2016-2017人教版新课标二年级数学上册12月份月考卷

合集下载

人教版小学二年级数学上册12月月考试卷

汤口中心学校12月月考检测二年级数学试卷（试卷满分100分，检测时间60分钟）一、填一填（第10题每空0.5分，其余没空1分，共24分。

） 1. 填上合适的单位名称。

一本数学书的宽度是18（）。

操场跑道一圈是400（）一节数学课的时间是40（）。

从黄山坐高铁到北京需要5（） 2. 2和5相乘是（），2个5相乘是（）。

3. 一个三角尺中有( )个角，其中有（）个直角。

4. （）比54多18， 75比（）少16。

5. 最大的两位数加上（）是最小的三位数，最小的两位数比34少（）。

6. 8只青蛙8张嘴，（）只眼睛，（）条腿。

7. ，从（）面观察到的是，从（）面观察到的是。

8.找规律填空。

19 21 23 25 （）（）（）9.天润发超市开展“3周年店庆活动”，满50元减10元，君君买了一辆26元的玩具小汽车，还买了一盒24元的积木，君君需要付（）元。

10.( )里最大能填几？（）×6<25 42>6×( ) 8×( )<36 ( ) ×4<3439>( ) ×5 ( )×7<30 40>8×( ) ( )+5<20二、请你选一选。

（每题2分，共10分。

） 1. 算式3+3+3+3+2不可以改写成算式（）。

A. 34+2 B. 3 5 C. 35-1 2.一块橡皮5角钱，7块橡皮（）钱。

A ．3元B ．35元C ．3元5角 3.小学生的书包高（）。

A.5米B.50厘米.C.5厘米4.爸爸今年31岁，去年爷爷比爸爸大26岁，爷爷今年 ( )。

A ．56岁 B ．57岁 C ．58岁5.如图右图正方体有（）个直角。

A.4 B.8 C.24 三、辨一辨（对的打√，错的打×，共12分）1．，这支铅笔的长度是10厘米。

二年级年级数学上册全套试卷附完整答案

二年级年级数学上册全套试卷附完整答案
本试卷共有22份，为最新人教版教材（2016~2017年）配套试卷，包括第一单元至第七单元的测评卷、期中测评卷、第八单元至第十一单元的分类测评卷，以及期末测评卷。

每份试卷均为对应单元的测评卷，旨在测试学生对该单元所学知识的掌握情况。

除此之外，还有阶段测评卷和期末测评卷，以全面评估学生的研究成果。

每份试卷均附有参考答案，方便学生和家长进行自我评估和纠错。

本套试卷适用于2018-201年，为学生的数学研究提供有力的辅助和支持。

2016-2017学年人教版二年级数学上册12月份月考试卷

2016-2017 学年上期 12 月份月考卷阅卷人得分三、选择题。

（把正确答案的序号填入（）二年级数学（时间：100 分钟满分 100 分）里，共 5分））。

题号得分一二三四五六七总分C.25-10A ．7×6—6 3.小华早上大概是（）到学校的。

A.2时B.7时B.7×4—6 C ．4×7+6 阅卷人得分C.12时 4.一把剪刀 4元钱，买 6把剪刀需要（）元钱。

A.10B.32C.24 5.9个十与 2个一组成的数是（）A.92B.29C.99（）种不同的穿法。

2.钟面上时针走 1格是（）小时；分针走一小格是（）分，走 1大格是（）分，走 1圈是（）分，即（）时。

3.长方形和正方形都是有（）角，并且都是（）角。

4.一块直角三角板中，有（）个角，其中有（）个直角。

5.6个 7相加的和是（），9乘 3是（）相加的和是（），比 35多 45的数是（）。

阅卷人得分6.8×5表示（ 7．19比 10多了（ 8.用 3,7,2可以组成（最小的数是（）。

）个（）。

）。

四、计算（35分）1.口算。

（12分））个不同的两位，最大的数是（）， 10+28= 19-0= 9×8= 63+15-7= 27-7+8= 6×9+5= 2×9-8= 7×8-24= 7×5= 4×4= ）元。

）29+39= 55-（6+7）= 2．笔算下面各题。

（每题 2分，共 12分） 67+23= 85-80= 48-42=阅卷人得分二、判断。

（共 5分）对的在（）里打“√”，错的打“×”52-（16+28）=37+21+35=61-7+32=1.我们用的三角板有一个直角。

( )2.５＋５＋５＋５— 5＝５×４（）（）3.4×8和 8×4所用的乘法口诀不相同。

人教版二年级数学上册12月测试试卷1

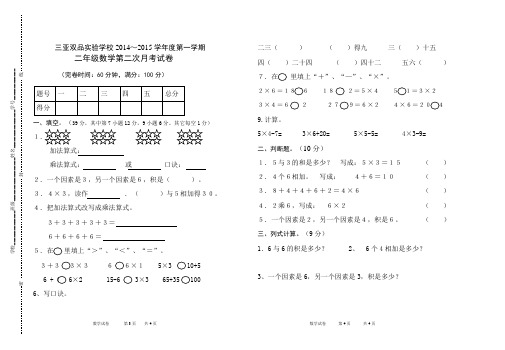
三亚双品实验学校2014～2015学年度第一学期二年级数学第二次月考试卷（完卷时间：60分钟，满分：100分）题号一二三四五总分得分一、填空。

（39分，其中第7小题12分，9小题6分。

其它每空1分）１．加法算式：乘法算式：或口诀：２．一个因素是３，另一个因素是６，积是（）。

３．４×３，读作 . （）与５相加得３０。

４．把加法算式改写成乘法算式。

３＋３＋３＋３＋３＝６＋６＋６＋６＝５．在里填上“＞”、“＜”、“＝”。

３＋３３×３６６×１ 5×3 10+56 + 6 6×2 15-6 3×3 65+35 1006、写口诀。

二三（）（）得九三（）十五四（）二十四（）四十二五六（）７．在里填上“＋”、“—”、“×”。

２×６＝１８６１８２＝５×４５１＝３×２３×４＝６２２７９＝６×２４×６＝２０４9.计算。

5×4-7= 3×6+20= 5×5-5= 4×3-9=二、判断题。

（10分）１．５与３的和是多少？写成：５×３＝１５（）２．４个６相加。

写成：４＋６＝１０（）３．８＋４＋４＋６＋２＝４×６（）４．２乘６，写成：６×２（）５．一个因素是２，另一个因素是４，积是６。

（）三、列式计算。

（9分）1．6与6的积是多少？ 2、 6个4相加是多少？3、一个因素是6，另一个因素是3，积是多少？学校线封密学校______________班级__________________姓名________________学号_____________四、看图列式计算。

（12分）1．☆☆☆☆☆☆☆☆2. ♂♂♂♂ ♂♂？个？个==3、五、解决问题。

湖北省随州市二年级上学期数学12月月考试卷

湖北省随州市二年级上学期数学12月月考试卷姓名:________ 班级:________ 成绩:________亲爱的小朋友们，这一段时间的学习，你们收获怎么样呢？今天就让我们来检验一下吧！一、直接写得数。

（20分） (共1题；共20分)1. （20分）(2019·肇庆模拟) 能简便的要用简便的方法计算：①4.6×9+② +36÷ ﹣0.35×③4÷9+7÷9+16÷9④[（）÷ ]×（2.5+7.5）⑤ +（15× ）÷（）二、列竖式计算。

（14分） (共1题；共14分)2. （14.0分）小树叶下藏着几呢？三、填一填。

（23分） (共8题；共23分)3. （2分） (2019五上·微山期中) 教室里小红坐在第二列第四行，用数对（2，4）来表示，小丽坐在第六列第一行，可以用数对________来表示。

4. （2分） (2019二上·新会月考) 笔算两位数加减法注意________对齐，从________位算起。

5. （4分） (2019二上·新会月考) 在横线上填上“厘米”或“米”。

一支粉笔长约9________。

大树高约6________。

教室高约4________。

小明身高约120________。

6. （3分） (2019二上·新会月考) 把口诀补充完整。

四九________ ________七四十二________八五十六7. （3分） (2019二上·新会月考) 把算式补充完整。

5×________＝30 3×________＝27 8×________＝328. （3分） (2019二上·新会月考) 在横线上最大能填几？9×________＜60 ________×7＜36 ________×6＜229. （3分） (2019二上·新会月考) 3+3+3+3+3=________，改写成乘法算式是________，口诀是：________。

2016-2017学年度高二年级数学12月月考试卷 (1)

九月教育2016-2017学年度11月月考试卷高二数学（上）考试范围：基本初等函数、统计、概率、圆锥曲线；考试时间：120分钟；总分：150分；命题人：郑周立姓名：___________班级：___________总分：___________第I卷（选择题）一、选择题（本题共12道小题，每小题0分，共0分）集合A={x|1＜log2x＜3，x∈Z}，B={x|5≤x＜9}，则A∩B=（）A．C．{5，6，7} D．{5，6，7，8}答案及解析：1.C【考点】交集及其运算．【专题】对应思想；定义法；集合．【分析】化简集合A，再求A∩B的值．【解答】解：集合A={x|1＜log2x＜3，x∈Z}={x|2＜x＜8，x∈Z}={3，4，5，6，7}，B={x|5≤x＜9}，∴A∩B={5，6，7}．故选：C．【点评】本题考查了集合的化简与运算问题，是基础题目．2.下列命题中是假命题的是（）A．∃m∈R，使是幂函数B．∃α，β∈R，使cos（α+β）=cosα+cosβC．∀φ∈R，函数f（x）=sin（x+φ）都不是偶函数D．∀a＞0，函数f（x）=ln2x+lnx﹣a有零点答案及解析：2.C【考点】命题的真假判断与应用．【分析】A．根据幂函数的定义进行求解即可．B．利用特殊值法进行判断．C．利用特殊值法进行判断．D．利用函数与方程的关系将函数进行转化，结合一元二次函数的性质进行判断．【解答】解：A．∵函数f（x）是幂函数，则m﹣1=1，则m=2，此时函数f（x）=x﹣1为幂函数，故A正确，B．当α=，β=﹣时，cos（α+β）=cos（﹣）=cos=，而cosα+cosβ=cos+cos（﹣）=，即此时cos（α+β）=cosα+cosβ成立，故B正确，C．当φ=，k∈Z时，f（x）=sin（x+φ）=cosx是偶函数，故C错误，D．由f（x）=ln2x+lnx﹣a=0得ln2x+lnx=a，设y=ln2x+lnx，则y=（lnx+）2﹣≥﹣，∴当a＞0时，ln2x+lnx=a一定有解，即∀a＞0，函数f（x）=ln2x+lnx﹣a有零点，故D正确故选：C3.如果log x＜log y＜0，那么（）A．0＜y＜x＜1 B．1＜y＜x C．1＜x＜y D．0＜x＜y＜1答案及解析：3.C【考点】对数函数的图象与性质．【分析】利用换底公式化简，结合对数函数的图象及性质，即可得到答案．【解答】解：∵真数在，对数值小于0，由对数函数的图象及性质，可知：底数必须大于1，即x＞1，y＞1．换成以底的对数：可得：log x=； log y=．∵log x＜log y，∴log ＞，由于底数为＜1，是减函数，∴y ＞x ，所以：1＜x ＜y故选：C ．4.已知f （x ）的定义在（0，3）上的函数，f （x ）的图象如图所示，那么不等式f （x ）cosx ＜0的解集是（）A ．（0，1）∪（2，3）B ．C ．D ．（0，1）∪（1，3）答案及解析：4.C【考点】其他不等式的解法；函数的图象；余弦函数的单调性．【分析】根据函数的图象可得，f （x ）小于0时，x 大于0小于1；f （x ）大于0时，x 大于1小于3，；且根据余弦函数图象可知，cosx 大于0时，x 大于0小于；当cosx 小于0时，x 大于小于3，则把所求的式子化为f （x ）与cosx 异号，即可求出不等式的解集．【解答】解：由函数图象可知：当f （x ）＜0时，0＜x ＜1；当f （x ）＞0时，1＜x ＜3；而cosx 中的x ∈（0，3），当cosx ＞0时，x ∈（0，）；当cosx ＜0时，x ∈（，3），则f （x ）cosx ＜0，可化为：或即或，解得：＜x ＜3或0＜x ＜1，所以所求不等式的解集为：（0，1）∪（，3），故选C ．5.已知奇函数f （x ）在区间[0，+∞）上是单调递增函数，则满足f （2x ﹣1）＜f （）的x 的取值范围是（）A ．（﹣∞，）B ．[，）C ．（，）D ．[，）答案及解析：5.A【考点】奇偶性与单调性的综合．【专题】计算题；函数的性质及应用．【分析】由奇函数的性质可知，f （x ）在区间（﹣∞，+∞）上是单调递增函数，从而可求得f （2x ﹣1）＜f （）的x 的取值范围．【解答】解：令x 1＜x 2＜0，则﹣x 1＞﹣x 2＞0，∵奇函数f （x ）在区间[0，+∞）上是单调递增函数，∴f（﹣x 1）＞f （﹣x 2）＞f （0）=0，∵f（x ）为奇函数，∴﹣f （x 1）＞﹣f （x 2）＞0，∴f（x 1）＜f （x 2）＜0，∴f（x ）在区间（﹣∞，+∞）上是单调递增函数；∵f（2x ﹣1）＜f （），∴2x﹣1＜，∴x＜．∴满足f （2x ﹣1）＜f （）的x 的取值范围是（﹣∞，）．故选A ．【点评】本题考查函数奇偶性与单调性的综合，分析得到f （x ）在区间（﹣∞，+∞）上是单调递增函数是关键，属于中档题．6.已知3.0log ,2,3.023.02===c b a ，则（）A ．c b a <<B ．b a c <<C ．a b c <<D ．b c a <<答案及解析：6.B:试题分析：由题意可知，最小，所以均大于而c b a c 0,,03.0log 2<=，因为a,b 不是同底数幂故无法直接比大小，因此需要将他们取相同的对数，再比较大小，即03.0log 23.0log log 2222<==a ，c a b a b b >>>>==:,,03.02log log 3.022综合所以，故选B考点：指数比较大小，指数函数，对数函数相关性质7.奇函数f （x ）的定义域为R ，若f （x+2）为偶函数，且f （1）=1，则f （8）+f （9）=（）A ．﹣2B ．﹣1C ．0D ．1答案及解析：7.D【考点】函数奇偶性的性质．【专题】函数的性质及应用．【分析】根据函数的奇偶性的性质，得到f （x+8）=f （x ），即可得到结论．【解答】解：∵f（x+2）为偶函数，f （x ）是奇函数，∴设g （x ）=f （x+2），则g （﹣x ）=g （x ），即f （﹣x+2）=f （x+2），∵f（x ）是奇函数，∴f（﹣x+2）=f （x+2）=﹣f （x ﹣2），即f （x+4）=﹣f （x ），f （x+8）=f （x+4+4）=﹣f （x+4）=f （x ），则f （8）=f （0）=0，f （9）=f （1）=1，∴f（8）+f （9）=0+1=1，故选：D ．【点评】本题主要考查函数值的计算，利用函数奇偶性的性质，得到函数的对称轴是解决本题的关键．8.不等式的解集为（）A ．[﹣1，3]B ．[﹣3，﹣1]C ．[﹣3，1]D ．[1，3]答案及解析：8.C【考点】指、对数不等式的解法．【专题】转化思想；数学模型法；不等式的解法及应用．【分析】根据指数函数的单调性，把原不等式化为≤2﹣1，求出解集即可．【解答】解：不等式可化为≤2﹣1，即x2+2x﹣4≤﹣1，整理得x2+2x﹣3≤0，解得﹣3≤x≤1，所以原不等式的解集为[﹣3，1]．故选：C．【点评】本题考查了利用指数函数求不等式的解集的应用问题，是基础题目．9.函数y=2cos（﹣x）﹣cos（+x）的最小值为（）A．﹣3 B．﹣2 C．﹣1 D．﹣答案及解析：9.D【考点】两角和与差的余弦函数．【分析】根据诱导公式和辅助角公式得到y=sin（+x﹣φ），再根据正弦函数的性质即可求出最小值．【解答】解：y=2cos（﹣x）﹣cos（+x）=2sin（（+x）﹣cos（+x）=sin（+x﹣φ），它的最小值为﹣，故选：D．10.已知角α的终边落在直线y=﹣2x上，则tanα的值为（）A．2 B．﹣2 C．±2 D．答案及解析：10.B【考点】任意角的三角函数的定义．【分析】由条件利用任意角的三角函数的定义，求得tanα的值．【解答】解：角α的终边落在直线y=﹣2x上，在直线y=﹣2x上任意取一点（a，﹣2a），a≠0，则由任意角的三角函数的定义可得tanα===﹣2，故选：B．11.以椭圆+=1的顶点为顶点，离心率为2的双曲线方程是（）A．B．C．或D．以上都不对答案及解析：11.C【考点】双曲线的标准方程．【分析】根据题意，椭圆的顶点为（4，0）、（﹣4，0）、（0，3）、（0，﹣3）；则双曲线的顶点有两种情况，即在x轴上，为（4，0）、（﹣4，0）；和在y轴上，为（0，3）、（0，﹣3）；分两种情况分别讨论，计算可得a、b的值，可得答案．【解答】解：根据题意，椭圆的顶点为（4，0）、（﹣4，0）、（0，3）、（0，﹣3）；故分两种情况讨论，①双曲线的顶点为（4，0）、（﹣4，0），焦点在x轴上；即a=4，由e=2，可得c=8，b2=64﹣16=48；此时，双曲线的方程为；②双曲线的顶点为（0，3）、（0，﹣3），焦点在y轴上；即a=3，由e=2，可得c=6，b2=36﹣9=27；此时，双曲线的方程为；综合可得，双曲线的方程为或；故选C12.执行如图的程序框图，如果输入的n是4，则输出的p是（）A．8 B．5 C．3 D．2答案及解析：12. C【考点】循环结构．【分析】根据输入的n是4，然后判定k=1，满足条件k＜4，则执行循环体，依此类推，当k=4，不满足条件k＜4，则退出执行循环体，求出此时p的值即可．【解答】解：k=1，满足条件k＜4，则执行循环体，p=0+1=1，s=1，t=1k=2，满足条件k＜4，则执行循环体，p=1+1=2，s=1，t=2k=3，满足条件k＜4，则执行循环体，p=1+2=3，s=2，t=3k=4，不满足条件k＜4，则退出执行循环体，此时p=3 故选：C第II卷（非选择题）二、填空题（本题共4道小题，每小题0分，共0分）函数y=2x﹣4+3恒过定点．答案及解析：13.（4，4）【考点】指数函数的图象与性质．【分析】由函数y=a x恒过（0，1）点，令函数y=2x﹣4+3指数为0，可得定点坐标．【解答】解：由函数y=2x恒过（0，1）点，可得当x﹣4=0，即x=4时，y=4恒成立，故函数恒过（4，4）点，故答案为：（4，4）．14.已知函数，若f（x）为奇函数，则a= ．答案及解析：14.【考点】函数奇偶性的性质．【分析】因为f（x）为奇函数，而在x=0时，f（x）有意义，利用f（0）=0建立方程，求出参数a的值．【解答】解：函数．若f（x）为奇函数，则f（0）=0，即，a=．故答案为15.一个总体分为A，B两层，用分层抽样方法从总体中抽取一个容量为10的样本．已知B层中每个个体被抽到的概率都为，则总体中的个体数为．答案及解析：15.120【考点】分层抽样方法；等可能事件的概率．【分析】本题考查分层抽样，抽样过程中每个个体被抽到的可能性相同，这是解决一部分抽样问题的依据，样本容量、总体个数、每个个体被抽到的概率，这三者可以知二求一．【解答】解：∵B层中每个个体被抽到的概率都为，∴总体中每个个体被抽到的概率是，∴由分层抽样是等概率抽样得总体中的个体数为10÷=120故答案为：120．16.某公司的班车在8：00，8：30发车，小明在7：50至8：30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是．答案及解析：16.【考点】几何概型．【分析】求出小明等车时间不超过10分钟的时间长度，代入几何概型概率计算公式，可得答案．【解答】解：设小明到达时间为y，当y在7：50至8：00，或8：20至8：30时，小明等车时间不超过10分钟，故P==．故答案为：．三、解答题（本题共6道小题,第1题0分,第2题0分,第3题0分,第4题0分,第5题0分,第6题0分,共0分）已知函数f（x）=x2+（2a﹣8）x，不等式f（x）≤5的解集是{x|﹣1≤x≤5}．（1）求实数a的值；（2）f（x）≥m2﹣4m﹣9对于x∈R恒成立，求实数m的取值范围．答案及解析：17.【考点】函数恒成立问题．【分析】（1）由函数f （x ）=x 2+（2a ﹣8）x ，不等式f （x ）≤5的解集是{x|﹣1≤x ≤5}，知x=﹣1，x=5是方程x 2+（2a ﹣8）x ﹣5=0的两个实数根，由此能求出实数a ．（2）由f （x ）=x 2﹣4x=（x ﹣2）2﹣4≥﹣4，f （x ）≥m 2﹣4m ﹣9对于x ∈R 恒成立，知﹣4≥m 2﹣4m ﹣9，由此能求出实数m 的取值范围．【解答】解：（1）∵函数f （x ）=x 2+（2a ﹣8）x ，不等式f （x ）≤5的解集是{x|﹣1≤x ≤5}，∴x=﹣1，x=5是方程x 2+（2a ﹣8）x ﹣5=0的两个实数根，所以﹣1+5=8﹣2a ，解得a=2．（2）∵a=2，∴f （x ）=x 2﹣4x=（x ﹣2）2﹣4≥﹣4，因为f （x ）≥m 2﹣4m ﹣9对于x ∈R 恒成立，所以﹣4≥m 2﹣4m ﹣9，即m 2﹣4m ﹣5≤0，解得﹣1≤m ≤5，故实数m 的取值范围是{m|﹣1≤m ≤5}．18.(本小题满分12分) 已知函数)sin cos 3)(cos sin 3()(x x x x x f -+=.(1)求)(x f 的最小正周期；(2)求)(x f 的单调递增区间. 答案及解析：18.(1).22ππ==T （2）).](12,125[Z k k k ∈+-ππππ试题分析：(1)利用二倍角公式进行化简运算，然后构造成)sin()(φω+=x A x f 的形式求最小正周期；（2）熟练掌握sinx 的单调区间即可求解；试题解析：（1）x x x x x x x f sin cos cos 3sin 3cos sin 3)(22-+-= )sin (cos 3cos sin 222x x x x -+= ).32sin(22cos 32sin π+=+=x x x ……… 5分因此)(x f 的最小正周期.22ππ==T .............. (6分) （2）令223222πππππ+≤+≤-k x k ，得12125ππππ+≤≤-k x k ）Z (∈k ……… 11分因此)(x f 的单调递增区间为).](12,125[Z k k k ∈+-ππππ.............. (12分) 19. (本小题满分12分) ABC ∆的内角C B A ,,的对边分别为c b a ,,，已知2cos cos cos cos c C A b C B a =+. (1)求角C ；(2)若5,7=+=b a c ，求ABC ∆的面积. 答案及解析：19.(1).3π=C （2）233试题分析：(1)利用正弦定理对2cos cos cos cos c C A b C B a =+进行化简即可得出答案；（2）由余弦定理加上.3π=C 可得出ab=6,进而求出ABC ∆的面积；试题解析：（1）由已知及正弦定理得，C B A B A C sin 21)sin cos cos (sin cos =+，即.sin )sin(cos 2C B A C =+故C C C sin sin cos 2=，可得21cos =C ，所以.3π=C …………6分(2)由已知及余弦定理得，7cos 222=-+C ab b a ，故7cos 22)(2=--+C ab ab b a ，又,3,5π==+C b a因此，6=ab ，所以ABC ∆的面积.233sin 21==C ab S ……12分考点：1.正弦定理应用；2.余弦定理的应用；20.北京某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如表所示．（1）求频率分布表中n ，p 的值，并补充完整相应的频率分布直方图；（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第4、5组中用分层抽样的方法抽取6名学生进入第二轮面试，则第4、5组每组各抽取多少名学生进入第二轮面试？（3）在（2）的前提下，学校决定从6名学生中随机抽取2名学生接受甲考官的面试，求第4组至多有1名学生被甲考官面试的概率答案及解析：20.考点：古典概型抽样频率分布表与直方图试题解析：（1）由题意可知，第2组的频数n=0．35×100=35人，第3组的频率p==0．30；（2）∵第4、5组共有30名学生，∴利用分层抽样在30名学生中抽取6名学生，每组分别为：第4组：×6=4人，第5组：×6=2人，∴第4、5组分别抽取4人、2人；（3）试验发生包含的事件是从六位同学中抽两位同学有15种满足条件的事件是第4组至多有一名学生被考官甲面试有9种结果，∴至少有一位同学入选的概率为：=21.某种产品的广告费支出与销售额（单位：万元）之间有如下对应数据：（1）求广告费支出与销售额回归直线方程（，）；已知，（2）在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过的概率．答案及解析：21.考点：统计案例变量相关试题解析：（1）由题意得，，所求回归直线方程为。

新人教版二年级数学上册第二次月考试题及答案真题(四套)

新人教版二年级数学上册第二次月考试题及答案真题(四套)目录：新人教版二年级数学上册第二次月考试题及答案真题一新人教版二年级数学上册第二次月考试题及答案精编二新人教版二年级数学上册第二次月考试题及答案通用三新人教版二年级数学上册第二次月考试题附参考答案四新人教版二年级数学上册第二次月考试题及答案真题一班级：姓名：满分：100分考试时间：90分钟题序一二三四五六七总分得分一、填空题。

（20分）1、在测量物体时，尺子的_____要对准物体的左端，再看物体的_____端对着几。

2、妈妈每天工作8小时，一周工作5天，妈妈一周工作（______）小时。

3、8050读作：（_________________）；二千零二写作：（____________）4、6只小动物聚餐，每一位一双筷子，需要（_______）根筷子。

5、认一认，填一填。

过10分是（___）过一刻是（___）过半小时是（___）过25分是（___）6、用2、0、9、3组成一个四位数，其中最大的数（___________），最小的是（____________）。

7、时针从3走到9走了（____）时，分针从12走到5走了（____）分钟。

8、长度单位有（_______）和（_________）。

9、这把小刀长________厘米。

10、锐角都比直角（______），钝角都比直角（______）。

二、我会选（把正确答案前面的序号填在（）里）（10分）1、小朋友每天的睡眠时间应不少于10（）。

A．时B．分C．秒2、如下图，如果x点的位置表示为（2，3），则点y的位置表示为（）A．（4，4）B．（4，5）C．（5，4）3、小红的身高是98厘米，小丽比小红矮4厘米，小丽的身高是（）A．94米B．102厘米C．1米D．94厘米4、以雷达站为观测点，海洋舰的位置是（）。

A．东偏北60° B．东偏北30° C．北偏西60° D．西偏南30°5、在有余数的除法中,除数是5,商是6,被除数最大是( )。

二年级数学上册12月测试卷

二年级数学12月测试卷一、直接写出得数。

（每小题2分，共40分）45+32= 6+73= 18+6= 30+29= 36+22+4= 25-4= 46-30= 49-9= 39-39= 8×3+6= 37-0= 0×3= 4×7= 5×3= 53-3+9= 8×8= 66+35= 70-8+24= 9×3-7= 37-32-5=二、填空。

（每空2分，共22分）1、数学课本的宽大约是厘米，100条1厘米长的线段一条接一条，接成一条长线段，这条长线段是米。

2、小明有两件颜色不同的上衣和两条颜色不同的裤子，他可以有种不同的穿法。

3、三个小朋友，进行乒乓球比赛，每两人进行一次，一共要进行次比赛。

4、小明、小红、小丽三人玩拍球比赛，三人拍球的次数分别是36下35下、33下，小明拍的次数最多，小丽拍了33下，小红拍了下。

5、把“8+8+8+8+8”写成乘法算式是或。

6、把下列各数按从小到大的顺序排列。

5米 50厘米 5米50厘米 5厘米三、选择题，选择正确答案的序号填入括号内。

（每小题2分，共8分）1、下列图形中，有二个直角的是（）。

①②③④2、下列线中，线段是（）。

① ② ③ ④3、下列口诀中，只能用来计算一个乘法算式的是（）。

①二三得六 ②四三十二 ③八九七十二 ④七七四十九4、下列计算正确的是（）。

① 6 5 ② 2 1 ③ 8 0 ④ 7 8+ 3 5 + 3 9 - 4 9 - 3 81 0 0 6 4 1 5 0 四、在“ ”里填上“+”、“-”、“×”、“＜”、“＞”、“＝”。

（共16分）73-25 45 54+4 60 4 4=8 5×7 32 90 19+71 5 6=30 4 4=16 34-20 15五、用数学解决问题。

（共14分）（3分）1、小明有47张图片，小刚的图片张数比小明多29。

小刚有几张图片？（5分）2、二年级（2）班上体育课，老师让23名同学打蓝球，19名同学做操。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

人教版新课标（2017秋）二年级数学上册12月份月考卷
二年级数学（时间：100分钟满分100分）题号一二三四五六七总分
得分
一、填空题。

（每空1分，共23分）
1.有两件不同的上衣和三条不同的裤子，一共有（）种不同的穿法。

2.钟面上时针走1格是（）小时；分针走一小格是（）分，走1大格是（）分，走1圈是（）分，即（）时。

3.长方形和正方形都是有（）角，并且都是（）角。

4.一块直角三角板中，有（）个角，其中有（）个直角。

5.6个7相加的和是（），9乘3是（）。

6.8×5表示（）个（）相加的和是（）。

7．19比10多了（），比35多45的数是（）。

8.用3,7,2可以组成（）个不同的两位，最大的数是（），最小的数是（）。

9.妈妈买米用了69元，买菜用了21元，她一共花了（）元。

10. 分针从12走到6是（）分钟，从8走到10是（）分钟。

二、判断。

对的在（）里打“√”，错的打“×”（共5分）
1.我们用的三角板有一个直角。

( )
2.５＋５＋５＋５— 5＝５×４（）
3.4×8和8×4所用的乘法口诀不相同。

（）
4．钟面上有两根针，时针和分针。

（）
5.黑板上的直角比三角板上的直角大。

（）
三、选择题。

（把正确答案的序号填入（）里，共5分）
1．下面的算式中，积是15的是（）。

A.3×5 B .5+10 C.25-10
2.7+7+7+7-6改写成含有乘法的算式是（）。

A．7×6—6 B.7×4—6 C．4×7+6
3.小华早上大概是（）到学校的。

A.2时
B.7时
C.12时
4.一把剪刀4元钱，买6把剪刀需要（）元钱。

A.10
B.32
C.24
5.9个十与2个一组成的数是（）
A.92
B.29
C.99
四、计算（35分）
1.口算。

（12分）
10+28= 9×8= 63+15-7= 6×9+5= 19-0= 7×5= 27-7+8= 2×9-8= 29+39= 4×4= 55-（6+7）= 7×8-24= 2．笔算下面各题。

（每题2分，共12分）
67+23= 85-80= 48-42=
52-（16+28）= 37+21+35= 61-7+32=
3. 我会比较大小。

（在○里填上“＞”“＜”或“＝”）（6分）
10米○10厘米 2时○20分 6×9○6×8
59分○1时 5元○50角 3×8○6×4
4.在（）里填上适当的数。

（５分）
5×（）=40 8×（）＝４８8×（）＝72
( )×（）＝６×６ 7×5＝（）+5
五、看钟面写时间。

（10分）
六．列式计算（ 6分 )
(1)、两个乘数都是8，积是多少？
（2）、5个9的和减去15，差是多少？
（3）、31与12的差，再加上50，和是多少？
七、解决问题。

（16分）
1.小明写8个毛笔字，小丽、小亮、小强写得和他的一样多，他们一共写了多少个毛笔字？（4分）
2．2名老师带领9名学生去参观书法作品展，买门票一共需多少钱?（4分）
3.公交车上原有27人，到光明站后下去11人，又上来8人。

现在车上有多少人？。

（4分）
4.（1）同学们种了两行树，一行5棵，另一行4棵，一共种了多少棵？（2分）（2）同学们种了两行树，每行5棵，一共种了多少棵？（2分）。