三角形的内心与外心的性质
三角形四心及性质

三角形四心三角形四心要点诠释:(1)三角形的内心、重心都在三角形的内部.(2)钝角三角形的垂心、外心都在三角形的外部.(3)直角三角形的垂心为直角顶点,外心为直角三角形斜边的中点.(4)锐角三角形的垂心、外心都在三角形的内部.1、三角形外心:三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心) 。
三角形的三条垂直平分线必交于一点已知:△ABC中,AB,AC的垂直平分线DO,EO相交于点O求证:O点在BC的垂直平分线上证明:连结AO,BO,CO,∵DO垂直平分AB,∴AO=BO∵EO垂直平分AC,∴AO=CO∴BO=CO即O点在BC的垂直平分线上三角形的外心的性质:1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
3. 锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合4.OA=OB=OC=R5.∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA(圆心角=2同弧圆周角)6.S△ABC=abc/4R2、三角形的内心:三角形的内心是三角形三条内角平分线的交点(或内切圆的圆心)。
三角形三条角平分线必交于一点证明己知:在△ABC中,∠A与∠B的角平分线交于点O,连接OC求证:OC平分∠ACB证明:过O点作OD,OE,OF分别垂直于AC,BC,AB,垂足分别为D,E,F∵AO平分∠BAC,∴OD=OF;∵BO平分∠ABC,∴OE=OF ;∴OD=OF∴O在∠ACB角平分线上∴CO平分∠ACB三角形内心的性质:1.三角形的三条角平分线交于一点,该点即为三角形的内心2.三角形的内心到三边的距离相等,都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中,∠C=90°,r=(a+b-c)/2.5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/26.S△ABC=[(a+b+c)r]/2 (r是内切圆半径)3、三角形的垂心:三角形的垂心是三角形三边上的高的交点(通常用H表示)。
三角形的外心与内心的性质

三角形的外心与内心的性质三角形是几何学中最基本的图形之一,而三角形的外心与内心则是三角形内外接圆的特殊点。
本文将重点讨论外心与内心的性质及其与三角形的关系。
一、外心的性质外心是三角形外接圆的圆心,也被称为三角形的Circumcenter。
对于任意的三角形ABC,我们可以通过以下性质来确定外心的位置:1. 外心是三角形三个垂直平分线的交点。
垂直平分线是指从三角形的各个顶点到对边中点的垂直平分线。
2. 外心到三角形的每条边的距离都相等,即OC=OA=OB。
其中,O 表示外心,A、B、C表示三角形ABC的顶点。
3. 三角形的外接圆的直径等于三角形的最长边,即2R=BC,其中R 表示外接圆的半径,BC表示三角形的最长边。
二、内心的性质内心是三角形内切圆的圆心,也被称为三角形的Incenter。
内切圆是唯一与三角形的三个边相切的圆,因此内心也是三角形三个角的角平分线的交点。
对于任意的三角形ABC,我们可以通过以下性质来确定内心的位置:1. 内心是三角形三条角平分线的交点。
角平分线是指从三角形的各个顶点出发,将相邻两边的夹角平分的线。
2. 三条角平分线的交点到三个顶点的距离相等,即ID=IE=IF。
其中,I表示内心,D、E、F表示三角形ABC的顶点。
3. 内接圆的半径可以通过公式r = S / p来计算,其中r表示内接圆的半径,S表示三角形的面积,p表示三角形的半周长。
三、外心与内心之间的关系1. 外心、内心和重心共线。
重心是三角形三条中线的交点。
这条共线性质被称为欧拉线。
2. 外心到三个顶点的距离大于内心到三个顶点的距离,并且外心到顶点的距离之间存在大小关系。
3. 外心和内心的连线与三角形的三个角相对应。
四、实际应用外心和内心的性质在实际应用中有广泛的应用。
例如,在三角测量中,可以通过求解外心和内心的位置来计算三角形的形状和尺寸。
此外,在工程设计中,外心和内心的性质也被用于定位和计算结构的稳定性。
总结:三角形的外心与内心是三角形内外接圆的特殊点,它们具有一系列的性质。
三角形的内心外心与垂心性质

三角形的内心外心与垂心性质三角形是几何学中最基本、最常见的图形之一。
在三角形中,内心、外心和垂心是三个重要的点,它们分别具有独特的性质和作用。
本文将探讨三角形的内心、外心和垂心的性质以及它们在几何学中的应用。
一、内心内心是指三角形内切圆的圆心,由三角形的三条边所确定。
内心与三角形的顶点连线相交于三角形的角平分线上。
因为内心到三角形三边的距离相等,所以内心是三角形的重心。
内心具有以下几个性质:1. 内心到三角形三个顶点的距离相等。
2. 内心到三角形三个边的距离之和最小。
3. 内心是三角形角平分线的交点,三角形的角平分线经过内心。
内心在几何学中有广泛的应用。
例如,内心是解三角形问题中的重要点之一。
通过利用内心到三边的距离相等的性质,我们可以求解三角形的边长和角度。
此外,内心还与关于三角形面积、垂直平分线和中位线等性质的证明中起到重要的作用。
二、外心外心是指三角形外接圆的圆心,该圆通过三角形的三个顶点。
外心具有以下几个性质:1. 外心到三角形的三个顶点距离相等。
2. 外心到三角形的边的距离最大。
3. 外心是三角形外接圆的圆心,三角形的三边均与外接圆的弧相切。
外心在几何学中也有广泛的应用。
外心的特性使其成为解决三角形问题的重要工具,特别是在涉及三角形的外接圆、直角三角形和旋转问题中。
外心的性质还可以用于判断三角形是否锐角、钝角或直角。
三、垂心垂心是指三角形三条高的交点,垂心可以位于三角形的内部、外部或顶点上。
垂心具有以下几个性质:1. 垂心到三角形三个顶点的距离之和最小。
2. 垂心是三角形的最小外接圆心,即垂心到三角形的三个顶点的距离相等,且最小。
垂心在几何学中也有重要的应用。
在解决涉及高、中位线、外心和内心的问题时,垂心是一个重要的参考点。
此外,在计算三角形的性质,如面积、周长和角度时,垂心的位置和性质也经常被考虑。
总结:三角形的内心、外心和垂心是三个重要的点,它们分别具有独特的性质和作用。
内心是三角形内切圆的圆心,具有与三角形角平分线有关的性质;外心是三角形外接圆的圆心,与三角形的外接圆有关;垂心是三角形三条高的交点,与三角形的高和最小外接圆有关。
三角形的内心,外心,重心,垂心,旁心及性质分别是指什么?
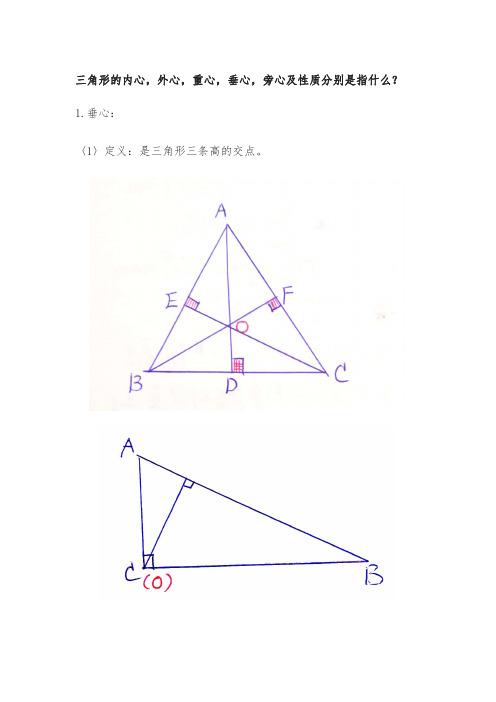
三角形的内心,外心,重心,垂心,旁心及性质分别是指什么?1.垂心:〈1〉定义:是三角形三条高的交点。
〈2〉性质:[性质1]锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
[性质2]三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
[性质3]垂心O关于三边的对称点,均在△ABC的外接圆圆上。
[性质4]△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,。
[性质5]O、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为--垂心组)。
[性质6]△ABC,△ABO,△BCO,△ACO的外接圆是等圆。
[性质7]三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
[性质8]设O、H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA.[性质9]锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍,即AH+BH+CH=2(r+R)。
[性质10]锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短。
[性质11]设H为非直角三角形的垂心,且D、E、F分别为H在BC,CA,AB.上的射影,H1,H2,H3分别为△AEF,△BDF,△CDE的垂心,则△DEF≌△H1H2H3.[性质12]三角形垂心H的垂足三角形的三边,分别平行于原三角形外接圆在各顶点的切线。
2.内心〈1〉定义:是三角形三条内角平分线的交点即内接圆的圆心。
交于点O,点O即为△ABC的内心。
〈2〉性质:[性质1]三角形的内心到三边的距离相等,都等于内切圆半径r. [性质2]∠BOC=90°+∠BAC/2。
[性质3]在Rt△ABC中,∠A=90°,三角形内切圆切BC于D,则S△ABC=BDxCD3.重心:〈1〉重心的定义:重心是三角形三条中线的交点。
初中数学知识点:三角形的内心、外心、中心、重心

三角形的四心定义:1、内心:三角形三条内角平分线的交点,即内切圆的圆心。
内心是三角形角平分线交点的原理:经圆外一点作圆的两条切线,这一点与圆心的连线平分两条切线的夹角(原理:角平分线上点到角两边距离相等)。
2、外心:是三角形三条边的垂直平分线的交点,即外接圆的圆心。
外心定理:三角形的三边的垂直平分线交于一点。
该点叫做三角形的外心。
3、中心:三角形只有五种心重心、垂心、内心、外心、旁心,当且仅当三角形是正三角形的时候,四心合一心,称做正三角形的中心。
4、重心:重心是三角形三边中线的交点。
三角形的外心的性质:1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心;2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合;3.锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合。
在△ABC中4.OA=OB=OC=R5.BOC=2BAC,AOB=2ACB,COA=2CBA6.S△ABC=abc/4R三角形的内心的性质:1.三角形的三条角平分线交于一点,该点即为三角形的内心2.三角形的内心到三边的距离相等,都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中,C=90,r=(a+b-c)/2.5.BOC = 90 +A/2 BOA = 90 +C/2 AOC = 90 +B/26.S△=[(a+b+c)r]/2 (r是内切圆半径)三角形的垂心的性质:1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
2.三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
例如在△ABC中3. 垂心O关于三边的对称点,均在△ABC的外接圆圆上。
4.△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AO?OD=BO?OE=CO?OF5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一垂心组)。
初中数学八年级三角形的四心及特点

三角形的内心、外心、中心、重心三角形的四心定义:1、内心:三角形三条内角平分线的交点,即内切圆的圆心。
内心是三角形角平分线交点的原理:经圆外一点作圆的两条切线,这一点与圆心的连线平分两条切线的夹角(原理:角平分线上点到角两边距离相等)。
2、外心:是三角形三条边的垂直平分线的交点,即外接圆的圆心。
外心定理:三角形的三边的垂直平分线交于一点。
该点叫做三角形的外心。
3、中心:三角形只有五种心重心、垂心、内心、外心、旁心,当且仅当三角形是正三角形的时候,四心合一心,称做正三角形的中心。
4、重心:重心是三角形三边中线的交点。
三角形的重心:三角形的重心是三角形三条中线的交点。
三角形的三条中线必交于一点已知:△ABC的两条中线AD、CF相交于点O,连结并延长BO,交AC于点E。
求证:AE=CE证明:延长OE到点G,使OG=OB∵OG=OB,∴点O是BG的中点又∵点D是BC的中点∴OD是△BGC的一条中位线∴AD∥CG∵点O是BG的中点,点F是AB的中点∴OF是△BGA的一条中位线∴CF∥AG∵AD∥CG,CF∥AG,∴四边形AOCG是平行四边形∴AC、OG互相平分,∴AE=CE三角形的重心的性质1.重心到顶点的距离与重心到对边中点的距离之比为2:1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/35.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
6.重心是三角形内到三边距离之积最大的点。
三角形的重心坐标:数学中,重心坐标是由单形(如三角形或四面体等)顶点定义的坐标。
重心坐标是齐次坐标的一种。
设v1, ..., vn 是向量空间V 中一个单形的顶点,如果V 中某点p 满足,(\lambda_{1}+\cdots +\lambda _{n})\,p=\lambda_{1}\,v_{1}+\cdots +\lambda _{n}\,v_{n}, 那么我们称系数(λ1, ..., λn) 是p 关于v1, ..., vn 的重心坐标。
内心、外心、重心、垂心定义及性质总结-外心的定义

内⼼、外⼼、重⼼、垂⼼定义及性质总结-外⼼的定义内⼼、外⼼、重⼼、垂⼼定义及性质总结
1.内⼼:
(1)三条⾓平分线的交点,也是三⾓形内切圆的圆⼼。
(2)性质:到三边距离相等。
2外⼼:
(1)三条中垂线的交点,也是三⾓形外接圆的圆⼼。
(2)性质:到三个顶点距离相等。
3 重⼼:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂⼼:三条⾼所在直线的交点。
5 重⼼: 三条中线定相交,交点位置真奇巧,
交点命名为“重⼼”,重⼼性质要明了,
重⼼分割中线段,数段之⽐听分晓;
长短之⽐⼆⽐⼀,灵活运⽤掌握好.
6 垂⼼: 三⾓形上作三⾼,三⾼必于垂⼼交.
⾼线分割三⾓形,出现直⾓三对整,
直⾓三⾓形有⼗⼆,构成六对相似形,四点共圆图中有,细⼼分析可找清.
7内⼼: 三⾓对应三顶点,⾓⾓都有平分线,
三线相交定共点,叫做“内⼼”有根源;
点⾄三边均等距,可作三⾓形内切圆,
此圆圆⼼称“内⼼”如此定义理当然.
8外⼼: 三⾓形有六元素,三个内⾓有三边.
作三边的中垂线,三线相交共⼀点.
此点定义为“外⼼”,⽤它可作外接圆.
“内⼼”“外⼼”莫记混,“内切”“外接”是关键.如有侵权请联系告知删除,感谢你们的配合!。
三角形的五“心”及其性质

三角形的五“心”及其性质
三角形的五心是指三角形内部的五个特殊点,包括重心、外心、内心、垂心和旁心。
1. 重心:三角形三个顶点与其对边的中点连接所交于一点,这个点被
称为重心。
重心到三角形三边的距离相等,重心将三角形划分为三个
面积相等的小三角形。
2. 外心:三角形三个顶点的垂直平分线相交于一点,这个点被称为外心。
外心是三角形外接圆圆心,即三角形三个顶点与外心的连线的长
度相等。
3. 内心:三角形三个顶点的角平分线相交于一点,这个点被称为内心。
内心是三角形内切圆圆心,即三角形三条边与内心的连线的垂直距离
相等。
4. 垂心:三角形三个顶点的高的延长线相交于一点,这个点被称为垂心。
垂心是三角形三条高的交点,即垂心到三角形三个顶点所在的直
线距离相等。
5. 旁心:三角形的旁心有三个,分别对应三条边。
旁心是指三角形的
外切圆圆心,即三角形的一条边外边的一条角的角平分线与另外两条
边延长线的交点。
这些五心有一些重要的性质:
- 重心是三角形的重要重心之一,它将三角形分成三个面积相等的小三
角形。
- 外心是三角形外接圆圆心,外接圆的直径是三角形的边长,外心到三
个顶点的距离相等。
- 内心是三角形内切圆圆心,内接圆与三个边相切,内心到三个边的距
离相等。
- 垂心是三角形三条高的交点,垂心到三个顶点所在的直线距离相等。
- 旁心是三角形外切圆圆心,外切圆与三条边相切,旁心到相对应的边
的距离相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的内心与外心的性质
三角形是平面几何中最基本的图形之一,而三角形的内心和外心则
是这个图形中具有重要性质的点。
本文将介绍三角形内心和外心的定义、性质以及它们在解决几何问题中的应用。
一、三角形的内心
内心是指三角形内一个特殊的点,它与三角形的三个顶点之间的距
离之和最短。
我们将这个点称为三角形的内心,用I来表示。
内心具有以下性质:
1. 内心是三角形的内切圆的圆心。
所谓内切圆,是指与三角形的三
条边相切于各边的中点,且与三边的交点构成的圆。
2. 内心到三角形的三条边的距离相等。
这是因为内切圆相切于三边
的中点,所以到各边的距离相等。
3. 内心所在的直径和三角形的内角平分线重合。
因此,通过内心可
以得到三角形内角平分线的重要性质。
二、三角形的外心
外心是指三角形外接圆的圆心,此圆恰好与三角形的三个顶点共线。
我们将这个点称为三角形的外心,用O来表示。
外心具有以下性质:
1. 外心位于三角形的三边的垂直平分线交点上。
所谓垂直平分线,
是指与三边垂直且通过三边中点的直线。
2. 外心到三角形的三个顶点的距离相等。
外心是外接圆的圆心,而外接圆与三个顶点相切,所以到各个顶点的距离相等。
3. 外心所在的直径和三角形的外角平分线重合。
因此,通过外心可以获得三角形外角平分线的重要性质。
三、内心和外心的应用
内心和外心是三角形中非常重要的点,它们在解决几何问题中有着广泛的应用。
以下是一些常见的应用场景:
1. 定位:内心和外心可以用来定位三角形在平面坐标系中的位置,帮助我们准确地画出三角形。
2. 证明:内心和外心可以用来证明三角形性质。
通过利用内心和外心所在的直径与角平分线重合的性质,可以推导出许多三角形性质的定理。
3. 问题求解:内心和外心在解决三角形相关问题时提供了有用的信息。
例如,通过外心可以确定三角形的外接圆半径和外接圆心坐标,从而帮助我们计算三角形的面积和周长。
总结:
三角形内心和外心是基于三角形内切圆和外接圆的特殊点。
它们具有许多重要的性质,可以应用于几何证明、问题求解等方面。
通过深入理解和应用内心和外心的性质,我们可以更好地理解和解决与三角形相关的几何问题。
