三角形三个内角三角函数关系
六个三角函数相互关系记忆图
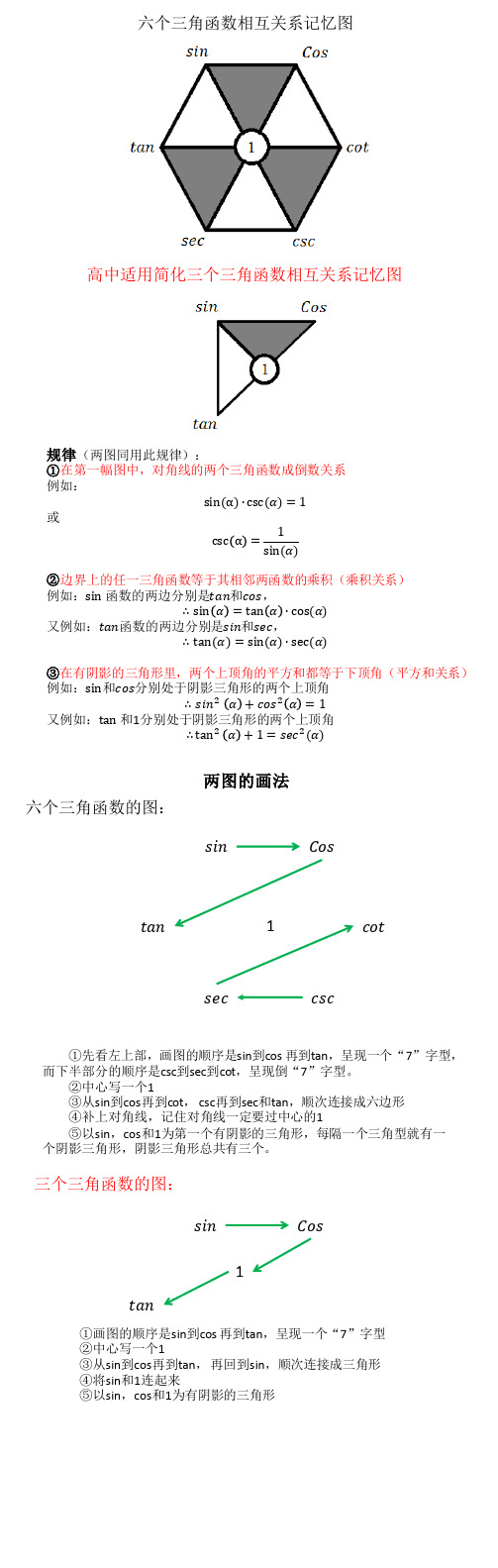
规律(两图同用此规律):①在第一幅图中,对角线的两个三角函数成倒数关系例如:sin(α)∙csc(α)=1或 csc α=1sin(α) ②边界上的任一三角函数等于其相邻两函数的乘积(乘积关系) 例如:sin函数的两边分别是tan 和cos ,∴sin α=tan α∙cos(α)又例如:tan 函数的两边分别是sin 和sec ,∴tan(α)=sin(α)∙sec(α)③在有阴影的三角形里,两个上顶角的平方和都等于下顶角(平方和关系) 例如:sin 和cos 分别处于阴影三角形的两个上顶角∴sin 2α+cos 2α=1又例如:tan和1分别处于阴影三角形的两个上顶角∴tan 2α+1=sec 2(α)六个三角函数相互关系记忆图高中适用简化三个三角函数相互关系记忆图两图的画法六个三角函数的图:sin Costan cotcscsec ①先看左上部,画图的顺序是sin 到cos 再到tan ,呈现一个“7”字型,而下半部分的顺序是csc 到sec 到cot ,呈现倒“7”字型。
②中心写一个1③从sin 到cos 再到cot , csc 再到sec 和tan ,顺次连接成六边形④补上对角线,记住对角线一定要过中心的1⑤以sin ,cos 和1为第一个有阴影的三角形,每隔一个三角型就有一个阴影三角形,阴影三角形总共有三个。
1 三个三角函数的图:sin Costan1①画图的顺序是sin 到cos 再到tan ,呈现一个“7”字型②中心写一个1③从sin 到cos 再到tan , 再回到sin ,顺次连接成三角形④将sin 和1连起来⑤以sin ,cos 和1为有阴影的三角形。
直角三角形的关系

直角三角形的关系
直角三角形是一种特殊的三角形,其中一个角度为90度(直角)。
直角三角形具有如下关系:
1. 边长关系:直角三角形的两条边与直角边之间有特定的关系。
根据勾股定理,直角边的平方等于直角三角形另外两条边的平方和。
即a² + b² = c²,在此公式中,c表示斜边,a和b分别表示其他两条边。
2. 正弦、余弦和正切关系:直角三角形的三个边与其内角度之间有特定的三角函数关系。
正弦函数(sin)、余弦函数(cos)和正切函数(tan)是直角三角形中常用的三角函数。
对于一个直角三角形的角度A:sin(A) = 对边/斜边;cos(A) = 邻边/斜边;tan(A) = 对边/邻边。
3. 特殊比例关系:直角三角形中还存在一些特殊的比例关系。
例如,在一个以斜边长为1的直角三角形中,对边与邻边的比值为较为常见的三角函数值,即sin(A)、cos(A)和tan(A)。
直角三角形的关系和特性在几何学和三角学中有广泛的应用和研究,对于测量、计算和解决实际问题都具有重要意义。
三角函数的基本关系定理

三角函数的基本关系定理三角函数是数学中研究角和边之间关系的重要工具,它们包括正弦函数、余弦函数和正切函数。
三角函数的基本关系定理是一个重要的数学定理,它描述了三角函数之间的基本关系和性质。
1. 正弦函数的基本关系在一个直角三角形中,边长比例可以用正弦函数来描述。
根据三角形的定义,正弦函数等于对边与斜边的比值。
假设三角形的一个角度为θ,对边为a,斜边为c,则有以下关系:sin(θ) = a/c这个关系称为正弦函数的基本关系。
根据这个关系,我们可以计算任意角度的正弦值,并在三角函数表中查找对应的数值。
2. 余弦函数的基本关系余弦函数描述了直角三角形中斜边与邻边之间的关系。
根据三角形的定义,余弦函数等于邻边与斜边的比值。
假设三角形的一个角度为θ,邻边为b,斜边为c,则有以下关系:cos(θ) = b/c这个关系称为余弦函数的基本关系。
通过这个关系,我们可以计算任意角度的余弦值,并在三角函数表中查找相应的数值。
3. 正切函数的基本关系正切函数描述了直角三角形中对边与邻边的比例关系。
根据三角形的定义,正切函数等于对边与邻边的比值。
假设三角形的一个角度为θ,对边为a,邻边为b,则有以下关系:tan(θ) = a/b这个关系称为正切函数的基本关系。
根据这个关系,我们可以计算任意角度的正切值,并在三角函数表中查找相应的数值。
三角函数的基本关系定理为我们提供了计算角度和边长比例的方法。
通过这些基本关系,我们可以解决各种实际问题,如建筑物高度的测量、航海中的导航以及天文学中的星体运动等。
在实际运用中,我们也经常遇到使用反三角函数的情况,反三角函数与正弦函数、余弦函数和正切函数互为反函数,可以通过求解三角方程来计算角度的值。
综上所述,三角函数的基本关系定理是一个重要的数学定理,它描述了正弦函数、余弦函数和正切函数之间的基本关系。
通过这些关系,我们可以计算角度和边长比例,并在实际问题中应用三角函数来解决各种数学和科学问题。
三角形角与边的关系公式

三角形角与边的关系公式在三角形中,角度和边的长度是密切相关的。
三角形的每个角度和每条边都有一定的关系公式。
下面将介绍三角形中最常用的角和边的关系公式。
1.三角形的内角和公式:在任何三角形中,三个内角的和始终为180度。
设三角形的三个内角分别为A、B和C,则有A+B+C=180度。
2.直角三角形中的角和边的关系公式:直角三角形是一种特殊的三角形,其中一个角度是90度。
在直角三角形ABC中,设边AC是斜边,边AB和边BC是直角的两条边,我们可以根据边长之间的关系来确定三角形的角度:a.边长关系公式:根据勾股定理,边长AB、BC和AC之间存在关系:AB^2+BC^2=AC^2b.三角函数关系公式:对于直角三角形,正弦、余弦和正切是常用的三角函数。
设角A是直角三角形的一个角,边长分别为AC、AB和BC,则有以下角和边的关系公式:- 正弦公式:sinA = AB / AC- 余弦公式:cosA = BC / AC- 正切公式:tanA = AB / BC3.等腰三角形中的角和边的关系公式:等腰三角形是一种特殊的三角形,其中两边的长度相等。
在等腰三角形ABC中,假设AB=AC,B和C是等腰三角形的两个顶点,A是底角的顶点。
我们可以根据边长之间的关系来确定三角形的角度:a.角度关系公式:由于等腰三角形的两边相等,所以角B=角C。
b.角平分线关系公式:等腰三角形的底边上的角平分线也是同时是三角形的高,可以利用角平分线来求解角度。
-角A的角平分线:角平分线AE将角A平分为两个相等的角。
根据角平分线定理,有AB/BE=AC/CE。
-角B和角C的角平分线:角平分线BD和CE均平分角B和C。
同样根据角平分线定理,有AB/BD=AC/CE。
4.任意三角形中的角和边的关系公式:对于一般的三角形,我们可以使用三角函数来确定角和边的关系。
假设三角形的三个内角为A、B和C,边长分别为a、b和c。
a. 正弦定理:sinA / a = sinB / b = sinC / c。
解三角形知识点归纳(附三角函数公式)

高中数学必修五 第一章 解三角形知识点归纳1、三角形三角关系:A+B+C=180°;C=180°—(A+B);2、三角形三边关系:a+b>c; a-b<c3、三角形中的基本关系:sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=-4、正弦定理:在C ∆AB 中,a 、b 、c 分别为角A 、B 、C 的对边,R 为C ∆AB 的外接圆的半径,则有2sin sin sin a b cR C===A B . 5、正弦定理的变形公式:①化角为边:2sin a R =A ,2sin b R =B ,2sin c R C =;②化边为角:sin 2a R A =,sin 2b R B =,sin 2c C R=; ③::sin :sin :sin a b c C =A B ;④sin sin sin sin sin sin a b c a b cC C++===A +B +A B . 6、两类正弦定理解三角形的问题:①已知两角和任意一边,求其他的两边及一角.②已知两角和其中一边的对角,求其他边角.(对于已知两边和其中一边所对的角的题型要注意解的情况(一解、两解、三解))7、余弦定理:在C ∆AB 中,有2222cos a b c bc =+-A 等,变形: 222cos 2b c a bc+-A =等,8、余弦定理主要解决的问题:①已知两边和夹角,求其余的量。
②已知三边求角) 9、三角形面积公式:111sin sin sin 222C S bc ab C ac ∆AB =A ==B .=2R 2sinAsinBsinC=R abc 4=2)(c b a r ++=))()((c p b p a p p ---10、如何判断三角形的形状:判定三角形形状时,可利用正余弦定理实现边角转化,统一成边的形式或角的形式设a 、b 、c 是C ∆AB 的角A 、B 、C 的对边,则:①若222a b c +=,则90C =;②若222a b c +>,则90C <;③若222a b c +<,则90C >.11、三角形的四心:垂心——三角形的三边上的高相交于一点重心——三角形三条中线的相交于一点(重心到顶点距离与到对边距离之比为2:1) 外心——三角形三边垂直平分线相交于一点(外心到三顶点距离相等) 内心——三角形三内角的平分线相交于一点(内心到三边距离相等) 12同角的三角函数之间的关系(1)平方关系:sin²α+cos²α=1 (2)倒数关系:tanα·cotα=1 (3)商的关系:ααααααsin cos cot ,cos sin tan ==特殊角的三角函数值三角函数值0 111不存在三角函数诱导公式:“ (2k πα+)”记忆口诀: “奇变偶不变,符号看象限”,是指(2kπα+),k ∈Z 的三角函数值,当k 为奇数时,正弦变余弦,余弦变正弦(正切,余切;正割、余割也同样);当k 为偶数时,函数名不变。
三角形度数计算公式

三角形度数计算公式三角形是初中数学中的基础内容,它的周长、面积、角度等都是我们需要掌握的知识点。
其中,角度是三角形中最基本的概念之一,而三角形中的角度又可分为内角和外角两种。
接下来,我们将详细介绍三角形中的度数计算公式。
一、内角计算公式内角是指三角形内部的角度,由于三角形的内角和为180度,因此我们可以通过已知两个内角,来计算第三个内角的度数。
具体的计算公式如下:第三个内角的度数 = 180度 - 已知的两个内角之和例如,已知一个三角形的两个内角分别是30度和60度,那么第三个内角的度数就是:第三个内角的度数 = 180度 - (30度 + 60度) = 90度二、外角计算公式外角是指三角形任意一条边的延长线与另外一条边所成的角度,它的度数等于与它相邻的两个内角之和。
具体的计算公式如下:外角的度数 = 相邻的两个内角之和例如,已知一个三角形的两个内角分别是30度和60度,那么与60度相邻的外角的度数就是:外角的度数 = 30度 + 60度 = 90度需要注意的是,三角形的任意一个外角的度数都等于与它不相邻的两个内角的度数之差。
三、利用三角函数计算角度在三角形中,我们还可以通过三角函数来计算角度。
三角函数是指正弦、余弦、正切等函数,它们可以帮助我们计算三角形中的各种角度。
具体的计算公式如下:1. 正弦函数:sin A = 对边 / 斜边其中,A表示三角形中的某个角度,对边表示该角度所对应的边的长度,斜边表示三角形的斜边长度。
2. 余弦函数:cos A = 邻边 / 斜边其中,A表示三角形中的某个角度,邻边表示该角度所对应的边的长度,斜边表示三角形的斜边长度。
3. 正切函数:tan A = 对边 / 邻边其中,A表示三角形中的某个角度,对边表示该角度所对应的边的长度,邻边表示与该角度相邻的边的长度。
需要注意的是,在使用三角函数计算角度时,我们需要已知三角形中的两个边长或者一个边长和一个角度,才能确定第三个角度的大小。
三角形三个内角三角函数关系

三角形三个内角三角函数关系三角形是一种三边和三角度角的形状。
对于任何三角形,它的三个内角之和总是等于 180 度。
假设我们把这三个内角记为 A、B 和 C,那么:A +B +C = 180在三角形中,我们可以使用三角函数来描述角度和边的关系。
在这篇文章中,我们将探讨三角形三个内角与三角函数之间的关系。
首先,我们需要知道三角函数的定义。
在直角三角形中,我们定义三角函数为:sin(A) = opposite / hypotenusecos(A) = adjacent / hypotenusetan(A) = opposite / adjacent其中,opposite 表示角 A 的对边长度,adjacent 表示角 A 的邻边长度,hypotenuse 表示斜边长度。
在非直角三角形中,我们可以使用正弦定理、余弦定理和正切定理来求解角度和边的关系。
这些公式可以表示为:正弦定理:a / sin(A) = b / sin(B) = c / sin(C)余弦定理:a = b + c - 2bc cos(A)正切定理:tan(A) = (b sin(A)) / (c - b cos(A))其中,a、b 和 c 分别表示三角形的三条边,A、B 和 C 分别表示相应的内角。
利用这些公式,我们可以发现三角形的三个内角与三角函数之间存在一定的关系。
例如,我们可以利用余弦定理来表示角 A 的余弦值:cos(A) = (b + c - a) / 2bc同样地,我们还可以利用正弦定理和正切定理来表示角 A 的正弦值和正切值。
这些公式可以表示为:sin(A) = (a / 2R) = √[(s - b)(s - c) / sc]tan(A) = 2R sin(A) / (b - c)其中,R 表示三角形的外接圆半径,s 表示三角形的半周长。
在实际应用中,我们可以利用这些公式来求解各种三角形问题,例如求解三角形的面积、周长、角度以及边长等。
三角函数关系

三角函数关系三角函数关系是数学中非常重要的一部分,涉及到三角函数之间的各种关系及其应用。
在解决各种数学、物理、工程等问题时,我们经常会用到三角函数关系,因此对其有深刻的理解是非常重要的。
三角函数包括正弦函数、余弦函数、正切函数等。
这些函数是与三角形内角度相关的数学函数。
正弦函数被定义为一个角的对边与斜边之比,余弦函数则是一个角的邻边与斜边之比,而正切函数则是一个角的对边与邻边之比。
三角函数之间存在着各种重要的关系。
最基本的关系就是勾股定理,即在一个直角三角形中,正弦函数、余弦函数和正切函数之间的关系可以通过勾股定理推导出来。
具体而言,如果一个直角三角形的斜边长度为c,其中一个锐角的对边长度为a,那么正弦函数、余弦函数和正切函数之间的关系可以表示为:sinθ = a/c;cosθ = b/c;tanθ = a/b;其中,θ是这个锐角的度数。
此外,三角函数之间还存在着一些重要的恒等式。
例如,根据三角恒等式,我们可以得到:sin^2θ + cos^2θ = 1;1 + tan^2θ = sec^2θ;1 + cot^2θ = csc^2θ。
这些恒等式对于解决各种三角题非常有用,有时候甚至可以简化问题的求解过程。
三角函数关系在解决各种实际问题时也有广泛的应用。
例如,在物理学中,三角函数关系可以用来描述波动的性质,例如声音和光的传播。
在工程学中,三角函数关系可以用来计算各种结构的力学性质,例如桥梁和建筑物的稳定性。
此外,三角函数还可以用来解决各种几何问题,例如计算三角形的面积、高度等。
在解决这些问题时,我们可以利用三角函数的定义和它们之间的关系来进行计算。
总之,三角函数关系是一门重要的数学分支,它不仅在理论上有重要的意义,而且在实际应用中也发挥着重要的作用。
通过深入的学习和了解三角函数关系,我们可以在解决各种数学、物理、工程等问题时更加得心应手。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形三个内角三角函数关系
在数学中,三角形是一个非常重要的概念。
它是由三条边和三个内角组成的平面图形。
三角形的内角和总是等于180度,这是一个基本的几何定理。
在三角形中,三个内角的大小和三角函数之间有着密切的关系。
三角函数是数学中的一种基本函数,它们是正弦函数、余弦函数和正切函数。
这些函数在三角形中有着广泛的应用。
在三角形中,正弦函数、余弦函数和正切函数分别表示三个内角的正弦值、余弦值和正切值。
这些函数可以帮助我们计算三角形的各种属性,如边长、角度和面积等。
正弦函数是三角形中最常用的函数之一。
它表示一个角的对边与斜边的比值。
在三角形ABC中,角A的正弦值可以表示为sin A = a/c,其中a是角A的对边,c是三角形的斜边。
同样地,角B和角C的正弦值可以表示为sin B = b/c和sin C = a/c。
余弦函数也是三角形中常用的函数之一。
它表示一个角的邻边与斜边的比值。
在三角形ABC中,角A的余弦值可以表示为cos A = b/c,其中b是角A的邻边。
同样地,角B和角C的余弦值可以表示为cos B = a/c和cos C = b/c。
正切函数是三角形中最有用的函数之一。
它表示一个角的对边与邻边的比值。
在三角形ABC中,角A的正切值可以表示为tan A = a/b,
其中a是角A的对边,b是角A的邻边。
同样地,角B和角C的正切值可以表示为tan B = b/a和tan C = c/b。
三角形的三个内角三角函数关系是非常重要的。
它们可以帮助我们计算三角形的各种属性,如边长、角度和面积等。
在实际应用中,三角函数在物理、工程、计算机科学等领域中都有着广泛的应用。
因此,学习三角函数和三角形的相关知识是非常重要的。
