生活中的立体图形练习题
(最新)北师大版七年级数学上册《生活中的立体图形》试卷(附答案)

第1页 共4页
11.将下列几何体分类,柱体有: ,锥体有 (填序号) ;
12.长方体由_______________个面_______________条棱_______________个顶点;
13.半圆面绕直径旋转一周形成__________;
4. 围成几何体的侧面中,至少有一个是曲面的是______________;(举一例)
5. 正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________;
6. 圆柱、圆锥、球的共同点是_____________________________;
7.线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________;
8. 圆可以分割成_____ 个扇形,每个扇形都是由___________________;
9. 从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成__________个三角形;
10.在乒乓球、橄榄球、足球、羽毛球、冰球中,是球体的有 ;
《生活中的立体图形》试卷
第1.1.1课时家庭作业 (生活中的立体图形1) 姓名 学习目标:
1.经历从现实世界中抽象出几何图表的过程,感受图形世界的丰富多彩。
2.在具体情境中认识圆柱、圆锥、正方体、长方体、棱柱、棱台、球,并能用自已的语言描述它们的某些特征。
一.填空题:
1.立体图形的各个面都是__________的面,这样的立体图形称为多面体.;
2.图形是由________,_________,________构成的;
生活中的立体图形含答案

1.生活中的立体图形一.选择题1.观察下图,请把左边的图形绕着给定的直线旋转一周后可能形成的几何体选出来( )2.下列说法错误的是( )A.长方体、正方体都是棱柱B.三棱柱的侧面是三角形C.直六棱柱有六个侧面、侧面为长方形D.球体的三种视图均为同样大小的图形3.从多边形一条边上的一点(不是顶点)发出发,连接各个顶点得到2003个三角形,则这个多边形的边数为 ( )A.2001B.2005C.2004D.20064.如图所示立体图形,是由____个面组成,面与面相交成____条线( )A.3,6B.4,5C.4,6D.5,7第4题 第5题5.如图,在一个棱长为6cm 的正方体上摆放另一个正方体,使得上面正方体的四个顶点恰好均落在下面正方体的四条棱上,则上面正方体体积的可能值有( )A .1个B .2个C .3个D .无数个二.填空题1.如图所示的几何体是由一个正方体截去41后而形成的,这个几何体是由( )个面围成的,其中正方形有( )个,长方形有( )个.第1题2.用一长20cm ,宽8cm 的纸片卷成(无重合部分)一个高为8cm 的圆柱,那么这个圆柱的底面圆的半径是( ),圆柱的体积是( )。
3.如图所示的几何体是由若干个棱长为1的正方体堆放而成的,则这个几何体的体积是( )。
第3题 第4题4.将棱长为1cm 的正方体组成如图所示的几何体,那么这个几何体的表面积是( )。
5.如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中; 共有1个小立方体,其中1个看得见,0个看不见;如图②中;把共有8个小立方体,其中7个看得见,1个看不见;如图③中;共有27个小立方体,其中19个看得见,8个看不见;……,则第⑥个图中,看得见的小立方体有______________个。
三.解答题1.在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,如图拼成一个长方体,请判断涂红、黄、白三种颜色的对面分别涂着哪一种颜色?2.如图,已知一个正方体的六个面上分别写着六个连续的整数,且每两个相对面上的两个数的和都相等,图中所能看到的数是16,19和20,求这6个整数的和.答案一选择题1.D2.B3.B4.C5.D 解析:因为上面正方体的棱长不确定,所以根据正方体体积公式可知,上面正方体体积的可能值有无数个. 二填空题1.8,2,42.π10,π800 3.6 4.362cm 5.125 三解答题1.绿 蓝 黑(分析:红不与蓝、白、黄、黑相对,所以红与绿相对;黄不与白、黑、绿、红相对,黄必与蓝相对;剩下黑与白相对。
北师大数学七年级上册第一单元《丰富的图形世界1.生活中的立体图形(一) - 同步练习

1.生活中的立体图形(一)陈锦辉一、学习目标1经历从现实世界中抽象出图形的过程,感受图形世界的丰富多彩。
2在具体的情境中,认识圆柱、圆锥、正方体、长方体、棱柱、球,并能用自己的语言描述它们的某些特征。
二、同步练习:活动一:从现实世界中抽象出图形1、下列几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱。
其中属于立体图形的是()A、③⑤⑥B、①②③C、③⑥D、④⑤2、在下列物体的几何图形中,是四棱锥是()3、下列图形中不是棱柱的是()A、B、C、D、4、(2008年湖北宜昌中考题)下列物体的形状类似于球的是()A、茶杯B、羽毛球C、乒乓球D、白炽灯泡6.长方体属于( )A.棱锥B.棱柱C.圆柱D.以上都不对7下列几何体中(如图)属于棱锥的是( )(1) (2) (3) (4) (5) (6)A.(1)(5)B.(1)C.(1)(5)(6)D.(5)(6)7.下列所讲述的物体,_______与圆锥的形状类似( )A.香烟盒B.铅笔C.西瓜D.烟囱帽8.机器零件中的六角螺母,圆筒形的易拉罐、足球、火柴盒、铅垂体中,•类似于棱柱的物体有________,•类似于球体的物体有_________,••类似于圆锥的物体有________,类似于圆柱的物体有__________.9下列图形中,是柱体的有。
(填序号)①②③④⑤活动二:认识棱柱及其他几何体的特征1、如果一个物体有七个顶点七个面,那么这个物体一定是()A、五棱锥B、五棱柱C、六棱锥D、七棱锥2、(2008年广东肇庆中考题)一个正方体的面共有()A、1个B、2个C、4个D、6个3、如图,下列图形()是柱体.4、把下列图形的名称填在括号内:5、如图4-5是一些具体的图形—三棱镜、方砖、帆布帐篷、笔筒、铅锤、粮囤、天文台,图4-6中是一些立体图形,找出与图4-6立体图形类似的图形。
6、判断题:(每题2分)1.柱体的上、下两个面一样大...........................()2.圆柱的侧面展开图是长方形.......................... ()3.球体不是多面体....................................()4.圆锥是多面体.......................................()5.长方体是多面体.....................................()6.柱体都是多面体.....................................()击中考1(2008年湖北宜昌中考题)下列物体的形状类似于球的是()A、茶杯B、羽毛球C、乒乓球D、白炽灯泡2、(2008年广东肇庆中考题)一个正方体的面共有()A、1个B、2个C、4个D、6个3(2009年浙江杭州中考题)直四棱柱,长方体和正方体之间的包含关系是()。
生活中的立体图形(家庭作业)
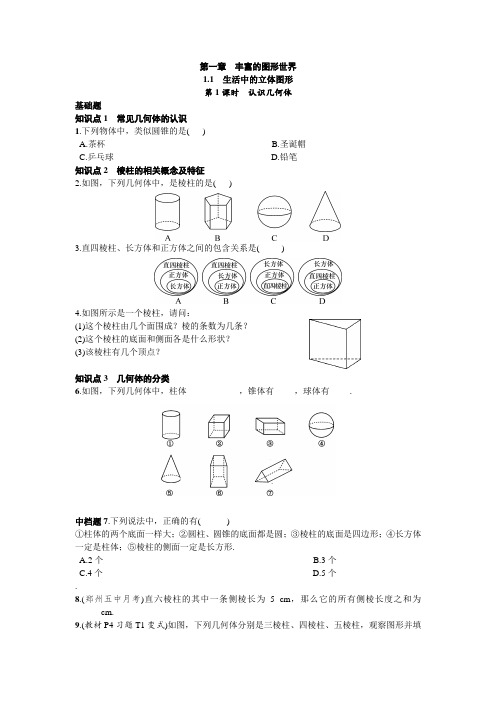
第一章丰富的图形世界1.1生活中的立体图形第1课时认识几何体基础题知识点1常见几何体的认识1.下列物体中,类似圆锥的是( )A.茶杯B.圣诞帽C.乒乓球D.铅笔知识点2棱柱的相关概念及特征2.如图,下列几何体中,是棱柱的是( )3.直四棱柱、长方体和正方体之间的包含关系是( )4.如图所示是一个棱柱,请问:(1)这个棱柱由几个面围成?棱的条数为几条?(2)这个棱柱的底面和侧面各是什么形状?(3)该棱柱有几个顶点?知识点3几何体的分类6.如图,下列几何体中,柱体--------------- ,锥体有-------,球体有-------.中档题7.下列说法中,正确的有( )①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.A.2个B.3个C.4个D.5个.8.(郑州五中月考)直六棱柱的其中一条侧棱长为 5 cm,那么它的所有侧棱长度之和为---------cm.9.(教材P4习题T1变式)如图,下列几何体分别是三棱柱、四棱柱、五棱柱,观察图形并填空.(1)三棱柱有-- 个面,--- 条棱,--- 个顶点;(2)四棱柱有---- 个面,----- 条棱----- 个顶点;(3)五棱柱有---- 个面,----- 条棱,---- 个顶点;(4)由此猜想:六棱柱有----- 个面,------ 条棱,----- 个顶点.10.指出图中各物体是由哪些几何体组成的.第2课时点、线、面、体基础题知识点1图形的构成元素1.下列几何体中,有五个面的是( )A.圆柱B.三棱柱C.四棱柱D.五棱柱2.圆锥有两个面,其中一个是------- 面,另一个------- 面,这两个面相交成一条--------- 线.知识点2点动成线、线动成面、面动成体3.流星划过天空时留下一道明亮的光线,用数学知识解释为( )A.点动成线B.线动成面C.面动成体D.以上都不对4.下雨时汽车的雨刷把玻璃上的雨水刷干净属于下列哪个选项的实际应用( )A.点动成线B.线动成面C.面动成体D.以上都不对6.以如图所示的三角形的边为轴旋转一周后所得到的几何体可以是右图中的--------------)(填序号).中档题7.将右边图形绕直线l旋转一周,可以得到如图所示的立体图形的是( )A B C D8.(太原五中检测)观察下图,请把如图的图形绕着给定的直线旋转一周后可能形成的几何体选出来( )A B C D9.我们曾学过圆柱的体积计算公式:V=Sh=πr2h(r是圆柱底面半径,h为圆柱的高).现有一个长方形,长为2 cm,宽为1 cm,以它的一边所在的直线为轴旋转一周,得到的几何体的体积是多少?1.2展开与折叠第1课时正方体的展开与折叠基础题知识点正方体的展开与折叠1.(长春中考)下列图形中,可以是正方体表面展开图的是( )2.(仙桃中考)如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )A.传B.统C.文D.化3.(河北中考改编)图1和图2中所有的正方形都相同,将图1的正方形放在图2中的①、②、③、④某一位置,所组成的图形不能围成正方体的位置是( )图1图2A.①B.②C.③D.④中档题5.(包头中考)将一个无盖正方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )6.(资阳中考)如图是一个正方体纸盒的外表面展开图,则这个正方体是( )7.(宝鸡期中)水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.下图是一个正方体的平面展开图,若图中的“似”表示正方体的前面,“锦”表示右面,“程”表示上面,则“祝”、“你”、“前”分别表示正方体的-------------------.8.如图,在图中增加1个小正方形使所得图形经过折叠能够围成一个正方体,则一共有---------种方式.综合题9.如图是一个正方体的表面展开图,把1,2,3,4,5,6分别填入六个小正方形内,使按虚线折成正方体后,相对的两个面上的数字之和相等.请你尝试不同的填法,并与同伴交流.第2课时棱柱、圆柱、圆锥的展开与折叠基础题知识点1棱柱的展开与折叠1.(北京中考)如图是某个几何体的展开图,该几何体是( )A.三棱柱B.圆锥C.四棱柱D.圆柱2.如图是一个长方体包装盒,则它的平面展开图是( )知识点2圆柱、圆锥的展开与折叠4.如图,圆柱的表面展开后得到的平面图形是( )5.如图所示的平面图形中,不可能围成圆锥的是( )6.(宝鸡渭滨区期中)圆锥的侧面展开图是---------------(填图形的名称).中档题7.下列图形中,能通过折叠围成一个三棱柱的是( )8.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )9.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面(字母朝外),那么在上面的字母是------------。
生活中的立体图形同步练习2024—2025学年东华师大版数学七年级上册

3.1生活中的立体图形同步练习一、单选题1.下列几何体,都是由平面围成的是( )A .圆柱B .三棱柱C .圆锥D .球2.用一个平面去截圆锥,得到的截面形状不可能是( )A .B .C .D . 3.以AB 为轴旋转一周后得到的立体图形是( )A .B .C .D . 4.如图所示的两个长方体容器中液体体积相同,根据图中信息,以下结论正确的是()A .8136(5)x x =+B .()81365x x =-C .甲容器中液体的体积为405D .乙容器中液面的高度为105.下列说法不正确的是( ).①长方体一定是柱体;①八棱柱有10个面;①六棱柱有12个顶点;①用一个平面去截几何体,若得到的图形是三角形,则这个几何体一定有一个面的形状是三角形.A.①B.①C.①①D.①①6.下列几何体中,圆锥是()A.B.C.D.7.下面几何体中,是圆锥的为()A.B.C.D.8.用一个平面去截下列几何体,截面不可能是圆的是()A.B.C.D.9.将一个直角三角形绕一条直角边所在的直线旋转一周后得到的几何体可能是()A.B.C.D.10.将一张正方形纸片按图①、图①所示的方式依次对折后,再沿图①中的虚线剪裁,最后将图①中的纸片打开铺平,所得到的图案是()A.B.C.D.二、填空题11.如图,这个几何体的名称为.12.用平面去截下列几何体:①三棱柱;①正方体;①圆柱;①圆锥;①球,则截面的形状可能是三角形的有个.13.一个棱长为6cm的正方体,它是由216个棱长为1cm的小正方体组成的,点P为上底面ABCD的中心,如果挖去(如图)的阴影部分为四棱锥,剩下的部分还包括个完整的棱长是1cm的小正方体.14.如果一个棱柱有12个顶点,那么它的面的个数是.15.已知一个直角三角形的两直角边分别是3和4,将这个直角三角形绕它的直角边所在直线旋转一周,可以得到圆锥,则圆锥的体积是 .(213π圆锥V r h =,结果保留π) 16.如图,一个正方体截去一个角后,剩下的几何体面的个数和棱的条数的和是 .三、解答题17.下列几何体可以由平面图形绕其中一条直线旋转一周得到吗?18.我们知道,将一个长方形绕它的一条边所在的直线旋转一周,得到的几何体是圆柱.现有一个长为6cm ,宽为4cm 的长方形,将这个长方形绕某条边所在直线旋转一周,求所得圆柱的体积是多少?(结果保留π)19.用一个平面去截一个正方体,请你画出三种不同的截面情况.20.如图,图①所示的几何体叫三棱柱,它有6个顶点,9条棱,5个面,图①和图①所示的几何体分别是四棱柱和五棱柱.(1)四棱柱有 个顶点, 条棱, 个面;(2)五棱柱有 个顶点, 条棱, 个面;(3)那么n 棱柱有 个顶点, 条棱, 个面.21.五棱柱、六棱柱各有多少个面?多少个顶点?多少条棱?猜测七棱柱的情形并设法验证你的猜测.22.如图1至图3是将正方体截去一部分后得到的多面体.(1)根据要求填写表格:面数(f)顶点数(v)棱数(e)图1图2图3(2)猜想f、v、e三个数量间有何关系;(3)根据猜想计算,若一个多面体有顶点数2013个,棱数4023条,试求出它的面数.。
生活中的立体图形单元测试
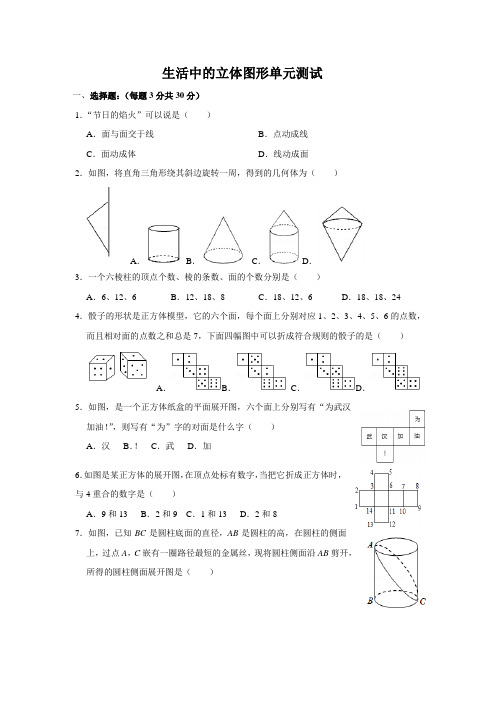
生活中的立体图形单元测试一、选择题:(每题3分共30分)1.“节日的焰火”可以说是()A.面与面交于线B.点动成线C.面动成体D.线动成面2.如图,将直角三角形绕其斜边旋转一周,得到的几何体为()A.B.C.D.3.一个六棱柱的顶点个数、棱的条数、面的个数分别是()A.6、12、6B.12、18、8C.18、12、6D.18、18、24 4.骰子的形状是正方体模型,它的六个面,每个面上分别对应1、2、3、4、5、6的点数,而且相对面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是()A.B.C.D.5.如图,是一个正方体纸盒的平面展开图,六个面上分别写有“为武汉加油!”,则写有“为”字的对面是什么字()A.汉B.!C.武D.加6.如图是某正方体的展开图,在顶点处标有数字,当把它折成正方体时,与4重合的数字是()A.9和13 B.2和9 C.1和13 D.2和87.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是()A.B.C.D.8.已知一个不透明的正方体的六个面上分别写着1﹣6六个数字,如图是我们能看到的三种情况,那么数字5的对面的数字是()A.6B.4C.3D.6或4或3 9.用一个平面去截一个圆柱体,截面图形不可能是()A.长方形B.梯形C.圆形D.椭圆形10.用一个平面去截一个几何体,截面是三角形,这个几何体不可能是()A.棱柱B.圆柱C.圆锥D.棱锥二、填空:(每题4分,共32分)11.如图是一个正方体的表面沿着某些棱剪开后展成的一个平面图形,若这个正方体的每两个相对面上的数字的和都相等,则这个正方体的六个面上的数字的总和为.11题图12题图13题图12.如图,将甲、乙、丙、丁四个小正方形中的一个剪掉,使余下的部分不能围成一个正方体,则剪掉的这个小正方形是.13.一个无盖长方体的包装盒展开图如图所示,则该长方体的体积为cm3.14.钻石原石看起来并不起眼,但经过精心设计、切割、打磨,就会成为璀璨夺目的钻石.钻石切割是多面体截面在实际生活中的一个应用.将已经加工成三棱柱形状的钻石原石进行切割,只切一刀,切截面的形状可能是.15.如果用平面截掉一个长方体的一个角(即切去一个三棱锥),则剩下的几何体最多有顶点,最少有条棱.16.如图从边长为10的正方体的一顶点处挖去一个边长为1的小正方体,则剩下图形的表面积为.17.用一个平面去截一个正方体,图中画有阴影的部分是截面,下面有关截面画法正确的序号有.18.有一个盛有水的圆柱体玻璃容器,它的底面半径为10cm,容器内水的高度为12cm,把一根半径为2cm的玻璃棒垂直插入水中直达容器底部,容器里的水升cm.三、解答题:19.用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.(8分)如A(1、5、6);则B();C();D();E().20.已知一个直棱柱,它有21条棱,其中一条侧棱长为20,底面各边长都为4.(7分)(1)这是几棱柱?(2)它有多少个面?多少个顶点?(3)这个棱柱的所有侧面的面积之和是多少?21.如图所示,两个圆和一个长方形(阴影部分)恰好可以围成一个圆柱,求这个圆柱的体积(π取3.14).(7分)22.如图所示的长方形是圆柱的侧面展开图,如果这个长方形相邻的两边长分别为6,4π,求圆柱的体积(温馨提示:考虑问题要全面哦!).(8分)23.如图是一个棱柱形状的食品包装盒的侧面展开图.(8分)(1)请写出这个包装盒的几何体的名称:;(2)若AC=3,BC=4,AB=5,DF=6,计算这个多面体的侧面积.。
立体图形练习题

一、基础概念题1. 请列举出三种常见的立体图形。
2. 立体图形的体积和表面积分别是什么?3. 立体图形的三视图分别是什么?4. 简述长方体、正方体、圆柱体、圆锥体的特征。
二、计算题1. 已知长方体的长、宽、高分别为10cm、6cm、4cm,求其体积和表面积。
2. 一个正方体的边长为8cm,求其体积和表面积。
3. 圆柱体的底面半径为5cm,高为10cm,求其体积和表面积。
4. 圆锥体的底面半径为3cm,高为4cm,求其体积和表面积。
三、应用题1. 一个长方体木块,长、宽、高分别为15cm、10cm、6cm,将其切割成最大的正方体,求正方体的边长。
2. 一个圆柱体水池,底面直径为10m,深为2m,求水池的容积。
3. 一个圆锥形帐篷,底面半径为6m,高为10m,求帐篷的占地面积。
4. 一块长方体铁块,长、宽、高分别为20cm、15cm、10cm,将其熔铸成一个球体,求球体的半径。
四、作图题1. 请画出长方体的三视图。
2. 请画出正方体的三视图。
3. 请画出圆柱体的三视图。
4. 请画出圆锥体的三视图。
五、判断题1. 立体图形的体积和表面积都是固定的。
()2. 长方体和正方体都是特殊的立方体。
()3. 圆柱体的底面一定是圆形。
()4. 圆锥体的侧面展开是一个扇形。
()六、选择题1. 下列哪个立体图形的体积公式是V = πr²h?A. 长方体B. 正方体C. 圆柱体D. 圆锥体2. 下列哪个立体图形的表面积公式是S = 2πrh + 2πr²?A. 长方体B. 正方体C. 圆柱体D. 圆锥体3. 一个正方体的边长为2cm,其体积为多少?A. 4cm³B. 8cm³C. 12cm³D. 16cm³4. 一个圆锥体的底面半径为3cm,高为4cm,其体积为多少?A. 12πcm³B. 36πcm³C. 48πcm³D. 144πcm³七、填空题1. 一个立方体的边长为5cm,其体积是______cm³,表面积是______cm²。
1.1生活中的立体图形练习题
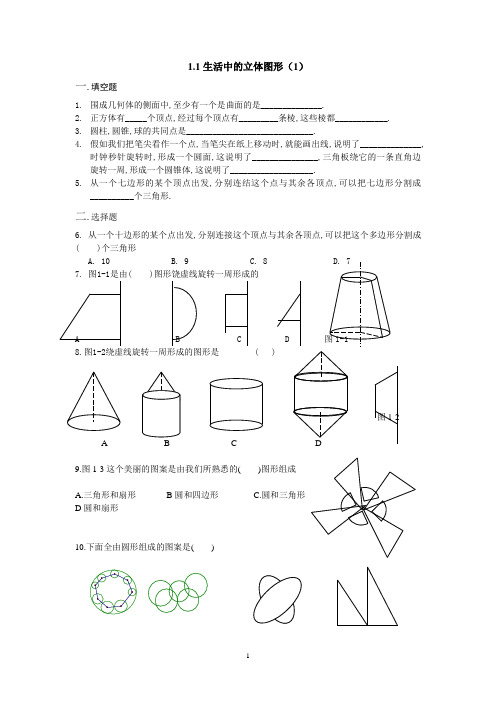
1.1生活中的立体图形(1)一.填空题1.围成几何体的侧面中,至少有一个是曲面的是______________.2.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.3.圆柱,圆锥,球的共同点是_____________________________.4.假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.5.从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成__________个三角形.二.选择题6. 从一个十边形的某个点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成( )个三角形A. 10B. 9C. 8D. 77. 图1-1是由( )图形饶虚线旋转一周形成的A B C D 图1-18.图1-2绕虚线旋转一周形成的图形是 ( )图1-2A B C D9.图1-3这个美丽的图案是由我们所熟悉的( )图形组成A.三角形和扇形B圆和四边形 C.圆和三角形D圆和扇形10.下面全由圆形组成的图案是( )A B C D三.解答题11.请写出下列几何体的名称( ) ( ) ( ) ( ) ( )1.1生活中的立体图形(2)一、判断题:1.柱体的上、下两个面一样大.………………………………………………..()2.圆柱的侧面展开图是长方形.………………………………………………()二、选择题:3、如图,下列图形()是柱体.4、下面给出的图形中,绕虚线旋转一周能形成圆锥的是()5、如下图,下列图形中有十四条棱的是()三、填空题:6、把下列图形的名称填在括号内7、长方体有个顶点,经过每个顶点有条棱,共有条棱。
8、一个七棱柱共有个面,条棱,个顶点,形状和面积完全相同的只有个面.9、如图4-5是一些具体的图形—三棱镜、方砖、帆布帐篷、笔筒、铅锤、粮囤、天文台,图4-6中是一些立体图形,找出与图4-6立体图形类似的图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
生活中的立体图形
十分钟测试
1、棱柱的两个底面是形,侧面是形;圆柱的两个底面是形,
侧面是面,展开图形是形。
2、棱柱和圆柱统称体。
3、棱锥的底面是形,侧面是形;圆锥的底面是形,侧面是面。
4、棱锥和圆锥统称体。
5、常见的立体图形分为体,体,体。
6、如图,下列图形()是柱体.
7、把下列立体图形的名称填到下面括号里。
8、判断下列的陈述是否正确
(1)柱体的上、下两个面不一样大( )
(2)圆柱、圆锥的底面都是圆()
(3)棱柱的底面不一定是四边形()
(4)圆柱的侧面是平面()
(5)棱锥的侧面不一定是三角形()
(6)柱体都是多面体()
小测试(1)
一、选择
1.与易拉罐类似的几何体是()
A、圆锥
B、圆柱
C、棱锥
D、棱柱
2.下图中是三棱锥的立体图形是( )
3.埃及金字塔类似于几何体 ( )
A 、圆锥
B 、圆柱
C 、棱锥
D 、棱柱 4.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线、面、体
C.角、三角形、正方形、圆
D.点、相交线、线段、长方体 5.下列说法正确的是 ( ) A .有六条侧棱的棱柱的底面一定是三角形 B .棱锥的侧面是三角形 C .长方体和正方体不是棱柱
D .柱体的上、下两底面可以大小不一样
二、填空
6.立体图形的各个面都是__________的面,这样的立体图形称为多面体. 7.篮球、排球、足球、乒乓球都是球形的,不是球形的球是。
8.棱柱的长相等,上下底面是的多边形,侧面是。
9.一个棱锥有7个面,这是棱锥,有个侧面。
10.长方体ABCD -A ′B ′C ′D ′有个面,条棱,个顶点。
与棱AB 垂直相交的棱有条,与棱AB 平行的棱有条。
11.如图所示立体图形中,(1)球体有___________;(2)柱体有_________;(3)锥体有____________.
12.如图,是一座粮仓,它可以看作是
由和几何体组成的.
13.如图,用边长为4的正方形,做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分的面积是
______.
14、判断
(1)柱体上下两个面一样大。
( ) (2)圆柱、圆锥的底面都是圆。
( ) (3)棱柱的底面是三角形。
( ) (4)棱锥的侧面是三角形。
( ) (5)球体不是多面体。
( ) (6)圆锥是多面体。
( ) (7)柱体都是多面体。
( )
A
B
C
D A
B C D ///
/
(8)棱锥、棱柱是多面体。
()
三、解答
15.正方体是由六个面围成的几何体,有由一个面围成的几何体吗?举例说明由三个、四个、五个面围成的几何体?
16.对于一个铅球,列出的如下特性:(1)是由金属制成的;(2)表面很硬,摸上去很凉;(3)是灰黑色的;
(4)是球形的;(5)质量是5千克;(6)放在水中会沉下去;(7)直径是10厘米;(8)小亮可以掷4米远.你能说出在这些特性中哪些是几何研究的内容吗?
17.连一连:
棱柱圆锥球正方体长方体圆柱
18.如图 3.1-4,是工厂烟囱,由圆锥和圆柱组成,举出由圆柱和棱柱,圆柱和球,棱柱和球组成的几何体。
你还能举出其他图形的组合吗?
19.你能否将下列几何体进行分类?并请说出分类的依据。
20.由平的面围成的立体图形又叫做多面体,有几个面,就叫做几面体。
三棱锥有四个面,所以三棱锥又叫四面体;正方体又叫做面体,有五条侧棱的棱柱又叫做面体。
(1)探索:如果把一个多面体的顶点数记为V,棱数记为E,面数记为F,填表:
多面体V F E V+F–E
四面体
长方体
五棱柱
(2)猜想:由上面的探究你能得到一个什么结论?
21.引人入胜的火柴问题,成年人和少年儿童都很熟悉,如图是由火柴搭成的图形,拿走其中的4根火柴,
使之留下5个正方形,且留下的每根火柴都正方形的边或边的一部分,请你给出两种方案,并将它们分别画在图(2)、图(3)中,要求:在拿走的火柴上作标记“°”“如图(1)所示”.
1.围成几何体的侧面中,至少有一个是曲面的是______________.
2.图1-2绕虚线旋转一周形成的图形是 ( )
图1-2
A B C D。
