逐点比较插补算法设计
逐点比较法圆弧插补算法

二、 逐点比较法圆弧插补加工一个圆弧,很容易联想到把加工点到圆心的距离和该圆的名义半径相比较来反映加工偏差。
这里,我们以第Ⅰ象限逆圆弧为例导出其偏差计算公式。
设要加工图2—3所示第Ⅰ象限逆时针走向的圆弧,半径为R ,以原点为圆心,起点坐标为A(00x ,y ),对于圆弧上任一加工点的坐标设为P( i j x ,y ),P 点与圆心的距离 P R 的平方为 222Pi j R =x +y ,现在讨论这一加工点的加工偏差。
图 2 - 2 圆 弧 差 补 过 程图2-3 圆弧插补过程点击进入动画观看逐点比较法圆弧插补若点P(i j x ,y )正好落在圆弧上,则下式成立:22222i j 00x +y =x +y =R若加工点P(i j x ,y )在圆弧外侧,则P R >R ,即:2222i j 00x +y >x +y若加工点P(i j x ,y )在圆弧内侧,则P R <R ,即:2222i j 00x +y >x +y将上面各式分别改写为下列形式:2222i 0j 0(x -x )+(y -y )=0(加工点在圆弧上) 2222i 0j 0(x -x )+(y -y )>0(加工点在圆弧外侧)2222i 0j 0(x -x )+(y -y )<0(加工点在圆弧内侧)取加工偏差判别式为:2222ij i 0j 0F =(x -x )+(y -y )运用上述法则,利用偏差判别式,即获得图2—2折线所示的近似圆弧。
若P(i j x ,y )在圆弧外或圆弧上,即满足 ij F ≥0的条件时,应向x 轴发出一个负向运动的进给脉冲(—Δx),即向圆内走一步。
若P(i j x ,y )在圆弧内侧,即满足ij F <0的条件,则向y 轴发出一个正向运动的进给脉冲(+Δy),即向圆弧外走一步。
为了简化偏差判别式的运算,仍用递推法来推算下一步新的加工偏差。
设加工点P(i j x ,y )在圆弧外侧或圆弧上,则加工偏差为2222ij i 0j 0F =(x -x )+(y -y )0≥x 坐标需向负方向进给一步(—Δx),移到新的加工点P(i+1j x ,y )位置,此时新加工点的x 坐标值为i x -1,y 坐标值仍为 i y ,新加工点P( i+1j x ,y )的加工偏差为:22222i+1,j i 0j 0F =(x -1)-x +y -y经展开并整理,得:i +1,j i j F =F 21i x -+(2-3)设加工点P(i j x ,y )在圆弧的内侧,则:ij F <0那么,y 坐标需向正方向进给一步(+Δy),移到新加工点P( i j+1x ,y ),此时新加工点的x 坐标值仍为i x ,y 坐标值则改为 j y 1+,新加工点P( i j+1x ,y )的加工偏差为:2222i,j+1i 0j 0F =x -x +(y +1)y -,展开上式,并整理得:i,j+1ij F =F 21i y ++综上所述可知:当ij F ≥0时,应走—Δx ,新偏差为 i+1,j ij F =F 21i x -+,动点(加工点)坐标为i+1i x =x -1, j j y y =;当 ij F <0时,应走+Δy ,新偏差为 i,j+1ij F =F 21i y ++,动点坐标为 j j y y =, i+1i =y +1y 。
实验一 逐点比较法圆弧和直线插补实验

Y B(xe,ye)
M(xm,ym)
Rm R
A(x0,y0)
O 图3 圆弧插补原理图 X
圆弧插补原理参见上图,对于第一象限逆圆,设圆弧的起点为 A(x0,y0),终点为 B(xe,ye), 圆弧半径为 R。加工点为 M(xm,ym),它与圆心的距离为 Rm,则
(1)偏差计算
Fm
=
Rm2
− R2
=
xm2
p102=p102-p104 p101=p101+1 x-0.1 else p102=p102+p103 p101=p101+1 y0.1
;计算新的偏差值(Fi+1=Fi-ya) ;步数计数器加一 ;X方向进分别是(-0.1 -0.5 -1.0) ;偏差判别(若P102小于0表示刀具在直线下方) ;计算新的偏差值(Fi+1=Fi+xa) ;步数计数器加一 ;Y方向进给分别是(0.1 0.5 1.0)
endif
endwhile
close
(3)根据直线插补编成格式,编写所给圆弧插补程序。 各组的圆弧的插补任务是: u 第一组:圆弧半径 50,第二象限顺圆;
第二组:圆弧半径 50,第二象限逆圆; 第三组:圆弧半径 60,第三象限顺圆; 第四组:圆弧半径 60,第三象限逆圆; 第五组:圆弧半径 70,第四象限顺圆; 第六组:圆弧半径 70,第四象限逆圆; open prog7 clear linear inc p101=0 p102=0 p103=0 p104=50 while(p101!>100) if(p102!<0) y0.5 p101=p101+1 p102=p102-2*p104+1 p104=p104-1 else -x0.5 p101=p101+1 p102=p102-2*p103+1 p103=103-1 endif endwhile close
圆弧插补(逐点比较法)20页文档

Fi<0
O Fi≥0
X Fi<0 Fi≥0
2、圆弧插补的象限处理
前面的圆弧插补(顺圆、逆圆)只限于第一象限,其他 情况如图所示: Y
O
X
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
代入偏差函数,得Pi+1点的偏差为: Fi+1 = Fi-2Yi + 1
当Fi<0时,向+X方向进给一步,动点由Pi(Xi,Yi) 移动到 Pi+1(Xi +1,Yi),则新动点的坐标为 Xi+1=Xi +1
代入偏差函数,得Pi+1点的偏差为:
Fi+1 = Fi + 2Xi + 1
所以,第一象限顺时针圆弧插补加工时偏差加工的递推 公式为:
10 F9=1 -X F10=F9-2X9+1 = 0, X10=0,Y10=5 ∑=0
加工过程为: Y 5
4 3
2 1
O
1 23 45
X
(三)象限处理 1、直线插补的象限处理 前面的公式只适用于第一象限,对于其他象限直线,偏
差函数用│X│和 │Y│代替X,Y。则进给方向为:
Y Fi<0 Fi≥0 Fi≥0
X
同理,对于第一象限顺圆加工时,即B→A,当Fi≥0时, 应向-Y方向进给一步,当Fi<0时,应向+X方向进给 一步。
Y
B(Xe,Ye)
Pi(Xi,Yi)
逐点比较法

即
Fi1 Fi X e
6
在插补计算、进给的同时还要进行终点判别。常用终点判 别方法是:
设置一个长度计数器,从直线的起点走到终点,刀具沿
X 轴应走的步数为X e,沿Y 轴走的步数为Ye,计数器中存入 X和Y两坐标进给步数总和∑=∣Xe∣+∣Ye∣,当X 或Y
坐标进给时,计数长度减一,当计数长度减到零时,即∑= 0时,停止插补,到达终点。
终点判别:判断是否到达终点,若到 达x ,结束插补;否则,继续以上四个
步骤(如图3-3所示)。
图3-3 逐点比较法工作循环图
3
2. 直线插补
图3-4所示第一象限直线OE为给定轨迹,其方程为
XeY-XYe=0
(3-1)
P(X,Y)为动点坐标,与直线的关系有三种情况:
(1)若P1点在直线上方,则有XeY-XYe>0 E (2) 若P点在直线上,则有 XeY-XYe=0
2.由偏差方程确定加工动点引起的偏 差符号(若要计算偏差量,则偏差方程系数不能简 化)。
3.下一步插补方向确定原则:向使加 工偏差减小、并趋向轨迹终点的方向插补
.(将偏差等于零的情况并入偏差大于零的情况)。
4.关于插补量:每次插补一个脉冲当 量的位移
12
3. 圆弧插补
在圆弧加工过程中,可用动点到圆心的距离来描述刀具位置与 被加工圆弧之间关系。
b) 逆圆弧
图3-9 第一象限顺、逆圆弧
14
偏差递推简化:对第一象限顺圆,Fi≥0,动点Pi(Xi,Yi)应 向-Y向进给,新的动点坐标为(Xi+1,Yi+1),且Xi+1=Xi,Yi +1=Yi-1,则新点的偏差值为:
15
若Fi<0时,沿+X向前进一步,到达(Xi+1,Yi)点,新点
逐点比较法插补的连续轨迹控制设计

综合设计课程设计设计要求1 设计要求1.1 设计要求(1)设计出逐点比较法插补软件流程图;(2)编写出逐点比较法插补程序;(3)要求用软件能够实现任意象限圆弧(G03)的插补计算;(4)要求软件能够处理特殊轮廓的插补,例如坐标中任意圆弧等;(5)插补结果要求能够以图形模拟进行输出。
2 设计目的2.1 设计目的(1)了解连续轨迹控制数控系统的组成原理;(2)了解逐点比较法插补的基本原理;(3)掌握逐点比较法插补的软件实现方法。
3 总体方案比较3.1 各多种方案的特点第一:采用逐点比较法插补。
逐点比较法的基本原理是被控对象在按要求的轨迹运动时,每走一步都要与规定的轨迹进行比较,由此结果决定下一步移动的方向。
逐点比较法既可以作直线插补又可以作圆弧插补。
这种算法的特点是,运算直观,插补误差小于一个脉冲当量,输出脉冲均匀,而且输出买成速度变化小,调节方便,因此在两坐标数控机床中应用较为普遍第二:数学积分法插补。
又称为微分分析法。
这种插补方法可实现一次、二次、甚至高次曲线的插补,也可以实现多坐标联动控制。
只要输入不多的几个数据,就能加工出圆弧等形状较为复杂的轮廓曲线。
作直线插补时,脉冲分配也较均匀。
第三:数据采样插补。
数据采样插补实际上是一种粗插补过程,它所产生的微小线段仍然比较大,必须进一步对其密化(即精插补)。
粗插补算法比较复杂,综合设计课程设计多CPU结构CNC系统硬件原理图大多用高级语言编制;精插补算法比较简单,多用汇编语言或硬件插补器实现。
3.2 方案选择根据课题要求,对逆圆插补。
根据两种方案的比较,都是很好的方法,但由于圆是二次,用采用逐点比较法插补进行设计比较方便、简单,所以根据各种插补方法的特点,选择用逐点比较法来实现。
4 多CPU结构CNC系统硬件原理图4.1 CNC系统原理图图4.1 共享总线的多CPU结构的CNC系统结构框图4.2 原理图极其说明共享总线机构,只有主模块有权控制系统的总线,在某一时刻只能有一个猪模块占有总线。
数控机床逐点比较法圆弧插补
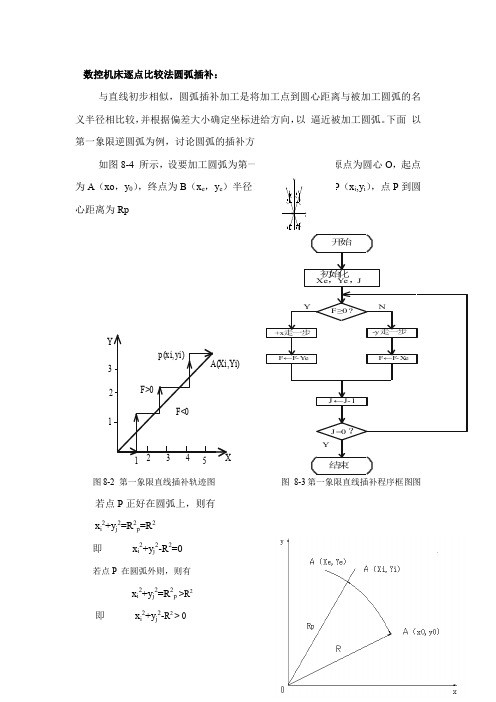
第一象限逆圆弧为例,讨论圆弧的插补方法。
如图8-4 所示,设要加工圆弧为第一象限逆圆弧AB ,原点为圆心O ,起点为A (xo ,y 0),终点为B (x e ,y e )半径R ,瞬时加工点为P (x i ,y i ),点P 到圆心距离为Rp<0+△y>0-△x <0+△x <0+△y>0-△x<0-△y <0-△y>0+△x yx图8-2 第一象限直线插补轨迹图 图 8-3第一象限直线插补程序框图图12345X123YF>0p(xi,yi)A(Xi,Yi)F<0开始初始化Xe ,Y e ,JF≥0?+x 走一步F←F -Y e F←F -X e-y 走一步YNJ ←J-1J =0?Y结束若点P 在圆弧内则,则有x i2+y j2=R2p<R2即x i2+y j2-R2 < 0显然,若令F i,j= x i2+y j2-R2(8-4)图8-4 逆圆弧插补则有:(1)F i,j= F i,j=0, 则点P在圆弧上(2)F i,j >0则点P在圆弧外则(3)F i,j<0则点P在圆弧不则常将8-4称为圆弧插补偏差判别式。
当F i,j≥时,为逼近圆弧,应向-x方向进给一步;当F i,j<0时,应向+y 方向走一步。
这样就可以获得逼近圆弧的折线图。
与直线插补偏差计算相似,圆弧插补的偏差的计算也采用递推的方法以简化计算。
若加工点P(x i,y i)在圆弧外或者圆弧上,则有:F i,j=x i2+y j2-R2≥0 为逼近该圆沿-x方向进给一步,移动到新加工点P(x i=1,y i),此时新加工点的坐标值为x i+1=x i-1,y i=y i新加工点的偏差为:F i+1,j=(x i-1)2+y i2-R2=x i2-2x i+1+ y i2-R2= x i2+ y i2-R2+1即F i+1,j= F i,j-2x i+1 (8-5)若加工P(x i,y i)在圆弧内,则有F i,j=x i2+y j2-R2<0若逼近该圆需沿+y方向进给一步,移到新加工点P(x i,y i),此时新加工点的坐标值图8-5 第一象限圆弧插补程序框图为新加工点的偏为:F i,j+1=x i2+(y i+1)2-R2=x i2+ y i2+1 -R2= x i2+ y i2-R2+1+2y iF i,j+1= F i,j-2y i+1 (8-6)从(8-5)和式(8-6)两式可知,递推偏差计算仅为加法(或者减法)运算,大大降低了计算的复杂程度。
逐点比较法第一象限直线插补

逐点比较法第一象限直线插补编程逐点比较法是以折线来逼近给定的轨迹,就是每走一步控制系统都要将加工点与给定的图形轨迹相比较,以决定下一步进给的方向,使之逼近加工轨迹。
逐点比较法以折线来逼近直线或圆弧,其最大的偏差不超过一个最小设定单位。
只要将脉冲当量取得足够小,就可以达到精度要求。
逐点比较插补法在脉冲当量为0.01mm,系统进给速度小于3000mm/min时,能很好的满足要求。
一、逐点比较法直线插补如下图所示设直线 oA 为第一象限的直线,起点为坐标原点o (0 , 0) ,终点坐标为, A( ) , P() 为加工点。
若 P 点正好处在直线 oA 上,由相似三角形关系则有即点在直线 oA 上方 ( 严格为直线 oA 与 y 轴正向所包围的区域 ) ,则有即若 P 点在直线 oA 下方 ( 严格为直线 oA 与 x 轴正向所包围的区域 ) ,则有图 3 — 1 逐点比较法第一象限直线插补即令则有:①如,则点 P 在直线 oA 上,既可向 +x 方向进给一步,也可向 +y 方向进给一步;②如,则点 P 在直线 oA 上方,应向 +x 方向进给一步,以逼近oA直线;③如,则点 P 在直线 oA 下方,应向 +y 方向进给一步,以逼近 oA直线一般将及视为一类情况,即时,都向 +x 方向进给一步。
当两方向所走的步数与终点坐标相等时,停止插补。
这即逐点比较法直线插补的原理。
对第一象限直线 oA 从起点 ( 即坐标原点 ) 出发,当 F时, +x 向走一步;当 F<0 时,y 向走一步。
特点:每一步都需计算偏差,这样的计算比较麻烦。
递推的方法计算偏差:每走一步后新的加工点的偏差用前一点的加工偏差递推出来。
采用递推方法,必须知道开始加工点的偏差,而开始加工点正是直线的起点,故。
下面推导其递推公式。
设在加工点 P( ) 处,,则应沿 +x 方向进给一步,此时新加工点的坐标值为新加工点的偏差为即若在加工点 P( ) 处,,则应沿 +y 方向进给一步,此时新加工点的坐标值为,新加工点的偏差为即综上所述,逐点比较法直线插补每走一步都要完成四个步骤 ( 节拍 ) ,即:(1) 位置判别根据偏差值大于零、等于零、小于零确定当前加工点的位置。
逐点比较法直线插补原理

四个象限插补计算统一起来; 不同象限的坐标进给方向由坐 F<0 F≥0
F≥0
L1 F<0
标值的符号来确定。
➢ 按照以上的插补规律,
可编制出逐点比较法直
F<0
线插补的程序。下面是
编制的演示程序。
L3
O
F≥0 F≥0
x F<0
L4
携手共进,齐创精品工程
Thank You
世界触手可及
数字增量插补算法中,粗插补由软件完成,精插补可以由 软件,也可以由硬件完成。
精插补由硬件完成: 如日本FANUC公司 的FANUC-3、6, 见图4-1
粗、精插补由软件完 成:如美国AllenBradley(A-B公司) 的9/260,见图4-2
二、脉冲增量插补算法
特点:
➢ 行程标量插补 每次插补的结果仅产生一个单位的行
环系统。
(一)逐点比较法
基本思路: 当刀具按要求的轨迹移动时,每走一步都要与规定的
轨迹比较,根据比较的结果决定下一步的移动方向,使 刀具向减小偏差的方向并趋向终点移动。
特点:
Y
运算直观,插补误差小于
一个脉冲当量,输出脉冲均匀,
速度变化小,调节方便。
(2,2) (3,2)
(1,1)
(2,1)
X
(0,0)
插补开始
偏差判别 坐标进给
偏差计算
终点判别
N
Y
插补结束
Y
例4-1:加工第一象限直线OA
起点偏差: F0,0=0
总步数:n=3+2=5
(2,2) A(3,2)
(1,1)
(2,1)
插补运算过程
O(0,0) (1,0)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学院毕业论文(设计) 2015 届机械设计制造及其自动化专业 13 班级题目逐点比较插补算法设计姓名学号 1指导教师职称教授二О一五年五月二十一日摘要逐点比较法是数控加工中常用的插补方法,通过控制刀具每次移动的位置与理想位置的误差函数进而实现零件加工,鉴于VB编程简单、直观,采用VB可以实现逐点比较插补原理的相关程序设计及加工过程虚拟化。
插补技术是机床数控系统的核心技术,逐点比较法可以实现直线和圆弧插补算法,其算法的优劣直接影响零件直线和圆弧轮廓的加工精度和加工速度。
文章在传统的逐点比较直线插补与圆弧插补算法的基础上,提出以八方向进给取代传统的四方向进给,研究了偏差最小的走步方向的实现方法,同时研究了保证数控机床坐标进给连续的偏差递推计算过程。
结果表明,新算法可以提高零件轮廓的逼近精度且减少了插补计算次数,从而提高了零件直线和圆弧轮廓的加工精度和加工速度。
关键词数控;插补;逐点比较;逼近;偏差函数The algorithm design of point-to-point comparisonAuthor: LI Zhiyuan Tutor: Chen LiangjiAbstractAbstract: The algorithm of point-to-point comparison is a typical plugging method in processing of numerical control,manufacturing parts by controlling error function between the position the cutting tool moves to and the perfect program is simple and visual,which can visualize the programming and processing of The algorithm of point-to-point comparison. Interpolation technology is the core technology of machine tool’s CNC system. The algorithm of point-to-point comparison can achieve the algorithms of linear and circular algorithm of point-to-point comparisonlinear and circular interpolation affects the machining accuracy and rate on the conventional algorithm of point-to-point comparison linear and circular interpolation,it was put forward in the article that feed in eight directions takes place of feed in four directions,the achievement method of feed direction was researched that can result in the least deviation,the deviation recursive calculation process was researched that can ensure a continuous CNC coordinate result showed that the approximation accuracy of parts’ contour was improved and the number of interpolation calculation was reduced by use of new algorithm,and then the machining accuracy and rate of parts’ linear and circular contour was improved. Keywords:CNC;interpolation;point-to-point comparison ;error function目录第一章绪论0设计与研究的重要性0本设计的主要工作0第二章逐点比较法1基准脉冲插补1逐点比较法1逐点比较法直线插补算法2逐点比较法圆弧插补8第三章逐点比较法算法的改进16改进的逐点比较直线插补算法 17改进的逐点比较圆弧插补算法 20第4章V B插补程序代码23逐点比较法直线插补的程序设计方案23程序实现23工作界面23源程序代码24逐点比较法圆弧插补V B程序26第五章结论29参考文献31第一章绪论在现代制造系统中数控系统占有非常重要地位,数控技术是一门不仅具有理论性而且具有实践性的多学科融合技术。
尤其,插补技术是数控技术的一个重要组成部分,数控加工中常采用的插补方法是逐点比较法插补法。
逐点比较插补法通过控制刀具每次移动的位置与理想位置误差函数进行比较,从而使实现零件的加工。
由于Visual Basic 在实际当中的广泛应用及编程简单、直观,采用Visual Basic 可以实现逐点比较法插补原理的相关程序设计。
随着科技水平的不断提高,人类对机械制造技术提出了更高的要求。
机械制造技术的基础是数控技术。
数控系统编程影响着数控机床的各种性能,不但决定着加工过程而且还决定着加工精度,所以,对数控系统的加工有着非常重大的意义。
设计与研究的重要性插补技术是机床数控系统的核心技术。
插补是机床数控系统按照一定方法控制执行部件运动、进而产生零件轮廓的过程。
插补的本质是在所需路径或轮廓上的两个已知点间,依据某一数学函数确定其中中间点的位置坐标值。
数控系统依据其坐标值控制执行部件的运动,从而实现数控加工。
插补算法的优劣直接影响数控系统的各性能指标,其计算精度也将直接影响零件轮廓的加工精度。
因此,插补算法对数控系统的性能非常重要。
设计的相关技术及现状在现代计算机数控系统中,插补算法大部分都是采用计算机的程序软件来实现。
由于直线和圆弧是构成工件轮廓的基本要素,因此一般的数控系统都具有直线和圆弧插补功能。
数控系统的插补算法可划分为基准脉冲插补和数据采样插补这两大类,逐点比较插补法是基准脉冲插补计算方法中的一种常采用的方法。
脉冲增量法实现起来相对比较简单而且易用硬件实现,从而被广泛应用在开环数控系统中。
因此,大多数的CNC 系统都具有直线和圆弧插补功能。
由于大多数非圆轮廓曲线均可以采用圆弧来逼近,在系统不具备高级曲线输出功能时,若有一个简单精确而且快速的圆弧插补功能则显得非常必要。
本设计的主要工作逐点比较插补法不但能进行过象限处理和终点判别,而且能对译码后的结果进行插补运算。
本设计在传统的逐点比较圆弧插补算法的基础上,提出一种改进算法。
这种改进的算法不仅减少数控系统的插补次数而且还提高插补精度,从而提高零件轮廓的加工精度。
本设计还采用了VB程序编写插补算法并调试其程序在计算机中实现模拟数控插补方法。
第二章逐点比较法基准脉冲插补脉冲增量插补为行程标量插补。
这类插补算法的特点是每次插补结束仅产生一个行程增量,以一个个脉冲的方式输出。
脉冲增量插补算法主要应用在开环数控系统中。
基准脉冲插补在插补计算过程中不断地向各坐标轴发出互相协调的进给脉冲,驱动各坐标轴进给电动机的运动,一个脉冲所产生的移动量称为脉冲当量,通常用δ表示。
脉冲当量δ值越小,数控机床的加工精度就越高,对数控系统的计算能力的要求也越高。
采用脉冲增量插补算法的CNC系统,其坐标轴进给速度受插补程序运行时间的限制。
逐点比较法是基于脉冲增量插补方法之一。
逐点比较法逐点比较插补法就是每走一步(即一个脉冲当量)都要将加工点的瞬时坐标与规定的图形轨迹相比较,判断实际加工点在给定轨迹的什么位置, 从而决定下一步的进给方向,这样就能得出一个非常接近规定图形的轨迹。
逐点比较法又称区域判别法,又称代数运算法,或醉步式近似法。
逐点比较法的基本原理是计算机在控制加工过程中,能逐点地计算和判别加工偏差,以控制坐标进给,按规定图形加工出所需要工件,在数控装置的控制下,按要求的轨迹运动时,每走一步都要和规定的轨迹比较,根据比较的结果决定下一步的移动方向。
每走一步都要完成四个工作节拍(如图2-1)。
图2-1 逐点比较的工作节拍(1) 偏差判别:判别加工点对规定图形的偏离位置,确定进给方向。
(2) 坐标进给:使加工点向规定的图形趋进,缩小偏差。
(3) 偏差计算:计算新的加工点与给定的图形之间的偏差,作为下一步判别依据。
(4) 终点判别:判断是否到达终点,若到达则停止插补;否则,在回到第一拍,如此不断重复上述循环过程,加工出所需要的轮廓形状。
逐点比较法可以实现直线和圆弧插补。
其特点是运算直观,插补误差小于一个脉冲当量,而且输出脉冲均匀,输出脉冲的速度变化小,调节方便。
逐点比较法直线插补算法 1. 逐点比较法直线插补原理直线插补时,以直线的起点为坐标原点,给出终点坐标()e e Y X A ,,见图如图2-2所示,则直线方程为eY X Y X e=改写为 0=-e e XY Y X (2-1)式中 X,Y 为该直线上任一点 P 的坐标。
对XY 平面第一象限直线段进行插补,直线段起点位于坐标原点O ,终点位于()e e Y X A ,,设点()i i Y X P ,为任一动点。
图2-2 逐点比较法直线插补 1)偏差判别设()i i Y X P ,为加工动点,则如下若P 点在该直线OA 上,则:0=-e i i e Y X Y X若P 点在该直线OA 上方,则:0>-e i i e Y X Y X若P 点在该直线OA 下方,则:0<-e i i e Y X Y X 由此,可取偏差判别函数i F 为e i i e i Y X Y X F 11++-= (2-2)则可得到如下结论:当i F =0时,加工动点P 落在给定直线上; 当i F >0时,加工动点P 落在给定直线上方; 当i F <0时,加工动点P 落在给定直线下方。
2) 坐标进给坐标进给是向使偏差缩小的方向。
根据这个原则,就有:①当i F >0时,应该向X 的正向进给一步,使点接近直线OA; ②当i F <0时,应该向Y 的正向进给一步,使点接近直线OA;③当i F =0时,既可以向X 的正向进给一步,也可以Y 的正向进给一步,但通常将F=0和F >0做同样的处理,既都向X 的正向进给一步。
