苏教版必修一函数练习题
新教材苏教版高中数学必修第一册第五章 函数概念与性质 课时分层练习题 精选最新配套习题,含解析

第五章函数概念与性质1函数的概念(一) ............................................................................................................ - 1 - 2函数的概念(二) ............................................................................................................ - 5 - 3函数的图象 ................................................................................................................ - 10 - 4函数的表示方法......................................................................................................... - 15 - 5分段函数 .................................................................................................................... - 20 -6.函数的单调性............................................................................................................. - 26 -7函数的最大值、最小值............................................................................................. - 35 - 8函数奇偶性的概念..................................................................................................... - 46 - 9函数奇偶性的应用..................................................................................................... - 50 -1函数的概念(一)基础练习1.已知集合A={x|0≤x≤8},集合B={y|0≤y≤4},则下列对应关系中,不能看作是从A到B的函数关系的是( )A.f:x→y=xB.f:x→y=xC.f:x→y=xD.f:x→y=x【解析】选D.对于A中的任意一个元素,在对应关系f:x→y=x;f:x→y=x;f:x→y=x下,在B中都有唯一的元素与之对应,故能构成函数关系.对于A中的元素8,在对应关系f:x→y=x下,在B中没有元素与之对应,故不能构成函数关系.2.(2020·朝阳高一检测)函数f(x)=的定义域为( )A.{x|x≤2或x≥3}B.{x|x≤-3或x≥-2}C.{x|2≤x≤3}D.{x|-3≤x≤-2}【解析】选A.由x2-5x+6≥0,解得x≤2或x≥3,所以函数f(x)=的定义域为{x|x≤2或x≥3}.3.函数f(x)=的定义域为 ( )A.[2,+∞)B.(2,+∞)C.(2,3)∪(3,+∞)D.[2,3)∪(3,+∞)【解析】选C.函数f(x)=中,解得x>2且x≠3;所以f(x)的定义域为(2,3)∪(3,+∞).4.已知集合M={x,y,z},N={-1,1},则从M到N的函数中,满足f(x)=1的有______个.【解析】由题意满足f(x)=1的有共4个.答案:45.求下列函数的值域.(1)f(x)=.(2)y=2x2+4x-3.【解析】(1)函数的定义域为R,f(x)==≤=2,且f(x)>0,所以其值域为(0,2].(2)因为y=2x2+4x-3=2(x+1)2-5≥-5,故函数y=2x2+4x-3的值域为{y|y≥-5}.提升训练一、选择题(每小题5分,共20分)1.若两个函数的对应关系相同,值域也相同,但定义域不同,则称这两个函数为同族函数.那么与函数y=x2,x∈{-1,0,1,2}为同族函数的有( )A.5个B.6个C.7个D.8个【解析】选D.由题意知同族函数是只有定义域不同的函数,函数解析式为y=x2,值域为{0,1,4}时,定义域中,0是肯定有的,正负1,至少含一个,正负2,至少含一个.它的定义域可以是{0,1,2},{0,1,-2},{0,-1,2},{0,-1,-2},{0,1,-2,2},{0,-1,-2,2},{0,1,-1,-2},{0,1,-1,2,-2},共有8种不同的情况.2.(2020·启东高一检测)函数f(x)=的定义域为( )A.B.C.(-∞,-2)∪D.(-∞,-2)∪【解析】选C.由解得x≤且x≠-2.所以函数f(x)=的定义域为(-∞,-2)∪.3.已知f(x)满足f(ab)=f(a)+f(b),且f(2)=p,f(3)=q,那么f(72)= ( )A.p+qB.3p+2qC.2p+3qD.p3+q2【解析】选B.因为f(ab)=f(a)+f(b),所以f(9)=f(3)+f(3)=2q,f(8)=f(2)+f(2)+f(2)=3p,所以f(72)=f(8×9)=f(8)+f(9)=3p+2q.4.(多选题)已知集合M={-1,1,2,4},N={1,2,4,16},给出下列四个对应关系,请由函数定义判断,其中能构成从M到N的函数的是 ( )A.y=B.y=x+1C.y=2|x|D.y=x2【解析】选CD.在A中,当x=-1时,y=-1∉N,故A错误;在B中,当x=-1时,y=-1+1=0∉N,故B错误;在C中,任取x∈M,总有y=2|x|∈N,故C正确;在D中,任取x∈M,总有y=x2∈N,故D正确.二、填空题(每小题5分,共10分)5.设函数f(x)=x0+,则其定义域为________.【解析】函数f(x)=x0+,则解得-3≤x≤3且x≠0.所以函数f(x)的定义域是[-3,0)∪(0,3].答案:[-3,0)∪(0,3]6.函数y=的定义域为R,则a∈________.【解析】因为任意x∈R,根式恒有意义,所以ax2+ax+1≥0的解集为R,①a=0时,1≥0恒成立;②a≠0时,解得0<a≤4,综上得,a∈{a|0≤a≤4}.答案:{a|0≤a≤4}三、解答题7.(10分)已知集合A={1,2,3,k},B={4,7,a4,a2+3a},a∈N*,k∈N*,x∈A,y∈B,f:x→y=3x+1是从定义域A到值域B的一个函数,求a,k,A,B.【解析】根据对应关系f,有1→4;2→7;3→10;k→3k+1.若a4=10,则a∉N*,不符合题意,舍去;若a2+3a=10,则a=2(a=-5不符合题意,舍去).故3k+1=a4=16,得k=5.综上a=2,k=5,集合A={1,2,3,5},B={4,7,10,16}.2函数的概念(二)基础练习1.与函数y=2x2+1不是同一个函数的是( )A.y=|x2|+|x2+1|B.y=C.y=|2x2+1|D.y=【解析】选 D.函数y=2x2+1的定义域为R,值域为[1,+∞),选项A中的函数y=|x2|+|x2+1|=x2+x2+1=2x2+1,它的定义域为R,值域为[1,+∞),和已知函数为同一个函数;选项B中的函数即y==2x2+1,它的定义域为R,值域为[1,+∞),和已知函数为同一个函数;选项C中的函数y=|2x2+1|=2x2+1,它的定义域为R,值域为[1,+∞),和已知函数为同一个函数;选项D中的函数的定义域为{x|x≠-1},故它和已知函数不是同一个函数.2.(2020·哈尔滨高一检测)下列函数中,表示同一个函数的是( )A.y=x2与y=()4B.y=x2与y=t2C.y=与y=D.y=·与y=【解析】选B.A.y=x2的定义域为R,y=()4的定义域为[0,+∞),定义域不同,不是同一个函数;B.y=x2与y=t2显然是同一个函数;C.y=的定义域为{x|x≠0},y=的定义域为R,定义域不同,不是同一个函数;D.y=·的定义域为[1,+∞),y=的定义域为(-∞,-1]∪[1,+∞),定义域不同,不是同一个函数.3.(2020·杭州高一检测)已知函数f(x)的定义域为(-1,1),则函数g(x)=f+f(x-2)的定义域为( )A.(0,2)B.(1,2)C.(2,3)D.(-1,1)【解析】选B.函数f(x)的定义域为(-1,1),则对于函数g(x)=f+f(x-2),应有解得1<x<2,故g(x)的定义域为(1,2).4.(2020·宜春高一检测)已知函数f(x)的定义域为A={1,2,3,4},值域为B={7,8,9},且对任意的x<y,恒有f(x)≤f(y),则满足条件的不同函数共有________个.【解析】如图,满足条件的函数共有3个.答案:35.(2020·同仁高一检测)已知f(x)=(x∈R,x≠-2),g(x)=x2+1(x∈R).(1)求f(2),g(2)的值.(2)求f(g(3))的值.(3)作出f(x),g(x)的图象,并求函数的值域.【解析】(1)f(2)==,g(2)=22+1=5.(2)f(g(3))=f(32+1)=f(10)==.(3)作出图象如图,则f(x)的值域为(-∞,0)∪(0,+∞),g(x)的值域为[1,+∞). 【补偿训练】已知f(x)=(x∈R,x≠2),g(x)=x+4(x∈R).(1)求f(1),g(1)的值.(2)求f(g(x)).【解析】(1)f(1)==1,g(1)=1+4=5.(2)f(g(x))=f(x+4)===-(x∈R,且x≠-2).提升训练一、选择题(每小题5分,共20分)1.若f(x)=2x-1,则f(f(x))= ( )A.2x-1B.4x-2C.4x-3D.2x-3【解析】选C.因为f(x)=2x-1,所以f(f(x))=2f(x)-1=2(2x-1)-1=4x-3.2.若函数y=f(x)的定义域为{x|0<x<1},则函数y=f(|2x-3|)的定义域为( )A.(0,1)B.(1,2)C.∪D.(1,3)【解析】选C.函数y=f(x)的定义域为{x|0<x<1},则对于函数y=f(|2x-3|),应有0<|2x-3|<1,即-1<2x-3<1,且2x-3≠0,解得1<x<2,且x≠.3.函数f(x)对于任意实数x均满足f(x+2)=-f(x),若f(1)=-5,则f(f(9))=( ) A.2 B.5C.-5D.-【解析】选B.因为f(x+2)=-f(x),所以f(x+4)=f(x),所以f(f(9))=f(f(1))=f(-5),因为f(x)=-f(x+2),所以f(-5)=-f(-3)=f(-1)=-f(1)=5.4.(多选题)(2020·济南高一检测)下列各组函数是同一个函数的是( )A.f(x)=x2-2x-1与g(s)=s2-2s-1B.f(x)=与g(x)=xC.f(x)=与g(x)=D.f(x)=x与g(x)=【解析】选AC.对于A,f(x)=x2-2x-1的定义域为R,g(s)=s2-2s-1的定义域为R,定义域相同,对应关系也相同,是同一个函数;对于B,f(x)==-x的定义域为{x|x≤0},g(x)=x的定义域为{x|x≤0},对应关系不同,不是同一个函数;对于C,f(x)==1的定义域为{x|x≠0},g(x)==1的定义域为{x|x≠0},定义域相同,对应关系也相同,是同一个函数;对于D,f(x)=x的定义域为R,g(x)==|x|的定义域为R,对应关系不同,不是同一个函数.二、填空题(每小题5分,共10分)5.已知y=f(x+1)的定义域是[-2,3],则函数y=f(x)的定义域为________,y=f(2x)+的定义域为________.【解析】因为y=f(x+1)的定义域是[-2,3],所以-2≤x≤3,则-1≤x+1≤4,即函数f(x)的定义域为[-1,4].由得得-<x≤2,即函数y=f(2x)+的定义域为.答案:[-1,4]6.一个变量y随另一变量x变化.对应关系是“2倍加1”:(1)填表.x … 1 2 3 4 …y ……(2)根据表格填空:x=2α时,y=________.(3)写出解析式:y=________.【解析】因为变量y随另一变量x变化,对应关系是“2倍加1”:(1)完整的表格如表所示:x … 1 2 3 4 …y … 3 5 7 9 …(2)根据表格填空:x=2α时,y=2×2α+1=4α+1.(3)函数的解析式:y=2x+1.答案:(1)3 5 7 9 (2)4α+1 (3)2x+1三、解答题7.(10分)已知函数f(x)=+的定义域为集合A,B={x|x<a}.(1)求集合A;(2)若A⊆B,求a的取值范围;(3)若全集U={x|x≤4},a=-1,求U A及A∩(UB).【解析】(1)使有意义的实数x的集合是{x|x≤3},使有意义的实数x的集合是{x|x>-2}.所以,这个函数的定义域是{x|x≤3}∩{x|x>-2}={x|-2<x≤3}.即A={x|-2<x≤3}.(2)因为A={x|-2<x≤3},B={x|x<a}且A⊆B,所以a>3.即a的取值范围为(3,+∞).(3)因为U={x|x≤4},A={x|-2<x≤3},所以UA=(-∞,-2]∪(3,4].因为a=-1,所以B={x|x<-1},所以UB=[-1,4],所以A∩(UB)=[-1,3].3函数的图象基础练习1.(2020·朝阳高一检测)图中,能表示函数y=f(x)的图象的是( )【解析】选D.根据题意,对于A,B两图,可以找到一个x与两个y对应的情形;对于C图,当x=0时,有两个y值对应;对于D图,每个x都有唯一的y值对应.因此,D图可以表示函数y=f(x).2.已知函数f(x)=x-,且此函数图象过点(5,4),则实数m的值为( )A.3B.4C.5D.6【解析】选C.将点(5,4)代入f(x)=x-,得m=5.3.将反比例函数y=(k为非零常数)的图象向左平移1个单位,再向下平移2个单位,所得的图象过点(-3,1),则k=________.【解析】将反比例函数y=(k为非零常数)的图象向左平移1个单位,再向下平移2个单位,平移后的函数为y=-2,根据所得的图象过点(-3,1),则-2=1,所以k=-6.答案:-64.若函数y=f(x)的定义域为{x|-3≤x≤8且x≠5},值域为{y|-1≤y≤2且y≠0},则y=f(x)的图象可能是________(填序号).【解析】①中函数的值域为{y|-1≤y<2},不满足条件,③中图象出现了一个x对多个y的情况,不满足函数的定义.只有②符合条件.答案:②5.作出下列函数的图象.(1)y=(-2≤x≤2,且x≠0);(2)y=x2-2x(x∈[0,3)).【解析】(1)描点作出图象,如图所示.(2)因为x∈[0,3),所以这个函数的图象是抛物线y=x2-2x在0≤x<3之间的一段弧,描点作出图象,如图所示.提升训练一、选择题(每小题5分,共20分)1.已知函数y=ax2+b的图象如图所示,则a和b的值分别为( )A.0,-1B.1,-1C.1,0D.-1,1【解析】选B.由图象可知,当x=1时,y=0;当x=0时,y=-1,即解得2.如图所示,函数y=x+的图象是 ( )【解析】选C.对于y=x+,当x>0时,y=x+1,当x<0时,y=x-1,即y=故图象为C.3.函数y=-x2+2x与函数y=1(x∈R)的图象的公共点个数是( )A.0B.1C.2D.3【解析】选B.在同一坐标系里画出两函数的图象(图略)可知有一个交点.4.(多选题)如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论,其中正确的是( )A.b2>4acB.2a-b=1C.a-b+c=0D.5a<b【解析】选AD.因为图象与x轴交于两点,所以b2-4ac>0,即b2>4ac,A正确.对称轴为x=-1,-=-1,2a-b=0,B错误.结合图象,当x=-1时,y>0,即a-b+c>0,C错误.由对称轴为x=-=-1知,b=2a.又函数图象开口向下,所以a<0,所以5a<2a,即5a<b,D正确.二、填空题(每小题5分,共10分)5.函数y=-3x2+bx+c的图象是由函数y=-3x2+6x+1的图象向上平移3个单位长度,再向左平移2个单位长度得到的,则b=________,c=________.【解析】y=-3x2+6x+1=-3(x-1)2+4向上平移3个单位,得y=-3(x-1)2+7,再向左平移2个单位,得y=-3(x-1+2)2+7=-3x2-6x+4=-3x2+bx+c,比较系数得b=-6,c=4.答案:-6 4【补偿训练】如图所示某购物中心食品柜在4月份的营业情况统计图象,根据图象回答下列问题:(1)在这个月中,日最低营业额是在4月________日,达到________万元.(2)这个月中最高营业额是在4月________日,达到________万元.【解析】(1)由图象可知当日期在9日时,日营业额最小,此时为2万元.(2)由图象可知当日期在21日时,日营业额最大,此时为6万元.答案:(1)9 2 (2)21 66.已知二次函数f(x)=x2+x+a(a>0),若f(m)<0,则f(m+1)与0的大小关系是________.【解析】因为二次函数f(x)=x2+x+a(a>0)的对称轴是x=-,且图象与y轴正半轴相交,所以由图象可知f(x)<0的解集的区间长度小于1,故若f(m)<0,则必有f(m+1)>0.答案:f(m+1)>0三、解答题7.(10分)函数y=f(x)的图象如图所示.(1)比较f,f,f的大小;(2)若-1<x1<x2<2,试比较f与f的大小.【解析】(1)根据函数的图象,容易发现,f<f<f.(2)根据函数的图象,容易发现若-1<x1<x2<2,则f>f.4函数的表示方法基础练习1.已知一次函数的图象过点(1,0)和(0,1),则此一次函数的解析式为( )A.f(x)=-xB.f(x)=x-1C.f(x)=x+1D.f(x)=-x+1【解析】选D.设f(x)=ax+b(a≠0),则有所以a=-1,b=1,所以f(x)=-x+1.2.已知g(x)=1-2x,f(g(x))=(x≠0),则f= ( )A.15B.1C.3D.30【解析】选A.令g(x)=,得1-2x=,解得x=.所以f=f===15.3.一次函数g(x)满足g(g(x))=9x+8,则g(x)的解析式是( )A.g(x)=9x+8B.g(x)=3x-2C.g(x)=-3x-4或g(x)=3x+2D.g(x)=3x+8【解析】选C.因为g(x)是一次函数,所以设g(x)=kx+b(k≠0),所以g(g(x))=k(kx+b)+b,又因为g(g(x))=9x+8,所以解得:或所以g(x)=3x+2或g(x)=-3x-4.【光速解题】逐一代入验证是否满足g[g(x)]=9x+8.4.(2020·南京高一检测)已知f(x)=2x+1,g(x+1)=f(x),则g(x)=__________. 【解析】依题意,g(x+1)=2x+1=2(x+1)-1,所以g(x)=2x-1.答案:2x-1【补偿训练】已知f(x+1)=x2,则f(x)=________.【解析】由f(x+1)=x2,得到f(x+1)=(x+1-1)2,故f(x)=(x-1)2.答案:(x-1)25.已知二次函数f(x)满足f(x+1)-f(x)=2x,f(0)=1.(1)求f(x)的解析式.(2)求y=f(x)在[-1,1]上的最大值.【解析】(1)设f(x)=ax2+bx+c(a≠0),因为f(x+1)-f(x)=2x,所以a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x,即解得a=1,b=-1,又由f(0)=1,得c=1,所以f(x)=x2-x+1.(2)由(1)知,函数f(x)=x2-x+1的图象开口方向朝上,以x=为对称轴的抛物线,故在区间[-1,1]上,当x=-1时,函数取最大值f(-1)=3.【补偿训练】设二次函数f(x)满足f(x-2)=f(-x-2),且f(x)的图象与y轴交点的纵坐标为1,被x轴截得的线段长为2,求f(x)的解析式.【解析】设f(x)=ax2+bx+c(a≠0).由f(x-2)=f(-x-2)得4a-b=0,①又因为|x1-x2|==2,所以b2-4ac=8a2,②又由已知得c=1.③由①②③解得b=2,a=,c=1,所以f(x)=x2+2x+1.提升训练一、选择题(每小题5分,共20分)1.已知f=2x+3,则f(6)的值为( )A.15B.7C.31D.17【解析】选C.令-1=6,则x=14,则f(6)=2×14+3=31.2.若f(x)对于任意实数x恒有3f(x)-2f(-x)=5x+1,则f(x)= ( )A.x+1B.x-1C.2x+1D.3x+3【解析】选A.因为3f(x)-2f(-x)=5x+1,所以3f(-x)-2f(x)=-5x+1,解得f(x)=x+1.3.下表表示y是x的函数,则函数的值域是( )x 0<x<5 5≤x<10 10≤x<15 15≤x≤20y 2 3 4 5A.[2,5]B.{2,3,4,5}C.(0,20]D.N*【解析】选B.由表格可知,y的值为2,3,4,5.故函数的值域为{2,3,4,5}.4.(多选题)(2020 ·宿迁高一检测)已知f(2x-1)=4x2,则下列结论正确的是( )A.f(3)=9B.f(-3)=4C.f(x)=x2D.f(x)=(x+1)2【解析】选BD.f(2x-1)=(2x-1)2+2(2x-1)+1,故f(x)=x2+2x+1=(x+1)2,故选项C错误,选项D正确;f(3)=16,f(-3)=4,故选项A错误,选项B正确.二、填空题(每小题5分,共10分)5.(2020·淮安高一检测)已知f(+2)=x+4,则f(x)的解析式为____,f=______.【解析】令t=+2,则x=(t-2)2且t≥2,因为f(+2)=x+4,所以f(t)=t2-4,则f(x)=x2-4(x≥2),f=-.答案:f(x)=x2-4(x≥2) -6.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次试验的数据.根据该函数模型和试验数据,可以得到最佳加工时间为________分钟.【解析】由题意知,函数关系p=at2+bt+c(a,b,c是常数)经过点(3,0.7),(4,0.8),(5,0.5),所以解得a=-0.2,b=1.5,c=-2,所以p=-0.2t2+1.5t-2=-0.2(t-3.75)2+0.812 5,所以得到最佳加工时间为3.75分钟.答案:3.75三、解答题7.(10分)在未实行大规模绿化造林之前,我国是世界上受荒漠化危害最严重的国家之一,如图1表示我国土地沙化总面积在1950-2000年的变化情况,由图1中的相关信息,试将上述有关年份中,我国从1950-1970、1970-1990、1990-2000年的平均土地沙化面积在图2中表示出来.【解析】由题图1可知:1950-1970:土地沙化面积增加了3.2(万平方千米), 年平均沙化面积为:0.16(万平方千米)=16(百平方千米)1970-1990:年平均沙化面积为:0.21(万平方千米)=21(百平方千米)1990-2000:年平均沙化面积为:0.25(万平方千米)=25(百平方千米)如图:5分段函数基础练习1.已知函数f(x)=若f(x)=5,则x的值是 ( )A.-2B.2或-C.2或-2D.2或-2或-【解析】选A.由题意知,当x≤0时,f(x)=x2+1=5,得x=-2(x=2舍去);当x>0时,f(x)=-2x=5,得x=-,舍去.【误区警示】本题容易出现忽视各段自变量的取值对x值的限制,出现错解.2.函数f(x)=x2-2|x|的图象是( )【解析】选C.f(x)=分段画出.3.已知f(x)=则不等式xf(x)+x≤2的解集是( )A.{x|x≤1}B.{x|x≤2}C.{x|0≤x≤1}D.{x|x<0}【解析】选A.当x≥0时,f(x)=1,xf(x)+x≤2⇔x≤1,所以0≤x≤1;当x<0时,f(x)=0,xf(x)+x≤2⇔x≤2,所以x<0.综上,x≤1.4.(2020·西城高一检测)因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况的是________(写出所有正确的图标序号).【解析】图①③所反映的是公司会挣钱,而图②公司会亏本;所以反映了这种物资每份价格(单位:万元)的可能变化情况的是①③.答案:①③5.已知函数f(x)=(1)画出函数f(x)的简图(不必列表).(2)求f(f(3))的值.(3)当-4≤x<3时,求f(x)取值的集合.【解析】(1)由分段函数可知,函数f(x)的简图为:(2)因为f(3)=4-32=4-9=-5,所以f(f(3))=f(-5)=1-2×(-5)=1+10=11.(3)当-4≤x<0时,1<f(x)≤9;当x=0时,f(0)=2;当0<x<3时,-5<f(x)<4,综上f(x)取值的集合为(-5,9].提升训练一、选择题(每小题5分,共20分)1.(2020·武汉高一检测)AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地3月1日到12日AQI指数值的统计数据,图中点A表示3月1日的AQI指数值为201.则下列叙述不正确的是( )A.这12天中有6天空气质量为“优良”B.这12天中空气质量最好的是3月9日C.这12天的AQI指数值的中位数是90.5D.从3月4日到9日,空气质量越来越好【解析】选C.根据图象:有6天AQI指数小于100,所以这12天中有6天空气质量为“优良”,所以A叙述正确;这12天中,AQI指数的最小值是3月9日的67,所以12天中空气质量最好的是3月9日,所以B叙述正确;由图象知,AQI指数值的中位数是=99.5,所以C叙述错误;通过图象可以看出,从3月4日到9日,AQI 的值逐渐减小,即空气质量越来越好,所以D叙述正确.2.已知f(x)=g(x)=3-2x,则f(g(2))= ( )A.-3B.-2C.3D.-1【解析】选 C.因为g(x)=3-2x,所以g(2)=3-2×2=-1<0,所以f(g(2))=f(-1)=-1+4=3.3.已知f(x)=则f(x)的图象大致为( )【解析】选A.由f(2)=-<0,排除选项B;f=-2+<0,排除选项D;函数在x=1处是连续的,排除C.4.(多选题)已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t和t1,下列判断中一定正确的是( )A.在t1时刻,甲车的速度大于乙车的速度B.t时刻后,甲车的速度小于乙车的速度C.在t时刻,两车的位置相同D.在t时刻,甲车在乙车前面【解析】BD.由图可知,当时间为t1时,甲车的速度小于乙车的速度;t时刻之前,甲车的速度一直大于乙车,时间相同的情况下,甲车行驶路程大于乙车行驶路程,故t时刻甲车在乙车前面;t时刻后,甲车的速度小于乙车的速度.二、填空题(每小题5分,共10分)5.(2020·徐州高一检测)若函数f(x)=的值域为R,则实数a的取值范围是__________.【解析】当x≤1时,f(x)≤2+a;当x>1时,f(x)=(x-a)2+1-a2,所以①a>1时,f(x)≥1-a2,由于f(x)的值域为R,所以2+a≥1-a2,解得a∈R,所以a>1;②a≤1时,f(x)>(1-a)2+1-a2=2-2a,由于f(x)的值域为R,所以2+a≥2-2a,解得a≥0,所以0≤a≤1,综上,实数a的取值范围是[0,+∞).答案:[0,+∞)【补偿训练】若函数f(x)=则f(-3)=__________________.【解析】f(-3)=f(-3+2)=f(-1)=f(-1+2)=f(1)=f(1+2)=f(3)=2×3=6.答案:66.已知函数f(x)=则f(1)=________,若f(f(0))=a,则实数a=________.【解析】依题意知f(1)=3+2=5;f(0)=3×0+2=2,则f(f(0))=f(2)=22-2a=a,求得a=.答案:5三、解答题7.(10分)已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.(1)在平面直角坐标系里作出f(x),g(x)的图象.(2)∀x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).(3)求满足f(x)>g(x)的x的取值范围.【解析】(1)f(x)=g(x)=则对应的图象如图:(2)min(x)图象如图:解析式为min(x)=(3)若f(x)>g(x),则由图象知在A点左侧,B点右侧满足条件.此时对应的x满足x>0或x<-2,即不等式f(x)>g(x)的解集为(-∞,-2)∪(0,+∞).6.函数的单调性基础练习1.函数f(x)=在R上( )A.是减函数B.是增函数C.先减后增D.先增后减【解析】选B.画出该分段函数的图象,由图象知,该函数在R上是增函数.【补偿训练】函数f(x)=在( )A.(-∞,1)∪(1,+∞)上是增函数B.(-∞,1)∪(1,+∞)上是减函数C.(-∞,1)和(1,+∞)上是增函数D.(-∞,1)和(1,+∞)上是减函数【解析】选C.f(x)的定义域为{x|x≠1}.f(x)==-1=-1,因为函数y=-在(-∞,0)和(0,+∞)上是增函数,由平移关系得,f(x)在(-∞,1)和(1,+∞)上是增函数.2.函数y=x2-6x+10在区间(2,4)上( )A.是增函数B.是减函数C.先减后增D.先增后减【解析】选C.函数y=x2-6x+10图象的对称轴为直线x=3,此函数在区间(2,3)上是减函数,在区间(3,4)上是增函数.3.函数y=的减区间是( )A.(-∞,1),(1,+∞)B.(-∞,1)∪(1,+∞)C.{x∈R|x≠1}D.R【解析】选A.单调区间不能写成单调集合,也不能超出定义域,故C,D不对,B表达不当.4.(2020·海淀高一检测)下列函数中,在区间(1,+∞)上是增函数的是( )A.y=-3x-1B.y=C.y=x2-4x+5D.y=|x-1|+2【解析】选D.由一次函数的性质可知,y=-3x-1在区间(1,+∞)上是减函数,故A错误;由反比例函数的性质可知,y=在区间(1,+∞)上是减函数,故B错误,由二次函数的性质可知,y=x2-4x+5在(-∞,2)上是减函数,在(2,+∞)上是增函数,故C错误;由一次函数的性质及图象的变换可知,y=|x-1|+2在(1,+∞)上是增函数.5.(2020·淮安高一检测)已知函数f(x)=x|x-4|,则不等式f(2x)≤f(2)的解集为________.【解析】因为f(x)=x|x-4|,所以由f(2x)≤f(2)得,2x|2x-4|≤4,所以x|x-2|≤1,所以或,解得x≤+1,所以f(2x)≤f(2)的解集为{x|x≤+1}.答案:{x|x≤+1}6.已知函数f(x)=,证明函数在(-2,+∞)上是增函数.【证明】设x1,x2是(-2,+∞)上的任意两个值,且x1>x2>-2,则f(x1)-f(x2)=-=,因为x1>x2>-2,所以x1-x2>0,x1+2>0,x2+2>0,所以>0,所以f(x1)>f(x2),所以f(x)在(-2,+∞)上是增函数.提升训练一、单选题(每小题5分,共20分)1.若定义在R上的函数f(x)对任意两个不相等的实数a,b,总有>0成立,则必有 ( )A.f(x)在R上是增函数B.f(x)在R上是减函数C.函数f(x)先增后减D.函数f(x)先减后增【解析】选A.由>0知f(a)-f(b)与a-b同号,即当a<b时,f(a)<f(b),或当a>b时,f(a)>f(b),所以f(x)在R上是增函数.2.设函数f(x)是(-∞,+∞)上的减函数,则( )A.f(a)>f(2a)B.f(a2)<f(a)C.f(a2+a)<f(a)D.f(a2+1)<f(a)【解析】选D.对A,B,C三个选项,令a=0就都排除了,对D项,由a2+1-a= +>0,得a2+1>a,从而f(a2+1)<f(a),故D正确.3.已知四个函数的图象如图所示,其中在定义域内具有单调性的函数是( )【解析】选B.已知函数的图象判断其在定义域内的单调性,应从它的图象是上升的还是下降的来考虑.根据函数单调性的定义可知选项B中的函数在定义域内为增函数.【补偿训练】下列函数y=f(x)的图象中,满足f>f(3)>f(2)的只可能是( )【解析】选D.因为f>f(3)>f(2),所以函数y=f(x)有增有减,排除A,B.在C中,f<f(0),f(3)>f(0),即f<f(3),排除C.在D中,由图象知,D正确.4.(2020·常州高一检测)若f(x)=是R上的单调函数,则实数a 的取值范围是( )A. B.C. D.【解析】选D.函数f(x)=-x+3a在(-∞,1)上是减函数,又f(x)=是R上的单调函数,所以f(x)=在[1,+∞)上是减函数,即a>0,并且≤-1+3a,即a≥.综上所述,a的取值范围为.【误区警示】解答本题时易只考虑两段上的单调性,忽视分界点处函数值之间的大小关系或者考虑到了函数值之间的大小关系,但是忽视了取等号的情况而导致结果错误.二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)5.下列四个函数中,在(-∞,0]上是减函数的是( )A.f(x)=x2-2xB.f(x)=2x2C.f(x)=x+1D.f(x)=【解析】选AB.在A中,f(x)=x2-2x的减区间为(-∞,1],故A正确;在B中,f(x)=2x2的减区间为(-∞,0],故B正确;在C中,f(x)=x+1在R上是增函数,故C错误;在D中,f(x)=中,x≠0,故D错误.6.设函数f(x)在R上为增函数,则下列结论不一定正确的是 ( )A.y=在R上为减函数B.y=|f(x)|在R上为增函数C.y=-在R上为增函数D.y=-f(x)在R上为减函数【解析】选ABC.根据题意,依次分析选项:对于A,若f(x)=x,则y==,在R上不是减函数,A错误;对于B,若f(x)=x,则y=|f(x)|=|x|,在R上不是增函数,B错误;对于C,若f(x)=x,则y=-=-,在R上不是增函数,C错误;对于D,函数f(x)在R上为增函数,则对于任意的x1,x2∈R,设x1<x2,必有f(x1)<f(x2),对于y=-f(x),则有y1-y2=[-f(x1)]-[-f(x2)]=f(x2)-f(x1)>0,则y=-f(x)在R上为减函数,D正确.三、填空题(每小题5分,共10分)7.(2020·南京高一检测)定义区间[a,b]的长度为b-a,已知f(x)=2x+m,x∈[0,m],值域为[a,b],若区间[a,b]的长度比区间[0,m]的长度大3,则m=__________. 【解析】因为f(x)=2x+m在[0,m]上是增函数,所以m≤f(x)≤3m,由题意可得,a=m,b=3m,区间长度b-a=2m,所以2m=m+3,所以m=3.答案:38.(2020·南通高一检测)设函数f(x)=|x2-1|的定义域和值域都是[a,b](a<b),则a+b=______.【解析】作出f(x)的图象如图:则函数f(x)的值域为[0,+∞),则必有0≤a<b,①若b≤1,则f(x)在[a,b]上是减函数,则即两式作差得b2-a2=b-a,即b+a=1,由1-a2=b=1-a,得1+a=1,得a=0,b=1,此时满足条件,②若0≤a≤1<b,此时函数的最小值为f(1)=0,即值域为[0,b],此时a=0,f(b)=b2-1=b,得b2-b-1=0,解得b=(负值舍去),此时a+b=,③若1≤a<b,此时函数f(x)=x2-1为增函数,则满足即a,b是方程f(x)=x的两个根,即x2-x-1=0, 则a+b=1,与a+b>1矛盾.综上a+b=1或.答案:1或四、解答题(每小题10分,共20分)9.已知函数f(x)=(1)在图中画出函数f(x)的大致图象.(2)写出函数f(x)的递减区间.【解析】(1)函数f(x)的大致图象如图所示.(2)由函数f(x)的图象得出,函数的减区间为[2,4].10.(2020·辽阳高一检测)已知函数f(x)=mx+,点A(1,5),B(2,4)是f(x)图象上的两点.(1)求m,n 的值.(2)用定义法证明:f(x)在[2,+∞)上是增函数. 【解析】(1)由题意可得,解得(2)由(1)可得,f(x)=x+,设x 1,x 2是[2,+∞)上任意两个值,且x 1<x 2, 则f(x 1)-f(x 2)=x 1-x 2+-=x 1-x 2+=,因为2≤x 1<x 2, 所以<0,即f(x 1)<f(x 2),所以f(x)在[2,+∞)上是增函数.创新练习1.已知f(x)是定义在(-∞,0]上的增函数,且f(-2)=3,则满足f(2x-3)<3的x 的取值范围是________.【解析】由题意知,f(2x-3)<f(-2),因为f(x)在(-∞,0]上是增函数,则2x-3<-2,解得x<.答案:x<2.已知函数f(x)=.(1)判断并证明函数f(x)在(-2,+∞)上的单调性.(2)若函数f(x)的定义域为(-2,2),且满足f(-2m+3)>f(m2),求m的取值范围. 【解析】(1)f(x)==3+,f(x)在(-2,+∞)上是减函数,证明如下:设x1,x2是(-2,+∞)上的任意两个值,且x1>x2,则f(x1)-f(x2)=-=,因为x1>x2>-2,所以x1+2>0,x2+2>0,x2-x1<0,所以f(x1)<f(x2),所以f(x)在(-2,+∞)上是减函数.(2)由(1)可知,当x∈(-2,2)时,函数f(x)是减函数,所以由f(-2m+3)>f(m2)得,解得1<m<,所以m的取值范围为(1,).【补偿训练】已知函数f(x)=-x+,其定义域为(0,+∞).(1)判断函数f(x)在(0,+∞)上的单调性,并用定义证明.(2)若f(x+1)<f(2x),求x的取值范围.【解析】(1)是减函数,证明如下:设0<x1<x2,则f(x 1)-f(x 2)=x 2-x 1+-=x 2-x 1+=(x 2-x 1),因为0<x 1<x 2, 所以(x 2-x 1)>0,所以f(x 1)>f(x 2),函数f(x)在(0,+∞)上是减函数.(2)因为f(x+1)<f(2x), f(x)在(0,+∞)上是减函数, 所以x+1>2x>0,解得,0<x<1.7函数的最大值、最小值基础练习1.函数y=x 2+2x-1在[0,3]上的最小值为 ( ) A.0B.-4C.-1D.-2【解析】选C.因为y=x 2+2x-1=(x+1)2-2,其图象的对称轴为直线x=-1, 所以函数y=x 2+2x-1在[0,3]上是增函数, 所以当x=0时,此函数取得最小值,最小值为-1. 2.函数f(x)=的最大值是 ( )A. B. C. D.【解析】选D.令t=1-x(1-x)=+≥,所以0<f(x)≤,即f(x)的最大值为.3.(2020·海淀高一检测)设函数f(x)=4x+-1(x<0),则f(x) ( )A.有最大值3B.有最小值3C.有最小值-5D.有最大值-5【解析】选D.当x<0时,f(x)=4x+-1=-(-4x)+-1≤-2-1=-5.当且仅当-4x=-,即x=-时,上式取等号.所以f(x)有最大值为-5.4.(2020·成都高一检测)函数f(x)=2x-的最小值为________.【解析】因为f(x)=2-2=2-,所以f(x)min=f=-.答案:-5.对于函数f(x),在使f(x)≥M恒成立的所有实数M中,我们把M的最大值Mmax叫做函数f(x)的下确界,则对于a∈R,f(a)=a2-4a+6的下确界为________.【解析】f(a)=a2-4a+6,f(a)≥M,即f(a)min≥M.而f(a)=(a-2)2+2,所以f(a)min=f(2)=2.所以M≤2.所以Mmax=2.答案:26.(2020·温州高一检测)已知函数f(x)=x2+.求函数f(x)在区间[-3,-1]上的最值.【解析】设x1,x2是[-3,-1]上的任意两个值,且x1<x2,f(x1)-f(x2)=-=(x1-x2)(x1+x2)-,又由-3≤x1<x2≤-1,得x1-x2<0,-6<x1+x2<-2,4<(x1-1)(x2-1)<16,则有(x1+x2)-<0,则有f(x1)-f(x2)>0,故函数f(x)在区间[-3,-1]上是减函数,故f(x)max=f(-3)=4,f(x)min=f(-1)=-.提升训练一、单选题(每小题5分,共20分)1.函数y=x+的最值的情况为( )A.最小值为,无最大值B.最大值为,无最小值C.最小值为,最大值为2D.最大值为2,无最小值【解析】选A.因为y=x+在定义域,+∞上是增函数,所以函数最小值为,无最大值.2.(2020·连云港高一检测)已知a>,则函数f(x)=x2+|x-a|的最小值是( )A.a2+1B.a+C.a-D.a-【解析】选D.函数f(x)=x2+|x-a|=当x≥a>时,函数f(x)=x2+x-a的对称轴方程为x=-,函数在[a,+∞)上是增函数,其最小值为a2;当x<a时,f(x)=x2-x+a的对称轴方程为x=,当x=时函数求得最小值为a-.因为a2-=a2-a+=>0.所以a2>a-.所以函数f(x)=x2+|x-a|的最小值是a-.3.对任意x∈R,函数f(x)表示-x+3,x+,x2-4x+3中的最大者,则f(x)的最小值为( )A.2B.3C.4D.5【解析】选A.分别作出y=-x+3,y=x+,y=x2-4x+3的图象如图(阴影部分边界对应的曲线为ABCDE),则由图象可知函数f(x)在C处取得最小值,由得即f(x)的最小值为2.4.(2020·无锡高一检测)若关于x的不等式x2-mx+4>0在x∈[1,3]上有解,则实数m的取值范围为( )A.(-∞,5)B.(-∞,5]C.(-∞,4)D.(-∞,-4)∪(4,+∞)【解析】选A.关于x的不等式x2-mx+4>0在x∈[1,3]上有解,即m<x+在x∈[1,3]上能成立.设f(x)=x+,则f(x)在(0,2]上是减函数,在[2,+∞)上是增函数,故当x=2时,f(x)取得最小值4,又f(1)=5,f(3)=,故当x=1时,函数f(x)取得最大值.则实数m<5.二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)5.下列关于函数y=ax+1,x∈[0,2]的说法正确的是( )A.当a<0时,此函数的最大值为1,最小值为2a+1B.当a<0时,此函数的最大值为2a+1,最小值为1C.当a>0时,此函数的最大值为1,最小值为2a+1D.当a>0时,此函数的最大值为2a+1,最小值为1【解析】选AD.当a<0时,函数y=ax+1在区间[0,2]上是减函数,当x=0时,函数取得最大值为1;当x=2时,函数取得最小值为2a+1.当a>0时,函数y=ax+1在区间[0,2]上是增函数,当x=0时,函数取得最小值为1,当x=2时,函数取得最大值为2a+1.6.函数y=(x≠1)的定义域为[2,5),下列说法正确的是( )A.最小值为B.最大值为4C.无最大值D.无最小值【解析】选BD.函数y==1+在[2,5)上是减函数,即在x=2处取得最大值4,由于x=5取不到,则最小值取不到.三、填空题(每小题5分,共10分)7.二次函数y=ax2+4x+a的最大值是3,则a=________.【解析】根据题意,二次函数y=ax2+4x+a的最大值是3,则解得a=-1. 答案:-18.(2020·杭州高一检测)对于任意的实数x1,x2,min{x1,x2}表示x1,x2中较小的那个数,若f(x)=2-x2,g(x)=x,则集合{x|f(x)=g(x)}=________;min{f(x),g(x)}的最大值是________.【解析】由题作出函数f(x),g(x)的图象,令f(x)=g(x),即2-x2=x,解得x=-2或x=1,则集合{x|f(x)=g(x)}={-2,1},由题意及图象得min{f(x),g(x)}=由图象知,当x=1时,min{f(x),g(x)}最大,最大值是1.答案:{-2,1} 1四、解答题(每小题10分,共20分)9.(2020·常州高一检测)已知二次函数f(x)=ax2+bx+c(a>0),对称轴为直线x=2,且f(0)=1.(1)若函数f(x)的最小值为-1,求f(x)的解析式;(2)函数f(x)的最小值记为g(a),求函数H(a)=a·g(a)的最大值.【解析】(1)因为f(x)的对称轴为直线x=2,所以-=2,则b=-4a.又f(0)=1,所以c=1.所以f(x)=ax2-4ax+1=a(x-2)2+1-4a,因为a>0,所以当x=2时f(x)有最小值1-4a=-1,所以a=,所以f(x)=x2-2x+1.(2)由(1)知f(x)=ax2-4ax+1=a(x-2)2+1-4a.所以g(a)=f(2)=1-4a.所以H(a)=a(1-4a)=-4+,a∈(0,+∞),所以H(a)的最大值为.10.(2020·太原高一检测)已知函数f(x)=,g(x)=x-1.(1)求解不等式f(x)≥g(x).(2)若x>,求y=3f(x)+2g(x)的最小值.【解析】(1)当x>时,由f(x)≥g(x),得(2x-1)(x-1)≤3,解得<x≤2.当x<时,由f(x)≥g(x),得(2x-1)(x-1)≥3,解得x≤-.所以不等式f(x)≥g(x)的解集为x<x≤2或x≤-.。
苏教版高中数学必修一2.2函数的简单性质

9.已知 点 是定义域为 ∞ ∞ 的奇函数,满足 点
考点
.若 点 考 ,则 点
点
点
点
考( )
A. -2018
B. 0
C. 2
D. 50
【答案】 C
【考点】函数奇偶性的性质,奇偶函数图象的对称性
10.已知 y=f(x)是偶函数,而 y=f(x+1)是奇函数,且对任意 0≤x≤1,都有 f(x)≥0,f(x)是增函数,
则 a=f(2010),b=f( ),c=﹣f( )的大小关系是( )
A. b<c<a
B. c<b<a
【答案】A
【考点】奇偶性与单调性的综合
二、填空题(共 5 题;共 7 分)
C. a<c<b
D. a<b<c
11.若函数 点 考 ሻ
是奇函数,则 ሻ =( )
A. 2
B.
C. 3
D. 4
【答案】 B 【考点】函数奇偶性的判断 12.已知函数 f(x)=ax2+bx+3a+b 是偶函数,且其定义域为[a﹣1,2a],则( )
g'(x)=﹣4x3+4x 当 g'(x)>0 时,﹣1<x<0 或 x>1 当 g'(x)<0 时,x<﹣1 或 0<x<1 故函数 g(x)的增区间为:(﹣1,0)和(1,+∞) 减区间为:(﹣∞,﹣1)和(0,1)
【考点】函数的单调性及单调区间 18.已知定义在[﹣3,3]上的函数 y=f(x)是增函数.
∴
, ∴﹣3<x≤2.
∴不等式的解集为{x|﹣3<x≤2}.
3/5
【考点】奇偶性与单调性的综合
19.已知函数 f(x)=ax+ 的图象经过点 A(1,1),B(2,﹣1).
苏教版高中数学高一必修一第二章《函数性质》测试题

1. D
2. D(p: ,q: ,则 ,及 ,∴p是q的既非充分也非必要条件)
3. B4. D5. B
6. C(先证明 为奇函数)
7. B
8. A(当x=2时, ,由 为函数定义域,设 ,显然在( )上u递减,又 递增, 在( )上递减)
9. C10. C11. B
12. B( , , )
.
16. (由①得 即方程有解,上式恒成立;即 ,∴①为其 ,由② ,则①、②至少有一个为真命题,则 即……)
17.(1)
则
令
(2)
为奇函数
18.(1)由不动点定义有
代入x=1,有
,再代入x=-3,有
又a=1,∴b=3,∴a=1,b=3
(2)对于任意实数b, 总有两个不动点,即方程 总有两个相异的实根,即 的判别式 ,即 恒成立,
14.如果函数 是奇函数,则 ______
15.将函数 的图象向左平移一个单位后得到 的图象,再将 的图象绕原点旋转 后仍与 的图象本身重合,则a的值为________
16.设有两个命题:
①关于x的方程 有解;
② 是减函数
当①与②至少有一个真命题时,实数a的取值范围是____________
三.解答题
5.函数 的值域是()
A.(0,3]B.(0,1)C.[ )D.
6.若a>0,a≠1,F(x)为偶函数,则 的图象()
A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线y=x对称
7.如果函数 在区间( ]上是减函数,那么实数a的取值范围是()
A. B. C. D.
8.已知函数 当x=2时,y>0,则此函数的单调递减区间为()
A. B. C. D.
苏教版高中数学必修一函数的概念和图象同步练习(1)(7)

第一轮复习 第3讲 函数的概念训练题一、选择题:1.设集合}21|{≤≤=x x A ,}41|{≤≤=y y B ,则下述对应法则f 中,不能构成A 到B 的映射的是( )A .2:x y x f =→ B .23:-=→x y x f C .4:+-=→x y x fD .24:x y x f -=→2.若函数)23(x f -的定义域为[-1,2],则函数)(x f 的定义域是( ) A .]1,25[--B .[-1,2]C .[-1,5]D .]2,21[3,设函数⎩⎨⎧<≥-=)1(1)1(1)(x x x x f ,则)))2(((f f f =( )A .0B .1C .2D .24.下面各组函数中为相同函数的是( ) A .1)(,)1()(2-=-=x x g x x fB .11)(,1)(2-+=-=x x x g x x fC .22)1()(,)1()(-=-=x x g x x fD .21)(,21)(22+-=+-=x x x g x x x f5.函数])4,0[(422∈+--=x x x y 的值域是( ) A .[0,2]B .[1,2]C .[-2,2]D .[-2,2]6.函数)(x f y =有反函数)(1x f y -=,将)(x f y =的图象绕原点顺时针方向旋转90°后得到另一个函数的图象,则得到的这个函数是( ) A .)(1x fy -=B .)(1x fy --=C .)(1x fy -=-D .)(1x fy --=-二、填空题:7.有下述对应:①集合A=R ,B=Z ,对应法则是⎩⎨⎧<-≥=→)0(1)0(1:x x y x f ,其中A x ∈,B y ∈. ②集合A 和B 都是正整数集N *,对应法则是|1|:-=→x y x f ,其中A x ∈, B y ∈. ③集合},2|{},|{Z k k y y B Z x x A ∈==∈=,对应法则是x y x f 2:=→.④集合x x A |{=是三角形},}0|{>=y y B ,对应法则是x y x f =→:的面积. 则其中是集合A 到集合B 的映射的是 ,是集合A 到集合B 的一一映射的是8.已知定义在),0[+∞的函数⎩⎨⎧<≤≥+=)20()2(2)(2x x x x x f 若425)))(((=k f f f ,则实数=k 9.若点(4,3)既在函数b ax y ++=1的图象上,又在它的反函数的图象上,则函数的解析式=)(x f 10.关于反函数给出下述命题:①若)(x f 为奇函数,则)(x f 一定有反函数. ②函数)(x f 有反函数的充要条件是)(x f 是单调函数.③若)(x f 的反函数是)(x g ,则函数)(x g 一定有反函数,且它的反函数是)(x f ④设函数)(x f y =的反函数为)(1x f y -=,若点P (a ,b )在)(x f y =的图象上,则点),(a b Q 一定在)(1x fy -=的图象上.⑤若两个函数的图象关于直线x y =对称,则这两个函数一定互为反函数.则其中错误的命题是三、解答题:11.已知)(x f 是二次函数,且满足)(,2)]([24x f x x x f f 求-=.12.设函数41)(2-+=x x x f , (Ⅰ)若定义域限制为[0,3],求)(x f 的值域; (Ⅱ)若定义域限制为]1,[+a a 时,)(x f 的值域为]161,21[-,求a 的值.13.若函数12)(22+--+=x x ax x x f 的值域为[-2,2],求a 的值.14.已知b a a x bx x f ,(21)(++=是常数,2≠ab ),且k xf x f =)1()((常数), (1)求k 的值; (2)若a kf f 求,2))1((=、b 的值.15.如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x ,两圆的面积之和为S ,将S 表示为x 的函数,求函数)(x f S =的解析式及)(x f 的值域.参考答案与解析一、1.D (提示:作出各选择支中的函数图象). 2.C (提示:由523121≤-≤-⇒≤≤-x x ). 3.B (提示:由内到外求出).4.D (提示:考察每组中两个函数的对应法则与定义域).5.A (提示:40,4)2(422≤≤∴+--=+-=u x x x u ,然后推得). 6.B (提示:作一个示意图,如令x x f 2)(=).二、7.①、③、④;③.(提示:对照“映射”、“一一映射”的定义). 8.23(提示:由外到里,逐步求得k ). 9.(提示:将(4,3)与(3,4)分别代入原函数解析式,不必求出反函数). 10.①、②(提示:①错的原因是:奇函数不一定是单调函数;例如xy 1=它不是单调函数(∵它有两个单调区间),但它的定义域是一一对应的,有反函数,∴②错).三、解答题:11.设)0()(2≠++=a c bx ax x f ,)()()]([222c bx ax b c bx ax a x f f +++++=∴+c)()2()2(2222223243c bc ac x b abc x ab c a ab bx a x a +++++++++=242x x -=,1)(,101002220212222223-=∴⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=+-=++==∴x x f c b a c bc ac b abc ab c a ab b a a . 12.21)21()(2-+=x x f ,∴对称轴为21-=x , (Ⅰ)2103->≥≥x ,∴)(x f 的值域为)]3(),0([f f ,即]447,41[-;(Ⅱ)∴-=,21)]([min x f 对称轴]1,[21+∈-=a a x ,212321121-≤≤-⇒⎪⎪⎩⎪⎪⎨⎧-≥+-≤∴a a a ,∵区间]1,[+a a 的中点为210+=a x , (1)当211,2121-≤≤--≥+a a 即时,16141)1()1(,161)1()]([2max =-+++∴=+=a a a f x f , 49(4302748162-=-=⇒=++∴a a a a 不合); (2)当123,2121-<≤--<+a a 即时,161)()]([max ==a f x f ,41(45051616,1614122=-=⇒=-+∴=-+∴a a a a a a 不合); 综上,4543-=-=a a 或.13.12+-x x 的判别式恒小于零,∴函数的定义域为R ,∴原函数等价于0)2)(1(4)(,0)2()()1(22≥+--+=∆=+++--y y a y y x a y x y ,即0)8()42(322≤++--a y a y 的解集为[-2,2](其中包含y =1),2,221=-=∴y y 是方程0)8()42(322=++--a y a y 的根, 24207400222121=⇒⎪⎩⎪⎨⎧==>+-⇒⎪⎩⎪⎨⎧-=⋅=+>∆∴a a a a a y y y y . 14.(1)k axxb a x bx x f x f =++⋅++=221)1()( ,0)2()41()2(222=-+--++-⇒ak b x k k a b x ak b ,上式是关于x 的恒等式,04140412222222=--+⇒⎩⎨⎧=--+=∴k k a k a k k a b ak b 4110)1)(14(22==⇒=--⇒k k a k a k 或,若41,,212122=∴=⇒⋅==k ab a a b k a 不合得, (2)812222))1((,)2()(2)()2())((2222=++++++=∴++++++=a b a b a b f f a x b a b a x b x f f , 而b a a b 2412=⇒⨯=,代入上式得07922=++b b , 解得2,21;271=-=-=-=-=ab a b b b 此时时当或,不合,7,27-=-=∴a b .15.设另一个圆的半径为y ,则222=+++y y x x 2))(12(=++⇒y x22122-=+=+⇒y x ,])22([)()(2222x x y x x f S --+=+==∴ππ)]223()222(2[)]246()22(22[22-+--=-+--=x x x ππ, ∵当一个圆为正方形内切圆时半径最大,而另一圆半径最小, ∴函数的定义域为21223≤≤-x (注意定义域为闭区间), ),223(23)21()223();223(],21,223[222min -==--=∴-∈-f f Sπ )223(23max -=∴πS , ∴函数)(x f S =的值域为)]223(23),223([--ππ.。
苏教版高中数学必修一函数与方程同步练习(10)
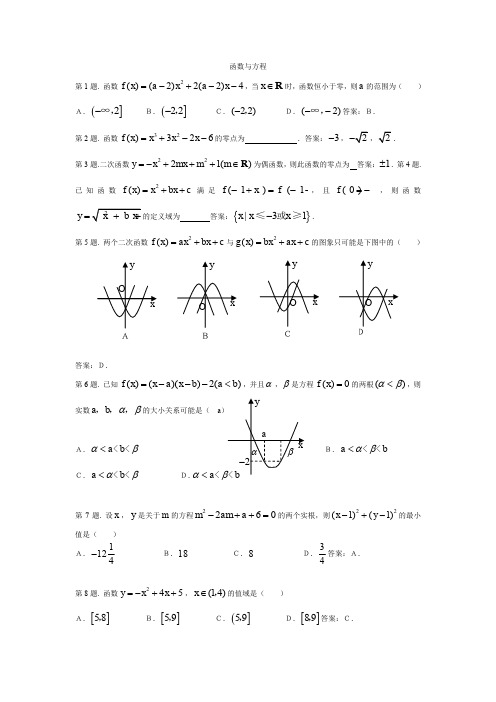
函数与方程第1题. 函数2()(2)2(2)4f x a x a x =-+--,当x ∈R 时,函数恒小于零,则a 的范围为()A.(]2-,∞ B.(]22-,C.(22)-, D.(2)--,∞答案:B.第2题. 函数32()326f x x x x =+--的零点为 .答案:3-,.第3题.二次函数2221()y x mx m m =-+++∈R 为偶函数,则此函数的零点为答案:1±.第4题.已知函数2()f x x bx c=++满足(1)(1f x f x-+=--,且(0)3f =-,则函数y c=的定义域为 答案:{}|31x x x -或≤≥.第5题. 两个二次函数2()f x ax bx c =++与2()g x bx ax c =++的图象只可能是下图中的()答案:D. 第6题. 已知()()()2()f x x a x b a b =---<,并且α,β是方程()0f x =的两根()αβ<,则实数ab αβ,,,的大小关系可能是( a A.a b αβ<<<B.a b αβ<<<C.a b αβ<<<D.a α<<第7题. 设x ,y 是关于m 的方程2260m am a -++=的两个实根,则22(1)(1)x y -+-的最小值是( ) A.1124-B.18C.8D.34答案:A.第8题. 函数245y x x =-++,(14)x ∈,的值域是()A.[]58,B.[]59,C.(]59,D.[]89,答案:C.ABCSt 02 3AB第9题. 如果函数2()f x x bx c =++对任意实数t 都有(2)(2)f t f t +=-,那么()A.(2)(1)(4)f f f <<B.(1)(2)(4)f f f <<C.(2)(4)f f <<D.(4)(2)(1)f f f <<答案:A.第10题. 已知函数2()f x ax bx c =++的图象如图所示,则b A.0b >B.0b <C.1b <-D.21b -<<-答案:C.第11题. 如果偶函数()f x 在[]04,上是增函数,那么()f π与(4)f -的关系是()A.()(4)f f π<- B.()(4)f f π>-C.()(4)f f π=--D.不能确定a第12题. 若函数2()2f x ax bx =++的两个零点是12-,13,则a b +的值为( )A.14B.14-C.10D.10- b第13题. 设函数y =R ,则k 的取值范围是()A.9k -≤或1k ≥ B.1k ≥C.91k -≤≤ D.01k <≤答案:B.第14题. 已知1x ,2x 是函数22(2)(35)y x k x k k =--+++(k 为实数)的两个零点,则2212x x +的最大值为( ) A.18B.19C.559D.不存 答案:A.第15题. 若函数2()21f x mx mx =-+有一个零点大于1,另一个零点小于1,则实数m的范围是 . 答案:0m <或1m >.第16题. 已知(11)x ∈-,时,2()02af x x ax =-+>恒成立,则a 的取值范围是答案:02a <≤. 第17题. 如果函数()f x 是定义在R 上的奇函数,在(10)-,上是增函数,且(2)()f x f x +=-,则下列关系式中正确的是( d )A.13((1)(32f f f <<B.31((1)(23f f f << C.31(()(1)23f f f << D.13(()(1)32f f f <<第18题. 在直角坐标系的第一象限内,AOB △是边长为2的等边三角形,设直线l :(02)x t t =≤≤截这个三角形所得位于此直线左侧的图形(阴影部分)的面积为()f t ,则函数()S f t =的图象只可能是()S答案:C.第19题. 如果关于x 的方程2350xx a -+=的一根大于2-但小于0,另一根大于1但小于3,那么实数a 的取值范围是 . 答案:120a -<<. 第20题. 已知一次函数()f x ax b =+与二次函数2()g x ax bx c =++满足a b c >>,且0()a b c a b c ++=∈R ,,.⑴求证:函数()y f x =与()y g x =的图象有两个不同的交点A ,B ;⑵设1A ,1B 是A ,B 两点在x 轴上的射影,求线段11A B 长的取值范围;⑶求证:当x ≤时,()()f x g x <恒成立.答案:⑴证明:由()f x ax b =+和2()g x ax bx c =++,得2()0ax a b x c b --+-=.它的2()4a b ac ∆=+-,又因为a b c >>,且0()a b c a b c ++=∈R ,,,则0a >,0c <,所以0∆>,因而函数()y f x =与()y g x =的图象有两个不同的交点A ,B ;⑵解:由12()/x x a b a +=-,12()/x x c b a =-,则1112A B x x =-=则21/2c a -<<.又因为a b c >>,且0()a b c a b c ++=∈R ,,,113(2A B ∈. ⑶证明:设2()()()()F x g x f x ax a b x c b =-=--+-的两根为1x ,2x 满足12x x <,则21x x -<()y f x =的对称轴为:02a b x a -=>,于是12a bx a--<122a b a bx a a--<<<,由此得:当x ≤时,12a b x x a -<<,又0a >,知()F x 在()2a ba --,∞上为单调递减函数,于是,1()()0F x F x <=,即当x ≤时,()()f x g x <恒成立.第21题. 对于任意定义在R 上的函数()f x ,若实数0x 满足00()f x x =,则称0x 是函数()f x 的一个不动点,若二次函数2()1f x x ax =-+没有不动点,则实数a的取值范围是 . 答案:(31)-,. 第22题. 已知函数5432()2288f x x x x x x =+----,求其零点,并求其非负值区间. 答案:解:分解因式2()(1)(2)(2)(2)f x x x x x =+-++,所以其零点是1-,2,2-.其非负值区间是[][)212--+,,∞. 第23题. 方程20x bx c ++=有两个不相等正根,则;有一正根,一负根,则 ;至少有一根为零,则 (填等价条件).答案:24000b c b c ⎧->⎪<⎨⎪>⎩;0c <;0c =.第24题. 设方程210xmx -+=的两个根为α,β,且01α<<,12β<<,则实数m 的取值范围是 . 答案:522m <<. 第25题. 关于x 的方程222320kx x k ---=的两实根,一个小于1,一个大于1,则实数k 的取值范围是 . 第26题. 已知函数2()(1)f x x a x a =-++⑴若()0f x <,则不等式()0f x <的解集是 ;⑵若()0f x =,则不等式()0f x <的解集是.答案:(1)a ,;(12),.第27题. 实数m 为何值时,函数2()(2)5f x mx m x m =+-+-的两个零点满足一个大于2,一个小于2?答案:解:由二次函数的图象可知:(2)0mf<,[]4(2)250m m m m +-⨯+-<∴,(79)0m m -<∴,907m <<∴. 第28题. 下列函数的自变量在什么范围内取值时,函数值大于零、小于零或等于零: ⑴2210y x x =--;⑵223y x x =--+.答案:解:⑴当(1(111)x ∈-++∞,,∞时,0y >;当(111)x ∈-时,0y<;当1x=-1x =+0y =第29题.求下列函数的定义域:a (1)y =(2)y =(3)y =答案:(1)(3][3)--+∞,,∞;(2)(4][1)--+∞,,∞;(3){|26}x x-剟.第30题. 求下列函数的图象与x 轴交点的坐标:(1)2()31f x x x =--;(2)2()382f x x x =-+-.答案:(1)0)0);(2)0)0).。
苏教版高中数学必修一函数的概念和图象同步练习(1)

2.1.1函数的概念和图象限时训练1.下列四种说法正确的一个是______________.⑴)(x f 表示的是含有x 的代数式 ⑵函数的值域也就是其定义中的数集B⑶函数是一种特殊的映射 ⑷映射是一种特殊的函数2.已知f 满足f(ab)=f(a)+ f(b),且f(2)=p ,f(3)=q ,那么f(72)=____________.3.下列各组函数中,表示同一函数的是______________.⑴x x y y ==,1 ⑵1,112-=+⨯-=x y x x y ⑶33,x y x y == ⑷2)(|,|x y x y == 4.已知函数23212---=x x x y 的定义域为_____________________. 5.设⎪⎩⎪⎨⎧<=>+=)0(,0)0(,)0(,1)(x x x x x f π,则=-)]}1([{f f f _____________.6.下列图中,画在同一坐标系中,函数bx ax y +=2与)0,0(≠≠+=b a b ax y 函数的图象只可能是 ( )7.设函数x y 111+=的定义域为M ,值域为N ,那么M =_________________,N =__________.8.已知二次函数)0()(2>++=a a x x x f ,若0)(<m f ,则)1(+m f 的值为__________.9.已知在x 克%a 的盐水中,加入y 克%b 的盐水,浓度变为%c ,将y 表示成x 的函数关系式______________________.10.若记号“*”表示的是2*b a b a +=,则用两边含有“*”和“+”的运算对于任意三个实数“a ,b ,c ”成立一个恒等式 .11.①.求函数|1||1|13-++-=x x x y 的定义域; ②求函数x x y 21-+=的值域; ③求函数132222+-+-=x x x x y 的值域.12.在同一坐标系中绘制函数x x y 22+=,||22x x y +=得图象.13.动点P 从边长为1的正方形ABCD 的顶点出发顺次经过B 、C 、D 再回到A ;设x 表示P 点的行程,y 表示PA 的长,求y 关于x 的函数解析式.14.已知函数)(x f ,)(x g 同时满足:)()()()()(y f x f y g x g y x g +=-;1)1(-=-f ,0)0(=f ,1)1(=f ,求)2(),1(),0(g g g 的值.参考答案1.⑴;2.3p +2q ;3.⑶;4.,1]2121,((-)--Y ∞;5.π+1;6.⑵; 7.(-∞,-1)(-1,+∞);8.正数; 9. x cb ac y --=;10. c b a c b a *+=+)()*(; 11.解:①.因为|1||1|-++x x 的函数值一定大于0,且1-x 无论取什么数三次方根一定有意义,故其值域为R ; ②.令t x =-21,0≥t ,)1(212t x -=,原式等于1)1(21)1(2122+--=+-t t t ,故1≤y 。
苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数测试卷(含答案)

苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数测试卷(满分150分,时间120分钟)班级姓名评价一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数f (x )2(3x +1)的定义域为()A.-13,+∞B.-∞,C.-13D.-13,12.设a =log 42.4,b =log 32.9,c =log 32.4,则a ,b ,c 的大小关系为()A.b >c >aB.b >a >cC.c >b >aD.a >c >b3.已知0<m <n <1,则指数函数①y =m x 和②y =n x 的图象为()A.B. C. D.4.已知函数f (x )=log 3(x -1),若f (a )=2,则实数a 的值为()A.3B.8C.9D.105.函数y 2+2的增区间为()A.(-∞,0)B.(-∞,-1]C.[-1,+∞)D.[-2,+∞)6.不论a 为何值,函数y =(a -1)2x-2恒过一定点,则这个定点为()A.1,B.1C.-1,D.-17.已知函数f (x )=log a x (0<a <1),则函数y =f (|x |+1)的图象大致是()A. B. C. D.8.春末夏初,南京玄武湖公园荷花池中的荷花枝繁叶茂,已知每天新长出的荷叶覆盖水面的面积是前一天的两倍,若荷叶20天可以完全长满荷花池水面,则当荷叶刚好覆盖水面面积18时,荷叶已生长了()A.4天B.15天C.17天D.18天二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.下列函数中定义域和值域相同的是()A.y = 23B.y = 15C.y =-xD.y =3x10.已知函数f (x )=log 3( -2), >2,3 -1, ≤2,则下列各式正确的是()A.f (5)=1B.f (f (5))=1C.f (3)=9D.f (f (3))=1311.设函数f (x )=(3-2 ) -1, ≤1,, >1,其中a >0且a ≠1,下列关于函数f (x )的说法正确的是()A.若a =2,则f (log 23)=3B.若f (x )在R 上是增函数,则1<a <32C.若f (0)=-1,则a =32D.函数f (x )为R 上的奇函数12.已知函数f (x )=lo g 12x ,下列四个命题正确的是()A.函数f (|x |)为偶函数B.若f (a )=|f (b )|,其中a >0,b >0,a ≠b ,则ab =1C.函数f (-x 2+2x )在(1,3)上为增函数D.若0<a <1,则|f (1+a )|<|f (1-a )|三、填空题:本题共4小题,每小题5分,共20分.其中第15题第一个空2分,第二个空3分.13.若幂函数y =f (x 2,则f .14.设函数f (x )=lg x ,若f (2x )<f (2),则实数x 的取值范围是.15.函数f (x )=a 2-x-1(a >0,a ≠1)恒过定点,当0<a <1时,f (x 2)的增区间为.16.已知函数f (x )=x 2+log 2|x |,则不等式f (x -1)-f (1)<0的解集为.四、解答题:本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.17.(10分)比较下列各组数的大小:(1)1.8,2.2;(2)0.70.8,0.80.7.18.(12分)已知关于x 的方程5x=15- 有负根,求实数a 的取值范围.19.(12分)已知函数f (x )=log a (-x 2+2x +3)(其中a >0且a ≠1)的值域为[-2,+∞).(1)求实数a 的值;(2)求函数f (x )的单调区间.20.(12分)已知函数f (x )=(a 2-a +1)x a +1为幂函数,且为奇函数.(1)求实数a 的值;(2)求函数g (x )=f (x )+1-2 ( )在0.21.(12分)设函数f (x )=lg (ax )·lg2.(1)当a =0.1时,求f (1000)的值;(2)若f (10)=10,求实数a 的值;(3)若对一切正实数x 恒有f (x )≤98,求实数a 的取值范围.22.(12分)为了预防流感,某学校对教室用药薰消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y (单位:mg )与t 时间(单位:h )成正比,药物释放完毕后,y 与t之间的函数关系式为y 2+0.9 +(a 为常数),其图象如图所示,根据图中提供的信息回答下列问题:(1)从药物释放开始,求每立方米空气中的含药量y 与时间t 之间的函数关系式.(2)据测定,当空气中每立方米的含药量降低到116mg 以下时,学生方可进入教室,那么从药物释放开始至少需要经过多少小时,学生才可以回到教室?(第22题)参考答案1.D2.A3.C4.D5.B6.C7.A8.C9.BC 10.ABD 11.AB 12.ABD 13.-214.(0,1)15.(2,0)[0,+∞)16.(0,1)∪(1,2)17.(1)1.82.2(2)0.70.8<0.80.718.方程5x=15- 有负根,即0<15-<1,解得a <4,即a ∈(-∞,4)19.(1)a =12(2)函数f (x )的减区间为(-1,1],增区间为[1,3)20.(1)a =0(2)g (x )=x +1-2 ,x ∈0t =1-2 ,t ∈[0,1],则g (t )=t +1- 22=-12(t -1)2+1,所以12≤g (t )≤121.(1)f (1000)=-14(2)f (10)=lg (10a )·lg 100=(1+lg a )(lg a -2)=(lg a )2-lg a -2=10,即(lg a )2-lg a -12=0,解得lg a =4或-3,即a =104或10-3(3)因为对一切正实数x 恒有f (x )≤98,所以lg (ax )·lg 2≤98在(0,+∞)上恒成立,即(lg a +lg x )(lg a -2lg x )≤98,即2(lg x )2+lg a ·lg x -(lg a )2+98≥0在(0,+∞)上恒成立.因为x >0,所以lg x ∈R .由二次函数的性质可知,Δ=(lg a )2-8-(lg )2+,所以(lg a )2≤1,则-1≤lg a ≤1,所以110≤a ≤1022.(1)当0≤t ≤1时,设y =kt ,将点(0.1,1)代入得k =10,所以y =10t ,再将点(0.1,1)代入y 2+0.9 +,得a =-0.1,所以y 0≤ ≤1,2+0.9 -0.1, >1(2)2+0.9 -0.1≤116,所以( 2+0.9 -0.1),所以5(t 2+0.9t -0.1)≥4,所以10t 2+9t -9≥0,所以t ≥35或t ≤-32(舍去),所以学生要在0.6h 后才可以进入教室。
苏教版高中数学必修一函数的概念和图象同步练习(1)(6)

函数图象一、选择题1.(2010·天津南开区调研)已知ab =1,函数f (x )=a x 与函数g (x )=-log b x 的图象可能是 ( )解析:∵ab =1,∴⎩⎪⎨⎪⎧a >1,0<b <1,a x为增函数,-log b x 为增函数0<a <1,b >1,a x为减函数,-log bx 为减函数. 答案:B2.函数y =ln cos x (-π2< x < π2)的图象是( )解析:本小题主要考查复合函数的图像识别.y =ln cos x (-π2< x < π2)是偶函数,可排除B 、D ,由cos x ≤1⇒ln cos x ≤0排除C ,选A. 答案:A3.(2009·安徽)设a <b ,函数y =(x -a )2(x -b )的图象可能是( )解析:由已知条件可知:答案:C4.(2010·山东烟台调研)已知函数y =f (x )(x ∈R)满足f (x +2)=f (x ),且x ∈(-1,1]时, f (x )=|x |,则y =f (x )与y =log 7x 的交点的个数为( ) A .4 B .5 C .6 D .7解析:y =f (x )与y =log 7x 的交点即为图象的交点如图,由图象可知有6个交点.答案:C 二、填空题5.(2009·湖南十二校联考)已知函数f (x )=x -52x +m的图象关于直线y =x 对称,那么m = ________.解析:f (x )=x -52x +m 的反函数为f-1(x )=-mx -52x -1.因为函数图象关于直线y =x 对称,所以 f (x )=f-1(x ),即x -52x +m =-mx -52x -1, 对一切x ≠12的实数恒成立.∴m =-1.答案:-16.(2010·江苏扬州调研)若曲线|y |=2x +1与直线y =b 没有公共点,则b 的取值范围是________.解析:曲线|y |=2x +1与直线y =b 的图象如图所示.由图象可得|y |=2x +1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]7.(情景题)一水池有2个进水口,1个出水口,进出水速度如下图甲、乙所示.某天0点到6点,该水池的蓄水量如下图丙所示.(至少打开一个水口)给出以下3个论断:① 0点到3点只进水不出水; ② 3点到4点不进水只出水; ③ 4点到6点不进水不出水;则一定能确定正确的论断序号是________.解析:由题中图丙,可知0点到3点时水增加速度等于2个进水口的进水速度,则①正 确;3点到4点时“一进一出”,所以②错误;③与已知(至少打开一个水口)不符. 答案:① 三、解答题 8.已知函数f (x )=x 1+x. (1)画出f (x )的草图; (2)指出f (x )的单调区间.解:(1)f(x)=x 1+x =1-x x +1,函数f(x)的图象是由反比例函数y=-1x 的图象向左平移1个单位后,再向上平移1个单位得到,图象如图所示. (2)由图象可以看出,函数f(x)有两个单调递增区间: (-∞,-1),(-1,+∞).9.(2010·福建厦门模拟)设函数f (x )=x +1x 的图象为C 1,C 1关于点A (2,1)对称的图象为 C 2,C 2对应的函数为g (x ). (1)求g (x )的解析式;(2)若直线y =m 与C 2只有一个交点,求m 的值和交点坐标.解:(1)设点P (x ,y )是C 2上的任意一点,则P (x ,y )关于点A (2,1)对称的点为P ′(4-x,2-y ),代入f (x )=x +1x ,可得2-y =4-x +14-x ,即y =x -2+1x -4,∴g (x )=x -2+1x -4.(2)由⎩⎪⎨⎪⎧y =m ,y =x -2+1x -4, 消去y 得x 2-(m +6) x +4m +9=0, Δ=(m +6)2-4(4m +9),∵直线y =m 与C 2只有一个交点, ∴Δ=0,解得m =0或m =4.当m =0时,经检验合理,交点为(3,0); 当m =4时,经检验合理,交点为(5,4).10.已知函数y =f (x )的定义域为R ,并对一切实数x ,都满足f (2+x )=f (2-x ).(1)证明:函数y =f (x )的图象关于直线x =2对称;(2)若f (x )是偶函数,且x ∈[0, 2]时,f (x )=2x -1,求x ∈[-4, 0]时的f (x )的表达式. 证明:(1)设P (x 0,y 0)是函数y =f (x )图象上任一点,则y 0=f (x 0),点P 关于直线x =2的 对称点为P ′(4-x 0,y 0).因为f (4-x 0)=f [2+(2-x 0)]=f [2-(2-x 0)]=f (x 0)=y 0, 所以P ′也在y =f (x )的图象上,所以函数y =f (x )的图象关于直线x =2对称. (2)解:当x ∈[-2,0]时,-x ∈[0,2], 所以f (-x )=-2x -1. 又因为f (x )为偶函数,所以f (x )=f (-x )=-2x -1,x ∈[-2,0]. 当x ∈[-4,-2]时,4+x ∈[0,2],所以f (4+x )=2(4+x )-1=2x +7,而f (4+x )=f (-x )=f (x ),所以f (x )=2x +7,x ∈[- 4,-2].所以f (x )=⎩⎪⎨⎪⎧2x +7,x ∈[-4,-2],-2x -1,x ∈(-2,0].1.某地一年内的气温Q(t)(单位:℃)与时间t(月份)之间的关系如右图所示,已知该年的平均气温为10℃.令C(t)表示时间段[0,t]的平均气温,C(t)与t之间的函数关系用下列图象表示,则正确的应该是(),解析:由图可以发现当t=6时,C(t)=0,排除C;t=12时,C(t)=10,排除D项;在大于6的某一段气温超于10,所以排除B项,故选A项.答案:A2. (★★★★★)不等式1-x2<x+a在x∈[-1,1]上恒成立,则实数a的取值范围是()A.(-∞,-2) B.(-1,2)C.[2,+∞) D.(2,+∞)解析:设y=1-x2,y=x+a,在同一直角坐标系内作出y=1-x2的图象,再将函数y=x 的图象沿y轴方向上、下平行移动,如右图所示,考查在x∈[-1,1]上,使不等式1-x2<x+a恒成立.答案:D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 -函数练习题1. 判断下列对应是否为函数:(1),,;x y y x x R y Z →∈∈其中为不大于的最大整数,(2)2,,,x y y x x N y R →=∈∈;(3)x y x →=,{|06}x x x ∈≤≤,{|03}y y y ∈≤≤;(4)16x y x →=,{|06}x x x ∈≤≤,{|03}y y y ∈≤≤.2.函数1()2f x x=-的定义域为 .3. 函数f (x )=x -1(x z ∈且[1,4]x ∈-)的值域为 .4. 已知函数()b ax x f +=,且()(),15,73-==f f 求()()1,0f f 的值.5. 求下列函数的定义域(1)43523--+=x x x y (2)xxx y 3121112--++=6.求函数()f x =的定义域和值域.7. 已知)(2)(R x x x f ∈=(1)当函数值域为]4,2[时,求函数定义域; (2) 当函数值域为}2,8,4{-时,求函数定义域; 8.函数y =+的定义域为 . 12999 . c o m9. 函数24y x x =-+的值域是 .10. 函数()1x y x x-=+的定义域为11.函数[]22,1,3y x x =+∈-的值域是_____________. 12.函数y =的定义域是____________.13.已知2()21,()1f x x g x x =-=+. (1)[](2)f g 与()1g f -⎡⎤⎣⎦的值; (2)求[]()f g x 与()g f x ⎡⎤⎣⎦14.已知函数2()1f x x x =+-. (1)若()5f x =,求x 的值;(2)若()()f x f a ≥对一切x R ∈恒成立,求实数a 的取值范围.- 3 -15.画出下列函数的图象.(1))2,1[,12)(-∈-=x x x f (2)),0(,11)(+∞∈+=x xx f(3)]3,0[,)1()(2∈-=x x x f (4){}2,1,0,1,2,1)(--∈+=x x x f ;(5)2()2f x x x =+ (6)2()6f x x x =--16.设M ={x |0≤x ≤2},N ={y |0≤y ≤3},给出下列四个图形(如图所示),其中能表示从集合M 到集合N 的函数关系的是 .(填序号).17.已知一次函数()f x 满足(0)5f =,图象过点(2,1)-,则()f x = ;已知二次函数()h x 与x 轴的两交点为(2,0)-,(3,0),且(0)3h =-,则()h x = .18.函数1y x =+与两条坐标轴围成的封闭图形的面积为 . 19.若函数⎩⎨⎧<+≥=0130)(2x x x x x f ,则(3)f = ;20.若函数52)(+=x x f ,则=)(2x f ; 21.已知函数()21)1(+=+x x f ,则=)(x f ;22.若2(21)2,f x x x +=-则(1)f -= ; 23.若函数⎩⎨⎧>-≤+=)0(2)0(12x xx x y ,则使得函数值为10的x 的集合为 ;24.已知1)(2+=x x f ,则)1(+x f = ,[]=)(x f f ; 25.若2211()f x x x x-=+,则()f x = ;26.已知5(6)()(2)(6)x x f x f x x -≥⎧=⎨+<⎩,则(3)f = ;27.已知()f x 是二次函数,且(2)3,(2)7,(0)3,f f f =--=-=-求()f x28.已知函数c bx ax x f ++=2)(,若0)0(=f ,且x x f x f ++=+1)()1( 对任意的Rx ∈成立,求)(x f29.函数2y x=-的单调递_____区间是______________________.30.函数221y x x =+-的单调递增区间为_______________________.31.已知()(21)f x k x b =++在R 上是增函数,则k 的取值范围是______________.- 5 -32.下列说法中,正确命题的个数是______________. ①函数2y x =在R 上为增函数; ②函数1y x=-在定义域内为增函数;③若()f x 为R 上的增函数且12()()f x f x >,则12x x >; ④函数1y x=的单调减区间为(,0)(0,)-∞⋃+∞.33.函数()1f x x =+的增区间为 . 34.函数1()1f x x =+的单调减区间为 .35.函数14)(2+-=mx x x f 在]2,(--∞上递减,在),2[+∞-上递增,则实数m = . 36.证明函数1()1g x x=-在()1,+∞是减函数.37.求证函数1()f x x x =-在()0,+∞是单调增函数.38.函数()f x =的单调减区间 .39. 函数)(x f 在),0(+∞上是减函数,那么)1(2+-a a f 与)43(f 的大小关系是 .40.函数1||22+-=x x y 的单调增区间为 . 41.设定义在R 上的函数f (x )=|x |,则()f x ( )A .既是奇函数,又是增函数B .既是偶函数,又是增函数C .既是奇函数,又是减函数D .既是偶函数,又是减函数42.y =f (x )(x ∈R )是奇函数,则它的图象必经过点 ( ) A .(-a ,-f (-a )) B .(a ,-f (a )) C .(a ,f (a1)) D .(-a ,-f (a ))43.如果偶函数在],[b a 具有最大值,那么该函数在],[a b --有 ( ) A .最大值 B .最小值C .没有最大值D .没有最小值44.设奇函数f (x )的定义域为[-5,5],若当x ∈[0,5]时,f (x )的图象如下图,则不等式()0f x <的解是 .45.设()f x 为定义在R 上的奇函数,满足()()2f x f x +=-,当01x ≤≤时()f x x =,则()7.5f 等于 .46.设f (x )=ax 5+bx 3+cx -5(a ,b ,c 是常数)且(7)7f -=,则f (7)= . 47.判断下列函数的奇偶性 ①xx y 13+=; ②x x y 2112-+-=;③x x y +=4;48.已知函数()y f x =是定义在实数集R 上的偶函数,当0x ≥时,2()23f x x x =--。
(1)写出函数()y f x =的表达式; (2)作出()y f x =的图象; (3)指出函数的单调区间及单调性。
(4)求函数的最值。
49. 已知函数2()f x ax bx c =++是定义在[]1,2a a -上的偶函数,则a = ,________b =50. 已知函数()f x 是定义在R 上的奇函数,当0x <时,2()2f x x x =-,则(1)f =51、已知集合A ={a ,b },B ={c ,d },则从A 到B 的不同的映射有 个。
52.若2x =-,则x 的取值范围是 。
- 7 -53.计算20032004+⋅-的值是 。
54.化简:()⎪⎭⎫⎝⎛<+-2391246322b a b ab a 的结果是( ) (A )23a b - (B )32b a - (C ) (23)a b ±- (D )32b a -55.求值(1)3= ; (2= ; (3= . 56.当810x <<= .57.化简:2+58.下列运算中,正确的是( )(A )5552a a a ⋅= (B )56a a a += (C )5525a a a ⋅= (D )5315()a a -=- 59.下列根式与分数指数幂的互化中.正确的是( )(A )12()(0)x x =-> (B 13(0)y y =< (C)340)xx -=> (D)130)x x -=≠60.化简(1)131121373222[()()()]a b ab b ---⋅⋅⋅= .(2) 21131133344()()x y z x y z ---⋅⋅⋅⋅⋅= .(3)20a >= .61.若103,104xy ==,则10x y-= .62.求值: 341681⎛⎫ ⎪⎝⎭, 12100-, 314-⎛⎫ ⎪⎝⎭63.函数2(232)x y a a a =-+是指数函数,则a 的取值范围是( )()A 0,1a a >≠ ()B 1a = ()C 12a =()D 1a =或12a =64.函数y =)()A (2,)-+∞ ()B [1,)+∞()C (,1]-∞- ()D (,2)-∞- 65.(1)函数y =的定义域是 ;值域是 ;(2)函数y =的定义域是 ;值域是 . 66.要得到函数122x y -=的图象,只要将函数1()4xy =的图象 ( )(A )向左移1个单位 (B )向右移1个单位 (C )向左移0.5个单位 (D )向右移0.5个单位67.函数21x y a +=-(0,1)a a >≠的图象过定点 .68.函数22363x x y -+=的单调递减区间是 .69.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3小时,这种细菌由1个可繁殖成 ( ) A . 511个 B . 512个 C . 1023个 D . 1024个70.某商场进了A B 、两套服装,A 提价20%后以960元卖出,B 降价20%后以960元卖出,则这两套服装销售后 ( )()A 不赚不亏 ()B 赚了80元 ()C 亏了80元 ()D 赚了2000元71.将下列对数式改写成指数式.(1) log 5 125 = 3 (2) log31 3 = -2(3) log 10 a = -1.699 (4) ln 15 = b- 9 -72.求下列各式的值.(1) log 2 64 (2) log 9 27(3) log 51125 (4) 32log95 (5) 2 2-log2573.计算103132(1)log 27+-+74.已知函数()lg 11,a a +==则__________75.2log ______________76.已知函数3,1,(),1,x x f x x x ⎧≤=⎨->⎩若()2f x =,则x = 。
77. 解方程96370xx-⋅-=78.已知()643log log log 0x =⎡⎤⎣⎦,求x 的值79.求下列各式的值(1) log 2(47×25) (2) lg 5100(3) lg 2 + lg 5 (4) 21+log 2380. 设lg 3.14=a , 则lg 314=____________________81. 1lg 25lg 4-=___________________82. 计算2lg 5lg 2lg 50+⨯83. 已知b a ==3lg ,2lg ,则=12lg 3lg 2=__________;84.已知c b a x lg 21)lg 3((lg 2lg -+=,则=x ;85.化简 lg 1001 + log 391 - log 5125 - log 44186. 计算327log 2log 6487.化简:=⋅⋅9log8log 25log532___________88.函数()f x =的定义域为 ;89.函数()()1()log 3x f x x -=-的定义域为 ;90. 函数)12(log 2-=x y 的值域为 ; 91. 已知4log4log nm<,试比较n m ,的大小关系92. 方程3log (21)1x -=的解x = ;93.函数0.5log (41)y x =+的单调减区间为 ;94. 解下列方程:(1) log 5 (2x +3) = log 5 (3x –2) (2) ln (x 2+2) = 2ln (2x –1)- 11 -95.下列函数中是偶函数的是 ;(1)x y 3-= (2)(]3,3,2-∈=x x y (3)32-=x y (4)3)1(2+-=x y96.幂函数()f x的图像过点(,则()f x 的解析式是97.函数x x y 1-=的零点是 ;98.函数)0(12≠--=a x ax y 只有一个零点,则实数a 的值为 ;99.函数f (x )=-2x +4x -4在区间[1,3]上 ;A .没有零点B .有一个零点C .有两个零点D . 有无数个零点 100.求实数m 的取值范围,使关于x 的方程032=++mx x 有两个实根1x ,2x ,且满足41021<<<<x x 。
