第三章 酶促反应动力学
合集下载
生物化学 第三章 酶(共65张PPT)

概念: 抑制剂和底物的结构相似,能与底物竞争酶的活性中心,从而阻碍酶底物复合物的形成,使酶的活性降低。
含多条肽链则为寡聚酶,如RNA聚合酶,由4种亚基构成五聚体。
(cofactor)
别构酶(allosteric enzyme):能发生别构效应的酶
9 D-葡萄糖6-磷酸酮醇异构酶 磷酸葡萄糖异构酶
esterase)活性中心丝氨酸残基上的羟基结合,使酶失活。
酶蛋白
酶的磷酸化与脱磷酸化
五、酶原激活
概念
酶原(zymogen):细胞合成酶蛋白时或者初分 泌时,不具有酶活性的形式
酶原 切除片段 酶
(–)
(+)
酶原激活
本质:一级结构的改变导致构象改变,激活。
胰蛋白酶原的激活过程
六、同工酶
同工酶(isoenzyme)是指催化相同的化学反应, 而酶蛋白的分子结构、理化性质乃至免疫学性质 不同的一组酶。
正协同效应(positive cooperativity) 后续亚基的构象改变增加其对别构效应剂
的亲和力,使效应剂与酶的结合越来越容易。
负协同效应(negative cooperativity) 后续亚基的构象改变降低酶对别构效应剂
的亲和力,使效应剂与酶的结合越来越难。
协同效应
正协同效应的底物浓度-反应速率曲线为S形曲线
/ 即: Vmax = k3 [Et]
Km 和 Vmax 的测定
双倒数作图法 Lineweaver-Burk作图
将米氏方程式两侧取倒数
1/v = Km/Vmax[S] + 1/Vmax = Km/Vmax •1/ [S] + 1/Vmax 以 1/v 对 1/[S] 作图, 得直线图
斜率为 Km/Vmax
含多条肽链则为寡聚酶,如RNA聚合酶,由4种亚基构成五聚体。
(cofactor)
别构酶(allosteric enzyme):能发生别构效应的酶
9 D-葡萄糖6-磷酸酮醇异构酶 磷酸葡萄糖异构酶
esterase)活性中心丝氨酸残基上的羟基结合,使酶失活。
酶蛋白
酶的磷酸化与脱磷酸化
五、酶原激活
概念
酶原(zymogen):细胞合成酶蛋白时或者初分 泌时,不具有酶活性的形式
酶原 切除片段 酶
(–)
(+)
酶原激活
本质:一级结构的改变导致构象改变,激活。
胰蛋白酶原的激活过程
六、同工酶
同工酶(isoenzyme)是指催化相同的化学反应, 而酶蛋白的分子结构、理化性质乃至免疫学性质 不同的一组酶。
正协同效应(positive cooperativity) 后续亚基的构象改变增加其对别构效应剂
的亲和力,使效应剂与酶的结合越来越容易。
负协同效应(negative cooperativity) 后续亚基的构象改变降低酶对别构效应剂
的亲和力,使效应剂与酶的结合越来越难。
协同效应
正协同效应的底物浓度-反应速率曲线为S形曲线
/ 即: Vmax = k3 [Et]
Km 和 Vmax 的测定
双倒数作图法 Lineweaver-Burk作图
将米氏方程式两侧取倒数
1/v = Km/Vmax[S] + 1/Vmax = Km/Vmax •1/ [S] + 1/Vmax 以 1/v 对 1/[S] 作图, 得直线图
斜率为 Km/Vmax
酶促反应动力学

ES + I Ki ESI
E+P
非竞争性抑制的双倒数方程:
3. 反竞争性抑制作用
• 抑制剂仅与酶和底物形成的中间产物(ES) 结合,使ES的量下降。这样,既减少从 ES转化为产物的量,也同时减少从ES解 离出游离酶和底物的量。
• 特点:Vmax和Km均降低。
E+S
ES + I Ki ESI
(三)Km值和Vmax值的测定
双倒数方程式: Km 1 1 1 + v = V Vmax max [S]
.
双倒数做图法: • 用于测Km值和Vmax值 • 用于判断可逆性抑制反应的性质
二、酶浓度对反应速度的影响
• 当[S]>>[E]时, [E]与v呈正比 关系。
三、温度对反应速度的影响
双重影响 • 最适温度:酶促反应速度最快时的环境 温度。 • 体内大多数酶的最适温度在35~40℃之 间。 • 最适温度不是酶的特征性常数。 • 低温不使酶破坏。
第三节
酶促反应动力学
研究的是酶促反应速度及其影响因素的 关系。 酶促反应速度:用单位时间内底物的 消耗量或产物的生成量表示 研究酶促反应动力学要采用初速度 初速度:反应速度与时间呈正比的阶 段。 反应10min. 或底物消耗在5%
影响因素: • 底物浓度([S]) • 酶浓度([E]) • 温度 • pH
1. 竞争性抑制作用
• 概念:抑制剂与酶的底物结构相似,可 与底物竞争酶的活性中心,从而阻碍酶 与底物结合形成中间产物,而抑制酶的 活性。
E+S +
ES
E+P
I
Ki
v= EI
Vmax [S] Km (1+
第03章酶催化作用机制

V
Vmax
[S]
随着底物浓度的增高 反应速度不再成正比例加速。
V
Vmax
[S]
当底物浓度高达一定程度 反应速度不再增加,达最大速度,说明酶已 经被底物所饱和。
1. 米氏方程
第 三 章 酶 催 化 作 用 机 制
1913年,米彻利斯(Michaelis)和曼吞 (Menton)在前人研究的基础上,推导出 著名的米氏方程: v——反应速度; S——底物浓度; v m —— 最大反应速度; K m —— 米氏常数,为 酶催化反应速度等于最大反应速度一半时 的底物浓度。
(一)酶的刚性与“琐和钥匙”学说
第 三 章 酶 催 化 作 用 机 制
1890年,德 国化学家费舍 尔(Fisher) 提出了著名的 “琐和钥匙” 此学说认为:酶与底物都是刚性的,二者 学说。 结构间天然存在互补的关系,就像锁和钥
匙一样。此学说较好的解释了酶对底物选 择的专一性,但不能解释酶能够高效催化 反应的原因。
中间产物学说
中间产物
第 三 章 酶 催 化 作 用 机 制
酶促反应速度与底物浓度的关系,可以用 中间产物学说加以解释。 酶促反应模式——中间产物学说
E+S
k1 k2
ES
k3
E+P
推导过程
米-曼氏方程式推导基于两个假设:
第 三 章 酶 催 化 作 用 机 制
E与S形成ES复合物的反应是快速平衡反应,
Dixon plot
Cornish-Bowden plot
酶的转换数
定义 — 当酶被底物充分饱和时,单位时间内 (每秒钟)每个酶分子催化底物转变 为产物的分子数(微摩尔数)。 意义 — 可用来比较每单位酶的催化能力。
第三章 酶促反应动力学(简)-1

10
(1)快速平衡学说 在推导动力学方程时,有下述四点假设。
① 在反应过程中,酶的浓度保持恒定,即 [ E 0] = [ E ] + [ ES ] ② 与底物浓度[S]相比,酶的浓度是很小的,因而可以忽略 由于生成中间复合物[ES]而消耗的底物。 ③ 产物的浓度是很低的,因而产物的抑制作用可以忽略,也 不必考虑P+E─→[ES]这个逆反应的存在。换言之,据 此假设所确定的方程仅适用于反应初始状态。 ④ 生成产物的速率要慢于底物与酶生成复合物的可逆反应 速率,因此,生成产物的速率决定整个酶催化反应的速 率,而生成复合物的可逆反应在初速度测定时间内已达 到平衡状态。因此,又称为“快速平衡”假设。
v Vmax -Km
Vmax Km
v
[S]
20
(3) Hanes-Woolf 作图法 在 1 Km 1 1 — = —— . — + —— 两边均乘以[S]: v Vmax [S] Vmax
Km [S] [S] ——=——+—— v Vmax Vmax [S] v 1 Vmax
以
[S] ~[S]作图 v
11
k +1 k +2 ⎯⎯→ ES ⎯⎯→ P + E E + S← ⎯⎯ k −1
产物的生成决定反应的总速度,因此整个酶促反 应速度决定于:v=k+2[ES]
k −1 [ E ][ S ] ES复合物解离常数为: K S = k = [ ES ] (1) +1
设[E0]为酶的总浓度,则平衡时游离酶浓度为:
k +2 ⎯ E + S←⎯→ ES ⎯⎯→ P + E ⎯⎯
k +1
k −1
Vmax [ S ] v= K s + [S ]
(1)快速平衡学说 在推导动力学方程时,有下述四点假设。
① 在反应过程中,酶的浓度保持恒定,即 [ E 0] = [ E ] + [ ES ] ② 与底物浓度[S]相比,酶的浓度是很小的,因而可以忽略 由于生成中间复合物[ES]而消耗的底物。 ③ 产物的浓度是很低的,因而产物的抑制作用可以忽略,也 不必考虑P+E─→[ES]这个逆反应的存在。换言之,据 此假设所确定的方程仅适用于反应初始状态。 ④ 生成产物的速率要慢于底物与酶生成复合物的可逆反应 速率,因此,生成产物的速率决定整个酶催化反应的速 率,而生成复合物的可逆反应在初速度测定时间内已达 到平衡状态。因此,又称为“快速平衡”假设。
v Vmax -Km
Vmax Km
v
[S]
20
(3) Hanes-Woolf 作图法 在 1 Km 1 1 — = —— . — + —— 两边均乘以[S]: v Vmax [S] Vmax
Km [S] [S] ——=——+—— v Vmax Vmax [S] v 1 Vmax
以
[S] ~[S]作图 v
11
k +1 k +2 ⎯⎯→ ES ⎯⎯→ P + E E + S← ⎯⎯ k −1
产物的生成决定反应的总速度,因此整个酶促反 应速度决定于:v=k+2[ES]
k −1 [ E ][ S ] ES复合物解离常数为: K S = k = [ ES ] (1) +1
设[E0]为酶的总浓度,则平衡时游离酶浓度为:
k +2 ⎯ E + S←⎯→ ES ⎯⎯→ P + E ⎯⎯
k +1
k −1
Vmax [ S ] v= K s + [S ]
酶促反应动力学

k1 k 1
ES
ES
k2 P E
[ES]生成速度: v1
k1 Et ESS ,[ES]分解速度: v2 k1ES k2 ES
当酶反应体系处于恒态时: 即: 令:
k1 Et ESS k1ES k2 ES
恒态法推导:
1925年Briggs和Haldame对米氏方程作了一次重要 的修正,提出了恒态的概念。
k1 k3
E+S
k2
ES
E+P
所谓恒态是指反应进行一定
时间后,ES的生成速度和ES的分 解速度相等,亦即ES的净生成速
度为零,此时ES的浓度不再改变,
达到恒态,也称稳态。
SE
S
Et ES
2.米氏常数的意义 (1). 物理意义: Km值等于酶反应速度为最大速度一半时的底物浓度。 (2). Km 值愈大,酶与底物的亲和力愈小;Km值愈小, 酶与底物亲和力愈大。酶与底物亲和力大,表示不需要很 高的底物浓度,便可容易地达到最大反应速度。 (3). Km 值是酶的特征性常数,只与酶的性质,酶所催 化的底物和酶促反应条件(如温度、pH、有无抑制剂等)有 关,与酶的浓度无关。酶的种类不同,Km值不同,同一种 酶与不同底物作用时,Km值也不同。各种酶的Km值范围很 广,大致在 10-1~10-6 M 之间。
为解释酶被底物饱和现象,Michaelis和Menten 做了大量的定量研究,积累了足够的实验数据, 提出了酶促反应的动力学方程:
中间复合物学说:
第一步: E+S
第二步: ES→E+P
ES
V∝[ES]
1913年Michaelis和 Menten推导了米氏方程
酶(part2)
经整理得:[ES ]=[Et ][S ] K m +[S ]
(1)
由于酶促反应速度由[ES]决定,即 决定, 由于酶促反应速度由 决定
v = k2 [ES ]
,所以
[ES ] =
将(2)代入(1)得: )代入( ) 当[Et]=[ES]时, 时
[Et ][S ] v = k2 K m + [S ]
所以
Vmax 2
Vmax[S] = Km + [S] Km=[S]
∴Km值等于酶促反应速度为最大反应速度一半时 的底物浓度,单位是mol/L。 的底物浓度,单位是 。
小结: 小结:Km的物理意义 的物理意义
Km值
① Km等于酶促反应速度为最大反应速度一半时的底物浓 度。 ② 意义: 意义:
a) Km是酶的特征性常数之一; 是酶的特征性常数之一; b) Km可近似表示酶对底物的亲和力; 可近似表示酶对底物的亲和力; c) 同一酶对于不同底物有不同的 同一酶对于不同底物有不同的Km值。 值
2.酶活力单位和比活力表示方式 (1)酶活力单位
惯用单位 :酶促反应在单位时间内生成一定量的产物或消 耗一定数量的底物所需的酶量 。 国际单位(IU):在特定条件下,每分钟催化1μ mol底物 国际单位(IU):在特定条件下,每分钟催化1μ mol底物 ):在特定条件下 转化为产物所需的酶量为一个国际单位。(1976) 转化为产物所需的酶量为一个国际单位。 1催量(1 kat)是指在特定条件下,每秒钟使 催量( 催量 )是指在特定条件下,每秒钟使1mol底物转化 底物转化 产物所需的酶量。 产物所需的酶量。(1979) Kat与IU的换算:1IU=16.67×10-9Kat, 与 的换算 的换算: = × , 1Kat=6×107IU = ×
第三章 酶反应动力学

引起酶反应速度降低的原因: 底物浓度的降低;酶的部分失
斜率=[P]/ t = V初速度 活;产物对酶的抑制;产物增
加引起的逆反应速度的增加
时间
t •研究酶反应速度以酶促反应的
初速度(initial speed)为准
酶反应速度曲线
二、底物浓度对反应速度的影响
1、单底物酶促反应动力学
(1))米氏方程(Michaelis-Menten equation
所以 Vm k2 Et
(4)
v
Vm ax S Km S
2.2.3 米氏常数的意义
•当v=Vmax/2时,Km=[S]( Km的单位为浓度单位),即 米氏常数是反应速度为最大值的一半时的底物浓度。
* 是酶在一定条件下的特征物理常数,通过测定Km的
数值,可鉴别酶。
* 可近似表示酶和底物亲合力,Km愈小,E对S的亲合
以 对作图,绘出曲线,横轴截距即 为-值,纵轴截距则是
双倒数作图
米氏常数(Michaelis-constant)的意义
a Km的物理意义
当V=1/2Vmax时的底物浓度,为Km的物理意义。 即[S]=Km
Km单位:m(mol)/L
b Km是酶的特征性常数
不同酶,Km是不一样的。 底物种类,pH(opt),T(opt) 要定下来。
分变性; (3) 随时间延长,产物增加,产物对酶的抑制作用; (4) 产物增加,逆反应速度增加。
因此,只有初速度才是酶的反应速度。
一、酶浓度的影响
酶促反应的速度和酶浓度成正比
[S]>>[E]
V∝[E]
反 应 速 度
0
酶浓度
[P] 产 物 浓 度
反应速度:用单位时间内、单 位体积中底物(S)的减少量或产 物(P)的增加量来表示。单位: 浓度/单位时间
第三章 酶催化反应动力学

如何避免影响?
测定反应初速度的方法来测定相关制剂中酶的含量(活性)。
1.2 酶活力的测定原理
酶蛋白的含量很低,很难直接测定其蛋白质的 含量,且常与其他各种蛋白质混合存在,将其 提纯耗时费力。故不能直接用重量或体积等指 标来衡量。
分光光度法 荧光法 同位素法 电化学方法 其他方法:如旋光 法、量气法、量热 法和层析法等
E
+
S
ES
ESI
E
+
P
图3-7 反竞争性抑制曲线
特点: ⑴ Vm值和Km值都随[I]的增加而降低; ⑵ 双倒数作图所得为一组平行线; ⑶必须有底物存在,抑制剂才能对酶产生抑制作用;抑制程 度随底物浓度的增加而增加。
举例:
这种抑制作用在单底物反应中比较少见,而常
见于多底物反应中。
目前已经证明,肼类化合物对胃蛋白酶的抑制
举例:磺胺类药物的抑菌机制
•与对氨基苯甲酸竞争性抑制二氢叶酸合成酶
Glu + H2N COOH PAB A + 二氢蝶呤
FH2合成酶
FH 2
FH2还原酶
FH 4
氨甲蝶呤 H2N 磺胺药 SO2NHR
②非竞争性抑制(noncompetitive inhibition) : 非竞争性抑制剂(I)和底物(S)可以同时与酶(E) 结合,两者之间不存在竞争关系。 但是在酶与抑制剂结合后,还可以进一步与底 物结合形成酶-底物-抑制剂复合物ESI;酶与 底物结合后,也可以进一步与抑制剂结合形成 酶-底物-抑制剂复合物ESI。
4.2 不可逆的抑制作用
根据不可逆抑制剂选择性的差异,通常把不可
逆抑制剂分为两种类型,即非专一性不可逆抑
制剂和专一性不可逆抑制剂。
测定反应初速度的方法来测定相关制剂中酶的含量(活性)。
1.2 酶活力的测定原理
酶蛋白的含量很低,很难直接测定其蛋白质的 含量,且常与其他各种蛋白质混合存在,将其 提纯耗时费力。故不能直接用重量或体积等指 标来衡量。
分光光度法 荧光法 同位素法 电化学方法 其他方法:如旋光 法、量气法、量热 法和层析法等
E
+
S
ES
ESI
E
+
P
图3-7 反竞争性抑制曲线
特点: ⑴ Vm值和Km值都随[I]的增加而降低; ⑵ 双倒数作图所得为一组平行线; ⑶必须有底物存在,抑制剂才能对酶产生抑制作用;抑制程 度随底物浓度的增加而增加。
举例:
这种抑制作用在单底物反应中比较少见,而常
见于多底物反应中。
目前已经证明,肼类化合物对胃蛋白酶的抑制
举例:磺胺类药物的抑菌机制
•与对氨基苯甲酸竞争性抑制二氢叶酸合成酶
Glu + H2N COOH PAB A + 二氢蝶呤
FH2合成酶
FH 2
FH2还原酶
FH 4
氨甲蝶呤 H2N 磺胺药 SO2NHR
②非竞争性抑制(noncompetitive inhibition) : 非竞争性抑制剂(I)和底物(S)可以同时与酶(E) 结合,两者之间不存在竞争关系。 但是在酶与抑制剂结合后,还可以进一步与底 物结合形成酶-底物-抑制剂复合物ESI;酶与 底物结合后,也可以进一步与抑制剂结合形成 酶-底物-抑制剂复合物ESI。
4.2 不可逆的抑制作用
根据不可逆抑制剂选择性的差异,通常把不可
逆抑制剂分为两种类型,即非专一性不可逆抑
制剂和专一性不可逆抑制剂。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
rS rmax
即:
或:
( 3-16)
rmaxt CS0 CS
CS CS0 rmaxt
当CS与Km的数量关系处于上述两者之间的范 围时,即符合米氏方程所表示的关系式。在 t=0时,CS=CS0,对(2-13)式积分得到:
rmaxt (CS0 CS ) K m ln CS0 CS
CE0 CE C[ ES ]
CS0 CS C[ ES ] CP
dC S k 1 (C E0 C[ ES ] )( CS0 C[ ES ] C P ) k 1C[ ES ] dt
dC[ ES ] dt
k1 (CE0 C[ ES ] )(CS0 C[ ES ] CP ) (k1 k 2 )C[ ES ]
式中:
(3-5)
(3-6)
(3-7)
a, b, c
k1 , k2
—— A,B,C的浓度;
——各步反应的速率常数;
如果A的初始浓度为a0, B和C的初始浓度为0, 并且a+b+c=a0,则可求得:
k1t
(3-8)
a a0 e
k1a0 k1t k2t b (e e ) k2 k1
压力 pH值 与离子强度
外部因素(环境因素): 溶液的介电常数
温度
内部因素(结构因素):
底物浓度及效应物
酶结构
零级反应—— 酶促反应速率与底物浓度无关。
d[S ] rmax dt
式中:[S]——底物浓度;
(3-1)
rmax——最大反应速率。
一级反应——
酶促反应速率与底物浓度的一次方成正比。
根据上述假设和式(3-11),有:
dC S dC P rP k 2C[ ES ] dt dt
和
k1CECS k1C[ ES ]
C[ ES ] k1 C[ ES ] CE KS k1 CS CS
或表示为:
式中:CE—游离酶的浓度,mol/L; CS—底物的浓度,mol/L; KS—解离常数, mol/L;
均相酶催化反应: 指酶与反应物系同处液相的酶催化 反应. 因此不存在相间的物质传递. 均相酶催化反应动力学所描述的反应 速率与反应物系的基本关系,反映了该 反应过程的本征动力学关系,而且酶与 反应物的反应是分子水平上的反应.
一、酶促反应动力学基础
影响酶促反应的因素:
浓度:
酶浓度 底物浓度 产物浓度
反应速率:单位时间、单位反应体系中某一组 分的变化量来表示。对均相酶催化反应,单位 反应体系常用单位体积表示。反应速率为:
1 dCS 1 dC P rS , rP V dt V dt
式中:rs —底物S的消耗速率,mol/(L.s);
rP—产物P的生成速率, mol/(L.s);
V—反应体系的体积,L; CS—底物S的物质的量,mol; CP—产物P的物质的量,mol; t—时间,s;
酶催化A→B的反应
db k1 (a0 b) dt
1
(3-2)
式中:k ——一级反应速率常数;
a0
——底物A的初始浓度;
b——t时产物B的浓度。
二级反应—— 酶催化A+B→C的反应
dc k2 (a0 c)(b0 c) dt
式中: 2 ——二级反应速率常数; k
(3-3)
a0 , b0
生物反应工程原理
李艳 教授 生物科学与工程学院
Ly5885@ Lymdh5885@
第三章
酶促反应动力学
学习目的: 1、了解酶促反应特点及与一般化学反应的区别。 2、掌握0、1级和米氏酶促反应动力学及应用原理; 3、了解存在抑制时的酶促反应动力学特征; 4、具备固定化酶反应中的过程分析能力和内外不同 阶段的固定化酶动力学的应用能力; 5、熟悉酶的失活动力学与反应过程中酶失活动力学 行为。
( 3-12 )
式中: r P,max—产物的最大生成速率,mol/(L . s); CE0—酶的总浓度,亦为酶的初始浓度,mol/L;
式(3-12)即米氏方程,式中的两个动 力学参数是KS和rP,max。其中:
k1 CS CE KS k1 C[ ES ]
KS表示了酶与底物相互作用的特性。KS的单位和CS的单位相同, 当rP=1/2 rP,max 时,存在KS=CS关系。 rP,max =k+2CE0。表示当全部酶都呈复合物状态时的反应速率。 k+2又叫酶的转换数。表示单位时间内一个酶分子所能催化底 物发生反应的分子数,因次,它表示酶催化反应能力的大小, 不同的酶反应其值不同。 rP,max正比于酶的初始浓度CE0。实际应用中将k+2和CE0合并应 用为一个参数。
②Michaelis-Menten方程推导过程:
“快速平衡学说”(rapid equilirium): 假设:酶与底物反应生成复合物,和复合物又 解离成酶和底物的反应之间快速建立平衡,而 复合物解离成产物和酶,即ES→E+P是整个反应 的限速步骤,即由酶和底物反应生成中间复合 物的可逆反应在初速度测定时间内已经达到平 衡。
根据反应机理和上述假设,有下述方程式:
dC P k 2C[ ES ] dt dC S k 1C E C S k 1C[ ES ] dt
dC[ ES ] dt
又因为有:
k 1CE CS k 1C[ ES ] k 2C[ ES ] 0
CE0 CE C[ ES ]
(3-9)
a0 k1t k2t c [k2 (1 e ) k1 (1 e )] k2 k1
(3-10)
二、单底物酶促反应动力学
单底物酶促反应指一种反应物(底物)参 与的不可逆反应。如:水解酶、异构酶和 多数裂解酶催化的反应。
1、米氏方程
① Henri中间复合物学说 ② Michaelis-Menten方程 ③ Briggs-Haldane方程 ④动力学特征(米氏方程的讨论) ⑤动力学参数的求取
——底物A和底物B的初始浓度;
c——t时产物C的浓度。 积分上式,得:
b0 (a0 c) 1 ln k2t a0 b0 a0 (b0 c) (3-4)
连锁反应—— k1 k2 酶催化A → B → C的反应
da k1a dt db k1a k2b dt dc k2 a dt
第三章
酶促反应动力学
第一节 均相酶促反应动力学 第二节 固定化酶促反应动力学 第三节 酶的失活动力学
酶促反应(Enzymatic reaction):
研究酶促反应
酶促反应动力学
研究生物反应的基础
酶催化反应机制
对酶促反应速率的规律 进行定性或定量的描述
建立反应动力学方程
确定适宜的操作条件
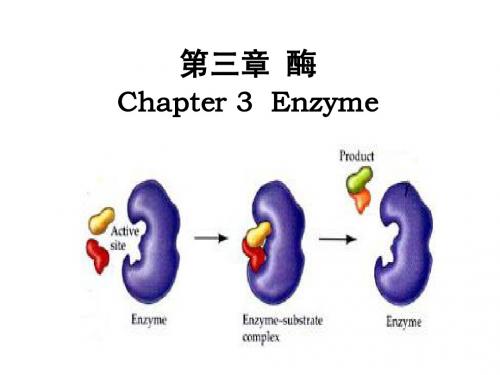
① Henri中间复合物学说:
SE
k+1 k -1
ES
k +2
EP
式中: efree——游离酶; CS——底物浓度; C[ES] ——酶-底物复合物浓度; CP——产物浓度; K+1——酶与底物形成复合物的反应速度常数; K-1——复合物解离为酶和底物的反应速度常数; K+2——ES复合物分解生成产物的反应速度常数。
dC P k 2C[ ES ] dt
④动力学特征(米氏方程的讨论)
根据米氏方程, 酶反应的速度 与底物浓度的 关系为一双曲 线,P30图3-1。 该曲线表示了 三个不同动力 学特点的区域。
当CS《Km,即底物浓度比Km值小很多时,该 曲线近似为一直线。表示反应速率与底物浓度 近似成正比关系,此时酶催化反应成为一级反 应速率方程。
根据质量作用定律,P的生成速率可表示为:
rP k2CES
式中:
( 3-11 )
C[ES] —中间复合物[ES]的浓度,它
为一难测定的未知量,因而不能用它
来表示最终的速率方程。
对上述反应机理,推导动力学方 程时的三点假设:
(1)在反应过程中,酶的浓度保持恒定,即: CE0=CE+C[ES]。 (2)与底物浓度CS相比,酶的浓度是很小的, 因而可以忽略由于生成中间复合物[ES]而消耗 的底物。 (3)产物的浓度是很低的,因而产物的抑制 作用可以忽略,也不必考虑P+E→[ES]这个逆 反应的存在。 据此假设所确定的方程仅适用于反应初始状态。
CS 0 CS
rmax CS CS0 exp t Km
式中:CS0—底物的初始浓度,mol/L; 这个原理在酶法分析中被应用。利用 酶测定底物时,可使用足够量的酶以 便在较短时间内,使反应达到完全。 这样测定形成的产物总量就与待测物 的量相等或相关。
当CS》Km时,该曲线近似为一水平线,表示 当底物浓度继续增加时,反应速率变化不大。 此时酶反应可视为零级反应,反应速率将不随 底物浓度的变化而变化。这是因为当Km值很 小时,绝大多数酶呈复合物状态,反应体系内 游离的酶很少,因而即使提高底物的浓度,也 不能提高其反应速率。
( 3-14 )
当k+2《k-1时,Km=Ks,即生成产物的速率大 大慢于酶底物复合物解离的速率。 Km值的大小与酶、反应物系的特性以及反应条 件有关。
某些酶促反应的Km值:P30表3-1 M-M方程与B-H方程比较见下表
在M-M方程和B-H方程的推导中都假设CE0《CS0,因 而C[ES]值也很小。如果酶的浓度很高, C[ES]值在反应 过程中有可能是很高的。若仍然采用上述方程会带来 较大误差。此时物料平衡和速率方程可表示为:
