浙江省杭州市西湖区2014-2015学年第一学期期末考试八年级数学试卷
2014-2015学年八年级上学期期末考试成绩表
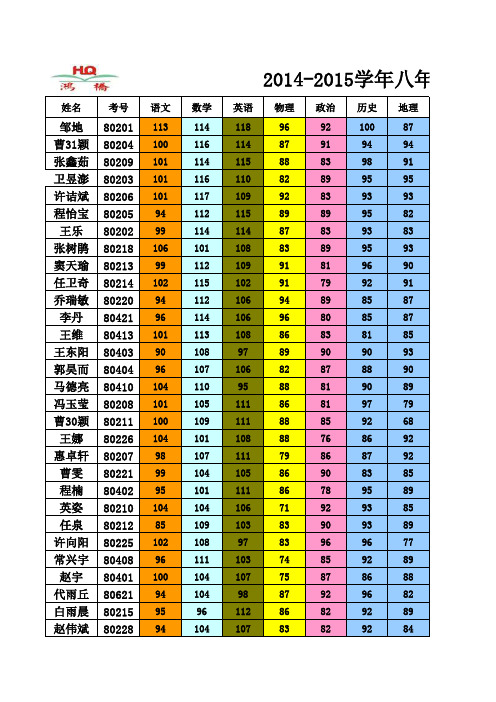
邹地 曹31颖 张鑫茹 卫昱澎 许诘斌 程怡宝 王乐 张树鹃 窦天瑜 任卫奇 乔瑞敏 李丹 王维 王东阳 郭昊而 马德亮 冯玉莹 曹30颖 王娜 惠卓轩 曹雯 程楠 英姿 任泉 许向阳 常兴宇 赵宇 代雨丘 白雨晨 赵伟斌
80201 80204 80209 80203 80206 80205 80202 80218 80213 80214 80220 80421 80413 80403 80404 80410 80208 80211 80226 80207 80221 80402 80210 80212 80225 80408 80401 80621 80215 80228
2014-2015学年八年级上学期
姓名 考号 语文 113 100 101 101 101 94 99 106 99 102 94 96 101 90 96 104 101 100 104 98 99 95 104 85 102 96 100 94 95 94 数学 114 116 114 116 117 112 114 101 112 115 112 114 113 108 107 110 105 109 101 107 104 101 104 109 108 111 104 104 96 104 英语 118 114 115 110 109 115 114 108 109 102 106 106 108 97 106 95 111 111 108 111 105 111 106 103 97 103 107 98 112 107 物理 96 87 88 82 92 89 87 83 91 91 94 96 86 89 82 88 86 88 88 79 86 86 71 83 83 74 75 87 86 83 政治 92 91 83 89 83 89 83 89 81 79 89 80 83 90 87 81 81 85 76 86 90 78 92 90 96 85 87 92 82 82 历史 100 94 98 95 93 95 93 95 96 92 85 85 81 90 88 90 97 92 86 87 83 95 93 93 96 92 86 96 92 92 地理 87 94 91 95 93 82 83 93 90 91 87 87 85 93 90 89 79 68 92 92 85 89 85 89 77 89 88 82 89 84
2014-2015学年第一学期期末八年级数学模拟试卷(A)

2014-2015学年第一学期期末八年级数学模拟试卷(A卷)一、选择题(每小题2分,共28分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母代号填写在下表相应题号的方格内.2±=±4 B﹣382227.(2分)某人将一枚质量均匀的硬币连续抛10次,落地后正面朝上6次,反面朝上4次,下9.(2分)如图,已知AD=CB,AB=CD,AC与BD交于点O,则图中全等三角形共有()10.(2分)如图,△ABC中,AB=AC,∠BAC=100°,AD是BC边上的中线,且BD=BE,则∠ADE 的大小为()11.(2分)如图,在△ABC中,DE垂直平分BC,若AB=8,AC=6,则△ADC的周长等于()12.(2分)如图,OC平分∠AOB,CD⊥OB于D,点P是射线OA上的一个动点,若CD=8,OD=6,则PC的最小值为()13.(2分)如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形()14.(2分)如图,在△ABC中,∠ACB=90°,AC=BC,顶点A、B、C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是2个单位长度,则△ABC的面积是()二、填空题(每小题3分,共12分)15.(3分)(2002•汕头)比较大小:_________0.5.16.(3分)若m2+6m=2,则(m+3)2=_________.17.(3分)如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为_________.18.(3分)如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为_________.三、解答题(共60分)19.(14分)计算(1)(3x﹣1)(3x+2)﹣(﹣3x)2;(2)(2a﹣3b)2﹣2a(2a﹣3b);(3)先化简,再求值:(x﹣2y)(﹣2y﹣x)﹣(x﹣2y)2,其中x=3,.20.(8分)把下列多项式分解因式.(1)4x3﹣xy2;(2)4(x+y)2﹣16xy.21.(6分)如图是我国古代数学家赵爽的“勾股方圆图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是12,小正方形的面积是2,直角三角形的两直角边分别是a和b,求(a+b)2的值.22.(9分)某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调查(每人只选一种书籍).图1和图2是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:(1)这次活动一共调查了_________名学生;(2)在图2中,“漫画”所在扇形圆心角为_________度;(3)补全条形统计图.23.(10分)如图,已知△ABC.利用直尺和圆规,根据要求作图,并解决后面的问题.(1)作△ABC的角平分线AD;(2)作∠CBE=∠ADC,BE交CA的延长线于点E;(要求:保留作图痕迹,不需写作法和证明)(3)图中线段AB与线段AE相等吗?证明你的结论.24.(13分)如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN 绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.(1)求证:△ADE≌△CDF;(2)求四边形AEDF的面积;(3)连结EF.①当点F在AC边上时总有BE_________EF(填“>”或“<”或“=”),请说明理由;②若BE=2,求EF的长.2014-2015学年第一学期期末八年级数学模拟试卷(A卷)参考答案与试题解析一、选择题(每小题2分,共28分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母代号填写在下表相应题号的方格内.1.解:∵(﹣3)2=9,∴(﹣3)2的平方根是±3,故选B.2.解:A、=4,故本选项错误;B、﹣32=﹣9,根据负数没有平方根,故本选项错误;C、1的立方根是1,故本选项错误;D、﹣是7的一个立方根,故本选项正确.故选D.3.解:∵a•2•23=28,∴a=28÷24=24=16.故选C.4.解:(﹣2xy)2÷xy2=4x2y2÷xy2=4x.故选B.5.解:x2﹣x﹣12=(x+3)(x﹣4),则(x+3)(x﹣4)=x2﹣x﹣12.故选A6.解:①若AB=AC=2cm,则BC=8﹣2﹣2=4(cm),∵2+2=4,不能组成三角形,舍去;②若AB=BC=2cm,则AC=8﹣2﹣2=4(cm),∵2+2=4,不能组成三角形,舍去;③若AB=2cm,则AC=BC==3(cm),故选B.7.解:∵某人抛硬币抛10次,其中正面朝上6次,反面朝上4次,∴出现正面的频数是6,出现反面的频数是4,出现正面的频率为6÷10=60%;出现反面的频率为4÷10=40%.故选B8.解:A、三个角的比为1:2:3,设最小的角为x,则x+2x+3x=180°,x=30°,3x=90°,故是直角三角形;B、三条边满足关系a2=b2﹣c2,故是直角三角形;C、三条边的比为1:2:3,12+22≠32,故不是直角三角形;D、三边之比为3:4:5,所以设三边长分别为3x,4x,5x,则(3x)2+(4x)2=(5x)2,故是直角三角形;故选:C.9.解:△ADC≌△CBA;△ADB≌△CBD;△AOB≌△COD;△AOD≌△COB共四对.在△ADC和△CBA中,,∴△ADC≌△CBA(SSS),∴∠DCA=∠BAC,在△ABD和△CDB中,,∴△ADB≌△CBD(SSS),∴∠ADB=∠CBD,,∴△AOB≌△COD(ASA),∴DO=CO,BO=DO,在△DOA和△BOC中,,∴△AOD≌△COB(SSS).故选:D.10.解:∵△ABC中,AB=AC,∠BAC=100°∴∠B=∠C=(180°﹣∠BAC)=(180°﹣100°)=40°∵BD=BE∴∠BED=∠BDE=(180°﹣∠B)=(180°﹣40°)=70°∴∠ADE=90°﹣70°=20°.故选B.11.解:∵DE垂直平分BC,∴DB=DC,∵AB=8,AC=6,∴△ADC的周长为:AD+DC+AC=AD+BD+ACAB+AC=14.故选C.12.解:当CP⊥OA时,PC的值最小,∵OC平分∠AOB,CD⊥OB于D,∴PC=CD=8.故选C.13.解:(1)∵∠ABC=60°,∠ACB=45°,AD是高,∴∠DAC=45°,∴CD=AD,∴△ADC为等腰直角三角形,∵∠ABC=60°,BE是∠ABC平分线,∴∠ABE=∠CBE=30°,在△ABD中,∠BAD=180°﹣∠ABD ﹣∠ADB=180°﹣60°﹣90°=30°,∴∠ABF=∠BAD=30°,∴AF=BF即△ABF是等腰三角形,在△ABC中,∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣45°=75°,∵∠AEB=∠CBE+∠ACB=30°+45°=75°,∴∠BAE=∠BEA,∴AB=EB即△ABE是等腰三角形,∴等腰三角形有△ACD,△ABF,△ABE;故选B.14.解:过C作EF⊥该组平行线,交A所在直线于点E,交B所在直线于点F,∵∠ACE+∠BCF=90°,∠ACE+∠CAE=90°,∴∠CAE=∠BCF,,∴△ACE≌△CBF(AAS),∴AE=CF=8,∴AC2=AE2+CE2=100,∴S△ABC=AC2=50,故选C.二、填空题(每小题3分,共12分)15.(3分)(2002•汕头)比较大小:>0.5.解:∵0.5=,2<<3,∴>1,∴故填空答案:>.16.(3分)若m2+6m=2,则(m+3)2=11.解:∵m2+6m=2,∴(m+3)2=m2+6m+9=2+9=11.故答案为:11.17.(3分)如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为9.解:∵正方形A、B的面积依次为2、4,∴正方形E的面积为2+4=6,又∵正方形C的面积为3,∴正方形D的面积3+6=9,故答案为9.18.(3分)如图,在△ABC中,AB=AC=12,BC=8,D为AB的中点,点P在线段BC上以每秒2个单位的速度由B点向C点运动,同时,点Q在线段CA上以每秒x个单位的速度由C点向A点运动.当△BPD与以C、Q、P为顶点的三角形全等时,x的值为2或3.解:设经过t秒后,使△BPD与△CQP全等,∵AB=AC=12,点D为AB的中点,∴BD=6,∵∠ABC=∠ACB,∴要使△BPD与△CQP全等,必须BD=CP或BP=CP,即6=8﹣2t或2t=8﹣2t,t1=1,t2=2,t=1时,BP=CQ=2,2÷1=2;t=2时,BD=CQ=6,6÷2=3;即点Q的运动速度是2或3,故答案为:2或3.三、解答题(共60分)19.(14分)计算(1)(3x﹣1)(3x+2)﹣(﹣3x)2;(2)(2a﹣3b)2﹣2a(2a﹣3b);(3)先化简,再求值:(x﹣2y)(﹣2y﹣x)﹣(x﹣2y)2,其中x=3,.解:(1)原式=9x2+6x﹣3x﹣2﹣9x2=3x﹣2;(2)原式=4a2﹣12ab+9b2﹣4a2+6ab=﹣6ab+9b2;(3)(x﹣2y)(﹣2y﹣x)﹣(x﹣2y)2=4y2﹣x2﹣x2+4xy﹣4y2=﹣2x2+4xy,当x=3,时,原式=﹣2×32+4×3×=﹣10.20.(8分)把下列多项式分解因式.(1)4x3﹣xy2;(2)4(x+y)2﹣16xy.解:(1)原式=x(4x2﹣y2)=x(2x+y)(2x﹣y);(2)原式=4(x2+y2+2xy﹣4xy)=4(x﹣y)2.21.(6分)如图是我国古代数学家赵爽的“勾股方圆图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是12,小正方形的面积是2,直角三角形的两直角边分别是a和b,求(a+b)2的值.解:∵大正方形的面积是12,小正方形的面积是2,∴四个直角三角形面积和为12﹣2=10,即4×ab=10,∴2ab=10,a2+b2=12,∴(a+b)2=a2+b2+2ab=12+10=22.答:(a+b)2的值为22.22.(9分)某校为了了解本校八年级学生课外阅读的喜好,随机抽取该校八年级部分学生进行问卷调查(每人只选一种书籍).图1和图2是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:(1)这次活动一共调查了200名学生;(2)在图2中,“漫画”所在扇形圆心角为72度;(3)补全条形统计图.解:(1)调查的总人数是:80÷40%=200(人),故答案是:200;(2)“漫画”所在扇形圆心角为:360°×=72°,故答案是:72;(3)喜好科普常识的人数是:200×30%=60(人)..23.(10分)如图,已知△ABC.利用直尺和圆规,根据要求作图,并解决后面的问题.(1)作△ABC的角平分线AD;(2)作∠CBE=∠ADC,BE交CA的延长线于点E;(要求:保留作图痕迹,不需写作法和证明)(3)图中线段AB与线段AE相等吗?证明你的结论.解:(1)如图:(2)如图:(3)AB=AE,∵AD是角平分线,∴∠BAD=∠ADC,∴AD∥BE,∴∠E=∠CAD,∠EBA=BAD,∴∠E=∠EBA,∴AB=AE.24.(13分)如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN 绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.(1)求证:△ADE≌△CDF;(2)求四边形AEDF的面积;(3)连结EF.①当点F在AC边上时总有BE<EF(填“>”或“<”或“=”),请说明理由;②若BE=2,求EF的长.(1)证明:∵∠BAC=90°,AB=AC,D为BC中点,∴∠B=∠C=∠BAD=∠CAD=45°,∠ADC=90°,∴AD=DC=BD,∵∠ADE+∠ADF=90°,∠ADF+∠CDF=90°,∴∠ADE=∠CDF,在△ADE和△CDF中,,∴△ADE≌△CDF(ASA);(2)解:∵△ADE≌△CDF,∴四边形AEDF的面积=S△ADC =S△ABC,∵S△ABC =AB•AC=,∴四边形AEDF的面积=;(3)解:①∵△ADE≌△CDF,∴AE=CF,∵AB=AC,∴BE=AF,∵FA⊥EA,∴AF<EF,即BE<EF;②∵AB=AC=3,BE=2,∴AE=1,AF=BE=2,∴EF==.。
2014-2015学年八年级上学期阶段性测试数学试题及答案

2014-2015学年度八年级上学期阶段性测试数 学 试 卷时间120分钟 满分100分2015、1、2 一、选择题(每小题3分,共24分)1、下列运算中,正确的是( ) A.+336x x 2x = B.()222a b a b +=+ C.()=325x x D.336x x x ⋅= 2、计算()()()+2x 1x 1x 1-+的结果是( )A.-2x 1B.-3x 1C.+4x 1D.-4x 1 3、下列各式可以分解因式的是 ( ) A .()-22x y - B .+224x 2xy y + C. 22x 4y -+ D.-22x 2xy y - 4、用尺规作角平分线的依据是 ( ) A . SAS B .ASA C.AAS D. SSS5、如图BC=BD ,AD=AE ,DE=CE ,∠A=36°,则∠B= ( ) A .36° B .45° C .72° D .30°6.在三角形内部,到三角形三边距离相等的点是 ( )A .三条中线的交点B .三条高线交点C .三个内角平分线交点D .三边垂直平分线交点7.如图,在等腰△ABC 中,∠BAC=120°,DE 是AC 的垂直平分线,线段DE=1cm ,则BD 的长为 ( )A .6cmB .8cmC .3cmD .4cm8.如图,在Rt△ABC 中,∠ACB=90°,AB=2BC ,在直线BC 或AC 上取一点P ,使得△PAB 为等腰三角形,则符合条件的点P 共有) A.4个 B.5个 C.6个 D.7个二、填空题(每小题3分,共18分)9、计算:(直接写结果)()-233x 2xy ⋅ = ,()()-3x 12x 1+ = . 10、已知一个多边形的内角和等于900°,则这个多边形的边数是 . 11.汉字“王、中、田”等都是轴对称图形,请再写出一个这样的汉字 . 12、若x 2﹣kxy+25y 2是一个完全平方式,则k 的值是 ____ .13、三角形周长是奇数,其中两边的长是2和5,则第三边长是 .14、如图,在ABC 中,AP=DP ,DE=DF ,DE⊥AB 于E ,DF⊥AC 于F ,则下列结论: ①.AD 平分∠BAC;②.△BED≌△FPD;③.DP∥AB;④.DF 是PC 的垂直平分线. 其中正确的是= .(写序号)三、解答题(每小题5分,共25分)15、因式分解:322x 2x y xy ++16、先化简,再求值:)2)(2(4)84223b a b a ab b a ab -++÷-(,其中 .1,2==b a17、如图,在△ABC 中,D 是AB 上一点,DF 交AC 于点E ,DE=FE ,AE=CE ,AB 与CF 有什么位置关系?证明你的结论.18、如图,已知PB ⊥AB , PC ⊥AC ,且PB =PC ,D 是AP 上的一点,求证:CDBD =.19、已知(a+2b )(2a+b )=2a 2+5ab+2b 2,如图是正方形和长方形卡片(各有若干张),你能用拼图的方法说明上式吗?四、解答题(每小题6分,共18分)20、(6分)作图题(不写作法) 已知:如下图所示.①. 作出△ABC 关于y 轴对称的△A 1B 1C 1,并②. 写出△A 1B 1C 1三个顶点的坐标; ②.在x 轴上确定点P ,使PA+PC 最小.21、(6分)仔细阅读下面例题,解答问题:例题:已知二次三项式x 2﹣4x+m 有一个因式是(x+3),求另一个因式以及m 的值. 解:设另一个因式为(x+n ),得 x 2﹣4x+m=(x+3)(x+n ) 则x 2﹣4x+m=x 2+(n+3)x+3n ∴解得:n=﹣7,m=﹣21 ∴另一个因式为(x ﹣7),m 的值为﹣21 问题:仿照以上方法解答下面问题:已知二次三项式2x 2+3x ﹣k 有一个因式是(2x ﹣5),求另一个因式以及k 的值.22、(6分)D 是等边三角形内一点,DB=DA ,BP=AB ,∠DBP=∠DBC,求∠BPD 的度数.五、解答题(第1小题7分,第2小题8分,共15分)23、(7分)已知:如图所示,在A B C△和A D E △中,A B A C =,A D A E =,B A C D A E ∠=∠,且点B A D,,在同一条直线上,连接B E C D M N ,,,分别为B E C D ,的中点, 连接MNANAM,,.⑴.求证:B E C D; (4分)⑵.求证:A M N△是等腰三角形.(3分)24、(8分)数学课上,李老师出示了如下的题目:“在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.小敏与同桌小聪讨论后,进行了如下解答:⑴.特殊情况,探索结论(2分)当点E为AB的中点时,如图①,确定线段AE与DB的大小关系,请你直接写出结论:AE ______ DB(填“>”,“<”或“=”).⑵.特例启发,解答题目(4分)解:题目中,AE与DB的大小关系是:AE _____ DB(填“>”,“<”或“=”).理由如下:如图②,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)⑶.拓展结论,设计新题(2分)在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为2,AE=1,求CD的长(请你直接写出结果).参考答案一、选择题(每小题3分,共24分)1.D 2.D 3.C 4.D 5.A 6.C 7.A 8.B 二、填空题(每小题3分,共18分) 9.,3326x y 6x x 1-+-; 10. 7 ; 11.一(答案不唯一); 12.10±;13.4或6;14. ①、③.三、解答题(每小题5分,共25分)15.略解:()()=232222x 2x y xy x x 2xy y x x y ++++=+16.略解: 原式=()2222b 2ab 4a b 4a 2ab 2a 2a b -+-=-=- 当.a 2b 1==时,原式=()-==222214312⨯⨯⨯ 17.答:AB EF 理由如下:∵在ADE 和CFE 中,,,DE FE AED CEF AE CE =∠=∠=,∴ADE ≌CFE ∴ADE F ∠=∠, ∴AB EF . 18. 略证:∵PB ⊥AB , PC ⊥AC ∴PBA PCA 90∠=∠= ∵在Rt ADE 和Rt CFE 中.PB PC PA PA == ∴ PBA ≌PCA (HL) ∴BPA CPA ∠=∠ 即BPD CPD ∠=∠ ∵在BPD 和CPD 中 ,,PB PC BPD CPD PD PD =∠=∠= ∴ BPD ≌CPD ∴BD CD = 19.由拼图可知:四、解答题(每小题6分,共18分)20.略解:①的作图如图所示111A B C 三个顶点的坐标分别为:()()()111A 12B 31C 44---,,,,,②的作图如图所示:P 就是所求作的点,此时PA+PC 最小.21.略解: 设另一个因式为()x m +,则()()+22x 3x k 2x 5x m -=-+整理:()+222x 3x k 2x 2m 5x 5m -=+--;则:2m 53k 5m -=⎧⎨=⎩解得:m 4k 20=⎧⎨=⎩. ()()222222a 2b 2a b a a 5ab b b 2a 5ab 2b S =++=++++=++矩形PA'B 1A C 122.略解:五、解答题(第23小题7分,第24小题8分,共15分) 23.略证: 24、略解: ⑴.AE DB =;⑵.AE DB =.理由:⑶.CD 3=⑴.∵BAC CAD ∠=∠ ∴BAC CAE CAD CAE ∠+∠=∠+∠ 即BAE CAD ∠=∠在BAE 和CAD 中AB ACBAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩ ∴BAE ≌CAD∴CE CD =⑵.由BAE ≌CAD 知:=12∠∠ 又∵M N 、分别为BE CD 、的中点,且CE CD = ∴BM CN = 在BAM 和BM CN 12AB AC =⎧⎪∠=∠⎨⎪=⎩∴BAM ≌CAN∴AM AN = 即AMN 是等腰三角形。
杭州市西湖区2014-2015学年第一学期期末考试七年级数学试卷(含详细解答)

杭州市西湖区2014-2015学年第一学期期末考试七年级数学试卷考生须知:1.本试卷分试题卷和答题卷两部分.满分120分,考试时间100分钟. 2.答题前,必须在答题卷上填写校名,班级,姓名,座位号.3.不允许使用计算器进行计算,凡题目中没有要求取近似值的,结果中应保留根号或π. 一.仔细选一选(本题有10个小题,每小题3分,共30分)每小题给出的四个选项中,只有一个是正确的,注意可以用多种不同的方法来选取正确答案. 1. 下列四个数中,结果为负数的是( ) A .1()2-- B .12-C .21()2-D .12--2. 下列计算正确的是( ) A .39±= B .283-=- C .36412585= D .72)3()2(23=-⨯- 3. 用代数式表示:“a ,b 两数的平方和与a ,b 乘积的差”,正确的是( ) A .a 2+b 2-ab B .2)(b a +-ab C .a 2b 2-ab D .(a 2+b 2)ab4. 据统计,2013年我国用义务教育经费支持了13940000名农民工随迁子女在城市里接受义务教育,这个数字用科学计数法可表示为( )A .1.394×107B .13.94×107C .1.394×106D .13.94×106 5. 若212b am --与n ab 5可以合并成一项,则n m +的值是( )A .1B .2C .3D .4 6. 如图,A 是直线l 外一点,点B 、C 、E 、D 在直线l 且AD ⊥l ,D 为垂足,如果量得AC =8cm ,AD =6cm ,AE AB =13cm ,那么,点A 到直线l 的距离是( ) A. 13cm B. 8cm C. 7cm D. 6cm 7. 下列式子变形正确的是( ) A .1)1(--=--a a B .a a a 253-=- C .b a b a +=+2)(2 D .ππ-=-338. 若有理数m 在数轴上对应的点为M ,且满足1m m <<-,则下列数轴表示正确的是( )9.下列说法:①两点确定一条直线;②射线AB 和射线BA 是同一条射线;③相等的角是对顶角;④三角形任意两边和大于第三边的理由是两点之间线段最短. 正确的是( ) A. ①③④ B. ①②④ C. ①④ D. ②③④1BMxDC M 1Amx10. 已知线段AB =8cm ,在直线AB 上有一点C ,且BC =4cm ,点M 是线段AC 的中点,则线段AM 的长为( )A. 2 cmB. 4 cmC. 2 cm 或6 cmD. 4 cm 或6 cm 二.认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案.11. 若∠1=40°50′,则∠1的余角为 ▲ ,∠1的补角为 ▲ .12. 在实数5,227,0,π2,36, -1.414,0.131131113…(两个“3”之间依次多一个“1其中无理数是 ▲ .13. 关于x 的方程326x a +=的解是1-a ,则a 的值是 ▲ . 14. 如果36a b -=,那么代数式539a b -+的值是___ ▲ _____.15. 若当x =3时,代数式2(34)7x m ++与122mx -的值相等,则m= ▲ .16. 下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字m 为▲ ,第n 个正方形的中间数字为 ▲ . (用含n 的代数式表示)……21121110913876554321……第1个 第2个 第3个 第4个 第n 个 三.全面答一答(本题有7个小题,共66分)解答应写出必要的文字说明、证明过程或推理步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.(本题满分6分)计算 (1)(-2.25)-(+85)+(-43)-(-0.125) (2)2235(6)(4)(2)-+⨯---÷- 18.(本题满分8分)解方程(1)423x x -=- (2)2112236x x+-=- 19.(本题满分8分)如图,O 在直线AC 上,OD 是∠AOB 的平分线,OE 在∠BOC 内. (1)若OE 是∠BOC 的平分线,则有OD ⊥OE ,试说明理由;(2)若∠BOE =21∠EOC ,∠DOE =72°,求∠EOC 的度数.20. (本题满分10分)在同一平面内有n 条直线,当n =1时,如图①,一条直线将一个平面分成两个部分;当n =2时,如图②,两条直线将一个平面最多分成四个部分.(1)在作图区分别画出当n =3时,三条直线将一个平面分成最少部分和最多部分的情况; (2)当n =4时,请写出四条直线将一个平面分成最少部分的个数和最多部分的个数;(3)若n 条直线将一个平面最多分成n a 个部分,(n +1)条直线将一个平面最多分成1+n a 个部分,请写出n a ,EDC BAO1+n a ,n 之间的关系式.图①图② 作图区(最少部分) 作图区(最多部分) 21. (本题满分10分)在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所.已知青少年宫在学校东500m 处,商场在学校西300m 处,医院在学校东600m 处.若将马路近似地看作一条直线,以学校为原点,向东方向为正方向,用1个单位长度表示100m.(1)请画一条数轴并在数轴上表示出四家公共场所的位置; (2)列式计算青少年宫与商场之间的距离; (3)若小新家也位于这条马路旁,在青少年宫的西边,且到商场与青少年宫的距离之和等于到医院的距离,试求小新家与学校的距离. 22. (本题满分12分)图1为全体奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为a (如图2). (1)请用含a 的代数式表示框内的其余4个数;(2)框内的5个数之和能等于2015,2020吗?若不能,请说明理由;若能,请求出这5个数中最小的一个数,23. (本题满分12分)某超市在“元旦”促销期间规定:超市内所有商品按标价..的75%出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额=商品的折扣+相应的奖券金额,例如:购买标价为440元的商品,则消费金额为:440×75%=330元,获得的优惠额为:440×(l-75%)+40=150元.(1)购买一件标价为800元的商品,求获得的优惠额;(2)若购买一件商品的消费金额在450≤a <800之间,请用含a 的代数式表示优惠额;(3)对于标价在600元与900元之间(含600元和900元)的商品,顾客购买标价为多少元的商品时可以得到1332的优惠率?(设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价)参考答案评分标准一、仔细选一选(本大题共10个小题;每小题3分,共30分)(每小题4分,共24分)11.49°10′, 139°10′; 12.5, π2, 0.131131113…(两个“3”之间依次多一个“1”); 13.1.8;14.-13 ;15.2524-;16.29,8n -3 . 三、全面答一答(本题共7小题,共66分)17. (本题满分6分) 解:(1)原式=-2.25-85-43+0.125 -------2分 = -213 -------1分(2)原式=-9-30+8 -------2分 =-31 -------1分 18.(本题满分8分)解:(1)432x x -=- -------2分 (2)2(21)1212x x +=-- -------1分2x ∴=- -------2分 42211x x +=-- -------1分 613x =- -------1分 ∴136x =--------1分 19.(本题满分8分)解:(1)∵OD 、OE 分别是 ∠AOB 和∠BOC 的平分线∴∠DOB=12∠AOB , ∠BOE=12∠BOC ------------2分 ∴∠DOB+∠BOE=12(∠AOB+∠BOC )=90°,∴OD ⊥OE ------------2分(2)设∠BOE=x ,∵∠BOE=21∠EOC ,∴∠EOC=2x , ∵∠DOE=72°,∴∠DOB=12∠AOB =72-x , -------------1分 ∴2(72-x )+x +2x =180 -------------1分 解得,x =36°------------1分∴∠EOC=72°-------------1分20. (本题满分10分) (1)。
浙江省杭州市西湖区2013-2014学年八年级(上)期末数学试卷(含答案解析)

2013-2014学年浙江省杭州市西湖区八年级(上)期末数学试卷一、仔细选一选(共10小题,每小题3分,满分30分)1.(3分)在平面直角坐标系中,点(﹣2,3)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限2.(3分)(2002•福州)等腰三角形的两边长分别为2和7,则它的周长是()A.9 B.11 C.16 D.11或163.(3分)(2013•宾阳县一模)不等式组的解集在数轴上表示为()ABCD4.(3分)下列函数中,y的值随着x值的增大而增大的是()A.y=x+1 B.y=﹣x C.y=1﹣x D.y=﹣x﹣15.(3分)如图,一次函数y=kx+b的图象与y轴的交点坐标是(0,1),则关于x的不等式kx+b>1的解是()A.x>1 B.x<1 C.x>0 D.x<06.(3分)若a>b,则下列各式中一定成立的是()A.ma>mb B.c2a>c2b C.1﹣a>1﹣b D.(1+c2)a>(1+c2)b7.(3分)甲、乙、丙、丁4个人步行的距离和花费的时间如图,按平均值计算,则走的最慢的是()A.甲B.乙C.丙D.丁8.(3分)(2012•江干区一模)将一根铁丝围成一个等腰三角形,围成的三角形的底边长y与腰长x之间的函数关系可能为()A B C D9.(3分)如图,△ABC中,BC=8,AD是中线,∠ADB=60°,将△ADB沿AD折叠至△ADB′,则点C到B′的距离是()A.4 B.2C.3 D.210.(3分)如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+∠C;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是()A.①B.②③C.①②D.①③二、认真填一填(共6小题,每小题3分,满分18分)11.(3分)证明命题“x(x﹣5)=0,则x=5”是假命题,反例是_________.12.(3分)如图,在△ABC中,AB=AC,外角∠ACD=110°,则∠A=_________°.13.(3分)直角三角形的两直角边长分别为6和8,则斜边中线的长是_________.14.(3分)(2004•金华)△ABO中,OA=OB=5,OA边上的高线长为4,将△ABO放在平面直角坐标系中,使点O 与原点重合,点A在x轴的正半轴上,那么点B的坐标是_________.15.(3分)(2014•宝坻区二模)如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC 上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为_________.16.(3分)无论a取什么实数,点P(2a﹣1,a﹣3)都在直线l上,Q(m,n)是直线l上的点,则(m﹣2n﹣1)2的值为_________.三、全面答一答(共7小题,满分0分)17.下列四个图象中,哪些是y关于x的函数?请用函数定义判断之.18.有一张图纸被损坏,但上面有如图的两个标志点A(﹣3,1),B(﹣3,3)可认,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中C点的位置,并求△ABC的周长.19.尺规作图画线段AB的中垂线CD(E为垂足)时,为了方便起见,通常把四段弧的半径取成相等;其实不必如此,如图,若能确保弧①、②的半径相等(即AC=BC),再确保弧③、④的半径相等(即AD=BD),直线CD同样是线段AB的中垂线.请你给出证明.20.如图,已知△ABC、△DEF都是正三角形,D、E、G、H均在边上(1)写出图中与∠AGF必定相等的所有角.(2)对于(1)中的几个角,请你选择一个角证明与∠AGF相等.21.已知y是x的一次函数,且当x=﹣4时,y的值是9,当x=2时,y的值是﹣3.(1)求y关于x的函数关系式;(2)求过点P(1,2)且与原一次函数平行的直线与坐标轴围成的面积;(3)若函数图象上有一点P(m,n),点P到x轴的距离大于3且小于5,求m的取值范围.22.为了保护环境,某开发区综合治理指挥部决定购买A、B两种型号(每种至少购买1台)的污水处理设备共10台,经调查:购买一台A型设备比购买一台B型设备多4万元,购买3台B型设备比购买2台A型设备多6万元,每台设备处理污水量如下表所示(1)求A、B两种型号设备的价格各为多少万元?(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过148万元,问有几种购买方案?哪种方案每月能处理的污水量最多?污水量最多为多少吨?A型B型220 180处理污水量(吨/月)23.如图,在直角坐标系中,一次函数y=x+2的图象与x轴交于点A,与y轴交于点B,点C的坐标为(2,0),连接BC.(1)判断△ABC是不是等腰直角三角形,并说明理由;(2)若点P在线段BC的延长线上运动(P不与点C重合),连结AP,作AP的垂直平分线交y轴于点E,垂足为D,分别连结EA,EP;①当点P在运动时,∠AEP的度数是否变化?若变化,请说明理由;若不变,求出∠AEP的度数;②若点P从点C出发,运动速度为每秒1个单位长度,设△AOE的面积为S,点P的运动时间为t秒,求S关于t的函数关系式.参考答案与试题解析一、仔细选一选(共10小题,每小题3分,满分30分)1.(3分)在平面直角坐标系中,点(﹣2,3)所在的象限是()A .第一象限B.第二象限C.第三象限D.第四象限考点:点的坐标.分析:根据各象限内点的坐标特征解答.解答:解:点(﹣2,3)在第二象限.故选B.点评:本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).2.(3分)(2002•福州)等腰三角形的两边长分别为2和7,则它的周长是()A .9 B.11 C.16 D.11或16考点:等腰三角形的性质;三角形三边关系.专题:分类讨论.分析:在三角形中,两边之和大于第三边.所以,据此很容易找到等腰三角形的腰与底边.解答:解:(1)假设等腰三角形的腰是2,则2+2=4,4<7,也就是说两边之和小于第三边,所以假设不成立;(2)假设等腰三角形的腰是7,则7+7=14,14>7,也就是说两边之和大于第三边;7﹣7=0,则0<2,即两边之差小于第三边,所以假设成立,所以等腰三角形的周长是7+7+2=16,即等腰三角形的周长是16.故选C.点评:解答本题的难点是分清等腰三角形的腰的长度与底边的长度,如何来区分呢?根据三角形中的三边关系,即两边之和大于第三边,两边之差小于第三边.3.(3分)(2013•宾阳县一模)不等式组的解集在数轴上表示为()A .B.C.D.考点:在数轴上表示不等式的解集;解一元一次不等式组.分析:首先解不等式组中的每个不等式,然后再数轴上表示即可.解答:解:解不等式①得:x≥﹣1;解不等式②得:x<1.则不等式组的解集是:故选B.点评:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.4.(3分)下列函数中,y的值随着x值的增大而增大的是()A .y=x+1 B.y=﹣x C.y=1﹣x D.y=﹣x﹣1考点:一次函数的性质;正比例函数的性质.分析:根据一次函数的性质对各选项进行逐一分析即可.增大而增大,故本选项正确;B、∵函数y=﹣x中k=﹣1<0,∴y的值随着x值的增大而减小,故本选项错误;C、∵函数y=1﹣x中k=﹣1<0,∴y的值随着x值的增大而减小,故本选项错误;D、∵函数y=﹣x﹣1中k=﹣1<0,∴y的值随着x值的增大而减小,故本选项错误.故选A.点评:本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,k>0,y随x的增大而增大;k<0,y随x的增大而减小.5.(3分)如图,一次函数y=kx+b的图象与y轴的交点坐标是(0,1),则关于x的不等式kx+b>1的解是()A .x>1 B.x<1 C.x>0 D.x<0考点:一次函数与一元一次不等式.分析:根据一次函数y=kx+b的图象过点(0,1),得出y的值小于1的点都符合条件,从而得出x的解集.解答:解:∵y=kx+b的图象过点(0,1),∴由图象可知y>1,∴kx+b>1的解集是x<0.故选D.点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.6.(3分)若a >b ,则下列各式中一定成立的是( ) A . ma >mb B .c 2a >c 2b C .1﹣a >1﹣b D . (1+c 2)a >(1+c 2)b考点: 不等式的性质.分析:根据不等式的性质:①不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;③不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变进行计算,即可选出正确答案.解答:解:A 、当m <0时,ma <mb ,故此选项错误; B 、当c =0时,c 2a =c 2b ,故此选项错误; C 、a >b ,则1﹣a <1﹣b ,故此选项错误; D 、a >b ,1+c 2>0,则(1+c 2)a >(1+c 2)b ,故此选项正确; 故选:D .点评:此题主要考查了不等式的基本性质,关键是熟练掌握不等式的性质.7.(3分)甲、乙、丙、丁4个人步行的距离和花费的时间如图,按平均值计算,则走的最慢的是( )A . 甲B .乙 C .丙 D .丁 考点: 勾股定理的应用.解答:解:由图可知,甲的速度==0.02(千米/分);乙的速度==0.05(千米/分);丙的速度==0.1(千米/分);丁的速度==0.25(千米/分).∵0.02<0.05<0.1<0.25,∴甲的速度最慢.故选A.点评:本题考查的是有理数的大小比较,熟知正数比较大小的法则是解答此题的关键.8.(3分)(2012•江干区一模)将一根铁丝围成一个等腰三角形,围成的三角形的底边长y与腰长x之间的函数关系可能为()A .B.C.D.考点:函数的图象;三角形三边关系;等腰三角形的性质.分析:根据周长公式即可得到x和y之间的等式,变形即可得到y 与x之间的函数关系.利用三角形的边长是正数和两边和大于第三边求得自变量的取值范围.解答:解:根据题意,得y=等腰三角形的周长﹣2x,根据三角形的三边关系得,2x>y,y>0,所以y与x之间的函数图象为一次函数,图象在第一象限,y随x的增大而减小,则符合条件的图象是B.故选B.点评:本题考查了函数的图象,现实生活中存在大量成一次函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.9.(3分)如图,△ABC中,BC=8,AD是中线,∠ADB=60°,将△ADB沿AD折叠至△ADB′,则点C到B′的距离是()A .4 B.2C.3 D.2考点:翻折变换(折叠问题).分析:先根据中线的性质得BD=DC=4,再由轴对称的性质得B′D=BD=4,∠ADB′=∠ADB=60°,那么根据平角的定义求出∠B′DC=60°,从而判定△B′DC为等边三角形即可求解.解答:解:△ABC中,∵BC=8,AD是中线,∴BD=DC=4.由轴对称的性质可得:B′D=BD=4,∠ADB′=∠ADB=60°,∴∠B′DC=60°,∴△B′DC为等边三角形,∴B′C=B′D=DC=4.故选A.点评:本题考查翻折变换(折叠问题),判断出△B′DC是等边三角形是解决本题的突破点,本题难度适中.用到的知识点为:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;有一个角是60°的等腰三角形是等边三角形.10.(3分)如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+∠C;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是()A .①B.②③C.①②D.①③考点:角平分线的性质;三角形内角和定理;等腰三角形的判定与性质.分析:根据三角形的内角和定理可得∠BAC+∠ABC=180°﹣∠C,再根据角平分线的定义可得∠OAB+∠OBA=(∠BAC+∠ABC),然后根据三角形的内角和定理列式整理即可得解,判断出①正确;根据角平分线的定义判断出点O在∠ACB的平分线上,从而得到点O不是∠ACB的平分线的中点,然后判断出②错误;根据角平分线上的点到角的两边距离相等可得点D到AC的距离等于OD,再利用三角形的面积公式列式计算即可得到S△CEF=ab,判断出③正确.解答:解:在△ABC中,∠BAC+∠ABC=180°﹣∠C,∵∠BAC和∠ABC的平分线相交于点O,∴∠OAB+∠OBA=(∠BAC+∠ABC)=90°﹣∠C,在△AOB中,∠AOB=180°﹣(90°﹣∠C)=90°+∠C,故①正确;∵∠BAC和∠ABC的平分线相交于点O,∴点O在∠ACB的平分线上,∴点O不是∠ACB的平分线的中点,∵EF∥AB,∴E,F一定不是AC,BC的中点,故②错误;∵点O在∠ACB的平分线上,∴点D到AC的距离等于OD,∴S△CEF=(CE+CF)•OD=•2b•a=ab,故③正确;综上所述,正确的是①③.故选D.点评:本题考查了角平分线的定义,三角形的内角和定理,角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记各性质并准确识图是解题的关键.二、认真填一填(共6小题,每小题3分,满分18分)11.(3分)证明命题“x(x﹣5)=0,则x=5”是假命题,反例是x=0.考点:命题与定理.分析:举出一个能使得方程成立的非5的根即可.解答:解:当x=0时,0×(0﹣5)=0,故反例为x=0,故答案为:x=0.点评:本题考查了命题与定理的知识,判断一个命题是假命题时,往往举出反例.12.(3分)如图,在△ABC中,AB=AC,外角∠ACD=110°,则∠A=40°.考点:等腰三角形的性质.分析:先得到∠ACB的度数,利用等腰三角形的性质和三角形内角和求出顶角A.解答:解:∵AB=AC,∴∠ABC=∠ACB.而∠ACD=110°,∴∠ACB=∠ABC=180°﹣110°=70°,∴∠A=180°﹣70°﹣70°=40°.故答案为:40.点评:考查了三角形的内角和定理与等腰三角形的两底角相等的性质.13.(3分)直角三角形的两直角边长分别为6和8,则斜边中线的长是5.考点:勾股定理.专题:计算题.分析:已知直角三角形的两条直角边,根据勾股定理即可求斜边的长度,根据斜边中线长为斜边长的一半即可解题.解答:解:已知直角三角形的两直角边为6、8,则斜边长为=10,故斜边的中线长为×10=5,故答案为5.点评:本题考查了勾股定理在直角三角形中的运用,考查了斜边中线长为斜边长的一半的性质,本题中正确的运用勾股定理求斜边的长是解题的关键.14.(3分)(2004•金华)△ABO中,OA=OB=5,OA边上的高线长为4,将△ABO放在平面直角坐标系中,使点O 与原点重合,点A在x轴的正半轴上,那么点B的坐标是(3,4),(﹣3,4),(﹣3,﹣4),(3,﹣4).考点:坐标与图形性质;勾股定理.专题:压轴题.分析:建立如图所示的平面直角坐标系,再以O为圆心,5为半径作圆,作直线y=±4,与⊙O交于四点B1,B2,B3,B4,即为所求.解答:解:如图,建立平面直角坐标系,以O为圆心,5为半径作圆,作直线y=±4,与⊙O交于点B1,B2,B3,B4,即为所求.易求点B1的坐标为(3,4);点B2的坐标为(﹣3,4);点B3的坐标为(﹣3,﹣4);点B4的坐标为(3,﹣4).故点B的坐标是(3,4),(﹣3,4),(﹣3,﹣4),(3,﹣4).点评:考查三角形的高、解直角三角形与点的坐标等知识.综合运用所学知识,去解决此题.15.(3分)(2014•宝坻区二模)如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB 、BC AC=18,GF=6,则F点到AC的距离为6﹣6.上,且BD=BE.若考点:分析:过点B作BH⊥AC于H,交GF于K,根据等边三角形的性质求出∠A=∠ABC=60°,然后判定△BDE是等边三角形,再根据等边三角形的性质求出∠BDE=60°,然后根据同位角相等,两直线平行求出AC∥DE,再根据正方形的对边平行得到DE∥GF,从而求出AC∥DE∥GF,再根据等边三角形的边的与高的关系表示出KH,然后根据平行线间的距离相等即可得解.解答:解:如图,过点B作BH⊥AC于H,交GF于K,∵△ABC是等边三角形,∴∠A=∠ABC=60°,∵BD=BE,∴△BDE是等边三角形,∴∠BDE=60°,∴∠A=∠BDE,∴AC∥DE,∵四边形DEFG是正方形,GF=6,∴DE∥GF,∴AC∥DE∥GF,∴KH=18×﹣6×﹣6=9﹣3﹣6=6﹣6,∴F点到AC的距离为6﹣6.故答案为:6﹣6.点评:本题考查了正方形的对边平行,四条边都相等的性质,等边三角形的判定与性质,等边三角形的高线等于边长的倍,以及平行线间的距离相等的性质,综合题,但难度不大,熟记各图形的性质是解题的关键.16.(3分)无论a取什么实数,点P(2a﹣1,a﹣3)都在直线l上,Q(m,n)是直线l上的点,则(m﹣2n﹣1)2的值为16.考点:一次函数图象上点的坐标特征.分析:先令a=0,求出P点坐标,再令a=1得出P点坐标,利用待定系数法求出直线l的解析式,再把Q(m,n)代入求出m、n的关系,代入代数式进行计算即可.解答:解:令a=0,则P(﹣1,﹣3);令a=1,则P(1,﹣2),∵设直线l的解析式为y=kx+b(k≠0),则,解得,∴直线l的解析式为y=x﹣,∵Q(m,n)是直线l上的点,∴m﹣=n,即m﹣2n=5,∴(m﹣2n﹣1)2=(5﹣1)2=16.故答案为:16.点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.三、全面答一答(共7小题,满分0分)17.下列四个图象中,哪些是y关于x的函数?请用函数定义判断之.考点:函数的概念.分析:根据函数的定义,设在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,x是自变量,进而判断得出即可.解答:解:由函数的定义可得出:①②③都是y关于x的函数,④中当x每取一个值y有2个值对应,则y不是x的函数.点评:此题主要考查了函数的概念,正确把握函数定义得出是解题关键.18.有一张图纸被损坏,但上面有如图的两个标志点A(﹣3,1),B(﹣3,3)可认,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中C点的位置,并求△ABC的周长.考点:坐标确定位置.分析:先根据A点坐标画出直角坐标系,再描出点C,然后利用两点间的距离公式计算出AB、AC、BC,再计算三角形的周长.解答:解:根据A(﹣3,1),B(﹣3,﹣3)画出直角坐标系,描出点C(3,2),如图,AC==,AB=1+3=4,BC==,所以△ABC的周长=+4+.点评:本题考查了坐标确定位置:直角坐标平面内点的位置可由点的坐标确定,点与有序实数对一一对应.也考查了两点间的距离公式.19.尺规作图画线段AB的中垂线CD(E为垂足)时,为了方便起见,通常把四段弧的半径取成相等;其实不必如此,如图,若能确保弧①、②的半径相等(即AC=BC),再确保弧③、④的半径相等(即AD=BD),直线CD同样是线段AB的中垂线.请你给出证明.考点:作图—基本作图;全等三角形的判定与性质;线段垂直平分线的性质.分析:利用全等三角形的对应角相等、对应边成比例即可证得CD是线段AB的中垂线.解答:证明:∵AC=BC,AD=BD,CD=CD,∴△ACD≌△BCD,∴∠ACE=∠BCE,∴AE=BE,CD⊥AB,即CD是AB的中垂线.点评:本题考查了线段的垂直平分线、全等三角形的判定与性质及基本作图的知识,属于基础题,比较简单.20.如图,已知△ABC、△DEF都是正三角形,D、E、G、H均在边上(1)写出图中与∠AGF必定相等的所有角.(2)对于(1)中的几个角,请你选择一个角证明与∠AGF相等.考点:等边三角形的性质.分析:(1)根据等边三角形的三个角都是60°和三角形的一个外角等于与它不相邻的两个内角的和以及对顶角相等解答;(2)根据对顶角相等和三角形的外角性质进行证明.解答:(1)解:与∠AGF必定相等的角有:∠DGH、∠ADE、∠BEH;(2)证明:①∠DGH=∠AGF(对顶角相等);②在△ADG中,∠AGF=∠A+∠ADG=60°+∠ADG,∵∠ADE=∠ADG+∠EDF=∠ADG+60°,∴∠ADE=∠AGF;③∵△ABC、△DEF均为正三角形,∴∠F=60°=∠C,∴∠AGF=∠F+GHF=∠C+CHE=∠BEH.点评:本题考查了等边三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,对顶角相等的性质,熟记各性质并准确识图是解题的关键.21.已知y是x的一次函数,且当x=﹣4时,y的值是9,当x=2时,y的值是﹣3.(1)求y关于x的函数关系式;(2)求过点P(1,2)且与原一次函数平行的直线与坐标轴围成的面积;(3)若函数图象上有一点P(m,n),点P到x轴的距离大于3且小于5,求m的取值范围.考点:待定系数法求一次函数解析式;一次函数图象上点的坐标特征;两条直线相交或平行问题.专题:计算题.分析:(1)设y=kx+b,将x与y两对值代入计算求出k与b的值,即可确定出解析式;(2)根据题意设出直线方程,将P坐标代入确定出解析式,即可确定出直线与坐标轴围成的面积;(3)P到x轴的距离即为P纵坐标,求出横坐标范围即为m的范围.解答:解:(1)设y=kx+b,将x=﹣4,y=9;x=2,y=﹣3代入得:,解得:k=﹣2,b=1,则y与x的关系式为y=﹣2x+1;(2)设与一次函数y=﹣2x+1平行的直线解析式为y=﹣2x+p,将P(1,2)代入得:2=﹣2+p,即p=4,所求直线解析式为y=﹣2x+4,令x=0,得到y=4;令y=0,得到x=2,则直线与坐标轴围成的面积为×4×2=4;(3)根据P(m,n),3<n<5,且n=﹣2m+1,得到3<﹣2m+1<5,解得:﹣2<m<﹣1.点评:此题考查了待定系数法求一次函数解析式,以及一次函数的性质,熟练掌握待定系数法是解本题的关键.22.为了保护环境,某开发区综合治理指挥部决定购买A、B两种型号(每种至少购买1台)的污水处理设备共10台,经调查:购买一台A型设备比购买一台B型设备多4万元,购买3台B型设备比购买2台A型设备多6万元,每台设备处理污水量如下表所示(1)求A、B两种型号设备的价格各为多少万元?(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过148万元,问有几种购买方案?哪种方案每月能处理的污水量最多?污水量最多为多少吨?A型B型220 180处理污水量(吨/月)考点:一元一次不等式的应用;二元一次方程组的应用.分析:(1)设A、B两种型号设备的价格各为x万元,y万元,根据购买一台A型设备比购买一台B型设备多4万元,购买3台B型设备比购买2台A型设备多6万元,列方程组求解;(2)设购买A型号a台,B型号(10﹣a)台,根据总资金不超过148万元,列不等式,求出a的取值范围,然后求出购买方案.解答:解:(1)设A、B两种型号设备的价格各为多x万元,y万元,由题意得,,解得:,答:A、B两种型号设备的价格各为18万元,14万元;(2)设购买A型号a台,B型号(10﹣a)台,由题意得,18a+14(10﹣a)≤148,解得:a≤2,则共有2种购买方案:A种型号买1台,B种型号买9台,处理污水量为:220+180×9=1840(吨);A种型号买2台,B种型号买8台,处理污水量为:220×2+180×8=1880(吨).答:A种型号买2台,B种型号买8台,处理污水量最多,为1880吨.点评:本题考查了一元一次不等式和二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出题目中的等量关系和不等关系,列方程和不等式求解.23.如图,在直角坐标系中,一次函数y=x+2的图象与x轴交于点A,与y轴交于点B,点C的坐标为(2,0),连接BC.(1)判断△ABC是不是等腰直角三角形,并说明理由;(2)若点P在线段BC的延长线上运动(P不与点C重合),连结AP,作AP的垂直平分线交y轴于点E,垂足为D,分别连结EA,EP;①当点P在运动时,∠AEP的度数是否变化?若变化,请说明理由;若不变,求出∠AEP的度数;②若点P从点C出发,运动速度为每秒1个单位长度,设△AOE的面积为S,点P的运动时间为t秒,求S关于t的函数关系式.考一次函数综合题.点:分析:(1)由一次函数y=x+2求出A、B两点,再根据A、B、C的坐标求得OA=OB=OC=2,AC=4,进而求得∠ABO=∠BAO=∠CBO=∠BCO=45°,AB=BC=2,∠ABC=90°,则可证△ABC为等腰直角三角形.(2)连接EC,由于E在y轴上,即E在AC的垂直平分线上,所以EA=EC,故∠ECA=∠EAC,而E在AP的垂直平分线上,同理可求得EA=EP,即EC=EP=EA,那么∠ECP=∠EPC;由三角形的外角的性质可知∠ACP=∠ECA+∠ECP=135°,那么∠EAC、∠EPC的度数和也是135°,由此可求得∠AEP=360°﹣270°=90°,即∠AEP的度数不变.(3)过E作EM⊥PC于M,由(2)知△ECP是等腰三角形,则CM=PM=,在Rt△BEM中,∠EBM=45°,BM=2+,通过解直角三角形即可求得BE的长,从而可得到OE的长,到此,可根据三角形的面积公式表示出△ACE的面积,从而求得S的表达式,由此得解.解答:解:(1)如图1,由一次函数y=x+2,则A(﹣2,0),B(0,2),C(2,0).∴OA=OB=OC=2,AC=4,∴△AOB和△COB是等腰直角三角形,∴∠ABO=∠BAO=∠CBO=∠BCO=45°,∴AB=BC=2,∠ABC=90°∴△ABC为等腰直角三角形.(2)∠AEP的度数不变化;如图2,连接EC,∵E点在y轴上,且A、C关于y轴对称,∴E点在线段AC的垂直平分线上,即EA=EC;∵E点在线段AP的垂直平分线上,则EA=EP,∴EA=EP=EC,∴∠EAC=∠ECA,∠ECP=∠EPC;∵∠BCA=45°,即∠ACP=∠ECA+∠ECP=∠BAC+∠ABC=135°,∴∠EAC+∠EPC=135°,即∠EAC+∠EPC+∠ACP=270°,故∠AEP=360°﹣270°=90°,∴∠AEP的度数不会发生变化,为定值90°.(3)如图3,过E作EM⊥BP于M、过A作AN⊥BP于N;由(2)知:△CEP是等腰三角形,则有:CM=MP=CP=;∴BM=BC+CM=2+;在Rt△BEM中,∠MBE=45°,则有:BE=BM=(2+);∴OE=BE﹣OB=(2+)﹣2=2+t;∴S△AEC=AC•OE=×4×(2+t)=4+t,∴S=S△AEC=2+t.故S=t+2.点评:此题主要考查了一次函数与三角形的相关知识,涉及到:等腰直角三角形、等腰三角形的判定和性质,三角形面积的求法,解直角三角形等重要知识点.参与本试卷答题和审题的老师有:星期八;nhx600;zhjh;HJJ;sjzx;sd2011;CJX;lantin;499807835;mmll852;wangming;HLing;ZJX;gsls;sks;caicl;杨金岭(排名不分先后)21世纪教育网2014年12月12日。
杭州市滨江区2014-2015学年第一学期期末考试八年级数学试卷(含详细解答)

杭州市滨江区2014-2015学年第一学期期末考试八年级数学试卷考生须知:1.本试卷满分120分,考试时间100分钟.2.答题前,必须在答题纸指定位置填写学校、班级、姓名、座位号(写在学校上面). 3.必须在答题纸的对应答题位置上答题,写在其他地方无效. 答题方式详见答题纸上的说明. 4.不能使用计算器;考试结束后,上交答题纸.试题卷一、选择题:(本题共有10小题,每小题3分,共30分) 1.下列各组数不可能是一个三角形的边长的是( )A .1,2,3,B .4,4,4C . 6,6,8D .7,8,9 2.若x >y ,则下列式子错误的是( )D .55yx > A .x ﹣2>y ﹣2 B .x +1>y +1 C .﹣5x >﹣5y 3.如图,△ABC 中,∠ACB =90°,AD=BD ,且CD =4,则AB =( ) A .4 B .8 C .10 D .16 4.下列句子属于命题的是( )A .正数大于一切负数吗?B .将16开平方C .钝角大于直角D .作线段AB 的中点 5.对于一次函数y=kx-k(k 0≠),下列叙述正确的是( )A .当k >0时,函数图象经过第一、二、三象限B .当k >0时,y 随x 的增大而减小C .当k <0时,函数图象一定交于y 轴负半轴一点D .函数图象一定经过点(1,0) 6. 如图,在△ABC 和△DEF 中,B ,E ,C ,F 在同一条直线上,AB =DE ,AC=DF ,要使ΔABC ≌ΔDEF ,还需要添加一个条件是( ) A .BE=CF B . BE=EC C . EC=CF D .AC //DF 7. 若不等式组⎩⎨⎧<≥.2,x a x 有解,则a 的取值范围是( )A .2>aB .2<aC . 2≤aD .2≥a8. 已知点A (-3,2)与点B (x ,y )在同一条平行y 轴的直线上,且B 点到x 轴的矩离等于3,则B 点的坐标是( )A .(-3,3)B .(3,-3)C .(-3,3)或(-3,-3)D .(-3,3)或(3,-3) 9. 下列命题是真命题的是( ) A .等边对等角.B .周长相等的两个等腰三角形全等.C .等腰三角形的角平分线、中线和高线互相重合.D .三角形一条边的两个顶点到这条边上的中线所在直线的距离相等.DCAB(第3题)FEDCBA(第6题)10. 如图,等腰Rt △ABC 中,∠ABC =90°,O 是△ABC 内一点,OA =6,OB =24,OC =10, O '为△ABC 外一点,且△CBO ≌△AB O ',则四边形BO O A '的面积为( )A .10B .16C .40D . 80 二、填空题:(本题共有6小题,每小题4分,共24分) 11.使代数式x -4有意义的x 的取值范围是 ▲ .12.13.1415.如图,平面直角坐标系中有一正方形OABC ,点C 的坐标为 (-2,-1),则点A 坐标为 ▲ ,点B 坐标为 ▲ .16.如图,直线l :y=x+2交y 轴于点A ,以AO 为直角边长作等腰Rt ΔAOB , 再过B 点作等腰Rt Δ11BB A 交直线l 于点A 1 ,再过1B 点再作等腰Rt Δ212B B A 交直线l 于点A 2,以此类推,继续作等腰Rt Δ323B B A --- ,Rt Δn n n B B A 1-,其中点n A A A A ,...,,,21都在直线l 上, 点n B B B B ,...,,,21都在x 轴上,且1132321211,...,,,--∠∠∠∠n n n B B A B B A B B A BB A 都为直角.则点3A 的坐标为 ▲ ,点n A 的坐标为 ▲ . 三、解答题:(本题共有7小题,共66分) 17.(本小题满分10分) 解下列不等式(组):(1)2x -154≥+x ⎪⎩⎪⎨⎧≥+-+≤-x.-3)3(2,1512231)2(x x x )(3)82(32112+⨯-+18.(本小题满分6分)如图,已知△ABC ,其中AB=AC.(1)作AC 的垂直平分线DE ,交AC 于点D ,交AB 于点E ,连结CE (尺规作图,不写作法,保留作图痕迹);(2)在(1)所作的图中,若BC =7,AC =9,求△BCE 的周长.19.(本小题满分8分)已知y 是关于x 的一次函数,且当x =1时,y =-4;当x =2时,y =-6. (1)求y 关于x 的函数表达式;(第3题)O 'O BA(第15题)x y CBAO(第18题)CBA(第16题)yxlB 2A 2B 1A 1B AO(2)若-2<x <4,求y 的取值范围;(3)试判断点P (a ,-2a+3)是否在函数的图象上,并说明理由.20. (本小题满分10分)已知,△ABC 的三个顶点A ,B ,C 的坐标分别为A (4,0),B (0,-3),C (2,-4).(1) 在如图的平面直角坐标系中画出△ABC ,并分别写出点A ,B ,C 关于x 轴的对称点A',B’,C’的坐标; (2)将△ABC 向左平移5个单位,请画出平移后的''''''C B A ∆,并写出''''''C B A ∆各个顶点的坐标.(3)求出(2)中的△ABC 在平移过程中所扫过的面积.21. (本小题满分10分)如图,△ABC 中,AB=BC , ∠ABC =90°,F 为AB 延长线上一点,点E 在BC 上,且AE =CF(1)求证:△ABE ≌△CBF;(2)若︒=∠25CAE ,求.的度数ACF ∠22. (本小题满分10分)某商店销售A 型和B 型两种型号的电脑,销售一台A 型电脑可获利120元,销售一台B 型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中B 型电脑的进货量不超过A 型电脑的3倍.设购进A 型电脑x 台,这100台电脑的销售总利润为y 元. (1)求y 与x 的关系式;(2)该商店购进A 型、B 型电脑各多少台,才能使销售利润最大?(3)若限定商店最多购进A 型电脑60台,则这100台电脑的销售总利润能否为13600元?若能,请求出此时该商店购进A 型电脑的台数;若不能,请求出这100台电脑销售总利润的范围.23. (本小题满分12分)如图,直线l 1: y 1= 2+-x 与x 轴,y 轴分别交于A ,B 两点,点P (m ,3)为直线l 1上一点,另一直线l 2: y 2=b x +21过点P .(1)求点P 坐标和b 的值;(2)若点C 是直线l 2与x 轴的交点,动点Q 从点C 开始以每秒1个单位的速度向x 轴正方向移动.设点Q 的运动时间为t 秒.(第20题) xy–1–2–3–4–5–6–7–812345678–1–2–3–4–5–6–7–812345678O(第21题)EF BCA(第23题)xyQl 2l 1PCOA B①请写出当点Q 在运动过程中,△APQ 的面积S 与t 的函数关系式; ②求出t 为多少时,△APQ 的面积小于3;③是否存在t 的值,使△APQ 为等腰三角形?若存在,请求出t 的值;若不存在,请说明理由.八年级数学答案一、选择题:(本题共有10小题,每小题3分,共30分)二、 填空题:(本题6小题,每小题4分,共24分) 11. 4≤x 12. )1(;C 2分少一个变量扣,,r π 13 . 3; 14. 5 ; 15. A(-1,2) ,B(-3, 1);16.(14,16),(2n+1-2,2n+1)三:解答题(本题7小题,满分66分) 17.(本小题满10分)解:(1)6x ≥-4 ---------1分;32-≥x ---------1分(2)由①得,-19x ≤-13(或19x ≥13)---------1分,1913≥x ---------1分 由②得,,1-≥x ---------1分.1913≥∴x ---------1分 分分)原式(1-------------62223623222323-=-------+=18. (本小题满分6分)(1)图正确2分(痕迹不全不得分), 结论1分 (2)由垂直平分线性质得AE=CE-----1分ΔBCE 的周长=AB+BC ----------1分 =16----------------1分19.(本小题满分8分)(1)解:设y=kx+b ,把x =1时,y =-4,x =2时,y =-6代入y=kx+b 得⎩⎨⎧-----=+-=+分2624b k b k。
2012-2013学年浙江省杭州市西湖区八年级(下)期末数学试卷

2012-2013学年浙江省杭州市西湖区八年级(下)期末数学试卷2012-2013学年浙江省杭州市西湖区八年级(下)期末数学试卷一.仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内,注意可以用多种不同的方法来选取正确答案.1.(3分)要使式子有意义,则x的取值范围是()224.(3分)(2012•泰州)下列四个命题:①一组对边平行且一组对角相等的四边形是平行四边形;②对角线互相垂直且相等的四边形是正方形;③顺次连接矩形四边中点得到的四边形是菱形;5.(3分)(2007•滨州)关于x的一元二次方程(m+1)+4x+2=0的解为()6.(3分)(2012•泸州)已知三角形两边的长分别是3和6,第三边的长是方程x2﹣6x+8=0的根,则这个三角形的7.(3分)如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,若设计一种砌法,使矩形花园的面积为300m2.则AB长度为()8.(3分)阅读材料:对于任何实数,我们规定符号的意义是.按照这个规定,请你计算:当x2﹣4x+4=0时,的值()9.(3分)(2012•安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为()10.(3分)已知,在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3均在x轴正半轴上.若已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,且B1C1∥B2C2∥B3C3,则点A3的坐标是()),二.认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案11.(4分)化简:=_________.12.(4分)已知如图,在线段BG同侧作正方形ABCD和正方形CEFG,其中BG=10,BC:CG=2:3,则S△ECG= _________,S△AEG=_________.13.(4分)(2012•包头)关于x的两个方程x2﹣x﹣2=0与有一个解相同,则a=_________.14.(4分)已知下列命题:①若a>0,b>0,则a+b>0;②若a2≠b2,则a≠b;③对角线互相垂直的平行四边形是菱形;④直角三角形斜边上的中线等于斜边的一半.其中原命题与逆命题均为真命题的序号是_________.15.(4分)如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为_________米.16.(4分)如图,矩形ABCD的边AB在x轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点,则:(1)a的取值范围是_________;(2)若设直线PQ为:y=kx+2(k≠0),则此时k的取值范围是_________.三.全面答一答(本题有7个小题,共66分)解答应写出必要的文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.(6分)(1)解方程:(x+1)(x﹣5)=1(2)关于x的一元二次方程x2+bx+c=0(c<0)是否有实数解,请你作出判断并说明理由.18.(8分)已知在如图4×4的方格中,有一个格点三角形ABC(三个顶点均在格点上),其中AB=,BC=,AC=.(1)请你在方格中画出该三角形;(2)求△ABC的面积;(3)求△ABC中AC边上的高的长(结果保留根号).19.(8分)一次测试八年级若干名学生1分钟跳绳次数的频数分布直方图如图所示,请根据这个直方图回答下列问题:(1)已知自左至右第2、3组(组中值分别为145、155)的频率之和为0.28,第3、4、5组(组中值分别为155、165、175)的频率之和为0.8,则参加测试的总人数有_________人,第3组的频数为_________人,第4组的频率为_________,并将直方图补充完整;(2)若图中自左至右各组的跳绳平均次数分别为137次,146次,156次,164次,177次,则参加测试的学生跳绳的平均次数为_________(只需列出算式,不用计算结果);(3)若测试所得数据的中位数是160次,则测试次数为160次的学生至少有_________人.(直方图中每一组包括前一个边界值,不包括后一个边界值)20.(10分)如图,已知AG⊥BD,AF⊥CE,BD,CE分别是∠ABC和∠ACB的角平分线,若BF=2,ED=3,GC=4.(1)求FG的长;(2)求△ABC周长.21.(10分)平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是线段AC上的两动点,分别从A、C 两点以1cm/s的速度向C、A运动,若BD=12cm,AC=16cm.(1)四边形DEBF是平行四边形吗?请说明理由;(2)当运动时间t为多少时,四边形DEBF是矩形.22.(12分)(2012•南京)某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.(1)若该公司当月售出3部汽车,则每部汽车的进价为_________万元;(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)23.(12分)已知直角梯形ABCD如图放置在平面直角坐标系中,∠DCB=30°,AB边在y轴上,点D的横坐标为6,CQ⊥x轴,垂足为Q,点Q的横坐标为12,过CD的直线l交x轴于点E,E点坐标为(18,0).(1)求直线l的解析式,以及点A和点B的坐标;(2)P为线段CD上一动点,连结PQ、OP,探究△POQ的周长,并求出当周长最小时,P的坐标及此时的该三角形的周长;(3)点N从点Q(12,0)出发,沿着x轴以每秒1个单位长度的速度向点O运动,同时另一动点M从点B开始沿B﹣C﹣D﹣A的方向绕梯形ABCD运动,运动速度为每秒为2个单位长度,当其中一个点到达终点时,另一点也停止运动,设运动时间为t秒,连结MO和MN,试探究当t为何值时MO=MN.2012-2013学年浙江省杭州市西湖区八年级(下)期末数学试卷参考答案与试题解析一.仔细选一选(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内,注意可以用多种不同的方法来选取正确答案.1.(3分)要使式子有意义,则x的取值范围是()224.(3分)(2012•泰州)下列四个命题:①一组对边平行且一组对角相等的四边形是平行四边形;②对角线互相垂直且相等的四边形是正方形;③顺次连接矩形四边中点得到的四边形是菱形;5.(3分)(2007•滨州)关于x的一元二次方程(m+1)+4x+2=0的解为()6.(3分)(2012•泸州)已知三角形两边的长分别是3和6,第三边的长是方程x2﹣6x+8=0的根,则这个三角形的7.(3分)如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,若设计一种砌法,使矩形花园的面积为300m2.则AB长度为()8.(3分)阅读材料:对于任何实数,我们规定符号的意义是.按照这个规定,请你计算:当x2﹣4x+4=0时,的值()∴9.(3分)(2012•安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为()AC=BC===AC=BC=××,正八边形周围是四个全等三角形,面积和为:10.(3分)已知,在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3均在x轴正半轴上.若已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,且B1C1∥B2C2∥B3C3,则点A3的坐标是()),1=,=,×,=×==×==×=×=,M=+×=N=×=××)﹣=+++++,,二.认真填一填(本题有6个小题,每小题4分,共24分)要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案11.(4分)化简:=π﹣3.二次根式的性质:=12.(4分)已知如图,在线段BG同侧作正方形ABCD和正方形CEFG,其中BG=10,BC:CG=2:3,则S△ECG= 18,S△AEG=18.×××﹣13.(4分)(2012•包头)关于x的两个方程x2﹣x﹣2=0与有一个解相同,则a=4.代入=中得:=14.(4分)已知下列命题:①若a>0,b>0,则a+b>0;②若a2≠b2,则a≠b;③对角线互相垂直的平行四边形是菱形;④直角三角形斜边上的中线等于斜边的一半.其中原命题与逆命题均为真命题的序号是③④.15.(4分)如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为1米.16.(4分)如图,矩形ABCD的边AB在x轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点,则:(1)a的取值范围是﹣2≤a≤2;(2)若设直线PQ为:y=kx+2(k≠0),则此时k的取值范围是k≤﹣1或k≥1.三.全面答一答(本题有7个小题,共66分)解答应写出必要的文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.(6分)(1)解方程:(x+1)(x﹣5)=1(2)关于x的一元二次方程x2+bx+c=0(c<0)是否有实数解,请你作出判断并说明理由.;18.(8分)已知在如图4×4的方格中,有一个格点三角形ABC(三个顶点均在格点上),其中AB=,BC=,AC=.(1)请你在方格中画出该三角形;(2)求△ABC的面积;(3)求△ABC中AC边上的高的长(结果保留根号).,;.19.(8分)一次测试八年级若干名学生1分钟跳绳次数的频数分布直方图如图所示,请根据这个直方图回答下列问题:(1)已知自左至右第2、3组(组中值分别为145、155)的频率之和为0.28,第3、4、5组(组中值分别为155、165、175)的频率之和为0.8,则参加测试的总人数有50人,第3组的频数为8人,第4组的频率为0.4,并将直方图补充完整;(2)若图中自左至右各组的跳绳平均次数分别为137次,146次,156次,164次,177次,则参加测试的学生跳绳的平均次数为(只需列出算式,不用计算结果);(3)若测试所得数据的中位数是160次,则测试次数为160次的学生至少有8人.(直方图中每一组包括前一个边界值,不包括后一个边界值)=0.12;20.(10分)如图,已知AG⊥BD,AF⊥CE,BD,CE分别是∠ABC和∠ACB的角平分线,若BF=2,ED=3,GC=4.(1)求FG的长;(2)求△ABC周长.21.(10分)平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是线段AC上的两动点,分别从A、C 两点以1cm/s的速度向C、A运动,若BD=12cm,AC=16cm.(1)四边形DEBF是平行四边形吗?请说明理由;(2)当运动时间t为多少时,四边形DEBF是矩形.AO=CO=BD=6cm22.(12分)(2012•南京)某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.(1)若该公司当月售出3部汽车,则每部汽车的进价为26.8万元;(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)23.(12分)已知直角梯形ABCD如图放置在平面直角坐标系中,∠DCB=30°,AB边在y轴上,点D的横坐标为6,CQ⊥x轴,垂足为Q,点Q的横坐标为12,过CD的直线l交x轴于点E,E点坐标为(18,0).(1)求直线l的解析式,以及点A和点B的坐标;(2)P为线段CD上一动点,连结PQ、OP,探究△POQ的周长,并求出当周长最小时,P的坐标及此时的该三角形的周长;(3)点N从点Q(12,0)出发,沿着x轴以每秒1个单位长度的速度向点O运动,同时另一动点M从点B开始沿B﹣C﹣D﹣A的方向绕梯形ABCD运动,运动速度为每秒为2个单位长度,当其中一个点到达终点时,另一点也停止运动,设运动时间为t秒,连结MO和MN,试探究当t为何值时MO=MN.∴∴;当y=),x∴,,∴s6+综上可得:参与本试卷答题和审题的老师有:dbz1018;sjzx;yangwy;WWF;gsls;lanyan;zhjh;sd2011;星期八;HLing;zjx111;HJJ;caicl;xiawei(排名不分先后)菁优网2014年6月19日。
2014——2015学年度第一学期八年级数学期中考试卷(含答案)

2014——2015学年度第一学期 八年级数学期中考试卷(含答案)(考试时间:100分钟 满分:120分)一、选择题:(每小题3分,共42分)下列各题都有A 、B 、C 、D 四个答案供选择,其中只有一个答案是正确的,请把认为正确1、4的算术平方根是A . 2B . 2-C . 2±D . 2±2、与数轴上的点成一一对应关系的数是A . 有理数B . 无理数C . 实数D . 整数 3、下列从左边到右边的变形,属于因式分解的是A . 1)1)(1(2-=-+x x x B . 1)2(122+-=+-x x x xC . )4)(4(422y x y x y x -+=-D . 22)3(96-=+-x x x4、下列命题中是真命题的是A .三角形的内角和为180°B .同位角相等C .三角形的外角和为180°D .内错角相等 5、使式子32+x 有意义的实数x 的取值范围是A .32>x B . 23>x C . 23-≥x D . 32-≥x6、在实数73,1+π,4,3.14,38,8,0, 11.21211211中,无理数有A . 2个B . 3个C . 4个D . 5个7、一个正方形的边长增加了cm 2,面积相应增加了232cm ,则这个正方形的边长为 A . 6cm B . 5cm C . 8cm D . 7cm8、计算:()20132013125.08-⨯等于A . 1-B . 1C . 2013D . 2013- 9、下列条件中,不能证明△ABC ≌△'''C B A 的是 A .''''C A AC B B A A =∠=∠∠=∠,,学校:班别: 姓名: 座号:………………………………………………………………装………………订………………线………………………………………………得分 B'C BB .''''B A AB B B A A =∠=∠∠=∠,,C .'''''C A AC A A B A AB =∠=∠=,,D .'''''C B BC B A AB A A ==∠=∠,, 10、下列算式计算正确的是A .523a a a =+B .623a a a =⋅C .923)(a a =D . a a a =÷2311、估计15的大小在A . 2和3之间B . 3和4之间C . 4和5之间D . 5和6之间12、若(x+a)(x-5)展开式中不含有x 的一次项,则a 的值为A . 5-B . 5C . 0D . 5± 13、如右图,△ABC ≌△EDF ,DF =BC ,AB=ED ,AF =20,EC =10,则AE 等于 A . 5 B . 8 C .10 D . 15 14、如果则的值分别是A . 2 和 3B . 2和-3C . 2和D .二、填空题:(每小题4分,共16分) 15、计算:=⨯-2016201020132________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
杭州市西湖区2014-2015学年第一学期期末考试八年级数学试卷考生须知:1.本试卷分试题卷和答题卷两部分.满分120分,考试时间100分钟.2.答题前,必须在答题卷上填写校名,班级,姓名,座位号.3.不允许使用计算器进行计算,凡题目中没有要求取精确值的,结果中应保留根号或π.一.仔细选一选(本题有10个小题,每小题3分,共30分)每小题给出的四个选项中,只有一个是正确的,注意可以用多种不同的方法来选取正确答案.1. 在平面直角坐标系中,点A坐标为(1,3),将点A向左平移2个单位长度,得到点A′,则点A′的坐标为()A. (3,3)B. (-1,3)C. (0,3)D. (3,-1)2. 下列说法中:①法国数学家笛卡尔首先建立了坐标思想②全等三角形对应边上的中线长相等③若a2>b2,则a>b④有两边和其中一条边所对的一个角对应相等的两个三角形一定全等,说法正确的为()A.①②B.②④C.②③④D.①③④3.已知A(x1,1),B(x2,2)是一次函数y=-2x+3的图象上的两点,则下列判断正确的是()A.x1< x2B.x1> x2C.x1<0,x2>0 D.以上结论都不正确4.已知点P1(-a+1,-3)和点P2(3,b)关于y轴对称,则(a+b)2015的值为()A. 72015B. -1C. 1D.(-3)20155.如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=780,则∠FOG的度数为()A. 78°B. 102°C. 120°D. 112°第5题图6.已知P为△ABC的边AB上的点,且AP2+BP2+CP2-2AP-2BP-2CP+3=0,则△ABC的形状为()A. 等腰三角形B. 直角三角形C. 等腰直角三角形D. 等边三角形7. 观察图中的函数图象,可以得到关于x 的不等式 ax-bx <c 的解为( )A . x <-2B .x <4C .x >-2D .x >48. 已知点M 为某封闭图形边界上一定点,动点P 从点M 出发,沿其边界顺时针匀速运动一周.设点P 运动的时间为x ,线段MP 的长为y .表示y 与x 的函数关系的图象大致如右图所示,则该封闭图形可能是( )9. 如图,在长方形网格中,每个小长方形的长为3,宽为1,A 、B 两点在网格格点上.若点C 也在网格格点上,以A 、B 、C 为顶点的三角形面积为3,则满足条件的点C 有( )A. 4个B. 6个C. 9个D. 10个10. 已知平面直角坐标系上的动点A (x ,y ),满足x =1+2a ,y =1-a ,其中-2≤a ≤3,有下列四个结论:①-3≤x ≤7 ②-2≤y ≤0 ③ 0≤x +y ≤5 ④若x ≤0,则0≤y ≤3. 其中正确的结论是( ) A .②④ B .② C .①③ D .③④二.认真填一填(本题有6个小题,每小题4分,共24分) 要注意认真看清楚题目的条件和要填写的内容,尽量完整地填写答案. 11. 已知点P (a +1,9)在直线y =-2x +7上,则a = ▲ .12. 若关于x 的方程3mx+8x=-3的解是负数,则m 的取值范围是 ▲ . 13. 如图,正方形OABC 的两边OA 、OC 分别在x 轴、y 轴上,点D (5,3)在边AB 上,以C 为中心,把△CDB 顺时针旋转90°,则旋转后点D 的对应点D ′的坐标是 ▲ .第7题图第8题图第9题图第13题图14. 如图,已知在长方形纸条ABCD 中,点G 在边BC 上,BG =2CG ,将该纸条沿着过点G 的直线翻折后,点C 、D 分别落在边BC 下方的点E 、F 处,且点E 、F 、B 在同一条直线上,折痕与边AD 交于点H ,HF 与BG 交于点M .设AB =t ,那么△GHM 的周长为 ▲ (用含t 的代数式表示)15. 如图,是一个底面半径为1cm ,高度为 2cm 的无盖圆柱形玻璃容器,A 、B 两点在容器顶部一条直径的两端,现有一只小甲虫在容器外.A 点正下方1cm 的M 处,要爬到容器内.B 点正下方距离底部1cm 的N 处,则这只小甲虫最短爬行的距离是__▲___cm .16. 有一组平行线a //b //c ,过点A 作AM ⊥b 于M ,作∠MAN =600,且AN =AM ,过点N 作CN ⊥AN 交直线c 于点C ,在直线b 上取点B 使BM =CN ,则△ABC 为 ▲ 三角形,若直线a 与b 间的距离为1,b 与c 间的距离为2,则AC = ▲ .三.全面答一答(本题有7个小题,共66分) 解答应写出必要的文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17. (本题满分6分)已知两条线段a ,b 和一个直角,请借助直角,以这两条线段的长度为两条边长构造直角三角形,请画出符合条件的直角三角形.18. (本题满分8分)小明放学骑车回家一共用了20分钟,回家的过程中,路程s 与时间t 的关系如图.请根据图像回答下列问题: (1)开始10分钟内的平均速度是多少?最后5分钟内的平均速度是多少呢?第14题图第15题图第16题图第17题图(2)经过15分钟后离家路程还有多远? (3)小明回家途中有没有停留?停留多少时间?19. (本题满分8分) 关于x 的不等式组⎩⎨⎧<->+2b x 53a x 2的解为-1<x <1,求ab 的值.20. (本题满分10分)等腰三角形ABC 中AB =AC =13,一边上的高为5,求底边BC 的长.21. (本题满分10分)某年级380名师生秋游,计划租用7辆客车,学校可提供租车费用共4000元,现有甲、乙两种型号客车,它们的载客量和租金如右表.(1)设租用甲种客车x 辆,租车总费用为y 元.求出y (元)与x (辆)之间的函数关系式;(2)有几种可行的租车方案?哪种租车方案能使预支的租车费用剩余最多?最多可剩余多少元?22. (本题满分12分)直线CP 是经过等腰直角三角形ABC 的直角顶点C ,并且在三角形的外侧所作的直线,点A 关于直线CP 的对称点为E ,连接BE ,CE ,其中BE 交直线CP 于点F . (1)若∠PCA =25°,求∠CBF 的度数.(2)连接AF ,设AC 与BE 的交点为点M ,请判断△AFM 的形状.第18题图甲种客车 乙种客车载客量(座/辆) 60 45 租金(元/辆)550450(3)求证:EF 2+BF 2=2BC 2.23. (本题满分12分)如图,在平面直角坐标系中,已知直线与x 轴交于点A (-1,0),与y 轴交于点C (0,-2).线段AC 的中垂线交x 轴于点B (23,0),垂足为点D . (1)求直线AC 的表达式.(2)求出点D 的坐标和△BAD 的面积.(3)过点B 作y 轴的平行线BH ,借助△BAD 的一边构造与△BAD 面积相等的三角形,第三个点P 在直线BH 上,求出符合条件的点P 的坐标.参考答案评分标准一、仔细选一选(本大题共10个小题;每小题3分,共30分)题号12345678910第22题图第23题图答案 B A B C D B C A C C二、认真填一填(每小题4分,共24分)11. -2; 12. m 83>-;13.(﹣2,0);14.t 32; 15.π5; 16. 等边,2132. . 三、全面答一答(本题共7小题,共66分)17. (本小题满分6分)形如△AOB 和△COB 的两种图形: 在△AOB 中,直角边OB =a ,斜边AB =b ; 在△COB 中,直角边OB =a ,直角边CO =b . 说明:正确做出一图4分,两图都正确得6分. 18.(本小题满分8分)解:(1)开始10分钟内的速度是0.2km /min ,最后5分钟0.3km /min .(4分) (2)经过15分钟后离家路程还有1.5km . (2分) (3)小明回家途中停留了5分钟. (2分) 19.(本小题满分8分) 解:不等式2x +a >3的解为32ax ->,(2分); 不等式5x -b <2的解为25b x +<,(2分)不等式组的解为-1<x <1,由题意得3-12215ab ⎧=-⎪⎪⎨+⎪=⎪⎩(2分),∴a =5,b =3;ab =15. (2分)20. (本小题满分10分)BC 长为:24或26或265 (做对1个得4分,做对2个得8分,做对3个得10分) 21. (本小题满分10分)解: (1)y =550x +450(7-x ) ∴y =100x +3150 (4分)(2)()1003150400060457380x x x +≤⎧⎨+-≥⎩ (2分)解得131732x ≤≤,又因为7x ≤,所以x 可以取5,6,7 (2分) ∵y =100x +3150是递增的一次函数,所以当x =5时可以取得最小值3650, ∴x =5时费用剩余最多,剩余350元. (2分) 22. (本小题满分12分)(1)由题意可知直线CP 是线段AB 的中垂线, ∵∠PCA =25°,∴∠PCE =25°,∴∠BCE =140°,∵CA =CB ,CE =CB , ∴∠CBF =20°. (4分) (2)△AFM 是直角三角形. (2分) ∵直线CP 是线段AB 的中垂线,∴FA =FE ,CE =CA ,CE =CB , ∴△ECF ≌△ACF ,∴∠CEM =∠CAF ,∠CEM =∠CBM , ∴∠CAF =∠CBM .在△AFM 与△BCM 中,∠CAF =∠CBM ,∠AMF =∠CMB∴∠AFM =∠BCB =90°,即:△AFM 是以AM 为斜边的直角三角形. (2分) (3)∵△AFM 是以AM 为斜边的直角三角形,∴∠AFB =∠ACB =90°, ∴AF 2+BF 2=AB 2 ,即:EF 2+BF 2=2BC 2. (4分) 23. (本小题满分12分)解:(1)直线AC 的表达式为y =-2x -2 (4分) (2)D (1-21-,), (2分) △BAD 的面积为45. (2分) (3)借助△BAD 的一边构造与△BAD 面积相等的三角形,如图,有5个点:P 135()24,,P 235(-)24,,P 33(1)2,,P 43(-1)2,,P 53(-10)2,. (4分)(4个或以上均满分)。
