高一数学必修二立体几何练习题含答案

合集下载

高中数学高一必修2空间立体几何试卷(有详细答案)

高中数学立体几何测试试卷学校：___姓名：___班级：___考号：__一．单选题1．一个圆锥的侧面展开图的圆心角为90°，它的表面积为a，则它的底面积为（）A．B．C．D．2．设α为平面，m，n为直线（）A．若m，n与α所成角相等，则m∥nB．若m∥α，n∥α，则m∥nC．若m，n与α所成角互余，则m⊥nD．若m∥α，n⊥α，则m⊥n3．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（）A．75°B．60°C．45°D．30°4．设α是空间中的一个平面，l，m，n是三条不同的直线，①若m⊂α，n⊂α，l⊥m，l⊥n，则l⊥α；②若l∥m，m∥n，l⊥α，则n⊥α；③若l∥m，m⊥α，n⊥α，则l∥n；④若m⊂α，n⊥α，l⊥n，则l∥m；则上述命题中正确的是（）A．①②B．②③C．②④D．③④5．已知一个铜质的五棱柱的底面积为16cm2，高为4cm，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（）A．2cm B．C．4cm D．8cm6、在正方体ABCD-A l B1C1D1中，P是正方体的底面A l B1C1D1（包括边界）内的一动点（不与A1重合），Q是底面ABCD内一动点，线段A1C与线段PQ相交且互相平分，则使得四边形A1QCP面积最大的点P有（）A．1个B．2个C．3个D．无数个7．如图所示几个空间图形中，虚线、实线使用不正确的有（）A．②③B．①③C．③④D．④二．填空题8、如图，在四棱锥S-ABCD中，SB⊥底面ABCD．底面ABCD为梯形，AB⊥AD，AB∥CD，AB=1，AD=3，CD=2．若点E是线段AD上的动点，则满足∠SEC=90°的点E的个数是______．9、一个正方体的六个面上分别标有字母A、B、C、D、E、F，如图是此正方体的两种不同放置，则与D面相对的面上的字母是______．10．设α、β为互不重合的平面，m、n为互不重合的直线，下列四个命题中所有正确命题的序号是______．①若m⊥α，n⊂α，则m⊥n；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β．③若m∥α，n∥α，则m∥n．④若α⊥β，α∩β=m，n⊂α，n⊥m，则n⊥β．三．简答题11、在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，S D=，在线段SA上取一点E（不含端点）使EC=AC，截面CDE与SB交于点F．（1）求证：四边形EFCD为直角梯形；（2）设SB的中点为M，当的值是多少时，能使△DMC为直角三角形？请给出证明．12、正三棱台的高为3，上、下底面边长分别为2和4，求这个棱台的侧棱长和斜高．13、已知三棱椎D-ABC，AB=AC=1，AD=2，∠BAD=∠CAD=∠BAC=90°，点E，F分别是BC，DE的中点，如图所示，（1）求证AF⊥BC（2）求线段AF的长．参考答案一．单选题1．一个圆锥的侧面展开图的圆心角为90°，它的表面积为a，则它的底面积为（）A．B．C．D．答案：A解析：解：设圆锥的母线为l，所以圆锥的底面周长为：，底面半径为：=，底面面积为：．圆锥的侧面积为：，所以圆锥的表面积为：+=a，底面面积为：=．故选A．2．设α为平面，m，n为直线（）A．若m，n与α所成角相等，则m∥nB．若m∥α，n∥α，则m∥nC．若m，n与α所成角互余，则m⊥nD．若m∥α，n⊥α，则m⊥n答案：D解析：解：对于选项A，若m，n与α所成角相等，m，n也可能相交、平行、异面；故A错误；对于选项B，若m∥α，n∥α，直线m，n也可能平行，也可能相交，还有可能异面；故B 错误；对于选项C，若m，n与α所成角互余，如与α所成角分别为30°和60°，直线m，n所成的角有可能为30°；故C错误；对于选项D，根据线面垂直的性质，容易得到m⊥n；故D正确；故选D．3．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（）A．75°B．60°C．45°D．30°答案：C解析：解析：如图，四棱锥P-ABCD中，过P作PO⊥平面ABCD于O，连接AO则AO是AP在底面ABCD上的射影．∴∠PAO即为所求线面角，∵AO=，PA=1，∴cos∠PAO==．∴∠PAO=45°，即所求线面角为45°．故选C．4．设α是空间中的一个平面，l，m，n是三条不同的直线，①若m⊂α，n⊂α，l⊥m，l⊥n，则l⊥α；②若l∥m，m∥n，l⊥α，则n⊥α；③若l∥m，m⊥α，n⊥α，则l∥n；④若m⊂α，n⊥α，l⊥n，则l∥m；则上述命题中正确的是（）A．①②B．②③C．②④D．③④答案：B解析：解：①根据线面垂直的判定，当m，n相交时，结论成立，故①不正确；②根据平行线的传递性，可得l∥n，故l⊥α时，一定有n⊥α，故②正确；③由垂直于同一平面的两直线平行得m∥n，再根据平行线的传递性，即可得l∥n，故③正确．④m⊂α，n⊥α，则n⊥m，∵l⊥n，∴可以选用正方体模型，可得l，m平行、相交、异面都有可能，如图所示，故④不正确故正确的命题是②③故选B．5．已知一个铜质的五棱柱的底面积为16cm2，高为4cm，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（）A．2cm B．C．4cm D．8cm答案：C解析：解：∵铜质的五棱柱的底面积为16cm2，高为4cm，∴铜质的五棱柱的体积V=16×4=64cm3，设熔化后铸成一个正方体的铜块的棱长为acm，则a3=64解得a=4cm故选C6、在正方体ABCD-A l B1C1D1中，P是正方体的底面A l B1C1D1（包括边界）内的一动点（不与A1重合），Q是底面ABCD内一动点，线段A1C与线段PQ相交且互相平分，则使得四边形A1QCP面积最大的点P有（）A．1个B．2个C．3个D．无数个答案：C解：∵线段A1C与线段PQ相交且互相平分，∴四边形A1QCP是平行四边形，因A l C的长为定值，为了使得四边形A1QCP面积最大，只须P到A l C的距离为最大即可，由正方体的特征可知，当点P位于B1、C1、D1时，平行四边形A1QCP面积相等，且最大．则使得四边形A1QCP面积最大的点P有3个．故选C．7．如图所示几个空间图形中，虚线、实线使用不正确的有（）A．②③B．①③C．③④D．④答案：D解析：解：根据棱柱的放置和“看见的棱用实线、看不见的棱用虚线”，则①②③正确，④错误，故选D．二．填空题8、如图，在四棱锥S-ABCD中，SB⊥底面ABCD．底面ABCD为梯形，AB⊥AD，AB∥CD，AB=1，AD=3，CD=2．若点E是线段AD上的动点，则满足∠SEC=90°的点E的个数是______．答案：2解：连接BE，则∵SB⊥底面ABCD，∠SEC=90°，∴BE⊥CE．故问题转化为在梯形ABCD中，点E是线段AD上的动点，求满足BE⊥CE的点E的个数．设AE=x，则DE=3-x，∵AB⊥AD，AB∥CD，AB=1，AD=3，CD=2，∴10=1+x2+4+（3-x）2，∴x2-3x+2=0，∴x=1或2，∴满足BE⊥CE的点E的个数为2，∴满足∠SEC=90°的点E的个数是2．故答案为：2．9、一个正方体的六个面上分别标有字母A、B、C、D、E、F，如图是此正方体的两种不同放置，则与D面相对的面上的字母是______．答案：B解析：解：由此正方体的两种不同放置可知：与C相对的是F，因此D与B相对．故答案为：B．10．设α、β为互不重合的平面，m、n为互不重合的直线，下列四个命题中所有正确命题的序号是______．①若m⊥α，n⊂α，则m⊥n；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β．③若m∥α，n∥α，则m∥n．④若α⊥β，α∩β=m，n⊂α，n⊥m，则n⊥β．答案：①④解析：解：①若m⊥α，n⊂α，利用线面垂直的性质，可得m⊥n，正确；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；两条相交直线才行，不正确．③m∥α，n∥α，则m与n可能平行、相交、异面，不正确．④若α⊥β，α∩β=m，n⊂α，n⊥m，则由面面垂直的性质定理我们易得到n⊥β，正确．故答案为：①④．三．简答题11、在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，S D=，在线段SA上取一点E（不含端点）使EC=AC，截面CDE与SB交于点F．（1）求证：四边形EFCD为直角梯形；（2）设SB的中点为M，当的值是多少时，能使△DMC为直角三角形？请给出证明．答案：解：（1）∵CD∥AB，AB⊂平面SAB，∴CD∥平面SAB面EFCD∩面SAB=EF，∴CD∥EF．∵∠D=90°，∴CD⊥AD，又SD⊥面ABCD，∴SD⊥CD，∴CD⊥平面SAD，∴CD⊥ED又EF＜AB＜CD，∴EFCD为直角梯形．（2）当=2时，能使DM⊥MC．∵AB=a，∴，∴，∴SD⊥平面ABCD，∴SD⊥BC，∴BC⊥平面SBD．在△SBD中，SD=DB，M为SB中点，∴MD⊥SB．∴MD⊥平面SBC，MC⊂平面SBC，∴MD⊥MC，∴△DMC为直角三角形．12、正三棱台的高为3，上、下底面边长分别为2和4，求这个棱台的侧棱长和斜高．答案：解：如图所示，正三棱台ABC-A1B1C1中，高OO1=3，底面边长为A1B1=2，AB=4，∴OA=×AB=，O1A1=×A1B1=，∴棱台的侧棱长为AA1==；又OE=×AB=，O1E1=×A1B1=，∴该棱台的斜高为EE1==．13、已知三棱椎D-ABC，AB=AC=1，AD=2，∠BAD=∠CAD=∠BAC=90°，点E，F分别是BC，DE的中点，如图所示，（1）求证AF⊥BC（2）求线段AF的长．答案：解：（1）分别以AB、AC和AD为x、y、z轴，建立空间直角坐标系O-xyz，如图所示：记A（0，0，0），B（1，0，0），C（0，1，0），D（0，0，2），∴E（，，0），F（，，1）；∴（，，1），=（-1，1，0），∴•=×（-1）+×1+1×0=0，∴⊥，即AF⊥BC；（2）∵=（，，1），∴||===，即线段AB=．。

高中数学必修2立体几何测试题(含参考答案)

高中数学必修2立体几何测试题参考答案一、选择题（每小题5分，共60分）ADDCB BDADD BB二、填空题（每小题4分，共16分）13、小于 14、平行 15、菱形 16、1111AC B D 对角线与互相垂直三、解答题（共74分,要求写出主要的证明、解答过程）17、【解析】(1)方法一：如图，取AD 的中点H ，连结GH ，FH.∵E 、F 分别为PC 、PD 的中点，∴EF ∥CD.∵G 、H 分别为BC 、AD 的中点，∴GH ∥CD.∴EF ∥GH.∴E 、F 、H 、G 四点共面.∵F 、H 分别为DP 、DA 的中点，∴PA ∥FH.∵PA ⊄平面EFG ，FH ⊂平面EFG ，∴PA ∥平面EFG.方法二：∵E 、F 、G 分别为PC 、PD 、BC 的中点.∴EF ∥CD,EG ∥PB.∵CD ∥AB,∴EF ∥AB.∵PB ∩AB=B,EF ∩EG=E,∴平面EFG ∥平面PAB.∵PA ⊂平面PAB ，∴PA ∥平面EFG.(2)由三视图可知，PD ⊥平面ABCD ，又∵GC ⊂平面ABCD ，∴GC ⊥PD.∵四边形ABCD 为正方形，∴GC ⊥CD.∵PD ∩CD=D,∴GC ⊥平面PCD.∵PF=12PD=1，EF= 12CD=1， ∴S △PEF = 12EF ·PF= 12. ∵GC= 12BC=1, ∴V P-EFG =V G-PEF = 13S △PEF ·GC= 13×12×1=16.19、证明：（1）连结11A C ，设11111AC B D O = 连结1AO ， 1111ABCD A B C D -是正方体 11A ACC ∴是平行四边形11A C AC ∴且 11A C AC = 2分又1,O O 分别是11,A C AC 的中点，11O C AO ∴且11O C AO =11AOC O ∴是平行四边形 4分111,C O AO AO ∴⊂面11AB D ，1C O ⊄面11AB D∴1C O 面11AB D 6分（2）1CC ⊥面1111A B C D 11!CC B D ∴⊥ 7分又1111A C B D ⊥， 1111B D AC C ∴⊥面 9分111AC B D ⊥即 11分同理可证11A C AB ⊥， 12分又1111D B AB B =∴1A C ⊥面11AB D 14分20.【解析】(1)在△ABE中，P，Q分别是AE，AB的中点，所以PQ∥EB，又DC∥EB，所以PQ∥DC，又PQ⊄平面ACD，DC⊂平面ACD，所以PQ∥平面ACD.(2)连接DP，CQ，在△ABC中，AC=BC=2，AQ=BQ，所以CQ⊥AB，因为DC⊥平面ABC，EB∥DC，所以EB⊥平面ABC，又EB⊂平面ABE，所以平面ABE⊥平面ABC，平面ABE∩平面ABC=AB,所以CQ⊥平面ABE，由(1)知四边形DCQP是平行四边形,所以DP∥CQ,所以DP⊥平面ABE,所以AD在平面ABE内的射影是AP, 所以∠DAP是AD与平面ABE所成的角.在Rt △APD 中，AD ==，DP=CQ=2sin ∠CAQ=1,所以sin ∠DAP= DPAD 5==.故AD 与平面ABE 21.【解析】(1)由条件知PDAQ 为直角梯形.因为QA ⊥平面ABCD ，所以平面PDAQ ⊥平面ABCD ，交线为AD.又四边形ABCD 为正方形，DC ⊥AD ，所以DC ⊥平面PDAQ ，可得PQ ⊥DC.在直角梯形PDAQ 中可得DQ=PQ=2PD ，则PQ ⊥QD. 所以PQ ⊥平面DCQ.(2)设AB=a.由题设知AQ 为棱锥Q-ABCD 的高，所以棱锥Q-ABCD 的体积V 1=13a 3.由(1)知PQ 为棱锥P-DCQ 的高,而，△DCQ 的面积为2a 2，所以棱锥P-DCQ 的体积V 2=13a 3.故棱锥Q-ABCD 的体积与棱锥P-DCQ 的体积的比值为1.22、解:如图,设所截等腰三角形的底边边长为xcm .在Rt EOF 中, 15,2EF cm OF xcm ==, 3分所以EO = 6分于是13V x = 10分依题意函数的定义域为{|010}x x << 14分。

高一数学必修二立体几何点线面专项练习(含答案)

（2）证明: 平面；
（3）求直线与平面所成角的正切值.
15. （本题13分）在几何体ABCDE中, ∠BAC= , DC⊥平面ABC, EB⊥平面ABC, F是BC的中点, AB=AC=BE=2, CD=1.
（1）求证: DC∥平面ABE；
（2）求证: AF⊥平面BCDE；
（3）求几何体ABCDE的体积.
16. 如图, 在正三棱柱ABC—A1B1C1中, 底面边长及侧棱长均为2, D是棱AB的中点,
(1)求证 ;
(2)求异面直线AC1与B1C所成角的余弦值.
17.如图,在正方体中,为底面的中心,是的中点,设是上的中点,求证:（1）;
(2)平面 ∥平面 .
18. (14分)如图, 在直三棱柱中, , 点是的中点.
（Ⅰ）求证: ；
（Ⅱ）求证: 平面；
（Ⅲ）求异面直线与所成角的余弦值.
参考答案
Hale Waihona Puke 1．D2．D3．C
4．D
5．B
6．②④
7.平行或相交（直线在平面外）
8．1, 2, 3
9．
10. ②④⑤
11. （1）见解析（2）见解析
12. 见解析。
13. （Ⅰ）见解析；（Ⅱ）见解析。
14. （1）证明: 见解析；（2）证明: 见解析；（3）
二、填空题:
6.设是三个不重合的平面,是直线,给出下列四个命题:
①若
②若
③若
④若
其中正确的命题序号是
7. 已知两条相交直线, , ∥平面, 则与的位置关系是 .
8．如图, 空间中两个有一条公共边AD的正方形ABCD和ADEF．设M、N分别是BD和AE的中点, 那么
①AD⊥MN；②MN∥平面CDE；③MN∥CE；④MN、CE异面

高一数学必修2经典习题与答案

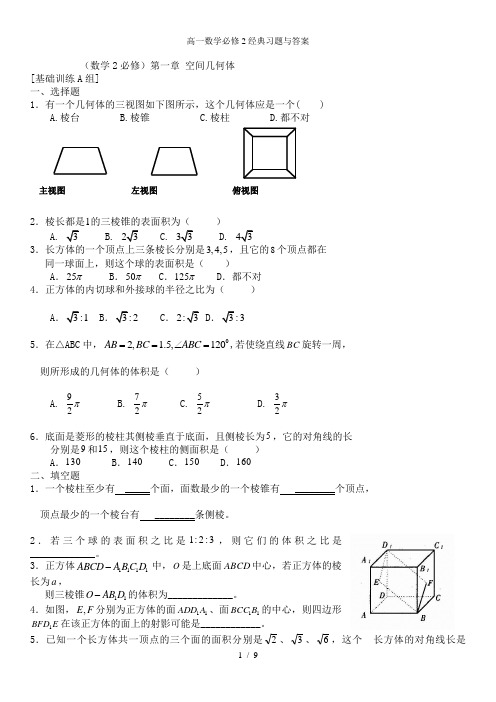
（数学2必修）第一章空间几何体[基础训练A 组] 一、选择题1．有一个几何体的三视图如下图所示，这个几何体应是一个( )A.棱台B.棱锥C.棱柱D.都不对2．棱长都是1的三棱锥的表面积为（）A. 3B. 23C. 33D. 433．长方体的一个顶点上三条棱长分别是3,4,5，且它的8个顶点都在同一球面上，则这个球的表面积是（） A ．25π B ．50π C ．125π D ．都不对 4．正方体的内切球和外接球的半径之比为（）A ．3:1B ．3:2C ．2:3D ．3:35．在△ABC 中，02, 1.5,120AB BC ABC ==∠=,若使绕直线BC 旋转一周，则所形成的几何体的体积是（）A. 92πB. 72πC. 52πD. 32π6．底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是（） A ．130 B ．140 C ．150 D ．160 二、填空题1．一个棱柱至少有 _____个面，面数最少的一个棱锥有 ________个顶点，顶点最少的一个棱台有 ________条侧棱。

2．若三个球的表面积之比是1:2:3，则它们的体积之比是_____________。

3．正方体1111ABCD A B C D - 中，O 是上底面ABCD 中心，若正方体的棱长为a ，则三棱锥11O AB D -的体积为_____________。

4．如图，,E F 分别为正方体的面11A ADD 、面11B BCC 的中心，则四边形 E BFD 1在该正方体的面上的射影可能是____________。

5．已知一个长方体共一顶点的三个面的面积分别是2、3、6，这个长方体的对角线长是主视图左视图俯视图C ___________；若长方体的共顶点的三个侧面面积分别为3,5,15，则它的体积为___________. 三、解答题1．养路处建造圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用），已建的仓库的底面直径为12M ，高4M ，养路处拟建一个更大的圆锥形仓库，以存放更多食盐，现有两种方案：一是新建的仓库的底面直径比原来大4M （高不变）；二是高度增加4M (底面直径不变)。

部编版高中数学必修二第八章立体几何初步带答案知识总结例题

(名师选题)部编版高中数学必修二第八章立体几何初步带答案知识总结例题单选题1、如图1，已知PABC是直角梯形，AB∥PC，AB⊥BC，D在线段PC上，AD⊥PC．将△PAD沿AD折起，使平面PAD⊥平面ABCD，连接PB，PC，设PB的中点为N，如图2．对于图2，下列选项错误的是（）A．平面PAB⊥平面PBC B．BC⊥平面PDCC．PD⊥AC D．PB＝2AN2、已知直线l⊥平面α，有以下几个判断：①若m⊥l，则m//α；②若m⊥α，则m//l；③若m//α，则m⊥l；④若m//l，则m⊥α；上述判断中正确的是（）A．①②③B．②③④C．①③④D．①②④3、某正方体被截去部分后得到的空间几何体的三视图如图所示，则该空间几何体的体积为（）A ．132B ．223C ．152D ．2334、南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148．5m 时，相应水面的面积为140．0km 2；水位为海拔157．5m 时，相应水面的面积为180．0km 2，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148．5m 上升到157．5m 时，增加的水量约为（√7≈2.65）（）A ．1.0×109m 3B ．1.2×109m 3C ．1.4×109m 3D ．1.6×109m 35、已知圆锥的母线长为3，其侧面展开图是一个圆心角为2π3的扇形，则该圆锥的体积为（）A ．√23πB ．2√23πC ．πD ．√2π 6、已知正四棱锥的底面边长为6，侧棱长为5，则此棱锥的侧面积为（） A ．6B ．12C ．24D ．487、如图，某圆锥的轴截面ABC 是等边三角形，点D 是线段AB 的中点，点E 在底面圆的圆周上，且BE ⌢的长度等于CE⌢的长度，则异面直线DE 与BC 所成角的余弦值是（）A ．√24B ．√64C ．√104D ．√1448、已知一个圆锥的体积为3π，其侧面积是底面积的2倍，则其底面半径为（） A ．2√3B ．3C ．√3D ．√33多选题9、如图所示，在棱长为2的正方体ABCD −A 1B 1C 1D 1中，M ，N 分别为棱C 1D 1，C 1C 的中点，则下列结论正确的是（）A．直线AM与BN是平行直线B．直线BN与MB1是异面直线C．直线MN与AC所成的角为60°D．平面BMN截正方体所得的截面面积为9210、如图所示，P为矩形ABCD所在平面外一点，矩形对角线交点为O，M为PB的中点，下列结论正确的是（）A．OM∥PD B．OM∥平面PCDC．OM∥平面PDA D．OM∥平面PBA11、如图，在棱长均相等的正四棱锥P−ABCD中，M、N分别为侧棱PA、PB的中点，O是底面四边形ABCD对角线的交点，下列结论正确的有（）A．PC//平面OMN B．平面PCD//平面OMNC．OM⊥PA D．PD⊥平面OMN填空题12、已知一个圆锥的底面半径为6，其体积为30π则该圆锥的侧面积为________.部编版高中数学必修二第八章立体几何初步带答案(十八)参考答案1、答案：A分析：由已知利用平面与平面垂直的性质得到PD⊥平面ABCD，判定C正确；进一步得到平面PCD⊥平面ABCD，结合BC⊥CD判定B正确；再证明AB⊥平面PAD，得到△PAB为直角三角形，判定D正确；可证明平面PBC⊥平面PDC，若平面PAB⊥平面PBC，则平面PAB与平面PDC的交线⊥平面PBC，矛盾，可判断A图1中AD⊥PC，则图2中PD⊥AD，又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，∴PD⊥平面ABCD，则PD⊥AC，故选项C正确；由PD⊥平面ABCD，PD⊂平面PDC，得平面PDC⊥平面ABCD，而平面PDC∩平面ABCD＝CD，BC⊂平面ABCD，BC⊥CD，∴BC⊥平面PDC，故选项B正确；∵AB⊥AD，平面PAD⊥平面ABCD，且平面PAD∩平面ABCD＝AD，∴AB⊥平面PAD，则AB⊥PA，即△PAB是以PB为斜边的直角三角形，而N为PB的中点，则PB＝2AN，故选项D正确．由于BC⊥平面PDC，又BC⊂平面PBC∴平面PBC⊥平面PDC若平面PAB⊥平面PBC，则平面PAB与平面PDC的交线⊥平面PBC由于AB//平面PDC，则平面PAB与平面PDC的交线//AB显然AB不与平面PBC垂直，故A错误故选：A2、答案：B分析：根据线面的位置关系，线面垂直的性质定理，线面平行的性质定理及线面垂直的性质逐项分析即得. 对于①，当m⊂平面α也可以有m⊥l，但m不平行于平面α，故①错；对于②，根据线面垂直的性质定理可知②正确；对于③，根据线面平行的性质定理可得存在n⊂α且m∥n．而直线l⊥平面α，故可根据线面垂直的性质得出l⊥n，故l⊥m正确；对于④，根据直线l⊥平面α，可在平面α内找到两条相交直线p，n，且l⊥p，l⊥n，又m∥l，所以m⊥p，m⊥n，故根据线面垂直的判定定理可知，m⊥α正确．即②③④正确．故选：B．3、答案：C分析：根据几何体的三视图，可知该几何体是棱长为2的正方体截去两个小三棱锥，根据三棱锥的体积公式即可求解．解：根据几何体的三视图，该空间几何体是棱长为2的正方体截去两个小三棱锥，由图示可知，该空间几何体体积为V=23−(13×12×12×1+13×12×12×2)=152，故选：C.4、答案：C分析：根据题意只要求出棱台的高，即可利用棱台的体积公式求出．依题意可知棱台的高为MN=157.5−148.5=9(m)，所以增加的水量即为棱台的体积V．棱台上底面积S=140.0km2=140×106m2，下底面积S′=180.0km2=180×106m2，∴V=13ℎ(S+S′+√SS′)=13×9×(140×106+180×106+√140×180×1012)=3×(320+60√7)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m3)．故选：C ． 5、答案：B分析：根据弧长计算公式，求得底面圆半径以及圆锥的高，即可求得圆锥的体积. 设圆锥的底面圆半径为r ，故可得2πr =2π3×3，解得r =1，设圆锥的高为ℎ，则ℎ=√32−12=2√2，则圆锥的体积V =13×πr 2×ℎ=13×π×2√2=2√23π. 故选：B. 6、答案：D分析：首先由勾股定理求出斜高，即可求出侧面积；解：正四棱锥的底面边长为6，侧棱长为5，则其斜高ℎ′=√52−(62)2=4，所以正四棱锥的侧面积S =12×4×6×4=48 故选：D 7、答案：A分析：过点A 作AO ⊥BC 于点O ，过点A 作DG ⊥BC 于点G ，取AO 的中点F ，连接GE 、OE 、EF ，则有∠DEF （或其补角）就是异面直线DE 与BC 所成的角，设圆锥的底面半径为2，解三角形可求得答案. 解：过点A 作AO ⊥BC 于点O ，过点A 作DG ⊥BC 于点G ，取AO 的中点F ，连接GE 、OE 、EF ，则DF //BC ，且DF =12BC ，所以∠DEF （或其补角）就是异面直线DE 与BC 所成的角，设圆锥的底面半径为2，则DF =1，OE =2，AO =2√3，所以DG =OF =√3，在Rt △GOE 中，GO =1，OE =2，所以GE =√GO 2+OE 2=√5，在Rt△GDE中，GE=√5，DG=√3，所以DE=√GD2+GE2=2√2，在Rt△FOE中，FO=√3，OE=2，FE=√FO2+OE2=√7，所以在△DFE中，满足DF2+FE2=DE2，所以∠DFE=90∘，所以cos∠DEF=DFDE =2√2=√24，故选：A.8、答案：C分析：根据圆锥的侧面展开图和圆锥体积公式以及侧面积公式，即可求出结果. 设底面半径为r，高为ℎ，母线为l，如图所示：则圆锥的体积V=13πr2ℎ=3π，所以r2ℎ=9，即ℎ=9r2，S 侧=12⋅2πrl=2πr2，则l=2r，又ℎ=√l2−r2=√3r，所以√3r3=9，故r=√3．故选：C．9、答案：BCD解析：根据异面直线的定义直接判断AB选项，根据MN//D1C，转化求异面直线所成的角，利用确定平面的依据，作出平面BMN 截正方体所得的截面，并求面积. A.直线AM 与BN 是异面直线，故A 不正确； B.直线BN 与MB 1是异面直线，故B 正确；C. 由条件可知MN//D 1C ，所以异面直线MN 与AC 所成的角为∠ACD 1，△ACD 1是等边三角形，所以∠ACD 1=60∘，故C 正确；D.如图，延长MN ，并分别与DD 1和DC 交于E,F ，连结EA,GB 交于点F ，连结A 1M,BN ，则四边形A 1BNM 即为平面BMN 截正方体所得的截面，由对称性可知，四边形A 1BNM 是等腰梯形，MN =√2,A 1B =2√2，A 1M =BN =√5，则梯形的高是ℎ=√(√5)2−(√22)2=3√22，所以梯形的面积S =12×(√2+2√2)×3√22=92，故D 正确.故选：BCD小提示：关键点点睛：本题考查以正方体为载体，判断异面直线，截面问题，本题关键选项是D ，首先要作出平面BMN与正方体的截面，即关键作出平面EFG.10、答案：ABC分析：通过直线与平面平行的判定定理，即可判断ABC正确；由线面的位置关系，即可得到直线在平面内，故D错误；解：对于A，由于O为BD的中点，M为PB的中点，则OM∥PD，故正确；对于B，由于OM∥PD，OM⊄平面PCD，PD⊂平面PCD，则OM∥平面PCD，故正确；对于C，由于OM∥PD，OM⊄平面PAD，PD⊂平面PAD，则OM∥平面PAD，故正确；对于D，由于M∈平面PAB，故错误．故选：ABC．小提示：本题考查线面平行的判定定理及应用，考查直线与平面的位置关系，考查空间想象能力.11、答案：ABC分析：A选项，由中位线证明线线平行，推导出线面平行；B选项，在A选项的基础上证明面面平行；从而推导出D错误；由勾股定理的逆定理得到PA⊥PC，从而得到OM⊥PA.因为O为底面四边形ABCD对角线的交点，所以O为AC的中点，由M是PA的中点，可得PC∥MO，因为PC⊄在平面OMN，OM⊂平面OMN，所以PC//平面OMN，A正确；同理可推得PD//平面OMN，而PC∩PD=P，所以平面PCD//平面OMN，B正确；因为PD⊂平面PCD，故PD不可能垂直平面OMN，D错误；设该正四棱锥的棱长为a，则PA=PC=a,AC=√2a，所以PA⊥PC，因为PC∥MO，所以OM ⊥PA ，C 正确.故选ABC ．12、答案：39π分析：利用体积公式求出圆锥的高，进一步求出母线长，最终利用侧面积公式求出答案. ∵V =13π62⋅ℎ=30π ∴ℎ=52∴l =√ℎ2+r 2=√(52)2+62=132 ∴S 侧=πrl =π×6×132=39π.所以答案是：39π.。

部编版高中数学必修二第八章立体几何初步带答案考点题型与解题方法

(名师选题)部编版高中数学必修二第八章立体几何初步带答案考点题型与解题方法单选题1、某正方体被截去部分后得到的空间几何体的三视图如图所示，则该空间几何体的体积为（）A ．132B ．223C ．152D ．2332、已知直线a 与平面α,β,γ，能使α//β的充分条件是（） ①α⊥γ,β⊥γ ②α//γ,β//γ ③a //α,a //β ④a ⊥α,a ⊥β A ．①②B ．②③C ．①④D ．②④3、下列命题中，正确的是（） A ．三点确定一个平面B ．垂直于同一直线的两条直线平行C ．若直线l 与平面α上的无数条直线都垂直，则l ⊥αD ．若a 、b 、c 是三条直线，a ∥b 且与c 都相交，则直线a 、b 、c 在同一平面上4、如图.AB 是圆的直径，PA ⊥AC ，PA ⊥BC ，C 是圆上一点(不同于A ，B )，且PA =AC ，则二面角P −BC −A 的平面角为（）A ．∠PACB ．∠CPAC ．∠PCAD ．∠CAB5、如图，“蘑菇”形状的几何体是由半个球体和一个圆柱体组成，球的半径为2，圆柱的底面半径为1，高为3，则该几何体的表面积为（）A ．18πB ．20πC ．22π3D ．26π6、如图，某圆锥的轴截面ABC 是等边三角形，点D 是线段AB 的中点，点E 在底面圆的圆周上，且BE ⌢的长度等于CE⌢的长度，则异面直线DE 与BC 所成角的余弦值是（）A ．√24B ．√64C ．√104D ．√1447、如图，“十字歇山”是由两个直三棱柱重叠后的景象，重叠后的底面为正方形，直三棱柱的底面是顶角为120°，腰为3的等腰三角形，则该几何体的体积为（）A ．23B ．24C ．26D ．278、如图，在梯形ABCD 中，AB ∥DC 且AB =2DC ，点E 为线段BC 的靠近点C 的一个四等分点，点F 为线段AD 的中点，AE 与BF 交于点O ，且AO⃑⃑⃑⃑⃑ =xAB ⃑⃑⃑⃑⃑ +yBC ⃑⃑⃑⃑⃑ ，则x +y 的值为（）A ．1B ．57C ．1417D ．56多选题9、《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”；底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”；四个面均为直角三角形的四面体称为“鳖膈”．如图在堑堵ABC −A 1B 1C 1中，AC ⊥BC ，且AA 1=AB =2．下列说法正确的是（）A ．四棱锥B −A 1ACC 1为“阳马” B ．四面体A 1C 1CB 为“鳖膈” C ．四棱锥B −A 1ACC 1体积最大为23D ．过A 点分别作AE ⊥A 1B 于点E ，AF ⊥A 1C 于点F ，则EF ⊥A 1B10、在正方体ABCD−A1B1C1D1中，点P在线段AD1上运动，则下列命题正确的是（）A．异面直线C1P和CB1所成的角为定值B．直线CD和平面BPC1相交C．三棱锥D−BPC1的体积为定值D．直线CP和直线A1B可能相交11、已知PA⊥矩形ABCD所在的平面，则下列结论中正确的是（）A．PB⊥BCB．PD⊥CDC．PD⊥BDD．PA⊥BD填空题12、对于任意给定的两条异面直线，存在______条直线与这两条直线都垂直．部编版高中数学必修二第八章立体几何初步带答案(四)参考答案1、答案：C分析：根据几何体的三视图，可知该几何体是棱长为2的正方体截去两个小三棱锥，根据三棱锥的体积公式即可求解．解：根据几何体的三视图，该空间几何体是棱长为2的正方体截去两个小三棱锥，由图示可知，该空间几何体体积为V=23−(13×12×12×1+13×12×12×2)=152，故选：C.2、答案：D解析：根据线面的平行关系，结合相关性质，逐个分析判断即可得解.对①，若α⊥γ,β⊥γ，垂直于同一个平面的两个平面可以相交，故①错误；对②，若α//γ,β//γ，则α//β，平面的平行具有传递性，故②正确；对③，若a//α,a//β，平行于同一直线的两平面可以相交，故③错误；对④，a⊥α,a⊥β，垂直于同一直线的两平面平行，故④正确.综上：②④正确，故选：D.3、答案：D分析：利用空间点、线、面位置关系直接判断.A.不共线的三点确定一个平面，故A错误；B.由墙角模型，显然B错误；C.根据线面垂直的判定定理，若直线l与平面α内的两条相交直线垂直，则直线l与平面α垂直，若直线l与平面α内的无数条平行直线垂直，则直线l与平面α不一定垂直，故C错误；D.因为a//b，所以a、b确定唯一一个平面，又c与a、b都相交，故直线a、b、c共面，故D正确；故选：D.4、答案：C解析：由圆的性质知：AC⊥BC，根据线面垂直的判定得到BC⊥面PAC，即BC⊥PC，结合二面角定义可确定二面角P−BC−A的平面角.∵C是圆上一点(不同于A，B)，AB是圆的直径，∴AC⊥BC，PA⊥BC，AC∩PA=A，即BC⊥面PAC，而PC⊂面PAC，∴BC⊥PC，又面ABC∩面PBC=BC，PC∩AC=C，∴由二面角的定义：∠PCA为二面角P−BC−A的平面角.故选：C5、答案：A分析：由题意可知该几何体的体积是由半球的表面积加上圆柱的侧面积，再加上圆的面积即可解：由题意得，球的半径R=2，圆柱的底面半径r=1，高ℎ=3，则该几何体的表面积为S=2πR2+πR2+2πrℎ=8π+4π+2π×1×3=18π故选：A.6、答案：A分析：过点A作AO⊥BC于点O，过点A作DG⊥BC于点G，取AO的中点F，连接GE、OE、EF，则有∠DEF （或其补角）就是异面直线DE与BC所成的角，设圆锥的底面半径为2，解三角形可求得答案.解：过点A作AO⊥BC于点O，过点A作DG⊥BC于点G，取AO的中点F，连接GE、OE、EF，BC，所以∠DEF（或其补角）就是异面直线DE与BC所成的角，则DF//BC，且DF=12设圆锥的底面半径为2，则DF=1，OE=2，AO=2√3，所以DG=OF=√3，在Rt△GOE中，GO=1，OE=2，所以GE=√GO2+OE2=√5，在Rt△GDE中，GE=√5，DG=√3，所以DE=√GD2+GE2=2√2，在Rt△FOE中，FO=√3，OE=2，FE=√FO2+OE2=√7，所以在△DFE中，满足DF2+FE2=DE2，所以∠DFE=90∘，所以cos∠DEF=DFDE =2√2=√24，故选：A.7、答案：D分析：作出几何体直观图，由题意结合几何体体积公式即可得组合体的体积.该几何体由直三棱柱AFD−BHC及直三棱柱DGC−AEB组成，作HM⊥CB于M，如图，因为CH=BH=3,∠CHB=120∘，所以CM=BM=3√32,HM=32，因为重叠后的底面为正方形，所以AB=BC=3√3,在直棱柱AFD−BHC中，AB⊥平面BHC，则AB⊥HM, 由AB∩BC=B可得HM⊥平面ADCB，设重叠后的EG与FH交点为I,则V I−BCDA =13×3√3×3√3×32=272,V AFD−BHC =12×3√3×32×3√3=814则该几何体的体积为V =2V AFD−BHC −V I−BCDA =2×814−272=27.故选：D. 8、答案：C分析：由向量的线性运算法则化简得到AO ⃑⃑⃑⃑⃑ ==(x −y2)AB ⃑⃑⃑⃑⃑ +2yAF ⃑⃑⃑⃑⃑ 和BO ⃑⃑⃑⃑⃑ =(1−x)BA ⃑⃑⃑⃑⃑ +4y 3BE⃑⃑⃑⃑⃑ ，结合B,O,F 三点共线和A,O,E 三点共线，得出2x +3y −2=0和3x −4y =0，联立方程组，即可求解. 根据向量的线性运算法则，可得AO⃑⃑⃑⃑⃑ =xAB ⃑⃑⃑⃑⃑ +yBC ⃑⃑⃑⃑⃑ =xAB ⃑⃑⃑⃑⃑ +y(BA ⃑⃑⃑⃑⃑ +AC ⃑⃑⃑⃑⃑ ) =xAB ⃑⃑⃑⃑⃑ −yAB ⃑⃑⃑⃑⃑ +yAC ⃑⃑⃑⃑⃑ =(x −y)AB ⃑⃑⃑⃑⃑ +y ⋅(AD ⃑⃑⃑⃑⃑ +DC⃑⃑⃑⃑⃑ ) =(x −y)AB ⃑⃑⃑⃑⃑ +y ⋅(2AF ⃑⃑⃑⃑⃑ +12AB ⃑⃑⃑⃑⃑ )=(x −y)AB ⃑⃑⃑⃑⃑ +2yAF ⃑⃑⃑⃑⃑ +12yAB ⃑⃑⃑⃑⃑ =(x −y2)AB ⃑⃑⃑⃑⃑ +2yAF ⃑⃑⃑⃑⃑ ，因为B,O,F 三点共线，可得x −y 2+2y =1，即2x +3y −2=0；又由BO ⃑⃑⃑⃑⃑ =BA ⃑⃑⃑⃑⃑ +AO ⃑⃑⃑⃑⃑ =BA ⃑⃑⃑⃑⃑ +xAB ⃑⃑⃑⃑⃑ +yBC ⃑⃑⃑⃑⃑ =BA ⃑⃑⃑⃑⃑ −xBA ⃑⃑⃑⃑⃑ +y ⋅43BE ⃑⃑⃑⃑⃑ =(1−x)BA ⃑⃑⃑⃑⃑ +4y 3BE ⃑⃑⃑⃑⃑ ，因为A,O,E 三点共线，可得1−x +4y 3=1，即3x −4y =0，联立方程组{2x +3y −2=03x −4y =0 ，解得x =817,y =617，所以x +y =1417.故选：C. 9、答案：ABD分析：根据“阳马”和“鳖膈”的定义，可判断A ，B 的正误；当且仅当AC =BC 时，四棱锥B −A 1ACC 1体积有最大值，求值可判断C 的正误；根据题意可证A 1B ⊥平面AEF ，进而判断D 的正误. 底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”， ∴在堑堵ABC −A 1B 1C 1中，AC ⊥BC ，侧棱AA 1⊥平面ABC ，A 选项，∴AA 1⊥BC ，又AC ⊥BC ，且AA 1∩AC =A ，则BC ⊥平面A 1ACC 1， ∴四棱锥B −A 1ACC 1为“阳马”，对；B 选项，由AC ⊥BC ，即A 1C 1⊥BC ，又A 1C 1⊥C 1C 且BC ∩C 1C =C ， ∴A 1C 1⊥平面BB 1C 1C ，∴A 1C 1⊥BC 1，则△A 1BC 1为直角三角形，又由BC⊥平面AA1C1C，得△A1BC为直角三角形，由“堑堵”的定义可得△A1C1C为直角三角形，∥CC1B为直角三角形．∴四面体A1C1CB为“鳖膈”，对；C选项，在底面有4=AC2+BC2≥2AC⋅BC，即AC⋅BC≤2，当且仅当AC=BC=√2时取等号，V B−A1ACC1=13S A1ACC1×BC=13AA1×AC×BC=23AC×BC≤43，错；D选项，因为BC⊥平面AA1C1C，则BC⊥AF，AF⊥A1C且A1C∩BC=C，则AF⊥平面A1BC，∴AF⊥A1B，又AE⊥A1B且AF∩AE=A，则A1B⊥平面AEF，所以则A1B⊥EF，对；故选：ABD．10、答案：AC解析：A：由正方体的性质判断B1C⊥平面ABC1D1，得出B1C⊥C1P，异面直线C1P与CB1所成的角为90°；B：由CD//AB，证明CD//平面ABC1D1，即得CD//平面BPC1；C：三棱锥D−BPC1的体积等于三棱锥的体积P−DBC1的体积，判断三棱锥D−BPC1的体积为定值；D：可得直线CP和直线A1B为异面直线.对于A，因为在正方体ABCD−A1B1C1D1中，B1C⊥BC1，B1C⊥C1D1，又BC1∩C1D1=C1，BC1，C1D1⊂平面ABC1D1，所以B1C⊥平面ABC1D1，而C1P⊂平面ABC1D1，所以B1C⊥C1P，故这两个异面直线所成的角为定值90°，所以A正确；对于B，因为平面BPC1与面ABC1D1是同一平面，DC//AB，AB⊂平面ABC1D1，CD⊂平面ABC1D1，故CD//平面ABC1D1，即CD//平面BPC1，故B错误；对于C，三棱锥D−BPC1的体积等于三棱锥P−DBC1的体积，而平面DBC1为固定平面，且△DBC1大小一定，又因为P∈AD1，因为AD1//BC1，AD1⊂平面BDC1，BC1⊂平面BDC1，所以AD1//平面DBC1，所以点A到平面DBC1的距离即为点P到该平面的距离，为定值，所以三棱锥D−BPC1的体积为定值，故C正确；对于D，直线CP和直线A1B是异面直线，不可能相交，故D错误.故选：AC.分析：本题考查线面平行的判定，线面垂直的判定及性质，异面直线所成的角，直线与平面所成的角，空间中的距离，正确理解判定定理和性质是解题的关键.11、答案：ABD分析：由PA⊥矩形ABCD，得PA⊥BD，若PD⊥BD，则BD⊥平面PAD，又BA⊥平面PAD，则过平面外一面有两条直线与平面垂直，不成立，故PD⊥BD不正确．解：∵PA⊥矩形ABCD，BD⊂矩形ABCD，∴PA⊥BD，故D正确．若PD⊥BD，则BD⊥平面PAD，又BA⊥平面PAD，则过平面外一面有两条直线与平面垂直，故PD⊥BD不正确，故C不正确；∵PA⊥矩形ABCD，∴PA⊥CD，AD⊥CD，∴CD⊥平面PAD，∴PD⊥CD，故B正确；∵PA⊥矩形ABCD，∴由三垂线定理得PB⊥BC，故A正确；故选：ABD．12、答案：无数分析：平移一条直线与另一条相交并确定一个平面，再由线面垂直的意义及异面直线所成角判断作答. 令给定的两条异面直线分别为直线a,b，平移直线b到直线b′，使b′与直线a相交，如图，则直线b′与a确定平面α，点A是平面α内任意一点，过点A有唯一直线l⊥α，因此，l⊥a,l⊥b′，即有l⊥b，由于点A的任意性，所以有无数条直线与异面直线a,b都垂直.所以答案是：无数。

高中数学必修二第八章立体几何初步考点题型与解题方法(带答案)

高中数学必修二第八章立体几何初步考点题型与解题方法单选题1、下列说法中正确的是（）A．如果一条直线与一个平面平行，那么这条直线与平面内的任意一条直线平行B．平面α内△ABC的三个顶点到平面β的距离相等，则α与β平行C．α//β，a//α，则a//βD．a//b，a//α，b⊄α，则b//α答案：D分析：根据线面关系，逐一判断每个选项即可.解：对于A选项，如果一条直线与一个平面平行，那么这条直线与平面内的无数条直线平行，而不是任意的直线平行，故错误；对于B选项，如图1，D，E，F，G分别为正方体中所在棱的中点，平面DEFG设为平面β，易知正方体的三个顶点A，B，C到平面β的距离相等，但△ABC所在平面α与β相交，故错误；对于选项C，a可能在平面β内，故错误；对于选项D，正确.故选：D.2、已知直三棱柱ABC−A1B1C1的各顶点都在同一球面上，且该棱柱的体积为√3，AB=2，AC=1，∠BAC=60°，则该球的表面积为（）A．4πB．4√2πC．8πD．32π答案：C解析：利用三棱柱ABC −A 1B 1C 1的侧棱垂直于底面，棱柱的体积为√3，AB =2，AC =1，∠BAC =60°，求出AA 1，再求出ΔABC 外接圆的半径，即可求得球的半径，从而可求球的表面积. ∵三棱柱ABC −A 1B 1C 1的侧棱垂直于底面，棱柱的体积为√3，AB =2，AC =1，∠BAC =60°， ∴12×2×1×sin60°×AA 1=√3，∴AA 1=2∵BC 2=AB 2+AC 2−2AB ⋅ACcos60°=4+1−2=3，∴BC =√3. 设ΔABC 外接圆的半径为R ，则BCsin60°=2R ，∴R =1.∴外接球的半径为√1+1=√2，∴球的表面积等于4π×(√2)2=8π. 故选：C.小提示：本小题主要考查根据柱体体积求棱长，考查几何体外接球有关计算，属于基础题.3、牟合方盖是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法，该方法不直接给出球体的体积，而是先计算牟合方盖的体积.刘徽通过计算，“牟合方盖”的体积与球的体积关系为V 牟V 球=4π，并且推理出了“牟合方盖”的八分之一的体积计算公式，即V 牟8=r 3−V 方盖差，从而计算出V 球=43πr 3.如果记所有棱长都为r 的正四棱锥的体积为V ，则V 方差盖:V =（） A ．√22B ．1C ．√2D ．2√2 答案：C分析：计算出V 方盖差，V ，即可得出结论.由题意，V 方盖差=r 3−18V 牟=r 3−18×4π×43×π×r 3=13r 3，所有棱长都为r 的正四棱锥的体积为V 正=13×r ×r ×r 2−(√2r 2)2=√26r 3， ∴V 方盖差V 正=13r 3√2r 36=√2，故选：C ．4、已知圆锥的底面半径为R ，高为3R ，在它的所有内接圆柱中，全面积的最大值是（） A ．2πR 2B ．94πR 2C ．83πR 2D ．πR 2答案：B分析：根据圆柱的表面积公式以及二次函数的性质即可解出．设圆柱的底面半径为r，圆柱的高为ℎ，所以在轴截面三角形中，如图所示：由相似可得，rR =3R−ℎ3R，所以，ℎ=3R−3r，即圆柱的全面积为S=2πr2+2πrℎ=2πr2+2πr(3R−3r)=2π(−2r2+3rR)=2π[−2(r−34R)2+98R2]≤9π4R2，当且仅当r=34R时取等号．故选：B．5、如图所示的是平行四边形ABCD所在的平面，有下列表示方法：①平面ABCD；②平面BD；③平面AD；④平面ABC；⑤AC；⑥平面α.其中不正确的是（）A．④⑤B．③④⑤C．②③④⑤D．③⑤答案：D解析：根据平面的表示方法判断．③中AD不为对角线，故错误；⑤中漏掉“平面”两字，故错误.故选：D.6、如图，矩形BDEF所在平面与正方形ABCD所在平面互相垂直，BD=2，DE=1，点P在线段EF上.给出下列命题：①存在点P，使得直线DP//平面ACF；②存在点P，使得直线DP⊥平面ACF；,1]；③直线DP与平面ABCD所成角的正弦值的取值范围是[√55④三棱锥A−CDE的外接球被平面ACF所截得的截面面积是9π.8其中所有真命题的序号（）A．①③B．①④C．①②④D．①③④答案：D分析：当点P是线段EF中点时判断①；假定存在点P，使得直线DP⊥平面ACF，推理导出矛盾判断②；利用线面角的定义转化列式计算判断③；求出△ACF外接圆面积判断④作答.取EF中点G，连DG，令AC∩BD=O，连FO，如图，在正方形ABCD中，O为BD中点，而BDEF是矩形，则DO//GF且DO=GF，即四边形DGFO是平行四边形，即有DG//FO，而FO⊂平面ACF，DG⊄平面ACF，于是得DG//平面ACF，当点P与G重合时，直线DP//平面ACF，①正确；假定存在点P，使得直线DP⊥平面ACF，而FO⊂平面ACF，则DP⊥FO，又DG//FO，从而有DP⊥DG，在Rt△DEF中，∠DEF=90∘，DG是直角边EF上的中线，显然在线段EF上不存在点与D连线垂直于DG，因此，假设是错的，即②不正确；因平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD=BD，则线段EF上的动点P在平面ABCD上的射影在直线BD上，于是得∠PDB是直线DP与平面ABCD所成角的，在矩形BDEF中，当P与E不重合时，∠PDB=∠DPE，sin∠PDB=sin∠DPE=DEDP =√DE2+EP2=√1+EP2，而0<EP≤2，则√55≤sin∠PDB<1，当P与E重合时，∠PDB=π2，sin∠PDB=1，因此，√55≤sin∠PDB≤1，③正确；因平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD=BD，BF⊥BD，BF⊂平面BDEF，则BF⊥平面ABCD，BC=√2，在△ACF中，AF=CF=√BC2+BF2=√3，显然有FO⊥AC，sin∠FAC=FOAF =√BO2+BF2AF=√2√3，由正弦定理得△ACF外接圆直径2R=CFsin∠FAC =√2，R=2√2，三棱锥A−CDE的外接球被平面ACF所截得的截面是△ACF的外接圆，其面积为πR2=9π8，④正确，所以所给命题中正确命题的序号是①③④.故选：D小提示：名师点评两个平面互相垂直，则一个平面内任意一点在另一个平面上的射影都在这两个平面的交线上.7、边长为5 cm的正方形EFGH是圆柱的轴截面，则从E点沿圆柱的侧面到相对顶点G的最短距离是（）A．10cm B．5√2cmC．5√π2+1cm D．52√π2+4cm答案：D分析：将圆柱展开，根据题意即可求出答案.圆柱的侧面展开图如图所示，展开后E′F=12×2π×52=52π(cm)，∴E′G=√52+(5π2)2=52√π2+4(cm)，即为所求最短距离．8、下面四个选项中一定能得出平面α/⁄平面β的是（）A．存在一条直线a，a//α，a//βB．存在一条直线a，a⊂α，a//βC．存在两条平行直线a，b，a⊂α，b⊂β，a//β，b//αD．存在两条异面直线a，b，a⊂α，b⊂β，a//β，b//α答案：D分析：对于A，B，C，举出符合条件的特例即可判断；对于D，过直线a作平面γ∩β=c，再证c//α即可. 如图，ABCD−A1B1C1D1是长方体，平面ABCD为平面α，平面ABB1A1为平面β，对于A，直线C1D1为直线a，显然a//α，a//β，而α与β相交，A不正确；对于B，直线CD为直线a，显然a⊂α，a//β，而α与β相交，B不正确；对于C，直线CD为直线a，直线A1B1为直线b，显然a⊂α，b⊂β，a//β，b//α，而α与β相交，C不正确；对于D，因a，b是异面直线，且a⊂α，b⊂β，过直线a作平面γ∩β=c，如图，则c//a，并且直线c与b必相交，而c⊄α，于是得c//α，又b//α，即β内有两条相交直线都平行于平面α，⁄平面β.因此，平面α/多选题9、(多选题)下列说法中，正确的结论有（）A．如果一个角的两边与另一个角的两边分别平行，那么这两个角相等B．如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角(或直角)相等C．如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补D．如果两条直线同时平行于第三条直线，那么这两条直线互相平行答案：BD分析：由等角定理可判断A的真假；根据直线夹角的定义可判断B的真假；举反例可判断C的真假；由平行公理可判断D的真假.对于选项A：如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补，故选项A错误；对于选项B：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角或直角相等，故选项B正确；对于选项C：如果一个角的两边和另一个角的两边分别垂直，这两个角的关系不确定，既可能相等也可能互补，也可能既不相等，也不互补.反例如图，在立方体中，∠A1D1C1与∠A1BC1满足A1D1⊥A1B，C1D1⊥C1B，但是∠A1D1C1=π2，∠A1BC1=π3，二者不相等也不互补.故选项C错误；对于选项D：如果两条直线同时平行于第三条直线，那么这两条直线平行，故选项D正确.故选：BD.10、矩形ABCD中，AB=2，BC=1，将此矩形沿着对角线BD折成一个三棱锥C−BDA，则以下说法正确的有（）A．三棱锥C−BDA的体积最大值为2√515B．当二面角C−BD−A为直二面角时，三棱锥C−BDA的体积为2√515C．当二面角C−BD−A为直二面角时，三棱锥C−BDA的外接球的表面积为5πD．当二面角C−BD−A不是直二面角时，三棱锥C−BDA的外接球的表面积小于5π答案：ABC分析：求出点C到平面ABD的最大距离即可计算棱锥的最大体积判断选项A，B；求出三棱锥C−BDA的外接球的半径即可判断选项C，D作答.过C作CE⊥BD于E，在平面DBA内过E作BD的垂线EG，则∠CEG为二面角C−BD−A的平面角，如图，平面CEG⊥平面DBA，过C作CF⊥EG于F，则CF⊥平面DBA，在直角△BCD中，∠BCD=90∘，BC=1,CD=2,CE=BC⋅CDBD =2√55，显然CF≤CE，当且仅当点E与F重合时取“=”，即点C到平面ABD距离的最大值为CE=2√55，而S△DBA=12AB⋅AD=1，则三棱锥C−BDA的体积最大值为13CE⋅S△DBA=2√515，A正确；当CF取最大值2√55时，CF⊂平面BCD，又CF⊥平面DBA，则平面BCD⊥平面DBA，即二面角C−BD−A为直二面角，三棱锥C−BDA的体积为2√515，B正确；取BD中点O，连接AO，CO，显然有AO=CO=12BD=BO=DO，于是得点A，B，C，D在以O为球心，AO=√52为半径的球面上，显然，无论二面角C−BD−A如何变化，点A，B，C，D都在上述的球O上，其表面积为5π，C正确，D不正确.故选：ABC11、如图，正方体ABCD−A1B1C1D1的棱长为1，则下列四个命题正确的是（）A．两条异面直线D1C和BC1所成的角为π4B．直线BC与平面ABC1D1所成的角等于π4C．点D到面ACD1的距离为√33D．三棱柱AA1D1−BB1C1外接球半径为√32答案：BCD分析：对于A：根据异面直线的求法易得：异面直线D1C和BC1所成的角为∠AD1C；对于B：可证B1C⊥平面ABC1D1，则直线BC与平面ABC1D1所成的角为∠CBC1；对于C：根据等体积转换V D−ACD1=V D1−ACD，求点D到面ACD1的距离；对于D：三棱柱AA1D1−BB1C1的外接球即为正方体ABCD−A1B1C1D1的外接球，直接求正方体外接球的半径即可．连接AC、AD1∵AB∥C1D1且AB=C1D1，则四边形ABC1D1为平行四边形，∴异面直线D1C和BC1所成的角为∠AD1C∵AC=AD1=D1C，则△ACD1为正三角形，即∠AD1C=π3A不正确；连接B1C在正方形BB1C1C中，BC1⊥B1C∵AB⊥平面BB1C1C，B1C⊂平面BB1C1C∴AB⊥B1CAB∩BC1=B，则B1C⊥平面ABC1D1∴直线BC与平面ABC1D1所成的角为∠CBC1=π4 B正确；根据等体积转换可知：V D−ACD1=V D1−ACD即13×ℎ×12×√2×√2×√32=13×1×12×1×1，则ℎ=√33C正确；三棱柱AA1D1−BB1C1的外接球即为正方体ABCD−A1B1C1D1的外接球则外接球的半径即为正方体ABCD−A1B1C1D1体对角线的一半，即R=√32 D正确；故选：BCD．填空题12、一个圆锥的母线长为20，母线与轴的夹角为60∘，则圆锥的高为________．答案：10分析：利用圆锥的几何性质可求得该圆锥的高.由题意可知，该圆锥的高为ℎ=20cos60∘=10.所以答案是：10.13、若将两个半径为1的铁球熔化后铸成一个球，则该球的半径为______．答案：√23分析：根据球的体积等于两个半径为1的球的体积之和即可求其半径．设大球的半径为r，则根据体积相同，可知43π+43π=43πr3，则r3=2，解得r=√23.所以答案是：√23．14、已知一三角形ABC用斜二测画法画出的直观图是面积为√3的正三角形A′B′C′(如图)，则三角形ABC中边长与正三角形A′B′C′的边长相等的边上的高为______．答案：2√6分析：根据面积公式求出三角形的边长，以及高，利用斜二测画法的原理还原出原三角形的高，并求出答案. 设正三角形A′B′C′的边长为a，∵S△A′B′C′=√34a2=√3∴a=2，DC′=√3O′C′=√6∴O′C=2√6所以答案是：2√6.解答题15、如图，在正方体ABCD−A1B1C1D1中，A1C1与B1D1交于点O1，求证：(1)直线A1B∥平面ACD1；(2)直线BO1∥平面ACD1．答案：(1)证明见解析(2)证明见解析分析：(1)根据题意，先证得四边形A1D1CB是平行四边形，从而证得A1B∥D1C，即可证得线面垂直；(2)连接BD，交AC于O，连接D1O，只需证明O1B∥D1O，即可证得线面垂直；（1）证明：直线A1B在平面ACD1外，因为A1D1∥BC，A1D1=BC，所以四边形A1D1CB是平行四边形，所以A1B∥D1C，而D1C是平面ACD1内的直线，根据判定定理可知，直线A1B∥平面ACD1．（2）证明：如图，连接BD，交AC于O，连接D1O，易知D1O1∥OB，D1O1=OB，则四边形D1O1BO是平行四边形，所以O1B∥D1O，所以D1O在平面ACD1上，根据判定定理可知，O1B∥平面ACD1．。

高中数学必修二第八章立体几何初步考点精题训练(带答案)

高中数学必修二第八章立体几何初步考点精题训练单选题1、南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148．5m时，相应水面的面积为140．0km2；水位为海拔157．5m时，相应水面的面积为180．0km2，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148．5m上升到157．5m时，增加的水量约为（√7≈2.65）（）A．1.0×109m3B．1.2×109m3C．1.4×109m3D．1.6×109m3答案：C分析：根据题意只要求出棱台的高，即可利用棱台的体积公式求出．依题意可知棱台的高为MN=157.5−148.5=9(m)，所以增加的水量即为棱台的体积V．棱台上底面积S=140.0km2=140×106m2，下底面积S′=180.0km2=180×106m2，∴V=13ℎ(S+S′+√SS′)=13×9×(140×106+180×106+√140×180×1012)=3×(320+60√7)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m3)．故选：C．2、如图已知正方体ABCD−A1B1C1D1，M，N分别是A1D，D1B的中点，则（）A．直线A1D与直线D1B垂直，直线MN//平面ABCDB．直线A1D与直线D1B平行，直线MN⊥平面BDD1B1C．直线A1D与直线D1B相交，直线MN//平面ABCDD．直线A1D与直线D1B异面，直线MN⊥平面BDD1B1答案：A分析：由正方体间的垂直、平行关系，可证MN//AB,A1D⊥平面ABD1，即可得出结论.连AD1，在正方体ABCD−A1B1C1D1中，M是A1D的中点，所以M为AD1中点，又N是D1B的中点，所以MN//AB，MN⊄平面ABCD,AB⊂平面ABCD，所以MN//平面ABCD.因为AB不垂直BD，所以MN不垂直BD则MN不垂直平面BDD1B1，所以选项B,D不正确；在正方体ABCD−A1B1C1D1中，AD1⊥A1D，AB⊥平面AA1D1D，所以AB⊥A1D，AD1∩AB=A，所以A1D⊥平面ABD1，D1B⊂平面ABD1，所以A1D⊥D1B，且直线A1D,D1B是异面直线，所以选项C错误，选项A正确.故选：A.小提示：关键点点睛：熟练掌握正方体中的垂直、平行关系是解题的关键，如两条棱平行或垂直，同一个面对角线互相垂直，正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.3、在正方体ABCD −A 1B 1C 1D 1中，三棱锥A −B 1CD 1的表面积为4√3，则正方体外接球的体积为（）A ．4√3πB ．√6πC ．32√3πD ．8√6π答案：B解析：根据三棱锥的表面积进一步求出正方体的棱长，最后求出正方体的外接球的半径，进一步求出结果．解：设正方体的棱长为a ，则B 1D 1=AC =AB 1=AD 1=B 1C =D 1C =√2a ，由于三棱锥A −B 1CD 1的表面积为4√3，所以S =4S △AB 1C =4×12×√32(√2a)2=4√3所以a =√2所以正方体的外接球的半径为√(√2)2+(√2)2+(√2)22=√62，所以正方体的外接球的体积为43π·(√62)3=√6π故选：B ．小提示：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.4、已知三棱锥P −ABC ，其中PA ⊥平面ABC ，∠BAC =120°，PA =AB =AC =2，则该三棱锥外接球的表面积为（）A ．12πB ．16πC ．20πD ．24π答案：C分析：根据余弦定理、正弦定理，结合球的性质、球的表面积公式进行求解即可.根据题意设底面△ABC 的外心为G ，O 为球心，所以OG ⊥平面ABC ，因为PA ⊥平面ABC ，所以OG//PA ，设D 是PA 中点，因为OP =OA ，所以DO ⊥PA ，因为PA ⊥平面ABC ，AG ⊂平面ABC ，所以AG ⊥PA ，因此OD//AG ，因此四边形ODAG 是平行四边形，故OG =AD =12PA =1，由余弦定理，得BC =√AB 2+AC 2−2AB ⋅AC ⋅cos120°=√4+4−2×2×2×(−12)=2√3，由正弦定理，得2AG =√3√32⇒AG =2，所以该外接球的半径R 满足R 2=(OG )2+(AG )2=5⇒S =4πR 2=20π，故选：C ．小提示：关键点睛：运用正弦定理、余弦定理是解题的关键.5、牟合方盖是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法，该方法不直接给出球体的体积，而是先计算牟合方盖的体积.刘徽通过计算，“牟合方盖”的体积与球的体积关系为V 牟V 球=4π，并且推理出了“牟合方盖”的八分之一的体积计算公式，即V 牟8=r 3−V 方盖差，从而计算出V 球=43πr 3.如果记所有棱长都为r 的正四棱锥的体积为V ，则V 方差盖:V =（）A．√22B．1C．√2D．2√2答案：C分析：计算出V方盖差，V，即可得出结论.由题意，V方盖差=r3−18V牟=r3−18×4π×43×π×r3=13r3，所有棱长都为r的正四棱锥的体积为V正=13×r×r×r2−(√2r2)2=√26r3，∴V方盖差V正=13r3√2r36=√2，故选：C．6、如图，已知正方体的棱长为a，沿图1中对角面将它分割成两个部分，拼成如图2的四棱柱，则该四棱柱的全面积为（）A．(8+2√2)a2B．(2+4√2)a2C．(4+2√2)a2D．(6−4√2)a2答案：C分析：拼成的几何体比原正方体的表面增加了两个截面，减少了原来两个正方形面，据此变化，进行求解. 由题意，拼成的几何体比原正方体的表面增加了两个截面，减少了原来两个正方形面，由于截面为矩形，长为√2a，宽为a，所以面积为√2a2，所以拼成的几何体的表面积为4a2+2√2a2=(4+2√2)a2.故选：C.7、如图所示的正方形SG1G2G3中，E ， F分别是G1G2，G2G3的中点，现沿SE，SF，EF把这个正方形折成一个四面体，使G1，G2，G3重合为点G，则有（）A．SG⊥平面EFG B．EG⊥平面SEFC．GF⊥平面SEF D．SG⊥平面SEF答案：A解析：根据正方形的特点，可得SG⊥FG，SG⊥EG，然后根据线面垂直的判定定理，可得结果. 由题意：SG⊥FG，SG⊥EG，FG∩EG=G，FG，EG⊂平面EFG所以SG⊥平面EFG正确，D不正确；.又若EG⊥平面SEF，则EG⊥EF，由平面图形可知显然不成立；同理GF⊥平面SEF不正确；故选：A小提示：本题主要考查线面垂直的判定定理，属基础题.8、如图，PA垂直于矩形ABCD所在的平面，则图中与平面PCD垂直的平面是（）A．平面ABCD B．平面PBCC．平面PAD D．平面PCD答案：C分析：由线面垂直得到线线垂直，进而证明出线面垂直，面面垂直.因为PA⊥平面ABCD，CD⊂平面ABCD，所以PA⊥CD，由四边形ABCD为矩形得CD⊥AD，因为PA∩AD=A，所以CD⊥平面PAD．又CD⊂平面PCD，所以平面PCD⊥平面PAD．故选：C多选题9、沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图，某沙漏由上(细管长度忽略不下两个圆锥组成，圆锥的底面直径和高均为8cm，细沙全部在上部时，其高度为圆锥高度的23计).假设该沙漏每秒钟漏下0.02cm3的沙，且细沙全部漏入下部后，恰好堆成一个盖住沙漏底部的圆锥形沙堆.以下结论正确的是（）A．沙漏中的细沙体积为1024πcm381B．沙漏的体积是128πcm3C．细沙全部漏入下部后此锥形沙堆的高度约为2.4cmD．该沙漏的一个沙时大约是1565秒(π≈3.14)答案：AC解析：A．根据圆锥的体积公式直接计算出细沙的体积；B．根据圆锥的体积公式直接计算出沙漏的体积；C．根据等体积法计算出沙堆的高度；D．根据细沙体积以及沙时定义计算出沙时.A.根据圆锥的截面图可知：细沙在上部时，细沙的底面半径与圆锥的底面半径之比等于细沙的高与圆锥的高之比，所以细沙的底面半径r=23×4=83cm，所以体积V=13⋅πr2⋅2ℎ3=13⋅64π9⋅163=1024π81cm3B.沙漏的体积V=2×13×π×(ℎ2)2×ℎ=2×13×π×42×8=2563πcm3；C.设细沙流入下部后的高度为ℎ1，根据细沙体积不变可知：1024π81=13×(π(ℎ2)2)×ℎ1，所以1024π81=16π3ℎ1,所以ℎ1≈2.4cm；D.因为细沙的体积为1024π81cm3，沙漏每秒钟漏下0.02cm3的沙，所以一个沙时为：1024π810.02=1024×3.1481×50≈1985秒.故选：AC.小提示：该题考查圆锥体积有关的计算，涉及到新定义的问题，难度一般.解题的关键是对于圆锥这个几何体要有清晰的认识，同时要熟练掌握圆锥体积有关的计算公式.10、(多选题)在四棱锥A－BCDE中，底面四边形BCDE为梯形，BC∥DE.设CD，BE，AE，AD的中点分别为M，N，P，Q，则（）A．PQ＝1MN B．PQ∥MN2C．M，N，P，Q四点共面D．四边形MNPQ是梯形答案：BCD分析：根据中位线的性质，结合平行的性质逐个判定即可DE，且DE≠MN，由题意知PQ=12所以PQ≠1MN，故A不正确；又PQ∥DE，DE∥MN，2所以PQ∥MN，又PQ≠MN，所以B，C，D正确.故选：BCD11、给出以下关于斜二测直观图的结论，其中正确的是（）A．水平放置的角的直观图一定是角B．相等的角在直观图中仍然相等C．相等的线段在直观图中仍然相等D．两条平行线段在直观图中仍是平行线段答案：AD分析：根据直观图和斜二测画法的规则，判断选项.水平放置的角的直观图一定是角，故A正确；角的大小在直观图中都会发生改变，有的线段在直观图中也会改变，比如正方形的直方图中，故BC错误；由斜二测画法规则可知，直观图保持线段的平行性，所以D正确.故选：AD填空题12、如图所示，P为平行四边形ABCD所在平面外一点，E为AD的中点，F为PC上一点，若PA//平面EBF，则PF=_______FC答案：12##0.5 分析：连接AC 交BE 于点M ，连接FM ，由线面平行的性质得线线平行，由平行线性得结论．连接AC 交BE 于点M ，连接FM ，∵PA//平面EBF ，PA ⊂平面PAC ，平面PAC ∩平面EBF =EM ，∴PA//EM ，又AE//BC ，∴PF FC =AM MC =AE BC =12. 所以答案是：12． 13、已知一个圆锥的底面半径为6，其体积为30π则该圆锥的侧面积为________.答案：39π分析：利用体积公式求出圆锥的高，进一步求出母线长，最终利用侧面积公式求出答案. ∵V =13π62⋅ℎ=30π∴ℎ=52∴l =√ℎ2+r 2=√(52)2+62=132 ∴S 侧=πrl =π×6×132=39π. 所以答案是：39π.14、如图，拿一张矩形纸片对折后略微展开，竖立在桌面上，折痕与桌面的关系是______．答案：垂直分析：根据给定条件，利用线面垂直的判定推理作答.令桌面所在的平面为α，折痕所在直线为l，纸片与桌面公共部分所在直线为a,b，如图，依题意有a∩b=A，因l⊥a,l⊥b，a,b⊂α，所以l⊥α，所以折痕与桌面垂直.所以答案是：垂直解答题15、如图，四棱锥P−ABCD的底面是矩形，PD⊥底面ABCD，M为BC的中点，且PB⊥AM．（1）证明：平面PAM⊥平面PBD；（2）若PD=DC=1，求四棱锥P−ABCD的体积．答案：（1）证明见解析；（2）√23．分析：（1）由PD⊥底面ABCD可得PD⊥AM，又PB⊥AM，由线面垂直的判定定理可得AM⊥平面PBD，再根据面面垂直的判定定理即可证出平面PAM⊥平面PBD；（2）由（1）可知，AM⊥BD，由平面知识可知，△DAB~△ABM，由相似比可求出AD，再根据四棱锥P−ABCD的体积公式即可求出．（1）因为PD⊥底面ABCD，AM⊂平面ABCD，所以PD⊥AM，又PB⊥AM，PB∩PD=P，所以AM⊥平面PBD，而AM⊂平面PAM，所以平面PAM⊥平面PBD．（2）[方法一]：相似三角形法由（1）可知AM⊥BD．于是△ABD∽△BMA，故ADAB =ABBM．因为BM=12BC,AD=BC,AB=1，所以12BC2=1，即BC=√2．故四棱锥P−ABCD的体积V=13AB⋅BC⋅PD=√23．[方法二]：平面直角坐标系垂直垂直法由（2）知AM⊥DB,所以k AM⋅k BD=−1．建立如图所示的平面直角坐标系，设BC =2a(a >0)．因为DC =1，所以A(0,0)，B(1,0)，D(0,2a)，M(1,a)．从而k AM ⋅k BD =a−01−0×2a−00−1=a ×(−2a)=−2a 2=−1．所以a =√22，即DA =√2．下同方法一.[方法三]【最优解】：空间直角坐标系法建立如图所示的空间直角坐标系D −xyz ，设|DA|=t ，所以D(0,0,0)，C(0,1,0)，P(0,0,1)，A(t,0,0)，B(t,1,0)．所以M (t 2,1,0)，PB ⃑⃑⃑⃑⃑ =(t,1,−1)，AM ⃑⃑⃑⃑⃑⃑ =(−t 2,1,0)．所以PB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =t ⋅(−t 2)+1×1+0×(−1)=−t 22+1=0．所以t =√2，即|DA|=√2．下同方法一.[方法四]：空间向量法由PB ⊥AM ，得PB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0．所以(PD⃑⃑⃑⃑⃑ +DA ⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ )⋅AM ⃑⃑⃑⃑⃑⃑ =0．即PD ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +DA ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0．又PD ⊥底面ABCD ，AM 在平面ABCD 内，因此PD ⊥AM ，所以PD ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0．所以DA ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ ⋅AM ⃑⃑⃑⃑⃑⃑ =0，由于四边形ABCD 是矩形，根据数量积的几何意义，得−12|DA ⃑⃑⃑⃑⃑ |2+|AB ⃑⃑⃑⃑⃑ |2=0，即−12|BC ⃑⃑⃑⃑⃑ |2+1=0．所以|BC⃑⃑⃑⃑⃑ |=√2，即BC =√2．下同方法一. 【整体点评】(2)方法一利用相似三角形求出求出矩形的另一个边长，从而求得该四棱锥的体积；方法二构建平面直角坐标系，利用直线垂直的条件得到矩形的另一个边长，从而求得该四棱锥的体积；方法三直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的另一个边长,为最常用的通性通法，为最优解；方法四利用空间向量转化求得矩形的另一边长.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一．选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)
1、下列命题为真命题的是（）
A. 平行于同一平面的两条直线平行；
B.与某一平面成等角的两条直线平行；
C. 垂直于同一平面的两条直线平行；
D.垂直于同一直线的两条直线平行。

2、下列命题中错误的是：（）
A. 如果α⊥β，那么α内一定存在直线平行于平面β；
B. 如果α⊥β，那么α内所有直线都垂直于平面β；
C. 如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β；
D. 如果α⊥γ，β⊥γ，α∩β＝l,那么l ⊥γ. 3、右图的正方体ABCD-A ’B ’C ’D ’
中,异面直线AA ’与BC 所成的角是（） A. 300 B.450 C. 600 D. 900
4、右图的正方体ABCD- A ’B ’C ’D ’中，二面角D ’-AB-D 的大小是（）
A. 300
B.450
C. 600
D. 900
5.在空间中，下列命题正确的是 A.若三条直线两两相交，则这三条直线确定一个平面
B.若直线m 与平面α内的一条直线平行，则α//m
C.若平面βα⊥，且l =βαI ，则过α内一点P 与l 垂直的直线垂直于平面β
D.若直线a 与直线b 平行，且直线a l ⊥，则b l ⊥
6．设平面α∥平面β，A ，C ∈α，B ，D ∈β，直线AB 与CD 交于点S ，且点S 位于平面α，β之间，AS ＝8，BS ＝6，CS ＝12，则SD ＝（）
A ．3
B ．9
C ．18
D ．10
7．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )
A ．9π
B ．10π
C ．11π
D ．12π
8. 正方体的内切球和外接球的半径之比为（） A. 3 B. 3 C. 3 D. 39．已知△ABC 是边长为a 2的正三角形，那么它的斜二侧所画直观图A B C ⅱ?V 的面积为
( )
a 2 a 2 a 2 a 2
10．若正方体的棱长为2，则以该正方体各个面的中心为顶点的多面体的体积为
( )
11. 在空间四边形ABCD 中，AD=BC=2，E 、F 分别是AB 、CD 的中点，EF=2，求AD 与
BC 所成角的大小．( )
A B
D
A ’
B ’ D ’
C C ’
A B D C E F A. ο30 B.ο45 C. 60ο D.ο90
12.如图，在多面体ABCDEF 中，已知平面ABCD 是边长为3的
正方形，//EF AB ,32
EF =,且EF 与平面ABCD 的距离为2，则该多面体的体积为（）
A 92
B 5
C 6
D 152
二、填空题（共4小题，每小题5分，共20分，把答案填在题中的横线上） 13． Rt ABC ∆中，3,4,5AB BC AC ===，将三角形绕直角边AB 旋转一周所成的几何体的体积为 .
14．一个圆台的母线长为5 cm ，两底面面积分别为4πcm 2 和25π cm 2.则圆台的体积 ________．
15. 三棱锥S-ABC 中SA 平面 ABC ，AB 丄 BC,SA = 2,AB =B C
=1，则三棱锥S-ABC 的外接球的表面积等于______.
16．如图，在直角梯形ABCD 中，,,BC DC AE DC ⊥⊥M 、N 分别是AD 、BE 的中点，将三角形ADE 沿AE 折起。

下列说法正确的是．（填上所有正确的序号） ①不论D 折至何位置（不在平面ABC 内）都有
//MN 平面;DEC
②不论D 折至何位置都有;MN AE ⊥
③不论D 折至何位置（不在平面ABC 内）都有//;MN AB
④在折起过程中，一定存在某个位置，使.EC AD ⊥
三、解答题（本大题共6小题，共70分） 17.如图，在底面是直角梯形的四棱锥S-ABCD 中，
(1)求四棱锥S-ABCD 的体积;
(2)求证：;SBC SAB 面面⊥
(3)求SC 与底面ABCD 所成角的正切值。

18.如图，在边长为a 的菱形ABCD 中，ABCD PC ABC 面⊥=∠,60ο，E,F 是PA 和AB 的
中点。

（1）求证： EF||平面PBC ;
（2）求E 到平面PBC 的距离。

19．（本题12分）已知：一个圆锥的底面半径为R ＝2，高为H ＝4，在其中有一个高为x 的内接圆柱．（1）写出圆柱的侧面积关于x 的函数；
（2）x 为何值时，圆柱的侧面积最大．
20. （本题12分）如下图所示，在直三棱柱ABC －A 1B 1C 1中，
AC ＝3，BC ＝4，AB ＝5，AA 1＝4，点D 是AB 的中点．
(1)求证：AC ⊥BC 1；
(2)求证：AC 1∥平面CDB 1； A B C D P E F
S
C A
D B
(3)求异面直线AC 1与B 1C 所成角的余弦值．
21.已知DBC ∆∆和ABC 所在的平面互相垂直，且ＡＢ＝ＢＣ＝ＢＤ，
0120=∠=∠DBC CBA ，求：
⑴．直线AD 与平面BCD 所成角的大小；
⑵．直线AD 与直线BC 所成角的大小； ⑶．二面角A-BD-C 的余弦值． 22. (本小题满分12分）如图，已知四棱锥P —ABCD ，侧面PAD 为边长等
于2的正三角形，底面ABCD 为菱形，
.
(I)证明：；
(I I )若PB = 3，求四棱锥P—ABCD 的体积.
题
号
1 2 3 4 5 6 7 8 9 10 11 12
答
案 C B D B D B D C C B B D 13. 16π 14 52π 15. 6π 16．(1),(2),(4)
17. （1）解：4
111)121(61)(2
13131=⨯⨯+⨯=⨯⨯+⨯⨯==SA AB BC AD Sh v （2）证明：
又,A AB SA BC AB =⊥I Θ，
（3）解：连结AC,则SCA ∠就是SC 与底面ABCD 所成的角。

在三角形SCA 中，SA=1,AC=2112
2=+, 18.（1）证明：PB
EF BF AF PE AE ||,,∴==Θ……………………………2 又 ,,PBC PB PBC EF 平面平面⊂⊄
故 PBC EF 平面|| (5)
（2）解：在面ABCD 内作过F 作H BC FH 于⊥ (6)
ABCD PBC 面面⊥∴ (8)
又 BC ABCD PBC =面面I ，BC FH ⊥，ABCD FH 面⊂
又PBC EF 平面||，故点E 到平面PBC 的距离等于点F 到平面PBC 的距离FH 。

在直角三角形FBH 中，2,60a FB FBC ==∠ο，故点E 到平面PBC 的距离等于点F 到平面PBC 的距离，等于
a 43。

…………12 21.⑴如图，在平面ABC 内，过A 作AH ⊥BC ，垂足为H ，
则AH ⊥平面DBC ，∴∠ADH 即为直线AD 与平面BCD 所成的角
由题设知△AHB ≌△AHD ，则DH ⊥BH ，AH =DH ，∴∠ADH =45°
⑵∵BC ⊥DH ，且DH 为AD 在平面BCD 上的射影，
∴BC ⊥AD ，故AD 与BC 所成的角为90°
⑶过H 作HR ⊥BD ，垂足为R ，连结AR ，则由三垂线定理知，AR ⊥BD ，故∠ARH 为二面角A —BD —C 的平面角的补角设BC =a ,则由题设知，AH =DH =
2
,23a BH a =,在△HDB 中，HR =43a ，∴tan ARH =HR AH =2 故二面角A —BD —C 的余弦值的大小为55-
22.。