运筹学单纯形法的例题
合集下载
运筹学单纯形法
只要取 x5=min{-，8/2，12}=4 就有上式成立。 x5=4时， x4=0，故决定用x5换x4 x1 =4- 1/4 x4 x5 =4-1/2 x4 +2 x3 x2 =2+1/8 x4–1/2 x3 代入得 z=14-3/2 x3 –1/8 x4 ，令x3 ，x4=0得z=14。新基可 行解为 X(3) =(4,2,0,0,4) T –为最优解，新顶点Q2 最优目标值z=14 。
§3.4 最优性检验和判别定理
线性规划解的四种可能： 1、有唯一解； 2、无穷多最优解； 3、无界解； 4、无可行解。 何时达最优解, 何种最优解？
将基本可行解X(0)和X(1)分别代入目标函数得
z z
(0)
= ∑ ci xi0
i =1 m
mቤተ መጻሕፍቲ ባይዱ
(1)
= ∑ ci [ xi0 − θ aij ] + θ ci
§3.3 从初始基可行解转换为另一基可行解
0 0 记初始基可行解为X(0),有 X ( 0 ) = (x10 x 2 L x m 0 L 0
)
Pi xi0 = b 该解满足约束方程, 即 ∑
i =1
m
(1)
非基向量可以用基向量的线性组合表示
Pj = ∑ aij Pj
i =1 m
m
(2) (3)
Pj − ∑ aij Pj = 0
从实际例子中分析单纯形法原理的基本框架为 •第一步：将LP线性规划变标准型，确定一个初始可行解 （顶点）。 •第二步：对初始基可行解最优性判别，若最优，停止；否 则转下一步。 •第三步：从初始基可行解向相邻的基可行解（顶点）转 换，且使目标值有所改善—目标函数值增加，重复第二和 第三步直到找到最优解。
运筹学-单纯形法灵敏度对偶
若新增约束如下：
max z 50x1 100x2 x1 x2 300 2x1 x2 400 x2 250 10x1 30x2 5000(电力约束) x1, x2 , 0
x1 x2 s1
把最优解x1=50,x2 =250代入电力约束 1050+30 250=80005000 新约束不满足,最优解变化
例题：已知某线性规划初始可行基是（S1 S2 S3 a1）， 最终单纯形表如下，求对偶价格不变时的△bi变化范围
x1 x2 s1
50 100 0
X1 50
1
0
0
S3 0
0
0
0
X2 100 0
1
0
s1 0
0
0
1
Zj
50 100 0
δj
0
0
0
（1） △b1的变化范围： ?
（2） △b2的变化范围：?
（3） △b3的变化范围： ? （4） △b4的变化范围：?
1 0 1 2 0.5
B1 p6'
2
1
1
0.5
2
0 0 1 1.5 1.5
Z6' 50 0.5 0 (2) 100 1.5 175
' 6
C6
Z6'
150 175
25
δ6´<0，最优解不变，即仍生产Ⅰ50件，Ⅱ100件。
2、变量xk系数列由pk变为pk´，在最终单纯形表 上xk是基变量
x1 x2 s1
50 100 0
X1 50 1
0
0
S3 0
0
0
0
X2 100 0
1
0
s1 0
0
运筹学单纯形法的例题
可行域在x1+3x2=7与4x1+2x2=9之下__
3
.
05.07.2020
练习㈠用图解法
5
4 4x1+x2=9
3
2
1 (2.25,0)
0
1
2
3
4
5
6
7
4
.
05.07.2020
练习㈠. 单纯形表
1 31 0 7 4 20 1 9
填入第一个约束的数据.
填入第二个约束的数据.
5
.
05.07.2020
❖至少有一个非基变量的检验数为正,但它的系 数全为非正,则无有限最优解；
❖所有非基变量的检验数全为非正，已有最优解， 但若其中至少有一个的检验数为0，且它的系 数中有2正4 的，则可能有. 无穷多个最优0解5.07.。2020
基变量列中_x_5_换为_x_1_,
改CB列,_-_M__换为_4__.
Excel
17
.
05.07.2020
练习㈢用图解法和单纯形法求 如下线性规划问题的最优解：
Max z =4 x1 + x2 x1 + 3x2 ≥ 7
s.t. 4x1 + 2x2 ≥ 9 x1 , x2 ≥ 0
可行域在直线 x1+3x2=7之上__
s.t. 4x1 + 2x2 -x4+x6=9
基引是进谁两?个这 理x“1里?,x人“2 ,工x-”3 如变,x4何量,x5处”,x6≥0
x5 ,x620
.
05.07.2020
练习㈢.用单纯形法
Max z=4x1+x2+0x3+0x4 -Mx5 –Mx6
15单纯形法(运筹学)
几点说明： 几点说明： (1)、 (1)、例 maxZ=X1 +2X2 X1 ≤ 4 X2 ≤ 3 X1+2X2 ≤ 8 X1 , X2 ≥0 X1+X3 = 4 X2+X4 = 3 X1+2X2+X5= 8 X1 … X5 ≥0
1
2
3
4
X(1)= (2,3) X(2)= (4,2)
全部解： 全部解：X=α
(1) -4 0 1 -2 0
14
15
本问题无界。 本问题无界。 X2
O
X1
Z=0
16
1.5.4 初始基本可行解的求法 (一)、大M法： 一、 法 例1 ： maxZ= 6X1 +4X2 2X1 +3X2 ≤ 100 4X1 +2X2 ≤ 120 X1 X1 X2 ≥0
=14
X2 ≥ 22
17
λj <0
8
(3)、 (3)、maxZ=10X1 + 12X2 3X1+4X2 ≤ 6 4X1+ X2 ≤ 2 3X1 +2X2 ≤ 3 X1 , X2 ≥0
9
10
X =(0, 3/2, 0, 1/2, 0)T Zmax=18
退化解
*
11
例：maxZ= -3/4X4+20X5 -1/2X6+6X7 X1+1/4X4 -8X5 -X6+9X7 =0 X2+1/2X4-12X5 -1/2X6+3X7 =0 X3+X6 =1 X1 … X7 ≥0 (P1 P2 P3) → (P4 P2 P3) → (P1 P2 P3) → (P4 P5 P3) → (P6 P5 P3) → (P6 P7 P3) → (P1 P7 P3)
1
2
3
4
X(1)= (2,3) X(2)= (4,2)
全部解： 全部解：X=α
(1) -4 0 1 -2 0
14
15
本问题无界。 本问题无界。 X2
O
X1
Z=0
16
1.5.4 初始基本可行解的求法 (一)、大M法： 一、 法 例1 ： maxZ= 6X1 +4X2 2X1 +3X2 ≤ 100 4X1 +2X2 ≤ 120 X1 X1 X2 ≥0
=14
X2 ≥ 22
17
λj <0
8
(3)、 (3)、maxZ=10X1 + 12X2 3X1+4X2 ≤ 6 4X1+ X2 ≤ 2 3X1 +2X2 ≤ 3 X1 , X2 ≥0
9
10
X =(0, 3/2, 0, 1/2, 0)T Zmax=18
退化解
*
11
例：maxZ= -3/4X4+20X5 -1/2X6+6X7 X1+1/4X4 -8X5 -X6+9X7 =0 X2+1/2X4-12X5 -1/2X6+3X7 =0 X3+X6 =1 X1 … X7 ≥0 (P1 P2 P3) → (P4 P2 P3) → (P1 P2 P3) → (P4 P5 P3) → (P6 P5 P3) → (P6 P7 P3) → (P1 P7 P3)
运筹学习题解答(chap1 线性规划及单纯形法)
第一章 线性规划及单纯形法一、写出下列线性规划的标准形式，用单纯形法求解，并指出其解属于哪种情况。
1、P55,1.3(a)21510m ax x x Z +=⎪⎩⎪⎨⎧≥≤+≤+0x ,x 8x 2x 59x 4x 3.t .s 212121 解：将模型化为标准型21510x x Z Max +=⎪⎩⎪⎨⎧≥=++=++0,,,825943..4321421321x x x x x x x x x x t s 单纯形表如下因所有检验数0j ≤σ，已达最优解，最优解是)2,1(*=X ，最优目标值为2。
由检验数的情况可知，该问题有唯一最优解。
2、 P55,1.3(b)21x x 2Z m ax +=s.t⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,524261552121212x x x x x x x解：将模型化为标准型21x x 2Z Max +=t s . ⎪⎪⎩⎪⎪⎨⎧≥=++=++=+0x ,...,x ,x ,5x x x ,24x x 2x 6,15x x 552152142132 单纯形表如下因所有检验数0j ≤σ，已达最优解，最优解是)0,0,2,2,2(X *=，最有目标值为217。
由检验数的情况可知，该问题有唯一最优解。
3、3212x x x Z Min -+=，t s . ⎪⎪⎩⎪⎪⎨⎧≥≤++≤+-≤-+0,,,5,822,422321321321321x x x x x x x x x x x x 解：将模型化为标准型：3212x x x Z Min -+=t s . ⎪⎪⎩⎪⎪⎨⎧≥=+++=++-=+-+0,,,5,822,422321632153214321x x x x x x x x x x x x x x x 用单纯形法迭代最优解为（0，0，4），最优值为-4。
4、43213x x x x Z Min +++=t s . ⎪⎪⎩⎪⎪⎨⎧≥=++=++-0,,,,,63,4224321421321x x x x x x x x x x 解：因为所有检验数均已非负，故已是最优解，最优解为（0，2，0，4），--10分最优目标值：6Z =*。
运筹学 线性规划问题的单纯形法
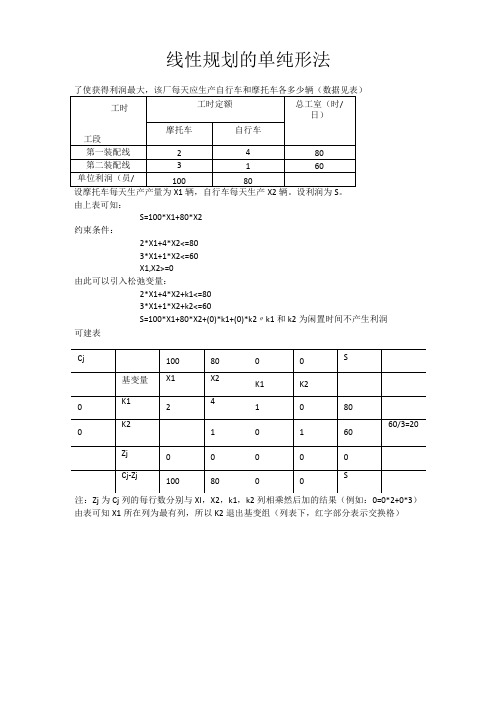
线性规划的单纯形法
由上表可知：
S=100*X1+80*X2
约束条件：
2*X1+4*X2<=80
3*X1+1*X2<=60
X1,X2>=0
由此可以引入松弛变量：
2*X1+4*X2+k1<=80
3*X1+1*X2+k2<=60
S=100*X1+80*X2+(0)*k1+(0)*k2〃k1和k2为闲置时间不产生利润
可建表
注：Zj为Cj列的每行数分别与XI，X2，k1，k2列相乘然后加的结果（例如：0=0*2+0*3）由表可知X1所在列为最有列，所以K2退出基变组（列表下，红字部分表示交换格）
而由表可知要消去图中绿字所在行必须是图中绿字所在行-2*红字所在行。
消去后的表的情
注：此时由上表可知X2所在列是最有解，切Cj-Zj依旧为正。
所以，此时K1出基（将k1行中各数据*3/10）得到如下表：
注：由表可知此时Cj-Zj为零，如果接续下去此值将会为负所以此时由最大利润为2560即：当摩托车生产16辆，自行车生产12辆是有最大利润。
本题只是为了让和我有一样迷惑的人有一个解题案例，如若真正搞懂线性规划问题的单纯形法还得去以参考书为准。
运筹学单纯形法的对偶问题
可以为负，即 y3 没有非负限制。
这样我们把原规划的对偶问题化为
min f 440 y1 100 y2 200 y3
s.t. 2 y1 6 y2 5y3 3,
3y1 4 y2 3y3 4,
6 y1 y2 y3 6,
y1, y2 0, y3 没有非负限制。
对照原线性规划问题，我们可以知道：
解：设x1为产品 的计划产量，x2 为产品Ⅱ的计划产量，则有
目标函数： 约束条件：
Max z=50 x1 + 100 x2
x1 x2 300
2x1 x2 400
x2 250
x1, x2 0
管理运筹学
1
§1 线性规划的对偶问题
现在我们从另一个角度来考虑这个问题。假如有另外一个工厂要求租用该厂的设备A、B、 c，那么该厂的厂长应该如何来确定合理的租金呢？
管理运筹学
14
§1 线性规划的对偶问题
首先在写对偶问题之前，我们先把第二个约束条件两边乘以-1得
2x1 3x2 x3 60
然后按照上面的规则，我们可以得到其对偶问题为
max z 180 y1 60 y2 240 y3;
y1 2 y2 5 y3 3
s.t.
2 y1 3y2 3y3 9
管理运筹学
16
§2 对偶规划的基本性质
3．最优性。如果 Xˆ是原问题的可行解，Yˆ 是对偶问题 的可行解，并且cXˆ bTYˆ，则 Xˆ 和 Yˆ分别为原问题和 对偶问题的最优解。
4．强对偶性。即若原问题及其对偶问题都有可行解，
则两者都有最优解，且它们的最优解的目标函数都 相等。
5．互补松弛性。在线性规划问题的最优解中，如果
决策变量都来源于原问题的第三个约束条件，记为
(完整word版)运筹学单纯形法
0*10+0*20
=0
σj=Cj- Zj
2
-1
1
0
0
0
1
S1
0
0
4
-5
1
-3
0
30
30/4
X1
2
1
-1
2
0
1
0
10
10/-1
S3
0
0
2
-3
0
-1
1
10
10/2
Zj
2
-2
4
0
2
0
Z=Z0=0*30+
2*10+0*10
=20
σj=Cj- Zj
0
1
-3
0
-2
0
2
S1
0
0
0
1
1
-1
-2
10
X1
2
1
0
1/2
0
s.t.
5x1+6x2-4x3-4x4+S1=20
3x1-3x2+2x3+8x4+S2=25
4x1-2x2+x3+3x4+S3=10
x1,x2,x3,x4,S1,S2,S3>=0
迭代次数
基变量
CB
(Ci)
X1
X2
X3
X4
S1
S2
S3
b
比值
bi/aij
6
2
10
8
0
0
0
0
S1
0
5
6
-4
-4
1
0
0
20
=0
σj=Cj- Zj
2
-1
1
0
0
0
1
S1
0
0
4
-5
1
-3
0
30
30/4
X1
2
1
-1
2
0
1
0
10
10/-1
S3
0
0
2
-3
0
-1
1
10
10/2
Zj
2
-2
4
0
2
0
Z=Z0=0*30+
2*10+0*10
=20
σj=Cj- Zj
0
1
-3
0
-2
0
2
S1
0
0
0
1
1
-1
-2
10
X1
2
1
0
1/2
0
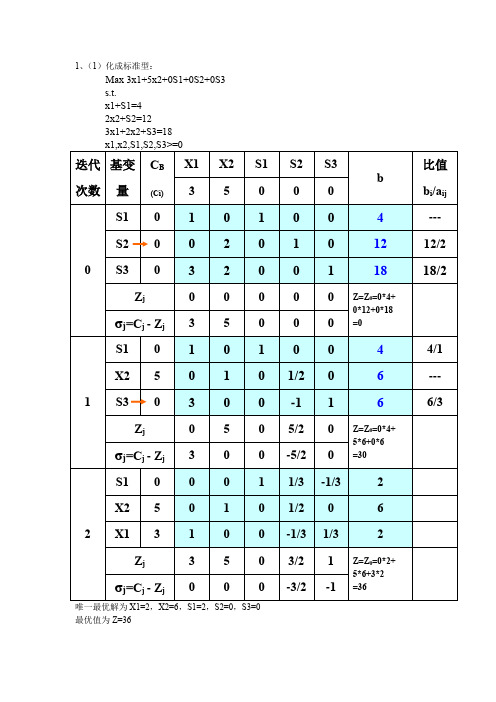
s.t.
5x1+6x2-4x3-4x4+S1=20
3x1-3x2+2x3+8x4+S2=25
4x1-2x2+x3+3x4+S3=10
x1,x2,x3,x4,S1,S2,S3>=0
迭代次数
基变量
CB
(Ci)
X1
X2
X3
X4
S1
S2
S3
b
比值
bi/aij
6
2
10
8
0
0
0
0
S1
0
5
6
-4
-4
1
0
0
20
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
s.t. 4x1 + 2x2 -x4+x6=9
基引是进谁两?个这 理x“1里?,x人“2 ,工x-”3 如变,x4何量,x5处”,x6≥0
x5 ,x620
编辑ppt
03.08.2020
练习㈢.用单纯形法
Max z=4x1+x2+0x3+0x4 -Mx5 –Mx6
x1+3x2-x3 +x5 =7 s.t. 4x1+2x2 -x4 +x6=9
x1,x2,x3,x4 ,x5,x6 ≥0
基是谁? x5,x6 它们的检验数为0 请它们出基,逼它们取值为0. 不能全出基,就无可行解. Excel
21
编辑ppt
03.08.2020
解LP问题单纯形法
❖LP问题解的几种可能：
唯一解 有解
无穷多解
无解
22
无有限最优解
无可行解
编辑ppt
03.08.2020
填入第一个约束的数据.
14
编辑ppt
03.08.2020
练习㈡. 单纯形表
填入第二个约束的数据. 基?
填目标函数系数,填基变量列,
填C 列,计算Z ,计算检验数σ , B 15
j编辑ppt
03.08.2020
j
练习㈡. 单纯形表
7 9/4
最优吗？查什么？不是！谁进基?
检x1验的数系最数大有的正x的1进吗基? ,求谁比出值基??
比
41 00
x3 0 0 2.5 1 -0.25 4.75
1
x1 4 1 0.5 0 0.25 2.25
zj
42 019
σj=Cj- zj 0 -1
9
编辑ppt
0 -1 03.08.2020
练习㈡用图解法和单纯形法求Biblioteka 如下线性规划问题的最优解：
Max s.t.
4zxxx1=11+4+, x321xxx2+22≤≥≥x2790
可行域在直线 x1+3x2=7之下__
可行域在直线4x1+2x2=9之上__
10
编辑ppt
03.08.2020
练习㈡用图解法
5 最优解是x1=7,x2=0,此时Max z=28
4 4x1+x2=28
3
2
(7,0) 1
0
1
2
3
4
5
6
7
11
编辑ppt
03.08.2020
练习㈡.用单纯形法 (大M法)
改CB列,__0_换为_4__.
8
编辑ppt
Excel
03.08.2020
练习㈠用单纯形法
迭代
基
CB
次数 变量
x1
4
x2
1
x3
0
x4
0
bi
比
x3 0 1 3 1 0 7 7
0
x4 0 4 2
zj
00
0 1 9 9/4 000
σj=Cj- zj 4 1 0 0
迭代
基
CB
次数 变量
x1
x2
x3
x4
bi
解LP问题单纯形法
❖LP问题解的几种可能： s.t. Ax≤b x≥0
❖无需引入人工变量.一定有可行 解,从而一定有基可行解,但还有 可能有无穷最优解或无有限最
优解.
23
编辑ppt
03.08.2020
解LP问题单纯形法
❖LP问题解的几种可能：
❖一般要引入人工变量. ❖人工变量不能全出基则无可行解,更
0 00 0 0
4 10 0
最优吗？查什么？不是！谁进基？
检x1验的数系最数大有的正x的1进吗基？求, 谁比出值基？？
7
编辑ppt
03.08.2020
练习㈠. 单纯形表
4 10 0 x3 0 1 3 1 0 7 7 x4 0 4 2 0 1 9 9/4
0 00 0 0
4 10 0
基变量列中_x_4_换为_x_1_,
16
编辑ppt
03.08.2020
练习㈡. 单纯形表：迭代
基变量列中_x_5_换为_x_1_,
改CB列,_-_M__换为_4__.
Excel
17
编辑ppt
03.08.2020
练习㈢用图解法和单纯形法求 如下线性规划问题的最优解：
Max z =4 x1 + x2 x1 + 3x2 ≥ 7
s.t. 4x1 + 2x2 ≥ 9 x1 , x2 ≥ 0
可行域在x1+3x2=7与4x1+2x2=9之下__
3
编辑ppt
03.08.2020
练习㈠用图解法
5
4 4x1+x2=9
3
2
1 (2.25,0)
0
1
2
3
4
5
6
7
4
编辑ppt
03.08.2020
练习㈠. 单纯形表
1 31 0 7 4 20 1 9
填入第一个约束的数据.
填入第二个约束的数据.
5
编辑ppt
03.08.2020
练习㈠. 单纯形表
4 10 0 x3 0 1 3 1 0 7 x4 0 4 2 0 1 9
0 00 0 0
4 1 0 0 基?
填目标函数系数,填基变量列,
填CB列,计算Zj,计算检验数σj,
6
编辑ppt
03.08.2020
练习㈠. 单纯形表
4 10 0 x3 0 1 3 1 0 7 7 x4 0 4 2 0 1 9 9/4
《运筹学》单纯形法
2
编辑ppt
03.08.2020
练习㈠用图解法和单纯形法求如
下线性规划问题的最优解：
Max z =4 x1 + x2 x1 + 3x2 ≤ 7
s.t. 4x1 + 2x2 ≤ 9 x1 , x2 ≥ 0
x1+3x2=7经过点(_7_,0)与(1,_2_)
4x1+2x2=9经过点(2,_0_.5_)与(0,_4_.5_)
可行域在直线 x1+3x2=7之上__
可行域在直线4x1+2x2=9之上__
18
编辑ppt
03.08.2020
练习㈢用图解法
5
有可行解,但无有限的最优解,z→+∞.
4
3
2
1
0
1
2
3
4
5
6
7
19
编辑ppt
03.08.2020
练习㈢.用单纯形法(大M法)
标准化为: M是一个大的正数
Max z=4x1+x2+0x3+0x-4Mx5 -Mx6 x1 + 3x2 - x3 +x5 =7
Max z =4x1+x2+0x3+0x4-Mx5
x1 + 3x2 + x3
=7
s.t. 4x1 + 2x2 -x4+x5 =9
x1, x2 , x3 , x4 , x5 ≥0
基是谁? x3,x5 x5的检验数为0
请它出基,逼它取值为0.
13
编辑ppt
03.08.2020
练习㈡. 单纯形表
两行，几列? 少一列?
无最优解. ❖不需人工变量或人工变量可以全部出 基则必有可行解.分:
❖至少有一个非基变量的检验数为正,但它的系 数全为非正,则无有限最优解；
标准化为: M是一个大的正数
Max z =4 x1+x2+0x3+0x4-Mx5
x1 + 3x2 + x3
=7
s.t. 4x1 + 2x2 -x4+x5=9
基再是引谁进?一这 理x个1个?, “x“2 人,-”x如工3 ,何变x4处, x5≥ 0
量”1x2 5
编辑ppt
03.08.2020
练习㈡.用单纯形法
基引是进谁两?个这 理x“1里?,x人“2 ,工x-”3 如变,x4何量,x5处”,x6≥0
x5 ,x620
编辑ppt
03.08.2020
练习㈢.用单纯形法
Max z=4x1+x2+0x3+0x4 -Mx5 –Mx6
x1+3x2-x3 +x5 =7 s.t. 4x1+2x2 -x4 +x6=9
x1,x2,x3,x4 ,x5,x6 ≥0
基是谁? x5,x6 它们的检验数为0 请它们出基,逼它们取值为0. 不能全出基,就无可行解. Excel
21
编辑ppt
03.08.2020
解LP问题单纯形法
❖LP问题解的几种可能：
唯一解 有解
无穷多解
无解
22
无有限最优解
无可行解
编辑ppt
03.08.2020
填入第一个约束的数据.
14
编辑ppt
03.08.2020
练习㈡. 单纯形表
填入第二个约束的数据. 基?
填目标函数系数,填基变量列,
填C 列,计算Z ,计算检验数σ , B 15
j编辑ppt
03.08.2020
j
练习㈡. 单纯形表
7 9/4
最优吗？查什么？不是！谁进基?
检x1验的数系最数大有的正x的1进吗基? ,求谁比出值基??
比
41 00
x3 0 0 2.5 1 -0.25 4.75
1
x1 4 1 0.5 0 0.25 2.25
zj
42 019
σj=Cj- zj 0 -1
9
编辑ppt
0 -1 03.08.2020
练习㈡用图解法和单纯形法求Biblioteka 如下线性规划问题的最优解：
Max s.t.
4zxxx1=11+4+, x321xxx2+22≤≥≥x2790
可行域在直线 x1+3x2=7之下__
可行域在直线4x1+2x2=9之上__
10
编辑ppt
03.08.2020
练习㈡用图解法
5 最优解是x1=7,x2=0,此时Max z=28
4 4x1+x2=28
3
2
(7,0) 1
0
1
2
3
4
5
6
7
11
编辑ppt
03.08.2020
练习㈡.用单纯形法 (大M法)
改CB列,__0_换为_4__.
8
编辑ppt
Excel
03.08.2020
练习㈠用单纯形法
迭代
基
CB
次数 变量
x1
4
x2
1
x3
0
x4
0
bi
比
x3 0 1 3 1 0 7 7
0
x4 0 4 2
zj
00
0 1 9 9/4 000
σj=Cj- zj 4 1 0 0
迭代
基
CB
次数 变量
x1
x2
x3
x4
bi
解LP问题单纯形法
❖LP问题解的几种可能： s.t. Ax≤b x≥0
❖无需引入人工变量.一定有可行 解,从而一定有基可行解,但还有 可能有无穷最优解或无有限最
优解.
23
编辑ppt
03.08.2020
解LP问题单纯形法
❖LP问题解的几种可能：
❖一般要引入人工变量. ❖人工变量不能全出基则无可行解,更
0 00 0 0
4 10 0
最优吗？查什么？不是！谁进基？
检x1验的数系最数大有的正x的1进吗基？求, 谁比出值基？？
7
编辑ppt
03.08.2020
练习㈠. 单纯形表
4 10 0 x3 0 1 3 1 0 7 7 x4 0 4 2 0 1 9 9/4
0 00 0 0
4 10 0
基变量列中_x_4_换为_x_1_,
16
编辑ppt
03.08.2020
练习㈡. 单纯形表：迭代
基变量列中_x_5_换为_x_1_,
改CB列,_-_M__换为_4__.
Excel
17
编辑ppt
03.08.2020
练习㈢用图解法和单纯形法求 如下线性规划问题的最优解：
Max z =4 x1 + x2 x1 + 3x2 ≥ 7
s.t. 4x1 + 2x2 ≥ 9 x1 , x2 ≥ 0
可行域在x1+3x2=7与4x1+2x2=9之下__
3
编辑ppt
03.08.2020
练习㈠用图解法
5
4 4x1+x2=9
3
2
1 (2.25,0)
0
1
2
3
4
5
6
7
4
编辑ppt
03.08.2020
练习㈠. 单纯形表
1 31 0 7 4 20 1 9
填入第一个约束的数据.
填入第二个约束的数据.
5
编辑ppt
03.08.2020
练习㈠. 单纯形表
4 10 0 x3 0 1 3 1 0 7 x4 0 4 2 0 1 9
0 00 0 0
4 1 0 0 基?
填目标函数系数,填基变量列,
填CB列,计算Zj,计算检验数σj,
6
编辑ppt
03.08.2020
练习㈠. 单纯形表
4 10 0 x3 0 1 3 1 0 7 7 x4 0 4 2 0 1 9 9/4
《运筹学》单纯形法
2
编辑ppt
03.08.2020
练习㈠用图解法和单纯形法求如
下线性规划问题的最优解：
Max z =4 x1 + x2 x1 + 3x2 ≤ 7
s.t. 4x1 + 2x2 ≤ 9 x1 , x2 ≥ 0
x1+3x2=7经过点(_7_,0)与(1,_2_)
4x1+2x2=9经过点(2,_0_.5_)与(0,_4_.5_)
可行域在直线 x1+3x2=7之上__
可行域在直线4x1+2x2=9之上__
18
编辑ppt
03.08.2020
练习㈢用图解法
5
有可行解,但无有限的最优解,z→+∞.
4
3
2
1
0
1
2
3
4
5
6
7
19
编辑ppt
03.08.2020
练习㈢.用单纯形法(大M法)
标准化为: M是一个大的正数
Max z=4x1+x2+0x3+0x-4Mx5 -Mx6 x1 + 3x2 - x3 +x5 =7
Max z =4x1+x2+0x3+0x4-Mx5
x1 + 3x2 + x3
=7
s.t. 4x1 + 2x2 -x4+x5 =9
x1, x2 , x3 , x4 , x5 ≥0
基是谁? x3,x5 x5的检验数为0
请它出基,逼它取值为0.
13
编辑ppt
03.08.2020
练习㈡. 单纯形表
两行，几列? 少一列?
无最优解. ❖不需人工变量或人工变量可以全部出 基则必有可行解.分:
❖至少有一个非基变量的检验数为正,但它的系 数全为非正,则无有限最优解；
标准化为: M是一个大的正数
Max z =4 x1+x2+0x3+0x4-Mx5
x1 + 3x2 + x3
=7
s.t. 4x1 + 2x2 -x4+x5=9
基再是引谁进?一这 理x个1个?, “x“2 人,-”x如工3 ,何变x4处, x5≥ 0
量”1x2 5
编辑ppt
03.08.2020
练习㈡.用单纯形法