数学错题案例共10页文档
人教版四年级数学上册错题集及分析

错题:第一周:1、30000406读作:三千万零四零六三千万四百零六分析原因:学生刚接触亿以内的读数,对数位顺表还不是很熟,顾上了万级,却顾不了个级。
特别是零出现很多个的情况下,学生就容易写错。
纠错措施:让学生记住数位表,并分级读数。
改正:300000406读作:三千万零四百零六2、一百万有10个(1千万)。
分析:学生没有仔细读题,想当然以为是10个一百万是多少。
改正:一百万有10个(十万)。
第二周1、服装厂去年出口创汇一千万零一百美元。
写作:(1000100)分析原因:学生对写数的方法还不够熟练,没有分级再读,不够仔细。
纠错措施:让学生对文字也进行分级,找到万字,再写数。
改正:服装厂去年出口创汇一千万零一百美元。
写作:(10000100)2、三个“8”分别表示8个千万、8个十万、8个千的数是(C)。
A. 83688000B.80848400C.800808000分析:学生没有分级就从高位开始看起,导致错误。
改正:B第三周1、5个千亿和5个千组成的数写作(50000005000 )。
分析原因:学生没有分级写数,导致漏了一个0。
纠错措施:让学生熟记数位表,左起右起都能记住。
再按数位写数。
改正:5个千亿和5个千组成的数写作(500000005000 )。
2、89□0039079≈90亿□里可以填的数是( 9 )。
分析原因:学生没有理解题意,可以填的数不是唯一的。
纠错措施:让学生明白省略的尾数是那一部分,最高位是什么,再判断填什么数。
改正:89□0039079≈90亿□里可以填的数是( 5~9 )。
第四周1、一个蛋糕长5厘米,20个蛋糕排成一排长(100)厘米,就是(1)米。
那么,(10000)个蛋糕排起来是1千米。
分析原因:学生对20个蛋糕排成一排长100厘米,就是1米的意思不理解。
纠错措施:帮助学生理解第二条信息的意思,知道排成一排1米需要20个蛋糕,那么排1千米需要1000个20。
改正:那么,(20000)个蛋糕排起来是1千米。
李梅英初中学生数学解题错误案例

初中数学学生错解剖析株洲市枫叶中学初二年级组 李梅英 2009、11、4一、概念上的错误例1 指出下列方程中的二元一次方程18;067)5(;921)4(;83)3(;37)2(;32)1(2=+=-=+=+-==+y x xy y xx x y y x 错解 (1)、(2)、(4)、(5)都是二元一次方程剖析 含有两个未知数,且未知数的最高次数为1的整式方程叫做二元一次方程。
此定义有三个要点:两个未知数;未知数的最高次数为1;整式方程。
方程(4)的左边不是整式;方程(5)的未知项7xy 的次数是2,故它们不是二元一次方程。
正解 只有(1)、(2)是二元一次方程例2 已知方程9)12()2(321=++---n m y n xm 是二元一次方程,求n m 、的值。
错解 由题意,得⎩⎨⎧=-=-13211n m 解之,得⎩⎨⎧=±=22n m 即n m 、的值分别为2,2±。
剖析 根据二元一次方程的定义可知,做给方程必须含有来那个个未知数,这就是这两个未知数的系数不能为0,即012,02≠+≠-n m ,上述错解正是忽视了这一点。
正解 (接上述过程),由于2=m 使x 的系数为0,故它不合题意,应舍去,故n m 、的值为别为-2、2。
二、相近概念混合例316的平方根是 错解 16的平方根是4±剖析 这里误将16得平方根当成16的平方根,其实是16的算术平方根的平方根,两个相近概念“算术平方根”和“平方根”有机地含在一起。
正解 答案应填2±。
三、连等于例4 解方程6336+=-x x错解 39336366336====+=-=+=-x x x x x x剖析 解方程时一定要注意同解变形与恒等变形的区别。
移项变形之后,等号两边的代数式的值发生了变化,导致出现了:“9=3=x ”的矛盾情况,所以方程之间不能用等号连接。
四、移项不变号例5 解方程512+-=-x x错解 移项,得152-=-x x 4=∴x剖析 把方程右边的x -移到方程左边和把方程左边的-1移到方程右边,都忘记了改变符号,破坏了方程的同解性。
初中数学经典错题

初中数学经典错题
题目一:
小明从家里骑自行车去学校,骑了一段时间后,小明觉得自行车的速度太慢,便下车向前跑。
假设小明骑自行车的速度是每小时20公里,而小明跑步的速度是每小时10公里。
小明从家到
学校的距离是8公里,请问小明骑自行车和跑步分别需要多长时间?
解答:
假设小明骑自行车的时间为t小时,则他跑步的时间为(8-20t)小时。
根据题意可列出方程:20t + 10(8-20t) = 8
化简方程得:20t + 80 - 200t = 8
合并同类项得:-180t + 80 = 8
移项得:-180t = -72
解得:t = -72/-180 = 0.4小时
代入可得:小明骑自行车需要0.4小时,跑步需要(8-20*0.4)= 8-8 = 0小时
答案分析:
该题的错误在于未考虑到小明跑步的时间不能为负值,因是不可能跑走比自行车骑行的距离更
多的距离。
正确的解答应是小明骑自行车需要0.4小时,跑步需要(8-20*0.4)= 8-8 = 0小时,即小明在0.4小时内骑自行车,然后用剩下的时间跑步到达学校。
小学三年级数学上册错题库及分析.docx
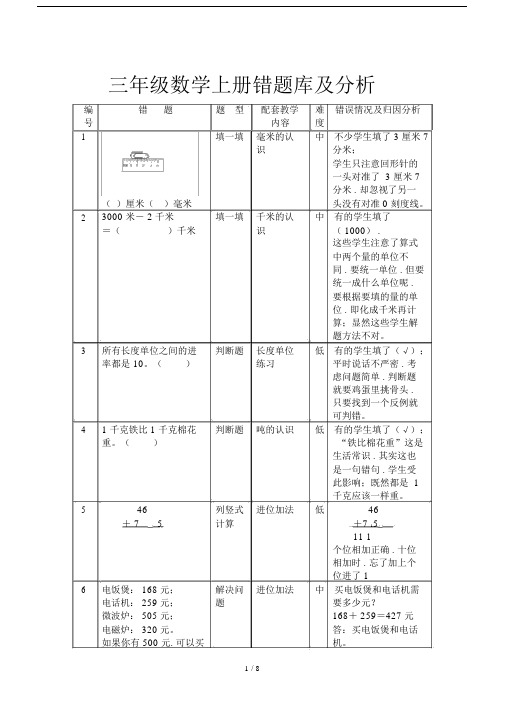
三年级数学上册错题库及分析编错题题型配套教学难错误情况及归因分析号内容度1填一填毫米的认中不少学生填了 3 厘米 7识分米;学生只注意回形针的一头对准了 3 厘米 7分米 . 却忽视了另一()厘米()毫米头没有对准 0 刻度线。
23000 米- 2 千米填一填千米的认中有的学生填了=()千米识( 1000) .这些学生注意了算式中两个量的单位不同 . 要统一单位 . 但要统一成什么单位呢 .要根据要填的量的单位 . 即化成千米再计算;显然这些学生解题方法不对。
3所有长度单位之间的进判断题长度单位低有的学生填了(√);率都是 10。
()练习平时说话不严密 . 考虑问题简单 . 判断题就要鸡蛋里挑骨头 .只要找到一个反例就可判错。
4 1 千克铁比 1 千克棉花判断题吨的认识低有的学生填了(√);重。
()“铁比棉花重”这是生活常识 . 其实这也是一句错句 . 学生受此影响;既然都是 1千克应该一样重。
546列竖式进位加法低46+ 75计算+7 1511 1个位相加正确 . 十位相加时 . 忘了加上个位进了 16电饭煲: 168 元;解决问进位加法中买电饭煲和电话机需电话机: 259 元;题要多少元?微波炉: 505 元;168+ 259=427 元电磁炉: 320 元。
答:买电饭煲和电话如果你有 500 元. 可以买机。
哪两器?明理些学生会解决由。
. 但一提得多余 . 看来教要注意范学生的解格式。
7先估一估 . 再算一算。
解决退位减法低便宜了( 200)元。
价比原价便宜了多少些学生有 .元?填了估算的果;“先手机:原价 924 元估一估”指口估算 .价 745 元而要填的是算的便宜了()元。
果。
8803-495=算退位减法中803- 495=408些学生在算退位减法 . 个位、十位相减都正确 . 但百位相减 . 忘了被减数已退了 1。
9805-397=397式减法的低把算的果 397 当805算: 805算 . 并算做算的果。
错题本整理范例

错题本整理范例一、错题原题题目:已知函数f(x)=x^2 + 2ax + 1在区间[-1, 2]上的最大值为4,求实数a的值。
二、错误答案及错误思路我当时是这么写的:因为函数f(x)=x^2 + 2ax + 1=(x + a)^2+1 - a^2,对称轴是x=-a。
我就想啊,当-a ≤ (-1 + 2)/(2)=(1)/(2)的时候,也就是a ≥ -(1)/(2),函数在x = 2处取得最大值。
所以就把x = 2代入函数得:4 + 4a + 1 = 4,解得a = -(1)/(4)。
当-a > (1)/(2),也就是a < -(1)/(2)时,函数在x = -1处取得最大值。
把x = -1代入函数得:1 - 2a + 1 = 4,解得a = -1。
我错就错在啊,只考虑了对称轴在区间中点左边和右边这两种情况,完全忽略了对称轴就在区间端点的时候。
这就好比我只看了路的左边和右边,没注意到自己就站在路口上,傻不傻呀!三、正确答案及正确思路1. 函数f(x)=x^2 + 2ax + 1=(x + a)^2+1 - a^2,对称轴为x=-a。
2. 分三种情况讨论:- 当-a ≤ -1,即a ≥ 1时,函数在[-1, 2]上单调递增,所以f(x)_max=f(2)=4 + 4a + 1 = 4,解得a = -(1)/(4),但是这个值不符合a ≥ 1,所以舍去。
- 当-1 < -a < 2,即-2 < a < 1时,f(x)_max=f(-a)=1 - a^2 = 4,这个方程无解。
- 当-a ≥ 2,即a ≤ -2时,函数在[-1, 2]上单调递减,所以f(x)_max=f(-1)=1 - 2a + 1 = 4,解得a=-1,这个值不符合a ≤ -2,所以舍去。
再回头看之前忽略的端点情况,当-a=-1,即a = 1时,f(x)=x^2 + 2x + 1=(x + 1)^2,f(2)=9不符合最大值为4;当-a = 2,即a=-2时,f(x)=x^2 - 4x + 1=(x - 2)^2 - 3,f(-1)=6也不符合最大值为4。
数学试卷典型错题(答案)

数学试卷典型错题(答案)姓名班级1、把⼀个圆平均分成若⼲份,可以拼成⼀个近似于长⽅形。
长⽅形的长相当于圆的(周长的⼀半),宽相当于圆的(半径),所以圆的⾯积S=(πr2)。
2、在⼀个长8厘⽶、宽6厘⽶的长⽅形纸板上剪⼀个最⼤的圆,圆的⾯积是( 9π)平⽅分⽶。
6厘⽶是直径 3是半径 3×3×π3、⼤圆的半径等于⼩圆的直径,则⼤圆⾯积是⼩圆⾯积的(4)倍,周长扩⼤(2)倍,⾯积扩⼤(4)倍。
4、把⼀个直径是4分⽶的圆分成两个半圆后,每个半圆的周长是(10.28)分⽶。
周长 4×π=4π半圆 2π还要加上直径 2π+45、判断:半圆的周长是与它等半径圆周长的⼀半。
(×)还有直径6、判断:半径是2厘⽶的圆,它的周长和⾯积相等。
(×)不能⽐较7、⼀个半圆,半径是r,它的周长是(C)A π÷4B πrC πr+2r9、宽阔的草地上有⼀头⽜⽤⼀条8⽶长的绳⼦拴着,这头⽜最多能吃到多少平⽅⽶的草?8×8×π=64π(平⽅⽶)10、花园⾥有⼀个半径为3⽶的圆形花坛,要在其周围铺设2⽶宽的⽔泥路,这条路的⾯积是多少平⽅⽶?⼤圆半径为5⽶,⼩圆半径为3⽶5×5×π-3×3×π=16π(平⽅⽶)11、⼀只⼤钟,它的时针长40厘⽶。
当从中午12时到13时,这根时针的尖端所⾛的路程是多少厘⽶?时针扫过的⾯积是多少平⽅厘⽶?从中午12时到13时把圆分成了12份周长 2×40×π=80π(厘⽶) 80π÷12≈⾯积 40×40×π=1600π(平⽅厘⽶) 1600π÷12≈12、从学校到⽂化宫,甲要25分钟,⼄要20分钟。
⼄的时间⽐甲少(20)%;⼄的速度⽐甲快(25)%。
⼄的时间⽐甲少:(25-20)÷25假设路程为100,那么甲速度100÷25=4 ,⼄速度100÷20=5⼄的速度⽐甲快(5-4)÷413、6⽶⽐12⽶少(50)%,⽐20⽶多5%是(21)⽶,20⽶⽐(25)⽶少20%。
小学数学错题典型案例

题目变式(类似题):从下面6张数字卡片中选择4张组成四位数。
2、5、9、0、8、3
解题思路:(写详细)【思路点拨】当题目中要求找“最接近几千”的数时,我们先要把比这个整千数“大一些”和“小一些”的数都找一找,再进行比较,最后找出“最接近”的那一个。这道题要找“最接近3000”的数,我们可以根据题意,把比3000“大一些”和“小一些”的数都找出来,有2903、2930、3029、3092,再把每个数和3000比一比,发现这四个数与3000分别相差97、70、29、92。所以,最接近3000的是3029。
小学数学错题典型案例
பைடு நூலகம்教师:吴日期:2023.5
题源
第四单元
题目
用0、2、3、9这四个数字组成一个最接近3000的四位数,这个数是()
题目所
属领域
数与代数
错误解答:【错因分析】有同学看到题目中的“最接近3000”,首先想到的就是2930,也有同学想到找比3000大一些的数,但是错误地填了3092。
错误
类型
知识性错误□√逻辑性错误□√
策略性错误□心理性错误□
错误原因
(对应错误类型写原因,尽量详细些)
【错因分析】有同学看到题目中的“最接近3000”,首先想到的就是2930,也有同学想到找比3000大一些的数,但是错误地填了3092。
知识点
关于"组数"问题,一定要考虑两种情况,一种是比要组成的数大一些,另一种是比要组成的数小一些,然后两者进行比较,选出符合题意"最 近"的数。
初一数学错题本范例

初一数学错题本范例
一、有理数运算
1. 题目:计算。
- 错误解法:
- 原式(错误原因:在去括号时,没有正确处理符号,应该变为,但是在计算过程中,将前面的符号也改变了,应该是
是计算结果正确,但是过程中存在对去括号理解的隐患)。
- 正确解法:
- 原式。
2. 题目:计算。
- 错误解法:
- 原式(错误原因:对幂运算的优先级理解错误,应该先计算指数,结果为,而不是)。
- 正确解法:
- 原式。
二、整式的加减
1. 题目:化简。
- 错误解法:
- 原式(错误原因:合并同类项时,正确,但是,而不是)。
- 正确解法:
- 原式。
2. 题目:先化简,再求值:,其中。
- 错误解法:
- 化简得:
- 原式。
- 当时,代入得:原式
(错误原因:在化简过程中,去括号后符号出现错误,计算正确,但是在前面的项去括号时,的符号错误,应该是正确)。
- 正确解法:
- 化简得:
- 原式。
- 当时,代入得:原式。
三、一元一次方程
1. 题目:解方程。
- 错误解法:
- 移项得,(错误原因:移项时没有变号,正确的应该是,移项后,移项后变为)。
- 正确解法:
- 移项得,。
2. 题目:解方程。
- 错误解法:
- 去分母得(错误原因:去分母时,等式右边没有乘以分母的最小公倍数6)。
- 正确解法:
- 去分母得,
- 去括号得, - 移项得, - 合并同类项得,
- 系数化为1得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例(一)关于数学错题集的五个材料①黑龙江07年高考状元禹奇锋(总分667分):我刚进高一时痴迷于网络,成绩一度滑落至全年级倒数,意识到问题的严重性后,我主动远离了网络,全身心投入到学习中。
学习上我紧跟老师的思路,我学习上的收获缘自我认真的投入,以及勤于回头看自己过去的失误。
在我的复习资料中,根据平时犯的错误整理出来的“错题本”是我的最爱。
复习中经常翻看这个小本子,对于我改正错误、避免失误起到了非常重要的作用。
②河南07年高考状元马冰一(总分667分):我高考数学考了满分,我的绝招是我那本快被磨破的“易错题宝典”,里面密密麻麻地记载了各种类型的数学考题,记录时间从高一到高三,这是我3年里数学考试中的所有错题,我用星号标出了犯错次数和难度,凡是错过两次的题目,就是我考试前复习的重点。
我建议高中生平时做题时,要善于分析、思考和总结,探索新方法,积极主动地追寻题目和答案之间必然的联系,把题做活。
③一个高考数学得了139分的人在其博客里说,我学数学的方法是,多做题,然后把做错的题目单独拿个本子记下来,标记出哪里不懂,错在什么地方了,搞一个专门的错题集,以后经常看看自己做错的题目,避免错误重犯。
④《思维与智慧》杂志登载的杨传良的文章:别浪费失败中考数学满分是120分的,我以118分的成绩位于全县第一。
老师让我谈谈成功经验时,我拿出了16本错题集。
我的错题集让老师大为赞赏。
那16本错题集囊括了初中三年我所有出错的数学题。
初一数学四本,初二数学四本,初三数学二本。
其余的六本是综合整理了三年中容易出错的数学题。
易错题有从作业本上摘录的,有从考卷中摘取的,还有的是从课外书上摘录下来的。
第11本、第12本错题集最厚,那是分门别类集合了初中三年中改错后又反复出错的题目。
第13本就开始变薄了,到第16本时就只剩下6道题,这6道题全是课外书上的,复杂而有难度,可以说是初中数学中的六座高峰。
在考场上,面对四张数学考卷,我体会到“读书破万卷,下笔如有神”的快感。
那些题目就像是老朋友一样向我热情地微笑,我从头到尾没遇到一个拦路虎。
我知道这次考试非常成功。
三年来我从书本中反复畅游,多少道易错的难题都让我做熟了。
我在一本书上看到过茅以升的故事,他的数学成绩特别好。
据说他成功的原因之一也是建立了多本错题集。
人生谁都有走错路做错事的时候。
错了,要走出一味自责的怪圈,如果走不出这个怪圈你会一错再错。
珍惜错误吧,它和成功一样重要,是我们人生宝贵的经验。
让人惋惜的是许多人不善于利用错误,而白白浪费了错误资源。
⑤内蒙古高考理科状元状元辛旺的自述《如何利用错题集延伸成功之路》[我为什么犯错]我一直自信自己能够在高考中取得好成绩,是因为我对学习中所犯错误的高度重视。
我有好几本错题集,只要是犯过的错误都被我认认真真记载下来,以备总结经验教训。
按照我的理解,错题不外分三种类型:第一种是特别愚蠢特别简单的错误,例如在粗心大意的时候把1+1算成3;第二种就是面对难度较大的题目所犯的错误,拿到题目一点思路都没有,不知道解题该从何下手,但是一看答案却恍然大悟;第三种就是题目难度中等,按道理有能力做对,但是却做错了。
掌握了自己犯错的类型,我就为防范错误做好准备。
我比较重视一些概念上的错误,我仔细分析过我的试卷,可以说一半以上的错误都是因为审题不清造成的。
每个经历过高考的人都知道,高考中审题特别重要。
因此在复习中遇到自己所犯的错误,首先分析是否由于审题不清造成,如果是,就要找出这种诱使你审题不清的小陷阱,熟悉之后就不容易掉进去了。
[绝不一错再错]对于学习中的错误,我有一个心得,绝不能一错再错!我把错题记下来后,会非常认真地对待。
对待错题的态度和方法不同,学习效果会有很大的差别。
如果只是把错题在试卷上标注,复习时随手翻看试卷,这种方法看上去节省时间,但是我觉得拿着一大沓试卷翻看错误,注意力会被分散,复习的效果就会大打折扣。
因此,把犯过的错误写在本子上是一个切实可行的好办法,一方面便于集中查阅自己犯过的错误,另一方面便于翻看。
把错题集中记录到一个本子上,看到曾经出现过的问题,同时翻看课本里面相应的内容,这样边记边看效果会更显著。
由于每一科学习的好坏程度不一样,所犯的错误肯定不同,这一点在我的错题集上也会有所反映,记载下来的错误越多,说明我对这一科的掌握还存在很大的不足,也需要投入更多的精力。
临近高考的时候,我把我的几个错题本集中在一起看,每个学科的错误都被我重新集中扫视了一遍,每一次错误都被我牢牢记在心里,并且以最佳状态做好了防范。
做错题集之初,可能看不到立竿见影的效果,但是坚持防范错误,一边记忆,一边翻阅课本,找准出错的原因,规避从前的错误,强化正确的知识,在潜移默化中培养一种良好的思维方式,对真正掌握知识大有裨益。
[及时改错,不让错误陪我过夜]对于错题,我是一个绝对的急性子,如果知道有什么错误,我不会把它放到第二天再去解决。
在及时改错的时候,我注意做到:一是不绕过,二是不拖拉,三是分析总结。
不绕过,就是正视自己的错误,不讳疾忌医,不为自己的错误找借口,搞不懂的知识就勇敢承认自己的缺陷,绝不能不懂装懂,害羞胆怯地自欺欺人。
不拖拉,意思是遇到错题,当场解决,不要隔一段时间再去解决,因为经过一段时间的间隔,很可能造成遗忘,让你想不起自己当初是怎样犯的错。
因此及时改错很有必要。
分析总结,就是对于每一个错题都要经过认认真真的分析,研究出错的原因,找准致错的症结,同时及时进行改错,避免再次犯错。
高三上学期,也就是11月份,我才开始建错题本。
复习时看完错题本之后觉得很充实,该解决的问题都解决了,觉得自己不害怕高考了。
果然,在高考中我取得了良好的成绩。
(二)数学错题集的建立与使用学习高中数学时,我们经常有这样的体会:上课听老师讲课听得懂,但到自己练习时,总感到困难重重;在做作业时,许多题目老师讲过了、自己做过了、甚至考过了,却无从入手;在测试或考试时,同学们都会有做错的题目,也许下次考试还是会错。
在这些错题的背后,往往是我们学习中的知识漏洞。
我们往往会处理一些直观的或是熟悉的数学问题,而对那些不具体的、抽象的数学问题常常不能抓住其本质,不能转化为已知的数学模型或过程去分析解决。
这主要是由于我们知识结构的残缺和认识上的盲点造成的,平时做习题很少进行反思,做错时只就题改题,不能对知识系统和数学方法进行归纳。
如何学会解题回顾和反思,从而提高学习的效率呢?从一些富有经验的教师和上述考试高分者的总结中可得知:最有效的途径是建立起数学错题集。
1、错题集的收集每一个同学,可对每天的练习和作业等出现的自己做错的题目,登记在自己的错题集上,每错必登,多错多登,少错少登,无错不登。
:错题集基本格式为:原题:……错解:……错误原因(种类):……正解:……例如,原题:已知定点A(-1,2)、B(2,3),直线:与线段AB恒相交,试求实数的取值范围。
错解:因为直线:恒过点P(0,-1),线段PA的斜率,线段PB的斜率,则实数的取值范围是。
错误原因:对斜率的图形认识不足,未能运用数形结合来解题。
正解:当直线:的斜率大于或等于直线PB的斜率2,或直线的斜率小于或等于直线PA的斜率-3时,直线与线段AB恒相交,所以实数的取值范围应为刚开始建立错题集时,会给我们增加很多负担,尤其错题多的同学,但使用错题集的目的是为了减少错题提高解题的正确性,表面上看是增加了麻烦,以后就可减少麻烦,还可以促使自己认真学习、认真作业、不做错题。
所以不要怕困难不要怕麻烦,要天天进行,坚持不懈,逐渐形成一种习惯。
同时上课要认真听讲,不懂就问,不留疑点,争取少出现错题。
2、错题集的整理一开始错题是很多的,要学会将错题分类。
一般有三种分类方法:按内容分类可使知识系统化;按题型分类可化繁为简集中目标;按错因分类,可举一反三事半功倍。
建议同学们按错因分类,认真看看解错的过程和关键错误,弄清解错的原因:概念模糊类、粗心大意类、顾此失彼类、图型类、技巧类、新概念类、数学思想类等等,然后分类整理。
整理后将做错的习题再做一遍,若是对错误的地方没弄清楚,就反复认真地思考,实在解决不了的要请教老师和同学。
3、错题集的使用错题集建立起来后,想发挥它的作用提高数学成绩,关键还在于使用。
要经常翻阅自己的错题集,把易错的地方拿出来复习强化,然后找与该题变化不大的题目作适当的重复性练习,使它变成自己的知识。
练多以后,不妨自己试着改变题目的条件或结论,进行变式练习;最后可自己根据要求进行编题,与同学互相练习,共同提高。
这样就可更好地掌握方法,减轻了负担,提高了效果,最大限度在发挥错题集的作用。
4、错题集的深化在课前预习时,我们对课本和课后练习会有自己的理解,经过老师课堂上的讲解、同学们回答之后,会发现自己在预习时存在着的错误和不足,此时可做好记录和分析;每次单元测试、期中、期末和模拟考试出现的错题,都要在错题集上作相应记载并将错误改正,然后分析错误发生的原因,与正确解法进行对比,培养自己的解题思维。
还可以归纳相关知识和技能的小规律小结论,提高对某类题型的解题技巧。
已进入高中的我们已有一定的解题经验,因此有时放弃不了一些陈旧的解题思路,对自己的某些想法深信不疑,不能根据新的问题的特点作灵活的反应,甚至造成歪曲的认识。
因此我们要善于思考,不满足于用常规方法取得正确答案,而尽量多尝试、多探索最简单、最好的方法,发展思维的创造性。
(三)活页型错题集的建立与使用错题集常有三种类型:一是订正形,即将所有做错的题目都抄下来,并做出订正;二是汇总型,将所有做错的题目按课本章节的顺序进行分类整理;三是纠错型,即将所有做错的题目按错误的原因进行分类整理。
下面介绍另一种错题集――活页型错题集的建立方法。
1、分类整理将所有的错题分类整理,分清错误的原因:概念模糊类、粗心大意类、顾此失彼类、图型类、技巧类、新概念类、数学思想类等等,并将各题注明属于某一章某一节,这样分类的优点在于既能按错因查找,又能按各章节易错知识点查找,给今后的复习带来简便,另外也简化了错题集,整理时同一类型问题可只记录典型的问题,不一定每个错题都记。
在整理错题集时,一定要有恒心和毅力,不要在乎时间的多少,对于相关错误知识点的整理与总结,虽然工作繁杂,但其作用绝不仅仅是明白了一道错题是怎样求解这么简单,更重要的是通过整理错题集,你将学会如何学数学、如何研究数学,避免这些知识点还会在将来犯错误,真正做到“吃一堑长一智”。
2、错题分析当老师讲评试卷时,要注意老师对自己做错的题的分析讲解,如讲评该题的引入语、解题的切入口、思路突破方法、解题的技巧、规范步骤及小结等等,自己在该题的旁边注释,写出自己解题时的思维过程,找出自己解题出错的原因及根源的分析。
这种方法开始时可能觉得较困难或写不出,不必强行要求自己,初始阶段可先用自己的语言写出小结即可,总结得多了,自然会有心得体会,渐渐认清思维的种种障碍(即做错的原因)。
