《流体力学》典型例题
流体力学例题

2013-8-1
6
图2-18
2013-8-1 7
【例2-4】 已知密闭水箱中的液面高度h4=60mm,测 压管中的液面高度h1=100cm,U形管中右端工作介质高 度,如图2-19所示。试求U形管中左端工作介质高度h3为 多少? 【解】 列1—1截面等压面方程,则 p 0 p a H 2 0 g (h1 h4 )
h4=300mm,h5=500mm,ρ1=1000㎏/m3,ρ2=800㎏
/m3,ρ3=13598㎏/m3,试确定A和B两点的压强差。
【解】 根据等压面条件,图中1—1,2—2,3—3均 为等压面。可应用流体静力学基本方程式(2-11)逐步推 算。 P1=p2+ρ1gh1 p2=p1-ρ3gh2 p3=p2+ρ2gh3
2013-8-1 23
由连续性方程:
d2 V1 V 2 d 1
2
将已知数据代入上式,得
V22 1 V22 20 2 15 0 16 2 g 2g
19.6 7 16 V2 12.(m/s) 1 15
管中流量
qV
4
2 d 2 V2
Ax=2sin300×1
2013-8-1 13
则气体作用在单位长度圆柱体上的垂直分力为
Fz=pAx=35×2sin300×1=35(kN) (b) Fx=ρghcAx=9.81×(1/2×3.73) ×(3.73×1)
×1000=68.1(kN)
Fz=ρgVp=9.81×1000×(2100/3600×22+1/2×1 ×1.732+1×2) ×1=100.5(KN)
《流体力学》试题及答案

《流体力学》试题及答案一、选择题(每题5分,共25分)1. 下列哪个选项不属于流体力学的三大基本方程?A. 连续性方程B. 动量方程C. 能量方程D. 牛顿第二定律答案:D2. 在不可压缩流体中,流速和压力之间的关系可以用下列哪个方程表示?A. 伯努利方程B. 欧拉方程C. 纳维-斯托克斯方程D. 帕斯卡方程答案:A3. 下列哪个现象表明流体具有粘性?A. 流体流动时产生涡旋B. 流体流动时产生湍流C. 流体流动时产生层流D. 流体流动时产生摩擦力答案:D4. 在下列哪种情况下,流体的动能和势能相等?A. 静止流体B. 均匀流动的流体C. 垂直下落的流体D. 水平流动的流体答案:C5. 下列哪个因素不会影响流体的临界雷诺数?A. 流体的粘度B. 流体的密度C. 流体的流速D. 流体的温度答案:D二、填空题(每题5分,共25分)6. 流体力学是研究______在力的作用下运动规律的科学。
答案:流体7. 不可压缩流体的连续性方程可以表示为______。
答案:ρV = 常数8. 在恒定流场中,流体质点的速度矢量对时间的导数称为______。
答案:加速度矢量9. 伯努利方程是______方程在不可压缩流体中的应用。
答案:能量10. 流体的湍流流动特点为______、______和______。
答案:随机性、三维性、非线性三、计算题(每题25分,共50分)11. 一个直径为10cm的管道,流体的流速为2m/s,流体的密度为800kg/m³,求管道中流体的流量。
解:流量Q = ρvA其中,ρ为流体密度,v为流速,A为管道截面积。
A = π(d/2)² = π(0.05)² = 0.00785m²Q = 800kg/m³ 2m/s 0.00785m² = 12.44 kg/s答案:管道中流体的流量为12.44 kg/s。
12. 一个直径为20cm的圆柱形储罐,储罐内充满水,水面高度为1m。
《流体力学》典型例题

《例题力学》典型例题例题1:如图所示,质量为m =5 kg 、底面积为S =40 cm ×60 cm 的矩形平板,以U =1 m/s 的速度沿着与水平面成倾角θ=30的斜面作等速下滑运动。
已知平板与斜面之间的油层厚度δ=1 mm ,假设由平板所带动的油层的运动速度呈线性分布。
求油的动力粘性系数。
解:由牛顿内摩擦定律,平板所受的剪切应力du Udy τμμδ== 又因等速运动,惯性力为零。
根据牛顿第二定律:0m ==∑F a ,即:gsin 0m S θτ-⋅=()324gsin 59.8sin 301100.1021N s m 1406010m U S θδμ--⋅⨯⨯⨯⨯==≈⋅⋅⨯⨯⨯ 例题2:如图所示,转轴的直径d =0.36 m 、轴承的长度l =1 m ,轴与轴承的缝隙宽度δ=0.23 mm ,缝隙中充满动力粘性系数0.73Pa s μ=⋅的油,若轴的转速200rpm n =。
求克服油的粘性阻力所消耗的功率。
解:由牛顿内摩擦定律,轴与轴承之间的剪切应力()60d d n d uy πτμμδ==粘性阻力(摩擦力):F S dl ττπ=⋅= 克服油的粘性阻力所消耗的功率:()()3223223230230603.140.360.732001600.231050938.83(W)d d n d n n lP M F dl πππμωτπδ-==⋅⋅=⨯⨯=⨯⨯⨯=⨯⨯=例题3:如图所示,直径为d 的两个圆盘相互平行,间隙中的液体动力黏度系数为μ,若下盘固定不动,上盘以恒定角速度ω旋转,此时所需力矩为T ,求间隙厚度δ的表达式。
解:根据牛顿黏性定律 d d 2d r r F A r r ωωμμπδδ== 2d d 2d r T F r r r ωμπδ=⋅=42420d d 232dd d T T r r πμωπμωδδ===⎰432d Tπμωδ=例题4:如图所示的双U 型管,用来测定比水小的液体的密度,试用液柱高差来确定未知液体的密度ρ(取管中水的密度ρ水=1000 kg/m 3)。
流体力学例题(动力学部分)
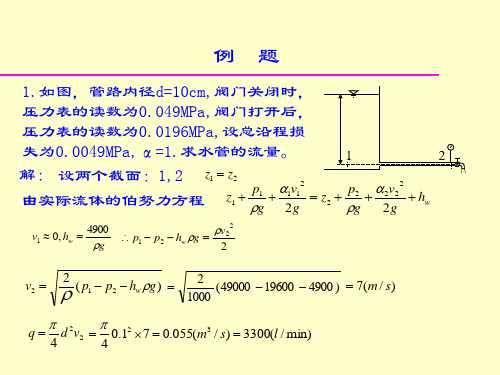
1000
q
49 7 m / s
d 2
4
v2
0 .12
4
7 55 10
3
m /s
3
2
6.一个100N的重物恰被一垂直水射 流所支承,其中d=6cm,出口速度 v=8m/s,不计沿程损失,求Y=? 解:水流接触重物后动量发生了变化
Fiy q ( 2 v y 2 1 v y 1 )
Fiy 100 N q v y2
d 2
4 0
v
0 . 06 2
z1 z 2 z
v2 q2
v1
q1
由伯努利方程: v1 v 2 v
v1 q1
令: 1 由动量方程:
v
A
F i 0 q1v q 2 v qv cos
q1 q 2 q cos v 2 q2 由连续性方程:q1 q 2 q
2 gH v
令: 2 1 1
带入动量方程: F q ( 2 v z 2 1v z1 )
F av ( v a A 2 gH v )
2
水流对水桶的作用为-F
W W 0 F W 0 av ( v a A 2 gH v )
4
8 0 . 0226 m / s
3
令: 2 1 1
则:
v y1
F
q
100 1000 0 . 0226
4 . 42 m / s
由出口和重物底面的伯努利方程:
z1 p
g
v1
流体力学例题及解答(一)

其它性质与水接近。试选择适宜管径。
选取φ108×4mm的无缝钢管(d=0.1m)。 核算流速:
【例2】20℃的空气在直径为80mm的水平管流过。现于 管路中接一文丘里管,如本题附图所示。文丘里管的 上游接一水银U管压差计,在直径为20mm的喉颈处接一 细管,基下部插入水槽中。空气流过文丘里管的能量 损失可忽略不计。当U管压差计读数R=25mm、h=0.5m时, 试求此时空气的流量为若干m3/h。当大气压强为 101.33×103Pa。 解:该题有两项简化,即 (1)当理想流体处理,Σhw=0 (2)可压缩流体当不可压缩流体对 待,取平均密度ρm。
(4)用连续性方程式确定u1与u2之 间关系,即
【例2】20℃的空气在直径为80mm的水平管流过。现于 管路中接一文丘里管,如本题附图所示。文丘里管的 上游接一水银U管压差计,在直径为20mm的喉颈处接一 细管,基下部插入水槽中。空气流过文丘里管的能量 损失可忽略不计。当U管压差计读数R=25mm、h=0.5m时, 试求此时空气的流量为若干m3/h。当大气压强为 101.33×103Pa。 (5)联立上两式解得 : 于是 :
【例2】20℃的空气在直径为80mm的水平管流过。现于 管路中接一文丘里管,如本题附图所示。文丘里管的 上游接一水银U管压差计,在直径为20mm的喉颈处接一 细管,基下部插入水槽中。空气流过文丘里管的能量 损失可忽略不计。当U管压差计读数R=25mm、h=0.5m时, 试求此时空气的流量为若干m3/h。当大气压强为 101.33×103Pa。 计算的基本过程是: (1)根据题意,绘制流程图,选取 截面和基准水平面,确定衡算范围。
确定管道中流体的流量
【例1】精馏塔进料量为 Wh=50000kg/h,ρ=960kg/s,
流体力学例题
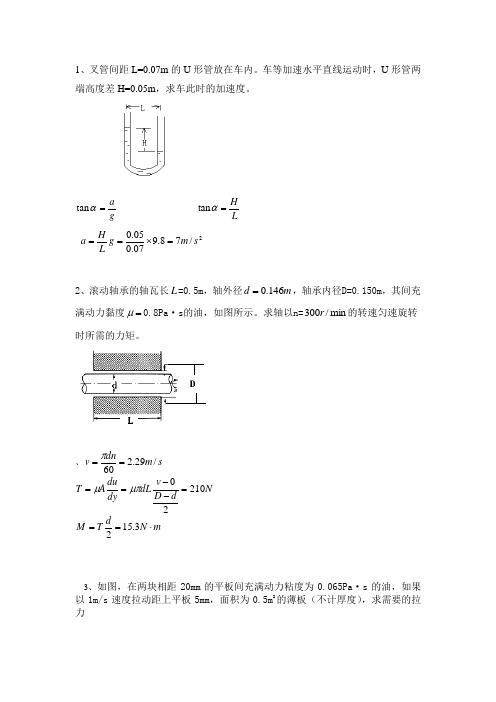
1、叉管间距L=0.07m 的U 形管放在车内。
车等加速水平直线运动时,U 形管两端高度差H=0.05m ,求车此时的加速度。
g a =αtan LH =αtan 2/78.907.005.0s m g L H a =⨯==2、滚动轴承的轴瓦长L =0.5m ,轴外径m d 146.0=,轴承内径D=0.150m ,其间充满动力黏度=μ0.8Pa ·s 的油,如图所示。
求轴以n=min /300r 的转速匀速旋转时所需的力矩。
、s m dnv /29.260==πN d D v dL dydu A T 2102=--==μπμm N dT M ⋅==3.1523、如图,在两块相距20mm 的平板间充满动力粘度为0.065Pa ·s 的油,如果以1m/s 速度拉动距上平板5mm ,面积为0.5m 2的薄板(不计厚度),求需要的拉力dy du AT μ= N huA dy du AT 5.61===μμ N hH u A dy du AT 17.22=-==μμ N T T T 67.821=+=4、用复式U 形管差压计测量A 、B 两点的压力差。
已知:mm h 3001=,mm h 5002=。
水31000m kg =ρ,水银内313600m kg m =ρ,3800m kg ='ρ。
求B A p p -。
A B p h h h g gh h h p =+∆++'-∆-)(211ρρρPa p p B A 32144-=-5、有一敞口容器,长=L 2米,高=H 1.5米,等加速水平直线运动,求当水深h 分别为1.3米和0.5米时,使容器中的液体开始溢出的最大加速度。
g a =αtan L h H )(2tan -=α 2/96.1)(2s m g Lh H a =-= xH hL 21=34=x x H g a ==αtan s m g a /11892==6、有一敞口容器,长2米,高1.3 米,宽B=1m ,等加速水平直线运动,水深0.5米。
流体力学考试试题(附答案)剖析

可编辑修改精选全文完整版流体力学考试试题(附答案)1、如图所示,有一直径=d 12cm 的圆柱体,其质量=m 5kg ,在力=F 100N 的作用下,当淹深=h 0.5m 时,处于静止状态,求测压管中水柱的高度H 。
解: 圆柱体底面上各点所受的表压力为:3.131844/12.014.3806.951004/22=⨯⨯+=+=d mg F p g π(Pa )由测压管可得:)(h H g p g +=ρ则:84.05.0806.910003.13184=-⨯=-=h gp H gρ(m )2、为测定90º弯头的局部阻力系数,在A 、B 两断面接测压管,流体由A 流至B 。
已知管径d =50 mm ,AB 段长度L AB = 0.8 m ,流量q = 15 m 3/h ,沿程阻力系数λ=0.0285,两测压管中的水柱高度差Δh = 20 mm ,已知水银的密度为13600kg/m 3,求弯头的局部阻力系数ξ。
解:)/(12.2405.0360015422s m d q v v v v B A =⨯⨯====ππ 对A 、B 列伯努利方程:f BB B A A A h gv z g P g v z g P +++=++2222水水ρρ 2211z gPz g P z g Pz g P B B A A +=++=+水水水水ρρρρf BA h gv z g P g v z g P +++=++∴22222211水水ρρ vv v B A == 又64.005.08.00285.0)1100013600(12.202.08.92)(2)2(222)(22222221212211=--⨯⨯⨯=-∆-∆=-=∴+=+=∆-∆=-+-=+-+=∴d l h h v g g v d l h v g gv g v d l h h h h gh g z z g P P z gP z gP h f f f λρρλξξλρρρρρξλ水汞水汞水水水又3、一变直径管段AB ,内径d A =0.2m ,d B =0.4m ,高度差Δh =1m ,压强表指示p A =40kPa ,p B =70kPa ,已知管中通过的流量q v =0.2m 3/s ,水的密度ρ=1000kg/m 3,试判断管中水流的方向。
流体力学练习题库+参考答案

流体力学练习题库+参考答案一、单选题(共50题,每题1分,共50分)1、离心泵抽空、无流量,其发生的原因可能有:①启动时泵内未灌满液体;②吸入管路堵塞或仪表漏气;③吸入容器内液面过低;④泵轴反向转动;⑤泵内漏进气体;⑥底阀漏液。
你认为可能的是( )A、①③⑤B、全都是C、全都不是D、②④⑥正确答案:B2、用离心泵向高压容器输送液体,现将高压容器改为常压容器,其它条件不变,则该泵输送液体流量( ),轴功率()。
A、增加B、不确定、不变C、减小D、增加、增加正确答案:D3、转子流量计的设计原理是依据 ( )A、液体对转子的浮力B、流动时在转子的上、下端产生了压强差C、流体的密度D、流动的速度正确答案:B4、为防止离心泵发生气缚现象,采取的措施是( )。
A、降低被输送液体的温度B、降低泵的安装高度C、关小泵出口调节阀D、启泵前灌泵正确答案:D5、单级单吸式离心清水泵,系列代号为( )A、ISB、DC、SHD、S正确答案:A6、某塔高30m,进行水压试验时,离塔底l0m高处的压力表的读数为500kPa,(塔外大气压强为100kPa)。
那么塔顶处水的压强( )A、698.1kPaB、无法确定C、600kPaD、403.8kPa正确答案:D7、离心泵内导轮的作用是( )A、密封B、转变能量形式C、改变叶轮转向D、增加转速正确答案:B8、一台离心泵开动不久,泵入口处的真空度正常,泵出口处的压力表也逐渐降低为零,此时离心泵完全打不出水。
发生故障的原因是( )A、忘了灌水B、吸入管路堵塞C、吸入管路漏气D、压出管路堵塞正确答案:B9、某泵在运行的时候发现有汽蚀现象应( )A、检查进口管路是否漏液B、停泵向泵内灌液C、降低泵的安装高度D、检查出口管阻力是否过大正确答案:A10、离心泵在正常运转时,其扬程与升扬高度的大小比较是( )A、扬程<升扬高度B、扬程>升扬高度C、扬程=升扬高度D、不能确定正确答案:B11、离心通风机铭牌上的标明风压是100mmH2O意思是( )A、输任何条件的气体介质的全风压都达到l00mmH2OB、输送任何气体介质当效率最高时,全风压为l00mmH2OC、输送20℃,l01325Pa、的空气,在效率最高时全风压为l00mmH2OD、输送空气时不论流量的多少,全风压都可达到100mmH2O正确答案:C12、泵将液体由低处送到高处的高度差叫做泵的( )A、吸上高度B、升扬高度C、扬程D、安装高度正确答案:B13、离心泵在启动前应()出口阀,旋涡泵启动前应( )出口阀A、关闭,打开B、关闭,关闭C、打开,关闭D、打开,打开正确答案:A14、离心泵发生气蚀可能是由于( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
水g h1 h2 g h3 h2 水g h4 h3
h1 h2 h3 h4 水 h3 h2
3
h
h1
h2
z
容器A
容器B
例题 5:如图所示,U 型管中水银面的高差 h=0.32 m,其他流体为水。容器 A 和容器 B 中 心的位置高差 z=1 m。求 A、B 两容器中心处的压强差(取管中水的重度 水 =9810 N/m3, 水银的重度 水银 =133416 N/m3) 。 解:图中 1-1、2-2 为 2 组等压面。根据等压面的性质和流体静力学基本方程 p p0 gh , 可36 m, 轴承的长度 l=1 m, 轴与轴承的缝隙宽度 =0.23
1
mm,缝隙中充满动力粘性系数 0.73Pa s 的油,若轴的转速 n 200rpm 。求克服油的粘性阻 力所消耗的功率。
n d l
解:由牛顿内摩擦定律,轴与轴承之间的剪切应力
=
粘性阻力(摩擦力) : F S dl 克服油的粘性阻力所消耗的功率:
n d 60 du dy
d n d n d n 2l P M F dl 2 30 2 30 602
3
3.14 0.36
dT dF r
r
2 r 2 dr
2
T
d 2 0
4 2 d 4 dT dr r 2 32 0 d 4
d
32T 例题 4:如图所示的双 U 型管,用来测定比水小的液体的密度,试用液柱高差来确定未知 液体的密度 (取管中水的密度 水 =1000 kg/m3) 。
2 2 2r 2 X x, Y y , Z g z H0 ,可推出自由水面(为一等压面)的方程: 2g d d d d p X x Y y Z z
根据在水没有溢出的情况下,旋转前后水的体积不变的性质,可得:
由此可求得: H 0 h
例题 6:如图所示,仅在重力场作用下的无盖水箱高 H=1.2m,长 L=3m,静止时盛水深度
h=0.9m 。 现 水 箱 以 a 0.98 m s 2 的 加 速 度 沿 水 平 方 向 做 直 线 运 动 。 若 取 水 的 密 度
1000 kg m3 ,水箱中自由水面的压强 p0 =98000Pa。试求:
2
2g H h D D 2 8 2
2
2 9.8 2.0 1.5 8.854 rad s 1 1 4 8
(2)旋转容器中任意一点的相对压强可表达为
2r 2 2r 2 2 D2 p g H0 z g h z 16g 2g 2g 将 G 点条件: r 0, z 0 带入得: 2 D2 62 12 pG g h 1000 9.8 1.5 12450Pa 16g 16 9.8 同理,将 C 点条件: r D 2, z 0 带入得: 2 D2 2 D2 62 12 h pC g 1000 9.8 1.5 16950Pa 16g 16 9.8 8g
d 2
0
2r 2 d2 2 r H 0 d r h 2g 4
2d 2
16g
,带入自由表面方程得:
d2 2 r 2g 8 若使 达到某一最大值而水不溢出,将 r d 2 时, z H ,带入上式,得 z h
2
例题 8:如图所示为一圆柱形容器,直径为 d 300mm ,高 H 500mm ,容器内装水,水深 为 h 300mm ,使容器绕垂直轴做等角速旋转,试确定水正好不溢出来的转速 n 。
6
z
H
H0
o
r
h
解:如图所示,将坐标原点 o 放在筒底的中心位置,并假设自由表面最低点的高度为
r 0, z H 0 ,则由:
2
2
h1
h3
h4
1
1
h2
水
解:经分析可知图中 1-1 和 2-2 为两组等压面。
水
根据等压面的性质和流体静力学基本方程 p p0 gh ,采用相对压强可得: 左侧: p1 水 g (h1 h2 ) , 右侧: p2 水 g (h4 h3 ) 中间: p1 p2 g (h3 h2 ) 联立可得:
(1)水箱中自由水面的方程和水箱中的压强分布。 (2)水箱中的水不致溢出时的最大加速度 amax 。
z H h O a L
4
x
解: (1)如图所示,将固定在水箱上的运动坐标系的原点置于静止时自由水面的中点,z 轴垂 直向上,x 轴与加速度的方向一致。则水箱运动时单位质量水受到的质量力和水的加速度分 量分别为 X a,Y 0 ,Z g 代入非惯性坐标系中的压力全微分公式 dp Xdx Ydy Zdz dW ,得
amax g H h L
③
②和③式联立求解,得:
amax
2 H h 2 1.2 0.9 g 9.8 1.96 m s 2 L 3
例题 7:有一盛水的旋转圆筒,直径 D=1 m,高 H=2 m,静止时水深为 h=1.5 m。求: (1)为使水不从筒边溢出,旋转角速度 应控制在多大? (2)当 =6 rad/s 时,筒底 G、C 点处的相对压强(相对于自由水面)分别为多少?
G=mg
又因等速运动,惯性力为零。根据牛顿第二定律: F ma 0 ,即:
mgsin S 0
mgsin 5 9.8 sin 30 1103 0.1021 N s m 2 4 U S 1 40 60 10
粘性是流体在运动状态下,具有的抵抗产生剪切变形速率能力的量度;粘性是流体的一种固有物理属 性;流体的粘性具有传递运动和阻滞运动的双重性。
根据在水没有溢出的情况下,旋转前后水的体积不变的性质,可得:
由此可求得: H 0 h
D2
0
2r 2 D2 2 r H 0 h dr 2g 4
2 D2
16g
,带入自由表面方程得:
D2 2 r 2g 8 若使 达到某一最大值而水不溢出,则有 r D 2 时, z H ,带入上式,得 z h
5
D
H h
G
则由:
C
解: (1)若将坐标原点放在筒底的中心位置,并假设自由表面最低点的高度为 r 0, z H 0 ,
2 2 2r 2 X x, Y y , Z g H0 ,可推出自由水面(为一等压面)的方程: z 2g dp Xdx Ydy Zdz
dp adx gdz
积分得
①
p ax gz c1
利用边界条件确定积分常数 c1 :在坐标原点 O( x z 0 )处, p p0 ,得 c1 p0 由式①可得水箱内的压强分布 p p0 ax gz 98000 1000 0.98 x 9.8 z 98000 980 x 9800 z 对于水箱中的等压面,有 dp 0 ,所以由式①可得等压面的微分方程 a dx gd z a 积分得 z x c2 g 上式给出了一簇斜率为 a g 的倾斜平面, 就代表水箱加速运动的一簇等压面, 自由水面是等 压面中的一个,因自由水面通过坐标原点,可确定积分常数 c2 0 。因此自由水面方程为
2g H h
2 2
D D 8 2 30 30 18.67 178.25 n
2 9.8 0.5 0.3 18.67 rad s 0.32 8
r
min
例 9:液体静压强分布图绘制要点及举例
例题 1:如图所示,质量为 m=5 kg、底面积为 S=40 cm×60 cm 的矩形平板,以 U=1 m/s 的速度沿着与水平面成倾角 = 30 的斜面作等速下滑运动。已知平板与斜面之间的油层厚度
=1 mm,假设由平板所带动的油层的运动速度呈线性分布。求油的动力粘性系数。
U
解:由牛顿内摩擦定律,平板所受的剪切应力 = du U dy
《流体力学》典型例题(9 大类)
要先把布置的各章作业题做熟练!举一反三。
例 1~例 3——牛顿内摩擦定律(牛顿剪切公式)应用 例 4~例 5——流体静力学基本方程式的应用——用流体静力学基本方程和等压面计算某点的压强或两点之 间的压差。 例 6~例 8——液体的相对平衡——流体平衡微分方程中的质量力同时考虑重力和惯性力(补充内容) (1)等加速直线运动容器中液体的相对平衡(与坐标系选取有关) (2)等角速度旋转容器中液体的平衡(与坐标系选取有关) 例 9 液体静压强分布图绘制 例 10~12 静止液体作用在平面上的总压力 例 13——求流线、迹线方程;速度的随体导数(欧拉法中的加速度) ;旋度计算及流动有旋、无旋判断 例 14~20——速度势函数、流函数、速度场之间的互求 例 21——计算流体微团的线变形率、角变形率及旋转角速度 例 22~24——动量定理应用(课件中求弯管受力的例子) 例 25~26——总流伯努利方程的应用 例 27——综合:总流伯努利方程、真空度概念、平均流速概念、流态判断、管路系统沿程与局部损失计算
z
a 0.98 x x 0.1x g 9.8
(2) 假设水箱以加速度 amax 运动时, 其中的水刚好没有溢出, 且此时水箱右侧水的深度为 h , 则根据加速前后水的体积不变的性质可得
