位移计算练习题
位移练习题

一、位移概念1. 位移的定义2. 位移与路程的关系3. 位移的方向4. 位移的表示方法5. 位移的计算公式二、位移计算1. 已知物体从A点出发,经过一段时间后到达B点,求位移大小2. 已知物体从A点出发,经过一段时间后到达B点,求位移方向3. 已知物体从A点出发,经过一段时间后到达B点,求位移与路程的关系4. 已知物体从A点出发,经过一段时间后到达B点,求位移的表示方法5. 已知物体从A点出发,经过一段时间后到达B点,求位移的计算公式三、位移应用1. 求物体在一段时间内的平均速度2. 求物体在一段时间内的瞬时速度3. 求物体在一段时间内的加速度4. 求物体在一段时间内的位移5. 求物体在一段时间内的路程四、位移与时间的关系1. 已知物体在一段时间内的位移,求时间2. 已知物体在一段时间内的速度,求时间3. 已知物体在一段时间内的加速度,求时间4. 已知物体在一段时间内的位移,求速度5. 已知物体在一段时间内的速度,求加速度五、位移与力的关系1. 已知物体受到的力,求位移2. 已知物体受到的力,求时间3. 已知物体受到的力,求加速度4. 已知物体受到的力,求速度5. 已知物体受到的力,求位移与力的关系六、位移与能量的关系1. 已知物体受到的力,求动能2. 已知物体受到的力,求势能3. 已知物体受到的力,求机械能4. 已知物体受到的力,求位移与能量的关系5. 已知物体受到的力,求能量与位移的关系七、位移与运动学的关系1. 已知物体受到的力,求运动轨迹2. 已知物体受到的力,求运动速度3. 已知物体受到的力,求运动时间4. 已知物体受到的力,求运动位移5. 已知物体受到的力,求运动学关系八、位移与几何的关系1. 已知物体受到的力,求几何图形2. 已知物体受到的力,求几何图形的面积3. 已知物体受到的力,求几何图形的周长4. 已知物体受到的力,求位移与几何的关系5. 已知物体受到的力,求几何与位移的关系九、位移与物理实验的关系1. 已知实验数据,求位移2. 已知实验数据,求时间3. 已知实验数据,求加速度4. 已知实验数据,求速度5. 已知实验数据,求位移与物理实验的关系十、位移与数学的关系1. 已知数学公式,求位移2. 已知数学公式,求时间3. 已知数学公式,求加速度4. 已知数学公式,求速度5. 已知数学公式,求位移与数学的关系十一、位移与实际应用1. 求汽车从甲地到乙地的平均位移2. 计算飞机在水平飞行中的位移3. 求火车在匀速直线运动中的位移4. 计算卫星绕地球运行的位移5. 求运动员在百米赛跑中的位移十二、位移与坐标系1. 在直角坐标系中,求点P到原点的位移2. 在极坐标系中,求点P的位移3. 在笛卡尔坐标系中,求点P的位移4. 在球坐标系中,求点P的位移5. 在任意坐标系中,求点P的位移十三、位移与物理定律1. 根据牛顿第一定律,求物体在无外力作用下的位移2. 根据牛顿第二定律,求物体在恒力作用下的位移3. 根据牛顿第三定律,求两物体相互作用时的位移4. 根据能量守恒定律,求物体在运动过程中的位移5. 根据动量守恒定律,求碰撞前后物体的位移十四、位移与曲线运动1. 求物体在圆周运动中的位移2. 计算物体在抛物线运动中的位移3. 求物体在螺旋线运动中的位移4. 计算物体在摆动运动中的位移5. 求物体在非匀速曲线运动中的位移十五、位移与实际问题1. 求地球自转一周的位移2. 计算地球绕太阳公转的位移3. 求地球表面两点间的位移4. 计算地球表面某点在一年内的位移5. 求地球表面某点在一天内的位移十六、位移与极限1. 求物体在极短时间内的位移2. 计算物体在极小位移下的速度3. 求物体在极小位移下的加速度4. 计算物体在极小位移下的动能5. 求物体在极小位移下的势能十七、位移与微积分1. 利用微积分求物体在某一时刻的位移2. 计算物体在某一时刻的速度3. 求物体在某一时刻的加速度4. 利用微积分求物体在某一时刻的动能5. 求物体在某一时刻的势能十八、位移与物理量转换1. 将位移转换为路程2. 将位移转换为速度3. 将位移转换为加速度4. 将位移转换为时间5. 将位移转换为能量十九、位移与数学证明1. 证明位移的计算公式2. 证明位移与路程的关系3. 证明位移与速度的关系4. 证明位移与加速度的关系5. 证明位移与时间的函数关系二十、位移与复杂运动1. 求多质点系统在复杂运动中的位移2. 计算多质点系统在复杂运动中的平均速度3. 求多质点系统在复杂运动中的加速度4. 计算多质点系统在复杂运动中的动能5. 求多质点系统在复杂运动中的势能二十一、位移与相对运动1. 计算两个相对运动的物体的位移差2. 求一个物体相对于另一个物体的位移3. 分析两个物体相对运动的位移关系4. 计算两个物体相对运动的相对位移5. 求两个物体相对运动的相对速度二十二、位移与振动1. 求简谐振动中质点的位移2. 计算振动周期内的位移变化3. 求振动位移的最大值4. 分析振动位移随时间的变化规律5. 计算振动位移的平均值二十三、位移与波动1. 求波动传播过程中的位移2. 计算波峰与波谷之间的位移3. 求波动中质点的位移4. 分析波动位移的周期性5. 计算波动位移的振幅二十四、位移与流体力学1. 求流体在管道中的位移2. 计算流体在流动过程中的位移变化3. 求流体在涡流中的位移4. 分析流体位移与流速的关系5. 计算流体位移对流动的影响二十五、位移与天体运动1. 求地球绕太阳公转的位移2. 计算月球绕地球公转的位移3. 求行星在椭圆轨道上的位移4. 分析天体运动的位移规律5. 计算天体运动中的轨道偏心率二十六、位移与光学1. 求光在介质中的位移2. 计算光在折射过程中的位移变化3. 求光在反射过程中的位移4. 分析光位移与折射率的关系5. 计算光位移对成像的影响二十七、位移与电磁学1. 求电荷在电场中的位移2. 计算电荷在磁场中的位移3. 求电荷在电磁场中的位移4. 分析电荷位移与电场强度、磁场强度的关系5. 计算电荷位移对电磁波传播的影响二十八、位移与量子力学1. 求粒子的位置位移2. 计算粒子在量子态中的位移3. 求粒子在势阱中的位移4. 分析粒子位移与波函数的关系5. 计算粒子位移对量子隧穿的影响二十九、位移与热力学1. 求热力学系统中的位移2. 计算热力学过程中的位移变化3. 求热力学系统中的热位移4. 分析热位移与温度的关系5. 计算热位移对热力学系统的影响三十、位移与生物力学1. 求肌肉收缩时的位移2. 计算骨骼运动过程中的位移3. 求关节活动范围内的位移4. 分析生物力学中的位移与力的关系5. 计算生物力学系统中的位移对运动的影响三十一、位移与材料科学1. 求材料在受力后的位移2. 计算材料在弹性范围内的位移3. 求材料在塑性变形时的位移4. 分析材料位移与应力、应变的关系5. 计算材料位移对结构稳定性的影响三十二、位移与地球物理学1. 求地震波在地壳中的位移2. 计算地球内部结构对地震波位移的影响3. 求地球表面地形变化引起的位移4. 分析地球物理学中的位移与地质构造的关系5. 计算地球物理学中的位移对地震预测的影响三十三、位移与气象学1. 求气象要素在空间中的位移2. 计算气象系统中的位移变化3. 求气象现象的位移4. 分析气象位移与气候模式的关系5. 计算气象位移对天气预报的影响三十四、位移与交通工程1. 求车辆在道路上的位移2. 计算交通流中的位移变化3. 求交通事故对车辆位移的影响4. 分析交通位移与交通规则的关系5. 计算交通位移对交通效率的影响三十五、位移与航空航天1. 求航天器在轨道上的位移2. 计算航天器在发射过程中的位移变化3. 求航天器在空间中的位移4. 分析航天位移与轨道力学的关系5. 计算航天位移对航天任务的影响三十六、位移与学1. 求关节的位移2. 计算臂的位移范围3. 求路径规划中的位移4. 分析位移与运动学的关系5. 计算位移对操作精度的影响三十七、位移与地质勘探1. 求地震勘探中的位移2. 计算地质勘探数据中的位移变化3. 求地质断层中的位移4. 分析地质位移与地质构造的关系5. 计算地质位移对矿产资源勘探的影响三十八、位移与生物医学1. 求生物体内的位移2. 计算生物组织在生理活动中的位移变化3. 求生物细胞内的位移4. 分析生物位移与生物生理学的关系5. 计算生物位移对疾病诊断的影响1. 求机器学习模型中的位移2. 计算神经网络中的位移变化四十、位移与数据分析1. 求数据集中的位移2. 计算数据分布中的位移变化3. 求数据挖掘中的位移4. 分析位移与数据分析方法的关系5. 计算位移对数据分析结果的影响答案一、位移概念1. 位移是物体位置的变化量,有大小和方向。
位移法习题

结构力学-位移法习题1.确定用位移法计算下图所示结构的基本未知量数目,并绘出基本结构。
2.判断题1)位移法基本未知量的个数与结构的超静定次数无关。
()2)位移法可用于求解静定结构的内力。
()3)用位移法计算结构由于支座移动引起的内力时,采用与荷载作用时相同的基本结构。
()4)位移法只能用于求解连续梁和钢梁,不能用于求解桁架。
()3.已知下图所示钢架的结点B产生转角,试用位移法概念求解所作用外力偶M。
4.若下图所示结构结点B向右产生单位位移,试用位移法概念求解应施加的力。
5.已知钢架的弯矩图如下图所示,各杆常数,杆长,试用位移法概念直接计算结点B的转角。
6.用位移法计算下图所示的连续梁,作弯矩图和剪力图。
EI=常数。
7.用位移法计算下图所示结构,作弯矩图。
常数。
8.用位移法计算下图所示各结构,并作弯矩图。
常数。
9.利用对称性计算下图所示结构,作弯矩图。
常数。
10.下图所示等截面连续梁,,已知支座C下沉,用位移法求作弯矩图。
11.下图所示的刚架支座A下沉,支座B下沉,求结点D的转角。
已知各杆。
12.试用位移法计算下图所示结构,并绘出其内力图。
13.试用位移法计算下图所示结构,并绘出其内力图。
14.试用位移法计算图示结构,并绘出M图。
15.试用位移法计算图示结构,并绘出M图。
16.试利用对称性计算图示刚架,并绘出M图。
6m 6m9ml lq(a)4m 4m4m(b)10kN/m6m6m 6m 6m6m(a)8m 4m 4m 4m 4m20kN/m17. 试计算图示结构在支座位移作用下的弯矩,并绘出M 图。
18. 试用位移法计算下图所示结构,并绘出其内力图。
19. 试用位移法求作下列结构由于温度变化产生的M 图。
已知杆件截面高度h =0.4m ,EI =2×104kN ·m 2,α=1×10-5。
20.试计算图示具有牵连位移关系的结构,并绘出M 图。
3EI lA D CB l EI EIϕl Δ=ϕa 2aa 2aaF P6m 4m A B C +20℃0℃ +20℃0℃ 20kN8m 8m 6m 3m A C D EB F G EI 1=∞EI 1=∞ 3EI3EI 3EI EI。
《建筑力学习题》-结构位移计算
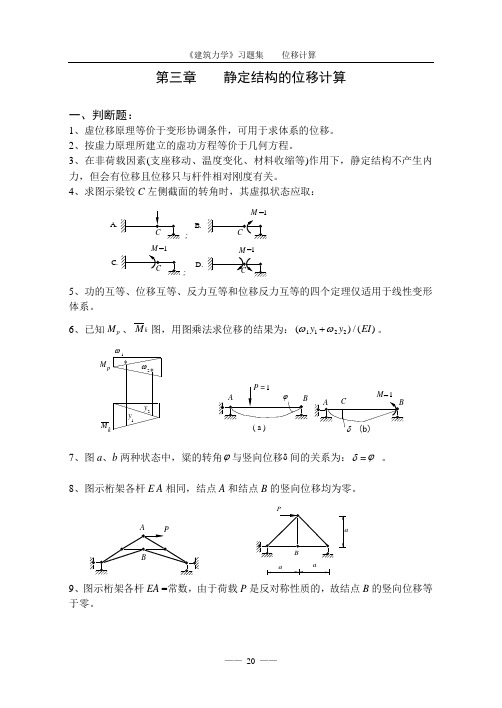
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形协调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A两侧截面的相对转角ϕA,EI = 常数。
q11、求图示静定梁D端的竖向位移∆DV。
EI = 常数,a = 2m 。
10kN/m12、求图示结构E点的竖向位移。
EI = 常数。
q13、图示结构,EI=常数,M=⋅90kN m, P = 30kN。
求D点的竖向位移。
P14、求图示刚架B端的竖向位移。
q15、求图示刚架结点C的转角和水平位移,EI = 常数。
q16、求图示刚架中D点的竖向位移。
EI = 常数 。
l/217、求图示刚架横梁中D点的竖向位移。
EI = 常数 。
18、求图示刚架中D 点的竖向位移。
E I = 常数 。
ql l l/219、求图示结构A、B两截面的相对转角,EI = 常数 。
l/23l/320、求图示结构A 、B 两点的相对水平位移,E I = 常数。
21、求图示结构B 点的竖向位移,EI = 常数 。
l l22、图示结构充满水后,求A 、B 两点的相对水平位移。
E I = 常数 ,垂直纸面取1 m 宽,水比重近似值取10 kN / m 3。
位移法习题

习题8-1 图示梁杆端弯矩=ABM, 侧受拉;杆端剪力Q AB F = 。
题8-1图 题8-2图8-2图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
8-3图示梁杆端弯矩ABM= ,侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
2EI AB题8-3图 题8-4图 8-4图示梁杆端弯矩ABM= , 侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
8-5图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q AB F = 。
Q B A F = 。
题8-5图 题8-6图8-6 图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
Q AB F = 。
8-7图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
题8-7图 题8-8图 8-8 图示梁杆端弯矩ABM= , 侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
8-9 图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
题8-9图 题8-10图8-10 图示梁杆端弯矩BA M = , 侧受拉;杆端剪力Q B A F = 。
8-11 图示梁杆端弯矩ABM = , 侧受拉;杆端剪力Q B A F = 。
设i =EI /l 。
6EI AB1题8-11图 题8-12图 8-12 试作图示梁弯矩图,并求B 支座的反力。
8-13 图示梁的跨度为l ,若使A 端截面的转角为零,在A 端施加的弯矩=ABM。
1M1Δ题8-13图 题8-14图8-14 已知图示结构的柱端水平位移为EIlF Δ93P 1=,试作弯矩图。
8-15 试用位移法计算图示结构,作弯矩图。
(a ) (b)题8-15图8-16 试用位移法计算图示结构,作弯矩图。
(a) (b) (c)题8-16图8-17 用位移法解图示结构,基本未知量最少为2个的结构是( )。
A.(a)、(b)B.(b)、(c)C.(c)、(a)D.(a)、(b)、(c)(a)(b) (c)题8-17图8-18 用位移法解图示结构,基本未知量最少为3个的结构是()。
位置位移练习题(打印版)

位置位移练习题(打印版)### 位置位移练习题#### 一、单选题(每题5分,共20分)1. 物体从A点移动到B点,位移大小为10米,方向由A指向B。
若物体再从B点返回A点,位移大小和方向如何?A. 10米,由B指向AB. 20米,由A指向BC. 10米,由A指向BD. 20米,由B指向A2. 一辆汽车从静止开始,沿直线加速行驶了100米,到达点B。
若汽车保持匀速行驶,则从B点再行驶100米到达点C,问汽车从A点到C 点的总位移是多少?A. 100米B. 200米C. 300米D. 400米3. 某物体在水平面上做匀速直线运动,经过时间t后,位移为s。
若物体速度不变,再经过时间t,物体的位移变为多少?A. 2sB. 3sC. sD. 无法确定4. 一物体从A点出发,先向东移动了5米,然后向北移动了3米,最后向西移动了2米。
物体最终的位移大小和方向如何?A. 5米,东偏北30°B. 5米,西偏北60°C. 6米,东偏北30°D. 6米,西偏北60°#### 二、填空题(每空5分,共20分)1. 位移是描述物体位置变化的物理量,其大小等于物体从初始位置到最终位置的直线距离,方向由______指向______。
2. 若物体的位移大小为0,说明物体的初始位置和最终位置______。
3. 位移和路程是两个不同的概念,位移是矢量,有大小和方向;而路程是标量,只有______。
4. 在计算位移时,需要考虑物体的初始位置和最终位置,而与物体运动的______无关。
#### 三、计算题(每题30分,共40分)1. 一物体从A点出发,先向东移动了8米,然后向南移动了6米,最后向西移动了3米。
求物体最终的位移大小和方向。
2. 一辆汽车从A点出发,沿直线加速行驶了150米到达B点,然后匀速行驶了250米到达C点。
若汽车从C点开始减速,最终在D点停止。
已知汽车从A点到D点的总位移为400米,求汽车从B点到D点的位移大小和方向。
高二物理练习题及答案

高二物理练习题及答案练习题一:1. 一个物体以3 m/s的速度匀速直线运动,经过4秒后,它的位移是多少?答:位移=速度×时间 = 3 m/s × 4 s = 12 m2. 一个物体静止,突然以2 m/s²的加速度向前运动,经过3秒后,它的速度是多少?答:速度=初速度+加速度×时间 = 0 m/s + 2 m/s² × 3 s = 6 m/s3. 一个火箭以20 m/s的速度垂直上升,加速度为10 m/s²,求它上升的位移。
答:位移 = 初速度×时间 + ½ ×加速度 ×时间² = 20 m/s ×t + ½ × 10 m/s² × t²(t为时间)练习题二:1. 如果力的大小为40牛顿,物体的质量为5千克,求该物体的加速度。
答:加速度 = 力 / 质量 = 40 N / 5 kg = 8 m/s²2. 如果物体的质量为8千克,加速度为4 m/s²,求作用于物体上的力的大小。
答:力 = 质量 ×加速度 = 8 kg × 4 m/s² = 32 N3. 弹簧常数为200牛/米,弹簧伸长了0.5米,求作用于弹簧上的力的大小。
答:力 = 弹簧常数 ×伸长的长度 = 200 N/㎡ × 0.5 m = 100 N练习题三:1. 如果两个物体的质量分别为2千克和4千克,它们之间的引力大小为多少?答:引力 = 万有引力常数 ×(质量1 ×质量2)/ 距离² = 6.67 ×10⁻¹¹ N·㎡/kg² ×(2 kg × 4 kg)/ 距离²(距离为两物体间的距离)2. 如果两个物体之间的距离为0.1米,它们之间的引力大小为10牛顿,求其中一个物体的质量。
位移路程练习题

位移路程练习题1. 问题描述:小明从学校出发,按照下列路线前往图书馆:向东行驶300米,然后转向南行驶200米,最后向西行驶400米。
请计算小明从学校到图书馆的位移和总路程。
2. 解答过程:根据题目描述,小明从学校到图书馆的路线可以用如下示意图表示:```北||西 ----------+---------- 东||南```小明按照题目的路线行驶,首先向东行驶300米,再向南行驶200米,最后向西行驶400米。
我们可以从坐标的角度来分析小明的位移。
首先,向东行驶300米会使小明的横坐标增加300,纵坐标不变,得到位置A。
(300, 0)然后,向南行驶200米会使小明的横坐标不变,纵坐标减少200,得到位置B。
(300, -200)最后,向西行驶400米会使小明的横坐标减少400,纵坐标不变,得到位置C.(-100, -200)根据以上计算,小明从学校到图书馆的位移可以用路径AC表示,位移向量的横坐标为-100,纵坐标为-200。
位移的数量可以用位移向量的长度来表示,即位移的总路程。
根据勾股定理,位移向量的长度计算公式为:位移长度= √((-100)^2 + (-200)^2) = √10000 + 40000 = √50000 ≈ 223.61米所以,小明从学校到图书馆的位移为(-100, -200),总路程为约223.61米。
3. 小结:本文根据位移路程练习题的要求,通过计算小明从学校到图书馆的位移和总路程,展示了解题的过程。
文章采用了分析和计算相结合的方式,清晰展示了解决问题的步骤。
同时,文章排版整洁美观,语句通顺,表达流畅,无影响阅读体验的问题。
这个练习题的解答可以帮助读者熟悉位移和总路程的概念,并提高解决类似问题的能力。
小学数学四年级位移练习题

小学数学四年级位移练习题在小学四年级的数学课程中,位移是一个重要的概念。
通过练习位移相关的题目,可以帮助学生巩固对位移的理解和运用。
下面是一些小学四年级的位移练习题,供同学们练习和掌握:1. 问题:小明从家里走到学校的路程是5千米,他又从学校走回家,这时他的总位移是多少?解答:小明从家走到学校的路程是5千米,这是正的位移。
然后他又从学校走回家,这是负的位移。
所以他的总位移是5千米 - 5千米 =0千米。
2. 问题:小华从她家走到公园的路程是3千米,接着又从公园走到图书馆,图书馆离公园有2千米的距离。
小华的总位移是多少?解答:小华从家走到公园的路程是3千米,这是正的位移。
然后她又从公园走到图书馆,这也是正的位移。
所以她的总位移是3千米 + 2千米 = 5千米。
3. 问题:小李从家骑自行车到了朋友家,这是一个位移为8千米的行程。
接着他又骑车回到了家。
请问他的总位移是多少?解答:小李从家骑自行车到朋友家的位移是8千米,这是正的位移。
然后他又从朋友家骑车回到家,这也是正的位移。
所以他的总位移是8千米 + 8千米 = 16千米。
4. 问题:小王从家骑自行车到了朋友家,这是一个位移为5千米的行程。
接着他在朋友家呆了一会儿又骑车回到了家。
请问他的总位移是多少?解答:小王从家骑自行车到朋友家的位移是5千米,这是正的位移。
然后他又从朋友家骑车回到家,这也是正的位移。
所以他的总位移是5千米 + 5千米 = 10千米。
通过以上的练习题,我们可以看到位移的概念在日常生活中非常普遍。
理解和计算位移有助于我们了解物体在空间中的位置变化,同时也培养了我们的逻辑思维和数学运算能力。
在实际中,位移的计算通常使用数值来表示,我们只需要注意位移的方向,正负号的运算即可。
通过练习位移的习题,我们可以更好地掌握位移的概念和计算方法,为解决更复杂的数学问题打下基础。
希望大家能够认真练习,提高自己的数学能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(a)(b) (c)
(d) (e)
题6-1图
6-2图(a)所示结构上的力在图(b)所示由温度变化引起的位移上作的虚功W=。
(a)(b)
题6-2图
6-3图示结构加 引起位移 、 ,再加 又产生新的位移 、 ,两个力所作的总功为()。
题6-6图题6-7图
6-7试求图示桁架K点水平位移。EA=常数。
*6-8图示变截面悬臂梁,已知 ,试求A点竖向位移和A截面转角。
题6-8图
6-9应用图乘法的条件是。
6-10试求图示结构的指定位移。
(a)(b)
(c) (d)
题6-10图
6-11试求图示结构的指定位移。
(a) (b) (c)
(d) (e)
(e)A铰右侧截面的转角
6-6 (↓);
6-7 (→ቤተ መጻሕፍቲ ባይዱ;
6-8 (↓); (逆时针)
6-9EI=常数,杆轴为直线,两个弯矩图中至少有一个是直线图形
6-10 (a) ( );(b) (↑);(c) (←);(d)0
6-11(a) ( ); (↓)
(b) (↑)
(c) (↓)
(d) (↓)
(e) (→ ←)
6-16试求图示结构支座位移引起的C铰两侧截面的相对转角。
题6-16图题6-17图
*6-17图示结构内部温度升高t度,外侧温度不变,已知线膨胀系数为α,试求C点竖向位移。
*6-18图示结构中,AB杆的温度上升t度,已知线膨胀系数为α,则C点的竖向位移为。
题6-18图
*6-19上题结构中的AB杆,由于加热而伸长了Δ,则由此产生的C点竖向位移为。
A. ;B. ;
C. ;D.
题6-3图
*6-4变形体虚功原理适用于()。
A.线弹性体系;B.任何变形体;C.静定结构;D.杆件结构
6-5图示单位力状态是求图(a)所示荷载引起的哪些位移的单位力状态?
(b),(c),(d),(e)。
(a) (b) (c)
(d) (e)
题6-5图
6-6试求图示桁架K点竖向位移。已知各杆截面相同, , 。
*6-20上题结构中的AB杆,由于制作时作长了Δ,则由此产生的C点竖向位移为。
*6-21互等定理包括定理、定理和定理,其中定理是最基本的。
*6-22虚功互等定理适用于()。
A.任意体系B.线弹性体系C.静定结构D.超静定结构
6-23图示两个简支梁的长度和抗弯刚度相同,在单位力作用下位移相等的有()。
A. B. C. D.
题6-23图
参考答案
6-1(a)A点竖向位移
(b)AB两点相对竖向位移
(c)AB两截面相对转角
(d)AB杆的转角(AB杆两端的力构成作用于该杆的力偶m,该力偶在杆件转角上作功)
(e)A截面转角
6-2
6-3 C
6-4 B
6-5 (b)A点竖向位移
(c)A铰左侧截面的转角
(d)A铰两侧截面的相对转角
题6-11图
6-12试求图示结构的指定位移。
(a) (b)
(c) (d)
题6-12图
6-13试求图示结构AB两截面间的相对竖向位移、相对水平位移和相对转角。已知:q=10kN/m,l=5m, 。
题6-13图
6-14若使图示结构的A点竖向位移为零,则应使 与 的比值为 =。
题6-14图题6-15图
6-15试求图示结构由于支座位移产生的A点水平位移。已知: , , 。
6-12(a) (↓)
(b) ( )
(c) (↓)
(d) (↓)
6-13 , (→←),
6-14 16/5
6-150.046m(→)
6-16 0
6-17 (↑)
6-18 4αtl(↑)
6-19 (↑)
6-20 (↑)
6-21虚功互等位移互等反力互等虚功互等
6-22 B
6-23 C
