电抗滤波器的谐振频率如何计算
滤波器计算公式

滤波器计算公式
滤波器的计算公式可以根据具体应用和设计要求而有所不同。
常见的滤波器计算公式包括低通滤波器的计算公式和带通滤波器的计算公式等。
1、低通滤波器的计算公式:
f=1/(2πRC)
其中,f为截止频率,R为电阻值,C为电容值。
这个公式可以帮助您计算低通滤波器的截止频率。
2、带通滤波器的计算公式:
f=(f_{c1}+f_{c2})/2
其中,f_{c1}和f_{c2}分别为上下限频率。
这个公式可以帮助您计算带通滤波器的中心频率。
另外,根据具体应用和设计要求,还可以采用其他类型的滤波器计算公式,如高通滤波器、陷波器等。
这些计算公式可以根据具体的应用和设计要求进行选择和使用。
RLC联谐振频率及其计算公式

RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ⇒I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即 Z =R+jX L−jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C⇒Q T=Q L−Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L−X C)当 f = f r时, Z = R 为最小值,电路为电阻性。
RLC串联谐振频率及其计算公式

RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ?I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
???????????? 图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即 Z =R+jX L?jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C?Q T=Q L?Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L?X C)当 f = f r时, Z = R 为最小值,电路为电阻性。
RLC串联谐振频率与其计算公式

RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ⇒I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即 Z =R+jX L−jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C⇒Q T=Q L−Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L−X C)当 f = f r时, Z = R 为最小值,电路为电阻性。
RLC串联谐振频率及其计算公式

创作编号:BG7531400019813488897SX创作者:别如克*RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大. 1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ⇒I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即 Z =R+jX L−jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C⇒Q T=Q L−Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
RLC串联谐振频率及其计算公式(完整资料).doc

【最新整理,下载后即可编辑】RLC串联谐振频率及其计算公式串联谐振是指所研究的串联电路部分的电压和电流达到同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收相同之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ⇒I2X L = I2 X C也就是X L =X C时,为R-L-C串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即Z =R+jX L−jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C⇒Q T=Q L−Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C使其达到谐振频率f r,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 πfL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L−X C)当f = f r时,Z = R 为最小值,电路为电阻性。
RLC串联谐振的频率及计算公式
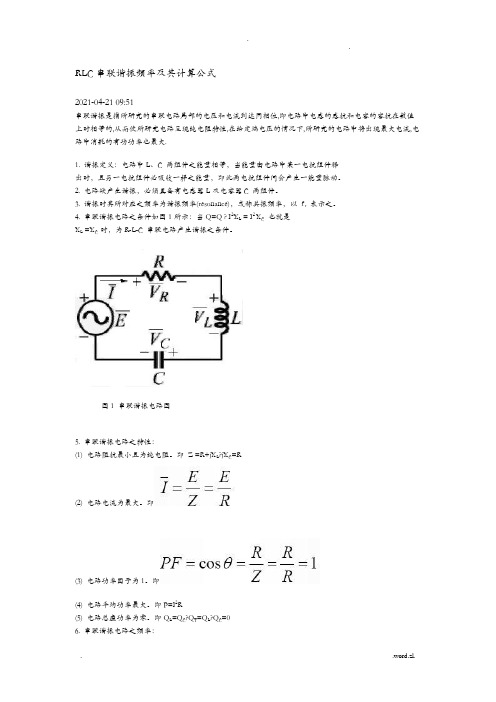
RLC串联谐振频率及其计算公式2021-04-21 09:51串联谐振是指所研究的串联电路局部的电压和电流到达同相位,即电路中电感的感抗和电容的容抗在数值上时相等的,从而使所研究电路呈现纯电阻特性,在给定端电压的情况下,所研究的电路中将出现最大电流,电路中消耗的有功功率也最大.1. 谐振定义:电路中L、C 两组件之能量相等,当能量由电路中某一电抗组件释出时,且另一电抗组件必吸收一样之能量,即此两电抗组件间会产生一能量脉动。
2. 电路欲产生谐振,必须具备有电感器L及电容器C 两组件。
3. 谐振时其所对应之频率为谐振频率(resonance),或称共振频率,以f r表示之。
4. 串联谐振电路之条件如图1所示:当Q=Q ? I2X L = I2 X C也就是X L =X C 时,为R-L-C 串联电路产生谐振之条件。
图1 串联谐振电路图5. 串联谐振电路之特性:(1) 电路阻抗最小且为纯电阻。
即Z =R+jX L?jX C=R(2) 电路电流为最大。
即(3) 电路功率因子为1。
即(4) 电路平均功率最大。
即P=I2R(5) 电路总虚功率为零。
即Q L=Q C?Q T=Q L?Q C=06. 串联谐振电路之频率:(1) 公式:(2) R - L -C 串联电路欲产生谐振时,可调整电源频率f 、电感器L 或电容器C 使其到达谐振频率f r ,而与电阻R完全无关。
7. 串联谐振电路之质量因子:(1) 定义:电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比,称为谐振时之品质因子。
(2) 公式:(3) 品质因子Q值愈大表示电路对谐振时之响应愈佳。
一般Q值在10~100 之间。
8. 串联谐振电路阻抗与频率之关系如图(2)所示:(1) 电阻R 与频率无关,系一常数,故为一横线。
(2) 电感抗X L=2 π fL ,与频率成正比,故为一斜线。
(3) 电容抗与频率成反比,故为一曲线。
(4) 阻抗Z = R+ j(X L ?X C)当f = f r时,Z = R 为最小值,电路为电阻性。
电抗电感和频率计算公式

电抗电感和频率计算公式电抗和电感是与电流的变化有关的电路元件。
在交流电路中,电感是由线圈产生的,具有抵抗电流变化的趋势。
而电抗是指电路对交流电的阻抗,是电感和电容的综合特性。
在计算电抗和电感时,我们需要考虑频率的影响。
首先,我们要了解一些基本的概念:1. 电感(Inductance):电流通过一个线圈时,产生的电磁感应现象。
单位是亨利(H)。
2. 电抗(Reactance):电路对交流电的阻抗。
单位是欧姆(Ω)。
3. 频率(Frequency):交流电的周期数。
单位是赫兹(Hz)。
接下来,我们介绍计算电抗和电感的公式:1.电感的计算公式:电感(L)与线圈的特性有关,具体计算公式为:L=(μ₀μᵣN²A)/l其中,L表示电感(亨利),μ₀是真空中的磁导率(4π×10⁻⁷H/m),μᵣ是相对磁导率,N是线圈的匝数,A是线圈的横截面积(m²),l是线圈的长度(m)。
2.电抗的计算公式:电抗(X)与电路中的电感(L)和频率(f)有关,具体计算公式为:X=2πfL当我们知道电抗和频率后,可以使用上述公式计算电感。
以下是一个具体的计算例子:假设有一个线圈,电流频率为50赫兹,线圈匝数为100,横截面积为0.01平方米,长度为0.1米。
我们可以使用上述公式计算电感和电抗:首先,根据电感的计算公式,我们可以计算电感的值:L=(μ₀μᵣN²A)/l=(4π×10⁻⁷H/m×1×100²×0.01m²)/0.1m然后,根据电抗的计算公式,我们可以计算电抗的值:X=2πfL≈0.3963Ω总结起来,电感和电抗是与电流的变化有关的电路元件。
我们可以使用特定的公式计算电感和电抗的值,其中电感的计算公式与线圈的特性有关,电抗的计算公式与电感和频率有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于电抗滤波器的问题,为什么在7%时189Hz时形成谐振?如何计算的?
今天一个厂家来做产品推荐,当谈到电抗滤波器抑制流经电容器的谐波电流时,突然想从理论计算出为何电抗为电容的7%时,形成谐振,而此时的频率F0=189Hz。
但是我发现凭我的能力算不出来。
麻烦会的朋友告诉我这个计算过程,现在很纠结这个问题。
一个所有样本上写出的东西是如何计算得出的。
我现在就知道f=/(2x3.14x(LC)^2)。
再往后如何计算啊?
问厂家的技术人员,他们也不能推导出整个过程,后来老总说你自己回去推倒吧。
算了半天还是算不出来,睡不着觉了。
没人回答吗?我查了一晚上文献,终于明白自己错在哪了。
所谓的7%是指电抗与电容器的有名值比,即感抗/容抗,单位都应该是欧姆。
而我一直是按照电感与电容来推导的,单位都不一样(H和F),根本不是一个概念。
正确的推导应该是:XL为基波下(即50Hz)电抗器的感抗,Xc为基波下电容器的容抗,假设n次谐波发生谐振,则nXL=Xc/n(XLn=2π n f0 L,Xcn=1/(2π n f0 C),导出n=√(Xc/XL)=√(1/0.07)=3.78,即3.78x50=189Hz时发生谐振。
或者说,7%是指基波电流下感抗与容抗的比值,f0=50Hz。
从这个角度出发,也可以通过f=/(2x3.14x(LC)^2)推导,只要把(XLn=2π n f0 L,Xcn=1/(2π n f0 C)搞懂就行。
另外推荐大家看看《串联电抗器抑制谐波的作用及电抗率的选择》,对谐波治理以及无功补偿能有一个数学模型上的认识。
看来我还是对基础概念有混淆,相信有部分和我一样年轻的工程师也有这个问题,希望大家以我为戒。
弄清这个问题实际上对做工程没有太大意义,因为样本上已经把想处理几次谐波选择多大的电抗器给出来,只要查数据就行了。
只是我这个人有些偏执狂,如果弄不懂一个非常想知道的问题就睡不着觉。
另外,这个论坛要是能贴mathtype的公式就好了,否则写的麻烦,看的也麻烦。
