数学符号念读
数学符号及读法大全

数学符号及读法大全一、基本符号及读法1. 加号(+):读作“加”或“正”。
例如,2 + 3 读作“二加三”或“二正三”。
2. 减号():读作“减”或“负”。
例如,5 2 读作“五减二”或“五负二”。
3. 乘号(×):读作“乘”。
例如,4 × 6 读作“四乘六”。
4. 除号(÷):读作“除以”。
例如,8 ÷ 2 读作“八除以二”。
5. 等号(=):读作“等于”。
例如,3 + 4 = 7 读作“三加四等于七”。
6. 不等号(≠):读作“不等于”。
例如,5 ≠ 6 读作“五不等于六”。
7. 大于号(>):读作“大于”。
例如,7 > 5 读作“七大于五”。
8. 小于号(<):读作“小于”。
例如,3 < 8 读作“三小于八”。
9. 大于等于号(≥):读作“大于等于”。
例如,x ≥ 5 读作“x大于等于五”。
10. 小于等于号(≤):读作“小于等于”。
例如,y ≤ 10 读作“y小于等于十”。
二、指数与对数符号及读法1. 指数符号(^):读作“的幂”。
例如,2^3 读作“二的三次幂”。
2. 对数符号(log):读作“以为底的对数”。
例如,log₂8 读作“以二为底八的对数”。
三、集合符号及读法1. 属于符号(∈):读作“属于”。
例如,3 ∈ {1, 2, 3} 读作“三属于集合{一、二、三}”。
2. 不属于符号(∉):读作“不属于”。
例如,4 ∉ {1, 2, 3} 读作“四不属于集合{一、二、三}”。
3. 空集符号(∅):读作“空集”。
例如,∅表示一个不包含任何元素的集合。
四、几何符号及读法1. 直线符号(→):读作“直线”。
例如,AB → 表示直线AB。
2. 射线符号(⇀):读作“射线”。
例如,AC ⇀表示射线AC。
3. 线段符号(|):读作“线段”。
例如,BC | 表示线段BC。
4. 角符号(∠):读作“角”。
例如,∠ABC 表示角ABC。
数学符号的读法

数学符号的读法α( 阿而法)β( 贝塔)γ(伽马)δ(德尔塔)ε(艾普西龙)ζ(截塔)η(艾塔)θ(西塔)ι约塔)κ(卡帕)λ(兰姆达)μ(米尤)ν(纽)ξ(可系)ο(奥密克戎)π (派)ρ (若)σ (西格马)τ (套)υ (英文或拉丁字母)φ(斐)χ(喜)ψ(普西))ω(欧米伽)α Α alpha 【'ælfə】β Β beta 【'bi:tə, 'beitə】γ Γ gamma 【'gæmə】δ Δ delta 【'deltə】ε Ε epsil on 【ep'sailən, 'epsilən】ζ Ζ zeta 【'zi:tə】η Η eta 【'i:tə】θ Θ theta 【'θi:tə】ι Ι iota 【ai'əutə】κ Κ kappa 【'kæpə】λ ∧lambda 【'læmdə】μ Μ mu 【mju:】ν Ν nu 【nju:】ξ Ξ xi 【ksai, ksi:】ο Ο omicron 【əu'maikrən】π ∏ pi 【pai】ρ Ρ rho 【rəu】σ ∑ sigma 【'sigmə】τ Τ tau 【tau】υ Υ upsilon 【ju:p'sailən】φ Φ phi 【fai】χ Χ chi 【kai, ki:】ψ Ψ psi 【psai】ω Ω omega 【'əumigə】更全面:1 Α α alpha a:lf 阿尔法角度;系数2 Β β beta bet 贝塔磁通系数;角度;系数3 Γ γ gamma ga:m 伽马电导系数(小写)4 Δ δ delta delt 德尔塔变动;密度;屈光度5 Ε ε epsilon ep`silon 伊普西龙对数之基数6 Ζ ζ zeta zat 截塔系数;方位角;阻抗;相对粘度;原子序数7 Η η eta eit 艾塔磁滞系数;效率(小写)8 Θ θ thet θit 西塔温度;相位角9 Ι ι iot aiot 约塔微小,一点儿10 Κ κ kappa kap 卡帕介质常数11 ∧λ lambda lambd 兰布达波长(小写);体积12 Μ μ mu mju 缪磁导系数;微(千分之一);放大因数(小写)13 Ν ν nu nju 纽磁阻系数14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 ∏ π pi pai 派圆周率=圆周÷直径=3.141617 Ρ ρ rho rou 肉电阻系数(小写)18 ∑ σ sigma `sigma 西格马总和(大写),表面密度;跨导(小写)19 Τ τ tau tau 套时间常数20 Υ υ upsilon jup`silon 宇普西龙位移21 Φ φ phi fai 佛爱磁通;角22 Χ χ chi phai 西23 Ψ ψ psi psai 普西角速;介质电通量(静电力线);角24 Ω ω omega o`miga 欧米伽欧姆(大写);角速(小写);角希腊字母读法Αα:阿尔法AlphaΒβ:贝塔BetaΓγ:伽玛GammaΔδ:德尔塔DelteΕε:艾普西龙Epsilonζ :捷塔ZetaΖη:依塔EtaΘθ:西塔ThetaΙι:艾欧塔IotaΚκ:喀帕Kappa∧λ:拉姆达LambdaΜμ:缪MuΝν:拗NuΞξ:克西XiΟο:欧麦克轮Omicron∏π:派PiΡρ:柔Rho∑σ:西格玛SigmaΤτ:套TauΥυ:宇普西龙UpsilonΦφ:fai PhiΧχ:器ChiΨψ:普赛PsiΩω:欧米伽Omega希腊字母怎么打打开Office文档之后,在你需要输入希腊字母的时候,先将输入法切换为英文状态,然后同时按下三个键Ctrl+Shift+Q ,工具栏上的“字体”就会发生变化此刻,你再对照下表输入a,b,c……即可得到您想要的希腊字母。
数学符号读法大全

大写小写英文注音国际音标注音中文注音Αα alpha alfa阿耳法Ββ beta beta贝塔Γγ gamma gamma伽马Δδ deta delta德耳塔Εε epsilon epsilon艾普西隆Ζζ zeta zet a 截塔Ηη eta et a 艾塔Θθ theta θita西塔Ιι iota iota约塔Κκ kappa kappa卡帕∧λ lambda lambda兰姆达Μμ mu miu缪Νν nu niu纽Ξξ xi ksi可塞Οο omicron omikron奥密可戎∏π pi pai派Ρρ rho rou柔∑σ sigma sigma西格马Ττtau ta u 套Υυ upsilon jupsilon 衣普西隆Φφ phifai 斐Χχ chikhai 喜Ψψ psi ps ai 普西Ωω omega omiga欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax 同 a^xlogba 以b为底a的对数; blogba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin yacos x y,余弦函数反函数在x处的值,即 x = cos yatan x y,正切函数反函数在x处的值,即 x = tan yacot x y,余切函数反函数在x处的值,即 x = cot yasec x y,正割函数反函数在x处的值,即 x = sec yacsc x y,余割函数反函数在x处的值,即 x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
(完整版)数学符号及读法大全
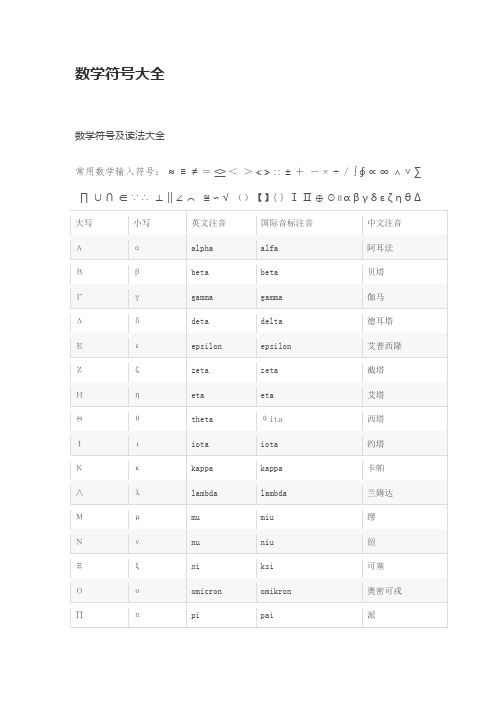
数学符号大全数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ公式输入符号≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√+:plus(positive正的)-:minus(negative负的)*:multiplied by÷:divided by=:be equal to≈:be approximately equal to():round brackets(parenthess)[]:square brackets{}:braces∵:because∴:therefore≤:less than or equal to≥:greater than or equal to∞:infinityLOGnX:logx to the base nxn:the nth power of xf(x):the function of xdx:diffrencial of xx+y:x plus y(a+b):bracket a plus b bracket closeda=b: a equals ba≠b: a isn't equal to ba>b : a is greater than ba>>b: a is much greater than ba≥b: a is greater than or equal to bx→∞:approches infinityx2:x squarex3:x cube√ ̄x:the square root of x3√ ̄x:the cube root of x3‰:three peimilln∑i=1xi:the summation of x where x goes from 1to nn∏i=1xi:the product of x sub i where igoes from 1to n ∫ab:integral betweens a and b数学符号(理科符号)——运算符号1.基本符号:+- × ÷(/)2.分数号:/3.正负号:±4.相似全等:∽≌5.因为所以:∵∴6.判断类:=≠<≮(不小于)>≯(不大于)7.集合类:∈(属于)∪(并集)∩(交集)8.求和符号:∑9.n次方符号:¹(一次方) ²(平方) ³(立方)⁴(4次方)ⁿ(n次方)10.下角标:₁₂₃₄(如:A₁B₂C₃D₄效果如何?)11.或与非的"非":¬12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:|21.弧:⌒22.圆:⊙11.或与非的"非":¬12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:|21.弧:⌒22.圆:⊙αβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯΔ。
数学符号读法大全(免费)
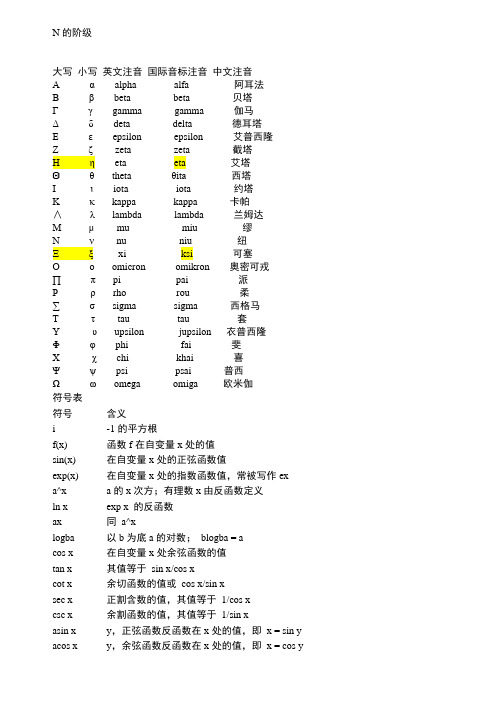
N的阶级大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Γδdeta delta 德耳塔Δεepsilon epsilon 艾普西隆Εδzeta zeta 截塔Ζεeta eta 艾塔Θζtheta ζita西塔Ηηiota iota 约塔Κθkappa kappa 卡帕∧ιlambda lambda 兰姆达Μκmu miu 缪Νλnu niu 纽Ξμxi ksi 可塞Ονomicron omikron 奥密可戎∏πpi pai 派Ρξrho rou 柔∑ζsigma sigma 西格马Τηtau tau 套Υυupsilon jupsilon 衣普西隆Φθphi fai 斐Φχchi khai 喜Χψpsi psai 普西Ψωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数;blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值,其值等于1/cos xcsc x 余割函数的值,其值等于1/sin xasin x y,正弦函数反函数在x处的值,即x = sin y acos x y,余弦函数反函数在x处的值,即x = cos yatan x y,正切函数反函数在x处的值,即x = tan y acot x y,余切函数反函数在x处的值,即x = cot y asec x y,正割函数反函数在x处的值,即x = sec y acsc x y,余割函数反函数在x处的值,即x = csc yζ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z 用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
数学符号读音
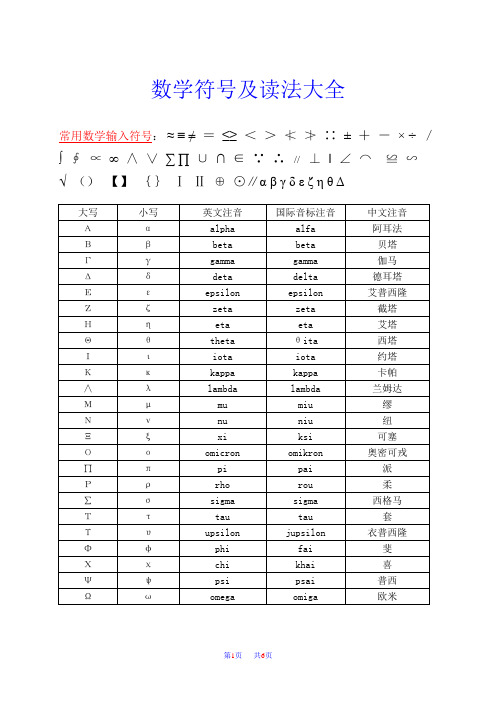
数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≦≧∷±+-× ÷/∫∬∝∞∡∢∑∏∪∩∈∮∭//≩‖∟≪≌∽√()【】{}ⅠⅡ⊕≨∠αβγδεδεζΓ符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作e x a^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数; b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin y acos x y,余弦函数反函数在x处的值,即 x = cos y atan x y,正切函数反函数在x处的值,即 x = tan y acot x y,余切函数反函数在x处的值,即 x = cot y asec x y,正割函数反函数在x处的值,即 x = sec y acsc x y,余割函数反函数在x处的值,即 x = csc yζ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到100 的和可以表示成:。
这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化,dy, dz, dr等类似ds 长度的微小变化ξ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积ζvw向量v和w之间的夹角A•B×C标量三重积,以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量,即 w/|w|df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数,同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数,自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
常用数学符号读法大全

常用数学符号读法大全大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Γδdeta delta 德耳塔Δεepsilon epsilon 艾普西隆Εδzeta zeta 截塔Ζεeta eta 艾塔Θζtheta ζita西塔Ηηiota iota 约塔Θθkappa kappa 卡帕ⅸιlambda lambda 兰姆达Μκmu miu 缪Νλnu niu 纽Ξμxi ksi 可塞Ονomicron omikron 奥密可戎∏πpi pai 派Ρξrho rou 柔∑ζsigma sigma 西格马Τηtau tau 套Υυupsilon jupsilon 衣普西隆Φθphi fai 斐Φχchi khai 喜Χψpsi psai 普西Ψωomega omiga 欧米伽常用数学符号大全1 几何符号ⅷⅶ↋ↆↄ△2 代数符号ⅴⅸⅹ~ⅼↅↇↈↃⅵↀ3运算符号×÷ⅳ±4集合符号ⅻⅺⅰ5特殊符号ⅲπ(圆周率)6推理符号|a| ↂ△ⅶⅺⅻↅↆ±ↈↇⅰⅬⅭⅮⅯ↖↗↘↙ⅷⅸⅹ&; §←↑→↓↔↕↖↗ΓΔΘΛΞΟΠΣΦΧΨΩαβγδεδεζηθικλμνπξζηυθχψωⅠ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹⅰⅱⅲ↚ⅳⅴⅵ↛ⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↀↁↂↃↄ↝ↅↆↇↈ↞↟↉↊⊕↋↠℃指数0123:o123上述符号所表示的意义和读法(中英文参照)+ plus 加号;正号- minus 减号;负号± plus or minus 正负号× is multiplied by 乘号÷ is divided by 除号= is equal to 等于号ↅ is not equal to 不等于号ↆ is equivalent to 全等于号ↄ is approximately equal to 约等于Ↄ is approximately equal to 约等于号< is less than 小于号> is more than 大于号ↇ is less than or equal to 小于或等于ↈ is more than or equal to 大于或等于% per cent 百分之…ⅵ infinity 无限大号ⅳ (square) root 平方根X squared X的平方X cubed X的立方ⅿ since; because 因为ⅾ hence 所以ⅶ angle 角 semicircle 半圆↋ circle 圆○ circumference 圆周△ triangle 三角形 perpendicular to 垂直于ⅻ intersection of 并,合集ⅺ union of 交,通集ⅼthe integral of …的积分ⅲ (sigma) summation of 总和° degree 度′ minute 分〃 second 秒#number …号@ at 单价CNN) -- Kezai started receiving professional tennis coaching at the age of eight. Since then his father has worked hard to cover his training costs.Two years on and it all seems to have paid off. In June, a local Chengdu company reached out to Li Chengpeng, Kezai's father, with an offer to sponsor Kezai.Soon after, a professional photographer took pictures of Kezai and his father for advertisements. But the family's happiness was short lived. The company withdrew the sponsorship.Though he says he was never given an explanation, Kezai's father believes it was because of his political activity. The company could not be reached for comment.As a controversial blogger and writer, Li announced his plan to run for office as an independent candidate for China's National People's Congress of Wuhou District, a legislative body at the local level in Sichuan province."You never know the benefit of standing up if you always stay on your knees," Li declared in a campaign statement on his microblog, where he has more than three million regular followers. Through the power of social media, Li's original message was forwarded more than 3,000 times within a few hours on micro-blogging site Sina Weibo, a popular twitter-like service.But such campaigns are rare in China.The Chinese do not choose their own president or premier because all government officials are pre-decided.However, elections are held on the local level, with all candidates approved by the party beforehand.China's electoral law stipulates that every Chinese citizen over 18 has the right to vote and run in local elections. Those, like Li Chengpeng, seeking to become candidates for county or township legislatures must first register and secure confirmation of their candidacy. They must then be nominated as "deputy candidate" by political parties, social organizations or have the signed support of at least 10 registered voters in their constituency.In practice, the government can rule candidates or any of their supporters unqualified and refuse to put them on the ballot, which critics say leaves ample opportunity for manipulation of the results."I know nobody on the ballot sheet. And I don't think my vote will make much difference," a retiree in Beijing said when she was asked to vote for the People's Congress district's last election.In recent months, an unprecedented number of Chinese citizens have declared themselves as independent candidates, according to Li Fan, founder of the World and China Institute that promotes democracy at the local levels.He said many candidates have grievances with the local government and feel they cannot get their voices out."They bid for the position as they think they can draw attention from the public for better solving of the problem," he said."Some local governments did think that their leadership was threatened by these (independent candidates), which is obviously not the case." Li Fan said.Some believe there are concerns among the central government as well. On June 8, state-run media Xinhua quoted the head of the Commission for Legislative Affairs of the National People's Congress Standing Committee as saying that "there is no such a thing as an'independent candidate' as it's not recognized by law." All candidates must follow the guidelines laid out by the government.But some do manage to meet the guidelines and run under the banner of an independent. The history of China's independent candidates dates back to 1998, when Yao Lifa, a teacher in Hubei Province, became the first self-described independent candidate elected to the local congress. He lost out when attempting a bid for a second term in 2003.With the government in control of the media and potential candidates subject to government approval, many question whether a truly independent candidate can win. Li Fan says morethan 100 people -- many using the internet -- have declared themselves as candidates for upcoming elections for people's congresses across the country."There are no fair and free elections in China," said Li Fan. "Chances are not good for these people leading the wave, but with their appeals, a lot more people will stand out to join in the election. They are the future."No matter what the chances are for Li Chengpeng, he says he is determined. "In China, there is so much unfairness and many choices in life are decided by the others," he explained during an interview with CNN. "I want to make decisions on my own."To achieve his goal, Li Chengpeng has visited more than 100 residents in his constituency, listening to their appeals to work out his campaign plan, trying to secure thegovernment-required support from 10 registered voters. He also continues to speak out on his blog.Li Chengpeng is not sure whether his name will appear on the ballot in September, when the election process officially begins, but he tries to be optimistic. "I'm confident. If I'm not confident, how can I convince my supporters?" he said.Li Chengpeng is not so confident about securing another tennis sponsorship for his son, if his political activities indeed caused him to lose the first one. He says he plans to fight on as an independent -- and he has his son's support.。
各种数学符号的读法

各种数学符号的读法在日常生活中,我们经常会遇到各种各样的数学符号,例如加减乘除、大于小于、平方根等等。
对于这些符号,我们需要了解它们的读法,以便正确理解和运用。
下面就让我们来一起学习各种数学符号的读法吧。
首先,我们来看看最基本的加减乘除符号。
加号“+”读作“加”,减号“-”读作“减”,乘号“×”读作“乘”,除号“÷”读作“除”。
这些符号在数学运算中经常出现,对于初学者来说,掌握它们的读法是非常重要的。
接下来,我们来学习一些比较常见的数学符号。
大于号“>”读作“大于”,小于号“<”读作“小于”,等于号“=”读作“等于”。
这些符号在比较大小或者表示相等关系时经常被使用。
除了基本的运算符号和比较符号外,还有一些特殊的数学符号需要我们了解。
例如平方根符号“√”读作“根号”,百分号“%”读作“百分之”,阶乘符号“!”读作“阶乘”。
这些符号在数学表达式中起着重要的作用,正确理解它们的读法可以帮助我们更好地理解数学问题。
此外,还有一些数学符号的读法可能会让人感到困惑。
例如π(圆周率)读作“派”,Σ(求和符号)读作“求和”,∞(无穷大符号)读作“无穷大”。
这些符号在数学中具有特殊的意义,掌握它们的读法有助于我们更好地理解数学概念。
总的来说,数学符号的读法在数学学习中起着至关重要的作用。
正确理解这些符号的读法可以帮助我们更好地理解和运用数学知识,提高数学学习的效率和水平。
希望通过学习各种数学符号的读法,能够让我们在数学学习中更加得心应手,取得更好的成绩。
让我们一起努力学习,掌握更多有关数学的知识吧!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mathematics Symbols and Their English Explanations1/2 a half or one half1/3 a third or one third2/3 two third1/4 a quarter or one quarter; a fourth or one fourth1/10 a tenth or one tenth1/100a [one] hundredth 1/1000a [one] thousandth 1/1234one over a thousand two hundred and thirty-four 3/4three fourths or three quarters 4/5three fifths or four over five 113/300one hundred and thirteen over three hundred 212two and a half 872two and seven over eight or two and seven eighths 813three and one eighth 314four and a third 43125a [one] hundred twenty-five and three fourths [quarters] 0.1(or .1)0 point one or zero point one or nought point one 0.01(or .01)0 point 0 one or zero point zero one or nougth point nought one 0.25(or .25)nougth point two five or point two five 0.045decimal [point] nought four five 2.35two point three five 4.9four point nine recurring 3.0362three point nought three two six , two six recurring 45.67four five [forth-five] point six seven 38.72three eight point seven two or thirty-eight decimal seven two0.001(or .001) 0 point 0 0 one nought point nought nought one or zero pointzero zero one or point nought nought one+ plus; positive_ minus; negative±plus or minus⨯(or.) multiplied by ; times÷(or/) divided by= is equal to ; equals≡is identically equal to≈(or≅;Ω;=) is approximately equal to ; approximately equals≡identical with= or ≠not equal to→or= approaches< less thangreater than<< much less than>> much greater than≤equal to or less than≥equal to or greater than( ) round brackets; parentheses[ ] square brackets[ ] angular brackets{ } braces⋂intersection⋃union∈is member of set⊂is a subset of~ similar to ; difference* denotes an operation⇔is equivalent to⇒implies{ }or∅empty set→maps into∴thereforebecause: ratio sign, divided by, is to:: equals, as (proportion)∝varies as∞infinitysquare root of3cube root of║ parallel to。
degrees, minutes” seconds∠angleAB length of line from A to BA⨯B vector product of A and B; magnitude of A times magnitudeof B times sine of the angle from A to B; AB sin ABA B∙scalar product of A to B ; magnitude of A times magnitudeof B times cosine of the angle form A to B ;AB cos ABI or j imaginary or square root of -1ωor 2ωthe imaginary cube roots of 1πpi ; the ratio of the circumference of a circle to its diameter,approx.3.14159e or ε①the base of natural logarithms, approx.2.71828② the eccentricity of a conic sectionx ! or x factorial xn log x log x to the base n10log x or lg x log x to the base 10 (common logarithm)e log x or ln x log x to the base (natural logarithm or Naperian logarithm ) Mmodulus of common logarithms 10log e = 0.4343, (10log x = e log x ⨯0.4343) 1-Me l o g 10 = 2.3026, (e log x = 10log x ⨯ 2.3026) n xx x.x …to n factors, the nth power of x, x to the power n n x or n x 1the nth root of x,x to the power one over n th X → ax approaches the limit a θ(the angle between the radius vector and the polar axis) the angle theta ∑sigma ∏the product of the terms indicated xthe absolute value of x xthe mean value of x ; x bar b 'b prime b ''b double prime ; b second prime b '''b triple prime 1bb sub one 2bb sub two m bb sub m xx dot ,first derivative of x with respect to time x x two dot , second derivative of x with respect to timeexp x = x e (e = naperian log base )(abbreviation for x e ) n m b b double prime sub mf or F functionf(x );F(x );∅(x )… function f(or ∅) of xy = f(x) y is a function of x∆ ( finite difference or increment) deltax ∆or σx(the increment of x ) delta x x d(an increment of x considered as tending to zero )dee of x ; dee x ; differential of x yxd d or xy Dthe differential coefficient of y with respect to xthe first derivative of y with respect to x 2y d /2x dthe second derivative of y with respect x ; n y d /nx dthe nth derivative of y with respect x y ∂/u ∂the partial derivative of y with respect u ,uwhere y is a function of u and another variable (or variables) F '(x)the first derivative of function F of x with respect to x ∇i ∂/x ∂+j ∂/y ∂+k ∂/z ∂ del ; nabla; vector differential operator ∇nnth del (nabla) ιLaplacian operator 4!Factorial =1432⨯⨯⨯ ⎰line integral around a closed path ⎰integral ⎰ab integral between limits a and bF vector Fx+y x plus y(a+b) bracket a plus b bracket closeda =b a equal b ; a is equal to b ; a is ba ≠b a is not equal b ; a is not ba±b a plus or minus ba≈b a is approximately equal to ba>b a is greater than ba>>b a is much [far] greater than ba≥b a is greater than or equal to ba b a is not greater than ba<b a is less than ba<<b a is much less than ba b≤a is less than or equal to ba ba is not less than ba b⊥a is perpendicular to bx=∞x approaches infinitya b≡ a is identically equal to b ; a is of identity∠angle aaa‖b a is parallel to ba∽b the difference between a and ba b∝a varies directly as b11⨯=1 one one is one22⨯=4 twice two is four65⨯=30 six times [multiplied by] five equals [is equal to; are;makes ; make] thirty30=65⨯thirty is five times as large as sixs=vt s equals [is equal to] v multiplied by t;s equals v times t 1:2 the ratio of one to two123÷=4 12 divided by 3 equals [is] 420:5=16:4 the ratio of 20 to 5 equals the ratio of 16 to 4 ; 20 is to 5as 16 is to 4a:b :: c:d a is to b as c is to da+b=c a plus b is [are; equals; is equal to] cc-b=a c minus b is [equals; is equal to] a ; b from c leaves a v=t sv equals s divided by t ; c is s over t 7+3<127 plus 3 is less than 12 12>7+312 is greater than 7 plus 3 72-16=5672 minus 16 is [equals; is equal to] 56; 16 from 72 leaves 56 2xx square ; x squared; the square of x ; the second power of x ; x to the second power 25=25the second power of 5 is 25 ; 5 square is 25 ; 5 to the second power is equal to 25 3yy cube ; y cubed ;the cube of y ; y to the third power ; y to the third 10-yy to the minus tenth(power) 4=2±the square root of 4 is [equals] plus or minus 2 3athe cube root of a 52xthe fifth root of x square 518the square root of five hundred and eighteen 3930the cube root of nine hundred and thirty 3x=5three times x equals 5 3x /5=2y x to the third power divided by five equals ysquared2x +2y =10 x squared with y squared equals 10 a=tV V t - a equals v sub t minus v over [divided by] t (a+b-c f e d =÷⨯) a plus b minus c multiplied by d , all divided by e equals f (8+6212)468.385÷⨯-eight plus six and five-eighths minus three decimal [point] six eight multiplied by four, all divided by two and a half 456719823=÷余1323 into 4567 goes 198 times, and 13 remainder 45+70+152=26745,70 and 152 added together are 267 %per cent 2%two per cent 000per mille 5000five per mille 83%three eighths (of one)per cent 0.3%point three per cent 21tonhalf ton 32tontow third of a ton 43kmthree quarters of a kilometer 1.75kmone point seven five kilometer 60hr misixty miles per hour 20C 0twenty degrees 6'① 6 minutes ② 6 feet 01''① 10 seconds ② 10 inches 0C 0 zero degree Centigrade [Celsius]100C 0 one [a] hundred degrees centigrade32F 0 thirty-two degrees FahrenheitSet theory, relations, functionsX , Y Setx X ∈ x is a member of the set Xx X ∉ x is not a member of XA X A X ⊆⊂, Set A is contained in set XX A X A ⊆⊄, A is not contained in XY X Y X +⋃, Union of sets X and YY X Y X .,⋂ Intersection of sets X and Y+,+,O Symmetric difference of sets∑⋃xi Xi , Union of all the sets Xxi Xi ∏⋂, Intersection of all the sets X,0,φ∧ Null set , empty setCX CX X ,,' Complement of the set XX-Y , X\Y Difference of sets X and Y)}(:{)},({)),((^x P x x P x x p x The set of all x with the property p(x , y , z), ( x, y, z) Ordered set of elements x , y, and z; to bedistinguished from (x, y, z), for example( x, y, z) Unordered set, the set whose elements are x, y,z, and no others{ ,...,,21a a },{i a } i=1,2...,n 1}{=i n i aThe set whose members are i a , where i isany whole number from 1 to n{ ,...,21a a },{i a } i=1,2...,∞=1}{i i aThe set whose members are i a , where i is anypositive whole numberY X ⨯ Cartesian product, set of all (x , y) such thatY y X x ∈∈,I i a i ∈}{ The set whose elements are a , where I i ∈ Xry ,R {x , y} Relation,,≅≡∽,≈ Equivalence relations, for example, congrucnce ≥,≧,>,>>,≦,≤,< Transitive relations, for example, numerical orderf : X f Y f Y X y X Y X ∈→−→−→,,, Function, mapping, transformationY X f f f −→−---111,, Inverse mapping g 。
