甘肃省白银十中2017届高三(上)期中数学试卷(理科)(解析版)
2017年甘肃白银数学中考试题及答案
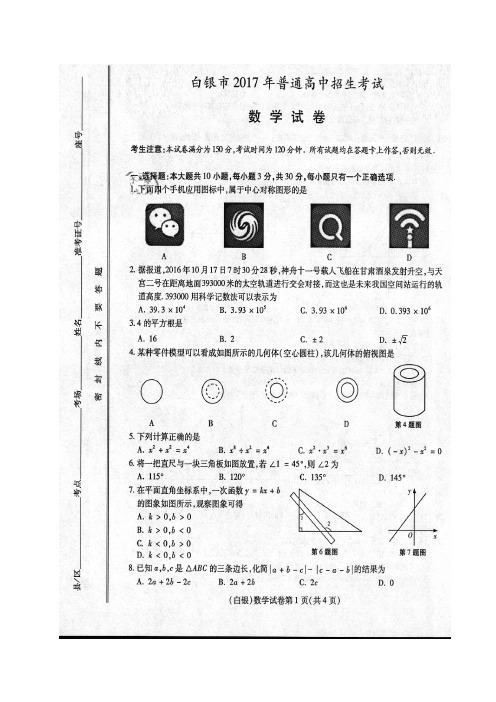
白银市2017年初中毕业、高中招生考试数学试题参考答案及评分标准一、选择题:本大题共10小题,每小题3分,共30分.每小题只有一个正确选项.二、填空题:本大题共8小题,每小题3分,共24分.11. 2(1)x - 12. > 13. 0 14. 5815. k ≤5且k ≠1 16. 154 17. 3π 18. 8(1分),6053(2分) 三、解答题(一):本大题共5小题,共26分.解答应写出必要的文字说明,证明过程或演算步骤.(注:解法合理、答案正确均可得分)19.(4分)解:原式=312-+- 2分=12- 3分1-. 4分20.(4分)解:解1(1)2x - ≤1得:x ≤3, 1分 解1-x <2得:x >-1. 2分则不等式组的解集是:-1<x ≤3. 3分 ∴该不等式组的最大整数解为3x =. 4分21.(6分)解:如图,5分 (注:作出一条线段的垂直平分线得2分,作出两条得4分,连接EF 得1分.)∴线段EF 即为所求作. 6分22.(6分) 解:过点D 作DE ⊥AC ,垂足为E ,设BE =x , 1分在Rt △DEB 中,tan DE DBE BE ∠=, ∵∠DBC =65°, ∴tan 65DE x =o . 2分又∵∠DAC =45°,∴AE =DE .∴132tan 65x x +=o , 3分∴解得115.8x ≈, 4分∴248DE ≈(米). 5分∴观景亭D 到南滨河路AC 的距离约为248米. 6分23.(6分)解:(1)画树状图:3分列表3分可见,两数和共有12种等可能性; 4分(2) 由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,∴李燕获胜的概率为61122=; 5分 刘凯获胜的概率为31124=. 6分 四、解答题(二):本大题共5小题,共40分.解答应写出必要的文字说明,证明过程或演算步骤.(注:解法合理、答案正确均可得分) B DC A E24.(7分) 解:(1)m =70, 1分 n =0.2; 2分(2)频数分布直方图如图所示,3分(3) 80≤x <90; 5分(4)该校参加本次比赛的3000名学生中成绩“优”等的约有:3000×0.25=750(人). 7分25.(7分) 解:(1)∵点P 在反比例函数的图象上,∴把点P (12,8)代入k y x=2可得:k 2=4, ∴反比例函数的表达式为4y x=, 1分 ∴Q (4,1) .把P (12,8),Q (4,1)分别代入1y k x b =+中,得 1118214k b k b ⎧=+⎪⎨⎪=+⎩, 解得129k b =-⎧⎨=⎩,∴一次函数的表达式为29y x =-+; 3分(2)P ′(12-,-8) 4分(3)过点P ′作P ′D ⊥x 轴,垂足为D. 5分∵P ′(12-,-8), ∴OD =12,P ′D =8, ∵点A 在29y x =-+的图象上,∴点A (92,0),即OA =92, ∴DA =5, ∴P ′A= 6分频数(人)频数分布直方图 成绩(分)∴sin ∠P ′AD P P D A ''=== ∴sin ∠P ′AO =. 7分 26.(8分) 解:(1)∵四边形ABCD 是平行四边形,O 是BD 的中点,∴A B ∥DC ,OB =OD , 1分∴∠OBE =∠ODF ,又∵∠BOE =∠DOF ,∴△BOE ≌△DOF (ASA ), 2分∴EO =FO ,∴四边形BEDF 是平行四边形; 4分(2)当四边形BEDF 是菱形时,设BE =x则 DE =x ,6AE x =-,在Rt △ADE 中,222DE AD AE =+,∴2224(6)x x =+-, ∴133x =, 135214332BEDF S BE AD =BD EF ,=∴⋅=⨯=⋅菱形 6分15223BD EF ,EF ===∴⨯=∴=又Q 8分27.(8分)解:(1)∵A 的坐标为(0,6),N (0,2)∴AN =4, 1分 ∵∠ABN =30°,∠ANB =90°,∴AB =2AN =8, 2分 ∴由勾股定理可知:NB=,∴B(,2) 3分(2)连接MC ,NC 4分 ∵AN 是⊙M 的直径,∴∠ACN =90°,∴∠NCB =90°, 5分 在Rt △NCB 中,D 为NB 的中点,∴CD =12NB =ND , ∴∠CND =∠NCD , 6分 ∵MC =MN , ∴∠MCN =∠MNC . ∵∠MNC +∠CND =90°,∴∠MCN +∠NCD =90°, 7分即MC ⊥CD .∴直线CD 是⊙M 的切线. 8分28.(10分)解:(1)将点B ,点C 的坐标分别代入24y ax bx =++,得:424064840a b a b -+=⎧⎨++=⎩, 1分 解得:14a =-,32b =. ∴该二次函数的表达式为213442y x x =-++. 3分 (2)设点N 的坐标为(n ,0)(-2<n <8),则2BN n =+,8CN n =-.∵B (-2,0), C (8,0),∴BC =10.令0x =,解得:4y =,∴点A (0,4),OA =4,∵MN ∥AC , ∴810AM NC n AB BC -==. 4分 ∵OA =4,BC =10, ∴114102022ABC S BC OA =⋅=⨯⨯=V . 5分 1122222810ABN AMN ABN S BN OA n+n+S AM CN n ,S AB CB =⋅=⨯-===()4=()又V V V QM N B C A O∴2811(8)(2)(3)51055AMN ABN n S S n n n -==-+=--+V V . 6分 ∴当n =3时,即N (3,0)时,△AMN 的面积最大. 7分(3)当N (3,0)时,N 为BC 边中点.∴M 为AB 边中点,∴12OM AB.= 8分∵AB ===,AC ===, ∴12AB AC,=9分 ∴14OM AC =. 10分。
甘肃省白银市第十中学2017-2018学年高一上学期期中考试数学模拟试题(解析版)

上是增函数, 对于 B, y
2
x 1 在(1,+ )上是增函数, 对于 C, y
x2
在 0,
上是减函数,对于 D, y 3 x 是减函数,所以选 A.
4.下列函数的图像关于 y 轴对称的是(
)
A. y ex e x
B. y 2x
C. y log 2 x
D. y x 3
【答案】 A 【解析】
因为函数图象关于 y 轴对称,所以函数为偶函数,因为
2
6. f ( x)
ex
1
的零点所在的区间是(
)
x
2
D.
点睛:判定两个函数是否为同一个函数,主要看定义域和对应法则,只有定义域与对应法则相同的函数才
是同一个函数,与函数的自变量名称无关 .
3.下列函数在区间 (0, A. y ln( x 1)
) 上是增函数的是( B. y ( x 1)2
)
C. y x 2
D. y 3 x
【答案】 A 【解析】
对于 A, y ln x 1 在 0,
B,
f ( x) =x ﹣1 ,定义域是 R, g (x) = x 2 ﹣1 ,定义域为 {x|x ≠ 0,} 定义域不同,不是同一函数;对于 x
4
=x 2,定义域为 R, g (x) = x =x 2,定义域是 [0 ,+ ∞),定义域不同,不是同一函数;对于
C, f( x) A,f ( x)
1
=|x| ,定义域是 R ,g( x)= x2 =|x| ,定义域是 R ,定义域相同,对应关系也相同,是同一函数.故选
D. 2 A
【答案】 B 【解析】
∵集合 A={x ∈ Q|x >﹣1} ,∴集合 A 中的元素是大于﹣ 1 的有理数,
甘肃省白银十中2016—2017学年第一学期高三年级第一次月考数学试题Word版含答案.doc

白银十中2016—2017学年第一学期高三年级第一次月考数学(理科)试题出题人:田学礼 审题人:王开泰第I 卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知全集U ={1,2,3,4,5,6},集合A ={2,3,4},集合B ={2,4,5},则下图中的阴影部分表示( )A .{5}B .{1,3}C .{2,4}D .{2,3,4,5} 2.下列函数中,与函数y =x 相同的是( ) A .y =x 2xB .y =(x)2C .y =lg 10xD . 2log 2x y =3. 下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数为 ( )A .2y x -=B .1y x -=C .2y x =D .13y x =4. 给出以下四个判断,其中正确的判断是 ( )A .函数f(x)的定义域关于原点对称是f(x)具有奇偶性的充分不必要条件B .命题“若x≥4且y≥2,则x +y≥6”的逆否命题为“若x +y <6,则x <4且y <2”C .若p :∂0x ≥ ,x 2-x +1>0,则¬p :∀x<0,x 2-x +1≤0D .己知n ∈N ,则幂函数y =x 3n-7为偶函数,且在x ∈(0,+∞)上单调递减的充分必要条件为n =15.已知函数220()log 0x x f x x x ⎧≤=⎨>⎩ ,则方程1()2f x =的解集为( ) A. B. C.{ D. 6. 如图给出了函数y =a x ,y =log a x ,y =log (a +1)x ,y =(a -1)x 2的图象,则与函数y =a x ,y =log a x ,y =log (a +1)x ,y =(a -1)x 2依次对应的图象是 ( )A .①②③④B .①③②④C .②③①④D .①④③②7. 已知函数f(x)是定义在(-∞,+∞)上的奇函数,若对于任意的实数x>0,都有1(2)()f x f x +=-,且当x ∈[0,2)时f(x)=log 2(x +1),则f(2 015)+f(2 016)的值为( )A .-1B .-2C .2D .18. 定义在区间[0,1]上的函数f(x)的图象如下图所示,以A(0,f(0))、B(1,f(1))、C(x ,f(x))为顶点的△ABC 的面积记为函数S(x),则函数S(x)的导函数S′(x)的大致图象为()9.函数2()(1)1f x x f x '=--+在x=1处的切线方程为( )A. 4y x =-+B. 3y x =C. 33y x =-D. 39y x =-10.已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数()y f x '=的图象如图所示.下列关于f(x)的命题:①函数f(x) 在x=0,4处取到极大值;②函数f(x)在区间[0,2]上是减函数;③如果当x ∈[-1,t]时,f(x)的最大值是2,那么t 的最大值为4;④当1<a <2时,函数y =f(x)-a 不可能有3个零点.其中所有真命题的序号是( )A.①②B. ①②③C. ①②④D. ①②③④11.函数f(x)在定义域R 内可导,f(x)=f(2-x),当(1,)x ∈+∞时,()()10x f x '<-,设352a=f(),b=f 22(),c=f(5)log log log ,则( )A .c<a<bB .c<b<aC .a<b<cD .b<a<c12. 设函数2sin 20()20a x x f x x a x +≥⎧=⎨+<⎩(其中a ∈R )的值域为S ,若[1,+∞)⊆S ,则a 的取值范围是( )A .(﹣∞,)B .[1,]∪(,2]C .(﹣∞,)∪[1,2]D .(,+∞)第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)13.函数f(x)= 1-2log 6x 的定义域为________. 14.已知函数()()21()0,1m f x log x m m =-+>≠且的图象恒过点P,且点P 在直线1,,ax by a b R +=∈上,那么ab 的最大值为____________________.15. 已知a≥0,函数f(x)=(x 2-2ax)e x ,若f(x)在[-1,1]上是单调减函数,则a 的取值范围是________.16. 设函数f(x)=e 2x 2+1x ,g(x)=e 2x e x ,对任意x 1,x 2∈(0,+∞),不等式g(x 1)k ≤f(x 2)k +1恒成立,则正数k 的取值范围是________.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17. (本小题满分10分)已知()f x xlnx =.(1)求曲线f(x)在x e =处的切线方程.(2)求函数f(x)的单调区间.18. (本小题满分12分)已知函数f(x)=ax 3+cx +d(a ≠0)是R 上的奇函数,当x =1时,f(x)取得极值-2.(1)求函数f(x)的解析式;(2)求函数f(x)的单调区间和极大值;19.(本小题满分12分)设函数f(x)=a x -(k -1)a -x (a>0且a ≠1)是定义域为R 的奇函数. (1)求k 值;(2)若f(1)<0,试判断函数单调性并求使不等式f(x 2+tx)+f(4-x)<0恒成立的t 的取值范围.20.(本小题满分12分)已知函数()f x 是定义在R 上的偶函数,现已画出函数()f x 在y 轴左侧的图象(二次函数图象的一部分),如图所示,请根据图象:(1)画出函数()f x 在y 轴右边的图像并写出函数()()f x x R ∈的解析式.(2)若函数()()[]2()2,1,2g x f x ax x =-+∈(a R ∈为常数),求函数()g x 的最小值及最大值.21.(本小题满分12分)已知函数f(x)=ax 2+bx +c e x(a >0)的导函数y =f ′(x)的两个零点为-3和0.(1)求f(x)的单调区间;(2)若方程()0f x m -=有三个不同的的解,求m 的取值范围(用a 表示)。
2016-2017学年甘肃省白银十中高三(上)开学数学试卷(理科)(解析版)

2016-2017学年甘肃省白银十中高三(上)开学数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合A={x|y=lg(2x﹣x2)},B={y|y=2x,x>0},R是实数集,则(∁R B)∩A=()A.[0,1]B.(0,1]C.(﹣∞,0]D.以上都不对2.(5分)“”是“一元二次方程x2+x+m=0有实数解”的()A.充分非必要条件B.充分必要条件C.必要非充分条件D.非充分非必要条件3.(5分)已知命题p:∀x∈R,x>sin x,则()A.非p:∃x∈R,x<sin x B.非p:∀x∈R,x≤sin xC.非p:∃x∈R,x≤sin x D.非p:∀x∈R,x<sin x4.(5分)设a=log3π,b=log2,c=log3,则()A.a>b>c B.a>c>b C.b>a>c D.b>c>a5.(5分)下列命题错误的是()A.命题“若m≤0,则方程x2+x+m=0有实数根”的逆否命题为:“若方程x2+x+m=0无实数根,则m>0”B.“x2﹣x﹣2=0”是“x=2”的必要不充分条件C.若p∧q为假命题,则p,q中必有一真一假D.命题“在△ABC中,a=b⇔A=B⇔sin A=sin B”为真6.(5分)函数y=的图象大致是()A.B.C.D.7.(5分)设函数,则下列结论错误的是()A.D(x)的值域为{0,1}B.D(x)是偶函数C.D(x)不是周期函数D.D(x)不是单调函数8.(5分)由方程x|x|+y|y|=1确定的函数y=f(x)在(﹣∞,+∞)上是()A.增函数B.减函数C.先增后减D.先减后增9.(5分)已知向量集合,,则M∩N=()A.{1,1}B.{1,1,﹣2,﹣2}C.{(﹣2,﹣2)}D.∅10.(5分)若函数f(x)=,若f(a)>f(﹣a),则实数a的取值范围是()A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(1,+∞)C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)11.(5分)已知定义在R上的奇函数f(x),满足f(x﹣4)=﹣f(x)且在区间[0,2]上是增函数,则()A.f(﹣25)<f(80)<f(11)B.f(80)<f(11)<f(﹣25)C.f(11)<f(80)<f(﹣25)D.f(﹣25)<f(11)<f(80)12.(5分)已知a>0且a≠1,f(x)=x2﹣a x,当x∈(﹣1,1)时均有f(x)<,则实数a的取值范围是()A.∪[2,+∞)B.∪(1,4]C.∪(1,2]D.∪[4,+∞)二、填空题(本大题共4小题,每小题5分,共20分.把最终结果写在横线上.)13.(5分)命题“∃x<0,有x2>0”的否定是.14.(5分)函数y=﹣(x﹣3)|x|的递增区间是.15.(5分)定义:区间[x1,x2](x1<x2)的长度为x2﹣x1.已知函数y=|log0.5x|定义域为[a,b],值域为[0,2],则区间[a,b]的长度的最大值为.16.(5分)设f(x)是定义在R上的偶函数,且对于∀x∈R恒有f(x)=f(x﹣2),已知当x∈[0,1]时,f(x)=()1﹣x,则下列四个命题:①f(x)的周期是2;②f(x)在(1,2)上递减,在(2,3)上递增;③f(x)的最大值是1,最小值是0;④当x∈(3,4)时,f(x)=()x﹣3其中正确命题的序号是.(把你认为正确的命题序号都填在横线上)三、解答题(本大题共6小题,第17小题10分,其余每题均为12分,共70分,解答应写出必要的文字说明、证明过程、计算步骤)17.(10分)设命题p:(4x﹣3)2≤1;命题q:x2﹣(2a+1)x+a(a+1)≤0,若¬p是¬q 的必要不充分条件,求实数a的取值范围.18.(12分)已知a>0,设命题p:函数y=a x在R上单调递增;命题q:不等式ax2﹣ax+1>0对∀x∈R恒成立.若p且q为假,p或q为真,求a的取值范围.19.(12分)已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式f(x)=﹣(a∈R).(1)写出f(x)在[0,1]上的解析式;(2)求f(x)在[0,1]上的最大值.20.(12分)已知函数f(x)=2x﹣.(Ⅰ)若f(x)=2,求x的值;(Ⅱ)若2t f(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.21.(12分)已知函数f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y),且x>0时f(x)<0,f(1)=﹣2.①求f(0);②求证:f(x)为奇函数;③求f(x)在[﹣3,3]上的最大值和最小值.22.(12分)已知函数f(x)=log a(a>0,b>0,a≠1).(1)求f(x)的定义域;(2)讨论f(x)的奇偶性;(3)讨论f(x)的单调性.2016-2017学年甘肃省白银十中高三(上)开学数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.【解答】解:由2x﹣x2>0,得x(x﹣2)<0,即0<x<2,故A={x|0<x<2},由x>0,得2x>1,故B={y|y>1},∁R B={y|y≤1},则(∁R B)∩A=(0,1]故选:B.2.【解答】解:由x2+x+m=0知,⇔.(或由△≥0得1﹣4m≥0,∴.),反之“一元二次方程x2+x+m=0有实数解”必有,未必有,因此“”是“一元二次方程x2+x+m=0有实数解”的充分非必要条件.故选:A.3.【解答】解:对全称命题的否定既要否定量词又要否定结论,p:∀x∈R,x>sin x,则非p:∃x∈R,x≤sin x故选:C.4.【解答】解:∵∵,故选:A.5.【解答】解:A.命题“若m≤0,则方程x2+x+m=0有实数根”的逆否命题为:“若方程x2+x+m=0无实数根,则m>0”,故A正确,B.由x2﹣x﹣2=0得x=﹣1或x=2,则“x2﹣x﹣2=0”是“x=2”的必要不充分条件,故B正确,C.若p∧q为假命题,则p,q中至少有一个为假命题.故C错误,D.在△ABC中,由边角关系正弦定理得a=b⇔A=B⇔sin A=sin B成立,故D正确,故选:C.6.【解答】解:∵f(﹣x)=﹣f(x)是奇函数,所以排除A,B当x=1时,f(x)=0排除C故选:D.7.【解答】解:A显然正确;∵=D(x),∴D(x)是偶函数,B正确;∵D(x+1)==D(x),∴T=1为其一个周期,故C错误;∵D()=0,D(2)=1,D()=0,显然函数D(x)不是单调函数,故D正确;故选:C.8.【解答】解:①当x≥0且y≥0时,x2+y2=1,②当x>0且y<0时,x2﹣y2=1,③当x<0且y>0时,y2﹣x2=1,④当x<0且y<0时,无意义.由以上讨论作图如右,易知是减函数.故选:B.9.【解答】解:对于M={=(1+3λ,2+4λ)},令=(x,y),则,化简可得y=x+,故M中的向量都在直线y=x+上.对于N={=(﹣2+4λ,﹣2+5λ)},同理可得N中的向量在直线y=x+上.再由,求得,可得这2条直线的交点是(﹣2,﹣2),故选:C.10.【解答】解:由题意.故选:C.11.【解答】解:∵f(x﹣4)=﹣f(x),∴f(x﹣8)=﹣f(x﹣4)=f(x),即函数的周期是8,则f(11)=f(3)=﹣f(3﹣4)=﹣f(﹣1)=f(1),f(80)=f(0),f(﹣25)=f(﹣1),∵f(x)是奇函数,且在区间[0,2]上是增函数,∴f(x)在区间[﹣2,2]上是增函数,∴f(﹣1)<f(0)<f(1),即f(﹣25)<f(80)<f(11),故选:A.12.【解答】解:由题意可知,a x>在(﹣1,1)上恒成立,令y1=a x,y2=,由图象知:0<a<1时a1≥=,即≤a<1;当a>1时,a﹣1≥=,可得1<a≤2.∴≤a<1或1<a≤2.故选:C.二、填空题(本大题共4小题,每小题5分,共20分.把最终结果写在横线上.)13.【解答】解:∵对命题“∃x∈A,P(X)”的否定是:“∀x∈A,¬P(X)”∴对命题“∃x<0,有x2>0”的否定是“∀x<0,有x2≤0”故答案为:∀x<0,有x2≤014.【解答】解:y=﹣(x﹣3)|x|=作出该函数的图象,观察图象知递增区间为[0,].故答案为:[0,]15.【解答】解:函数y=|log0.5x|的值域为[0,2],那么0≤log0.5x≤2 或﹣2≤log0.5x<0,即:log0.51<≤log0.5x≤log0.5(0.5)2或log0.5(0.5)﹣2≤log0.5x<log0.51,由于函数log0.5x是减函数,那么或1<x≤4.这样就求出函数y=|log0.5x|的定义域为[,4],所以函数定义域区间的长度为故答案为:16.【解答】解:∵对任意的x∈R恒有f(x+1)=f(x﹣1),∴f(x+2)=f(x)则f(x)的周期为2,故①正确;∵函数f(x)是定义在R上的偶函数,当x∈[0,1]时,f(x)=()1﹣x,∴函数f(x)在(0,1)上是增函数,函数f(x)在(1,2)上是减函数,在(2,3)上是增函数,故②正确;∴函数f(x)的最大值是f(1)=1,最小值为f(0)=,故③不正确;设x∈[3,4],则4﹣x∈[0,1],f(4﹣x)=()x﹣3=f(﹣x)=f(x),故④正确故答案为:①②④三、解答题(本大题共6小题,第17小题10分,其余每题均为12分,共70分,解答应写出必要的文字说明、证明过程、计算步骤)17.【解答】解:设A={x|(4x﹣3)2≤1},B={x|x2﹣(2a+1)x+a(a+1)≤0},易知A={x|≤x≤1},B={x|a≤x≤a+1}.由¬p是¬q的必要不充分条件,从而p是q的充分不必要条件,即A⊂B,且两等号不能同时取.故所求实数a的取值范围是[0,].18.【解答】解:∵y=a x在R上单调递增,∴a>1;又不等式ax2﹣ax+1>0对∀x∈R恒成立,∴△<0,即a2﹣4a<0,∴0<a<4,∴q:0<a<4.而命题p且q为假,p或q为真,那么p、q中有且只有一个为真,一个为假.①若p真,q假,则a≥4;②若p假,q真,则0<a≤1.所以a的取值范围为(0,1]∪[4,+∞).19.【解答】解:(Ⅰ)∵f(x)为定义在[﹣1,1]上的奇函数,且f(x)在x=0处有意义,∴f(0)=0,即f(0)=﹣=1﹣a=0.∴a=1.…(3分)设x∈[0,1],则﹣x∈[﹣1,0].∴f(﹣x)=﹣=4x﹣2x.又∵f(﹣x)=﹣f(x)∴﹣f(x)=4x﹣2x.∴f(x)=2x﹣4x.…(8分)(Ⅱ)当x∈[0,1],f(x)=2x﹣4x=2x﹣(2x)2,∴设t=2x(t>0),则f(t)=t﹣t2.∵x∈[0,1],∴t∈[1,2].当t=1时,取最大值,最大值为1﹣1=0.…(12分)20.【解答】解:(Ⅰ)当x≤0时f(x)=0,当x>0时,,有条件可得,,即22x﹣2×2x﹣1=0,解得,∵2x>0,∴,∴.(Ⅱ)当t∈[1,2]时,,即m(22t﹣1)≥﹣(24t﹣1).∵22t﹣1>0,∴m≥﹣(22t+1).∵t∈[1,2],∴﹣(1+22t)∈[﹣17,﹣5],故m的取值范围是[﹣5,+∞).21.【解答】解:①在f(x+y)=f(x)+f(y)中,令x=y=0可得f(0)=f(0)+f(0),变形可得f(0)=0②证明:因为x,y∈R时,f(x+y)=f(x)+f(y),令y=﹣x,可得f(x﹣x)=f(x)+f(﹣x)=f(0)所以f(﹣x)=﹣f(x)所以f(x)为奇函数.③设x1、x2∈R,且x1<x2,f(x2)﹣f(x1)=f(x2)+f(﹣x1)=f(x2﹣x1)因为x>0时f(x)<0,所以f(x2﹣x1)<0,即f(x2)﹣f(x1)<0,所以f(x)为减函数.所以f(x)在[﹣3,3]上的最大值为f(﹣3),最小值为f(3).因为f(3)=f(2)+f(1)=3f(1)=﹣6,f(﹣3)=﹣f(3)=6,所以函数在[﹣3,3]上的最大值为6,最小值为﹣6.22.【解答】解:(1)使f(x )有意义,则>0,∵b>0,∴x>b或x<﹣b,∴f(x)的定义域为{x|x>b或x<﹣b}.(2)由(1)知f(x)的定义域关于原点对称,∵f(﹣x)=log a=log a=log a﹣1=﹣log a=﹣f(x).∴f(x)为奇函数.(3)设u ===1+,设x1>x2,则u1﹣u2=1+﹣=,当x1>x2>b 时,<0,即u1<u2,此时,u为减函数,同理﹣b>x1>x2时,u也为减函数.∴当a>1时,f(x)=log a在(﹣∞,﹣b)上为减函数,在(b,+∞)上也为减函数.当0<a<1时,f(x)=log a在(﹣∞,﹣b)上为增函数,在(b,+∞)上也为增函数.第11页(共11页)。
甘肃省白银十中2017届高考数学一模试卷(解析版)(理科)

2017年甘肃省白银十中高考数学一模试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={y|y=x2},B={x|y=lg(1﹣x)},则A∩B=()A.[0,1]B.[0,1) C.(﹣∞,1)D.(﹣∞,1]2.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是()A.B.y=C.y=lg x D.y=|x|﹣13.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题的个数为()A.1 B.2 C.3 D.44.设函数f(x)=,则f(﹣2)+f(log212)=()A.3 B.6 C.9 D.125.“a=﹣1”是“直线ax+3y+3=0和直线x+(a﹣2)y+l=0平行”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件6.若cos(﹣α)=,则sin2α=()A.B.C.﹣ D.﹣7.已知数列{a n}的通项公式为a n=(n∈N+),其前n项和S n=,则直线+=1与坐标轴所围成三角形的面积为()A.36 B.45 C.50 D.558.已知A(3,﹣1),B=(x,y),C(0,1)三点共线,若x,y均为正数,则+的最小值是()A.B.C.8 D.249.某几何体的三视图如图所示,则该几何体的体积为()A.B.C. D.10.已知圆C:(x﹣1)2+(y﹣2)2=2与y轴在第二象限所围区域的面积为S,直线y=2x+b分圆C的内部为两部分,其中一部分的面积也为S,则b=()A.B.±C.D.±11.已知函数f(x)=ln(e x+e﹣x)+x2,则使得f(2x)>f(x+3)成立的x的取值范围是()A.(﹣1,3)B.(﹣∞,﹣3)∪(3,+∞)C.(﹣3,3)D.(﹣∞,﹣1)∪(3,+∞)12.设函数f(x)在R上的导函数为f′(x),且2f(x)+xf′(x)>x2,下面的不等式在R内恒成立的是()A.f(x)>0 B.f(x)<0 C.f(x)>x D.f(x)<x二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)13.已知||=1,||=,且⊥(﹣),则向量与向量的夹角是.14.已知直线x﹣y+2=0及直线x﹣y﹣10=0截圆C所得的弦长均为8,则圆C的面积是.15.已知变量x,y满足的约束条件,若x+2y≥﹣5恒成立,则实数a 的取值范围为.16.如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:①函数y=sinx具有“P(a)性质”;②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;③若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f (x)是周期函数.其中正确的是(写出所有正确命题的编号).三、解答题(本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(12分)等差数列{a n}的各项均为正数,a1=1,前n项和为S n;数列{b n}为等比数列,b1=1,且b2S2=6,b2+S3=8.(1)求数列{a n}与{b n}的通项公式;(2)求{a n•b n}的前n项和T n.18.(12分)在△ABC中,三个内角A,B,C所对的边分别为a,b,c,已知函数为偶函数,(1)求b;(2)若a=3,求△ABC的面积S.19.(12分)某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期的图象时,列表并填入的部分数据如下表:(Ⅰ)求x1,x2,x3的值及函数f(x)的表达式;(Ⅱ)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,求函数y=f(x)•g(x)在区间(0,)的最小值.20.(12分)将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=.(1)求证:DE⊥AC.(2)求DE与平面BEC所成角的正切值.(3)直线BE上是否存在一点M,使得CM∥平面ADE?若存在,求点M的位置;若不存在,请说明理由.21.(12分)已知函数f(x)=e x+ln(x+1).(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;(Ⅱ)当x≥0时,f(x)≥ax+1成立,求实数a的取值范围.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x 轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.(I)求直角坐标下圆C的标准方程;(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.2017年甘肃省白银十中高考数学一模试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={y|y=x2},B={x|y=lg(1﹣x)},则A∩B=()A.[0,1]B.[0,1) C.(﹣∞,1)D.(﹣∞,1]【考点】1E:交集及其运算.【分析】求出A中y的范围确定出A,求出B中x的范围确定出B,找出A与B 的交集即可.【解答】解:由A中y=x2≥0,得到A=[0,+∞),由B中y=lg(1﹣x),得到1﹣x>0,即x<1,∴B=(﹣∞,1),则A∩B=[0,1),故选:B.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是()A.B.y=C.y=lg x D.y=|x|﹣1【考点】3N:奇偶性与单调性的综合.【分析】分别函数的奇偶性、单调性,即可得出结论.【解答】解:A中函数是偶函数且在(0,+∞)上单调递减,故A错误;B中函数是偶函数且在(0,+∞)上单调递减,故B错误;C中函数不是偶函数,故C错误;D中函数是偶函数且在(0,+∞)上单调递增,故选D.【点评】本题考查函数的奇偶性、单调性,考查学生的计算能力,属于中档题.3.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题的个数为()A.1 B.2 C.3 D.4【考点】2K:命题的真假判断与应用.【分析】对①,运用长方体模型,找出符合条件的直线和平面,即可判断;对②,运用线面平行的性质定理和线面垂直的性质定理,即可判断;对③,运用面面平行的性质定理,即可判断;对④,由平行的传递性及线面角的定义,即可判断④.【解答】解:对于命题①,可运用长方体举反例证明其错误:如图,不妨设AA′为直线m,CD为直线n,ABCD所在的平面为α,ABC′D′所在的平面为β,显然这些直线和平面满足题目条件,但α⊥β不成立;命题②正确,证明如下:设过直线n的某平面与平面α相交于直线l,则l∥n,由m⊥α知m⊥l,从而m⊥n,结论正确;由平面与平面平行的定义知命题如果α∥β,m⊂α,那么m∥β.③正确;由平行的传递性及线面角的定义知命题:如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等,④正确.故选:C.【点评】本题考查命题的真假判断,考查空间线面、面面平行和垂直的位置关系,注意运用判定定理和性质定理,考查推理能力,属于中档题.4.设函数f(x)=,则f(﹣2)+f(log212)=()A.3 B.6 C.9 D.12【考点】3T:函数的值.【分析】先求f(﹣2)=1+log2(2+2)=1+2=3,再由对数恒等式,求得f(log212)=6,进而得到所求和.【解答】解:函数f(x)=,即有f(﹣2)=1+log2(2+2)=1+2=3,f(log212)==12×=6,则有f(﹣2)+f(log212)=3+6=9.故选C.【点评】本题考查分段函数的求值,主要考查对数的运算性质,属于基础题.5.“a=﹣1”是“直线ax+3y+3=0和直线x+(a﹣2)y+l=0平行”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】2L:必要条件、充分条件与充要条件的判断.【分析】根据直线平行的等价条件,结合充分条件和必要条件的定义进行判断即可.【解答】解:当a=﹣1,则直线分别为﹣x+3y+3=0和直线x﹣3y+l=0满足平行,即充分性成立,若直线ax+3y+3=0和直线x+(a﹣2)y+l=0平行,当a=0时,直线分别为3y+3=0,和x﹣2y+1=0,不满足条件,当a≠0时,满足,即a(a﹣2)=3,解得a=3或a=﹣1,当a=3时,两直线重合,故不满足条件,综上a=﹣1,即必要性成立,综上“a=﹣1”是“直线ax+3y+3=0和直线x+(a﹣2)y+l=0平行”的充要条件,故选:C【点评】本题主要考查充分条件和必要条件的判断,根据直线平行的等价条件是解决本题的关键.6.若cos(﹣α)=,则sin2α=()A.B.C.﹣ D.﹣【考点】GF:三角函数的恒等变换及化简求值.【分析】法1°:利用诱导公式化sin2α=cos(﹣2α),再利用二倍角的余弦可得答案.法°:利用余弦二倍角公式将左边展开,可以得sinα+cosα的值,再平方,即得sin2α的值【解答】解:法1°:∵cos(﹣α)=,∴sin2α=cos(﹣2α)=cos2(﹣α)=2cos2(﹣α)﹣1=2×﹣1=﹣,法2°:∵cos(﹣α)=(sinα+cosα)=,∴(1+sin2α)=,∴sin2α=2×﹣1=﹣,故选:D.【点评】本题考查三角函数的恒等变换及化简求值,熟练掌握诱导公式化与二倍角的余弦是关键,属于中档题.7.已知数列{a n}的通项公式为a n=(n∈N+),其前n项和S n=,则直线+=1与坐标轴所围成三角形的面积为()A.36 B.45 C.50 D.55【考点】8E:数列的求和;IE:直线的截距式方程.【分析】利用裂项相消法求出S n,由S n=求出n值,从而得到直线方程,易求该直线与坐标轴的交点,利用三角形面积公式可得答案.【解答】解:a n==,则S n=1﹣+=1﹣,由S n=,即1﹣=,解得n=9,所以直线方程为,令x=0得y=9,令y=0得x=10,所以直线与坐标轴围成三角形面积为×10×9=45.故选B.【点评】本题考查裂项相消法求数列的前n项和、考查直线的截距式方程、三角形面积公式,属中档题.8.已知A(3,﹣1),B=(x,y),C(0,1)三点共线,若x,y均为正数,则+的最小值是()A.B.C.8 D.24【考点】7F:基本不等式.【分析】根据题意,由A、B、C的坐标计算可得向量、的坐标,结合三点共线可得2x+3(y﹣1)=0,变形可得2x+3y=3,进而分析可得+=(2x+3y)(+)=(12++),由基本不等式分析可得答案.【解答】解:根据题意,A(3,﹣1),B=(x,y),C(0,1),则=(﹣3,2),=(x,y﹣1),若A、B、C三点共线,则有2x+3(y﹣1)=0,变形可得2x+3y=3,则+=(2x+3y)(+)=(12++)≥(12+2)=8,即+的最小值是8;故选:C.【点评】本题考查基本不等式的性质,关键由向量平行的坐标表示得到x、y的关系.9.某几何体的三视图如图所示,则该几何体的体积为()A.B.C. D.【考点】LF:棱柱、棱锥、棱台的体积;L!:由三视图求面积、体积.【分析】该几何体由一个圆柱和半个圆锥构成,半圆锥和圆柱的底面半径均为1,半圆锥的高为2,圆柱的高为2,代入圆锥和圆柱的体积公式,可得答案.【解答】解:该几何体由一个圆柱和半个圆锥构成,半圆锥和圆柱的底面半径均为1,半圆锥的高为2,圆柱的高为2,故组合体的体积:,故选B.【点评】本题考查的知识点是圆锥的体积和表面积,圆柱的体积和表面积,简单几何体的三视图,难度中档.10.已知圆C:(x﹣1)2+(y﹣2)2=2与y轴在第二象限所围区域的面积为S,直线y=2x+b分圆C的内部为两部分,其中一部分的面积也为S,则b=()A.B.±C.D.±【考点】J9:直线与圆的位置关系.【分析】由题意,圆心到直线y=2x+b的距离为1,建立方程,即可得出结论.【解答】解:由题意,圆心到直线y=2x+b的距离为1,∴=1,∴b=±,故选:D.【点评】本题考查点到直线的距离公式,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.11.已知函数f(x)=ln(e x+e﹣x)+x2,则使得f(2x)>f(x+3)成立的x的取值范围是()A.(﹣1,3)B.(﹣∞,﹣3)∪(3,+∞)C.(﹣3,3)D.(﹣∞,﹣1)∪(3,+∞)【考点】6E:利用导数求闭区间上函数的最值.【分析】先求出+2x,再由f(x)为偶函数,且在(0,+∞)上单调递增,故f(2x)>f(x+3)等价于|2x|>|x+3|,解之即可求出使得f(2x)>f(x+3)成立的x的取值范围.【解答】解:∵函数f(x)=ln(e x+e﹣x)+x2,∴+2x,当x=0时,f′(x)=0,f(x)取最小值,当x>0时,f′(x)>0,f(x)单调递增,当x<0时,f′(x)<0,f(x)单调递减,∵f(x)=ln(e x+e﹣x)+x2是偶函数,且在(0,+∞)上单调递增,∴f(2x)>f(x+3)等价于|2x|>|x+3|,整理,得x2﹣2x﹣3>0,解得x>3或x<﹣1,∴使得f(2x)>f(x+3)成立的x的取值范围是(﹣∞,﹣1)∪(3,+∞).故选:D.【点评】本题考查实数的取值范围的求不地,是中档题,解题时要认真审题,注意导数性质的合理运用.12.设函数f(x)在R上的导函数为f′(x),且2f(x)+xf′(x)>x2,下面的不等式在R内恒成立的是()A.f(x)>0 B.f(x)<0 C.f(x)>x D.f(x)<x【考点】63:导数的运算.【分析】对于这类参数取值问题,针对这些没有固定套路解决的选择题,最好的办法就是排除法.【解答】解:∵2f(x)+xf′(x)>x2,令x=0,则f(x)>0,故可排除B,D.如果f(x)=x2+0.1,时已知条件2f(x)+xf′(x)>x2成立,但f(x)>x 未必成立,所以C也是错的,故选A故选A.【点评】本题考查了运用导数来解决函数单调性的问题.通过分析解析式的特点,考查了分析问题和解决问题的能力.二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)13.已知||=1,||=,且⊥(﹣),则向量与向量的夹角是.【考点】9S:数量积表示两个向量的夹角.【分析】由条件利用两个向量垂直的性质、两个向量的数量积的定义求得cosθ的值,可得向量与向量的夹角θ的值.【解答】解:设向量与向量的夹角是θ,则由题意可得•(﹣)=﹣=1﹣1××cosθ=0,求得cosθ=,可得θ=,故答案为:.【点评】本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于基础题.14.已知直线x﹣y+2=0及直线x﹣y﹣10=0截圆C所得的弦长均为8,则圆C的面积是25π.【考点】J9:直线与圆的位置关系.【分析】判断两条直线为平行直线,求出两平行直线的距离,得到圆心到直线的距离,根据半径,半弦以及圆心距之间的关系求圆的半径即可.【解答】解:∵直线x﹣y+2=0与直线x﹣y﹣10=0平行,且截圆C所得的弦长均为8,∴圆心到两直线的距离相等,两平行直线的距离d=,即圆心到直线x﹣y+2=0的距离为d=3,则圆的半径R=,故圆C的面积是25π,故答案为:25π.【点评】本题主要考查圆的半径的求解,利用直线和圆的位置关系,求出圆的半径是解决本题的关键.15.已知变量x,y满足的约束条件,若x+2y≥﹣5恒成立,则实数a 的取值范围为[﹣1,1] .【考点】7C:简单线性规划.【分析】由题意作出其平面区域,则x+2y≥﹣5恒成立可化为图象中的阴影部分在直线x+2y=﹣5的上方,从而解得.【解答】解:由题意作出其平面区域,则x+2y≥﹣5恒成立可化为图象中的阴影部分在直线x+2y=﹣5的上方,则实数a的取值范围为[﹣1,1].故答案为:[﹣1,1].【点评】本题考查了简单线性规划,作图要细致认真,属于中档题.16.如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:①函数y=sinx具有“P(a)性质”;②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;③若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f (x)是周期函数.其中正确的是①③④(写出所有正确命题的编号).【考点】3P:抽象函数及其应用.【分析】根据新定义,得出f(x)的周期,结合函数奇偶性的性质即可判断.【解答】解:①∵sin(x+π)=﹣sin(x)=sin(﹣x),∴函数y=sinx具有“P(a)性质”;故①正确;②∵若奇函数y=f(x)具有“P(2)性质”,∴f(x+2)=f(﹣x)=﹣f(x),∴f(x)=f(2﹣x)=﹣f(x﹣2),∴f(x+2)=f(x﹣2),∴f(x)是周期为4的函数,∴f(2015)=f(﹣1)=﹣f(1)=﹣1,故②不正确;③∵若函数y=f(x)具有“P(4)性质”,∴f(x+4)=f(﹣x),∴f(x+2)=f(2﹣x),∴f(x)关于x=2对称,∵图象关于点(1,0)成中心对称,∴f(2﹣x)=﹣f(x),即f(2+x)=﹣f(﹣x),又f(x+2)=f(2﹣x),∴f(x)=f(﹣x),∴f(x)为偶函数,∵图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,∴图象也关于点(﹣1,0)成中心对称,且在(﹣2,﹣1)上单调递减,根据偶函数的对称得出:在(1,2)上单调递增;故③正确;④∵f(x)具有“P(0)性质”和“P(3)性质”,∴f(x)=f(﹣x),f(x+3)=f(﹣x)=f(x),∴f(x)为偶函数,且周期为3,故④正确.故答案为:①③④.【点评】本题考查了对新定义的理解与应用,函数周期性,奇偶性的性质,属于中档题.三、解答题(本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(12分)(2017•白银区校级一模)等差数列{a n}的各项均为正数,a1=1,前n项和为S n;数列{b n}为等比数列,b1=1,且b2S2=6,b2+S3=8.(1)求数列{a n}与{b n}的通项公式;(2)求{a n•b n}的前n项和T n.【考点】8M:等差数列与等比数列的综合;8E:数列的求和.【分析】(1)设等差数列{a n}的公差为d,d>0,{b n}的公比为q,运用等差数列和等比数列的通项公式和求和公式,解方程可得公差和公比,即可得到所求通项公式;(2)求得a n•b n=n•2n﹣1.运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.【解答】解:(1)设等差数列{a n}的公差为d,d>0,{b n}的公比为q,则a n=1+(n﹣1)d,b n=q n﹣1.由b2S2=6,b2+S3=8,有q(2+d)=6,q+3+3d=8,解得d=1,q=2,或q=9,d=﹣(舍去),故a n=n,b n=2n﹣1.(2)a n•b n=n•2n﹣1.前n项和为T n=1•20+2•21+3•22+…+n•2n﹣1,2T n=1•21+2•22+3•23+…+n•2n.两式相减可得﹣T n=1+21+22+…+2n﹣1﹣n•2n=﹣n•2n.化简可得T n=1+(n﹣1)•2n.【点评】本题考查等差数列和等比数列的通项公式和求和公式的运用,考查方程思想,以及数列的求和方法:错位相减法,考查化简整理的运算能力,属于中档题.18.(12分)(2016•合肥二模)在△ABC中,三个内角A,B,C所对的边分别为a,b,c,已知函数为偶函数,(1)求b;(2)若a=3,求△ABC的面积S.【考点】HP:正弦定理;GI:三角函数的化简求值.【分析】(1)利用三角函数的辅助角公式进行化简,结合三角函数是偶函数,建立方程关系进行求解即可.(2)根据正弦定理先求出A,然后根据三角形的面积公式进行求解即可.【解答】解:(1)在△ABC中,由f(x)为偶函数可知,所以又0<B<π,故所以…(6分)(2)∵,b=,∴由正弦定理得sinA==,∴A=或,当A=时,则C=π﹣﹣=,△ABC的面积S==当时,则C=π﹣﹣==,△△ABC的面积S===…(12分)【点评】本题主要考查三角函数的正弦定理的应用以及三角形面积的计算,根据正弦定理是解决本题的关键.19.(12分)(2017•白银区校级一模)某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期的图象时,列表并填入的部分数据如下表:(Ⅰ)求x1,x2,x3的值及函数f(x)的表达式;(Ⅱ)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,求函数y=f(x)•g(x)在区间(0,)的最小值.【考点】HI:五点法作函数y=Asin(ωx+φ)的图象;HJ:函数y=Asin(ωx+φ)的图象变换.【分析】(Ⅰ)由φ=0,φ=0可得ω,φ的值,由x1﹣=;x 2﹣=; x 3﹣=2π可得:x 1,x 2,x 3的值,又由Asin ()=2可求A 的值,从而求得解析式f (x )=2sin (x ﹣).(Ⅱ)先求解析式g (x )=f (x )=2cos (),从而可得解析式y=f (x )•g(x )=2sin (x ﹣),即可求解.【解答】(本小题满分13分)解:(Ⅰ)由φ=0,φ=0可得:ω=,φ=﹣,…(2分)由x 1﹣=; x 2﹣=; x 3﹣=2π可得:x 1=,x 2=,x 3=, 又∵Asin ()=2,∴A=2.∴f (x )=2sin (x ﹣),…(6分)(Ⅱ)由f (x )=2sin (x ﹣)的图象向左平移π个单位,得g (x )=f (x )=2sin (x ﹣+)=2cos ()的图象,…(8分)∴y=f (x )•g (x )=2×2sin ()cos ()=2sin (x ﹣)…(10分)∵x ∈(0,)时,x ﹣∈(﹣,π)∴当x ﹣=﹣时,即x=时,y min =﹣2,…(13分)注:若用运算,请参照给分.【点评】本题主要考察了五点法作函数y=Asin (ωx +φ)的图象,函数y=Asin (ωx +φ)的图象变换,三角函数的图象与性质,属于中档题.20.(12分)(2017•白银区校级一模)将边长为2的正方形ABCD 沿对角线BD折叠,使得平面ABD ⊥平面CBD ,AE ⊥平面ABD ,且AE=.(1)求证:DE ⊥AC .(2)求DE 与平面BEC 所成角的正切值.(3)直线BE上是否存在一点M,使得CM∥平面ADE?若存在,求点M的位置;若不存在,请说明理由.【考点】MI:直线与平面所成的角;LS:直线与平面平行的判定;LX:直线与平面垂直的性质.【分析】(1)以A为坐标原点,AB,AD,AE所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,求出所用点的坐标,然后利用=(0,﹣2,)•(1,1,)=0,可知DE⊥AC;(2)求出平面BCE的法向量为,设DE与平面BEC所成的角为θ,由sinθ=|cos<>|=,再求出cosθ,利用商的关系可得tanθ;(3)假设存在点M使得CM∥平面ADE,且,由此向量等式求出M的坐标,得到,再由AB⊥平面ADE,结合求得λ值得答案.【解答】(1)证明:以A为坐标原点,AB,AD,AE所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,则E(0,0,),B(2,0,0),D(0,2,0).取BD的中点F并连接CF,AF.由题意得,CF⊥BD且AF=CF=.又∵平面BDA⊥平面BDC,∴CF⊥平面BDA,∴C(1,1,),∴=(0,﹣2,),=(1,1,).∵=(0,﹣2,)•(1,1,)=0,∴DE⊥AC;(2)解:设平面BCE的法向量为=(x,y,z),则,令x=1,得=(1,﹣1,).设DE与平面BEC所成的角为θ,则sinθ=|cos<>|=,∴;(3)解:假设存在点M使得CM∥平面ADE,且,∵,∴,得M(2λ,0,),∴,又AB⊥平面ADE,∴=(2,0,0)为平面ADE的一个法向量.∵CM∥平面ADE,∴,即.即2(2λ﹣1)=0,∴λ=.故点M为BE的中点时,CM∥平面ADE.【点评】本题考查直线与平面平行的判定,考查直线与平面垂直的性质,训练了利用空间向量求线面角,是中档题.21.(12分)(2016•乌鲁木齐模拟)已知函数f(x)=e x+ln(x+1).(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;(Ⅱ)当x≥0时,f(x)≥ax+1成立,求实数a的取值范围.【考点】6E:利用导数求闭区间上函数的最值;6H:利用导数研究曲线上某点切线方程.【分析】(Ⅰ)由题意f(0)=1,,由此利用导数的几何意义能求出y=f(x)在点(0,f(0))处的切线方程.(Ⅱ)令g(x)=f(x)﹣ax﹣1,则,令,则,由此利用分类讨论思想和导数性质能求出实数a的取值范围.【解答】解:(Ⅰ)f(0)=e0+ln(0+1)=1,,∴y=f(x)在点(0,f(0))处的切线方程为:y﹣1=2(x﹣0),即y=2x+1.…(Ⅱ)令g(x)=f(x)﹣ax﹣1,则令,则,当x≥0时,e x>1,,∴h'(x)>0,∴函数y=h(x)(x≥0)为增函数,∴h(x)≥h(0)=2,∴g'(x)≥2﹣a ī)当a≤2时,2﹣a≥0,∴当a≤2时,g'(x)≥0∴函数y=g(x)(x≥0)为增函数,∴g(x)≥g(0)=0故对∀x≥0,f(x)≥ax+1成立.īī)当a>2时,a﹣1>1,由x≥0时,当x∈(0,ln(a﹣1))知e x+1﹣a<0,即g'(x)<0,∴函数y=g(x),x∈(0,ln(a﹣1))为减函数,∴当0<x<ln(a﹣1)时,g(x)<g(0)=0从而f(x)<ax+1这与题意不符,综上,对∀x≥0,f(x)≥ax+1成立时,实数a的取值范围为(﹣∞,2].…(12分)【点评】本题考查切线方程的求法,考查导数的几何意义的应用,是中档题,解题时要认真审题,注意导数性质和分类讨论思想的合理运用.[选修4-4:坐标系与参数方程]22.(10分)(2017•蚌埠一模)在直角坐标系xOy中,直线l的参数方程为(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ.(I)求直角坐标下圆C的标准方程;(Ⅱ)若点P(l,2),设圆C与直线l交于点A,B,求|PA|+|PB|的值.【考点】QH:参数方程化成普通方程.【分析】(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程,配方可得标准方程.(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1,t2.利用|PA|+|PB|=|t1﹣t2|,即可得出.【解答】解:(I)圆C的方程为ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐标方程:x2+y2=6y,配方为x2+(y﹣3)2=9.(II)直线l的参数方程为(t为参数),代入圆的方程可得:t2﹣7=0,解得t1=,t2=﹣.∴|PA|+|PB|=|t1﹣t2|=2.【点评】本题考查了直线的参数方程及其应用、圆的极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于中档题.。
甘肃省白银十中2016—2017学年第二学期高三年级第一次模拟考试数学(理科)试题

白银十中2016— 2017学年第二学期第一次模拟考试数学(理科)试题第I 卷(选择题,共60分)、选择题(本大题共 12小题,每小题5分,共60分•在每小题给出的四个选项中,只有 一项是符合题目要求的)、 21.已知集合 A={y|y=x }, B={x|y=lg (1 - x ) },则 A A B=([解析]B2•下列函数中,既是偶函数又在区间 (0,+^上单调递增的是(其中正确的命题的个数为(C . 3[解析]C 对于命题①,可运用长方体举反例证明其错误:如图,不妨设 AA 为直线m , CD 为直线n , ABCD 所在的平面为 a, ABC D 所在的平面 为B 显然这些直线和平面满足题目条件,但a 丄B 不成立. 命题②正确,证明如下:设过直线n 的某平面与平面 a 相交于直线I ,则I // n ,由m la 知 m l I ,从而 m l n ,结论正确. 由平面与平面平行的定义知命题③正确. A • [0, 1]B • [0 , 1)C .(十 1)D .(―汽 1]C . y = ig x[解析]D A 中函数 D . y = |x|— 1 y _ X 是偶函数且在(0 , 上单调递减, 2 x 故A 错误;B 中函数是偶函数且在(0 ,+R 上单调递减,故 B 错误;C 中函数不是偶函数,故 C 错误;D 中函数是 偶函数且在(0, + ^上单调递增,故选D. 3. a, ①如果 B 是两个平面,m , n 是两条直线,有下列四个命题:B 那么a 丄B m 丄n ,②如果 m 丄a, n // a ,那么 m 丄n.③如果m? a,那么 ④如果 m / n , all 那么m 与a 所成的角和n 与B 所成的角相等./ 上 ___B . y =A。
甘肃省白银市高三上学期期中数学试卷(理科)

甘肃省白银市高三上学期期中数学试卷(理科)姓名:________班级:________成绩:________一、 选择题 (共 12 题;共 24 分)1. (2 分) (2020 高一下·北京期末) 已知向量,A.1B . -1 C.4 D . -4,满足,则 ( )2. (2 分) 若 A.i B . -i C.1 D . -1,则复数 z 的虚部为( )3. (2 分) 已知向量 满足, 则向量 的夹角为 ( )A.B.C.D.4. (2 分) (2018 高二下·河南月考) 与曲线相切于点A.第 1 页 共 11 页处的切线方程是( )B. C. D. 5. (2 分) (2018·长春模拟) 在等差数列 中, 为前 项和, A. B. C. D.,则()6. (2 分) (2016 高一下·揭西开学考) 若将函数 移后图象的对称轴方程为( )的图象向左平移 个单位长度,则平A.B. C.D.7. ( 2 分 ) (2017 高 一 下 · 宜 昌 期 中 ) 等 比 数 列 {an} 各 项 均 为 正 数 , 且 a5a6+a4a7=54 , 则 log3a1+log3a2+…+log3a10=( )A.8B . 10C . 15D . 208. (2 分) (2018·凯里模拟) 已知的内角 , , 所对的边分别为 , , ,且满足第 2 页 共 11 页,则该三角形为( ) A . 等腰三角形 B . 等腰直角三角形 C . 等边三角形 D . 直角三角形9. (2 分) (2020 高二下·东莞期末) 设函数 能为( )的导函数图象如下图,则函数的图象可A. B. C.第 3 页 共 11 页D.10. (2 分) (2019 高一下·黄山期中) 已知数列 的前 项和 A . 15 B . 16 C . 31 D . 32,则()11. (2 分) (2019 高一下·宁波期中) 若关于 的不等式 取值范围为( )A. B. C. D.有实数解,则实数 的12. (2 分) 在直角坐标系 xOy 中, 分别是与 x 轴、y 轴正方向同向的单位向量,在直角三角形 ABC 中,若,则 k 的可能值个数是( )A.1B.2C.3D.4二、 填空题 (共 4 题;共 4 分)第 4 页 共 11 页13. (1 分) (2017·揭阳模拟) 设 Sn 为等差数列{an}的前 n 项和,且 a3=5,S6=42,则 S9=________.14. (1 分) 在平面直角坐标系 xOy 中,已知角 α 的顶点和点 O 重合,始边与 x 轴的非负半轴重合,终边上一点 M 坐标为,则=________.15. (1 分) (2016 高二上·杨浦期中) 以 AB 为直径的半圆,| |=2,O 为圆心,C 是三等分点,F 是 上的某一点,若 ∥ ,则=________.上靠近点 A 的16. ( 1 分 ) (2018 高 二 下 · 邱 县 期 末 ) 在 ,则 ________.三、 解答题 (共 5 题;共 50 分)中,角17. (10 分) 已知函数.(1) 求函数的单调递减区间;所对的边分别为(2) 若的内角 , , 所对的边分别为 , , ,,,,求.18. (10 分) (2017·渝中模拟) 在等差数列{an}中,公差 d≠0,a1=1,且 a1 , a2 , a5 成等比数列.(1) 求数列{an}的通项公式;(2) 若,求数列{bn}的前 n 项和 Tn .19. (10 分) 在中,角 、 、 所对的边分别为 、 、 ,已知,,且.(1) 求 ;(2) 若,且,求 的值.第 5 页 共 11 页20. (5 分) (2019·黄山模拟) 已知函数 f(x)=lnx+x,直线 l:y=2kx-1 (Ⅰ)设 P(x,y)是 y=f(x)图象上一点,O 为原点,直线 OP 的斜率 k=g(x),若 g(x)在 x∈(m,m+1) (m>0)上存在极值,求 m 的取值范围; (I)是否存在实数 k,使得直线/是曲线 y=f(x)的切线?若存在,求出 k 的值;若不存在,说明理由; (III)试确定曲线 y=f(x)与直线/的交点个数,并说明理由21. (15 分) (2016 高三上·巨野期中) 已知函数 f(x)=kx,(1) 求函数的单调递增区间;(2) 若不等式 f(x)≥g(x)在区间(0,+∞)上恒成立,求 k 的取值范围;(3) 求证:.四、 选考题 (共 2 题;共 20 分)22. (10 分) 在平面直角坐标系 xoy 中,以 O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线 C1 的极坐标方程为,曲线 C2 的参数方程为(1) 求曲线 C1 的直角坐标方程和曲线 C2 的普通方程;(φ 为参数且 0≤φ≤π).(2) 当曲线 C1 和曲线 C2 有两个公共点时,求实数 a 的取值范围.23. (10 分) (2017·泸州模拟) 设函数 f(x)=|x﹣ |+|x+a|(a>0). (1) 证明:f(x)≥4; (2) 若 f(2)<5,求 a 的取值范围.第 6 页 共 11 页一、 选择题 (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题;共 4 分)13-1、 14-1、 15-1、参考答案第 7 页 共 11 页16-1、三、 解答题 (共 5 题;共 50 分)17-1、17-2、 18-1、18-2、第 8 页 共 11 页19-1、 19-2、20-1、第 9 页 共 11 页21-1、21-2、21-3、四、 选考题 (共 2 题;共 20 分)22-1、第 10 页 共 11 页22-2、23-1、23-2、第11 页共11 页。
甘肃省白银十中2017-2018学年高三上学期周考练理科数学试题(第二周) Word版含答案

白银十中2017-2018学年高三第一学期周考练理科数学试题(第二周)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合A ={x |y =2x ,x ∈R },B ={x |x 2-1<0},则A B ()A.(-1,1)B.(0,1)C.(-∞,+∞)D.(0,+∞)2. 设函数f (x )=a x +b cos x ,x ∈R ,则“函数f (x )为奇函数”是“a=1,b =0”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件D.既不充分也不必要条件3. 下列有关的说法正确的是( )A.“若x 2=1,则x =1”的否为:“若x 2=1,则x ≠1”B.“x =-1”是“x 2-5x -6=0”的必要不充分条件C.“在∆ABC 中,a>b ⇔A>B ⇔sinA>sinB ”为真D.若p :∀x>0,x 2>0,则⌝p :∃2000,0x x ≤≤.4. 下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是( ) A.y =x 3 B.y =ln|x | C.y =||x -D.212x y ⎛⎫=⎪⎝⎭5. 定义运算“*”为:a *b =⎩⎪⎨⎪⎧ab ,a <0,2a +b ,a ≥0.若函数f (x )=(x +1)*x ,则该函数的图象大致是( )6.已知函数f (x )=2ax 2+4(a -3)x +5在区间(-∞,3)上是减函数,则a 的取值范围是( ) A .(0,34)B .(0,34]C .[0,34)D .[0,34]7.已知定义在R 上的偶函数f (x )在[0,+∞)上单调递增,且f (1)=0,则不等式f (x -2)≥0的解集是( ). A .[3,+ ∞] B .(-∞,3]C .[1,3]D .(-∞,1]∪[3,+∞)8.已知f (x )=⎩⎪⎨⎪⎧(2-a )x +1,x <1,a x ,x ≥1满足对任意x 1≠x 2,都有1212()[()()]0x x f x f x -->成立,那么a 的取值范围是( ) A .(1,2) B. [32,2)C.+∞(1,)D.32(1,] 9. 设函数f (x )=⎩⎪⎨⎪⎧x 2-6x +6,x ≥0,3x +4,x <0,若互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3),则x 1+x 2+x 3的取值范围是( ) A. ⎝⎛⎭⎫113,6 B.⎝⎛⎭⎫203,263C.⎝⎛⎦⎤113,6D. ⎝⎛⎦⎤203,26310.由方程x |x |+y |y |=1确定的函数y =f (x )在(-∞,+∞)上是 ( ) A .增函数B .减函数C .先增后减D .先减后增11.已知f (x )=⎩⎪⎨⎪⎧(1-2a )x +3a ,x <1,ln x ,x ≥1的值域为R ,那么a 的取值范围是( )A .(-∞,-1] B.⎝⎛⎭⎫-1,12 C.⎣⎡⎭⎫-1,12 D.⎝⎛⎭⎫0,12 12. f (x )是定义在(0,+∞)上的函数,满足f (xy )=f (x )+f (y ),f (3)=1,且1x >时f(x)>0;则不等式f (x )+f (x -6)≤3的解集为( ) A .(6,9] B .(6,+∞) C .(0,9]D .[-3,9]二、填空题(本大题共4小题,每小题5分,共20分.把最终结果写在横线上.)13. 函数y =3-2x -x 2的定义域是________.14.已知定义在R 上的函数f (x )满足f (-x )=-f (x ),f (x +2)=-1f (x ),且当x ∈[0,1]时,f (x )=log2(x+1),则f(35)=______________.=+____________.15.函数y x16.有下列4个:①若函数f(x)定义域为R,则g(x)=f(x)-f(-x)是奇函数;②若函数f(x)是定义在R上的奇函数,∀x∈R,f(x)+f(2-x)=0,则f(x)图象关于x=1对称;③已知x1和x2是函数定义域内的两个确定的数(x1<x2),若f(x1)>f(x2),则f(x)在定义域内单调递减;④若f(x)是定义在R上的奇函数,f(x+2)也是奇函数,则f(x)是以4为周期的周期函数.其中,正确是________(把所有正确结论的序号都填上).参考答案一、选择题(本大题共8小题,每小题7分,共56分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.解析:A [∵A =R ,B ={x |-1<x <1},∴AB =(-1,1) ,故选A.]2. 解析:B [当a=1,b =0时,函数f (x )为奇函数,反之不成立,故选B.]3. 解析:C [根据原与其逆否等价,具有共同的真假性,故选C.]4. 解析:B [A 为奇函数,B ,C ,D 为偶函数,B 在(0,+∞)上增, C 、D 在(0,+∞)上单减,故选B.]5. 解析:D [f (x )=(x +1)*x =⎩⎪⎨⎪⎧x (x +1)(x <-1),22x +1(x ≥-1).故选D.]6.解析 D 当a =0时,f (x )=-12x +5,在(-∞,3)上是减函数,当a ≠0时,由⎩⎨⎧a >0,-4(a -3)4a ≥3,得0<a ≤34,综上a 的取值范围是0≤a ≤34.7. 解析:D 由已知可得x -2≥1或x -2≤-1,解得x ≥3或x ≤1,∴所求解集是(-∞,1]∪[3,+∞).8.解析:B 由已知条件得f (x )为增函数, ∴⎩⎪⎨⎪⎧2-a >0,a >1,(2-a )×1+1≤a ,解得32≤a <2,∴a 的取值范围是[32,2).9. 解析:A [函数f (x )=⎩⎪⎨⎪⎧x 2-6x +6,x ≥0,3x +4,x <0的图象,如图,不妨设x 1<x 2<x 3,则x 2,x 3关于直线x =3对称,故x 2+x 3=6,且x 1满足-73<x 1<0;则x 1+x 2+x 3的取值范围是:-73+6<x 1+x 2+x 3<0+6;即x 1+x 2+x 3∈⎝⎛⎭⎫113,6.故选A.]10.解析:B [①当x ≥0且y ≥0时, x 2+y 2=1,②当x >0且y <0时,x 2-y 2=1, ③当x <0且y >0时,y 2-x 2=1, ④当x <0且y <0时,无意义.由以上讨论作图如右,易知是减函数.] 11.解析:选C 要使函数f (x )的值域为R ,需使⎩⎪⎨⎪⎧1-2a >0,ln 1≤1-2a +3a ,∴⎩⎪⎨⎪⎧a <12,a ≥-1,∴-1≤a <12. 即a 的取值范围是⎣⎡⎭⎫-1,12. 12.解析:A 方法一:2=1+1=f (3)+f (3)=f (9),f(27)=3,由f (x )+f (x -6)≤3,可得f [x (x -6)]≤f (27),因为f (x )是定义在(0,+∞)上的增函数,所以有060(6)27x x x x >⎧⎪->⎨⎪-≤⎩解得6<x ≤9.方法二:由题意可知3()log f x x =满足所有性质,代入求解即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年甘肃省白银十中高三(上)期中数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U=R,A={x|y=lg(2x﹣x2)},B={y|y=cos x},则图中阴影部分表示的区间是()A.[﹣1,2)B.(﹣1,2)C.(﹣∞,﹣1)∪[2,+∞)D.(﹣∞,﹣1]∪[2,+∞)2.若点P在角的终边上,且P的坐标为(﹣1,y),则y等于()A.B.C.D.3.给出以下四个判断,其中正确的判断是()A.命题p:∃α∈R,使幂函数y=xα图象经过第四象限;命题q:在锐角△ABC中,sinA>cosB,则p∧q为真B.命题:“正切函数y=tan x在定义域内为增函数”的逆否命题为真C.在区间(a,b)连续的函数f(x),f(a)•f(b)<0是f(x)在区间(a,b)内有零点的充要条件D.命题p:函数f(x)=x2﹣2x仅有两个零点,则¬p是真命题4.一个扇形OAB的面积是1cm2,它的周长是4cm,则弦长AB=()A.2 B.2sin 1 C.2sin 2 D.sin 15.已知α∈(,π),sin(α+)=,则=()A.B.C.D.6.关于函数y=tan(2x﹣),下列说法正确的是()A.最小正周期为πB.是奇函数C.在区间上单调递减D.为其图象的一个对称中心7.已知x1=dx,x2=e﹣1.1(其中e为自然对数的底数),实数x3满足,则x1,x2,x3的大小关系为()A.x1>x2>x3B.x2>x1>x3C.x3>x2>x1D.x3>x1>x28.把函数y=sin2x的图象向左平移个单位长度,再把函数图象上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=f(x)的图象,则函数y=f(x)的图象上最高点与最低点之间的距离的最小值为()A. B.C. D.9.如图放置的边长为1的正方形PABC沿x轴正方向滚动.设顶点P(x,y)的轨迹方程是y=f(x),设y=f(x)在其两个相邻零点间的图象与x轴所围区域为S,则直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数图象大致为()A.B.C.D.10.已知函数f(x)=的图象上恰好有两对关于原点对称的点,则实数a的取值范围是()A.(4,+∞)B.(﹣∞,0)∪(4,+∞)C.(0,4)D.(﹣∞,0)11.函数f(x)=﹣2ax+2a+1图象经过四个象限的必要而不充分条件是()A.﹣<x<﹣B.﹣2<a<0 C.﹣<a<﹣D.﹣1<a<﹣12.设函数f(x)(x∈R)满足f(﹣x)=f(x),f(x)=f(2﹣x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)﹣f(x)在上的零点个数为()A.6 B.7 C.8 D.9二、填空题(本大题共4小题,每小题5分,共20分,把最终答案填在题中的横线上)13.函数y=x与f(x)=2﹣x2围成的封闭图形的面积为.14.已知sinα﹣cosα=﹣,π<α<,求tanα的值.15.函数f(x)是定义在[﹣4,4]上的偶函数,其在[0,4]上的图象如图所示,那么不等式<0的解集为16.已知定义在R上的函数f(x)满足:f(x)>0,f(x)•f(y)=f(x+y),且f(1)=,当x∈(0,+∞)时f(x)<1,关于x的不等式f(a)•f(﹣2﹣xe x)﹣4>0(其中e为自然对数的底数)恒成立,则实数a的取值范围为.三、解答题(本大题共6小题,共70分,解答必须写出必要的文字说明、证明过程或演算步骤)17.(1)计算:﹣lg0.4﹣2lg0.5﹣14×(2)已知P(sinα,cosα)在直线y=x,求+2sinαcosα的值.18.已知函数f(x)=(sinx+cosx)2+cos2x.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.19.已知函数f(x)=x3+bx2+cx在x=1处的切线方程为12x+y﹣1=0.(1)求b,c的值;(2)若方程f(x)﹣m=0有三个解,求m的取值范围.20.已知函数f(x)=sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为.(1)求的值;(2)求函数g(x)=f(x)+f(x+)的对称轴与单调区间.21.已知函数f(x)=ax2﹣(a+2)x+lnx(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程(2)若对任意x1,x2∈(0,+∞),x1<x2,有f(x1)+2x1<f(x2)+2x2恒成立,求a的取值范围.22.己知函数f(x)=ae x+x2,g(x)=sin+bx,直线l与曲线y=f(x)切于点(0,f(0))且与曲线y=g(x)切于点(1,g(1)).(I)求a,b的值和直线l的方程.(Ⅱ)证明:f(x)>g(x)2016-2017学年甘肃省白银十中高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U=R,A={x|y=lg(2x﹣x2)},B={y|y=cos x},则图中阴影部分表示的区间是()A.[﹣1,2)B.(﹣1,2)C.(﹣∞,﹣1)∪[2,+∞)D.(﹣∞,﹣1]∪[2,+∞)【考点】Venn图表达集合的关系及运算.【分析】根据定义得到阴影部分的集合为∁U(A∪B),求出集合A,B的等价条件,结合集合的基本运算进行求解即可.【解答】解:由题意知,A={x|2x﹣x2>0}={x|0<x<2},B={y|﹣1≤y≤1},A∪B={x|﹣1≤x<2},则∁U(A∪B)即图中阴影部分所表示的区间,区间为(﹣∞,﹣1)∪[2,+∞),故选C.2.若点P在角的终边上,且P的坐标为(﹣1,y),则y等于()A.B.C.D.【考点】任意角的三角函数的定义.【分析】由条件利用任意角的三角函数的定义、诱导公式,求得y的值.【解答】解:∵点P在角的终边上,且P的坐标为(﹣1,y),∴tan(﹣)=﹣tan=﹣tan=﹣=,∴y=,故选:B.3.给出以下四个判断,其中正确的判断是()A.命题p:∃α∈R,使幂函数y=xα图象经过第四象限;命题q:在锐角△ABC中,sinA >cosB,则p∧q为真B.命题:“正切函数y=tan x在定义域内为增函数”的逆否命题为真C.在区间(a,b)连续的函数f(x),f(a)•f(b)<0是f(x)在区间(a,b)内有零点的充要条件D.命题p:函数f(x)=x2﹣2x仅有两个零点,则¬p是真命题【考点】命题的真假判断与应用.【分析】通过幂函数的性质判断A的正误;正切函数的单调性判断B的正误;零点判定定理以及充要条件判断C的正误;函数的零点个数判断D的正误;【解答】解:对于A,因为幂函数y=xα图象恒不过第四象限角,命题p是假命题;命题q 是真命题,则p∧q为假命题;对于B,正切函数y=tan x在每个周期内为增函数,故命题为假;对于C,f(a)•f(b)<0是f(x)在区间(a,b)内有零点的充分不必要条件;对于D,做出y=x2和y=2x,可知x=0时02﹣20<0,x=﹣1时,(﹣1)x2﹣2﹣1>0,可知x ∈(﹣1,0),x=2,x=4也是函数的零点,有三个交点,故命题p为假,¬p是真命题;故选:D.4.一个扇形OAB的面积是1cm2,它的周长是4cm,则弦长AB=()A.2 B.2sin 1 C.2sin 2 D.sin 1【考点】扇形面积公式.【分析】由已知利用扇形面积公式,可求扇形的半径和弧长,过O作OH⊥AB于H,解三角形即可得解AB的值.【解答】解:设扇形的半径为r cm,弧长为l cm,则:,解得:,∴圆心角α==2.如图,过O作OH⊥AB于H,则∠AOH=1 rad.∴AH=1•sin 1=sin 1(cm),∴AB=2sin 1(cm).故选:B.5.已知α∈(,π),sin(α+)=,则=()A.B.C.D.【考点】两角和与差的正弦函数.【分析】由已知利用同角三角函数基本关系式可求cos(α+)的值,进而利用诱导公式可求的值.【解答】解:∵α∈(,π),α+∈(,),sin(α+)=,∴cos(α+)=﹣=﹣,∴=sin(α++)=cos(α+)=﹣.故选:C.6.关于函数y=tan(2x﹣),下列说法正确的是()A.最小正周期为πB.是奇函数C.在区间上单调递减D.为其图象的一个对称中心【考点】正切函数的奇偶性与对称性.【分析】根据正切函数的图象与性质,求出函数y=tan(2x﹣)的最小正周期,判断它的奇偶性以及单调性、对称中心.【解答】解:函数y=tan(2x﹣)最小正周期为T==,A错误;令2x﹣≠+kπ,k∈Z,解得x≠+,k∈Z,∴f(x)的定义域为{x|x≠+,k∈Z},其定义域不关于原点对称,是非奇非偶函数,B错误;又周期函数在其定义域内无单调减区间,∴f(x)无单调减区间,C错误;令2x﹣=,k∈Z,解得x=+,k∈Z,∴f(x)的对称中心为(﹣+,0),k∈Z;当k=1时,f(x)的对称中心为(,0),D正确.故选:D.7.已知x1=dx,x2=e﹣1.1(其中e为自然对数的底数),实数x3满足,则x1,x2,x3的大小关系为()A.x1>x2>x3B.x2>x1>x3C.x3>x2>x1D.x3>x1>x2【考点】定积分.【分析】分别计算三个数的大小;x1利用定积分计算;x2结合指数函数判断,x3结合函数y=与函数y=lgx的交点进行判断.【解答】解:x1=dx=,x2=e﹣1.1<,实数x3是为函数y=与函数y=lgx的交点的横坐标,由作图可知x3>1.如图:所以x3>x1>x2.故选:D.8.把函数y=sin2x的图象向左平移个单位长度,再把函数图象上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=f(x)的图象,则函数y=f(x)的图象上最高点与最低点之间的距离的最小值为()A. B.C. D.【考点】正弦函数的对称性.【分析】由题意根据正弦函数的平移变换规律可求函数y=f(x)的解析式,利用正弦函数的图象和性质即可利用勾股定理计算得解.【解答】解:把函数y=sin2x的图象向左平移个单位长度得到y=sin(2x+)的图象,再把函数y=sin(2x+)图象上每一点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y=sin(x+)的图象,其周期为2π,最大值为1,最小值为﹣1,可得:最高点与最低点距离为:=.故选:A.9.如图放置的边长为1的正方形PABC沿x轴正方向滚动.设顶点P(x,y)的轨迹方程是y=f(x),设y=f(x)在其两个相邻零点间的图象与x轴所围区域为S,则直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数图象大致为()A.B.C.D.【考点】函数的图象.【分析】沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,先画出y=f(x)最终构成图象,即得到其两个相邻零点间的图象与x轴所围区域为S,再由图象选出直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数图象.【解答】解:由题意得,从顶点A落在x轴上的时候开始计算,到下一次A点落在x轴上,这个过程中四个顶点依次落在了x轴上,而每两个顶点间距离为正方形的边长1,下面考查P点的运动轨迹,知正方形向右滚动,P点从x轴上开始运动的时候,首先是围绕A点运动个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,再以C为圆心,旋转90°,这时候以CP为半径,因此y=f(x)最终构成图象如下:由图得,两个相邻零点间的图象与x轴所围区域S为曲线与x轴围成的封闭图形,则直线x=t从t=0到t=4所匀速移动扫过区域S的面积D与t的函数变化:从O到B面积相同时间内越来越大,D随着t变化得越来越快,从B到D面积相同时间内越来越小,D随着t变化得越来越慢,故D与t的函数变化图象大致为D中的图象,故选:D.10.已知函数f(x)=的图象上恰好有两对关于原点对称的点,则实数a的取值范围是()A.(4,+∞)B.(﹣∞,0)∪(4,+∞)C.(0,4)D.(﹣∞,0)【考点】分段函数的应用;二次函数的性质.【分析】若函数f(x)=的图象上恰好有两对关于原点对称的点,则当x>0时,x2﹣2ax+2a=﹣(﹣x)2即x2﹣ax+a有两个解,解得实数a的取值范围.【解答】解:若函数f(x)=的图象上恰好有两对关于原点对称的点,则当x>0时,x2﹣2ax+2a=﹣(﹣x)2即x2﹣ax+a有两个解,所以,解得a∈(4,+∞).故选:A.11.函数f(x)=﹣2ax+2a+1图象经过四个象限的必要而不充分条件是()A.﹣<x<﹣B.﹣2<a<0 C.﹣<a<﹣D.﹣1<a<﹣【考点】利用导数研究函数的单调性.【分析】由f(x),求导,f′(x)=ax2+ax﹣2a=a(x﹣1)(x+2),由题意可知:f(﹣2)<0,且f(1)>0,即可求得a的取值范围,根据a的取值范围,根据集合的关系,即可求得函数f(x)图象经过四个象限的必要而不充分条件为﹣2<a<0.【解答】解:由f(x)=﹣2ax+2a+1,求导f′(x)=ax2+ax﹣2a=a(x﹣1)(x+2).若a<0,令f′(x)<0,解得:x<﹣2或x>1,令f′(x)>0,解得:﹣2<x<1,由题意可知:f(﹣2)<0,且f(1)>0,,解得:﹣<a<﹣,若a≥0,则无解,∴数f(x)=﹣2ax+2a+1图象经过四个象限的充要条件为{a丨﹣<a<﹣},由题意可知:函数f(x)图象经过四个象限的必要而不充分条件为:﹣2<a<0.故选:B.12.设函数f(x)(x∈R)满足f(﹣x)=f(x),f(x)=f(2﹣x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)﹣f(x)在上的零点个数为()A.6 B.7 C.8 D.9【考点】根的存在性及根的个数判断.【分析】利用函数对称性,周期性得出图象判断即可,注意特殊值的运用.【解答】解:∵当x∈[0,1]时,f(x)=x3.∴当x∈[1,2]时,2﹣x∈[,0,1],∴f(x)=f(2﹣x)=(2﹣x)3,当x∈[0,]时,函数g(x)=|xcos(πx)|,当x∈[,]时,函数g(x)=﹣xcos(πx),∵f(x),g(x)都为偶函数,f(0)=g(0)=0,f(1)=g(1)=1,g()=g()=0据图象可知,函数还在(﹣,0)(0,)(,1)(1,)上各有一个零点,∴共有8个零点故选:C二、填空题(本大题共4小题,每小题5分,共20分,把最终答案填在题中的横线上)13.函数y=x与f(x)=2﹣x2围成的封闭图形的面积为.【考点】定积分.【分析】首先求出两个函数的交点,然后利用定积分表示封闭图形的面积,计算定积分.【解答】解:由得到,所以函数y=x与f(x)=2﹣x2围成的封闭图形的面积为==;故答案为:.14.已知sinα﹣cosα=﹣,π<α<,求tanα的值.【考点】同角三角函数间的基本关系.【分析】利用平方关系和商数关系即可得出.【解答】解:由sinα﹣cosα=﹣,sin2α+cos2α=1,得5cos2α﹣cos α﹣2=0∴cos α=或cos α=﹣∵π<α<,∴cos α<0.∴cos α=﹣,∴sin α=﹣.因此tan α==2.15.函数f(x)是定义在[﹣4,4]上的偶函数,其在[0,4]上的图象如图所示,那么不等式<0的解集为(﹣,﹣1)∪(1,)【考点】偶函数;函数奇偶性的性质.【分析】先求出不等式在[0,4]上的解集,再由偶函数的对称性求出在[﹣4,0)上,不等式的解集,将这2个解集取并集.【解答】解:在[0,1]上,f(x)≥0,cosx>0,不等式不成立.在(1,4]上,f(x)<0,要使不等式成立,必有cosx>0,∴x∈(1,),∴在[0,4]上,不等式的解集是(1,),再由偶函数的对称性知,在[﹣4,0)上,不等式的解集是(﹣,﹣1),∴不等式的解集是(1,)∪(﹣,﹣1).16.已知定义在R上的函数f(x)满足:f(x)>0,f(x)•f(y)=f(x+y),且f(1)=,当x∈(0,+∞)时f(x)<1,关于x的不等式f(a)•f(﹣2﹣xe x)﹣4>0(其中e为自然对数的底数)恒成立,则实数a的取值范围为(﹣∞,﹣).【考点】函数恒成立问题.【分析】利用定义判断函数的单调性,根据函数的单调性把恒成立问题转化为求函数最值问题解决.【解答】解:对于∀x1>x2,f(x1)﹣f(x2)=f(x2+x1﹣x2)﹣f(x2)=f(x2)[f(x1﹣x2)﹣1],又x1﹣x2>0,所以f(x1﹣x2)<1,从而f(x1)﹣f(x2)<0,所以f(x)在R上单调递减.f(0)•f(0)=f(0+0)得f(0)=1或0(舍),f(﹣1)•f(1)=f(﹣1+1)得f(﹣1)=2,从而f(﹣2)=4,所以原不等式f(a)•f(﹣2﹣xe x)﹣4>0等价于f(a﹣2﹣xe x)>f(﹣2)所以a﹣2﹣xe x<﹣2即a<xe x恒成立,令t=xe x,t'=e x(1+x),当x>﹣1时,函数递增,当x<﹣1时,函数递减,所以当x=1时,函数取最小值为﹣,所以a<﹣.故答案为(﹣∞,﹣).三、解答题(本大题共6小题,共70分,解答必须写出必要的文字说明、证明过程或演算步骤)17.(1)计算:﹣lg0.4﹣2lg0.5﹣14×(2)已知P(sinα,cosα)在直线y=x,求+2sinαcosα的值.【考点】运用诱导公式化简求值.【分析】(1)化根式为分数指数幂,然后利用有理指数幂的运算性质和对数的运算性质化简求值;(2)由题意可得tanα,进而利用诱导公式,同角三角函数基本关系式化简求值.【解答】解:(1)原式=()+|(﹣2)3|﹣(lg0.4+lg0.25)﹣14×=+8﹣(﹣1)﹣7=.(2)∵由题意可得:cos,可得:tanα=2,∴+2sinαcosα=+=+=﹣1+=﹣.18.已知函数f(x)=(sinx+cosx)2+cos2x.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.【考点】三角函数的周期性及其求法;三角函数的最值.【分析】(1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性得出结论.(2)利用定义域和值域求得f(x)在区间上的最值.【解答】解:(1)∵f(x)=sin2x+cos2x+2sin xcos x+cos 2x=1+sin 2x+cos 2x=sin(2x+)+1,∴函数f(x)的最小正周期为T==π.(2)由(1)的计算结果知,f(x)=sin(2x+)+1,当x∈[,]时,2x+∈[,],由正弦函数y=sin t在单调递减,在上单调递减.当2x+=,即x=时,f(x)取最大值2;当2x+=,即x=时,f(x)取最小值﹣+1.综上,f(x)在区间上的最大值为2,最小值为﹣+1.19.已知函数f(x)=x3+bx2+cx在x=1处的切线方程为12x+y﹣1=0.(1)求b,c的值;(2)若方程f(x)﹣m=0有三个解,求m的取值范围.【考点】利用导数研究曲线上某点切线方程;根的存在性及根的个数判断.【分析】(1)根据导数几何意义,导数的几何意义、切点坐标的应用,得到关于b,c的方程组,解得即可.(2)利用导数求出函数的单调区间,可得函数的极值,利用方程f(x)﹣m=0有三个解,即可求m的取值范围.【解答】解:(1)∵f'(x)=3x2+2bx+c,∴k=f'(1)=3+2b+c=﹣12①,又∵f(1)=﹣11,∴﹣,11=1+b+c②,由①②解得:b=﹣3,c=﹣9;(2)f'(x)=3x2﹣6x﹣9=3(x+1)(x﹣3),∴f(x)在(﹣∞,﹣1)单调递增,在(﹣1,3)单调递减,在(3,+∞)单调递增.∴f(x)得极大值f(﹣1)=5,极小值为f(3)=﹣27,∵方程f(x)﹣m=0有三个解,∴﹣27<m<5.20.已知函数f(x)=sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为.(1)求的值;(2)求函数g(x)=f(x)+f(x+)的对称轴与单调区间.【考点】正弦函数的单调性.【分析】(1)利用两角差的正弦函数公式化简函数解析式可得f(x)=2sin(ωx+φ﹣),由f(x)是偶函数,可得φ=+kπ(k∈Z),结合范围0<φ<π,可求φ,利用周期公式可求ω,即可求得函数解析式为f(x)=2cos 2x.利用诱导公式,特殊角的三角函数值即可求值得解.(2)利用三角函数恒等变换的应用可得解析式g(x)=2sin(2x+),令2x+=+kπ,k∈Z,即可解得对称轴方程,令﹣+2kπ≤2x+≤+2kπ,即可解得单调递增区间,令+2kπ≤2x+≤+2kπ,解得单调递减区间.【解答】解:(1)f(x)=sin(ωx+φ)﹣cos(ωx+φ)=2[sin(ωx+φ)﹣cos(ωx+φ)=2sin (ωx +φ﹣).因为f (x )是偶函数,则φ﹣=+k π(k ∈Z ), 所以φ=+k π(k ∈Z ),又因为0<φ<π, 所以φ=,所以f (x )=2sin ()=2cos ωx .由题意得=2•,所以ω=2.故f (x )=2cos 2x .因此=2cos=.(2)g (x )=2cos 2x +2cos 2(x +)=2cos 2x +2cos (2x +)=2cos 2x ﹣2sin 2x=2sin (2x +),令2x +=+k π,k ∈Z ,解得对称轴x=﹣+k π,k ∈Z ,令﹣+2k π≤2x +≤+2k π,解得:﹣+k π≤x ≤﹣+k π,k ∈Z ,令+2k π≤2x +≤+2k π,解得:﹣+k π≤x ≤+k π,k ∈Z ,所以函数g (x )的对称轴x=﹣+k π,k ∈Z ,单调递增区间为:[﹣+k π,﹣+k π],k ∈Z ,单调递减区间为:[﹣+k π,+k π],k ∈Z .21.已知函数f (x )=ax 2﹣(a +2)x +lnx(1)当a=1时,求曲线y=f (x )在点(1,f (1))处的切线方程 (2)若对任意x 1,x 2∈(0,+∞),x 1<x 2,有f (x 1)+2x 1<f (x 2)+2x 2恒成立,求a 的取值范围.【考点】利用导数研究曲线上某点切线方程;函数恒成立问题. 【分析】(1)a=1时,求f (x )的导函数,计算曲线y=f (x )在点(1,f (1))处的切线斜率k ,写出该点处的切线方程;(2)由题意设g(x)=f(x)+2x,(x>0),g(x)应是增函数,即g'(x)≥0在(0,+∞)上恒成立,求出a的取值范围.【解答】解:(1)a=1时,f(x)=x2﹣3x+lnx,f(1)=﹣2,∴,∴曲线y=f(x)在点(1,f(1))处的切线斜率k=f'(1)=0;所以在点(1,f(1))处的切线方程为y=﹣2;(2)令g(x)=f(x)+2x=ax2﹣ax+lnx,(x>0);由题意知g(x)在(0,+∞)单调递增,所以g'(x)=2ax﹣a+≥0在(0,+∞)上恒成立,即2ax2﹣ax+1≥0在(0,+∞)上恒成立;令h(x)=2ax2﹣ax+1,(x>0);则①若a=0,h(x)=1≥0恒成立,②若a<0,二次函数h(x)≥0不恒成立,舍去③若a>0,二次函数h(x)≥0恒成立,只需满足最小值,即,解得0<a≤8;综上,a的取值范围是[0,8].22.己知函数f(x)=ae x+x2,g(x)=sin+bx,直线l与曲线y=f(x)切于点(0,f(0))且与曲线y=g(x)切于点(1,g(1)).(I)求a,b的值和直线l的方程.(Ⅱ)证明:f(x)>g(x)【考点】利用导数研究曲线上某点切线方程;利用导数求闭区间上函数的最值.【分析】(Ⅰ)分别求出f(x)、g(x)的导数,求得切线的斜率和切线方程,再由切线唯一,即可求得a,b和切线方程;(Ⅱ)设F(x)=f(x)﹣(x+1)=e x+x2﹣x﹣1,运用导数,求得最小值大于0,再设G(x)=x+1﹣g(x),由正弦函数的值域可得G(x)≥0,即可得到f(x)>g(x),即可得证.【解答】解:(Ⅰ)f′(x)=ae x+2x,g′(x)=cos+b,即有f(0)=a,f′(0)=a,g(1)=1+b,g′(1)=b,曲线y=f(x)在点(0,f(0))处的切线为y=ax+a,曲线y=g(x)在点(1,g(1))处的切线为y=b(x﹣1)+1+b,即y=bx+1.依题意,有a=b=1,直线l方程为y=x+1.(Ⅱ)证明:由(Ⅰ)知f(x)=e x+x2,g(x)=sin+x.设F(x)=f(x)﹣(x+1)=e x+x2﹣x﹣1,则F′(x)=e x+2x﹣1,当x∈(﹣∞,0)时,F′(x)<F′(0)=0;当x∈(0,+∞)时,F′(x)>F′(0)=0.F(x)在(﹣∞,0)单调递减,在(0,+∞)单调递增,故F(x)≥F(0)=0.设G(x)=x+1﹣g(x)=1﹣sin,则G(x)≥0,当且仅当x=4k+1(k∈Z)时等号成立.由上可知,f(x)≥x+1≥g(x),且两个等号不同时成立,因此f(x)>g(x).2016年12月15日。
