在《几何画板》中使用数学公式或符号
几何画板中的勾股定理

几何画板中的勾股定理
勾股定理是数学中非常经典的定理,在几何画板上也有很好的应用。
通过几何画板可以直观地感受勾股定理的几何意义。
我们可以使用几何画板来构造勾股定理中的三角形。
首先,我们需要在画板上画一个直角三角形,即有一个角是90度的三角形。
然后,我们可以将这个直角三角形分成两个部分,一个是以直角为顶点的小三角形,另一个是以直角边为底边的大三角形。
我们可以将大三角形的底边和直角边分别标记为a和b,斜边标记为c。
根据勾股定理,a + b = c。
我们可以使用画板中的直线工具来测量a和b的长度,并使用勾股定理计算出斜边c的长度。
然后,我们可以使用画板中的角度工具来测量三角形中的角度,并确认其中一个角度是90度。
如果在画板中测量的结果与勾股定理中的结果一致,那么我们就成功地验证了勾股定理。
除了验证勾股定理外,几何画板还可以帮助我们探索勾股定理的一些性质。
例如,我们可以将直角三角形旋转90度,得到一个新的三角形,它也是直角三角形。
这个新的三角形的斜边长度和原来的三角形一样,但是它的底边和直角边交换了位置。
根据勾股定理,它们的长度关系仍然成立。
这个简单的旋转操作就展示了勾股定理的对称性。
总之,几何画板是一个非常有用的工具,它可以帮助我们更好地理解和应用勾股定理。
通过用画板构造和验证勾股定理,我们可以更加深入地了解几何学中的基本定理和概念。
几何画板中函数解析

几何画板中函数解析
几何画板中函数解析
Sin (三角函数中的正弦函数)
Cos(三角函数中的余弦函数)
Tan(三角函数中的正切函数)
Arcsin(反三角函数),如sin30=1/2,则arcsin1/2=30
Arcos, arctan 同上
Abs(<数值表达式>) 功能:求表达式的绝对值
sqrt(平方根计算)
log 如果a的x次方等于N(a>0,且a不等于1),那么数X叫做以a为底N的对数(logarithm),记作x=log a N。
其中,a叫做对数的底数N叫做真数,x叫做“以a为底N的对数”。
ln:自然对数:就是指log以e(无理数约等于2.71828………………)为底的对数,b=ln(a)表示e的b次方等于a。
lg : 就是指log以10为底的对数,b=lg(a)表示10的b次方等于a。
注:几何画板中的log就是lg
Sgn: 数学上的符号函数或者计算机语言中的返回函数。
中文名Sgn函数x>0,,sgnx=1 x=0 sgnx= 0 x<0 sgnx=-1
Round:
中文名round函数语法 ROUND(number, num_digits)
参数number 必需。
要四舍五入的数字返回值返回按指定位数进行四舍五入数值
Trunk:中文名trunc函数语法格式TRUNC (date,[fmt])其中 date 为必要参数
数字 TRUNC函数返回处理后的数值
例:=trunk(8.9) 返回的整数部分(8)。
应用几何画板解决初中数学的函数问题

应用几何画板解决初中数学的函数问题
几何画板是一款很好的应用软件,可以帮助初中生解决数学中的一些函数问题。
在初
中数学中,函数是一个很重要的概念,通过画图可以更直观地理解函数的性质和特点。
下
面我将详细介绍如何使用几何画板解决初中数学中的函数问题。
几何画板提供了丰富的几何图形绘制工具,包括直线、射线、线段、角等,可以用来
表示函数关系。
当我们遇到一个函数问题时,首先需要确定函数的表达式或者函数的性质,然后根据这些信息在几何画板上绘制相应的图形。
对于一元一次函数y=ax+b,我们可以通过绘制直线来表示。
我们需要确定直线的斜率a和截距b,并将其绘制在坐标系上。
在绘制时,可以调整直线的斜率和截距的值,观察直线在坐标系上的图像变化。
几何画板还提供了一些特殊函数的绘制工具,如指数函数、对数函数、正弦函数、余
弦函数等。
这些函数在初中数学中也经常出现,通过几何画板可以更好地理解这些函数的
性质和特点。
除了绘制函数图形外,几何画板还可以进行一些简单的运算和问题求解。
对于给定的
函数关系,可以通过几何画板求解函数的零点、极值点、拐点等。
还可以求解两个函数的
交点,求解函数的一些特殊点等。
通过使用几何画板,初中生可以更加直观地理解函数的性质和特点,提高数学学习的
效果。
几何画板的使用方法简单易懂,对于初学者来说也不会造成太大的困扰。
完整版)《几何画板》在初中数学教学中的应用实例

完整版)《几何画板》在初中数学教学中的应用实例几何画板》是一种有效的辅助教学工具,能够帮助初中数学教师实现“数形结合”的教学理念。
它具有很强的实用性,不仅能够减轻教师的工作负担,同时也能够改变教学环境,为问题的有效解决提供便利。
通过利用《几何画板》的大信息量储备,学生可以根据自身的需求进行查阅和研究,从而更好地掌握数学知识。
二、《几何画板》的主要功能几何画板》提供了多种绘图功能,包括画点、画圆、画线等,可以准确制作各种图形。
此外,它还提供了旋转、平移、缩放、反射等图形变换功能,并且具有强大的度量和计算功能,能够动态演示数据变化,制表等。
此外,它还提供了图表功能,可以建立直角坐标系、极坐标系,方便作出直线、二次曲线,绘制点和函数图象。
总之,《几何画板》是一种非常实用的辅助教学工具,可以帮助学生更好地掌握数学知识。
教师可以将其融入到几何学科的教学中去,使原本抽象的知识形象化、生活化,从而提高数学教学质量。
提供了一般软件所具备的编辑功能,同时能为所绘图形添加颜色。
最新版新增加了常用符号及数学公式编辑功能,并支持插入对象功能,如BMP位图、PowerPoint幻灯片、声音(.wav)、电影(.avt)、Excel表格、Word文档等。
甚至可以通过打“包”直接调用应用程序,进行超级链接(网),并可利用剪贴板将绘制图形转换到其它Windows应用程序中,以达到交换信息的目的。
教学中应用实例:例1:在《轴对称》这一节中,通过操作按钮,使学生更直观地感受轴对称的概念与性质。
如图所示,通过将图形沿着轴对称线进行翻转,可以得到对称的图形。
例2:对于“一次函数y=kx+b(k≠0)的性质”的研究,学生需要清楚y=kx+b(k≠0)在k>0或k0时,它的图象经过第一、三象限;当k<0时,它的图象经过第二、四象限。
在老师的演示下,学生可以自己动手作图与观察比较老师作图,从而更轻松地理解一次函数的图及性质。
例3:验证勾股定理。
几何画板计算命令详解
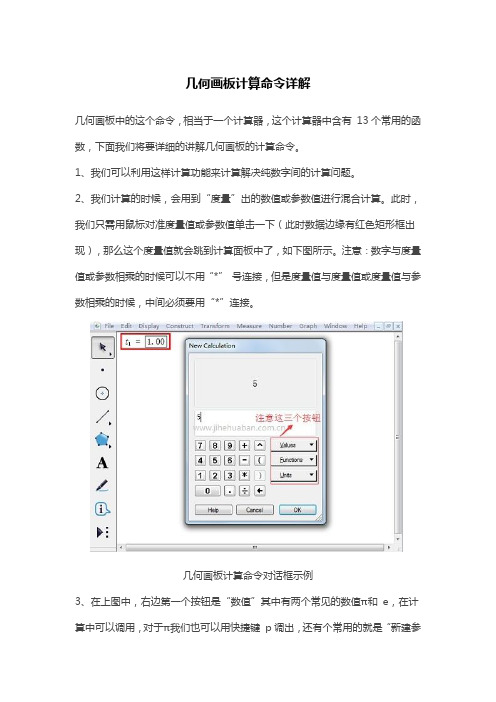
几何画板计算命令详解几何画板中的这个命令,相当于一个计算器,这个计算器中含有13个常用的函数,下面我们将要详细的讲解几何画板的计算命令。
1、我们可以利用这样计算功能来计算解决纯数字间的计算问题。
2、我们计算的时候,会用到“度量”出的数值或参数值进行混合计算。
此时,我们只需用鼠标对准度量值或参数值单击一下(此时数据边缘有红色矩形框出现),那么这个度量值就会跳到计算面板中了,如下图所示。
注意:数字与度量值或参数相乘的时候可以不用“*”号连接,但是度量值与度量值或度量值与参数相乘的时候,中间必须要用“*”连接。
几何画板计算命令对话框示例3、在上图中,右边第一个按钮是“数值”其中有两个常见的数值π和e,在计算中可以调用,对于π我们也可以用快捷键p调出,还有个常用的就是“新建参数”命令,这里“新建参数”命令与上面菜单中的新建参数命令效果一样,都可以新建一个参数,但是,在这里也是非常有用的。
例如,当我们已经写了很长的计算公式时,突然发现少建了一个参数,此时上面菜单中的“新建参数”命令又不可以调用,如果取消编辑的话,前面的输入公式就会白输,此时,我们就会用到数值按钮中的新建参数功能来弥补这一过失。
第二个按钮是“函数”其中,我们把它分成两部分,上半部是三角函数与反三角函数,下半部分是其它常用的函数。
如下图所示。
几何画板计算命令下的常用函数类型示例上半部分我们就不介绍了,我们主要介绍下半部分函数的用法。
1.Abs()这是个绝对值函数;2.Sqrt()这个是开平方函数;3.Ln()与log()函数是常用对数函数;4.sgn()是符号函数(也常把它叫做开关函数),当x>0时,sgn(x)=1;当x=0时,sgn(x)=0;当x<0时,sgn(x)=-1;5.round ()这是个四舍五入函数,最后取整;6.trunc()这个是去尾函数(也常叫取整函数),也就是去掉小数部分。
说明:对于一般的对数,我们可以利用换底公式,用ln()或log()都可以的;对于指数的运算,计算面板中有个“^”符号,它代表指数运算。
几何画板使用方法与技巧 函数图象的控制

(三)如何控制函数曲线的叠加?
1.构造两列波:f1(x)=ASIN(Bx+Q)+C 与 f2(x)=BCOS(Ax+Q)+C 在 宽度为H区间上的叠加波 f3(x)=f1(x)+f2(x) 。
方法:用符号函数控制波的宽度H;用x-x1或x-x2替代 自变量x来绘制函数曲线。
2.在x轴上取点X1、X2,度量其横坐标,改标签为x1、x2,并作 点X1、X2的动画按钮;
选弧度 返回
主菜单
在参数a上单击 右键、取属性
2. 建参数、定范围
请单击
单击新建参数/输入名称
a=1.0
b=1.0
C=1
10
设定参数的 范围和精度
返回
主菜单
3. 输入函数、绘制图形;
单击图表/绘 制新函数
二、一般函数作图 y1=ax2+bx+c y2=ax3+c y3=asin(bx+ )+c
几何画板使用方法与技巧
函数图象的控制
函数图像的各种控制
(一)函数图像的绘制和参数控制 (二) 如何绘制分段函数的图像?
(三)如何控制函数曲线的叠加?
(四) 如何控制函数曲线的波动?
返回
主菜单
(一)函数图像的绘制和参数控制
返回
主菜单
请单击
1.选择坐标系和弧度制
请单击
单击图表/网 格选项
单击编辑/参数选项
3.绘制新函数:f(x)=(sgn(x-x1)+sgn(x1+H-x))/2*F*sin(Z*(x-x1)) 选粗线和兰色;
拖动点X,或单击动画按钮,观察波的运动效果,改变各系数 参数F、Z、H,可以观看波的变化。
几何画板辅助初中数学教学

几何画板辅助初中数学教学
标记角的方法: (1)依次选中一个角的三个顶点,单击“变换/标 记角度”。 (2)选中某个角的度量值或选中新建参数值(单位 为度或弧度),单击“变换/标记角度”。
3.公式计算: 方法一:选中需要的所有度量值,单击“度量/计
算”,弹出“计算器”对话框,打开“数值”列表 框。
方法二:直接单击“度量/计算”,直接单击画板 上的度量值。
几何画板辅助初中数学教学
例2.8 绘制演示三角形内角和为180度的画板文件.
例2.9 绘制演示勾股定理的画板.
例2.10 在屏幕上画一条直线,度量这条直线的方程,并观 察由于直线的位置的变化而引起的相应直线方程参数的 变化情况.
T以圆心和圆周上的点画圆 两个点
R以圆心和半径画圆
一个点和一条线段
E圆上的弧
三个点
A过三点的弧
三个点
一组点,一个圆或一条弧
N内部
ctrl+P 一个对象和路径上的点
U轨迹
H作图帮助
几何画板辅助初中数学教学
2.构造几何关系
例2.6 绘制演示三角形三条高交于一点的图形.
3.构造三角形中其它图形
例2.7 连接四边形各边的中点.
几何画板辅助初中数学教学
例2.14 用反射变换制作菱形.(方法二) (方法三 旋转60度和-120度)
几何画板辅助初中数学教学
4)缩放变换 。按“固定比”缩放变换:直接输入像与原像缩放 的比值,分子是像值,分母是原像值。 。按“标记比”缩放变换:按事先标记好的缩放中心 和标记比作中心缩放。
几何画板软件在初中二次函数教学中的应用

几何画板软件在初中二次函数教学中的应用
几何画板软件是一种数学教学辅助工具,可以通过绘制图形、几何变换、求解方程等功能,帮助学生更好地理解和掌握数学知识。
在初中二次函数的教学中,几何画板软件可以为学生提供一个图形化的学习环境,帮助学生深入理解二次函数的相关概念和性质,提高数学学科的学习兴趣和成绩。
一、绘制二次函数图像
几何画板软件可以通过绘制坐标系和输入函数公式的方式,快速绘制出二次函数的图像。
比如,我们可以打开几何画板软件,先绘制出二维坐标系,然后在输入框输入二次函数的公式y=ax²+bx+c,设置a、b、c的取值,即可得到二次函数的图像,如图1所示。
通过几何画板软件,不仅可以绘制出二次函数图像,还可以根据具体的需求进行图形调整和变换,比如,平移、缩放、旋转等等。
二、探究二次函数的性质
在学习二次函数过程中,学生需要掌握二次函数的性质,如函数的对称性、解析式中参数的含义等等。
几何画板软件可以通过绘制图形以及相关定理的演示,帮助学生深入理解二次函数的性质和规律。
比如,我们可以利用几何画板软件绘制出二次函数的图像,并通过对称轴的绘制,演示二次函数的对称性。
如图2所示,我们可以绘制出二维坐标系和二次函数y=-x²+4的图像,并在函数图像上绘制出对称轴x=0。
这样,学生可以通过对称轴的演示,理解二次函数的对称性,并进一步分析函数图像的特点和性质。
图2 二次函数对称轴
三、解二次函数方程
在学习初中二次函数时,学生需要掌握利用二次函数将未知数的方程转化成解析式,并通过解析式求出方程的根的方法。
几何画板软件可以通过方程的绘制和演示,帮助学生巩固和加深对二次函数方程的理解和掌握。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在《几何画板》中使用数学公式或符号
发布:佚名时间:2008-12-19 18:22:00 来源:京翰教育中心录入:技艺人气:1166
【文字:大小】
在《几何画板》中使用数学公式或符号
《中国电脑教育报》朱建中
在使用《几何画板》的过程中,可能会经常使用到某些数学公式或符号,当然,可以在Word等软件中先编辑好,然后再粘贴到《几何画板》中,不过如果遇到如图所示的情况恐怕就不行了。
这是因为图中不仅要求显示数学符号,而且还要求这些符号能随着坐标系的变化而变化。
要想达到跟随变化的效果,需要用标签来解决问题,所以我们需要在标签上作点文章。
幸好,《几何画板》提供了简单的数学公式和符号的编辑功能,可以对标签、度量值和计算结果进行编辑修改。
下面我就以把标签改为π为例,说明这一编辑功能的具体操作步骤:
1.任意创建一个对象,接着用小手形状的工具按钮给它标上标签,然后按住数字小键盘上的“NumLock”键不放,与此同时用刚才的工具双击这一标签。
2.在随即弹出的“编辑数学格式文本”对话框中的“数学格式”编辑框中输入“{!:P}”(注意字母“P”一定要大写),然后按[确定]按钮退出。
重新回到《几何画板》中,你会发现原来的标签已经改成了π。
怎么样,是不是很简单啊。
其实,很多符号都可以在《几何画板》中通过编辑命令录入,详见附表。
