心理统计学第二章 统计图表
现代统计与教育心理学 第二章 统计图表
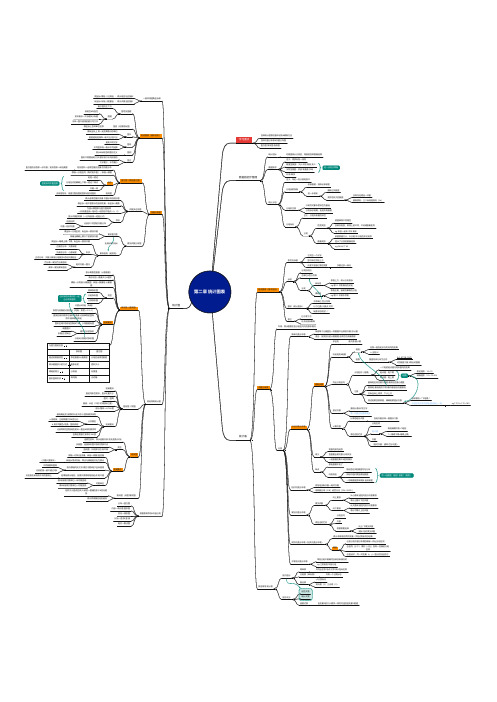
条形图直方图第二章 统计图表学习重点各种统计图表的基本结构&编制方法各种次数分布表&次数分布图直方图条形图线形图数据的初步整理统计指标对数据统计分类后,得到的各种数量结果数据排序含义:顺序标准→排列数值型数据:大小长短高低多少字符型数据:拼音笔画数字母升序/降序进一步划分等级统计分组含义:特征→划分到组别中分组前的准备校核数据:消除记录误差进一步核实删除过失数据变异性较大的数据没有充足理由→不删删除原则:三个标准差准则(3σ)分组时注意以研究对象本质特性为基础分类标志明确,包括所有数据分组标志含义:分组所依据的特性分类性质类别根据事物不同属性反映在组别、种类上的不同,不说明数量差异e g.年龄→老年中年青年数量类别依据取值大小,以分组/不分组的形式排序显示了分类的数量信息e g.96 86 77 63统计表组成要素(基本结构)表号及标题之间空一个汉字居中排在顶线上方长度不宜超过表的宽度字数过多→转行标目分类的项目含单位&百分号等分类纵标目表格上方,统计分析指标e g.表2-1 尽职情况的评定横标目表格左侧,被研究事物的分组e g.表2-1 非常不尽职数字(统计指标)不带单位百分号等以个位数/小数点对齐缺数字的项划“—”表注位于表下方补充说明&解释次数分布表作用:表示数据在各分组区间内的散布情况分类简单次数分布表依据每个分数值在一列数据中出现的次数/总计数适合:按类别分的计数数据连续性的测量数据分组次数分布表编制步骤求全距最大数最小数决定组距&组数组距任意一组的起点与终点间的距离=全距/K 组数数据总体分布为正态K =1.87*(N-1)2/5N 为数据个数 K 取近似整数列出分组区间分组区间(组限)一个组的起点值与终点值间的距离起点值:组下限终点值:组上限组限表述组限:10~19精确组限:9.5~19.499注意最高组区间含最大数据最低组含最小数据最高组/最低组的下限最好是组距的整数倍在纵坐标上排序,下小上大表述组限呈现表格,精确组限登记次数呈现表格→“下组限~”分组区间分界点的值登记到上一组e g.179.5→170~180登记次数画线计数卌/写正字第一次登记后要再核实计算次数计算各组总次数各组次数总和=数据总个数表包含的栏目分组区间组中值每组精确下限+½组距½(精确下限+精确上限)次数(相对次数:频率百分次数)意义将数列排列成序各数据出现次数分布状况一组数据的集中&差异情况缺点原始数据不见了归组效应假设各区间的数据均匀分布用组中值代表各原始数据→忽略数据原来情况造成误差同一组数据,组距↑误差↑(有限)相对次数分布表将各组实际次数→相对次数用频数比率(f/N )或百分比(f/N ×100%)累加次数分布表累加次数向上累加从小数端逐区间进行次数累加表示上限以下的次数向下累加从大数端逐区间进行次数累加表示下限以上的次数表包含的栏目分组区间次数根据需要选择向上/下累加次数实际/相对累加次数双列次数分布表(相关次数分布表)表示有联系的两列变量(同组/质被试的结果)编制①按分组次数分布表的编制→得出分组区间②竖列(小下)横列(小左)各有一变量的分组区间③登记时,同一对变量(x ,y )登记在相应格子不等距次数分布表等距分组不能确切反映实际情况时e g.工资级别年龄分组其他常用统计表按内容分简单表只列出名称地点时序统计指标名称分组表(单向表)只有一个分类标志复合表≥2分类标志双向表(2)三向表(3)按形式分定性式表统计式表函数式表自变量X 的大小顺序→排列对应的因变量Y 数值统计图一般采用直角坐标系横坐标/横轴(分类轴):表示组别/自变量X 纵坐标/纵轴(数值轴):表示次数/因变量Y 组成要素(基本结构)图号及图题置于图的正下方图题说明性&专指性资料复杂→大标题&小标题字体→图中使用的最大号文字图目(刻度线标签)横坐标上各种单位名称图尺横纵坐标上用一定距离表示的单位数据值相差悬殊→断尺法/回尺法图形避免书写文字不同图形线→表示不同结果图例表示&标明各种图形含义图注图形中需要借助文字/数字加以补充说明的文字要少,字号要小次数分布图直方图(等距直方图)矩形面积→连续性随机变量的次数分布直方图的总面积→总次数;矩形面积→该组频数横轴→分组区间(有时组中值);纵轴→频数制作组距→底边分组区间的精确上下限→底边二端点次数→高组织图没有画矩形,使直方图包围的面积成封闭图形各矩形间不留空隙次数多边形图表示连续性随机变量次数分布的线形图横坐标→组中值表示的连续变量;纵坐标→频数为使计算面积与直方图相等→折线画至前一组&后一组的组中值点(x ,0)作用显示次数的轮廓(→分布曲线→经验公式)比较多个同质的次数分布组距相同次数→相对次数累加次数分布图累加直方图横坐标→分组区间;纵坐标→累加次数能看出精确上限以下的累加次数累加曲线(递加线)横坐标→精确上限/下限;纵坐标→累加次数形状正偏态分布:大数端缓负偏态分布:小数端缓正态分布:大数小数端分组数目&各组次数相当相对次数→图尺百分数→累加百分数曲线频率→累加频率曲线其他常用统计图条形图(直条图)表示离散型数据(计数数据)条形长短→数量大小&差异横轴→分类轴计数数据;纵轴→数量轴计量数据类型简单条形图分组条形图分段条形图①比较的长条拼在一起②必须有图例绘制要点尺度从0开始(纵轴)条宽与间隔的比例适当(间隔:条宽=0.5~1)直条的排列顺序可按时间数量比较事物的固有序列具体情况来定图形区域中条形的顶端&下端,少用数据标签调节过长的条形调整图尺折叠法回转法分组&分段复式条形图与直方图的区别描述的数据类型称名数据/计数数据分组的连续性数据表示数据多少的方式直条长短面积大小横轴的意义分类轴刻度值图形直观形状有间隔无间隔圆形图(饼图)绘制要点描述间断性资料,显示比重大小图式:圆周基线:半径(12时时钟指针位置)部分/整体=X/360度绘制要点基线确定后按顺时针由大而小/固有顺序排列分开扇区a 用线条,注明简要文字&百分比b 用不同颜色/线条,图例说明比较两种性质类似的资料→直径&排列顺序同各扇区度数之和等于360度线形图连续性资料,表示函数关系/变化趋势/比较类型折线图:连接条形图中条形顶部中点曲线图:折线修匀后较平滑绘制要点横轴→时间/自变量;纵轴→频数/因变量纵轴从零点开始,零点与横轴相交处为原点(对数尺度除外)线与横轴间无文字/数目线条粗于坐标格线不同线要有图例比较的线一般不超过5条若横轴表示组距,刻度只需表明组距起点/组中值点应画在该组段中点的垂线上对数单位横/纵轴取对数单位→半对数曲线横&纵轴取对数单位→对数曲线散点图(点图散布图)相同大小圆点的多少/疏密→数量的多少&变化趋势表示两现象的相关趋势根据表现作用&内容分类分布→直方图内容→条形图圆形图变化→线形图比较→直条圆线相关→散点图连接矩形右端点。
心理与教育统计学第2章统计图表

表2-10 累加次数分布表
可以将次数、相对次数、累加次数等信息列入一张表中。
相对次数f/N
累加次数
表2-11 次数分布表
2.2.5 双列次数分布表
双列次数分布表又称相关次数分布表,是对有联系的两列变量用同一个表表示其次数分布。
所谓有联系的两列变量,一般是指同一组被试中每个被试两种心理能力的分数或两种心理特点的指标,或同一组被试在两种实验条件下获得的结果。
统计分组,根据被研究对象的特征,将所得数据划分到各个组别中去。
统计表是用来表达研究变量与被说明的事物之间数量关系的表格。它可以将大量数据的分类结果清晰、概括、一目了然地表达出来,便于分析、比较和计算。
表2-1 北京市四街道智力落后患者分布
街道
检查人数
病人数
患病率(‰)
甲
51841
2.1.2 数据排序
数据排序,就是按照某种标准,对收集到的杂乱无章的数据进行排列。
数值大小升序或降序排列
年龄、性别等
数据排序是整理数据最简单的方法
2.1.3 统计分组
数量类别:按数值大小进行分类,并排序。
性质类别:按事物的不同性质进行分类。
分类标志要明确,要能包括所有数据
分组要以被试对象的本质特征为基础。
02
分组表:只按一个标志分组的统计表称为分组表。
表2-2 各校学生数一览表
学校
A校
B校
C校
D校
人数
985
762
893
1051
表2-3 上海市区男幼儿20米跑步用时 资料来源:引自《华东师范大学学报》,1985年第2期第30页
年龄组
3岁~
4岁~
张厚璨《现代心理与教育统计学》书后习题详...
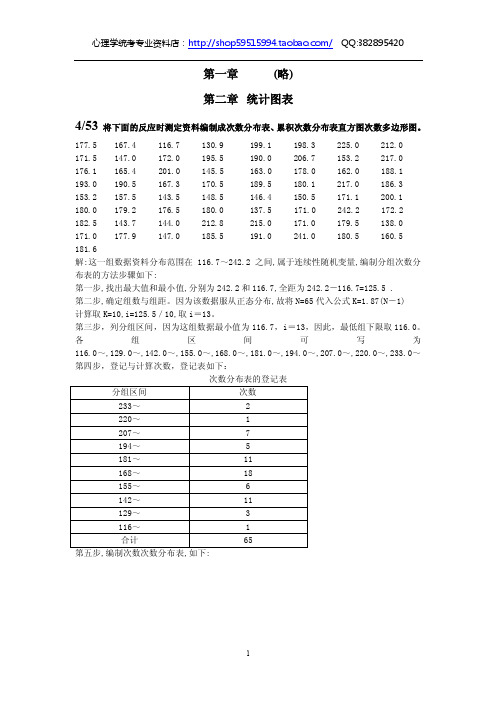
5 91 85
6 48 68
7 55 47
8 82 76
9 32 25
10 75 56
解: (1)用积差相关方法解答如下: A X 86 58 B Y 83 52
7
2 2
被试 1 2
X
Y
XY
7138 3016
7396 3364
6889 2704
心理学统考专业资料店:/ 3 4 5 6 7 8 9 10 79 64 91 48 55 82 32 670 670 89 78 85 68 47 76 25 56 659 6241 4096 8281 2304 3025 6724 1024 5625 48080
QQ:382895420
fXc 67 248 342 416 752 1000 1258 672 432 242 153 84 ∑fXc=5666
X=
fXc = 5666 =36.09
N
157
1 * 157 64 Md=34.5+ 2 *5=36.46 37
答:平均数为 36.09,中数为 36.46。
QQ:382895420 51 48 43
解: i 40 51 48 43 182 T
i i
i i 2 i 2 i
i
40 90.5 51 91.0 48 92.0 43 89.5 90.8 182
S d
ST
解 : 因为5厘米组与10厘米组的标准差单位相同(都是厘米), 但平均数差异很大,5厘米组 标准差直接比较5厘米组和10厘米组的离散程度大小是无意义的,应采用差异系数比较 其离散程度的大小。具体计算如下: s 0.7 CV1 100% 100% 11.1% 6.3 s 1.2 CV2 100% 100% 8.39% 14.3 答:通过比较差异系数可知, 5厘米组的离散程度比10厘米组的离散程度大。
(心理统计-2、3)第二章统计图表

VS
详细描述
折线图特别适合用于表示气温、股价、销 售量等随时间变化的数据。通过折线图, 可以直观地观察到数据的变化趋势和规律 ,有助于进行预测和决策。此外,折线图 还可以用于比较不同时间段的数据,以便 更好地了解数据的动态变化。
04
CATALOGUE
饼图
饼图的定义
01
饼图是一种以圆形表示数据的图 表,每个扇区代表一个分类数据 ,扇区面积的大小表示该分类数 据所占的比例。
柱状图的适用场景
总结词
柱状图适用于展示类别间的比较和趋势,适用于数据量较小 的情况。
详细描述
当需要比较不同类别之间的数值差异时,柱状图是一个很好 的选择。例如,展示不同产品的销售量、不同地区的降雨量 等。此外,当数据量较小,不需要过于复杂的图表时,也可 以使用柱状图来直观地呈现数据。
03
CATALOGUE
纵轴。
绘制点
根据数据点的值,在坐标轴上 绘制相应的点。
添加图例和标题
为了使图表易于理解,需要添 加适当的图例和标题。
散点图的适用场景
探索两个变量之间的关系
识别异常值
当需要了解两个变量之间是否存在某 种关系或趋势时,可以使用散点图进 行初步探索。
散点图可以用于识别异常值,即远离 其他数据点的点,这些点可能对整体 趋势产生影响。
02
饼图可以直观地展示数据的分布 情况,帮助我们快速了解各部分 在整体中所占的比重。
饼图的制作方法
选择数据
选择需要展示的数据,通常为分类数据和 对应的数值。
美化图表
根据需要,可以添加颜色、阴影等效果, 使图表更加美观。
设计布局
确定饼图的标题、图例、数据标签等元素 的位置。
添加标签
现代心理与教育统计-第二章统计图表PPT课件

5
10
15
20
25
图2-2b 某校初二.三班学生学习成绩和人数
.
14
复式纵条图
14 12
10
8
男生
6
女生
4
2
0
差
中
良
优
图2-3a 某校初二.三班男女生学习成绩和人数
.
15
复式横条图
优
良 女生
男生 中
差
0
5
10
15
图2-3b 某校初二.三班男女生学习成绩和人数
.
16
2.圆形图
优 良 中 差
图2-4 某校初二.三班学习成绩比较图
.
9
40 35 30 25 20 15 10
5 0
一年级 二年级 三年级 四年级
女生 男生
图2-1 某高校教育系各年级男女生人数
资料来源:表2-6
.
10
表2-6 某高校教育系各年级男女生人数统计表
一年级
二年级
三年级
四年级
女 男 女 男 女男 女 男
人数 26 33 26 36 24 37 25 35
2
.02
2
90-
92
4
.04
4
85-
87
9
.09
9
80-
82
16
.16
16
75-
77
20
.20
20
70-
72
15
.15
15
65-
67
13
.13
13
60-
62
8
.08
8
55-
《心理统计学》重要知识点

《心理统计学》重要知识点第二章 统计图表简单次数分布表的编制:Excel 数据透视表列联表(交叉表):两个类别变量或等级变量的交叉次数分布,Excel 数据透视表直方图(histogram ):直观描述连续变量分组次数分布情况,可用Excel 图表向导的柱形图来绘制 散点图(Scatter plot ):主要用于直观描述两个连续性变量的关系状况和变化趋向。
条形图(Bar chart ):用于直观描述称名数据、类别数据、等级数据的次数分布情况。
简单条形图:用于描述一个样组的类别(或等级)数据变量次数分布。
复式条形图:用于描述和比较两个或多个样组的类别(或等级)数据的次数分布。
圆形图(circle graph )、饼图(pie graph ):用于直观描述类别数据或等级数据的分布情况。
线形图(line graph ):用于直观描述不同时期的发展成就的变化趋势;第三章 集中量数● 集中趋势和离中趋势是数据分布的两个基本特征。
● 集中趋势:就是数据分布中大量数据向某个数据点集中的趋势。
● 集中量数:描述数据分布集中趋势的统计量数。
● 离中趋势:是指数据分布中数据分散的程度。
● 差异量数:描述数据分布离中趋势(离散程度)的统计量数 ● 常用的集中量数有:算术平均数、众数(M O )、中位数(M d ) 1.算术平均数(简称平均数,M 、X 、Y ):nx X i∑= Excel 统计函数AVERAGE算术平均数的重要特性:(1)一组数据的离均差(离差)总和为0,即0)(=-∑x x i(2)如果变量X 的平均数为X ,将变量X 按照公式bx a y +=转换为Y 变量后,那么,变量Y 2.中位数(median ,M d ):在一组有序排列的数据中,处于中间位置的数值。
中位数上下的数据出现次数各占50%。
3.众数(mode ,M O ):一组数据中出现次数最多的数据。
4.算术平均数、中数、众数之间的关系。
心理统计学重点知识

心理统计学一.描述统计(一)统计图表 1、统计图次数分布图——①直方图:用以矩阵的面积表示连续性随即变量次数分布的图形。
②次数多边形图:一种表示连续性随机变量次数分布的线形图,属于次数分布图。
③累加次数分布图:分为累加直方图和累加曲线图;其中累加曲线的形状大约有三种:一种是曲线的上枝长于下枝(正偏态),另一种是下枝长于上枝(负偏态),第三种是上枝,下枝长度相当(正态分布)。
其他统计图:条形图:用于离散型数据资料; 圆形图:用于间断性资料;线形图:更多用于连续性资料,凡预表示两个变量之间的函数关系,或描述某种现象在时间上的发展趋势,或一种现象随另一种现象变化的情况,用这种方法比较好。
散点图: 2、统计表①简单次数分布表 ②分组次数分布表③相对次数分布表:将次数分布表中各组的实际次数转化为相对次数,即用频数比率表示。
④累加次数分布表⑤双列次数分布表:对有联系的两列变量用同一个表来表示其次数分布。
(二)集中量数 1、算术平均数M1nii XX N==∑优点:反应灵敏;计算严密;计算简单;简明易解;适合于进一步用代数方法演算;较少受抽样变动的影响;缺点:受极端数据的影响;若出现模糊不清的数据时,无法计算平均数; 计算和运用平均数的原则: 同质性原则;平均数与个体数值相结合的原则; 平均数与标准差、方差相结合原则; 性质:①在一组数据中每个变量与平均数之差的总和等于零②在一组数据中,每一个数都加上一个常数C ,所得的平均数为原来的平均数加常数C ③在一组数据中,每一个数都乘以一个常数C ,所得的平均数为原来的平均数乘以常数C 2、中数:Md 按顺序排列在一起的一组数据中居于中间位置的数,即这组数据中,一般数据比它大,一般数据比它小。
注意计算方法;3、众数:Mo 是指在次数分布中出现次数最多的那个数值;三者的关系:正偏态分布中,M>Md>Mo 负偏态分布中,M<Md<MoMo=3Md-2M (自己推导一下)(三)差异量数差异量数就是对一组数据的变异性,即离中趋势特点进行度量和描述的统计量,也称为离散量数。
心理统计学-统计图表

69- 7
66- 3
63- 1
最后一组的累加次数应等于数据的总次数。 60- 1
∑ 100
cf
100 98 95 91 83 72 55 36 22 12 5 2 1 —
cf%
1.00 .98 .95 .91 .83 .72 .55 .36 .22 .12 .05 .02 .01 -
2021/6/16
心理统计学统计值25375赫兹28mm1786ns闪光融合错觉量反应时其他类型统计图表41其他常用的统计表类型分组表标目按一个分类标志分组心理统计学男生26女生24合计50性别不同年级控制组和实验组成绩的人数分布心理统计学复合表横标目按两个或两个以上分组标志进行多层分年级控制组22153033实验组35控制组23134816实验组332933控制组25203520实验组36243010心理统计学心理统计学42直条图条形图简单条形图分组条形图和分段条形图心理统计学102030405060708090第一季度第二季度第三季度第四季度东部西部北部存取款种类各类信用卡活期工资帐户定活两便活期三年以下定期三年以上定期16014012010080604020收入水平1500元以上8001500元300800元300元以下心理统计学绘制要求
︶
纵标目 (主语)
数字
(谓语)
2021/6/16
20
心理统计学
数字 统计表的基本语言。
原则 数位对齐 小数位数一致
空格处理 空白 ‘—’或‘…’ 0
未测或无此项 未发现
实测结果为0或极小数
2021/6/16
21
心理统计学
表体内的数字一般不带单位,百分数也不带百分号(%), 应把单位符号和百分号等归并在栏目中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.制作:编制双列次数分布表,先按照 分组次数分布表的编制方法,分别列出 各变量的分组区间,登记时,每次同一 对变量同时登记在相应的格内。
第三节 次数分布图
一、直方图 直方图就是用一系列宽度相等、高度不一的
矩形表示数据分布的统计图。以矩形的面积 表示连续性随机变量次数分布的图形。 一般用纵轴表示数据的频数,用横轴表示数 据的等距分组点,也就是各分组区间的上限 和下限,有时也使用组中值。
组效应。
三、相对次数分布表
1.含义:相对次数是指各组次数f对数据 总个数N的比值,用符号f/N表示。所有 相对次数之和(Σf/N)等于1。
2.制作:将分组次数分布表的各组次数 化为相对次数,用f/N或f/N×100%作 标志来表示次数,就制成了相对次数分 布表。
四、累加次数分布表(重点加难 点)
1.实际累加次数(cumulative frequency),把各组次数f由下而上或 由上而下依次累加的和,用符号cf表示。
2.相对累加次数(relative cumulative frequency),把各组的相对次数p由下 而上或由上而下依次累加的和,累加之 和为1。
五、双列次数分布表
1.含义:对有联系的两列变量用一个表 表示其次数分布,就称为双列次数分布 表,也称相关次数分布表。
300
200
100
0 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 66 69 72 75
Age in years
(四)散点图p48 用相同大小圆点的多少或疏密表示统计
资料数量的大小以及变化趋势等。
还可以表示相关程度。
100
90
80
70
60
当数据的取值过多时,不适合每一个值 记录一个频次。
将把所有数据先划分为若干个分组区间, 然后将数据按其数值大小划归相应组内, 分别计算各个组别中包括的数据个数, 再用列表形式呈现出来,就构成了分组 次数分布表(grouped frequency table)。
分组次数分布表的制作过程
1.求全距:全距 = 最大值-最小值
1200
1000
800
Under $25
$25 - $49
Income category in thousands
$50 - $74
$75+
条形图与直方图有本质的区别
1.数据类型:条形图—离散数据,直方图—连 续数据。
2.表示数据的方式:条形图—直条的长度
直方图—— 刻度值。
表述组限:10-19,20-29,30-39 精确组限:9.5-19.499,19.5-29.499,
29.5-39.455
5.登记次数 6.计算次数 7.编制分布表,计算组中值 组中值=(表述组限上限+表述组限下
限)/2 例如:求10~14的组中值 (10+14)/ 2=12
例题2-2
有80个员工参加民意调查,四个选项的 人数分别是9、30、10、25、6。要求 制作简单次数分布表。
表2-1 80名员工对部门主管尽职程度调查结果
员工对主管尽职情况的评定 1.非常不尽职 2.不尽职 3.不置可否 4.尽职 5.非常尽职 总计
人数 9* 30 10 25 6 80
二、分组次数分布表
(一)分组前的准备(异常值 和缺失值处理)
核对和校验:消除记录误差,删除一些错 误数据。删除变异性较大的数据应遵循 三个标准差准则
-3σ -2σ -1σ 0 +1σ +2σ +3σ
(二)统计分组应该注意的问题 1.以事物的本质特性为基础(分类依据) 2.分类标志要明确,要能包含所有数据 如:请判断下列分类好不好?
100名学生在某项测验中的成绩分数,把它制作成一个次数分布表。
76.0 88.0 89.0 75.0 79.5 66.0 71.5 77.5 73.5 94.0
77.5 81.0 78.0 84.0 80.5 83.0 83.0 75.0 76.0 79.0
82.0 76.6 78.0 90.0 73.0 87.0 91.0 79.0 88.5 80.0
4.直观形状:条形图——有间隔
直方图——没有间隔
(二)圆形图
以整个圆的面积代表被研究对象的总体, 按照组成部分占总体比重的大小,把圆 面积分成若干扇形,用来表示某一现象 的部分对总体的比例关系。
适合于离散性的资料。
图2.4 某城市居民关注不同类型广告的人数 构成
8% 5% 1% 5%
26%
男
女
优
10
15
中
20
20
差
10
5
表号
标题
顶线 表2-1 80名员工对部门主管尽职程度调查结果
员工对主管尽职情况的评定
人数
表线 1.非常不尽职
9*
2.不尽职
30
3.不置可否
10
标目
4.尽职
25
5.非常尽职
6
总计
80
表注 *表中数据源于xx
标目 数字 底线
四、统计图
统计图(graph或chart) 是用来表达统计指标与被说明的事物之
78---
79
77.5—80.5 |||| |||| |||||||
75---
76
74.5—77.5 |||| ||||||||
72---
73
71.5—74.5 |||| ||||
69---
70
68.5—71.5 |||| ||
66---
67
65.5—68.5 |||
63---
64
62.5—65.5 |
90.5 67.0 80.0 80.0 93.0 82.5 96.0 79.0 85.0 75.5
81.0 83.0 78.5 86.0 83.0 79.5 75.5 80.5 89.5 83.5
85.5 84.0 76.5 84.5 72.0 80.0 89.0 74.5 78.5 82.0
71.0 84.0 75.0 68.5 68.0 82.0 87.5 77.0 76.0 65.0
累加曲线形状
正偏态分布:小端的数据特别多,大端的数 据不是很多,比较分散,表现在曲线上就是 上枝长于下枝。
负偏态分布:大端的数据比较多,小端的数 据不是很多,但比较分散,表现在曲线上就 是下枝长于上枝。
正态分布:中间的数据最多,两头的数据少, 平均数两侧的数据个数相差不多。表现在曲 线上就是上枝和下枝的长度相当。
outline
第一节 数据的初步整理 第二节 次数分布表 第三节 次数分布图 第四节 其他类型的统计图表
重点:
各种统计图表的结构与编制方法 各种次数分布表与分布图的制作 直方图,条形图的区别 线形图折线图的做法
第一节 数据的初步整理
一、数据排序(sort) 排序就是按照某种标准,对收集到的杂
简单次数分布表是依据每一个分数值在 一列数据中出现的次数或总计数资料编 制成的统计表。
特点:对数据资料的来源没有过多要求, 编制过程简单,应用广泛
例题2-1
某公司为评估公司主管人员的绩效,做 民意调查,其中有一道题是:“你认为 本部门现任主管尽职尽责的程度如何?” 有四个答案:
1.非常不尽职;2.不尽职;3.不置可否;4尽职;5.非常尽职。
50
40
30
20
10
20
30
40
50
60
70
80
90
Propensity to leave
55
0.55
0.14
36
0.36
0.1
22
0.22
0.07
12
0.12
0.03
5
0.05
0.01
2
0.02
0.01
1
0.01
1
(二)分组次数分布表的意义与缺点 意义:显示数据的分布状况,集中情
况。 假设:各区间的数据均匀分布,并用
各组的组中值代表各原始数据。 缺点:由于假设所造成的误差称为归
对全世界人类的肤种分类:黄种人;白 种人;黑种人。
(三)分组的标志
1.性质类别
如:按照性别分:男、女
按照年龄分:青年、壮年、老年
按照优劣程度:优、良、中、差
2.数量类别
大小分组
三、统计表
统计表(tabulation)
是用来表达统计指标与被说明的事物之间 关系的表格。统计表具有简洁、清晰、准 确的特点,表中的数据易于比较分析。
间数量关系的图形,是统计数据资料的 可视化显示方式。
35
Y轴名称 30
25 人数
20
图尺
15
10
尺度单位 5
填充图案
轮廓线
基线
图号
非常 不尽 职
不尽 职
不置 可否
尽职
非常 尽职
评价
X轴名称
图1 80名员工对部门主管尽职程度评价条形图
图目 图题
第二节 次数分布表
一、简单次数分布表(simple frequency table)
1.全距 = 98-62 = 36 2.组数K = 1.87×(100-1)0.4 =
11.75 ≈ 12
3.组距 i = 全距÷组数 = 36÷12 = 3 4.分组区间:60.0 ~ (59.5 ~
62.499),63.0 ~ (62.5 ~ 65.499)………… 5.组中值:61、64、…………
60---
61
59.5—62.5 |
次数f 2 3 4 8 11 17 19 14 10 7 3 1 1 ∑f=100
