无机化学原子结构
北师大版无机化学第一章原子结构与元素周期表精品PPT课件

3
• 1732年: 尤拉 (Euler) 提出自然界存在多少种原子,就有多少种元素
• 定义 一种元素的1摩尔质量对核素12C的1摩尔质量
的1/12的比值(国际原子量与同位素丰度委员会1979
年)
• 特征 相对原子质量是纯数
单核素的相对原子质量等于该元素核素的相对原
子质量
多核素元素的相对原子质量等于该元素的天然同
位素相对原子质量的加权平均值
• 计算
Ar= ∑fi Mr,i fi : 同位素分度
不能正确给出许多元素的原子量。如设氢的原子量为1,作 为相对原子质量的标准,已知水中氢和氧的质量比是1:8,若水 分子是由1个氢原子和1个氧原子构成的,氧的原子量是8,若 水分子是由2个氢原子和1个氧原子构成的,氧的原子量便是16。 道尔顿武断地认为,可以从“思维经济原则”出发,认定水分子 由1个氢原子和1个氧原子构成,因而就定错了氧的原子量。
7
1-2-2 核素、同位素和同位素丰度
(1)核素(nuclide)---具有一定质子数和一定中子数的 原子称为一种核素
• 分类
稳定核素 --- 单核素元素和多核素元素
放射性核素 • 核素符号
Байду номын сангаас
162C 质量数
质子数
(2)同位素(isotope)---具有相同核电荷数,不同中子 数的核素互称同位素,这些核素在周期表中占同位置
化学和材料工作者着眼于化学变化,而化学变化则以 原子相互作用为基础的。通常在化学变化中,原子核不发 生变化。那么什么在变呢?电子的运动状态在变,通俗地 说,是核外电子在“跳来跳去”,所以研究核外电子的运动 的规律是研究者探索的重要问题。
天津大学无机化学课件第五章原子结构与元素周期性 共74页PPT资料

例外的还有: 41Nb、 44Ru、 45Rh、 57La、
58Ce、78Pt、89Ac、90Th、91Pa、92U、 93Np
29.11.2019
课件
36
基态原子的价层电子构型
价层——价电子所在的亚层 价层电子构型——指价层的电子分布式
29.11.2019
课件
30
无机化学多媒体电子教案
第五章 原子结构和元素周期性
第三节原子中电子的分布
第三节
原子中电子的分布
29.11.2019
课件
31
5-3-1 基态原子中电子的分布原理
泡利不相容原理——每一个原子轨道,最多
只能容纳两个自旋方向相反的电子.
能量5最-3低-原1理基—态—原原子子为中基态电时子,分电子布尽原可 能地分布在能级较低的理轨道上,使原子处于
课件
29
3. 磁量子数(m)
磁量子数(m)的取值决定于l值,可取(2l+1)个 从-l到+l(包括零在内)的整数。每一个m值代表 一个具有某种空间取向的原子轨道。
4.自旋量子数(ms)
自旋量子数(ms)只有+1/2或-1/2 这两个数值, 其中每一个值表示电子的一种自旋方向(如顺 时针或逆时针方向)。
课件
12
在量子力学中是用波函数和与其对应的 能量来描述微观粒子的运动状态的.
原子中电子的波函数ψ既然是描述电子云
运动状态的数学表达式,而且又是空间坐标的
函数,其空间图象可以形象地理解为电子运动
的空间范围,俗称”原子轨道”.为了避免与经
典力学中的玻尔轨道相混淆,又称为原子轨函
(原子轨道函数之意),亦即波函数的空间图象
激发态(电子处于能
无机化学内容精要及习题 第一章原子结构剖析
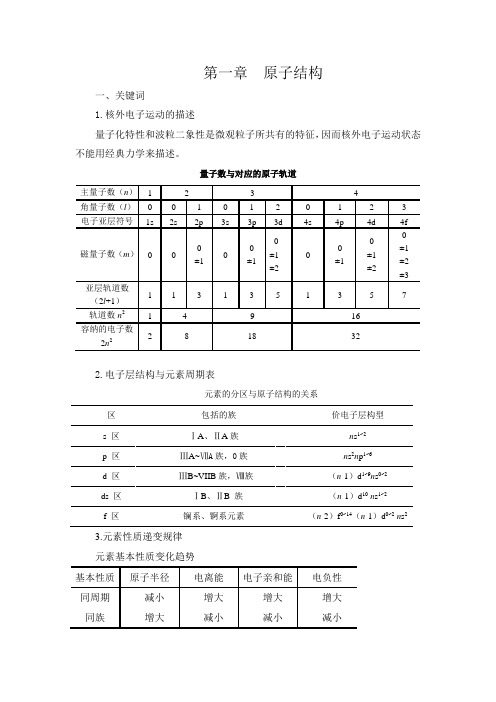
第一章原子结构一、关键词1.核外电子运动的描述量子化特性和波粒二象性是微观粒子所共有的特征,因而核外电子运动状态不能用经典力学来描述。
量子数与对应的原子轨道2.电子层结构与元素周期表元素的分区与原子结构的关系3.元素性质递变规律元素基本性质变化趋势二、学习感悟1.原子结构模型的演变历史给我们的启迪原子结构模型是科学家根据自己的认识,对原子结构的形象描摹。
一种模型代表了人类对原子结构认识的一个阶段。
人类认识原子的历史是漫长的、无尽的,随着科学技术的发展,人类对原子的认识过程还会不断深化。
①化学认识发展的规律和所有科学认识发展的规律一样是继承、积累和突破。
②实验方法是科学研究的一种重要方法,实验手段的不断改进促使化学理论向前发展。
人类对原子结构的认识体现了人类认识自然的历程,向我们提示了一个科学理论发展的模式:实践-认识-再实践-再认识。
2.研究原子结构涉及较深的数学知识和物理知识初学者往往觉得枯燥难懂,因此,学习时重点放在理解,接受相关的基本概念,加上一定的空间想像。
3.结构决定性质,性质体现结构元素的电离能、电子亲和能和电负性在衡量元素的金属性和非金属性强弱时,结果是大致相同的。
但由于元素的电负性的大小是表示分子中原子吸引电子的能力大小,所以它能方便地定性反映元素的某些性质,如:金属性与非金属性、氧化还原性;化合物中化学键的类型、键的极性等,故它在化学领域中被广泛地运用。
而元素的电子亲和能的数值一般较电离能小一个数量级,而且已知的元素的电子亲和能数据较少,测定的准确性也差,所以其重要性不如元素的电离能。
三、难点辅导1.微观粒子运动具有哪些特点?能量是量子化的。
量子化是相对于连续而言,也就是说变化过程是不连续的,是间隔的,是跳跃式的,一个一个的,不连续的。
与宏观物体的逐渐的、连续的运动有很大的区别。
打个比方说,光从微观角度讲就是不连续的,爱因斯坦的光子说中把每一个光子叫做光量子,是一个个不连续的能量包,虽然光没有静质量,但光有动质量,有质量就有能量。
大学无机化学原子结构试题及答案

第五章 原子结构和元素周期表本章总目标:1:了解核外电子运动的特殊性,会看波函数和电子云的图形2:能够运用轨道填充顺序图,按照核外电子排布原理,写出若干元素的电子构型。
3:掌握各类元素电子构型的特征4:了解电离势,电负性等概念的意义和它们与原子结构的关系。
各小节目标:第一节:近代原子结构理论的确立 学会讨论氢原子的玻尔行星模型213.6E eV n =。
第二节:微观粒子运动的特殊性1:掌握微观粒子具有波粒二象性(h h P mv λ==)。
2:学习运用不确定原理(2h x P mπ∆•∆≥)。
第三节:核外电子运动状态的描述1:初步理解量子力学对核外电子运动状态的描述方法——处于定态的核外电子在核外空间的概率密度分布(即电子云)。
2:掌握描述核外电子的运动状态——能层、能级、轨道和自旋以及4个量子数。
3:掌握核外电子可能状态数的推算。
第四节:核外电子的排布1:了解影响轨道能量的因素及多电子原子的能级图。
2;掌握核外电子排布的三个原则:○1能量最低原则——多电子原子在基态时,核外电子尽可能分布到能量最低的院子轨道。
○2Pauli 原则——在同一原子中没有四个量子数完全相同的电子,或者说是在同一个原子中没有运动状态完全相同的电子。
○3Hund原则——电子分布到能量简并的原子轨道时,优先以自旋相同的方式分别占据不同的轨道。
3:学会利用电子排布的三原则进行第五节:元素周期表认识元素的周期、元素的族和元素的分区,会看元素周期表。
第六节:元素基本性质的周期性掌握元素基本性质的四个概念及周期性变化1:原子半径——○1从左向右,随着核电荷的增加,原子核对外层电子的吸引力也增加,使原子半径逐渐减小;○2随着核外电子数的增加,电子间的相互斥力也增强,使得原子半径增加。
但是,由于增加的电子不足以完全屏蔽增加的核电荷,因此从左向右有效核电荷逐渐增加,原子半径逐渐减小。
2:电离能——从左向右随着核电荷数的增多和原子半径的减小,原子核对外层电子的引力增大,电离能呈递增趋势。
无机化学原子结构教案

无机化学课程工程教学设计方案熊颖单位:江西省医药学校2014年 3 月5 日教学过程一、新课导入二、教学步骤2 §2.1 原子构造理论的开展概述一、含核的原子模型,古中国和古希腊的物质构造学说;,道尔顿的原子学说(1808 ):原子不行分;,卢瑟福的含核原子模型(1911 )。
二、玻尔的原子模型(一)氢原子光谱玻尔氢原子理论(1913 )(二)玻尔氢原子理论,原子构造理论的几点假设:原子构造理论的几点 3 1、在原子中,电子不是在随意轨道上绕核运动,而是在一些符合肯定条件(从量子论导出的条件)的轨道上运动。
稳定轨道(stable orbital)具有固定的能量,沿此轨道运动的电子,称为处在定态的电子,它不汲取能量,也不放射能量2、电子在不同轨道上运动时具有不同的能量,通常把这些具有不连续能量的状态称为能级(energy level)。
玻尔氢原子能级为:玻尔氢原子能级为: B E=, 2 n n称为量子数(quantum number n quantum number),其值可取1,2,3…等任何1 2 3… 正整数。
B为常数,其值等于2.18×10-18J。
3、当电子从某一轨道跃迁到另一轨道时,有能量的汲取或放出。
其频率ν 可由两个轨道的能量差,E确定:E2- E1 = ,E = hν h为普朗克常量,其数值为6.62618×1034J,s。
4 (三)对玻尔理论的评价优点:,优点:首先引入量子化的概念,说明了氢原子光谱为不连续光谱。
,缺乏:缺乏:(1)未能完全冲破经典力学连续概念,只是牵强加进了一些人为的量子化条件和假定。
(2)不能说明多电子原子(核外电子数大于1的原子)、分子或固体的光谱。
亦不能说明氢光谱的每条谱线事实上还可分裂为两条谱线的现象。
(3)未考虑其运动的波动性,采纳了宏观轨道的概念。
5 (四)几个根本概念,稳定轨道在原子中一些符合肯定条件(从量子论导出的条件)的轨道。
无机化学 原子结构

1927年,德布罗依的假设为戴维逊(Davisson C J) 和盖革(Geiger H)的电子衍射实验所证实。
电子衍射图
1.1.3 微观粒子波粒二象性的特点
问题: 1. 是否波长越长,波动性越大?
2. 实物微粒波动性与光波动性的区别是什么? 或者是实物微粒波动性的特点是什么?
(3) 磁量子数(m)
m可取0,1,2,3,… l ,共2l +1个值。 m值反映了电子云(或原子轨道)在空间的伸展方向
同一亚层内的原子轨道其能量是相同的,称等价轨道或 简并轨道。但在磁场作用下,能量会有微小的差异,因而其 线状光谱在磁场中会发生分裂。
当一组合理的量子数n、l、m确定后,电子运动的波函 数 也随之确定,该电子的能量、核外的概率分布也确定了。
鲍林近似能级图: Pauling根据光谱 实验数据及理论 计算结果,把原 子轨道能级按从 低到高分为几个 能级组。
各能级的能量次序为:
轨道能量排序与n和l的关系:
1. l相同,n不同时 2. n相同,l不同时 3. n不同,l不同时------能级交错现象
当角量子数l相同时,原子轨道的能量随着主量子数n值增大而升高: 1s < 2s < 3s
原子核外电子排布三原则:
Hund 规则: 当电子在等价轨道(能量相同轨道)上分布时,将尽
可能分占等价轨道,且自旋相同。
半满和全满规则: 等价轨道中电子处于全空(s0,p0,d0,f0)、半空(p3,d5,f7)
或全满状态(p6,d10,f14)时能量较低.
泡利不相容原理里不是说每个轨道里得 电子自旋方向相反么?那洪特规则里怎 么写在等价轨道上电子自旋方向相同呢
无机化学大学课件第一章原子结构和元素周期律

• 意义:n 是决定电子层能量高低的主要因素,
n=1表示离核最近,能量最低的第一电子层;n=2表示离核
次近的能量次低的第二电子层,依此类推。能量越低,受核束 缚越大,能量越低。
(2) 角量子数(l)或副量子数(azimuthal quantum number)
电子绕核运动时,不仅具有一定的能量,而且也具有一定
电子层结构的特征,并结合原子参数熟悉元素性质周 期性的变化规律。
图1 道尔顿原子模型
§1.1 原子的含核模型
1. “枣糕模型”: 1903年W.汤姆生(1824~1907)提出, 原子是一个球体,正电荷均匀分布在整个球内,电子 则镶在球里,原子受到激发后,电子振动,产生光谱。
图2 汤姆生原子模型
r,q,R rQ qF
r,q,R rYq,
•
解薛定谔方程时,为了方便起见,将直角坐标x,y,z变
换 成 球 极 坐 标 r,q,f , 这 样 (x,y,z) 就 变 成 了 (r,q,f)=
R(r)Q(q)F(f) , 将 与 角 度 有 关 的 函 数 合 并 为 Y(q,f) , 则
要的,或者说,四个量子数确定了,核外电子的运动状态就确
定了。
• (1) 主量子数(n)(principle quantum number)
•
它是用来描述原子中电子出现概率最大区域离核远近的参
数,或者说,它是确定电子层数的。
n 的取值为:1, 2, 3, 4…n等正整数,表示电子层数。
光谱学上常用K,L,M,N…表示电子层数。
数E 就是粒子处在该定态时的总能量。
Figure 9 pherical polar coordinates(r,θ,φ) and Cartesian axes(x, y, z).
大学无机化学经典课件:原子结构

L
M
N
O
P…
35
2. 角量子数(l): 确定电子运动空间
形状的量子数 l 的取值 :0,1 ,2,3,…,n-1
n
l
1
2
3
4
…
n
0,
0, 1,
0, 1,
0
电子亚 层符号
0, 1
1, 2
2, 3
2,…,n-1
s
s, p
s, p,d
s, p,d, f
36
l =0, s 亚层, 球形
l =1, p 亚层, 亚铃型
粒子具有波粒二象性的假设。并预言了高速运动的电子的
物质波的波长
= h / P = h / mv
1927年,Davissson和Germer应用Ni晶体进行电子衍 射实验,证实电子具有波动性。
二、 波函数与原子轨道
1.
海森堡的测不准关系 :
测不准原理说明了微观粒子运动有其特殊的
规律,不能用经典力学处理微观粒子的运动,而 这种特殊的规律是由微粒自身的本质所决定的。
率成正比
11
E = h
式中 E 为光子的能量, 为光子的频率,h 为 Planck
常数,其值为 6.62610-34 Js。物质以光的形式吸收或放
出的能量只能是光量子能量的整数倍。 电量的最小单位是一个电子的电量。 电量是量子化的。量子化是微观领域的重要特征,后面我
我们将以上的说法概括为一句话,在微观领域中能量、
为自然数,且 n – 1 l
由解得的 R ( r )、 ( ) 和 ( ) 即可求得波函数
( r,, ) = R ( r ) ( ) ( )
34
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
51
1.原子轨道角度分布图
将角度波函数Yl,,m(θ,φ)随方位角θ、 φ变化作图,就得到原子轨道的角度分布图。
52
s,p,d原子轨道的角度分布图
53
2.电子云的角度分布图
将角度波函数Yl,,m(θ,φ)的平方随方 位角θ、φ变化作图,就得到电子云的角度分 布图。
54
s,p,d电子云角度分布图
最简单的就是 氢原子光谱
近代原子结构理论
4
5
将装有高纯度、低压氢气 的放电管通过高压电流,氢原 子被激发后,所发射的光谱在 可见光区有红、蓝绿、蓝、紫 四条特征谱线
Hδ 紫 410.2
Hγ 蓝 434.0
Hβ 蓝绿
Hα 红
486.1 656.3 (nm)
6
7
8
巴尔麦( J. Balmer)经验公式(1885)
电子在核外绕 核高速旋转运 动,与行星绕 太阳旋转相似。
2
原子的组成
原子
原子核 电子
质子 中子
正电 不带电
负电
3
按照经典 电动力学 电子绕原 子核运动 不断辐射 电磁波即 放出能量
事实上多数原 子能稳定存在
当原子被火焰、 电弧、电火花或 其他方法激发时
原子光谱:不连 续的线状光谱
连续光谱
电子离核越来 越近,最终落 在核上,原子 将不复存在。
为2.18×10-18 J
n=1,2,3,4,……
主量子数, 取正整数
在物理学里,如果某一物理量
的变化是不连续的,就说这一
物理量是量子化的
13
3.频率假设
原子中的电子可以吸收一定的能量从能量
较低的定态跃迁到能量较高的定态,也可以
辐射一定的能量从能量较高的定态跃迁到能
量较低的定态。
光子的频率
ΔE=E2-E1
47
(三)几率密度和电子云
|Ψ| 2 的物理意义: |Ψ| 2 表示电 子在原子核外空间某点P(x,y,z)处单 位体积内出现的几率,称为几率密度
48
基态氢原子电子的|Ψ|2 示意图
这种形象化地表示电子在核外出现几 率密度大小的图形称为电子云,它是|Ψ|2的 具体像。
几率密度的等值线图是连接在同一平 面上的|Ψ|2值相同点而成的曲线 。
同层轨道 数
n2
同层容纳电子 总数
2n2
1
2
4
8
9
18
43
量子数和电子运动状态
n 能量 距离
l 能量 形状
m 取向 mS 自旋
方向
例 轨道运动状态为2pz,可用来描述的量子 数为:
A. n=1, l =0, m =0; B. n=2, l =1, m=0; C. n=2, l =2, m=0 ; D. n=1, l =2, m=1。
如用主量子数来表示电子层,则角量子数 就表示同一电子层中的不同状态的分层——电 子亚层。
30
各电子层内的亚层数
n=1 l=0 1s
l=0
2s
n=2
l=1 2p
l=0 3s
n=3 l=1 3p
l=2 3d
31
每一个数值表示一种形状的原子轨道或 一个亚层 ,对于多电子原子,原子轨道的能 量由n、l共同决定。
n相同时,l值越大,轨道的能量越高,如 End>Enp>Ens
l相同时,n值越大,轨道的能量越高,如 E3s>E2s>E1s
32
重要物理意义:它表示原子轨道或电子云 的形状。 l =0,s 轨道,其轨道或电子云:球形 l =1,p 轨道,其轨道或电子云:哑铃形 l =2,d 轨道,其轨道或电子云:花瓣形
凡是与光的传播有关的现象如干涉、衍
射等,光表现为波动性;凡是与光和实物相
互作用有关的现象如光电效应、原子光谱等,
光表现为微粒性。
对于光: E mc2 hv
P = mc = h / c = h /
16
(二) 微粒的波粒二象性——物质波假设 (Louis de Broglie ,法国,1924)
①电子云角度分布图比原子轨道 分布图“瘦”一些,这是因为|Y|值小 于1,所以|Y|2 值更小;
②电子云角度分布图没有正负之 分,因为|Y|2均为正值。
第一章 原子结构
IF5
1
第一节 玻尔的氢原子模型
行星式原 子模型
1911年卢瑟福 (E.Rutherfor d)原子有核模 型
原子直径约为100pm 核的直径约为10-3pm 质子质量为1.6724×10-27kg 中子质量为1.6749×10-27kg 电子质量为9.1096×10-31kg
原子是由带 正电荷的原 子核和带负 电荷的电子 组成
45
练习: 1.用四个量子数分别表示7号、10号元素
核外所有电子的运动状态。 2. 4s2、3d5的含义是什么?分别用四个
量子数表示这两种轨道上各电子的运动状态。 4s轨道上2个电子的量子数哪些相同,哪些不 同?3d轨道上5个电子的量子数哪些相同,哪 些不同?
46
例 下列各组量子数哪些不合理?并分别 用轨道符号(如4s)和(n,l,m)表示合理的运动状 态。
11
玻尔(Bohr)理论的三个假设:
1.定态假设 电子只能在原子核外一定的轨道上运动, 运动着的电子既不放出能量也不吸收能,电 子处于稳定状态即定态。 基态和激发态
12
2.量子化条件假设
在定态轨道上运动的电子具有一定的能量
E,E是由某些量子化条件所决定的数值。
常量(n=1时基态能量),
E RH n2
1. n=2, l=1, m=0 4. n=2, l=3, m=2 2. n=2, l=0, m=-1 5. n=3, l=1, m=1 3. n=2, l=2, m=-1 6. n=3, l=0, m=-1
解:2, 3, 4, 6 不合理。
1. 2pz (2,1,0) 2pz
5. 3px (3,1,1) 3px
1 1
-1 1/2 -1 -1/2
42
主量子 数n
1 2
3
量子数组合和原子轨道表
角量子数 (副量子数)
l 0 0 1 0 1
2
磁量子数 m
波函数 Ψ
0
Ψ1s
0
Ψ2s
0
Ψ2pz
±1
Ψ2px Ψ2py
0
Ψ3s
0
Ψ3pz
±1
Ψ3px Ψ3py
0
Ψ3dz2
±1
Ψ3dxz Ψ3dyz
±2
Ψ3dxy Ψ3dx2—y2
v
1
RH
(1 22
1 n2
)
: 谱线波长的倒数, 波数(cm-1). n: 大于2的正整数. RH: 常数, 1.09677576107m-1 n = 3, 4 , 5, 6 分别对应氢光谱中四条谱线
↓ ↓ ↓↓ H、 H、 H、H 、 Balmer系
9
n=6
氢原子光谱图
10
1913年玻尔(Bohr) 综合了 Rutherford 的有核模型、 Planck的量子论 (P168)和Einstein 的光子学说 (P168),提出了 定态原子模型
“ 物质波”(substantial wave)的假
设:微观粒子如电子、原子等也具有和光
德布罗依
类似的波粒二象性。即
关系式
= h /P = h / m
17
1928年以后,人们陆续发现了质子射线、α 粒子射线、中子射线、原子射线和分子射线,这 就进一步证明了微观粒子的波粒二象性。
电子衍射图
电子波是几率波,反映电子运动中在空
26
(二)量子数
量子数n、l、m有一组合理取值和一定 组合,就有一个确定的波函数Ψ(一个原子 轨道),即有一种对应的电子空间运动状态。 电子的自旋运动状态由量子数ms来决定。
27
1.主量子数n :n = 1, 2, 3…正整数,有n个值 n值:1, 2, 3, 4, 5, 6, 7,……
光谱学符号:K,L, M,N,O, P, Q,…… n决定着电子离核的远近(即电子层)和能级。
间不同区域出现的几率。
18
(三)测不准原理
1927年德国科学家海森堡(W . Heisenberg)提出了著名的测不准原理 (uncertainly principle):
不可能同时准确地确定微观粒子的 空间位置和动量。测不准关系式为:
19
动量在坐标x方 向上的误差。
x P h 或x h
4
4m
运动速度 不确定量
微观粒子在坐标x方 向上的位置误差 (不确定量)
20
二、氢原子的量子力学模型 (核外电子运动状态的描述 )
由于微观粒子运动具有能量量子化、波 粒二象性和测不准关系这些特征,因此不能 用“在固定的圆形轨道上绕核运动”的经典 力学方法来描述微观粒子的运动,只能用量 子力学和统计力学的原理和方法来描述微观 粒子的运动状态。
ΔE=hν
即 hν = E2-E1
普朗克(Planck )常 数6.626×10-34J·s
14
贡献:1.解释了氢原子的线状光谱 2.解释了原子能稳定存在的原因
局限:1. 不能说明多电子原子光谱 2. 不能说明氢原子的精细光谱
15
第二节 氢原子的量子力学模型
一、微观粒子的波粒二象性
(一) 光的波粒二象性
直角坐标和球极坐标的关系
25
为了得到Schrödinger方程的合理解,要 求一些物理量是量子化的,这就必须引用三个 参数n、l、m,这三个参数称为量子数。
一个合理的波函数代表着电子的一种运动状 态或一个原子轨道,且可简化为用包含三个量 子数(n,l,m)的函数Ψ(n,l,m)来表示 。
