2-1谐振及阻抗变换电路
高频电子线路完整章节完整课件(胡宴如版)

第2章 小信号选频放大器
主要内容:
LC谐振回路
小信号谐振放大器
集中选频放大器
2.1 LC谐振回路—概述
LC 谐振回路是高频电路里最常用 的无源选频网络,包括并联回路和串联回路 两种结构类型。
利用LC谐振回路的幅(度)频(率) 特性和相(位)频(率)特性,不仅可以进 行选频,即从输入信号中选择出有用频率分 量而抑制掉无用频率分量或噪声(例如在选 频放大器和正弦波振荡器中),而且还可以
1.1、通信与通信系统
4)信道:信息的传送通道,又称传输媒介。信道 可分为无线信道和有线信道两大类;
5)接收机:把由信道传送过来的已调信号取出并 进行处理,得到与发送相对应的原基带信号, 把这一过程称为解调;
6)输出变换器:把基带信号恢复成原来形式的信 息。
1.1、通信与通信系统
通信系统按传输的基带信号不同,分为模拟通信系统和 数字通信系统两大类。 1)模拟通信系统:直接传输模拟信号(即基带信号为 模拟信号)的通信系统,称为模拟通信系统。 典型的模拟通信系统的发送设备的组成框图和接收 设备的组成框图分别如图2和图3所示。 图2为调幅发射机的组成框图。 图3为超外差式调幅接收机的组成框图。 2)数字通信系统:传输数字信号(即基带信号为数字 信号)的通信系统,称为数字通信系统。
2.1.1 并联谐振回路的选频特 性
谐振回路
谐振回路由电感线圈和电容器组成,它具有选择 信号及阻抗变换作用。
LC并联谐振回路
图2.1.1是电感L、电容C和外加信号源组成的
并联谐振回路。r是电感L的等效损耗电阻,电容的
.
损耗一般可以忽略。 I
S
为电流源,U
为并联回路两
O
端输出电压。
1谐振回路

2.1 谐振回路LC 谐振回路是通信电路中最常用的无源网络。
利用LC 谐振回路的幅频特性和相频特性,不仅可以进行选频,即从输入信号中选择出有用频率分量而抑制掉无用频率分量或噪声(例如,在小信号谐振放大器、谐振功率放大器和正弦波振荡器中),而且还可以进行信号的频幅转换和频相转换(例如,在斜率鉴频和相位鉴频电路中)。
另外,用L 、C 元件还可以组成各种形式的阻抗变换电路。
所以,LC 谐振回路虽然结构简单,但是在通信电路中却是不可缺少的重要组成部分。
陶瓷滤波器、声表面滤波器、晶体滤波器等是近几十年来利用固体滤波技术发展起来的新器仵,常被用作集中滤波器。
在选频放大电路集成化及改善电路特性方面起着重要的作用,目前已在各类通信设备中得到广泛的应用。
2.1.1 并联谐振回路的选频特性谐振回路由电感线圈和电容器组成,它具有选择信号及阻抗变换作用。
简单的谐振回路有串联谐振回路和并联谐振回路,有时为获得更好的选择效果,可把两个或更多个串、并联谐振回路连接起来,构成带通滤波器。
谐振放大器中,LC 并联谐振回路使用最为广泛。
1.并联谐振回路阻抗频率特性LC 并联谐振回路如图2-1所示。
图(a )中,r 代表线圈L 的等效损耗电阻,P R 为图(b )的等效电阻。
由于电容器的损耗很小,图中略去其损耗电阻。
sI为电流源,OU 为并联回路两端输出电压。
由图2-1可知并联谐振回路的等效阻抗为:由图(a )可得 C j L j r C j L j r I U Z SO ωωωω/1)/1)((+++== (2-1)由图(b )可得 ()22111L C R Z Pωω-+= (2-2)PR LC 11arctan ωωϕ--= (2-3)在实际电路中,通常r 很小,满足r <<L ω,因此,式(2-1)可近似为图2-1 LC 并联谐振回路Z ≈)/1(/C L j r CL ωω-+ (2-4)当L ω=C ω/1时,回路产生谐振,由式(2-4)可知并联谐振回路在谐振时其等效阻抗为纯电阻且为最大,可用符号P R 表示,即 Z =P R =CrL(2-5) 并联谐振回路的谐振频率为 LC10=ω 或 LCf π210=(2-6)在LC 谐振回路中,为了评价谐振回路损耗的大小,常引入品质因数Q ,它定义为回路谐振时的感抗(或容抗)与回路等效损耗电阻r 之比,即 Q =rL 0ω=rC0/1ω (2-7)将式(2-4)代入式(2-7),则得 Q =CLr(2-8)一般LC 谐振回路的Q 值在几十到几百范围内,Q 值愈大,回路的损耗愈小,其选频特性就愈好。
高频电子线路二版第二章.高频电路基础

次级回路自阻抗
M2
Zf1 Z22
初级回路自阻抗
M2
Zf2
Z11
Z22 次级回路自阻抗
Z11 初级回路自阻抗
广义失谐量: 0L ( 0 ) 2Q
r 0
0
耦合因子: A Q
临界耦合 A 1
欠耦合 A<1
过耦合 A>1
理相
1
0.7
实际
0.1
0
ω0
ω
② 选择性: 表征了对无用信号的抑制能力,
Q值越高,曲线越陡峭,选择性越好,但通频
带越窄。
③ 理想回路:幅频特性在通频带内应完全
平坦。是一个矩型.
矩型系数: 表征实际幅频特性与理想幅
频特性接近的程度.谐振曲线下降为谐振值( f0 处 )的0.1时对应的频带宽度B0.1与通频带B0.707 之比:
+
IS
RS
C
N1 N2 RL
+
R'L
IS
RS
C
L
分析:
由 N1:N2=1:n ,得 n = N2 / N1(接入系数)。利用ⅰ 的方法,也可求得负载RL等效到初级回路的等效电阻是:
பைடு நூலகம்RL
1 n2
RL
或 gL n2gL
ⅲ. 电容分压式阻抗变换电路
Ú
+
IS RS
L
C1 ÚT
C2
IS RS C L
C1 R'L
⑷ 分析几种常用的抽头并联谐振回路
ⅰ.自耦变压器阻抗变换电路
Ú1
+
IS
RS
C
N1 Ú2 L
N2
RL
通信电子线路(沈伟慈版)电子课件--第一章

ωC −
1 ωL
ge0
2010年9月11日星期六
齐怀琴主讲
1.1.2 阻抗变换电路
阻抗变换电路是一种将实际负载阻抗变换为前级 网络所要求最佳负载阻抗的电路。阻抗变换电路对于 提高整个电路的性能有重要的作用。 空载
Re 0 = Q0 = g e 0ω 0 L ω 0 L
有载
Qe = 1 g∑ ω0 L = R∑
2010年9月11日星期六
齐怀琴主讲
2 . LC选频匹配电路 选频匹配电路
X 2p R2 p Rp + j 2 Xp 由a图得: Z p = R p jX p = 2 2 2 R p+X p R p+X p
由b图得: Z s = Rs + jX s 要使Zp=Zs,必须满足
X 2p Rs = 2 Rp 2 R p+X p
2010年9月11日星期六
齐怀琴主讲
串联谐振曲线
并联谐振曲线
图1.4 串联、并联谐振曲线
2010年9月11日星期六
齐怀琴主讲
串联谐振回路特性
并联谐振回路特性
1 2 Z = r + (ωL − ) ωC
2
1 2 Z = r + (ωC − ) ωL
2
ϕ = arctan
ωL −
r
1 ωC
ϕ = − arctan
f0 f
请看谐振曲线
当失调不大时,即f与f0相差很 小时,
f 0 ( f + f 0 )( f − f 0 ) 2( f − f 0 ) 2∆f f ε= − = ≈ = f0 f f0 f f0 f0
所以
N( f ) =
1 2∆f 2 1+ Q 0 ( ) f0
第2讲LC谐振回路

)
1
j(L
0
1
0
)
1
jQ(
0 )
r rC
r 0 rC 0
0
LC谐振回路
失谐量 绝对失谐量 广义失谐量
f f f0 或 0
Q( 0 ) Q ( 0 )( 0 ) Q 2()
0
0
0
Q 2() Q 2(f )
0
f0
LC谐振回路
•
N( f )
1
1 j
•
N( f )
路上并联多大电阻才能满足放大器所需带 宽要求?
LC谐振回路
解: 1
L
1
02
1
(2 )2 f02C
L ( 1 )2
2
1 f02C
10 6
25330 f02C
5.07u
2
R0 Q0L 100 2 107 5.07 106 3.18 104
31.8k
B f0 100 kHz Q
LC谐振回路
并联回路适合与信号源和负载并联连接,使有 用信号在负载上的电压振幅增大。
LC谐振回路
例1 设一放大器以简单并联振荡回路为负载, 信 号中心频率fs=10MHz, 回路电容C=50 pF, (1) 试计算所需的线圈电感值。 (2) 若线圈品质因数为Q=100, 计算回路谐振电
阻及带宽。 (3) 若放大器所需的带宽B=0.5MHz, 则应在回
应使 Z S Z P
RS
X
2 P
RP2
X
2 P
RP
XS
RP2
RP2
X
2 P
XP
LC谐振回路
由于Q值不变,有
Qe
buck电路的阻抗变换

buck电路的阻抗变换Buck电路是一种常见的降压转换器,广泛应用于电源管理系统中。
在设计和分析Buck电路时,了解阻抗变换对电路性能的影响是非常重要的。
本文将介绍Buck电路的阻抗变换以及如何应用这些变换来分析电路。
1. Buck电路简介Buck电路是一种DC-DC转换器,用于将高输入电压转换为较低的输出电压。
它由功率开关、电感和输出电容组成。
根据电感和开关的工作状态,Buck电路可以实现电流连续和不连续两种模式。
2. 阻抗变换原理阻抗变换是指通过改变电路元件的参数来改变电路的输入输出特性。
在Buck电路中,常用的阻抗变换方法有:2.1 变换电感值:通过改变电感的数值,可以调节电路的谐振频率和输出电压范围。
2.2 变换负载电阻:改变负载电阻的数值可以调节电路的输出电压和电流。
2.3 变换开关频率:通过改变开关频率,可以调节电路的效率和输出电压波动。
3. 阻抗变换在Buck电路中的应用3.1 变换电感值:当需要调节Buck电路的输出电压时,可以通过改变电感的数值来实现。
增大电感值可以降低输出电压,减小电感值则可以提高输出电压。
3.2 变换负载电阻:负载电阻对Buck电路的输出电压和电流有较大影响。
通过改变负载电阻的数值,可以调节输出电压和电流到所需的数值。
3.3 变换开关频率:开关频率决定了Buck电路的工作速度和效率。
较高的开关频率可以提高电路的响应速度和效率,但也可能增加开关损耗。
通过调节开关频率,可以在输出电压和效率之间找到合适的平衡点。
4. 阻抗变换的分析方法在分析Buck电路中的阻抗变换时,一种常用的方法是采用频域分析。
通过将电路转换为复数形式,可以用相量和极坐标的形式来表示电路元件的阻抗。
在频域中,可以通过计算阻抗间的复数运算来得到电路的传输函数和频率响应。
5. 案例研究:变换电感值对Buck电路的影响以一个常见的Buck电路为例,假设电感的数值从L1变为L2,其他参数保持不变。
通过频域分析,可以计算出电路的新传输函数和频率响应。
1234串、并联阻抗等效互换与抽头变换双调谐
按幅频特性对滤波器的分类
A ( jω ) A ( jω )
低通 高通
ω
A ( jω ) A ( jω )
ω
带通
带阻
ω
ω
按所用器件的特点对滤波器分类
无源滤波器
由无源器件构成(电阻、电感和电容组成的RLC滤 波器)
晶体滤波器
利用石英晶体薄片构成
声表面波滤波器(SAW)
利用压电效应构成的。
有源滤波器
在所构成的滤波器中,除无源器件外还含有放大器 等有源电路。
相对衰减 衰减特性 ( jω ) Vo ( jω )
x(t )
延时与失真
τ
t
信号与延时后的信号(已知一信号是另一信 号的延时)
信号描述: 延时信号: 瞬时相位: 延时量:
x(t ) = A cos(ϕ (t )) = A cos(ωt ) x1(t) = A cos[ϕ1(t)] = x(t − τ ) = A cos(ω(t − τ ))
2串 § 1. 2串、并联阻抗等效互换
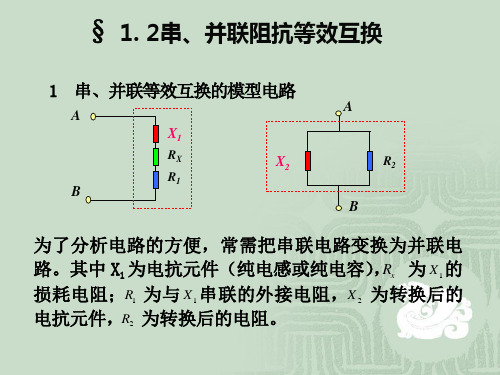
1 串、并联等效互换的模型电路
A X1
RX R1
A
X2 B
R2
B
为了分析电路的方便, 为了分析电路的方便 ,常需把串联电路变换为并联电 路。其中 X1 为电抗元件(纯电感或纯电容) Rx 为 X 1 的 为电抗元件(纯电感或纯电容) , 串联的外接电阻, 损耗电阻; 损耗电阻; R1 为与 X 1 串联的外接电阻, X 2 为转换后的 电抗元件, 为转换后的电阻。 电抗元件, R2 为转换后的电阻。
+ + Uab
-
+ + Ucb
-
Udb
-
Udb
-
高频第1章 谐振回路与阻抗变换

. .
第1章 谐振回路与阻抗变换
品质因数Q 回路的储能与耗能之比; (3) 品质因数Q:回路的储能与耗能之比; ω0 L ρ 1 Q= = = r ω0Cr r 电压特性: (4) 电压特性:谐振时通过电感与电容的电 压大小相等,方向相反。 压大小相等,方向相反。
V (ω0 ) V (ω0 ) V (ω ) = ≈ = V (ω ) • e jφ (ω ) ω − ω0 (ω + ω0 )(ω − ω0 ) 1 + jQ( ) 1 + j 2Q( )
. . .
ωω0
ω0
第1章 谐振回路与阻抗变换
(1) 幅频特性
V (ω0 ) V (ω ) = ω − ω0 2 1 + [2Q ( )]
ω =ω0
= −2
Q
ω0
可见,当输入频率发生变化时, 可见,当输入频率发生变化时,输出电压的幅度和 相位均发生变化。 相位均发生变化。
第1章 谐振回路与阻抗变换
电抗特性:若忽略损耗电阻R (3) 电抗特性:若忽略损耗电阻R
1 jX = jω L / / jωC
1 1 1 − ω 2 LC 1 1 = − ωC = = + jωC ⇒ X ωL ωL jX jω L
第1章 谐振回路与阻抗变换
例题
• 1 已知LC并联谐振回路的电感L在 f 0 = 30MHz 已知LC并联谐振回路的电感L LC并联谐振回路的电感 时测得 L = 1µ H, Q0 = 100 。 时的C和并联谐振电阻R 求谐振回路为 f 0 = 30 MHz 时的C和并联谐振电阻R.
2 已知并联谐振回路的谐振频率 f0 = 10MHz , C = 50 pF,调频带
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.谐振时的电流:
流经电感电流
流经电容电流
IL
Rp jw0 L
I jQ I
Rp IC I R p jw0C I j Q I 1 jw0C
谐振时有 I L IC
所以并联谐振又称为电流谐振。
结论: 谐振时流经电感和电容的电流大小相等,符号相反, 其大小都等于总电流的Q倍。
其中:
(2)电感分压阻抗变换电路
设L1、L2是无耗的,且RL>>wL2 自耦变压器的匝比
(3)电容分压阻抗变换电路 C1、C2 可看作是串联的,在串联电路中, 电压的分配与阻值成正比。
例2 并联谐振回路已知L=586μH,C=200pF,r=12Ω, RS=RL=200kΩ,试分析信号源、负载对谐振回路特性的影响。 (1)不考虑RS、RL影响 谐振频率 空载品质因数 谐振电阻 通频带
回路的品质因数为有载品质因数Qe
Re<RP ,Qe<Q ,Q值变小了,通频带展宽了,选择性变差了。
2、阻抗变换电路
为了减少信号源内阻及负载电阻对谐振回路的影响, 通常采用阻抗变换电路来增大Rs、RL的方法来解决 。
常用的阻抗变换电路有变压器、电感和电容分压电路。
(1)变压器阻抗变换电路 设变压器为无耗理想降 压变压器,其匝比为:
BW0.1 BW0.7
矩形系数K0.1越接近1,幅频特性曲线越接近矩形,选择性越好。 一般LC并联谐振回路的矩形系数为
K 0.1
BW0.1 10 BW0.7 10 BW0.7 BW0.7
因为10远大于1,所以,并联谐振回路的选择性比较差。
总之,并联谐振回路ቤተ መጻሕፍቲ ባይዱQ值越大,幅频特性曲 线越尖锐,通频带越窄,选择性越好。
电感线圈中r一般很小,wL>>r
1 L jw C C Z r j( wL 1 / wC) r j ( wL 1 ) wC j wL
Cr 1 Y j ( wc ) L wl
3、谐振频率
Cr 1 Y ( j 0 ) j (0C ) L 0 L
可解得谐振时 角频率 频率
第二章 小信号选频放大器
2.1 谐振回路
2.2小信号谐振放大器 2.3集中选频放大器 2.4放大器的噪声
2.1
谐振回路
谐振:含有电感电容的交流电路中,端口电压和电 流的相位一般不同,当电感电容参数选的合适时,可使 电压和电流的相位相同,电路呈纯阻性,这种工作状态 称为谐振。 并联谐振回路的应用最为广泛。
通频带
谐振电路频率选择性的好坏可以用通 频带BW0.7来衡量。在谐振频率f0两端,当电 流I下降至谐振电流I0的1/2 = 0.707倍 时所覆盖的频率范围,称为通频带
BW0.7=2△f=f2–f1,其中f2、f1分别叫做通频带的上限截止 频率和下限截止频率。BW0.7越小,谐振曲线越尖锐,表明电 路的频率选择性越好。 通频带与品质因数之间关系
U R r II U S Ur R
w0 L w0 U L j wL I jj U S jQ U S r R
1 1 UC I j US jQUS j w0C w0 rC
电容上电压
其中
Q
w0 L 1 r w0 rC r
【例21-2】
串联谐振回路的谐振频率f0=800kHz,回路电阻r=10Ω, 要求回路的通频带BW0.7= 104Hz,试求回路的品质因数Q、 电感L和电容C。 解: 因为
L
C
f0 800 10 3 Q 80 4 BW0.7 10
Q
w0 L 1 r w0CR
所以
Qr 80 10 159 10 6 H 159 μH w0 2 3 14 800 10 3
幅频特性曲线
相频特性曲线
可见,当ω =ω0时,即Δω=0时,电路发生谐振,Z=RP, 阻抗呈纯阻性,且最大。
当ω>ω0时,电路呈容性相移为负值,最大负值趋于-90º ; 当ω<ω0时,电路呈感性,电压相位超前电流,相移为正 值,最大正值趋于+90º 。 在谐振频率附近,相频特性曲线变化更陡峭。不同的Q值对 应不同的阻抗幅频特性曲线和相频特性曲线,Q值大,RP就 大,幅频特性曲线更尖锐。
1 1 249 10 12 F 249 pF w0 rQ 2 3 14 800 10 3 10 80
【例21-3】 由L = 200μH、C = 400 pF及r = 10Ω组成的串联回路, 试求其通频带BW0.7。 解: f 0
1 2 π LC 1 2 3 14 200 10 6 400 10 12 563 10 3 Hz 563 kH z
并联谐振回路输出电压幅频特性为
输出电压相频特性为
可见,Q值越大,电压幅频特性曲线越尖锐,相频 特性曲线越陡峭。
2.通频带 当 的值由1下降到0.707(即
1 2
)时所对应的频带
宽度即 2f ,称为通频带, 用 BW0.7表示。
1 2 1 2f 1 Q f0
L Q C R r
200 10 6 400 10 12 70 7 10
所以通频带 BW0.7
f 0 563 10 3 7 96 kHz Q 70 7
二、并联谐振回路的选频特性
1、并联电路
2、并联谐振的条件
1 (r j wL) ( j/ wC) Z (r jwL) // j wC r j( wL 1 / wC)
例1 并联谐振回路如图所示,已知L=180μH,C=140pF, r=10Ω。 试求: (1)该回路的谐振频率f0、品质因数Q及谐振电阻Rp; (2)Δf=±10kHZ、±5kHZ时并联回路的等效阻抗及相移。
三、并联谐振回路的通频带和选择性
1.电压谐振曲线
UO UP
1 2f 1 jQ f0
2
2
BW0.7 Q 2 1 f0 f0 BW0.7 Q f BW0.7 0 Q
(3)选择性 选择性是指回路从含有各种不同频率的信号总和中选 出有用信号、抑制干扰信号的能力。 在实际应用中,选择性常用 对应的频带宽度BW0.1表示。
1 10 1 2 f 1 Q f0
当电源频率正好等于谐振 频率w0时,电流的值最大,最 大值为I0 = U/R; 当电源频率向着w>w0或w <w0方向偏离谐振频率w0时, 阻抗∣Z∣都逐渐增大,电流 也逐渐变小至零。
只有在谐振频率附近,电路中电流才有较大值,偏离这 一频率,电流值则很小,这种能够把谐振频率附近的电流选 择出来的特性称为频率选择性。
一、串联谐振回路的选频特性
L Z ( j ) I R jj(L r
1
1、谐振及谐振条件 (1)谐振 电路的等效阻抗为
Us
1 j C
1 Z ( j ) r j (L ) C
当感抗wL等于容抗(1/wC)时,复阻抗Z=R,串联电 路的等效复阻抗变成了纯电阻,端电压与端电流同相, 这时就称电路发生了串联谐振。
解:
(1)电压源的角频率应为 1 1 w w0 10 6 rad/s LC 10 4 10 8
(2)电路的品质因数为
w0 L 10 6 0.1 10 3 Q 100 R 1
则
UL= UC = QUS =100×10 =1000V
(3) 通频带为
BW0.7 f0 1 w0 1 6 kHz Q 100 2 π
6.并联谐振回路的频率特性
L/C Z r j ( wL 1 / wC ) RP 1 1 j ( wL ) / r wC RP RP RP 2 2 0 1 jQ 0 0 w w0 1 jQ 1 jQ ( ) 0 w0 w 0
2
的值由1下降到0.1时所
BW0.1 100 1 Q f0 f0 BW0.1 10 10 BW0.7 Q
2
为提高选择性,有效抑制干扰信号, 要求谐振回路的幅频特性具有矩形形状, 如图所示,为此,引入“矩形系数”概念, 用K0.1表示。 定义: K 0.1
可见,回路的损耗电阻r越小,Q值越大,回路损耗越少。 Q值一般在几十到几百范围内。
2、谐振时的电压和电流 谐振时的电流:
I
US US Z r
可见谐振时电路中 电流最大,且与电 压源电压同相。这 就是收音机选择节 目的原理。
有效值为
U I Z
谐振时的电压: 电阻上电压 电感上电压
四、阻抗变换电路 1、信号源及负载对谐振回路的影响 在实际应用中,LC谐振回路一侧接信号源,另一侧接 负载,信号源的输出阻抗和负载阻抗都会对谐振回路产生 影响,使回路的等效品质因数下降、选择性变差、甚至谐 振频率发生偏移。
右图为一实用的LC并联谐振回路, 其中 为电压源,RS为电压源内阻、RL 为负载电阻。 将电压源变换成电流源,将 LrC等效变换成LRPC形式。 US L 其中, IS RP RS Cr 将RS 、RP 、RL 合并成Re,即
(2)串联谐振的条件
1 Z ( j ) R j (L ) C 1 固有角频率: 0 LC 1 固有频率: f0 2 LC
谐振电路的特性阻抗ρ,即 品质因数:
Q
1 0 L 0 0C
w0 L
1 w0 C
L C
w0 L 1 r w0 rC r
0
f0
1 LC 1
2 LC
