凸轮型线设计资料
LJ750发动机配气凸轮设计计算书

LJ750发动机配气凸轮型线设计计算书配气机构的设计思想:配气机构是发动机的重要组成部分,一台发动机的经济性能是否优越,工作是否可靠,噪声与振动能否控制在较低的限度,常常与其配其机构的设计是否合理密切关系。
特别对于高速大功率发动机,因对其较高性能指标的设计要求,配气机构的设计及其零部件的设计和制造就更加重要和严格。
配气机构的设计涉及到如下诸多问题:1.如果根据具体的机型的要求选取合理的函数凸轮型线并进行有关特性参数的计算和分析;2.配气机构方案选择及其气门的结构布置;3.对于高速配气机构来说,必须进行配气机构的动力学计算;4.在设计过程中,需要考虑很多重要的因素,如配气相位,平稳性(包括气门速度,加速度,脉冲数值大小及有无飞脱,落座反跳等),充气性能,润滑性能,凸轮与挺拄之间的接触应力等问题;因此,进行配气机构的设计往往需要很大的工作量,特别是为了获得一个最优的设计方案。
为了简化工作量,在目前国内外的设计中,常常采用参考某些成功机型的方法,来获得设计一台新发动机所需要的配气机构。
为此,在本设计了,参考了CBR900发动机的配气机构,通过对该机型配气机构的特性进行分析,并对提出的几种方案的凸轮型线进行的对比,最终获得了LJ750发动机配气机构的有关数据。
对比的结果最终还是采用了和CBR900发动机相同的配气结构,因此涉及到配气结构的许多动力学计算在这里都略去了。
本章主要介绍了多项动力凸轮设计的基本原理及其准则,并对CBR900发动机的凸轮型线进行了细致的分析和研究,在此基础上提出了LJ750发动机的配气机构。
一、凸轮型线类型的选择配气机构是发动机的一个重要系统,其设计好坏对发动机的性能、可靠性和寿命有极大的影响。
其中凸轮型线设计是配气机构设计中最为关键的部分,在确定了系统参数后,重要的问题是根据发动机的性能和用途,正确选择凸轮型线类型及凸轮参数。
凸轮型线有多种,如复合正弦,复合摆线,低次方,高次方,多项动力,谐波凸轮等。
第4.3节(盘形凸轮廓线的设计)

第三节 盘形凸轮廓线的设计当根据工作要求和结构条件选定了凸轮机构的类型、从动件的运动规律和凸轮的基圆半径(其确定将在下节中介绍)等结构参数后,就可以设计凸轮的轮廓曲线。
凸轮廓线的设计方法有图解法和解析法,其设计原理基本相同。
本节先简要介绍图解法,后重点介绍解析法设计凸轮廓线。
一、凸轮廓线设计的基本原理图4-13 反转法设计凸轮廓线基本原理图4-13所示为一尖顶对心盘形凸轮机构,设凸轮以等角速度ω逆时针转动,推动从动件2在导路中上、下往复移动。
当从动件处于最低位置时,凸轮轮廓曲线与从动件在A 点接触,当凸轮转过1ϕ角时,凸轮的向径A A 0将转到A A '0位置,而凸轮轮廓将转到图中虚线所示的位置。
从动件尖端从最低位置A 上升至B ',上升的位移为B A S '=1,这是从动件的运动位移。
若设凸轮不动,从动件及其运动的导路一起绕A 0点以等角速度-ω转过1ϕ角,从动件将随导路一起以角速度-ω转动,同时又在导路中作相对导路的移动,如图中的虚线位置,此时从动件向上移动的位移为B A 1。
而且,11S B A B A ='=,即在上述两种情况下,从动件移动的距离不变。
由于从动件尖端在运动过程中始终与凸轮轮廓曲线保持接触,所以从动件尖端的运动轨迹即为凸轮轮廓。
设计凸轮廓线时,可由从动件运动位移先定出一系列的B 点,将其连接成光滑曲线,即为凸轮廓线。
由于这种方法是假设凸轮固定不动而使从动件连同导路一起反转,故称为反转法。
对其它类型的凸轮机构,也可利用反转法进行分析和凸轮廓线设计。
二、图解法设计凸轮廓线1. 移动从动件盘形凸轮廓线的设计(1)尖端从动件 图4-14a 所示为一偏置移动尖端从动件盘形凸轮机构。
设已知凸轮的基圆半径为b r ,从动件导路偏于凸轮轴心A 0的左侧,偏距为e ,凸轮以等角速度ω顺时针方向转动。
从动件的位移曲线如图4-14b 所示,试设计凸轮的轮廓曲线。
图4-14 尖端从动件盘形凸轮廓线设计依据反转法原理,具体设计步骤如下。
车铣凸轮轴型线设计与曲线优化

车铣 凸轮轴 型线设 计与 曲线优 化
谷 丰
( 中国一重大连加氢反应器 制造有 限公 司 。辽宁 大连 1 1 6 0 0 0)
【 摘 要】 本 文根 据凸轮升程表数据 ,利用三次样条 函数方 法
对 凸轮列表 曲线拟合插值 ,实现 了连接 曲线的平滑过渡 ,有利 于保 证 凸轮轴建模轮廓精度 ,并进行轮廓 曲线误 差分析 ,为车铣模式下 刀具 中心轨迹数控加工模型的建立和车铣组合编程奠定 了基础 。
合 编 程 提 供 了理 论 基 础 。 Fra bibliotek等 +
+
( 1 . 5)
令 =X / , 得到左导数 :
一
)
( 1 . 6)
由式 ( 1 . 5 ) 、( 1 . 6 )得:
* + ) = 一 一 + ( 1 _ 7 )
由于 S ( x ) 的一阶导数连续 ,a P S t 一 + ) s 一 ・ , ,得
数求 出。可以利用 ( 在节点处 的连续 性来确定这些参数所满足 的 关系式。对式 ( 2 . 3 )求 导 得 :
) = 一 - 垒
一
+
+
【 关键词 】 车铣 ;凸轮轴 ;三 次样条 ;插值拟合
引 言
一 : 一
一
( 1 4)
.
令 =X i 一 1 ,得 到 右 导 数 :
一
。
6
h i +l  ̄
3
1凸轮 轮廓 曲线三次样条 函数拟 合插值 本文主要考虑 的是关于离散 点升程 表表示的 凸轮数控加工 的研 究,对于列表 曲线加 工其 最大特 点就是:在保证一定加工精度 的前 提下 ,要求 曲线 能平滑地通 过各个 坐标 点。对于列表 曲线的数学处 理 ,通常采用二次拟合法 。首先选 择多个插值方程来分段描述它 ,
D01长城柴油机性能计算及凸轮型线设计
D01柴油机性能计算及凸轮型线设计刘刚(长城汽车股份有限公司动力事业部,河北省保定市)摘 要:D01柴油机是长城公司研发的达到欧4排放标准的2.0L 柴油机。
当时,D01处在概念设计阶段,本文利用BOOST 进行D01柴油机性能预测并对气门升程曲线进行优化,确定了气门升程曲线,然后通过EXCITE TD 进行凸轮型线设计并进行运动学和动力学分析。
经过当前试验验证,D01柴油机达到了预期的性能。
关键词:气门升程曲线;凸轮型线 主要软件:BOOST ;EXCITE TD1.前言发动机通过气门来进行缸内的换气过程,因此气门升程曲线对发动机性能的影响很大。
本文通过BOOST 建立柴油机准确模型,在模型的基础上优化气门升程曲线,并通过EXCITE TD 设计凸轮型线,进行相应凸轮型线的运动学和动力学分析。
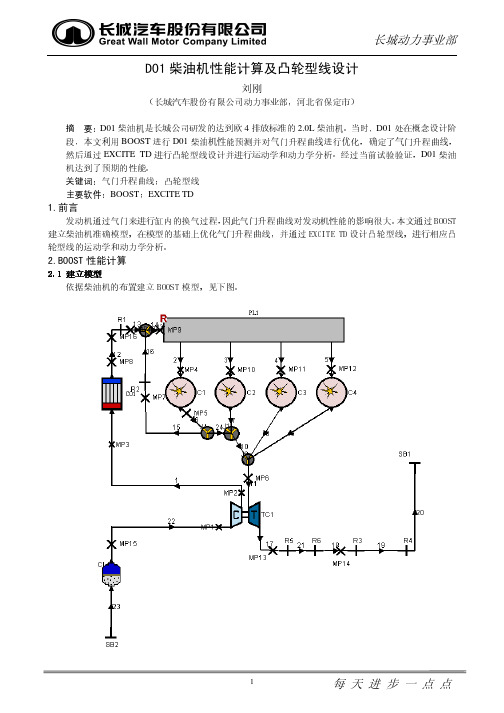
2.BOOST 性能计算2.1 2.1 建立模型建立模型建立模型依据柴油机的布置建立BOOST 模型,见下图。
图1 1 建立的模型建立的模型建立的模型2.22.2 计算结果和参考数据的比较计算结果和参考数据的比较由于D01处在概念设计阶段,没有样机进行台架试验,因此只能通过对比相似机型的性能数据来校核模型,下图是计算结果和参考数据的对比。
图2 2 计算结果计算结果计算结果从图中看到,扭矩和比油耗曲线和参考数据很接近,可以认定模型是准确的。
从功率图中看到,最大功率为100kw,为了达到目标值110kw,需要对气门升程曲线进行调整。
2.32.3 优化气门升程曲线优化气门升程曲线气门升程曲线的优化包括开启持续期的优化和相位的优化,而且必须将这两种优化方法结合起来以保证优化效果。
图3 4000rpm 下气门升程曲线优化结果上图是对D01功率在4000rpm 时进行开启持续期和相位的优化结果,分别将进气门的开启持续期设为183、193、203,同时将排气门的开启持续期设为188、198、208,并考虑相位的影响,综合考虑对功率的影响。
凸轮型线设计说明

内燃机课程设计凸轮说明书题目 90kW四行程四缸汽油机凸轮型线设计学院机电工程学院专业热能与动力工程专业班级热动1002 学号姓名指导老师刘军日期 2013-6-2590kW四行程四缸汽油机凸轮型线设计前言四冲程汽车发动机都采用气门式配气机构,其功用是按照发动机的工作顺序和工作循环要求,定时开启和关闭各缸的进、排气门,使新气进入气缸,废气从气缸排出。
其中,凸轮机构作为机械中一种常用机构,在自动学和半自动学当中应用十分广泛,凸轮外形设计在配气机构设计中极为重要,这是由于气门开关的快慢、开度的大小、开启时间的长短都取决于配气机构的形状。
因此,配气凸轮的外形设计和配气凸轮型线设计就决定了时间的大小、配气机构各零件的运动规律及其承载情况。
任务书首先对凸轮进行设计,然后利用最大速度和最大加速度位置基于高次方程凸轮运动规律进行凸轮型线的优化设计,建立数学模型,并设计图论过渡段和绘制图轮廓图。
凸轮的设计1.给定的参数及要求(1)凸轮设计转速nc=4636r/min;(2)进气门开启角233°(曲轴转角),凸轮工作段包角116.5°;(3)排气门开启角220°(曲轴转角),凸轮工作段包角110°;(4)气门重叠角15°(曲轴转角),凸轮转角7.5°;(5)凸轮基圆直径 28mm;(6)进气门最大气门升程hvmax =8.2,排气门最大气门升程hvmax=8。
2.凸轮型线类型的选择配气机构是发动机的一个重要系统,其设计好坏对发动机的性能、可靠性和寿命有极大的影响。
其中凸轮型线设计是配气机构设计中最为关键的部分,在确定了系统参数后,重要的问题是根据发动机的性能和用途,正确选择凸轮型线类型及凸轮参数。
凸轮型线有多种,如复合正弦,复合摆线,低次方,高次方,多项动力,谐波凸轮等。
其中,高次方、多项动力、谐波凸轮等具有连续的高阶倒数的凸轮型线,具有良好的动力性能,能满足较高转速发动机配气机构工作平稳性的要求。
用解析法设计凸轮廓线

二、凸轮基圆半径的确定
2、基圆半径r0的确定
(2)根据许用压力角 [ ] 确定 r0
推杆运动规律确定,lOP= ds/d 是定值 O取在m-m上→ P 必在n-n上, 不变;
(ds /d)i
m
90º - [ ]
ds/d
O取在m-m左侧→ P必在n-n左侧, 变小;
O取在m-m右侧→ P必在n-n右侧, 变大。
[ ] 40 — 50 (摆动从动件)
G F 2b cos( 1 ) (1 ) sin( 1 ) tan 2 l
回程: [ ] 70 — 80
结束
§ 9 - 4 凸轮机构基本尺寸的确定
基本尺寸:基圆半径,滚子半径,平底长度,中心距……
二、凸轮基圆半径的确定
结束
凸轮轮廓曲线的设计
三、用解析法设计凸轮廓线
1、偏置直动滚子推杆盘形凸轮机构
s0 r02 e 2
y
建立 B 点封闭矢量方程
s0
r e s0 s
向x 、y轴投影,得凸轮理论廓线:
r
x
x e cos ( s0 s) sin y e sin ( s0 s) cos
结束
§ 9 - 4 凸轮机构基本尺寸的确定
基本尺寸:基圆半径,滚子半径,平底长度,中心距……
一、凸轮机构的压力角与作用力
讨论: 定义:推杆受力方向与其运动方向 1、↑→ F↑ 传力性能 ↓ 的夹角为压力角 (不考虑摩擦)。 2、↑↑ → 分母为零时 F→ 自锁 推杆受力:G、F、FR1、FR2 临界压力角c :
内凹:a = + rr ·· · · · · · · · · · · · · · · · · · · · · ·
凸轮型线的优化设计

早期 的配气 凸轮 , 轮廓 一般 由几种 圆弧段 或 其
直线段 组成 , 称为几何 凸轮 , 现在 多数凸轮 为 函数 凸 轮, 函数凸轮 的设计 方 法是 从 确 定 的挺 柱升 程 函 数 出发 , 然后据此 确 定 凸 轮 的几 何 外形 .本 研 究 以某
Th tm a s g ft e Ca Pr fl e Op i lDe i n o h m o ie
LI Ji n s e g ,WA NG o g s e g N a — h n Y n —h n
( t t K yL b rt r f gn s S a e e a o ao yo ie ,Ti j ie s y En a i Unv ri ,Ti j 0 0 2 C ia ) nn t a i 3 0 7 , hn . nn
摘
要 : 对 高速 汽 油 机顶 置 凸轮 轴 的 设 计 , 立 了高 次 方 多项 式描 述 动 力 凸轮 特 性 的 数 学 模 型 , 给 出 了相 关 系 针 建 并
数 的 计 算公 式 , 最后 根 据 数 学 模 型 对一 台汽 油 机 的 凸轮 型 线进 行 了优 化 .
关 键 词 : 置 凸轮 轴 ;凸轮 型 线 ; 化 设 计 顶 优 中 图分 类号 : K4 2 T O 文 献标 识 码 :A
O
3 使配气机构工作平稳 , ) 振动和噪音较小 ; 4 凸轮与挺柱间 的接触应力不应过大 ; )
5 凸轮有 良好的润滑特性 ; )
阶段 X一 卫 一 1 其 中 ‰ 为 凸轮 基本工作 段 的半包 ,
0
6 气门与活塞不能相碰. )
微型汽车发动机凸轮型线仿真优化设计及应用研究

微型汽车发动机凸轮型线仿真优化设计及应用研究本文旨在探讨微型汽车发动机凸轮型线的仿真优化设计及其应用研究。
微型汽车发动机是一种小型、轻量化的发动机,具有体积小、重量轻、功率高、燃油经济性好等优点。
在内燃机领域中,微型汽车发动机获得了广泛的应用和研究。
凸轮是微型汽车发动机中的关键部件,控制着气门的开关和气门升程,直接影响发动机的性能。
凸轮型线的合理设计对发动机性能具有重要影响。
本文对微型汽车发动机凸轮型线进行仿真优化设计并进行了应用研究。
具体研究过程如下:一、凸轮型线的建模在仿真优化设计过程中,首先需要建立凸轮型线的数学模型。
本文采用MATLAB软件进行建模,绘制凸轮型线的曲线图并进行数据处理。
通过示波器观察发动机工作过程中气门的开关情况,得到气门开启和关闭的时刻,并将这些数据转换成MATLAB软件中的离散点数据。
二、凸轮型线的仿真优化设计在建立好凸轮型线的数学模型之后,本文采用遗传算法对凸轮型线进行仿真优化设计。
遗传算法是一种模仿自然进化机制的优化算法,通过模拟进化过程来搜索最优解。
将凸轮形状参数作为遗传算法的“基因”,设置适应度函数来衡量凸轮性能,不断演化优化得到最优解。
三、凸轮型线的应用研究通过仿真优化设计,本文得到了一组优化后的凸轮型线参数,再将这些参数应用于实际微型汽车发动机中,进行燃烧室压力测量和性能测试。
实验结果显示,优化后的凸轮型线可以明显提升发动机的输出功率和燃油经济性。
综上所述,通过对微型汽车发动机凸轮型线的仿真优化设计及应用研究,本文取得了一定的研究成果。
在未来的研究中,可以进一步探究凸轮型线的优化方案,并将其应用于更广泛的内燃机领域中,为内燃机的发展提供有价值的参考。
进一步探究凸轮型线的优化方案,可以从以下几个方面进行研究:一、不同工况下的凸轮型线优化不同工况下发动机对凸轮型线的要求不同,因此凸轮型线的优化也需要根据不同工况进行制定。
比如,在高速运转状态下,发动机需要更高的输出功率,因此凸轮型线的参数需要针对高负荷、高转速的要求进行优化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内燃机课程设计凸轮说明书题目90kW四行程四缸汽油机凸轮型线设计学院机电工程学院专业热能与动力工程专业班级热动1002学号姓名指导老师刘军日期2013-6-2590kW四行程四缸汽油机凸轮型线设计前言四冲程汽车发动机都采用气门式配气机构,其功用是按照发动机的工作顺序和工作循环要求,定时开启和关闭各缸的进、排气门,使新气进入气缸,废气从气缸排出。
其中,凸轮机构作为机械中一种常用机构,在自动学和半自动学当中应用十分广泛,凸轮外形设计在配气机构设计中极为重要,这是由于气门开关的快慢、开度的大小、开启时间的长短都取决于配气机构的形状。
因此,配气凸轮的外形设计和配气凸轮型线设计就决定了时间的大小、配气机构各零件的运动规律及其承载情况。
任务书首先对凸轮进行设计,然后利用最大速度和最大加速度位置基于高次方程凸轮运动规律进行凸轮型线的优化设计,建立数学模型,并设计图论过渡段和绘制图轮廓图。
凸轮的设计1.给定的参数及要求(1)凸轮设计转速nc=4636r/min;(2)进气门开启角233°(曲轴转角),凸轮工作段包角116.5°;(3)排气门开启角220°(曲轴转角),凸轮工作段包角110°;(4)气门重叠角15°(曲轴转角),凸轮转角7.5°;(5)凸轮基圆直径 28mm;(6)进气门最大气门升程hvmax =8.2,排气门最大气门升程hvmax=8。
2.凸轮型线类型的选择配气机构是发动机的一个重要系统,其设计好坏对发动机的性能、可靠性和寿命有极大的影响。
其中凸轮型线设计是配气机构设计中最为关键的部分,在确定了系统参数后,重要的问题是根据发动机的性能和用途,正确选择凸轮型线类型及凸轮参数。
凸轮型线有多种,如复合正弦,复合摆线,低次方,高次方,多项动力,谐波凸轮等。
其中,高次方、多项动力、谐波凸轮等具有连续的高阶倒数的凸轮型线,具有良好的动力性能,能满足较高转速发动机配气机构工作平稳性的要求。
由于凸轮设计转速为n c =2318 r/min ,即每分钟凸轮轴转2318圈,属于高速发动机,且为使发动机运动件少,传动链短,整个机构的刚度大,因此我们用双圆弧凸轮的凸轮轴上置式配置机构。
由于四冲程发动机每完成一个工作循环,每个气缸进、排气一次。
这时曲轴转两周,而凸轮轴只旋转一周,所以曲轴与凸轮轴的转速比或传动比为2:1,即由上式已知可知曲轴的转速为2318*2=4636r/min 。
3.计算凸轮的外形尺寸图一 圆弧凸轮的几何参数示意图由上图可知,圆弧凸轮有五个参数:基圆半径r 0=PR ,腹弧半径r 1=OA ,顶弧半径r 2=CB ,基本工作段作用角∠QPR=2φ0和挺住最大升程h tmax 。
其中有题中给出的已知数据有基圆半径r 0、基本工作段作用角2φ0和最大升程h tmax 。
为使圆弧凸轮能可靠地工作,凸轮型线外形应连续圆滑,这就要求各段圆弧在交接点处有公切线或公法线,所以各几何参数之间有一点的约束。
凸轮型线连续圆滑的条件是:腹弧与顶弧的交点B 、顶弧圆心C 、腹弧圆心O ,这三点应在一条直线上。
根据余弦定理,从 △OPC 中可得OPC cos PC OP 2-PC OP OC 222∠+= (1) 由凸轮的几何关系可知PO =r 1-r 0 PC =r 0+h tmax -r 2OC =r 1-r 2 OPC ∠=180o -φ将上式代入(1)可得公式(r 1-r 2)2=(r 0+h tmax -r 2)2+(r 1-r 0)2+2(r 0+h tmax -r 2)(r 1-r 0)∙cos φ0(2)可见,在五个参数中只有四个可以预先选择,其余一个必须满足上式要求。
基圆半径r 0、基本工作段作用角2φ0和最大升程h tmax 都为已知值,可以设计出凸轮的外形。
基圆半径r 0根据凸轮轴直径d t 决定,为了保证加工和维修的可能,常取r 0=0.5d t +1~3mm 。
可知凸轮轴的直径为22~26mm 。
我们取凸轮轴的直径为24mm 。
凸轮作用角2φ0 决定于已选定的配气机构,对进气凸轮有:2φ0 =0.5(180o +α1+α2) 式中 α1-进气提前角,单位(o );α2-排气提前角,单位(o )。
对排气凸轮有:2φ0 =0.5(180o +β 1+β2)式中 β1-进气提前角,单位(o);β2-排气提前角,单位(o )。
挺住的最大升程h tmax 决定与气门所要求的最大升程h qmax 。
h h qmax tmax i 1=式中 i-摇臂的摇臂比,一般i=1.2~1.7,常用为1.5.在凸轮直接驱动气门的顶置凸轮轴式气门机构中,i=1.由于r 0、2φ0、h tmax 三个参数在设计凸轮型线之前已初步确定,所以双圆弧凸轮的设计,实际上是在r 1、r 2两个参数中任选一个,确定一个即可。
由于r 1的选择范围很大,而r 2的选择范围很小,所以先选r 2再选r 1是很合理的。
在选择r 2时,应注意不要使r 2过小,以免凸轮变尖,导致凸轮尖端处接触应力过大,而使凸轮与挺住一对摩擦副产生早起损伤。
凸轮在长期使用尖端磨损超过极限后,必须重新磨削,因此必须留下磨削欲量。
一般认为r 2min 应大于2mm 。
(1)进气凸轮的设计: 设定进气凸轮的r 2=4mm ,则有: (r 1-4)2=(14+8.2-4)2+(r 1-14)2+2(14+8.2-4)(r 1-14)∙cos (58.25 o +7.5 o ) r 12-8r 1+16=18.22+r 12-28r 1+196+2*18.2*(r 1-14)*0.411 解,得5.0396r 1=301.7944 r 1=59.885mm 如下图所示:图二 进气凸轮的尺寸(2)排气凸轮的设计:设定排气凸轮的r2=3mm,则有:(r1-4)2=(14+8-4)2+(r1-14)2+2(14+8-4)(r1-14) cos(55o+7.5o)r 12-8r1+16=182+r12-28r1+196+2*18*(r1-14)*0.462解,得3.368r1=271.152r1=80.508mm图三排气凸轮的尺寸运动规律的分析下面进一步分析凸弧凸轮平面挺柱的运动规律,也即平面挺柱的升程ht、速度vt 、加速度at在凸弧凸轮型线上随凸轮转角α的变化规律。
图四凸弧凸轮平面的升程()r r 180a 21212maxD O O sin sin -==-︒O O φr r 210max Dsin sin -=φαr r C C C O O C C C h 0232322121Dcos t2-+=-+==β)(O A A A O A A A h 13321121t 1+-==为分析方便,计算分段进行。
第一阶段(即挺柱与腹弧相接触的阶段),当挺柱在A 点相接触(α=0)的时刻起即开始上升(图四中),当凸轮转过α角时,挺柱的升程为(3)式中 O A 11=r 1rA A 032=))((ααcos 1cos r r O O O A 01113--==代入(3)得()[]αcos t r r r r h 0111-+-=经整理得 ()()αcos 1t r r h 011--=第一阶段凸轮的最大转角αmax由△ OO 1O 2的关系决定,即由此得在计算挺柱第二阶段(即挺柱与顶弧接触段)的升程时(图四),为方便计算,凸轮转角将由相当与气门全开位置C 点开始,逆着凸轮的旋转方向计算。
在β角处挺柱的升程为同时加减一个h tmax ,则得 ()βcos 1D h h tmax t --= 第二阶段凸轮的最大转角βmax按下式计算αφβmax 0max -=将上面所得的挺柱升程与转角关系对时间求导,可得相应转角的速度。
挺柱在第一段上的速度为()αωsin dtdh r r v 01t t1t1-==βωDsin dt dh t t2t2v ==()αωcos dt dv r r a 012t t1t1-==βωDcos dtdv 2tt2t2a -==式中 t ω—凸轮旋转角速度,在第一阶段上,挺柱速度在max α时达到最大值。
在第二段上挺柱速度为在第二段上,挺住速度在βmax时达到最大值。
在第一段上挺柱的加速度为在第一段上,挺柱加速度在a=0时达到最大值。
在第二段上挺柱的加速度为在第二段上,挺柱加速度在β=0时达到最大值。
图五 第一阶段挺柱的速度图六第二阶段挺柱的速度图七第一阶段挺柱的加速度图八第二阶段挺柱的加速发动机进气凸轮型线发动机挺柱的升程图九凸轮整体运动情况图十凸轮工作段的情况配气机构在实际运动过程中,运动从凸轮开始,经过一长串传动链才传到气门。
过去在进行气门运动规律的计算时,人们通常把配气机构简单地视为刚性系统,认为气门的运动完全受凸轮外形控制,只要确定了凸轮从动件的运动规律,求出升程曲线丰满系数及最大正、负加速度,就足以判别凸轮设计的优劣,因而只进行运动学计算,是一个纯几何问题.但是,由于传动链本身具有一定的质量和弹性,工作时产生的弹性变形会使位于传动链末端气门处的运动产生很大畸变,即气门的升程、速度,特别是加速度曲线“失真”.气门的运动有时滞后于挺柱,有时又超越挺柱,使传动链脱节,气门开闭不正常、反跳,整个机构震动和噪音加大,甚至机构的正常工作遭到破坏。
随着发动机转速的提高,这种因传动链变形而产生的不利影响尤为明显,因此有必要对内燃机配气机构进行动力学分析,以便对配气机构的动力学性能进行评价,为配气机构的设计提供一种评价的理论依据。
为了验证所设计的型线符合动力学要求,对所优化的新型线进行了动力学仿真。
上图图是根据运动学与动力学分别计算出来的加速度,可以看出,挂动学公式计算的加速度与动力学差异比较大,说明对凸轮进行动力学仿真确实是非常必要的高次多项动力凸轮升程曲线数学模型的建立由于该发动机是一高速发动机,因此重点对高次多项式凸轮和多项动力凸轮进行分析对比首先从设计期望的气门升程规律开始,其气门升程函数一般采用七次多项式,其形式为:()x C x C x C x C x C x C C SS RR QQ PP 44220a h ++++++=式中,α----为凸轮转角(o );αB ----为凸轮基本工作段的半包角(o );h(a)----为气门升程;x----为转角比,在凸轮的上升阶段:x=1-a/a B ,有a=0时,x=1,α=αB 时,x=0;在下降阶段:x=a/a B -1。
C 2x 2----此项保证在气门升程最大处有一最大负加速度,因此要求C 2<0; C 4x 4----自由项,C 4可自由选取。
用于控制气门负加速度的曲线形状,使其vV d dh=αd h d 2v 2=α03d h d v3=α0d h d 4v 4=αC C C C C 4S R QP 242-S 1-S S 2-R 1-R R 2-Q 1-Q Q 2-P 1-P P -=+++))(())(())(())((与气门弹簧特性很好配合。
