电路分析四之积分微分电路
《积分和微分电路》课件

常见的积分电路实现方法有RC积分电路和运算 放大器积分电路。
二、微分电路
什么是微分电路
微分电路对输入信号进行微分, 输出信号表示输入信号的变化 率。
微分电路的符号表示
微分电路的符号使用一个d/dt符 号来表示。
பைடு நூலகம்
微分电路的基本原理
通过电容器对输入信号进行微 分运算。
微分电路的实现方法
《积分和微分电路》PPT 课件
本课件将介绍积分和微分电路的原理、应用和实验演示。通过丰富的布局和 图像,让您轻松理解和熟悉这一主题。
一、积分电路
什么是积分电路
积分电路将输入信号积分,输出信号表示输入信 号的累积。
积分电路的基本原理
通过电容器对输入信号进行积分运算。
积分电路的符号表示
积分电路的符号使用一个^∫符号来表示。
常见的微分电路实现方法有RC 微分电路和运算放大器微分电 路。
三、积分和微分电路的比较分析
1
积分电路与微分电路的区别
积分电路对输入信号进行积分,微分电路对输入信号进行微分。
2
积分和微分电路的应用场合
积分电路常用于信号处理和控制系统,微分电路常用于滤波和识别系统。
四、实验演示
积分电路实验装置
通过实验装置演示积分电路的原 理和应用。
微分电路实验装置
通过实验装置演示微分电路的原 理和应用。
实验演示步骤
详细步骤演示和讲解积分和微分 电路的实验操作。
五、总结
积分和微分电路的应用优缺点总结
通过总结积分和微分电路的应用优点和缺点,了解其在不同领域中的特点。
未来发展趋势
展望积分和微分电路在未来的发展方向和应用领域。
积分电路和微分电路实验报告

积分电路和微分电路实验报告篇一:积分电路与微分电路实验报告四、积分电路与微分电路目的及要求:(1)进一步掌握微分电路和积分电路的相关知识。
(2)学会用运算放大器组成积分微分电路。
(3)设计一个RC微分电路,将方波变换成尖脉冲波。
(4)设计一个RC积分电路,将方波变换成三角波。
(5)进一步学习和熟悉Multisim软件的使用。
(6)得出结论进行分析并写出仿真体会。
一.积分电路与微分电路1. 积分电路及其产生波形1.1运算放大器组成的积分电路及其波形设计电路图如图所示:图 1.1积分电路其工作原理为:积分电路主要用于产生三角波,输出电压对时间的变化率与输入阶跃电压的负值成正比,与积分时间常数成反比,即?U0?t??UinR1C式中,R1C积分时间常数,Uin为输入阶跃电压。
反馈电阻Rf的主要作用是防止运算放大器LM741饱和。
C为加速电容,当输入电压为方波时,输入端U01的高电平等于正电源?Vcc,低电平等于负电源电压?Vdd,比较器的U??U??0时,比较器翻转,输入U01从高电平跳到低电平?Vdd。
输出的是一个上升速度与下降速度相等的三角波形。
图1.2积分电路产生的波形1.2微分电路及其产生波形2. 运算放大器组成的微分电路及其波形设计的微分电路图:图2.1微分电路其工作原理为:将积分电路中的电阻与电容对换位子,并选用比较小的时间常数RC,便得到了微分电路。
微分电路中,输出电压与输入电压对时间的变化率的负值成正比,与微分时间常数成反比,所以RinU0??RfC?U?tin的主要作用是防止运放LM741产生自激振荡。
v0??RCdV/dt,输出电压正比与输入电压对时间的微商,符号表示相位相反,当输入电压为方波时,当t?o时输出电压为一个有限制。
随着C的充电,输出电压v0将逐渐衰减,最后趋于零,就回形成尖顶脉冲波。
微分电路中用信号发生器输入方波信号,经过微分电路就会产生输出脉冲波信号。
结论与体会:通过此设计学会了用运算放大器组成的积分电路和微分电路,还学会了Multisim 软件的应用和使用方法。
20种常见基本电路
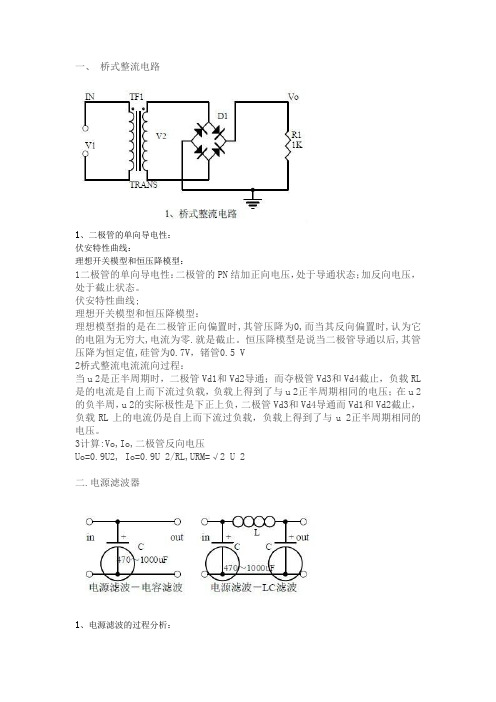
一、桥式整流电路1、二极管的单向导电性:伏安特性曲线:理想开关模型和恒压降模型:1二极管的单向导电性:二极管的PN结加正向电压,处于导通状态;加反向电压,处于截止状态。
伏安特性曲线;理想开关模型和恒压降模型:理想模型指的是在二极管正向偏置时,其管压降为0,而当其反向偏置时,认为它的电阻为无穷大,电流为零.就是截止。
恒压降模型是说当二极管导通以后,其管压降为恒定值,硅管为0.7V,锗管0.5 V2桥式整流电流流向过程:当u 2是正半周期时,二极管Vd1和Vd2导通;而夺极管Vd3和Vd4截止,负载RL 是的电流是自上而下流过负载,负载上得到了与u 2正半周期相同的电压;在u 2的负半周,u 2的实际极性是下正上负,二极管Vd3和Vd4导通而Vd1和Vd2截止,负载RL上的电流仍是自上而下流过负载,负载上得到了与u 2正半周期相同的电压。
3计算:Vo,Io,二极管反向电压Uo=0.9U2, Io=0.9U 2/RL,URM=√2 U 2二.电源滤波器1、电源滤波的过程分析:波形形成过程:1电源滤波的过程分析:电源滤波是在负载RL两端并联一只较大容量的电容器。
由于电容两端电压不能突变,因而负载两端的电压也不会突变,使输出电压得以平滑,达到滤波的目的。
波形形成过程:输出端接负载RL时,当电源供电时,向负载提供电流的同时也向电容C充电,充电时间常数为τ充=(Ri∥RLC)≈RiC,一般Ri〈〈RL,忽略Ri 压降的影响,电容上电压将随u 2迅速上升,当ωt=ωt1时,有u 2=u 0,此后u 2低于u 0,所有二极管截止,这时电容C通过RL放电,放电时间常数为RLC,放电时间慢,u 0变化平缓。
当ωt=ωt2时,u 2=u 0, ωt2后u 2又变化到比u 0大,又开始充电过程,u 0迅速上升。
ωt=ωt3时有u 2=u 0,ωt3后,电容通过RL放电。
如此反复,周期性充放电。
由于电容C的储能作用,RL上的电压波动大大减小了。
积分电路设计

积分电路是信号调理器实现加速 度信号转换为速度和位移的变换 电路。
一、基本概念
最简单的振动是简谐振动 特点: (1) 参量是时间的谐和函数; (2) 在时域为一正弦波; (3) 在频域为一直线谱(信号的傅立叶变换)。
X(ω) x(t)
0
t 0 ω0 ω
简谐振动的时域参数
振动时域参数间的幅度关系:微积分关系
设计要求
积分器低端截止频率 0.01Hz,衰减为-3dB; 高端频率为学号最末三位数,衰减取-25dB;
学号最末三位数
积分网络数目确定
一般要设计多条积分曲线; 第二条积分曲线的截止频率应该为第一条积分曲 线衰减-25dB处的频率,即第二条积分曲线在此 处衰减-3dB; 第三条曲线参照上述处理。
ieterceiodd????????rc分压电路rc微积分电路rc滤波电路rc耦合电路rcoeirc微分电路的频率特性四rc积分电积分曲线1速度积分曲线2积分器的阶跃方波响应积分器的正弦波响应?当积分器的输为正弦波时输出为余弦波相差为90度幅度增大倍
振动时域参数的相位关系
振动时域参数间的幅 度关系: 相位a、v、x依次超 前π/2。
v
x
a ω x、v、a三者的相位关系
二、传感器的动态特性
传感器的动态特性参数比较多,反映能测量参数 的频率线性范围。 (1)频率线性范围: 频率响应曲线,频率对灵敏度的影响; (2)幅度线性范围: 频率对测量幅度的影响(诺莫图); (3)相位线性范围:频率对相位的影响。
加速度传感器只能测量振动加速度; 速度和位移通过积分电路实现: (1) 通过一次积分电路输出位移; (2) 通过二次积分电路输出速度。 如果是测量振动位移,则速度和加速度分别通过 一次和二次微分电路来实现。 如如果是测量振动速度,则一次微分为加速度, 一次积分为位移。
RC微分、积分电路检测与分析

任何两个彼此绝缘(insulator)又相 隔很近的导体(conductor )就形成一个电 容器。它是容纳和释放电荷的电子元器件。
金属极板
电路图符号
绝缘物质 (电介质)
C
Capacitor
两个电极板在单位)。电压作用下,每一级 板上储存了电荷量。电容器带电时,它的两 个极板之间产生电势差U,电势差U随所带电 量Q的增加而增加,而 Q 是一恒量,该恒量叫
数字,第三环表示 ×10n(n:第三色环代表的数
字)。色环电容器的颜色数码对照表如下。
如:色环依次为黄、紫、橙,
黄在第一色环代表(4)、
紫在第二色环代表(7)、 47×103 pF=0.047 μF
橙在第三色环代表 103 。
3、电容器的主要参数(parameter )
(1)标称容量 (2)允许偏差 (3)额定工作电压
U
做电容器的电容(capacitance)。电容用符 号“C”表示。国际单位是法拉(F)。
1F=106μF=1012pF
1μF=106pF
电容器按其电容量是否可变,可分为固定电容
器,可变电容器和微调电容器。
电容器按其介质的不同,可分为空气介质电容器
和固体介质电容器(纸介、云母、陶瓷、涤纶、玻璃
釉、电解电容器)。
情境二
项目二 RC微分、Βιβλιοθήκη 分电路 检测与分析学习目标
1、会识别和测试电容器; 2、会使用示波器、信号源观测RC微分电路、积分电路波形; 3、会分析计算纯电容电路。
知识目标
技能目标
1、掌握电容器的特性和读取 1、会识别电容器;
知识;
2、会用万用表测试电容器;
2、掌握万用表测量电容器的 3、会使用示波器、信号源观
积分电路和微分电路的应用

积分电路和微分电路的应用积分电路和微分电路是电子工程中非常重要且广泛应用的两种电路。
积分电路可用于对输入信号进行积分运算,而微分电路则可以对输入信号进行微分运算。
这两种电路在不同领域中有着各自独特的应用。
一、积分电路的应用积分电路主要用于对信号进行时间积分运算,即对输入信号进行时间的累加。
其中最常见的应用就是在音频系统中,通过积分电路可以实现音频信号的频率分析和信号调制。
首先,积分电路可以对输入信号的幅度进行积分运算,从而得到输入信号的功率谱密度。
这对于音频系统来说尤为重要,因为它可以帮助我们了解音频信号的频谱分布情况,进而对音频信号进行合理的调整。
比如,在音乐录音室中,通过积分电路可以实时监测出音频信号在不同频段上的能量分布情况,从而调整音频设备的参数,使得音频产生的效果更加符合设计要求。
此外,积分电路还可以用于信号调制。
在通信系统中,调制是对输入信号进行编码和解码的过程,而积分电路可以用于信号的调制解调。
例如,在遥控器中,通过积分电路可以将输入信号进行编码,然后通过无线电波传输到接收端进行解码。
这种调制技术的应用,在遥控器、无线电和移动通信等领域得到广泛应用。
二、微分电路的应用微分电路则是对信号进行微分运算,可以对输入信号的变化率进行测量。
这种测量技术在很多领域中都有着重要的应用。
一个常见的应用就是在汽车领域中的刹车系统中。
刹车系统通过微分电路可以实时测量车轮的转速变化率,并将其与事先设定的规范进行比较,从而控制刹车力度。
这样可以实现自动刹车系统,在紧急情况下及时减速,保障行车安全。
此外,微分电路还被广泛应用于医疗设备中。
例如,在心电图仪中,通过微分电路可以实时检测心脏电信号的变化率,从而判断病人的心脏状况。
这对于医生来说非常重要,能够帮助他们及时发现心脏病变化,采取相应的治疗措施。
微分电路还可以应用于加速度计和陀螺仪等传感器中。
通过微分电路可以实时测量物体的加速度和角速度的变化率,从而判断物体的运动状态。
电路分析EDA设计性实验内容 有源RC微分、积分电路设计-1

实验三 一阶RC 微分、积分电路设计一、实验目的1. 掌握一阶RC 微分、积分电路的组成与工作原理;2. 掌握运用MULTISUM 软件实现一阶有源RC 微分、积分电路的设计方法;3. 掌握运用MULTISUM 软件实现RC 微分、积分电路的测试、分析方法;4. 培养学生对知识的综合运用能力,提高学生创新能力。
二、实验性质设计性实验,实验学时4学时。
三、设计任务及要求1. 一阶无源RC 微分、积分电路的设计设计简单的无源RC 微分和RC 积分电路。
讨论电路中元件参数的选取原则,注意微分电路和积分电路结构的区别和联系。
要求:(1)要有完整的理论分析及设计过程,根据理论分析结果讨论设计电路参数时应满足的条件。
(2)在MULTISUM 平台上完成电路搭建。
(3)利用所设计的电路分别对50HZ 的周期矩形信号进行测试,搭建测试电路并记录测试结果。
2. 一阶有源RC 积分电路的设计设计一个积分电路,用来将方波变换为三角波。
已知方波的幅值为2V ,频率为1kHz 。
要求积分电路的输入电阻Ω≥k R i 20。
要求:(1)要有完整的理论分析和设计过程,讨论设计电路时主要参数的选取原则。
(2)在MULTISUM 平台上完成电路搭建。
(3)按设计指标要求给所设计的电路输入方波电压信号,观察积分电路的输出波形。
记录输出波形的幅值和频率,若达不到设计指标要求,应调整电路参数,直到满足设计指标为止。
(4)再分别将三角波和正弦波信号作为测试的输入信号,观察电路的输入和输出信号的情况并记录结果(其中,测试信号频率自定,注意根据电路的参数适当选择测试信号的周期和频率)。
四、分析总结1.分析、总结测试过程中出现的问题及解决办法。
2. 对无源积分电路和有源积分电路进行简单的对比分析。
3. 分析误差及误差产生的原因。
注意:在进行实验前必须做好预习并完成理论设计内容,报告内容要力争完整、科学。
电路分析四之积分微分电路

微分与积分电路1、电路的作用,与滤波器的区别和相同点。
2、微分和积分电路电压变化过程分析,画出电压变化波形图。
3、计算:时间常数,电压变化方程,电阻和电容参数的选择。
积分电路和微分电路的特点:积分电路、微分电路可以分别产生尖脉冲和三角波形的响应 1:积分电路可以使输入方波转换成三角波或者斜波微分电路可以使使输入方波转换成尖脉冲波2:积分电路电阻串联在主电路中,电容在干路中微分则相反3:积分电路的时间常数t要大于或者等于10倍输入脉冲宽度 微分电路的时间常数t要小于或者等于1/10倍的输入脉冲宽度 4:积分电路输入和输出成积分关系微分电路输入和输出成微分关系积分电路:1.延迟、定时、时钟2.低通滤波3.改变相角(减)微分电路:1.提取脉冲前沿2.高通滤波3.改变相角(加)微分图像(在单位阶跃响应的前提下)微分电路可把矩形波转换为尖脉冲波,此电路的输出波形只反映输入波形的突变部分,即只有输入波形发生突变的瞬间才有输出。
而对恒定部分则没有输出。
输出的尖脉冲波形的宽度与RC有关(即电路的时间常数),RC越小,尖脉冲波形越尖,反之则宽。
积分图像(在单位阶跃响应的前提下)积分电路是使输出信号与输入信号的时间积分值成比例的电路RC电路的分类(1)RC 串联电路电路的特点:由于有电容存在不能流过直流电流,电阻和电容都对电流存在阻碍作用,其总阻抗由电阻和容抗确定,总阻抗随频率变化而变化。
RC 串联有一个转折频率: f0=1/2πR1C1当输入信号频率大于 f0 时,整个 RC 串联电路总的阻抗基本不变了,其大小等于 R1。
(2)RC 并联电路RC 并联电路既可通过直流又可通过交流信号。
它和 RC 串联电路有着同样的转折频率:f0=1/2πR1C1。
当输入信号频率小于f0时,信号相对电路为直流,电路的总阻抗等于 R1;当输入信号频率大于f0 时 C1 的容抗相对很小,总阻抗为电阻阻值并上电容容抗。
当频率高到一定程度后总阻抗为 0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微分与积分电路1、电路的作用,与滤波器的区别和相同点。
2、微分和积分电路电压变化过程分析,画出电压变化波形图。
3、计算:时间常数,电压变化方程,电阻和电容参数的选择。
积分电路和微分电路的特点:积分电路、微分电路可以分别产生尖脉冲和三角波形的响应 1:积分电路可以使输入方波转换成三角波或者斜波微分电路可以使使输入方波转换成尖脉冲波2:积分电路电阻串联在主电路中,电容在干路中微分则相反3:积分电路的时间常数t要大于或者等于10倍输入脉冲宽度 微分电路的时间常数t要小于或者等于1/10倍的输入脉冲宽度 4:积分电路输入和输出成积分关系微分电路输入和输出成微分关系积分电路:1.延迟、定时、时钟2.低通滤波3.改变相角(减)微分电路:1.提取脉冲前沿2.高通滤波3.改变相角(加)微分图像(在单位阶跃响应的前提下)微分电路可把矩形波转换为尖脉冲波,此电路的输出波形只反映输入波形的突变部分,即只有输入波形发生突变的瞬间才有输出。
而对恒定部分则没有输出。
输出的尖脉冲波形的宽度与RC有关(即电路的时间常数),RC越小,尖脉冲波形越尖,反之则宽。
积分图像(在单位阶跃响应的前提下)积分电路是使输出信号与输入信号的时间积分值成比例的电路RC电路的分类(1)RC 串联电路电路的特点:由于有电容存在不能流过直流电流,电阻和电容都对电流存在阻碍作用,其总阻抗由电阻和容抗确定,总阻抗随频率变化而变化。
RC 串联有一个转折频率: f0=1/2πR1C1当输入信号频率大于 f0 时,整个 RC 串联电路总的阻抗基本不变了,其大小等于 R1。
(2)RC 并联电路RC 并联电路既可通过直流又可通过交流信号。
它和 RC 串联电路有着同样的转折频率:f0=1/2πR1C1。
当输入信号频率小于f0时,信号相对电路为直流,电路的总阻抗等于 R1;当输入信号频率大于f0 时 C1 的容抗相对很小,总阻抗为电阻阻值并上电容容抗。
当频率高到一定程度后总阻抗为 0。
(3)RC 串并联电路RC 串并联电路存在两个转折频率f01 和 f02:f01=1/2πR2C1, f02=1/2πC1*[R1*R2/(R1+R2)]当信号频率低于 f01 时,C1 相当于开路,该电路总阻抗为 R1+R2。
当信号频率高于 f02 时,C1 相当于短路,此时电路总阻抗为 R1。
当信号频率高于 f01 低于 f02 时,该电路总阻抗在 R1+R2 到R1之间变化。
积分电路的作用是:消减变化量,突出不变量。
RC电路的积分条件:RC≥Tk,Tk是脉冲周期,积分电路可将矩形脉冲波转换为锯齿波或三角波,还可将锯齿波转换为抛物波。
电路原理很简单,都是基于电容的冲放电原理,这里就不详细说了,这里要提的是电路的时间常数R*C,构成积分电路的条件是电路的时间常数必须要大于或等于10倍于输入波形的宽度。
微分电路的作用是:消减不变量,突出变化量。
微分电路可把矩形波转换为尖脉冲波,电路的输出波形只反映输入波形的突变部微分电路分,即只有输入波形发生突变的瞬间才有输出。
而对恒定部分则没有输出。
输出的尖脉冲波形的宽度与R*C有关(即电路的时间常数),R*C越小,尖脉冲波形越尖,反之则宽。
此电路的R*C必须远远少于输入波形的宽度,否则就失去了波形变换的作用,变为一般的RC耦合电路了,一般R*C少于或等于输入波形宽度的微分电路1/10就可以了。
在模拟及脉冲数字电路中,常常用到由电阻R和电容C组成的RC电路,在些电路中,电阻R和电容C的取值不同、输入和输出关系以及处理的波形之间的关系,产生了RC电路的不同应用,下面分别谈谈微分电路、积分电路、耦合电路、脉冲分压器以及滤波电路。
1. RC微分电路如图1所示,电阻R和电容C串联后接入输入信号VI,由电阻R 输出信号VO,当RC 数值与输入方波宽度tW之间满足:RC<<tW,这种电路就称为微分电路。
在 R两端(输出端)得到正、负相间的尖脉冲,而且发生在方波的上升沿和下降沿,如图2 所示。
在t=t1时,VI由0→Vm,因电容上电压不能突变(来不及充电,相当于短路,VC=0),输入电压VI全降在电阻R上,即VO=VR=VI =V m 。
随后(t》t1),电容C的电压按指数规律快速充电上升,输出电压随之按指数规律下降(因VO=VI-VC=Vm-VC),经过大约3τ(τ=R × C)时,VCVm,VO0,τ(RC)的值愈小,此过程愈快,输出正脉冲愈窄。
t=t2时,VI由Vm→0,相当于输入端被短路,电容原先充有左正右负的电压V m开始按指数规律经电阻R放电,刚开始,电容C来不及放电,他的左端(正电)接地,所以VO=-Vm,之后VO随电容的放电也按指数规律减小,同样经过大约3τ后,放电完毕,输出一个负脉冲。
只要脉冲宽度tW>(5~10)τ,在tW时间内,电容C已完成充电或放电(约需3 τ),输出端就能输出正负尖脉冲,才能成为微分电路,因而电路的充放电时间常数τ必须满足:τ<(1/5~1/10)tW,这是微分电路的必要条件。
由于输出波形VO与输入波形VI之间恰好符合微分运算的结果[VO=RC( dVI/dt)],即输出波形是取输入波形的变化部分。
如果将VI按傅里叶级展开,进行微分运算的结果,也将是VO的表达式。
他主要用于对复杂波形的分离和分频器,如从电视信号的复合同步脉冲分离出行同步脉冲和时钟的倍频应用。
2. RC耦合电路图1中,如果电路时间常数τ(RC)>>tW,他将变成一个RC耦合电路。
输出波形与输入波形一样。
如图3所示。
(1)在t=t1时,第一个方波到来,VI由0→Vm,因电容电压不能突变(VC=0),VO=VR=VI=Vm。
(2)t1<t<t2时,因τ>>tW,电容C缓慢充电,VC缓慢上升为左正右负,V O=VR=VI-VC,VO缓慢下降。
(3)t=t2时,VO由Vm→0,相当于输入端被短路,此时,VC已充有左正右负电压Δ[Δ=(VI/τ)×tW],经电阻R非常缓慢地放电。
(4)t=t3时,因电容还来不及放完电,积累了一定电荷,第二个方波到来,电阻上的电压就不是Vm,而是VR=Vm-VC(VC≠0),这样第二个输出方波比第一个输出方波略微往下平移,第三个输出方波比第二个输出方波又略微往下平移,…,最后,当输出波形的正半周“面积”与负半周“面积”相等时,就达到了稳定状态。
也就是电容在一个周期内充得的电荷与放掉的电荷相等时,输出波形就稳定不再平移,电容上的平均电压等于输入信号中电压的直流分量(利用C的隔直作用),把输入信号往下平移这个直流分量,便得到输出波形,起到传送输入信号的交流成分,因此是一个耦合电路。
以上的微分电路与耦合电路,在电路形式上是一样的,关键是tW与τ的关系,下面比较一下τ与方波周期T(T》tW)不同时的结果,如图4所示。
在这三种情形中,由于电容C的隔直作用,输出波形都是一个周期内正、负“面积”相等,即其平均值为0,不再含有直流成份。
①当τ>>T时,电容C的充放电非常缓慢,其输出波形近似理想方波,是理想耦合电路。
②当τ=T时,电容C有一定的充放电,其输出波形的平顶部分有一定的下降或上升,不是 理想方波。
③当τ<<T时,电容C在极短时间内(tW)已充放电完毕,因而输出波形为上下尖脉冲,是微分电路。
3. RC积分电路如图5所示,电阻R和电容C串联接入输入信号VI,由电容C 输出信号V0,当RC (τ)数值与输入方波宽度tW之间满足:τ》》tW,这种电路称为积分电路。
在电容C两端(输出端)得到锯齿波电压,如图6所示。
(3)t=t2时,VI由Vm→0,相当于输入端被短路,电容原先充有左正右负电压VI(VI《Vm)经R缓慢放电,VO(VC)按指数规律下降。
这样,输出信号就是锯齿波,近似为三角形波,τ》》tW是本电路必要条件,因为他是在方波到来期间,电容只是缓慢充电,VC还未上升到Vm时,方波就消失,电容开始放电,以免电容电压出现一个稳定电压值,而且τ越大,锯齿波越接近三角波。
输出波形是对输入波形积分运算的结果,他是突出输入信号的直流及缓变分量,降低输入信号的变化量。
4. RC滤波电路(无源)在模拟电路,由RC组成的无源滤波电路中,根据电容的接法及大小主要可分为低通滤波电路(如图7)和高通滤波电路(如图8)。
(1)在图7的低通滤波电路中,他跟积分电路有些相似(电容C都是并在输出端),但他们是应用在不同的电路功能上,积分电路主要是利用电容C充电时的积分作用,在输入方波情形下,来产生周期性的锯齿波(三角波),因此电容C及电阻R是根据方波的tW来选取,而低通滤波电路,是将较高频率的信号旁路掉(因XC=1/(2πfC),f较大时,XC较小,相当于短路),因而电容C的值是参照低频点的数值来确定,对于电源的滤波电路,理论上C值愈大愈好。
(2)图8的高通滤波电路与微分电路或耦合电路形式相同。
在脉冲数字电路中,因RC与脉宽tW的关系不同而区分为微分电路和耦合电路;在模拟电路,选择恰当的电容C值,就可以有选择性地让较高频的信号通过,而阻断直流及低频信号,如高音喇叭串接的电容,就是阻止中低音进入高音喇叭,以免烧坏。
另一方面,在多级交流放大电路中,他也是一种耦合电路。
5. RC脉冲分压器当需要将脉冲信号经电阻分压传到下一级时,由于电路中存在各种形式的电容,如寄生电容,他相当于在负载侧接有一负载电容(如图9),当输入一脉冲信号时,因电容CL的充电,电压不能突变,使输出波形前沿变坏,失真。
为此,可在R1两端并接一加速电容 C1,这样组成一个RC脉冲分压器(如图10)。
(1)t=0+时,电容视为短路,电流只流经C1,CL,VO由C1和CL分压得到:但是,任何信号源都有一定的内阻,以及一些电路的需要,通常采取过补偿的办法,如电视信号中,为突出传送图像的轮廓,采用勾边电路,就是通过加大C1的取值。
求RC电路的放电时间为1分锺,电压从9V降到5v.放电电流为300mA左右,选择最佳的的R值和C值。
RC电路的放电方程是:UC=US*e-t/RC,其中,US=9,UC=5,t=60,代入公式可求出时间常数RC的值,现在关键的就是要确定R和C的值了,它只能通过你所要求的放电电路来选择了,由放电电流公式:I=C*dU/dt,再将此公式代入上面的公式中可得:I=-US*C/RCe-t/RC,将C看成一个未知参数,然后作出I-t曲线,计算出该曲线与直线I=300所围成的面积,这个积分上下限为t=0-60,去使面积最小的C 值就可.。
