LZW编码算法matlab实现
LZW-编码详解

待编码的数据序列为“dacab”,信源中各符号出现的概 率依次为P(a)=0.4,P(b)=0.2,P(c)=0.2, P(d)=0.2。
数据序列中的各数据符号在区间[0, 1]内的间隔(赋 值范围)设定为:
a=[0, 0.4) b=[0.4, 0.6) c=[0.6, 0.8) d=[0.8, 1.0 ]
8)读入code=3H,解码完毕。
解码过程
行号
1 2 3 4 5 6 7 8
输入数据 code 2H 0H 0H 1H 6H 4H 6H 3H
新串
aa ab bb bba aab
输出结果 oldcode 生成新字 符及索引
a
0H
a
0H aa<4H>
b
1H ab<5H>
bb
6H bb<6H>
aa
4H bba<7H>
输出S1=“aa”在字串表中的索引4H,并在字符串表末尾
为S1+S2=“aab”添加索引8H,且S1= S2=“b”
序号 输入数据 S1+S2 输出结果 S1
生成新字符及索引
S2
1 NULL
NULL 2H
NULL
2a
a
a
3a
aa
0H
a
aa<4H>
4b
ab
0H
b
ab<5H>
5b
bb
1H
b
bb<6H>
6b
4)读入code=1H,输出“b”,然后将 oldcode=0H所对应的字符串“a”加上 code=1H对应的字符串的第一个字符”b”, 即”ab”添加到字典中,其索引为5H,同 时oldcode=code=1H
LZW编码算法matlab实现

LZW编码算法,尝试使用matlab计算%encoder LZW for matlab%yu 20170503clc;clear;close all;%初始字典dic = cell(512,1);for i = 1:256dic{i} = {num2str(i)};end%输入字符串a,按空格拆分成A,注意加1对应范围1~256 a = input('input:','s');a = deblank(a);A = regexp(a,'\s+','split');L = length(A);for j=1:LA{j} = num2str(str2num(A{j})+1);endA_t = A{1};%可识别序列B_t = 'test';%待验证词条d = 256;%字典指针b = 1;%输出指针B = cell(L,1);%输出初始output = ' ';%输出初始j=1;for j = 2:Lm=1;B_t =deblank([A_t,' ',A{j}]);%合成待验证词条while(m <= d)if strcmp(dic{m},B_t)A_t = B_t;breakelsem=m+1;endendwhile(m == d+1)d = d+1;dic{d} = B_t;q=1;for q=1:dif strcmp(dic{q},A_t)B{b} = num2str(q);b = b+1;endendA_t = A{j};endendfor q=1:d%处理最后一个序列输出if strcmp(dic{q},A_t)B{b} = num2str(q);b = b+1;endendfor n = 1:(b-1)B{n} =num2str(str2num(B{n})-1);output=deblank([output,' ',B{n}]);endoutput运算结果计算结果为39 39 126 126 256 258 260 259 257 126LZW解码算法,使用matlab计算%decoder LZW for matlab%yu 20170503clc;clear;close all;%初始字典dic = cell(512,1);for i = 1:256dic{i} = {num2str(i)};end%输入字符串a,按空格拆分成A,注意加1对应范围1~256 a = input('input:','s');a = deblank(a);A = regexp(a,'\s+','split');L = length(A);for j=1:LA{j} = num2str(str2num(A{j})+1);endB_t = A{1};%待验证词条d = 256;%字典指针b = 1;%输出指针B = cell(L,1);%输出初始output = ' ';%输出初始j=1;B{b} = char(dic{str2num(A{j})});b = b+1;for j = 2:LBB = char(dic{str2num(A{j})});B_d = regexp(BB,'\s+','split');%按空格拆分L_B = length(B_d);p=1;for p=1:L_BB{(b+p-1)} = B_d{p};m=1;B_t =deblank([char(B_t),' ',char(B_d{p})]);%合成待验证词条while(m <= d)if strcmp(dic{m},B_t)B_t = B_t;breakelsem=m+1;endendwhile(m == d+1)d = d+1;dic{d} = B_t;B_t = B_d{p};endendb = b+L_B;endfor n = 1:(b-L_B)B{n} = num2str(str2num(B{n})-1);output=deblank([output,' ',B{n}]); endoutput运算结果运算结果为39 39 126 126 39 39 126 126 39 39 126 126 39 39 126 126。
LZW编码与译码编程实现
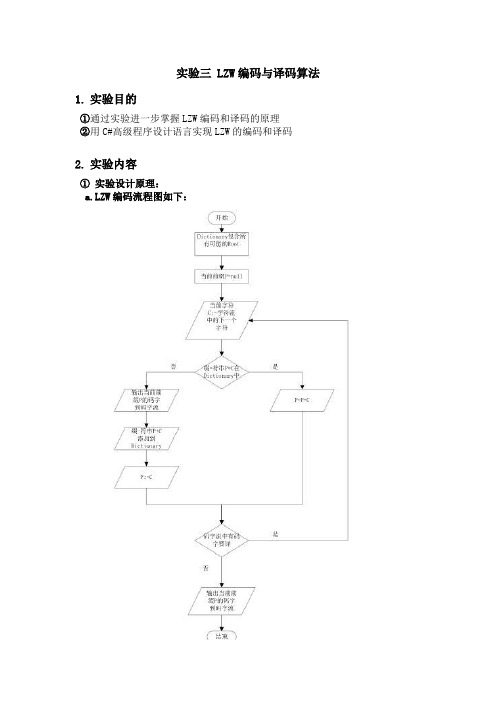
实验三 LZW编码与译码算法1.实验目的①通过实验进一步掌握LZW编码和译码的原理②用C#高级程序设计语言实现LZW的编码和译码2.实验内容①实验设计原理:a.LZW编码流程图如下:b.LZW译码流程图如下:②实验源代码:using System;using System.Collections.Generic; using System.Linq;using System.Text;using System.Threading.Tasks;namespace LZW{class Program{static void Main(string[] args){Encode();//编码Decode();//译码}public static void Encode()//编码函数{string Input = "ABBABABAC";//需要编码的字符流Console.WriteLine("编码前字符流:{0}",Input);Console.WriteLine();string P = null;//当前前缀P为空string X = null;int i = 0, j = 0, m = 3, n = 4, h = 0;string C = null;//当前字符Cstring[,] Dictionary=new string [9,2];//定义词典//词典初始化Dictionary[0,0]="1";Dictionary[0,1]="A";Dictionary[1,0]="2";Dictionary[1,1]="B";Dictionary[2,0]="3";Dictionary[2,1]="C";//LZW算法编码Console.Write("编码后码字流:");while (h<9){C = Input.ToCharArray()[h].ToString();X = P + C;for (i = 0; i < 9; i++){if (X.Equals(Dictionary[i, 1]))//缀-符串P+C在词典中{P = P + C;//P:=P+Cbreak;}}j = i;if (j >= 9)//缀-符串P+C不在词典中{for (i = 0; i < 9; i++){if (P.Equals(Dictionary[i, 1])){Console.Write(Dictionary[i, 0]);//把代表当前前缀P的码字输出到码字流Console.Write(" ");}}Dictionary[m, 0] = n.ToString();Dictionary[m, 1] = P + C;//把缀-符串P+C添加到词典P = C;//P:=Cm++;n++;}i = 0;j = 0;h++;}for (i = 0; i < 9; i++)//码字流中无码字要译{if (P.Equals(Dictionary[i, 1])){Console.Write(Dictionary[i, 0]);//把代表当前前缀P的码字输出到码字流Console.Write(" ");}}//输出DictionaryConsole.WriteLine();Console.WriteLine();Console.WriteLine("Dictionary如下:");for (i = 0; i < 9; i++, Console.WriteLine()){for (j = 0; j < 2; j++){Console.Write(Dictionary[i, j]);Console.Write(" ");}}}public static void Decode()//译码函数{string Output = "122473";//码字流string cW = null;//当前码字string pW = null;//先前码字string P = null;//当前前缀string C = null;//当前字符int i = 0, j = 0, h = 1, m = 3, n = 4;string[,] Dictionary = new string[20, 2];//定义词典//词典初始化Dictionary[0, 0] = "1";Dictionary[0, 1] = "A";Dictionary[1, 0] = "2";Dictionary[1, 1] = "B";Dictionary[2, 0] = "3";Dictionary[2, 1] = "C";Console.Write("解码后字符流:");cW = Output.ToCharArray()[0].ToString();//当前码字cW=码字流中的第一个码字Console.Write(Dictionary[int.Parse(cW) - 1, 1]);//输出当前缀-符串string.cW到字符流Console.Write(" ");while (h < 6){pW = cW;//先前码字=当前码字cW = Output.ToCharArray()[h].ToString();//当前码字递增for (i = 0; i < 9; i++){try{if (Dictionary[int.Parse(cW) - 1, 1].Equals(Dictionary[i, 1]))//当前缀-符串string.cW在词典中{Console.Write(Dictionary[int.Parse(cW) - 1, 1]);//当前缀-符串string.cW 输出到字符流Console.Write(" ");P = Dictionary[int.Parse(pW) - 1, 1];//当前前缀P:=先前缀-符串string.pWC = Dictionary[int.Parse(cW) - 1, 1].ToCharArray()[0].ToString();//当前字符C:=当前缀-符串string.cW的第一个字符Dictionary[m, 0] = n.ToString();Dictionary[m, 1] = P + C;//把缀-符串P+C添加到词典m++;n++;break;}}catch{continue;}}j = i;if (j >= 9)//当前缀-符串string.cW不在词典中{P = Dictionary[int.Parse(pW) - 1, 1];//当前前缀P:=先前缀-符串string.pWC = Dictionary[int.Parse(pW) - 1, 1].ToCharArray()[0].ToString();//当前字符C:=先前缀-符串string.pW的第一个字符Console.Write(P + C);//输出缀-符串P+C到字符流Console.Write(" ");Dictionary[m, 0] = n.ToString();Dictionary[m, 1] = P + C;//将缀-符串P+C添加到词典中m++;n++;}h++;i = 0;j = 0;}Console.WriteLine();Console.WriteLine();Console.WriteLine("Dictionary如下:");//输出词典for (i = 0; i < 9; i++,Console.WriteLine()){for (j = 0; j < 2; j++){Console.Write(Dictionary[i,j]);Console.Write(" ");}}}}}3.实验结果(截图)及分析①实验结果:②结果分析:由①中的实验结果可以看出,此次实验成功地对字符流ABBABABAC进行了编码和译码,并且在编码和译码过程中分别生成的Dictionary完全一致。
MATLAB中的数据的压缩与稀疏重建技术解析

MATLAB中的数据的压缩与稀疏重建技术解析引言随着数据量的快速增长和存储需求的提高,数据压缩和稀疏重建成为了一种非常重要的技术。
在MATLAB中,有许多强大的工具和技术可用于数据的压缩和稀疏重建。
本文将对MATLAB中的这些技术进行详细解析。
一、数据压缩1. 无损压缩无损压缩是指压缩后的数据可以完全恢复成原始数据,无任何失真。
MATLAB 中提供了多种无损压缩的方法,如Huffman编码、LZW压缩等。
这些方法通过统计数据中的频率分布来减少数据的冗余性,从而实现数据的压缩。
2. 有损压缩有损压缩是指在压缩数据的同时,对数据进行一定的损失,以减小数据的存储空间。
有损压缩在某些应用中具有重要的作用,如图像和音频压缩等。
在MATLAB中,我们可以使用一些经典的有损压缩算法,例如JPEG、MPEG等。
二、稀疏重建稀疏重建是指利用已知的部分采样数据,通过一定的算法或数学模型来估计原始信号的全部或部分。
在MATLAB中,有许多强大的稀疏重建技术可供使用。
1. 压缩感知压缩感知是一种新兴的稀疏重建技术,它基于信号的稀疏性假设,通过少量的测量来重建信号。
MATLAB中提供了一些方法来实现压缩感知,例如基于稀疏表示的信号重建算法。
2. 压缩采样匹配追踪压缩采样匹配追踪是另一种常用的稀疏重建方法。
它通过将信号表示为稀疏线性组合的方式,从而实现信号的重建。
在MATLAB中,我们可以使用OMP算法等方法来实现压缩采样匹配追踪。
3. 压缩感知重建的优化为了进一步提高压缩感知重建的性能,MATLAB中的优化方法也可以应用于该领域。
例如,我们可以使用凸优化算法,如最小二乘法、半正定规划等,来改进压缩感知重建的精度和速度。
三、案例研究为了进一步说明MATLAB中数据压缩与稀疏重建技术的应用,我们可以通过一个案例研究来进行分析。
假设我们有一个音频文件,需要对其进行压缩和稀疏重建。
我们可以使用MATLAB中的压缩感知算法来实现此目标。
Matlab函数实现哈夫曼编码算法

编写Matlab函数实现哈夫曼编码的算法一、设计目的和意义在当今信息化时代,数字信号充斥着各个角落。
在数字信号的处理和传输中,信源编码是首先遇到的问题,一个信源编码的好坏优劣直接影响到了后面的处理和传输。
如何无失真地编码,如何使编码的效率最高,成为了大家研究的对象。
哈夫曼编码就是其中的一种,哈夫曼编码是一种变长的编码方案。
它由最优二叉树既哈夫曼树得到编码,码元内容为到根结点的路径中与父结点的左右子树的标识。
所以哈夫曼在编码在数字通信中有着重要的意义。
可以根据信源符号的使用概率的高低来确定码元的长度。
既实现了信源的无失真地编码,又使得编码的效率最高。
二、设计原理哈夫曼编码(Huffman Coding)是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。
uffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫作Huffman编码。
而哈夫曼编码的第一步工作就是构造哈夫曼树。
哈夫曼二叉树的构造方法原则如下,假设有n个权值,则构造出的哈夫曼树有n个叶子结点。
n 个权值分别设为w1、w2、…、wn,则哈夫曼树的构造规则为:(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;(3)从森林中删除选取的两棵树,并将新树加入森林;(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
具体过程如下图1产所示:(例)图1 哈夫曼树构建过程哈夫曼树构造成功后,就可以根据哈夫曼树对信源符号进行哈夫曼编码。
具体过程为先找到要编码符号在哈夫曼树中的位置,然后求该叶子节点到根节点的路径,其中节点的左孩子路径标识为0,右孩子路径标识为1,最后的表示路径的01编码既为该符号的哈夫曼编码。
lzw编码实验报告

实验报告(一)——LZW编码的C++编程实现时间:2011.4.27一、实验目的及要求使用C++编程实现LZW编码、解码。
二、源程序设计思路1.编码程序:步骤一:开始时的词典包含所有可能的根,而当前前缀P是空的。
步骤二:当前字符C:=字符流中的下一个字符。
步骤三:判断P+C是否在词典中:(1)如果“是”,P:=P+C。
(2)如果“否”,则:①把代表当前前缀P的码字输出到码字流。
②把缀-符串P+C添加到词典中。
③令P:=C。
(3)判断字符流中是否还有字符需要编码:①如果“是”,返回到步骤二。
②如果“否”:输出相应于当前前缀P的码字。
结束编码。
2.译码程序:步骤一:在开始译码时,词典包含所有可能的前缀根。
步骤二:当前码字cW:=码字流中的第一个码字。
步骤三:输出当前缀-符串string.cW到字符流。
步骤四:先前码字pW:=当前码字cW。
步骤五:当前码字cW:=码字流中的下一个码字。
步骤六:判断当前缀-符串string.cW是否在词典中:(1)如果“是”,则:①当前缀-符串string.cW输出到字符流。
②当前前缀P:=先前缀-符串string.pW。
③当前字符C:=当前前缀-符串string.cW的第一个字符。
④把缀-符串P+C添加到词典。
(2)如果“否”,则:①当前前缀P:=先前缀-符串string.pW。
②当前字符C:=当前缀-符串string.pW的第一个字符。
③输出缀-符串P+C到字符流,然后把它添加到词典中。
步骤七:判断码字流中是否还有码字要译:(1)如果“是”,就返回到步骤四。
(2)如果“否”,结束。
三、程序框图词典初始化选择编码(1)或译码(2)?将第一个字符赋给前缀P结束是否有码字要译?字符串P+C 是否在词典中?是P :=P+C是输出代表当前前缀P 的码字否将P+C 添加到词典中P:=C 输出代表前缀P 的码字否C :=字符流中下一个字符 1 编码当前码字cW:=码字流中第一个码字输出对应字符string.cW先前码字pW:=当前码字cW;cW:=下一个码字是否有码字要译?否2 译码String.cW 是否在词典中?是输出string.cW是P :=string.pW C :=string.cW首字符将P+C 添加到词典P:=string.pW C:=string.pW 首字符输出P+C否四、程序设计代码及注释#include <iostream> #include <string> #include <iomanip> using namespace std;string dic[30]; int n;int find(string s) //字典中寻找,返回序号 { int temp=-1; for(int i=0;i<30;i++) { if(dic[i]==s) temp=i+1;}return temp;}void init() //字典初始化{dic[0]="a"; //开始时词典包含所有可能的根dic[1]="b";dic[2]="c";for(int i=3;i<30;i++) //其余为空{dic[i]="";}}void code(string str){init(); //初始化char temp[2];temp[0]=str[0]; //取第一个字符temp[1]='\0';string P=temp; //P为前缀int i=1;int j=3; //目前字典存储的最后一个位置cout<<"编码为:";while(1){char t[2];t[0]=str[i]; //取下一字符t[1]='\0';string C=t; //C为字符流中下一个字符if(C=="") //无码字要译,结束{cout<<" "<<find(P); //输出代表当前前缀的码字break; //退出循环,编码结束}if(find(P+C)>-1) //有码字要译,如果P+C在词典中,则用C扩展P,进行下一步:{P=P+C;i++;}else //如果P+C不在词典中,则将P+C添加到词典中,令P:=C{cout<<" "<<find(P);string PC=P+C;dic[j++]=PC;P=C;i++;}}cout<<endl;cout<<"生成的词典为:"<<endl;for(i=0;i<j;i++) //输出词典中的内容,j为词典的长度{cout<<setw(12)<<i+1<<setw(12)<<dic[i]<<endl;}cout<<endl;}void decode(int c[]){init(); //译码词典与编码词典相同,将a,b,c设为初始的前缀int pw,cw; //pw:先前码字,cw:当前码字cw=c[0]; //输入码字流的第一个码字,赋给当前码字int j=2,i;cout<<"译码为:";cout<<dic[cw-1]; //输出当前字符串到字符流for(int m=0;m<n-1;m++){pw=cw; //当前码字赋给先前码字cw=c[m+1];if(cw<=j+1) //若当前码字在词典中{cout<<dic[cw-1]; //输出当前码字锁代表的字符串char t[2];t[0]=dic[cw-1][0];t[1]='\0';string k=t;j++;dic[j]=dic[pw-1]+k; //将先前码字与当前码字所代表的字符串的首字符连接而成的字符串添加到词典中}else //若当前码字不在词典中{char t[2];t[0]=dic[pw-1][0];t[1]='\0';string k=t;j++;dic[j]=dic[pw-1]+k; //将先前码字与当前码字所代表的字符串的首字符连接而成的字符串添加到词典中cout<<dic[cw-1]; //输出该字符串}}cout<<endl;cout<<"生成的词典为:"<<endl;for(i=0;i<j;i++) //输出词典中的内容,j为词典的长度{cout<<setw(12)<<i+1<<setw(12)<<dic[i]<<endl;}cout<<endl;}int main() //主程序{string str;char choice;while(1){cout<<"\n\n\t"<<"1.编码"<<"\t"<<"2.译码\n\n";cout<<"请选择:";cin>>choice;if(choice=='1') //若选择a则编码{cout<<"\n输入要编码的字符串(由a、b、c组成):";cin>>str;code(str);}else if(choice=='2') //若选择b则译码{int c[30];cout<<"\n消息序列长度是:";cin>>n;cout<<"\n消息码字依次是:";for(int i=0;i<n;i++){cin>>c[i];}decode(c);}else return 0; //其他选择则退出程序}}五、程序运行结果。
Matlab函数实现哈夫曼编码算法讲解--实用.doc

编写 Matlab 函数实现哈夫曼编码的算法一、设计目的和意义在当今信息化代,数字信号充斥着各个角落。
在数字信号的理和中,信源是首先遇到的,一个信源的好坏劣直接影响到了后面的理和。
如何无失真地,如何使的效率最高,成了大家研究的象。
哈夫曼就是其中的一种,哈夫曼是一种的方案。
它由最二叉既哈夫曼得到,元内容到根点的路径中与父点的左右子的。
所以哈夫曼在在数字通信中有着重要的意。
可以根据信源符号的使用概率的高低来确定元的度。
既了信源的无失真地,又使得的效率最高。
二、设计原理哈夫曼 (Huffman Coding) 是一种方式,哈夫曼是可字 (VLC) 的一种。
uffman 于 1952 年提出一种方法,方法完全依据字符出概率来构造异字的平均度最短的字,有称之最佳,一般就叫作 Huffman 。
而哈夫曼的第一步工作就是构造哈夫曼。
哈夫曼二叉的构造方法原如下,假有 n 个,构造出的哈夫曼有 n 个叶子点。
n 个分 w1、 w2、⋯、wn,哈夫曼的构造:(1)将 w1、w2、⋯,wn 看成是有 n 棵的森林 (每棵有一个点 );(2)在森林中出两个根点的最小的合并,作一棵新的左、右子,且新的根点其左、右子根点之和;(3)从森林中除取的两棵,并将新加入森林;(4)重复 (2)、 (3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
具体过程如下图 1 产所示:(例)图 1哈夫曼树构建过程哈夫曼树构造成功后,就可以根据哈夫曼树对信源符号进行哈夫曼编码。
具体过程为先找到要编码符号在哈夫曼树中的位置,然后求该叶子节点到根节点的路径,其中节点的左孩子路径标识为 0,右孩子路径标识为 1,最后的表示路径的 01 编码既为该符号的哈夫曼编码。
可以知道,一个符号在哈夫曼树中的不同位置就有不同的编码。
而且,不同符号的编码长度也可能不一样,它由该结点到父结点的路径长度决定,路径越长编码也就越长,这正是哈夫曼编码的优势和特点所在。
LZW编码算法详解

LZW编码算法详解LZW(Lempel-Ziv & Welch)编码又称字串表编码,是Welch将Lemple和Ziv所提出来的无损压缩技术改进后的压缩方法。
GIF图像文件采用的是一种改良的LZW 压缩算法,通常称为GIF-LZW压缩算法。
下面简要介绍GIF-LZW的编码与解码方程解:例现有来源于二色系统的图像数据源(假设数据以字符串表示):aabbbaabb,试对其进行LZW编码及解码。
1)根据图像中使用的颜色数初始化一个字串表(如表1),字串表中的每个颜色对应一个索引。
在初始字串表的LZW_CLEAR和LZW_EOI分别为字串表初始化标志和编码结束标志。
设置字符串变量S1、S2并初始化为空。
2)输出LZW_CLEAR在字串表中的索引3H(见表2第一行)。
3)从图像数据流中第一个字符开始,读取一个字符a,将其赋给字符串变量S2。
判断S1+S2=“a”在字符表中,则S1=S1+S2=“a”(见表2第二行)。
4)读取图像数据流中下一个字符a,将其赋给字符串变量S2。
判断S1+S2=“aa”不在字符串表中,输出S1=“a”在字串表中的索引0H,并在字串表末尾为S1+S2="aa"添加索引4H,且S1=S2=“a”(见表2第三行)。
5)读下一个字符b赋给S2。
判断S1+S2=“ab”不在字符串表中,输出S1=“a”在字串表中的索引0H,并在字串表末尾为S1+S2=“ab”添加索引5H,且S1=S2=“b”(见表2第四行)。
6)读下一个字符b赋给S2。
S1+S2=“bb”不在字串表中,输出S1=“b”在字串表中的索引1H,并在字串表末尾为S1+S2=“bb”添加索引6H,且S1=S2=“b”(见表2第五行)。
7)读字符b赋给S2。
S1+S2=“bb”在字串表中,则S1=S1+S2=“bb”(见表2第六行)。
8)读字符a赋给S2。
S1+S2=“bba”不在字串表中,输出S1=“bb”在字串表中的索引6H,并在字串表末尾为S1+S2=“bba”添加索引7H,且S1=S2=“a”(见表2第七行)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LZW编码算法,尝试使用matlab计算
%encoder LZW for matlab
%yu 20170503
clc;
clear;
close all;
%初始字典
dic = cell(512,1);
for i = 1:256
dic{i} = {num2str(i)};
end
%输入字符串a,按空格拆分成A,注意加1对应范围1~256 a = input('input:','s');
a = deblank(a);
A = regexp(a,'\s+','split');
L = length(A);
for j=1:L
A{j} = num2str(str2num(A{j})+1);
end
A_t = A{1};%可识别序列
B_t = 'test';%待验证词条
d = 256;%字典指针
b = 1;%输出指针
B = cell(L,1);%输出初始
output = ' ';%输出初始
j=1;
for j = 2:L
m=1;
B_t =deblank([A_t,' ',A{j}]);%合成待验证词条
while(m <= d)
if strcmp(dic{m},B_t)
A_t = B_t;
break
else
m=m+1;
end
end
while(m == d+1)
d = d+1;
dic{d} = B_t;
q=1;
for q=1:d
if strcmp(dic{q},A_t)
B{b} = num2str(q);
b = b+1;
end
end
A_t = A{j};
end
end
for q=1:d%处理最后一个序列输出
if strcmp(dic{q},A_t)
B{b} = num2str(q);
b = b+1;
end
end
for n = 1:(b-1)
B{n} =num2str(str2num(B{n})-1);
output=deblank([output,' ',B{n}]);
end
output
运算结果
计算结果为39 39 126 126 256 258 260 259 257 126
LZW解码算法,使用matlab计算
%decoder LZW for matlab
%yu 20170503
clc;
clear;
close all;
%初始字典
dic = cell(512,1);
for i = 1:256
dic{i} = {num2str(i)};
end
%输入字符串a,按空格拆分成A,注意加1对应范围1~256
a = input('input:','s');
a = deblank(a);
A = regexp(a,'\s+','split');
L = length(A);
for j=1:L
A{j} = num2str(str2num(A{j})+1);
end
B_t = A{1};%待验证词条
d = 256;%字典指针
b = 1;%输出指针
B = cell(L,1);%输出初始
output = ' ';%输出初始
j=1;
B{b} = char(dic{str2num(A{j})});
b = b+1;
for j = 2:L
BB = char(dic{str2num(A{j})});
B_d = regexp(BB,'\s+','split');%按空格拆分
L_B = length(B_d);
p=1;
for p=1:L_B
B{(b+p-1)} = B_d{p};
m=1;
B_t =deblank([char(B_t),' ',char(B_d{p})]);%合成待验证词条
while(m <= d)
if strcmp(dic{m},B_t)
B_t = B_t;
break
else
m=m+1;
end
end
while(m == d+1)
d = d+1;
dic{d} = B_t;
B_t = B_d{p};
end
end
b = b+L_B;
end
for n = 1:(b-L_B)
B{n} = num2str(str2num(B{n})-1);
output=deblank([output,' ',B{n}]);
end
output
运算结果
运算结果为 39 39 126 126 39 39 126 126 39 39 126 126 39 39 126 126。
