画法几何练习题
画法几何期末考试练习题资料.

d′
d
e
c′
b
a
5、过点K作直线KL与直线MN垂直,并与△ABC平行。b′c′ Nhomakorabean′
a′
k′
m′
n
a
k
b
c
m
6、已知等腰△DEF的顶点D和一腰DE在直线DG上,另 一腰DF∥△ABC,且点F在MN上,试完成△DEF 的两面投影。
n′ b′
c′
m′
d′
g′
a′
b
g
n m c
d
7、五边形ABCDE为平面图形,BC∥H 面,AE∥BC, 试完成其正面投影。
b′
a′
c
e
b
d
a
8、求直线AB与CD间的距离,并作出过B点的垂线。
XV H
a′ c′
b′ d′
d
b c
a
9、如图所示,已知交叉两直线AB和CD的两面投影,用换 面法作出它们的公垂线EF,E、F分别是公垂线EF 与AB、 CD的交点,并作出AB和CD之间的真实距离。
10、做出该组合体的三面投影。
1、过空间一点作已知平面的垂线
a′
e′
b′
c′
c
e
a
b
2、过空间一直线作已知平面的垂面
a′
e′
b′
f′
c′ c
a
e
f
b
3、已知直角三角形ABC的水平投影,及直角边AB 的V投影,试完成其正面投影。
b′
a′
a
b
c
4、作一直线与两交叉直线AB和CD相交,同时与直 线EF平行。
f′
a′
e′
b′
c′
画法几何习题集答案
b’ p’ o’ n1’’
a’
c’
4’
m’
a c
po
4 m
n1 b
• 做法:
2’ • 延长 ac .34交
于m,求出 m’,
延长2‘1’交点
3’ 为o’,p,’ 在ab
求出p,bc利用
3 定比性求出o, 连接po交21
于n,求出n’,连
2
接mn,m’n’.
42 已知直线AB平行于平面CDE求直线的正面投影
b’ 55mm
高 度 差
a’
水平投影
a
水平投影
b
12判别下列各直线的空间位置, 并注明反映实际长度的投影
g’
d’
f’
a’
b’
e’
c’
h’
c
a
b
e
f
d
g (h)
直 线 AB CD
空间位 水平线 侧平线
置
实长投 ab
影
c’’d’’
EF GH
正平线 铅垂线
e’f’ g’h’
13 判别CDE 三点是否在直线AB上
• 1、在正立面上 分别连接m’c’交点 p’,n’a’交点q’,,n’b’ 交点r’.如图所示
• 2、做出三个点的 水平投影p,q,r
• 3、连接mp,nq,nr
• 4、做a’ ,b’,c’对应 的水平投影a,b,c, 并连接。
26 在∆ ABC内任作一条正平线和一条水平线
b’
n’ a’
m’ c’
20mm b1 X2
67用换面法确定两交错直线间的距离返回做出投影
c’ n’
b’
a’ m’
X
X1
a
重庆大学画法几何习题集及题解完整版

(b) 。
k′ b′b′ a′ k′
a′ X
xk a
k
b
a (a)
k′ b′
k′
a′
c′
a′
OX
cc ′
ox
a
c
k
b
a (b)
b′
b′
b
a′ c′
OX
k′ c′
a′ O k
c c′
c
aox
ck
b
a
(c)
k
15页
2005习题集第15页—平面2
4-5 △ABC属于平面P,试求作其H面投影。
b′
b′
4-6 取一点K属于 距H面15mm
N,n′
(1)
b
k′
a
X
m′
n O
b
k
a
B0
M,m
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK=25,求
作K点的投影k、k′,并求出直线的迹点。
N,n′
n〞
(2)
b′
b〞
k′
a′ m′
n b
k
a
M,m
a〞
m〞
10页
3–6 已知线段AB的投影,试取属于AB的一点K,使 AK=25,求
作K点的投影k、k′,并求出直线的迹点。 N,n′
(2)
a′ k′
b′
m′ n a
b
M,m
10页
2005习题集第11页—直线3
3–7 下列各图中,表示点M属于直线AB的是(a b ) 。
m′ b′ a′
a
m′
b
a
m′
b
画法几何习题集

【21-2】求作五棱柱与四棱柱的相贯线,并作侧面投影。
【21-3】求作四棱柱穿三棱柱孔后的正面投影。
【21-4】求作三棱锥与三棱柱的相贯线。
【21-5】补全房屋模型的正面投影和水平投影。
【21-6】求作房屋表面交线。
【22-1】求作四棱柱与圆锥的相贯线。
【23-1】求作两圆柱的相贯线。
【23-2】求作半个空心圆柱挖圆柱孔后的相贯线。
【23-3】求同轴异径圆柱穿圆柱通孔后的正面投影。
【23-4】求作圆柱与圆锥相贯的投影。
【23-5】求半圆柱与圆台相贯后的表面交线。
【23-6】求作圆柱和圆锥相交的投影。
【24-7】求作半球挖圆柱孔后的投影。
【22-2】作三棱柱与半圆柱的相贯线的正面投影。
【22-3】求作圆锥穿三棱柱孔后的相贯线,并作出侧面投影。
【22-4】求作1/2空心圆柱与空心长方体的相贯线。
【23-5】求半圆柱与圆台相贯后的表面交线。
【22-6】求作穿矩形孔圆球的表面相贯线。
对两曲面立体相贯线,其相贯线为空间曲线,首先应作 出相贯线上足够多的公有点(特殊点和一般点),然后 光滑连线。在特殊情况下,相贯线可以为椭圆、圆或直 线段。一般有以下四种类型:(非常重要)(不用想相 惯线的空间形状,实质是曲面立体定点的问题) 类型1:已知相贯线的两个投影,求相贯线第三投影。 如两圆柱体相贯,可依据相贯线上点的两投影求作第三 投影。(重点) 类型2:已知相贯线的一个投影,求相贯线另外两个 投影。如圆柱与圆锥、圆球等回转体相贯,可依据相贯 线上的一个投影,利用曲面上取点方法作出此相惯线的 另外两个投影。(重点) 类型3:特殊相惯线 ,两正交圆柱 相惯线简化画 法
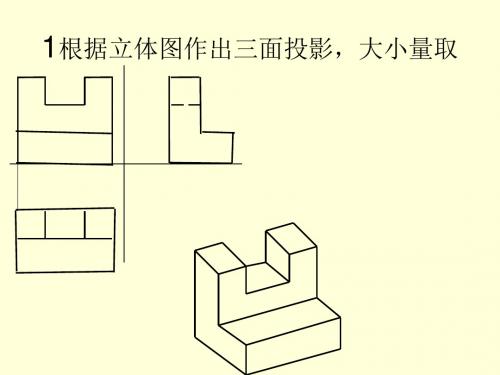
画法几何练习题

画法几何练习题一、基本概念与作图1. 判断题(1)在同一平面内,两条平行线的距离处处相等。
(2)垂直于同一直线的两条直线必定平行。
(3)等腰三角形的底角相等。
(4)圆的切线垂直于过切点的半径。
2. 填空题(1)两条平行线之间的距离是______。
(2)等腰三角形的底边与腰的比例为______。
(3)圆的半径为5cm,则圆的直径为______cm。
(4)若两个角的和为180°,则这两个角互为______角。
3. 作图题(1)已知线段AB,在AB上作一点C,使AC:CB=3:2。
(2)已知角α,画出角β,使β=2α。
(3)已知圆O的半径为5cm,画出圆的直径。
(4)已知等腰三角形底边长为8cm,腰长为6cm,画出该等腰三角形。
二、点、线、面的关系1. 判断题(1)任意两条直线必定相交。
(2)同一平面内,两条平行线与第三条直线所成的角度相等。
(3)空间中,一条直线与一个平面垂直,则该直线与平面内的任意直线都垂直。
(4)两条异面直线必定不平行。
2. 填空题(1)若直线a与直线b垂直,直线b与直线c垂直,则直线a与直线c的关系是______。
(2)两条平行线之间的距离是______。
(3)点到直线的距离是指______。
(4)若两平行线的斜率分别为k1和k2,则k1×k2=______。
3. 作图题(1)已知直线a和直线b,画出直线c,使直线c同时垂直于直线a和直线b。
(2)已知点A和直线l,画出直线l的垂线,并使垂线经过点A。
(3)已知平面α和平面β,画出它们的交线。
(4)已知正方体ABCDA1B1C1D1,画出对角线AC1。
三、平面图形的面积与体积1. 填空题(1)矩形的长为8cm,宽为6cm,其面积为______cm²。
(2)正三角形边长为10cm,其面积为______cm²。
(3)圆柱底面半径为3cm,高为5cm,其体积为______cm³。
(4)圆锥底面半径为4cm,高为6cm,其体积为______cm³。
画法几何随堂练习答案52题

A. B. D. 参考答案:AA. B. C. D. 参考答案:CA. B. D. 参考答案:BA. B. C. D. 参考答案:AA. B. D. 参考答案:AA. B. C. D. 参考答案:D答题: A. B. C. D. (已提交)参考答案:A问题解析:8.根据给定的形体的三面投影,与之相对应的立体图为(答题: A. B. C.D.参考答案:问题解析:9.根据给定的形体的三面投影,与之相对应的立体图为(B. C.参考答案:B.参考答案:11.根据给定的形体的三面投影,与之相对应的立体图为(B.参考答案:12.点A(10,15,18),则该点对V面的距离为((A)10 (B)15 (C)18 (D)25A. B. C. D.参考答案:BA. B. D.参考答案:AA. B. C. D.参考答案:BA. B. D. 参考答案:CA. B. C. D. 参考答案:BA. B. D. 参考答案:CA. B. C. D. 参考答案:AA. B. D. 参考答案:AA. B. D. 参考答案:CA. B. D. 参考答案:BA. B. C. D. 参考答案:BA. B. D. 参考答案:BA. B. C. D. 参考答案:BA. B. D. 参考答案:AA. B. C. D. 参考答案:BA. B. D. 参考答案:BA. B. C. D. 参考答案:CA. B. D. 参考答案:CA. B. D. 参考答案:CA. B. D. 参考答案:BA. B. C. D. 参考答案:AA. B. D. 参考答案:BA. B. C. D. 参考答案:BA. B. D. 参考答案:AA. B. C. D. 参考答案:BA. B. D. 参考答案:AA. B. C. D. 参考答案:BA. B. D. 参考答案:CA. B. D. 参考答案:BA. B. D. 参考答案:CA. B. C. D. 参考答案:CA. B. D. 参考答案:AA. B. C. D. 参考答案:CA. B. D.A. B. C. D. 参考答案:CA. B. D. 参考答案:CA. B. C. D. 参考答案:AA. B. D. 参考答案:BA. B. D. 参考答案:BA. B. C. D.A. B. C. D. 参考答案:A。
画法几何学第六版课后练习题含答案

画法几何学第六版课后练习题含答案什么是画法几何学画法几何学是一种使用直线和简单的几何图形构成复杂图案的技巧。
它可以帮助绘画者更加准确地捕捉形状和比例,并设计出视觉上令人愉悦的图案。
画法几何学不仅适用于绘画,也广泛应用于设计、建筑、艺术和制作手工等领域。
画法几何学第六版课后练习题本文将为大家提供画法几何学第六版课后练习题及其答案,帮助大家进一步巩固画法几何学的知识。
第一章问题一以下哪些是画法几何学中基本形状?A. 矩形,三角形,圆形B. 正方形,梯形,五边形C. 长方形,六边形,椭圆形D. 扇形,菱形,星形答案:A问题二以下哪些是画法几何学中用于衡量比例的工具?A. 直尺和三角板B. 圆规和锤子C. 手段和画刷D. 木棒和牛奶瓶答案:A第二章问题一在画法几何学中,什么是透视?A. 一种用于衡量形状和大小的基础技巧B. 一种用于营造深度和三维感的技巧C. 一种用于修剪画布和裁剪图案的技巧D. 一种用于防止颜料干燥的技巧答案:B问题二以下哪些形状可以用作透视中的“基准线”?A. 直线B. 圆弧C. 椭圆形D. 非正多边形答案:A第三章问题一以下哪些形状可以用作几何图案的“元素”?A. 直线B. 圆形C. 三角形D. 所有上述形状都可以用作元素答案:D问题二以下哪些工具可以用于制作几何图案?A. 视差镜B. 印章C. 压花工具D. 所有上述工具都可以用于制作几何图案答案:D总结画法几何学是一种非常实用的技能,它可以帮助人们更加准确地捕捉形状和比例。
通过本文提供的画法几何学第六版课后练习题及其答案,希望读者们能够加深对画法几何学的理解和掌握。
《画法几何》练习题

《画法几何》模拟试题(一)(考试时间:120分钟;考试方式:开卷)一、选择填空题:判断下列各对直线的相对位置(平行、相交、交叉、相交垂直、交叉垂直)。
(每小题2分,共12分)三、分析绘图题:已知平面△ABC 的H 、V 投影,求出其对V 面的倾角β。
(12分)二、分析绘图题:已知三点A (20,25,30)、B (20,0,25)和C (25,30,0),画出点A 、B 、C 的投影图。
(9分)五、分析绘图题:已知△ABC 和平行四边形DEFG 互相平行,完成平行四边形DEFG 的V 面投影。
(12分)四、判断填空题:根据形体投影图上的标注,判别指定的棱线和平面对投影面的相对位置。
(每空1分,共10分)AC 是 线 AF 是 线 BD 是 线 CE 是 线 EF 是 线 △ABC 是 面 △ACE 是 面 △AEF 是 面 △BCD 是 面 △CDE 是 面六、分析绘图题:已知球面上点的某个投影,求作点的其余投影。
(10分)七、分析绘图题:根据台阶的正等轴测投影,作出其三面投影(尺寸从轴测投影中量取)(12分)八、分析绘图题:根据形体的三面投影图,作出其正等轴测图(尺寸从投影图中量取)。
(11分)九、分析绘图题:已知圆锥被截切的V投影,试完成圆锥被截切后的H、W投影。
(12分)《画法几何》模拟试题(二) (考试时间:120分钟;考试方式:开卷)一、选择填空题:判断下列各对直线的相对位置(平行、相交、交叉、相交垂直、交叉垂直)。
(每小题2分,共12分)答: 答: 答: (1)(2(3)答:答:答:(4)(5) (6)二、分析绘图题:设F 点和E 点与H 面等距;G 点和E 点与V 面等距;D 点和E 点与W 面等距,完成点的其余投影(9分)。
三、分析绘图题:已知平面△ABC 的H、V 投影,求出其对H 面的倾角α。
(12分)五、分析绘图题:已知△ABC 与△DEF 相交,求两平面的交线并判别可见性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答: 答: 答: (1) (2) (3)答: 答: 答:(4) (5) (6)《画法几何》模拟试题(一) (考试时间:120分钟;考试方式:开卷)一、选择填空题:判断下列各对直线的相对位置(平行、相交、交叉、相交垂直、交叉垂直)。
(每小题2分,共12分)三、分析绘图题:已知平面△ABC 的H 、V 投影,求出其对V 面的倾角β。
(12分)二、分析绘图题:已知三点A (20,25,30)、B (20,0,25)和C (25,30,0),画出点A 、B 、C 的投影图。
(9分)五、分析绘图题:已知△ABC 和平行四边形DEFG 互相平行,完成平行四边形DEFG 的V 面投影。
(12分)四、判断填空题:根据形体投影图上的标注,判别指定的棱线和平面对投影面的相对位置。
(每空1分,共10分)AC 是 线 AF 是 线 BD 是 线 CE 是 线 EF 是 线 △ABC 是 面 △ACE 是 面 △AEF 是 面 △BCD 是 面 △CDE 是 面六、分析绘图题:已知球面上点的某个投影,求作点的其余投影。
(10分)七、分析绘图题:根据台阶的正等轴测投影,作出其三面投影(尺寸从轴测投影中量取)(12分)八、分析绘图题:根据形体的三面投影图,作出其正等轴测图(尺寸从投影图中量取)。
(11分)九、分析绘图题:已知圆锥被截切的V投影,试完成圆锥被截切后的H、W投影。
(12分)《画法几何》模拟试题(二) (考试时间:120分钟;考试方式:开卷)一、选择填空题:判断下列各对直线的相对位置(平行、相交、交叉、相交垂直、交叉垂直)。
(每小题2分,共12分)答: 答: 答:(1)(2(3)答: 答: 答: (4) (5) (6)二、分析绘图题:设F 点和E 点与H 面等距;G 点和E 点与V 面等距;D 点和E 点与W 面等距,完成点的其余投影(9分)。
三、分析绘图题:已知平面△ABC 的H、V 投影,求出其对H 面的倾角α。
(12分)五、分析绘图题:已知△ABC 与△DEF 相交,求两平面的交线并判别可见性。
(10分)四、分析绘图题:根据形体的两面投影图,补绘第三面投影图,并判别指定平面对投影面的相对位置。
(12分)六、分析绘图题:已知锥面上点的某个投影,求作点的其余投影。
(10分)七、分析绘图题:根据形体的正等轴测投影,作出其三面投影(尺寸从轴测投影中量取)(12分)八、分析绘图题:根据形体的三面投影图,作出其正等轴测图(尺寸从投影图中量取)。
(11分)九、分析绘图题:已知半圆球体被截切后的正面投影,求作截交线其余两面投影。
(12分)《画法几何》模拟试题(三) (考试时间:120分钟;考试方式:开卷)一、选择填空题:判断下列各对直线的相对位置(平行、相交、交叉、相交垂直、交叉垂直)。
(每小题2分,共12分)(6)答: 答:答: ((2)答: 答: 答:三、分析绘图题:已知平面图形ABCDEFG的不完全投影,试补全平面图形ABCDEFG的正面投影。
(10分)五、分析绘图题:已知台阶的V、W投影,试补绘其H投影。
(10分)七、分析绘图题:已知正五棱柱被截切后的V投影和部分W投影,求作其H、W投影。
(11分)九、分析绘图题:根据形体的投影图,绘制其正等轴测图。
(12分)(考试时间:120分钟;考试方式:开卷)二、分析绘图题:设线段AB 通过原点O ,α=30°,试完成AB 的三面投影图。
(10分)一、选择填空题:判断下列各对直线的相对位置(平行、相交、交叉、相交垂直、交叉垂直)。
(每小题2分,共12分)答: 答: 答: (1) (答: 答: 答: (4)(5)三、分析绘图题:已知平面五边形ABCDE的不完全投影,试完成平面五边形ABCDE的H面投影。
(9分)四、分析绘图题:已知点M和直线AB、CD的两投影,试五、分析绘图题:已知台阶的V、W投影,试补绘其H投影。
(11分)六、分析绘图题:补绘圆柱的W投影,并补全圆柱表面上的点的三面投影。
(12分)(12分)投影。
(12分)九、分析绘图题:根据形体的投影图,绘制其斜二等轴测图。
(10分)《画法几何》模拟试题(五)(考试时间:120分钟;考试方式:开卷)二、分析绘图题:已知线段AB ⊥BC ,且AB =BC ,点A 在V面上,求直线AB 的两面投影。
(10分)一、选择填空题:判断下列各对直线的相对位置(平行、相交、交叉、相交垂直、交叉垂直)。
(每小题2分,共12分)(1)(2)(3) 答: 答: (4) (5答: 答: 答:三、分析绘图题:已知平行四边形ABCD平面上K字的V 投影,求K字的H投影。
(10分)四、分析绘图题:已知平面ABC与平面DEFG相交,试求两平面交线的投影。
(10分)五、分析绘图题:根据台阶的H、V投影,补绘其W投影。
(12分)六、分析绘图题:已知圆锥台表面上点A、B及曲线MN的一个投影,求其它投影。
(10分)七、分析绘图题:已知圆柱体被截切后的正面投影,求作八、分析绘图题:已知两三棱柱相贯,试完成相贯线的投影。
(12分)九、分析绘图题:已知形体的正投影图,试完成斜二测轴测图。
(12分)模拟试题(一)答案要点及评分细则课程名称: 画法几何 ( A 卷) 专业年级: 建筑工程技术、建筑工程管理一、选择填空题:判断下列各对直线的相对位置(平行、相交、交叉、相交垂直、交叉垂直)(每小题2分,共12分)。
二、分析绘图题:已知三点A (20,25,30)、B (20,0,25)和C (25,30,0),画出点A 、B 、C 的投影图。
(9分)评分标准:作出每个点的1个投影1分,共9分。
(4(5)答: 平 行 答: 相 交 垂 直 答: 交 叉(1(2)答: 相 交 答: 交 叉 垂 直 答: 交 叉三、分析绘图题:已知平面△ABC 的H 、V 投影,求出其对V 面的倾角β。
(12分)评分标准:作出正平线的两个投影4分,作出最大斜度线的两个投影4分,利用直角三角形法求出β角的实形,4分,共12分。
四、判断填空题:根据形体投影图上的标注,判别指定的棱线和平面对投影面的相对位置。
(每空1分,共10分)评分标准:每空1分,共10分。
AC 是 水 平 线 AF 是 侧 平 线 BD 是 正 平 线 CE 是 一 般 线 EF 是 侧 垂 线 △ABC 是 水 平 面 △ACE 是 一 般 面 △AEF 是 侧 垂 面 △BCD 是 正 平 面 △CDE 是 正 垂 面五、分析绘图题:已知△ABC和平行四边形DEFG互相平行,完成平行四边形DEFG的V面投影。
(12分)评分标准:作出△ABC的平行面EⅠⅡ得3分,连接DF求出ⅢⅣ得3分,根据ⅢⅣ求出d’、f得2分,连接d’e’、e’f’得2分,作出d’g’、g’f’得2分,共12分。
评分标准:作出e’g’得4分,作出点d’、f’得6分,连接各点为平行四边形得2分,共12分。
六、分析绘图题:已知球面上点的某个投影,求作点的其余投影。
(10分)评分标准:作出每个点的一个其余投影,得1分,共10分。
七、分析绘图题:根据台阶的正等轴测投影,作出其三面投影(尺寸从轴测投影中量取)(12分)评分标准:作出台阶的每1个投影,得4分,共12分。
八、分析绘图题:根据形体的三面投影图,作出其正等轴测图(尺寸从投影图中量取)。
(11分)评分标准:作出形体底板的正等轴测图3分,作出右边四棱柱3分,作出中间四棱柱3分,作出左边三棱柱2分,共11分。
九、分析绘图题:已知圆锥被截切的V投影,试完成圆锥被截切后的H、W投影。
(12分)评分标准:分别求出截交线的H、V投影各得5分,整理轮廓线得2分,共12分。
尊敬的王厂长、赵厂长:经过多方面的考虑,我决定辞掉目前所从事的工作,此次申请,纯粹是个人兴趣的原因,非关其他原因。
我非常重视我在新光厂内的这段经历,也很荣幸自己成为新光厂的一员,我确信我在新光厂里的这段经历和经验,将为我今后的职业发展带来非常大的利益,对此,我表示衷心的感谢,感谢厂里领导为我提供这个的机会,我很遗憾自己在这个时候向厂里正式提出辞职。
来到新光厂也已经3-4年多了,正是在这里我开始踏上了社会,完成了自己从一个学生到社会人的转变。
有过欢笑,有过收获,也有过泪水和痛苦。
厂里平等的人际关系和开明的工作作风,一度让我有着找到了依靠的感觉,在这里我能开心的工作,开心的学习。
嫣然一个大家庭。
然而工作上的毫无成熟感。
管理上老是跟不厂里的节奏,思想上总是给厂里难以统一。
有时候感到彷徨无助。
经过多方面的考虑,我决定辞掉目前所从事的工作,我知道这样做辜负辛苦养育我的父母,辜负王长厂的信任和栽培~更加对不起我自己~以后想在有这样的机遇就很难了可能是因为还太小,太不懂事,太不懂去珍惜拥有的。
或许只有重新再跑到社会上去遭遇挫折,在不断打拼中去寻找属于自己的定位,才是我人生的下一步选择。
从小到大一直过得很不顺,这曾让我无奈,如今却让自己深深得痛苦,不能自拔,也许人真的要学会慢慢长大。
我也很清楚这时候向厂里对于自己都是一个考验,公司正值用人之际,公司新的制度的启动,所有的工作在新光厂上下极力重视下一步步推进。
也正是考虑到厂里今后在这个项目安排的合理性,本着对厂里负责的态度,为了不让厂里因我而造成的决策失误,所以我决定自己离开。
或许这对厂里对也是一种解脱吧。
离开工作3-4年的新光厂,离开这些曾经同甘共苦的同事,很舍不得,舍不得领导们的譐譐教诲,舍不得同事之间的那片真诚和友善。
更加不会忘记王长厂对我的知遇之恩。
也愿厂里在今后的工作中发挥优势,扬长避短,祝愿新光厂前程似锦!王长厂、赵厂长身体健康~工作顺心!同事们工作顺利!。
