三角函数章节复习专题
专题63 高中数学三角函数章末复习(原卷版)

专题63 三角函数章末复习一 知识系统整合二 规律方法1.在任意角和弧度制的学习中,要区分开角的各种定义,如:锐角一定是第一象限角,而第一象限角不全是锐角,概念要搞清;角度制和弧度制表示角不能混用,如:α=2k π+30°,k ∈Z ,这种表示法不正确. 2.任意角的三角函数,首先要考虑定义域,其次要深刻认识三角函数符号的含义,sin α=yr ≠sin ×α;诱导公式的记忆要结合三角函数的定义去记忆. 3.同角三角函数的基本关系式 sin 2α+cos 2α=1及sin αcos α=tan α,必须牢记这两个基本关系式,并能应用它们进行三角函数的求值、化简、证明,在应用中,注意掌握解题的技巧,能灵活运用公式.在应用平方关系求某个角的另一个三角函数值时,要注意根式前面的符号的确定.4.三角函数的诱导公式诱导公式一至六不仅要正确、熟练地掌握其记忆的诀窍,更要能灵活地运用. (1)-α角的三角函数是把负角转化为正角;(2)2k π+α(k ∈Z)角的三角函数是化任意角为[0,2π)内的角; (3)π2±α,π±α,3π2±α,2π-α角的三角函数是化非锐角为锐角; (4)化负为正→化大为小→化为锐角; (5)记忆规律:奇变偶同,象限定号. 5.正弦函数、余弦函数的图象与性质(1)五点法作图是画三角函数图象的基本方法,要切实掌握,作图时自变量要用弧度制,作出的图象要正规.(2)奇偶性、单调性、最值、周期是三角函数的重要性质,f (x +T )=f (x )应强调的是自变量x 本身加常数才是周期,如f (2x +T )=f (2x ),T 不是f (2x )的周期.解答三角函数的单调性的题目一定要注意复合函数单调性法则,更要注意定义域.6.使用本章公式时,应注意公式的正用、逆用以及变形应用.如两角和与差的正切公式tan(α±β)=tan α±tan β1∓tan αtan β,其变形公式:tan α±tan β=tan(α±β)(1∓tan αtan β)应用广泛;公式cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α的变形公式:1+cos2α=2cos 2α,1-cos2α=2sin 2α,cos 2α=1+cos2α2,sin 2α=1-cos2α2常用来升幂或降幂.7.函数y =A sin(ωx +φ)主要掌握由函数y =sin x 的图象到函数y =A sin(ωx +φ)的图象的平移、伸缩等变换. 注意各种变换对图象的影响,注意各物理量的意义,A ,ω,φ与各种变换的关系. 8.三角函数的应用 (1)根据图象建立解析式; (2)根据解析式作出图象;(3)将实际问题抽象为与三角函数有关的函数模型;(4)利用收集到的数据作出散点图,并根据散点图进行函数模拟.在建立三角函数模型的时候,要注意从数据的周而复始的特点以及数据变化趋势两个方面来考虑.考点一 三角函数的概念1.已知角α的终边在直线3x +4y =0上,求sin α,cos α,tan α的值.2.若角α的终边所在直线经过点P (-2,3),则有( )A .sin α=21313B .cos α=-21313C .sin α=31313D .tan α=-323.已知角θ的顶点为坐标原点,始边为x 轴的非负半轴.若P (4,y )是角θ终边上一点,且sin θ=-255,则y =_____.4.若角600°的终边上有一点(-4,a ),则a 的值是5.有一个扇形的弧长为π2,面积为π4,则该弧所对弦长为考点二 同角三角函数基本关系和诱导公式的应用1.若cos ⎝⎛⎭⎫3π2-α=-53,则sin(-5π+α)=2.已知1-cos x +sin x1+cos x +sin x =-2,则tan x 的值为3.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A (1,a ),B (2,b ), 且cos α=306,则|a -b |=4.已知tan α=-3,π2<α<π,则sin α-cos α=5.已知角α的终边上有一点P (1,3),则sin (π-α)-sin ⎝⎛⎭⎫π2+αcos ⎝⎛⎭⎫3π2-α+2cos (-π+α)的值为6.已知α∈⎝⎛⎭⎫π,3π2,tan α=2,则cos α=7.已知3sin (π+α)+cos (-α)4sin (-α)-cos (9π+α)=2,则tan α=8.已知sin(-π+θ)+2cos(3π-θ)=0,则sin θ+cos θsin θ-cos θ=________.9.已知tan α=-43,求下列各式的值:(1)2cos α+3sin α3cos α+sin α;(2)2sin 2α+sin αcos α-3cos 2α.10.已知2cos 2α+3cos αsin α-3sin 2α=1,α∈⎝⎛⎭⎫-3π2,-π.求: (1)tan α;(2)2sin α-3cos α4sin α-9cos α.11.已知tan α=-34.(1)求2+sin αcos α-cos 2α的值;(2)求sin (4π-α)cos (3π+α)cos ⎝⎛⎭⎫π2+αcos ⎝⎛⎭⎫152π-αcos (π-α)sin (3π-α)sin (-π-α)sin ⎝⎛⎭⎫132π+α的值.12.已知f (α)=sin 2(π-α)·cos (2π-α)·tan (-π+α)sin (-π+α)·tan (-α+3π).(1)化简f (α);(2)若f (α)=18,且π4<α<π2,求cos α-sin α的值;(3)若α=-47π4,求f (α)的值.13.已知-π2<x <0,sin x +cos x =15,则sin x -cos x 的值为________.14.已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ等于15.若sin θ=33,则cos (π-θ)cos θ⎣⎡⎦⎤sin ⎝⎛⎭⎫3π2-θ-1+cos (2π-θ)cos (π+θ)sin ⎝⎛⎭⎫π2+θ-sin ⎝⎛⎭⎫3π2+θ的值为________.16. 已知cos(π+α)=-12,且角α在第四象限,计算:(1)sin(2π-α);(2)sin[α+(2n +1)π]+sin (π+α)sin (π-α)cos (α+2n π)(n ∈Z).考点三 三角恒等变换的综合应用1.化简1-2sin (π+4)cos (π+4)等于( )A .sin4-cos4B .cos4-sin4C .-sin4-cos4D .sin4+cos42.2sin 215°-1的值是3.若sin2α=14,π4<α<π2,则cos α-sin α的值是4.已知α为锐角,cos α=55,则tan ⎝⎛⎭⎫π4+2α=5.在3sin x +cos x =2a -3中,a 的取值范围是A.⎣⎡⎦⎤12,52B.⎝⎛⎦⎤-∞,12C.⎝⎛⎭⎫52,+∞D.⎣⎡⎭⎫-52,-12 6.已知α∈⎝⎛⎭⎫π2,π,sin α=55,求sin ⎝⎛⎭⎫π4+α的值.7.在△ABC 中,3sin A +4cos B =6,4sin B +3cos A =1,则C 的大小为________.8.在△ABC 中,已知tan A +B2=sin C ,则△ABC 的形状为( )A .正三角形B .等腰三角形C .直角三角形D .等腰直角三角形9.已知sin α=55,且α为锐角,tan β=-3,且β为钝角,则α+β的值为10.已知α,β,γ∈⎝⎛⎭⎫0,π2,sin α+sin γ=sin β,cos β+cos γ=cos α,则β-α的值为________.11.求值:sin50°(1+3tan10°)-cos20°cos80°1-cos20°.12.化简:2sin130°+sin100°(1+3tan370°)1+cos10°.13.求证:sin θ(1+tan θ)+cos θ⎝⎛⎭⎫1+1tan θ=1sin θ+1cos θ.14.求证:sin α1-cos α·cos αtan α1+cos α=1.15.求证:1+2sin αcos αcos 2α-sin 2α=1+tan α1-tan α.16.求证:tan 2x +1tan 2x =2(3+cos4x )1-cos4x.17.已知tan 2α=2tan 2β+1,求证:sin 2β=2sin 2α-1.18.已知tan α=43,cos(α+β)=-1114,α,β均为锐角,求cos β的值.19.已知cos ⎝⎛⎭⎫α-β2=-277,sin ⎝⎛⎭⎫α2-β=12,且α∈⎝⎛⎭⎫π2,π,β∈⎝⎛⎭⎫0,π2,求: (1)cos α+β2;(2)tan(α+β).20.已知α,β为锐角,tan α=43,cos(α+β)=-55.(1)求cos 2α的值;(2)求tan(α-β)的值.21.已知函数f (x )=sin ⎝⎛⎭⎫π2-x sin x -3cos 2x .(1)求f (x )的最小正周期和最大值; (2)讨论f (x )在⎣⎡⎦⎤π6,2π3上的单调性.22.已知函数f (x )=4tan x sin ⎝⎛⎭⎫π2-x ·cos ⎝⎛⎭⎫x -π3- 3.(1)求f (x )的定义域与最小正周期; (2)讨论f (x )在区间⎣⎡⎦⎤-π4,π4上的单调性.23.已知函数f (x )=(sin x -cos x )sin 2xsin x.(1)求f (x )的定义域及最小正周期; (2)求f (x )的单调递减区间.24.已知函数f (x )=23sin x cos x +2cos 2x -1(x ∈R).(1)求函数f (x )的最小正周期及单调递增区间; (2)求f (x )在区间⎣⎡⎦⎤0,π2上的最大值和最小值.25.已知sin ⎝⎛⎭⎫α+3π4=513,cos ⎝⎛⎭⎫π4-β=35,且-π4<α<π4,π4<β<3π4,求cos[2(α-β)]的值.考点四 三角函数的图象与性质1.函数y =16-x 2+sin x 的定义域为______________.2.若f (x )是R 上的偶函数,当x ≥0时,f (x )=sin x ,则f (x )的解析式是__________________.3.对于函数f (x )=sin2x ,下列选项中正确的是( )A .f (x )在⎝⎛⎭⎫π4,π2上是递增的 B .f (x )的图象关于原点对称 C .f (x )的最小正周期为2π D .f (x )的最大值为24.函数y =2sin ⎝⎛⎭⎫π6-2x (x ∈[0,π])的单调递增区间是5.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π)是奇函数,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ).若g (x )的最小正周期为2π,且g ⎝⎛⎭⎫π4=2,则f ⎝⎛⎭⎫3π8=6.在△ABC 中,C >π2,若函数y =f (x )在[0,1]上为单调递减函数,则下列命题正确的是( )A .f (cos A )>f (cosB ) B .f (sin A )>f (sin B )C .f (sin A )>f (cos B )D .f (sin A )<f (cos B )7.已知函数f (x )=2sin ⎝⎛⎭⎫x +π4+φ是奇函数,当φ∈⎣⎡⎦⎤-π2,π2时,φ的值为________.8.若函数f (x )=sin x +a cos x 的图象关于直线x =π6对称,则a =________.9.关于函数f (x )=sin|x |+|sin x |有下述四个结论:①f (x )是偶函数;②f (x )在区间⎝⎛⎭⎫π2,π单调递增;③f (x )在[-π,π]有4个零点;④f (x )的最大值为2,其中所有正确结论的编号是( ) A .①②④ B .②④ C .①④ D .①③10.给出下列4个命题:①函数y =⎪⎪⎪⎪sin ⎝⎛⎭⎫2x -π12的最小正周期是π2;②直线x =7π12是函数y =2sin ⎝⎛⎭⎫3x -π4的一条对称轴;③若sin α+cos α=-15,且α为第二象限角,则tan α=-34;④函数y =cos(2-3x )在区间⎝⎛⎭⎫23,3上单调递减.其中正确的是________.(写出所有正确命题的序号).11.已知函数f (x )=sin ⎝⎛⎭⎫2x -3π2(x ∈R),下列说法错误的是( ) A .函数f (x )的最小正周期是π B .函数f (x )是偶函数C .函数f (x )的图象关于点⎝⎛⎭⎫π4,0中心对称D .函数f (x )在⎣⎡⎦⎤0,π2上是增函数12.已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|≤π2,x =-π4为f (x )的零点,x =π4为y =f (x )图象的对称轴,且f (x )在⎝⎛⎭⎫π18,5π36上单调,则ω的最大值为13.对于函数f (x )=⎩⎪⎨⎪⎧sin x ,sin x ≥cos x ,cos x ,sin x <cos x ,下列命题中正确的是( )A .该函数的值域是[-1,1]B .当且仅当x =2k π+π2(k ∈Z)时,函数取得最大值1C .当且仅当x =2k π-π2(k ∈Z)时,函数取得最小值-1D .当且仅当2k π+π<x <2k π+3π2(k ∈Z)时,f (x )<014.函数f (x )=sin x|cos x |在区间[-π,π]内的大致图象是下列图中的( )15.若函数f (x )的定义域为R ,最小正周期为2π,且满足f (x )=⎩⎪⎨⎪⎧cos x ,-π≤x <0,sin x ,0≤x <π,则f ⎝⎛⎭⎫-174π=________.16.已知f (x )=sin 2x +cos x ,x ∈⎣⎡⎦⎤-π3,2π3,则f (x )的值域为________.17.若函数f (x )=3sin(2x +θ)(0<θ<π)是偶函数,则f (x )在[0,π]上的单调递增区间是18.函数f (x )=sin x (1-sin x )1-sin x的奇偶性是( ) A .奇函数B .偶函数C .既是奇函数又偶函数D .非奇非偶函数19.求函数f (x )=2sin 2x +2sin x -12,x ∈⎣⎡⎦⎤π6,5π6的值域.20.已知|x |≤π4,求函数y =-sin 2x +sin x +1的最小值.21.函数f (x )=log 12cos x 的单调递增区间是___________.22.下列函数中,周期为4π的是( )A .y =sin4xB .y =cos2xC .y =tan x 2D .y =sin x 223.已知函数f (x )=log a cos ⎝⎛⎭⎫2x -π3(其中a >0,且a ≠1). (1)求它的定义域;(2)求它的单调区间;(3)判断它的奇偶性;(4)判断它的周期性,如果是周期函数,求出它的周期.24.已知函数f (x )=2sin ⎝⎛⎭⎫2x +π6+a +1(其中a 为常数). ①求f (x )的单调区间;②若x ∈⎣⎡⎦⎤0,π2时,f (x )的最大值为4,求a 的值.26.用“五点法”作出函数y =1-2sin x ,x ∈[-π,π]的简图,并回答下列问题:(1)观察函数图象,写出满足下列条件的x 的区间.①y >1;②y <1.(2)若直线y =a 与y =1-2sin x ,x ∈[-π,π]的图象有两个交点,求a 的取值范围.27.如图是函数y =A sin(ωx +φ)+2(A >0,ω>0,|φ|<π)的图象的一部分,则它的振幅、周期、初相分别是( )A .A =3,T =4π3,φ=-π6B .A =3,T =4π3,φ=-3π4C .A =1,T =4π3,φ=-π6D .A =1,T =4π3,φ=-3π428.函数f (x )=1-2a -2a cos x -2sin 2x 的最小值为g (a )(a ∈R).(1)求g (a );(2)若g (a )=12,求a 及此时f (x )的最大值.29.在已知函数f (x )=A sin(ωx +φ),x ∈R ⎝⎛⎭⎫其中A >0,ω>0,0<φ<π2的图象与x 轴的交点中,相邻两个交点之间的距离为π2,且图象上一个最低点为M ⎝⎛⎭⎫2π3,-2. (1)求f (x )的解析式;(2)当x ∈⎣⎡⎦⎤π12,π2时,求f (x )的值域.30.已知函数f (x )=2sin ⎝⎛⎭⎫2x -π3. (1)求函数f (x )的最小值及f (x )取到最小值时自变量x 的集合;(2)指出函数y =f (x )的图象可以由函数y =sin x 的图象经过哪些变换得到;(3)当x ∈[0,m ]时,函数y =f (x )的值域为[-3,2],求实数m 的取值范围.考点五 三角函数的图象变换问题1.已知曲线C 1:y =cos x ,C 2:y =sin ⎝⎛⎭⎫2x +2π3,则下面结论正确的是( ) A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 22.将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位长度后,得到一个偶函数的图象,则φ的一个可能取值为( )A.π2B.π4C .0D .-π43.将函数y =2sin ⎝⎛⎭⎫2x +π6的图象向右平移14个周期后,所得图象对应的函数为( ) A .y =2sin ⎝⎛⎭⎫2x +π4 B .y =2sin ⎝⎛⎭⎫2x +π3C .y =2sin ⎝⎛⎭⎫2x -π4D .y =2sin ⎝⎛⎭⎫2x -π3 4.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π2)的图象上的一个最低点为M ⎝⎛⎭⎫2π3,-2,周期为π. (1)求f (x )的解析式;(2)将y =f (x )的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),然后再将所得的图象沿x 轴向右平移π6个单位,得到函数y =g (x )的图象,写出函数y =g (x )的解析式.5.如图,是函数y =A sin(ωx +φ)+k (A >0,ω>0)的一段图象.(1)求此函数的解析式;(2)分析一下该函数的图象是如何通过y =sin x 的图象变换得来的?考点六 三角函数的应用1.直角走廊的示意图如图所示,其两边走廊的宽度均为2米,过点P 的一直线与走廊的外侧两边交于A ,B 两点,且与走廊的一边的夹角为θ⎝⎛⎭⎫0<θ<π2.(1)将线段AB 的长度l 表示为θ的函数;(2)一根长度为5米的铁棒能否水平(即铁棒与地面平行)通过该直角走廊?并说明理由.(铁棒的粗细忽略不计)2.福建沿海的超强台风过后,当地人民积极恢复生产,焊接工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1米,圆心角θ=π3,施工要求按图中所画的那样,在钢板OPQ 上裁下一块平行四边形钢板ABOC ,要求使裁下的钢板面积最大.试问王师傅如何确定A 的位置,才能使裁下的钢板符合要求?最大面积为多少?。
高一数学三角函数章节复习2(学生版)

学科教师辅导讲义【点拨】上述所给出的两种解法,均体现了一种转化与化归的数学思想方法,实际上,也给出了对求形如sin cos a x by c x d+=+值域的两种通法,另外,若以后学过《解析几何》之后,利用斜率的概念,还可以给出本题的另外一种数形结合的解题方法。
2、数形结合思想数形结合的思想,就是把问题的数量关系和空间形式结合起来考察的思想,根据解决问题的需要,可以把数量关系的问题转化为图形的性质问题去讨论,或者把图形的性质问题转化为数量关系的问题来研究,简言之“数形互相取长补短”。
例2、定义在R 上的函数()f x 满足()()2f x f x =+,当[]3,5x ∈时,()24f x x =--,则( ) A 、sincos 66f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭ B 、()()sin1cos1f f > C 、22cossin 33f f ππ⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭D 、()()cos2sin 2f f > 【分析】由()()2f x f x =+知()f x 是以2T =为周期的函数,又Q []3,5x ∈时,()24f x x =--,可知,当[]3,4x ∈,()2f x x =-;当(]4,5x ∈时,()6f x x =-+,如第一个图所示,知()f x 在[]1,0-上是增函数,在[]0,1上是减函数,由第二个图可知0cos2sin 2<<3、换元思想方法在求函数的定义域、周期、单调区间时,都可能用到了整体换元的思想方法。
例3、求函数()()43sin 43cos 16y x x =---的最值。
【分析】将函数式展开发现出现sin cos ,sin cos x x x x +,从而可以运用代数换元,转化为二次函数问题。
三角函数章节涉及的15个必考点全梳理

考点梳理:三角函数章节涉及的15个必考点全梳理必考点1 象限角及终边相同的角(1)任意角、角的分类:①按旋转方向不同分为正角、负角、零角. ②按终边位置不同分为象限角和轴线角. (2)终边相同的角:终边与角α相同的角可写成α+k ·360°(k ∈Z ). 【典例1】如果,那么与终边相同的角可以表示为A .B .C .D .【解析】由题意得,与终边相同的角可以表示为.故选B .【小结】象限角的两种判断方法(1)图象法:在平面直角坐标系中,作出已知角并根据象限角的定义直接判断已知角是第几象限角. (2)转化法:先将已知角化为k ·360°+α(0°≤α<360°,k ∈Z )的形式,即找出与已知角终边相同的角α,再由角α终边所在的象限判断已知角是第几象限角.【典例2】若α是第三象限的角, 则2απ-是 ( )A. 第一或第二象限的角B. 第一或第三象限的角C. 第二或第三象限的角D. 第二或第四象限的角【解析】α是第三象限角, 322,2k k k Z πππαπ∴+<<+∈, 3224k k παπππ∴+<<+, 31,422422k k k k παπππππππαπ∴--<-<--∴-+<-<-+,故当k 为偶数时, 12πα-是第一象限角;故当k 为奇数时, 12πα-是第三象限角,故选B.【小结】象限角与轴线角(终边在坐标轴上的角)的集合表示 (1)象限角:象限角 集合表示第一象限角 {α|k ·360°<α<k ·360°+90°,k ∈Z } 第二象限角 {α|k ·360°+90°<α<k ·360°+180°,k ∈Z } 第三象限角 {α|k ·360°+180°<α<k ·360°+270°,k ∈Z } 第四象限角{α|k ·360°+270°<α<k ·360°+360°,k ∈Z }(2)轴线角:角的终边的位置集合表示终边落在x 轴的非负半轴上 {α|α=k ·360°,k ∈Z } 终边落在x 轴的非正半轴上 {α|α=k ·360°+180°,k ∈Z } 终边落在y 轴的非负半轴上 {α|α=k ·360°+90°,k ∈Z } 终边落在y 轴的非正半轴上 {α|α=k ·360°+270°,k ∈Z } 终边落在y 轴上 {α|α=k ·180°+90°,k ∈Z } 终边落在x 轴上 {α|α=k ·180°,k ∈Z } 终边落在坐标轴上{α|α=k ·90°,k ∈Z }必考点2 弧度制、扇形的弧长及面积公式(1)弧度制:①1弧度的角:把长度等于半径长的弧所对的圆心角叫做1弧度的角.②规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,|α|=lr ,l 是以角α作为圆心角时所对圆弧的长,r 为半径.③用“弧度”做单位来度量角的制度叫做弧度制.比值lr 与所取的r 的大小无关,仅与角的大小有关.(2)弧度与角度的换算:360°=2π弧度;180°=π弧度. (3)弧度制下l =|α|·r ,S =12lr ,此时α为弧度.扇形面积公式,扇形中弦长公式,扇形弧长公式在角度制下,弧长l =n πr 180,扇形面积S =n πr 2360,此时n 为角度,它们之间有着必然的联系.【典例3】(2018·湖北高考模拟(理))《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为,弦长为的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中,)A .15B .16C .17D .18 【解析】因为圆心角为,弦长为,所以圆心到弦的距离为半径为40,因此根据经验公式计算出弧田的面积为,实际面积等于扇形面积减去三角形面积,为,因此两者之差为,选B.【典例4】(2019·河南高考模拟(理))已知圆O 与直线l 相切于A ,点,P Q 同时从点A 出发,P 沿着直线l 向右、Q 沿着圆周按逆时针以相同的速度运动,当Q 运动到点A 时,点P 也停止运动,连接OQ ,OP (如图),则阴影部分面积1S ,2S 的大小关系是( )A .12S S =B .12S S ≤C .12S S ≥D .先12S S <,再12S S =,最后12S S > 【解析】如图所示,因为直线l 与圆O 相切,所以OA AP ⊥, 所以扇形的面积为1122AOQ S AQ r AQ OA =⋅⋅=⋅⋅扇形,12AOP S OA AP ∆=⋅⋅, 因为AQ AP =,所以扇形AOQ 的面积AOP AOQ S S ∆=扇形, 即AOP AOQ AOB AOB S S S S ∆-=-扇形扇形扇形,所以12S S =,【典例5】一个扇形的周长为20 cm ,当扇形的圆心角α等于多少弧度时,这个扇形的面积最大?并求出这个扇形的最大面积.【解析】 设扇形的半径为r cm ,则弧长为l =(20-2r ) cm . 由0<l <2πr ,得0<20-2r <2πr ,∴10π+1<r <10.于是扇形的面积为S =12(20-2r )r =-(r -5)2+25(10π+1<r <10).当r =5时,l =10,α=2,S 取到最大值,此时最大值为25 cm 2.故当扇形的圆心角α等于2弧度时,这个扇形的面积最大,最大面积是25 cm 2. 【小结】应用弧度制解决问题的方法(1)利用扇形的弧长和面积公式解题时,要注意角的单位必须是弧度;(2)求扇形面积最大值的问题时,常转化为二次函数的最值问题,利用配方法使问题得到解决; (3)在解决弧长问题和扇形面积问题时,要合理地利用圆心角所在的三角形.必考点3 三角函数的定义1.任意角的三角函数定义:设α是一个任意角,角α的终边与单位圆交于点P (x ,y ),那么 (1)点P 的纵坐标叫角α的正弦函数,记作sin α=y ; (2)点P 的横坐标叫角α的余弦函数,记作cos α=x ;(3)点P 的纵坐标与横坐标之比叫角α的正切函数,记作tan α=yx .它们都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为: 正弦函数y =sinx ,x ∈R ; 余弦函数 y =cosx ,x ∈R ; 正切函数 y =tanx ,x ≠π2+k π(k ∈Z ).2.三角函数在各象限内的符号口诀是:一全正、二正弦、三正切、四余弦 【典例6】(2008·全国高考真题(文))若,且,则是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角 【解析】,则的终边在三、四象限;则的终边在三、一象限,,,同时满足,则的终边在三象限.【典例7】已知角的终边在射线上,则等于( )A. B. C. D.【解析】由题得在第四象限,且,所以【典例8】(江西高考真题(文))已知角θ的顶点为坐标原点,始边为x 轴的正半轴,若()4,p y 是角θ终边上一点,且25sin 5θ=-,则y=_______. 【解析】根据正弦值为负数,判断角在第三、四象限,再加上横坐标为正,断定该 角为第四象限角.=【典例9】已知角α的终边经过点(3a -9,a +2),且cos α≤0,sin α>0,则实数a 的取值范围是( ) A .(-2,3] B .(-2,3) C .[-2,3)D .[-2,3] 【解析】 ∵00cos ,sin αα≤>,∴角α的终边落在第二象限或y 轴的正半轴上. ∴39020a a ⎧-≤⎨+>⎩∴23-a <≤.故选A.【小结】1.已知角α终边上一点P 的坐标,则可先求出点P 到原点的距离r ,然后利用三角函数的定义求解.2.已知角α的终边所在的直线方程,则可先设出终边上一点的坐标,求出此点到原点的距离,然后利用三角函数的定义求解相关的问题.若直线的倾斜角为特殊角,也可直接写出角α的三角函数值.必考点4 同角三角函数的基本关系式同角三角函数的基本关系式(1)平方关系:sin 2α+cos 2α=1(α∈R ). (2)商数关系:tan α=sin αcos α⎝⎛⎭⎫α≠k π+π2,k ∈Z .【典例10】(2019·北京高考模拟(文))已知3(,)22ππα∈,且tan α=sin α=( )A .33-B .36-C .36 D【解析】因为3(,)22ππα∈,sin tan cos ααα==>0,故3(,)2παπ∈,即sin αα=, 又22sin cos 1αα+=, 解得:sin α=36-,故选 :B【典例11】(2020·金华市江南中学高一月考)已知sin cos sin cos x xx x+-=2,则tan x =____,sin x cos x =____.【解析】将sin cos sin cos x x x x +-=2左端分子分母同除以cos x ,得tan 12tan 1x x +=-,解得tan 3x =, 2222sin cos tan 33sin cos sin cos tan 13110x x x x x x x x ====+++. 【小结】1.同角三角函数关系式的三种应用方法--“弦切互化法”、““1”的灵活代换法”、“和积转换法” (1)利用sin 2α+cos 2α=1可实现α的正弦、余弦的互化,注意()222124sin cos sin cos sin cos tanπθθθθθθ=+=+-=等;(2)由一个角的任一三角函数值可求出这个角的另外两个三角函数值,因为利用“平方关系”公式,需求平方根,会出现两解,需根据角所在的象限判断符号,当角所在的象限不明确时,要进行分类讨论. 2. 利用sin αcos α=tan α可以实现角α的弦切互化.(1)若已知tan α=m ,求形如a sin α+b cos αc sin α+d cos α(或a sin 2α+b cos 2αc sin 2α+d cos 2α)的值,其方法是将分子、分母同除以cos α(或cos 2α)转化为tan α的代数式,再求值,如果先求出sin α和cos α的值再代入,那么运算量会很大,问题的解决就会变得繁琐.(2)形如a sin 2α+b sin αcos α+c cos 2α通常把分母看作1,然后用sin 2α+cos 2α代换,分子、分母同除以cos 2α再求解.必考点5 sin α±cos α与sin αcos α的关系及应用三角函数求值与化简必会的三种方法 (1)弦切互化法:主要利用公式tan α=;形如,22asin x bsinxcosx ccos x ++等类型可弦化切(2)“1”的灵活代换法: ()222124sin cos sin cos sin cos tanπθθθθθθ=+=+-=等.(3)和积转换法:利用()()22212,()2sin cos sin cos sin cos sin cos θθθθθθθθ±=±++-=的关系进行变形、转化.【典例12】(2018·河北高考模拟(理))已知,,则的值为( )A .B .C .D .【解析】∵,∴,∴,又∵,∴,∴,∴,故选B.【典例13】(2020·永州市第四中学高一月考)已知22sin 2sin cos 01tan 2k αααπαα+⎛⎫=<< ⎪+⎝⎭.试用k 表示sin cos αα-的值.【解析】()22sin sin cos 2sin 2sin cos sin 1tan 1cos ααααααααα++=++()2sin cos sin cos sin cos αααααα+=+2sin cos k αα== ()222sin cos sin cos 2sin cos αααααα-=+-12sin cos αα=-1k =-,当04πα<<时,sin cos αα<,此时sin cos 1k αα-=--, 当42ππα≤<时,sin cos αα≥,此时sin cos 1k αα-=-【典例14】(2019·天津高考模拟)已知,则的值是()A. B. C. D.【解析】,则即故选D.【典例15】(2019·山东高三期末(理))已知,,则()A. B. C.或 D.或【解析】由题意知,,①,即,,为钝角,,,,,②由①②解得,,故选B.【小结】(1)应用公式时注意方程思想的应用:对于sinα+cosα,sinαcosα,sinα-cosα这三个式子,利用(sinα±cosα)2=1±2sinαcosα,可以知一求二.(2)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.必考点6 诱导公式及其应用六组诱导公式角函数 2k π+α(k ∈Z )π+α-απ-απ2-α π2+α 正弦 sin_α -sin_α -sin_α sin_α cos_α cos_α 余弦 cos_α -cos_α cos_α -cos_α sin_α -sin_α 正切tan_αtan_α-tan_α-tan_α对于角“k π2±α”(k ∈Z )的三角函数记忆口诀“奇变偶不变,符号看象限”,“奇变偶不变”是指“当k 为奇数时,正弦变余弦,余弦变正弦;当k 为偶数时,函数名不变”.“符号看象限”是指“在α的三角函数值前面加上当α为锐角时,原函数值的符号”【典例16】(2016·全国高考真题(文))已知θ是第四象限角,且sin (θ+)=,则tan (θ–)= .【解析】∵θ是第四象限角, ∴,则,又sin (θ),∴cos(θ).∴cos()=sin (θ),sin ()=cos (θ).则tan (θ)=﹣tan ().故答案为:.【典例17】(2020·永州市第四中学高一月考)已知α是第四象限角,3sin cos tan()22()tan()sin()f ππααπααπαπα⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭=---.(1)化简()f α.(2)若33cos 25πα⎛⎫-= ⎪⎝⎭,求()f α的值. 【解析】(1)3sin()cos()tan()22()tan()sin()f ππααπααπαπα-+-=---sin()sin (tan )2tan sin πααααα---=-cos sin tan tan sin ααααα=-cos α=- (2)因为3cos()2πα-3cos()2πα=-3sin 5α=-=,所以3sin 5α=-.因为α是第四象限角,所以4cos 5α=,所以4()cos 5f αα=-=-.【小结】1.用诱导公式求值时,要善于观察所给角之间的关系,利用整体代换的思想简化解题过程.常见的互余关系有-α与+α,+α与-α,+α与-α等,常见的互补关系有-θ与+θ,+θ与-θ,+θ与-θ等.2. 利用诱导公式化简求值的步骤:(1)负化正;(2)大化小;(3)小化锐;(4)锐求值.必考点7 同角公式、诱导公式的综合应用【典例18】(2020·山东诸城�高一期中)已知3sin 5α=-,且α是第________象限角.从①一,②二,③三,④四,这四个选项中选择一个你认为恰当的选项填在上面的横线上,并根据你的选择,解答以下问题:(1)求cos ,tan αα的值;(2)化简求值:3sin()cos()sin 2cos(2020)tan(2020)πααπαπαπα⎛⎫--+ ⎪⎝⎭+-.【解析】(1)因为3sin 5α=-,所以α为第三象限或第四象限角; 若选③,24sin 3cos 1sin ,tan 5cos 4ααααα=--=-==; 若选④,24sin 3cos 1sin ,tan 5cos 4ααααα=-===-; (2)原式sin cos (cos )cos tan()ααααα-=-sin cos tan ααα-=-sin cos sin cos αααα=2cos α=2315⎛⎫=-- ⎪⎝⎭1625=【典例19】设tan(α+8π7)=m ,求证:sin (15π7+α)+3cos (α-13π7)sin (20π7-α)-cos (α+22π7)=m +3m +1.证法一:左=sin[π+(87π+α)]+3cos[(α+8π7-3π)]sin[4π-(α+87π)]-cos[2π+(α+8π7)]=-sin (α+8π7)-3cos (α+8π7)-sin (α+8π7)-cos (α+8π7)=tan (α+8π7)+3tan (α+8π7)+1=m +3m +1=右∴等式成立.证法二:由tan(α+8π7)=m ,得tan(α+π7)=m .左边=sin[2π+(π7+α)]+3cos[2π-(π7+α)]sin[2π+π-(π7+α)]-cos[2π+π+(π7+α)]=sin (π7+α)+3cos (π7+α)sin[π-(π7+α)]-cos[π+(π7+α)]=sin (π7+α)+3cos (π7+α)sin (π7+α)+cos (π7+α)=tan (π7+α)+3tan (π7+α)+1=m +3m +1=右边,∴等式成立. 【小结】1.利用诱导公式化简三角函数的基本思路:(1)分析结构特点,选择恰当公式;(2)利用公式化成单角三角函数;(3)整理得最简形式.2.化简要求:(1)化简过程是恒等变形;(2)结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值.3.三角恒等式的证明一般有三种方法:①一端化简等于另一端;②两端同时化简使之等于同一个式子;③作恒等式两端的差式使之为0.4证明条件恒等式,一般有两种方法:一是在从被证等式一边推向另一边的适当时候将条件代入,推出被证等式的另一边,这种方法称作代入法;二是直接将条件等式变形,变形为被证的等式,这种方法称作推出法,证明条件等式时,不论使用哪一种方法,都要依据要证的目标的特征进行变形.巩固1.(2020·甘肃省会宁县第四中学高二期末(文))sin780︒的值为( )A .B .12-C .12D .2【解析】()sin 780sin 72060sin 60︒=︒+︒=︒=,故选:D巩固2.(2020·昆明市官渡区第一中学高一月考)若-2π<α<0,则点P(tanα,cosα)位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【解析】∵-2π<α<0,∴tanα<0,cosα>0,∴点P(tanα,cosα)位于第二象限,故选B巩固3.(2019·伊美区第二中学高一月考)已知4sin 5θ=,()0,θπ∈,则tan θ等于( ). A .43B .34C .43±D .34±【解析】因为4sin 5θ=,()0,θπ∈,则由22sin cos 1θθ+=, 解得35cos θ=±,故可得43sin tan cos θθθ==±.故选:C .巩固4.(2020·河南项城市第三高级中学高一月考)α是第二象限角,且31cos 24πα⎛⎫+=⎪⎝⎭,则cos α=( )A .B .14-C .14D 【解析】因为31cos 24πα⎛⎫+=⎪⎝⎭,由诱导公式可得,1sin 4α=,因为22sin cos 1αα+=,α是第二象限角,所以cos 4α===-.故选:A巩固5.(2020·江西省铜鼓中学高一期末)一个扇形的圆心角为150°,面积为53π,则该扇形半径为( )A .4B .1CD .2【解析】圆心角为51506πα==,设扇形半径为R ,2215152326S R R ππα=⋅⇒=⨯,解得2R =.选D巩固6.(2020·吉林高三月考(理))若4sin cos 3θθ-=,且3π,π4θ⎛⎫∈ ⎪⎝⎭,则sin(π)cos(π)θθ---=( )A .3-B .3C .43-D .43【解析】由题意,416sin cos 12sin cos 39θθθθ-=⇒-=,则72sin cos 09θθ=-<,由于3π,π4θ⎛⎫∈ ⎪⎝⎭,则sin(π)cos(π)sin cos θθθθ---=+===.故选A.巩固7.(2018·全国延安�高三一模(文))已知()()sin 3cos sin 2πθπθθ⎛⎫++-=-⎪⎝⎭,则2sin cos cos θθθ+=( )A .15B .25C .35D .5【解析】由已知()()sin 3cos sin cos 3cos sin tan 2,2πθπθθθθθθ⎛⎫++-=-⇒-=-⇒=⎪⎝⎭则22222sin cos cos tan 13sin cos cos .sin cos tan 15θθθθθθθθθθ+++===++ 故选C.巩固8.(2020绵阳江油中学高三开学考试(文)已知()0,απ∈,1sin 23πα⎛⎫-=- ⎪⎝⎭,则()tan απ+=( )A B .-C .D .-【解析】因为1sin cos 23παα⎛⎫-==-⎪⎝⎭,且()0,απ∈所以sin 3α==,所以sin tan cos ααα==-()tan tan απα+==- D巩固9.(2019·历下·山东师范大学附中高三月考)【多选题】在平面直角坐标系xOy 中,角α顶点在原点O ,以x 正半轴为始边,终边经过点()()1,0P m m <,则下列各式的值恒大于0的是( ) A .sin tan ααB .cos sin αα-C .sin cos ααD .sin cos αα+【解析】由题意知sin 0α<,cos 0α>,tan 0α<. 选项Asin 0tan αα>; 选项B ,cos sin 0αα->; 选项C ,sin cos 0αα<; 选项D ,sin cos αα+符号不确定. 故选:AB.巩固10.(2020·山东临沂·高一期末)【多选题】对于①sin 0θ>,②sin 0θ<,③cos 0θ>,④cos 0θ<,⑤tan 0θ>,⑥tan 0θ<,则θ为第二象限角的充要条件为( ) A .①③B .①④C .④⑥D .②⑤【解析】若θ为第二象限角,则sin 0θ>,cos 0θ<,tan 0θ<. 所以,θ为第二象限角sin 0cos 0θθ>⎧⇔⎨<⎩或sin 0tan 0θθ>⎧⎨<⎩或cos 0tan 0θθ<⎧⎨<⎩.故选:BC.巩固11.(2020·福建泉州·高一期末)在平面直角坐标系中,角α的顶点在原点,始边与x 轴非负半轴重合,角α的终边经过点34,55P ⎛⎫-⎪⎝⎭,则sin α=___________,tan α=_________. 【解析】∵角α的终边经过点34,55P ⎛⎫- ⎪⎝⎭,∴||1OP =,∴4sin ,t 344455355an 1αα-=--===-.巩固12.(2019·北京顺义·牛栏山一中高三月考)已知tan 2α,且α为第二象限角,则sin α=______;cos α=_______.【解析】α为第二象限角 sin 0α∴>,cos 0α<,由22sin tan 2cos sin cos 1ααααα⎧==-⎪⎨⎪+=⎩得:sin cos αα⎧=⎪⎪⎨⎪=⎪⎩巩固13.(2018·浙江丽水·高一期末)在平面直角坐标系中,角α的顶点与原点重合,始边与x 轴的非负半轴重合,终边过点(1)P -,则tan α=_______;cos sin αα-=_______. 【解析】∵角α终边过点(1)P -,||2OP =,∴t an α==1sin 2α-=,cos α=cos sin αα-=.巩固14.(2019·海南高三月考)已知角α的终边经过点1(,33P -- (1)求sin ,cos ,tan ααα的值;(25sin(3)2cos()ππαα-++ 【解析】(1)由题意角α的终边经过点1(,3P -,可得1r OP ==,根据三角函数的定义,可得1sin ,tan 3ααα==-=. (25sin(3)2cos()ππαα-++=tan (14α===-⨯=.巩固15.(2020·全国高一课时练习)在平面直角坐标系中,角α的终边在直线3x +4y =0上,求sin α-3cos α+tan α的值.【解析】当角α的终边在射线y =-34x (x >0)上时,取终边上一点P (4,-3), 所以点P 到坐标原点的距离r =|OP |=5, 所以sin α=y r =35-=-35,cos α=x r =45,tan α=yx =-34. 所以sin α-3cos α+tan α=-35-125-34=-154. 当角α的终边在射线y =-34x (x <0)上时,取终边上一点P ′(-4,3), 所以点P ′到坐标原点的距离r =|OP ′|=5, 所以sin α=y r =35,cos α=x r =-45,tan α=yx =-34. 所以sin α-3cos α+tan α=35-3×45⎛⎫- ⎪⎝⎭-34=35+125-34=94.综上,sin α-3cos α+tan α的值为-154或94.巩固16.(2020·永州市第四中学高一月考)已知α是第四象限角,3sin cos tan()22()tan()sin()f ππααπααπαπα⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭=---. (1)化简()f α. (2)若33cos 25πα⎛⎫-= ⎪⎝⎭,求()f α的值. 【解析】(1)3sin()cos()tan()22()tan()sin()f ππααπααπαπα-+-=---sin()sin (tan )2tan sin πααααα---=-cos sin tan tan sin ααααα=-cos α=- (2)因为3cos()2πα-3cos()2πα=-3sin 5α=-=,所以3sin 5α=-因为α是第四象限角,所以4cos 5α=,所以4()cos 5f αα=-=-必考点8 “五点法”做函数()sin y A x h ωϕ=++的图象“五点法”作图:先列表,令30,,,,222x ππωϕππ+=,求出对应的五个错误!未找到引用源。
高一三角函数章节系统复习 (例题变式含解析)

高一三角函数章节教学设计【知识要点汇总】知识点一、任意角 1、角的概念一条射线OB 由原来的位置OB ,绕着它的端点O 按一定方向旋转到另一位置OA ,就形成了角α,其中射线OB 叫角α的始边,射线OA 叫角α的终边,O 叫角α的顶点.2、角的分类 (1)按旋转方向图形(2)按角的终边位置 36036090,}k k k Z α<<+∈ 36090360180,}k k k Z α+<<+∈360180360270,}k k k Z α+<<+∈36018036090,}k k k Z α-<<-∈{|360270360360,}k k k Z αα+<<+∈或{|36090360,}k k k Z αα-<<∈轴非负半轴为始边,终边落在坐标轴上的角360,k k ∈36090,}k k Z +∈360180,}k k Z +∈或360180,}k k Z -∈ 360270,}k k Z +∈或36090,}k k Z -∈{|180,k k ββ=∈18090,}k k Z +∈或{|18090,}k k Z ββ-∈{|90,k k ββ=∈3、终边相同的角所有与角α终边相同的角,连同角α在内,可构成一个集合{}Z k k S ∈⋅+==,360αββ,即任一与角α终边相同的角,都可以表示成角α与整数个周角的和. 【注】①相等的角终边一定相等,终边相同的角不一定相等 ①终边相同的角的表示不唯一 57.305718'=,1180π=、常用的角度与弧度对应表0 30 45 60 90 120 135 150 180知识点三、扇形的弧长和面积公式1、弧长公式:r l ·α=(α是圆心角的弧度数) 2、扇形面积公式:2·21·21r r l S α==.知识点四、三角函数的定义 1、单位圆定义法:如图,设α是一个任意角,R α∈,它的终边OP 与单位圆相交于点(,)P x y ①正弦函数:把点P 的纵坐标y 叫做α的正弦函数,记作sin α,即sin y α= ②余弦函数:把点P 的横坐标x 叫做α的余弦函数,记作cos α,即cos x α= ③正切函数:把点P 的纵坐标与横坐标的比值y x 叫做α的正切,记作tan α,即tan yxα=(0x ≠) 我们将正弦函数、余弦函数和正切函数统称为三角函数 2、终边上任意一点定义法:在角α终边上任取一点(,)P x y ,设原点到(,)P x y 点的距离为22||r OP x y ==+①正弦函数:sin yrα= ②余弦函数:cos xr α= ③正切函数:tan yxα=(0x ≠) 【注】任意角α的三角函数值只与α有关,而与点P 的位置无关. 3、三角函数值在各象限的符号(口诀:一全正,二正弦,三正切,四余弦)知识点五、特殊角的三角函数值角度α 0 15 30 45 60 75 90 120 135 150 180 弧度α 0 12π6π 4π 3π 512π2π 23π 34π 56π π正弦值sin α624- 122232624+ 13222121cos sin 22=+αα余弦值cos α1624+ 32 2212 624- 012- 22-32- 1-正切值tan α0 32-331 332+3-1- 33-知识点六、同角基本关系式 1、商数关系:αααcos sin tan =2、平方关系知识点七、诱导公式)2(απ+k本质是:奇变偶不变(对k 而言,指k 取奇数或偶数),符号看象限(看原函数,同时把α看成是锐角)(1)sin()sin παα+=- cos()cos παα+=- tan()tan παα+= (2)sin()sin αα-=-cos()cos αα-=tan()tan αα-=- (3)sin()sin παα-= cos()cos παα-=-tan()tan παα-=-(4)sin()cos 2παα-= cos()sin 2παα-=(5)sin()cos 2παα+=cos()sin 2παα+=-(6)3sin()cos 2παα-=- 3cos()sin 2παα-=-(7)3sin()cos 2παα+=- 3cos()sin 2παα+=知识点八、正弦函数、余弦函数、正切函数的图象与性质sin y x =cos y x = tan y x =图象222(sin cos )12sin cos (sin cos )(sin cos )4sin cos αααααααααα±=±-=+-k∈;注意:区分加πk与πk2的区别,有k一定要强调Z①由图可得:定义域、值域、周期、单调性、对称轴、对称中心知识点九、两角和与差的正余弦与正切①sin()sin cos cos sin αβαβαβ±=±;②cos()cos cos sin sin αβαβαβ±=;③tan tan tan()1tan tan αβαβαβ±±=;知识点十、二倍角公式①sin22sin cos ααα=;②2222cos2cos sin 2cos 112sin ααααα=-=-=-;③22tan tan 21tan ααα=-;知识点十一、降次(幂)公式2211cos 21cos 2sin cos sin 2;sin ;cos ;222ααααααα-+===知识点十二、半角公式sin22αα== sin 1cos tan.21cos sin aαααα-==+知识点十三、辅助角公式)sin(cos sin 22ϕααα++=+b a b a(其中abb a a b a b =+=+=ϕϕϕtan cos sin 2222,,). 【典型例题】例1. 已知cos (α−π6)=√33,则sin (4π3+α)=( ) A. √33B. −√33C. √63D. −√63解:∵cos(α−π6)=cos(π6−α)=√33,∴sin(π3+α)=sin[π2−(π6−α)] =cos(π6−α)=√33,∴sin(4π3+α)=sin[π+(π3+α)]=−sin(π3+α)=−√33. 故选B .变1. 已知sin (π6−α)=13,0<α<π2,则sin (π3+α)=( )A. 13B. −13C. 2√23D. −2√23解:∵sin(π6−a)=13,∴cos[π2−(π6−a)]=13,即cos(π3+a)=13, ∵0<a <π2,∴π3<a +π3<5π6.∴sin(π3+a)=2√23.故选C .例2. 已知sin(α+π6)−cosα=14,则sin(5π6−2α)的值为( ) A. −1516B. −78C. 78D. 1516解:∵sin(α+π6)−cosα=√32sinα+12cosα−cosα=√32sinα−12cosα=sin(α−π6)=14,∴cos(2α−π3)=1−2sin 2(α−π6)=1−2×(14)2=78. 又sin(5π6−2α)=cos(π2−(5π6−2α))=cos(2α−π3)所以sin(5π6−2α)的值为78.故选C .变2 .已知cos(α+π6)=34,则sin(2α+5π6)=( )A. −18B. 18C. −14D. 14解:因为cos(α+π6)=34,所以 sin(2α+5π6)=sin[π2+(2α+π3)]=cos(2α+π3)=2cos 2(α+π6)−1=2×(34)2−1=18.故选B .例3. 函数y =3sin(2x +π3)的图象,可由函数y =sin x 的图象经过下述哪项变换而得到( ) A. 向右平移π3个单位长度,横坐标缩短到原来的12,纵坐标伸长到原来的3倍 B. 向左平移π3个单位长度,横坐标缩短到原来的12,纵坐标伸长到原来的3倍 C. 向右平移π6个单位长度,横坐标伸长到原来的2倍,纵坐标缩短到原来的13 D. 向左平移π6个单位长度,横坐标缩短到原来的12,纵坐标缩短到原来的13解:将由y =sinx 的图象向左平移π3得到函数y =sin(x +π3),再横坐标缩小到原来的12倍,纵坐标不变得到函数y =sin(2x +π3),再横坐标不变,纵坐标变为原来的3倍得到y =3sin(2x +π3).故选B .变3 . 为了得到函数f(x)=sin(3x +π4)的图象,需对函数g(x)=sinx 的图象所作的变换可以为( )A. 先将图象上所有的横坐标压缩为原来的13倍,纵坐标不变,再向左平移π12个单位B. 先将图象上所有的横坐标伸长为原来的3倍,纵坐标不变,再向右平移π12个单位 C. 先将图象上所有的横坐标压缩为原来的13倍,纵坐标不变,再向左平移π4个单位 D. 先将图象上所有的横坐标伸长为原来的3倍,纵坐标不变,再向右平移π4个单位解:函数g(x)=sinx 要转换成函数f(x)=sin(3x +π4),先需要将函数g(x)=sinx 的图象上所有的横坐标压缩为原来的13倍变成y =sin3x ,再将y =sin3x 的图象再向左平移π12个单位,纵坐标不变,得到f(x)=sin [3(x +π12)]=sin (3x +π4)的图象,故选A .例4. 下列结论中正确的是( )A. 终边经过点(a,a)(a ≠0)的角的集合是{α|α=π4+kπ,k ∈Z } B. 将表的分针拨快10分钟,则分针转过的角的弧度数是π3 C. 若α是第三象限角,则α2是第二象限角,2α为第一或第二象限角D. M ={x|x =45°+k ⋅90°,k ∈Z},N ={y|y =90°+k ⋅45°,k ∈Z},则M ⊆N解:对于A ,终边经过点(a,a)(a ≠0)的角的正切值等于aa =1,所以终边经过点(a,a)(a ≠0)的角的集合是{α|α=π4+kπ,k ∈Z},所以A 正确;对于B ,将表的分针拨快10分钟,则分针顺时针旋转60°,即分针转过的角的弧度数是−π3,所以B 错误;对于C ,若α是第三象限角,则π+2kπ<α<3π2+2kπ,k ∈Z ,则π2+kπ<α2<3π4+kπ,k ∈Z ,2π+4kπ<2α<3π+4kπ,k ∈Z ,所以2α为第一或第二象限角,若k 为偶数,设k =2n ,n ∈Z ,则π2+2nπ<α2<3π4+2nπ,n ∈Z ,则α2是第二象限角;若k 为奇数,设k =2n +1,n ∈Z ,则3π2+2nπ<α2<7π4+2nπ,n ∈Z ,则α2是第四象限角,所以C错误;对于D ,M ={x|x =45°+k ·90°,k ∈Z}={x|x =(2k +1)×45°,k ∈Z},N ={x|x =90°+k ·45°,k ∈Z}={x|x =(k +2)×45°,k ∈Z},所以M 中的元素是45°的奇数倍的角,N 中元素是45°的整数倍的角,所以M ⊆N ,所以D 正确. 故选AD .变4 .下列结论中正确的是( )A. 终边经过点(a,a)(a ≠0)的角的集合是{α|α=π4+kπ,k ∈Z }B. 将表的分针拨慢10分钟,则分针转过的角的弧度数是π3 C. 若α是第三象限角,则α2是第二象限角,2α为第一或第二象限角D. M ={x|x =45°+k ⋅90°,k ∈Z},N ={y|y =90°+k ⋅45°,k ∈Z},则M ⊆N解:对于A ,终边经过点(a,a)(a ≠0)的角正切等于aa =1,所以终边经过点(a,a)(a ≠0)的角的集合是{α|α=π4+kπ,k ∈Z},所以A 正确;对于B ,将表的分针拨慢10分钟,则分针逆时针旋转60°,即分针转过的角的弧度数是π3,所以B 正确;对于C ,若α是第三象限角,则π+2kπ<α<3π2+2kπ,k ∈Z ,因此π2+kπ<α2<3π4+kπ,k ∈Z ,若k 为偶数,设k =2n ,n ∈Z ,则π2+2nπ<α2<3π4+2nπ,n ∈Z ,则α2是第二象限角,若k 为奇数,设k =2n +1,n ∈Z ,则3π2+2nπ<α2<7π4+2nπ,n ∈Z ,则α2是第四象限的角,所以C 错误;对于D ,M ={x|x =45°+k ·90°,k ∈Z}={x|x =(2k +1)45°,k ∈Z},N ={x|x =90°+k ·45°,k ∈Z}={x|x =(k +2)45°,k ∈Z},所以M 中的元素是45°的奇数倍的角,N 中元素是45°的整数倍的角,所以M ⊆N ,所以D 正确. 故选ABD .例5. 已知半径为1的扇形面积为π3,则此扇形的周长为 .解:设扇形的圆心角为α,则扇形的弧长为l =αr =α;扇形的面积为S =12lr =12α=π3,解得α=2π3; ∴弧长为l =2π3,扇形的周长为l +2r =2π3+2.故答案为:2π3+2.变5 .若半径为2cm 的扇形面积为8cm 2,则该扇形的周长是 cm解: 设该扇形的圆心角为α,则扇形面积为S =12×22×α=8,即α=4, 所以该扇形的弧长为4×2=8,因此该扇形的扇形周长为2×2+8=12.故答案为12.例6. 已知角α的终边经过点(2a +1,a −2),且cosα=−35,则实数a = . 解:由余弦函数的定义知,√(2a+1)+(a−2)=−35.化简并整理,得11a 2+20a −4=0.解得a =−2或a =211,又因为2a +1<0,所以a =−2.故答案为−2.变6 .已知角α的终边经过点P(−x,−6),且cos α=−513,则x 的值为 .解:因为cos α=√(−x)+(−6)=√x 2+36=−513,所以{x >0,x 2x 2+36=25169,,解得x =52.故答案为52. 例7. 若sinθ−cosθ=√2,则tanθ+1tanθ= .解析由已知得(sinθ−cosθ)2=2,∴sinθcosθ=−12, ∴tanθ+1tanθ=sinθcosθ+cosθsinθ=1sinθcosθ=−2.变7 .若tanα=2,则5sinα+2cosαsinα−4cosα=______.解:5sinα+2cosαsinα−4cosα=5tanα+2tanα−4=5×2+22−4=−6.故答案为−6.例8. 已知f (x )=2sin (2x −π3).(1)求函数f (x )的单调递增区间;(2)当x ∈[0,m ]时,函数f (x )的值域为[−√3,2],求实数m 的范围. 解:(1)对于函数f(x)=2sin(2x −π3),令2kπ−π2⩽2x −π3⩽2kπ+π2,k ∈Z ,求得kπ−π12⩽x ⩽kπ+5π12,k ∈Z .故函数f(x)的单调减区间为[kπ−π12,kπ+5π12],k ∈Z .(2)如图,因为当x ∈[0,m]时,y =f(x)取到最大值2,所以m ≥5π12.又函数y =f(x)在[5π12,11π12]上是减函数,f(0)=−√3,故m 的最大值为[5π12,11π12]内使函数值为−√3的值,令2sin (2x −π3)=−√3,即sin (2x −π3)=−√32,因为x ∈[5π12,11π12],所以2x −π3∈[π2,3π2], 所以2x −π3=4π3,解得x =5π6,所以m 的取值范围是[5π12,5π6]. 变8 .已知函数f (x )=1+2sin (2x −π3),(1)求f (x )的单调递增区间和对称中心;(2)若不等式|f (x )−m |<2在x ∈[π4,π2]上恒成立,求实数m 的取值范围.解:(1)∵函数f(x)=1+2sin(2x −π3),由−π2+2kπ≤2x −π3≤π2+2kπ(k ∈Z)得−π12+kπ≤x ≤5π12+kπ(k ∈Z),∴f(x)的单增区间为:[−π12+kπ,5π12+kπ](k ∈Z),又由2x −π3=kπ(k ∈Z)得x =π6+kπ2(k ∈Z)∴f(x)的对称中心为(π6+kπ2,1)(k ∈Z).(2)若不等式|f(x)−m|<2在x ∈[π4,π2]上恒成立,即m−32<sin(2x −π3)<m+12在x ∈[π4,π2]上恒成立,∴m−32<12,且m+12>1,由此求得m >1,且m <4,故实数m 的取值范围为(1,4). 例9. 若函数f(x)=cos (ωx +φ)(ω>0,|φ|<π2)的一个零点和与之相邻的对称轴之间的距离为π4,且当x =2π3时,f(x)取得最小值. (1)求f(x)的解析式;(2)若x ∈[π4,5π6],求f(x)的值域. 解:(1)函数f(x)=cos (ωx +φ)(ω>0,|φ|<π2),由函数f(x)的一个零点和与之相邻的对称轴之间的距离为π4,可得f(x)的周期T =π,即2πω=π,解得ω=2,又因为当x =2π3时,f(x)取得最小值,所以f(2π3)=cos(4π3+φ)=−1,所以4π3+φ=2kπ+π(k ∈Z),解得φ=2kπ−π3(k ∈Z),因为|φ|<π2,所以φ=−π3,所以函数f(x)=cos(2x −π3); (2)由(1)可得函数f(x)=cos(2x −π3),因为x ∈[π4,5π6],可得π6⩽2x −π3⩽4π3, 所以当2x −π3=π时,函数f(x)取得最小值−1,当2x −π3=π6时,函数f(x)取得最大值√32,所以函数f(x)的值域是[−1,√32].变9 .已知函数f(x)=2cos(4x −π4).(1)求函数f(x)的最大值以及相应的x 的取值集合; (2)若直线x =m 是函数f(x)的对称轴,求实数m 的值.解:(1)∵f(x)=2cos(4x −π4).∴f(x)的最大值为2,此时4x −π4=2kπ,k ∈Z , 则x 的取值集合为{x|x =12kπ+π16,k ∈Z} (2)函数f(x)=2cos(4x −π4).令4x −π4=kπ(k ∈Z),则x =kπ4+π16(k ∈Z).∵x =m 是函数f(x)的对称轴,∴m =kπ4+π16(k ∈Z).例10. 已知函数f(x)=2cosx( √3sinx +cosx)−1.(1)求f(x)的最小正周期和单调区间; (2)若f(α)=85,α∈(π4,π2),求cos2α的值.(1)f(x)=2cosx(√3sinx +cosx)−1=2√3sinxcosx +2cos 2x −1=√3sin2x +cos2x =2sin(2x +π6),所以f(x)的最小正周期为π;令−π2+2kπ≤2x +π6≤π2+2kπ,k ∈Z ,解得−π3+kπ≤x ≤π6+kπ,k ∈Z ; 令π2+2kπ≤2x +π6≤3π2+2kπ,k ∈Z ,解得π6+kπ≤x ≤2π3+kπ,k ∈Z .所以f(x)的单调递增区间为[−π3+kπ,π6+kπ],k ∈Z ;单调递减区间为[π6+kπ,2π3+kπ],k ∈Z ;(2)若f(α)=85,则sin(2α+π6)=45,因为α∈(π4,π2),所以2α+π6∈(2π3,7π6),所以cos(2α+π6)=−√1−sin 2(2α+ π 6)=−√1−(45)2=−35,所以cos2α=cos[(2α+π6)−π6]=cos(2α+π6) cos π6+sin(2α+π6) sin π6=−35× √32+45×12=4−3√310.变10 .已知函数f (x )=sinxcosx −√3cos 2x .(Ⅰ)求f (x )的最小正周期和单调增区间; (Ⅱ)当x 0∈(0,π2)时,f (x 0)=−√36,求cos2x 0. 解:(Ⅰ)f(x)=12sin2x −√3(1+cos2x)2=sin(2x −π3)−√32,∴最小正周期T =2π2=π.由−π2+2kπ≤2x −π3≤π2+2kπ,k ∈Z ,则−π12+kπ≤x ≤5π12+kπ,k ∈Z ,所以单调递增区间为[−π12+kπ,512π+kπ](k ∈Z).(Ⅱ)∵f(x 0)=−√36,∴sin(2x 0−π3)=√33,又0<x 0<π2,则−π3<2x 0−π3<2π3,结合sin(2x 0−π3)=√33,则0<2x 0−π3<π2,那么cos(2x 0−π3)=√63,从而cos2x 0=cos[(2x 0−π3)+π3]=cos(2x 0−π3)cos π3−sin(2x 0−π3)sin π3=√66−12.例11. 弹簧上挂的小球上下振动时,小球离开平衡位置的距离s(cm)随时间t(s)的变化曲线是一个三角函数曲线,其图象如图所示.(1)求这条曲线对应的函数解析式.(2)小球在开始振动时,离开平衡位置的位移是多少? 解:(1)设这条曲线对应的函数解析式为s =Asin(ωt +φ), 由图象可知:A =4,周期T =2×(7π12−π12)=π,所以ω=2ππ=2,此时所求函数的解析式为s =4sin(2t +φ),以点(π12,4)为“五点法”作图的第二关键点,则有2×π12+φ=π2,所以φ=π3, 故函数解析式为s =4sin(2t +π3);(2)当t =0时,s =4sin (2×0+π3)=4sin π3=4×√32=2√3(cm),所以小球在开始振动时,离开平衡位置的位移是2√3cm .变11 .若单摆从某一点开始来回摆动,离开平衡位置的距离S(单位:cm)和时间t(单位:s)的函数关系为S=6sin(2πt+π6 ).(1)求单摆开始摆动(t=0)时,离开平衡位置多少厘米;(2)求单摆来回摆动一次需要多长时间.解:(1)当t=0时,S=6sin π6=3cm,即单摆开始摆动时,离开平衡位置3cm.(2)S=6sin(2πt+π6)的振幅为6,∴单摆摆动到最右边时,离开平衡位置6cm,函数S的周期T=2π2π=1,∴单摆来回摆动一次需要时间1s.。
高考三角函数复习专题知识点涵盖齐全答案详细

6
6
2
3 sin 2x 1
....5
分
2
2
由 f ( ) 1,可得 sin 2
3
......7
分
3
所以 sin cos
1 sin 2 2
......8 分
3
.......9 分
6
( 2)当
2k
2
2x
2k , k Z , 换元法 ..11
2
即x [
k , k ], k Z 时, f (x) 单调递增 .
k 1.
时, y min
1.
周期性
2
2
奇偶性
奇函数
偶函数
既无最大值也无最小值 奇函数
在 2k
, 2k
2
2
单调性
k
上是增函数;在
3
2k
, 2k
2
2
k
上是减函数.
对称中心 k ,0 k
对称轴 对称性
xk
k
2
在 2k ,2 k k
上 是增 函数 ;在 在k
2k ,2 k k
k
上是减函数.
,k
2
2
上是增函数.
和差角公式逆用
……………… 3 分
(Ⅰ)函数 f ( x) 的最小正周期 T 2π π. 2
…………………………………… 5 分
令 2kπ
π ≤ 2xπFra bibliotekπ≤ 2kπ (k
Z) ,
……………………………………
6分
2
4
2
所以 2kπ
3π
≤
2x
≤
2kπ
π
.
高中数学三角函数知识点专题复习

高中数学三角函数知识点专题复习高中数学三角函数知识点专题复一、任意角及其三角函数1.已知α为第三象限的角,则在第二或四象限。
2.正确的命题是:终边相同的角必相等。
3.sin570等于-3/2.4.已知扇形的周长是8cm,圆心角是2rad,则扇形的面积是4cm²。
二、同角基本关系式和诱导公式1.已知cosα=3/5,α为第四象限角,则tanα=-4/3.2.设π≤x<2π,且1-sin2x=sinx-cosx,则x的取值范围是[π,5π/3]。
3.已知cos(-α)=4/3,则sin(α-π/2)=-3/5.4.已知sinβ+cosβ=1/5,且-π/2<β<π/2,求sinβcosβ、sinβ-cosβ、sinβ、cosβ、tanβ的值。
5.已知tanα=2,求2cosα-3sinα、sinαcosα、(cosα-sin²α)/2的值。
三、三角函数的图像和性质一)求定义域、值域1.函数y=cosx+1/2的定义域是全体实数,值域是[-1/2,3/2]。
2.y=sinx/2+3cosx在区间[0,2π]上的值域为[1/2,7/2]。
3.y=2cosx在区间[0,2π]上的值域为[-2,2]。
4.y=cosxsin²x在区间R上的值域为[-1/4,1/4]。
二)单调区间、对称轴(中心)、最值1.函数y=sin(x+π/4)的图象的一个对称中心是(π/4,-1)。
2.函数y=sin(2x-π/6)的单调递增区间是[π/12,7π/12]。
3.函数y=cos2x的单调递减区间是[π/4,3π/4]。
三)正弦函数的图象与性质正弦函数公式为y = Asin(ωx + φ),其中A为振幅,ω为角频率,φ为初相位。
正弦函数的最小正周期为2π/ω。
正弦函数的图象为一条在坐标系中上下振动的曲线,对称轴为x轴,振动中心为原点。
B.三角函数的周期性sin函数的周期为2π,即在区间[0,2π]上,sin函数的图象是一个完整的正弦波。
(完整版)高中数学三角函数复习专题

高中数学三角函数复习专题一、知识点整理 :1、角的看法的推行:正负,范围,象限角,坐标轴上的角;2、角的会集的表示:①终边为一射线的角的会集:x x2k, k Z=|k 360o, k Z②终边为向来线的角的会集:x x k, k Z;③两射线介定的地域上的角的会集:x 2k x2k, k Z④两直线介定的地域上的角的会集:x k x k, k Z;3、任意角的三角函数:(1)弧长公式: l a R R 为圆弧的半径,a为圆心角弧度数, l 为弧长。
(2)扇形的面积公式:S 1lR R 为圆弧的半径, l 为弧长。
2(3)三角函数定义:角中边上任意一点 P 为 ( x, y) ,设 | OP |r 则:sin y, cos x ,tan y r= a 2b2 r r x反过来,角的终边上到原点的距离为r 的点P的坐标可写为:P r cos, r sin 比如:公式 cos()cos cossin sin的证明(4)特别角的三角函数值α032 64322sin α012310-10222cosα13210-101222tan α0313不存不存0 3在在(5)三角函数符号规律:第一象限全正,二正三切四余弦。
(6)三角函数线:(判断正负、比较大小,解方程或不等式等)y T 如图,角的终边与单位圆交于点P,过点 P 作 x 轴的垂线,P 垂足为 M ,则Ao 过点 A(1,0)作 x 轴的切线,交角终边OP 于点 T,则M x。
(7)同角三角函数关系式:①倒数关系: tana cot a 1sin a ②商数关系: tan acosa③平方关系: sin 2 a cos2 a1( 8)引诱公试sin cos tan三角函数值等于的同名三角函数值,前方-- sin+ cos- tan加上一个把看作锐角时,原三角函数值的- tan-+ sin- cos符号;即:函数名不变,符号看象限+- sin- cos+ tan2-- sin+ cos- tan2k++ sin+ cos+ tansin con tan2+ cos+ sin+ cot三角函数值等于的异名三角函数值,前方2+ cos- sin- cot加上一个把看作锐角时,原三角函数值的3- cos- sin+ cot2符号 ;3- cos+ sin- cot2即:函数名改变,符号看象限 : sin x cos x cos x比方444cos x sin x444.两角和与差的三角函数:(1)两角和与差公式:cos() cos a cos sin a sin sin( a) sin a coscosa sintan a(atan a tan注:公式的逆用也许变形)1 tan a tan.........(2)二倍角公式:sin 2a 2sin acosa cos 2a cos2 a sin 2 a12 sin2 a 2 cos2 a 12 tan atan 2a1 tan2 a(3)几个派生公式:①辅助角公式:a sinx bcosx a2b2 sin(x)a22 cos()b x比方: sinα± cosα= 2 sin4= 2 cos4.sinα±3 cosα= 2sin3=2cos3等.②降次公式: (sin cos) 21sin 2cos21cos2,sin 21cos222③ tan tan tan()(1 tan tan)5、三角函数的图像和性质:(此中 k z )三角函数y sin x定义域(- ∞, +∞)值域[-1,1]最小正周期T2奇偶性奇[ 2k,2k]22单调性单调递加[ 2k,2k3 ]22单调递减x k对称性2(k ,0)零值点x ky cosx(- ∞, +∞)[-1,1]T 2偶[( 2k 1) ,2k ]单调递加[( 2k , (2k 1) ]单调递减x k(k,0)2x k2y tan xx k2(-∞,+∞)T奇(k,k)22单调递加k(,0)x kx k2x 2 k,最值点y max1ymax 1;无x k2x(2k 1) ,y min1y min1 6、 .函数y Asin( x) 的图像与性质:(本节知识观察一般能化成形如y Asin( x) 图像及性质)( 1)函数 y Asin( x) 和 y Acos( x2 ) 的周期都是T( 2)函数y A tan( x) 和 y Acot( x) 的周期都是T( 3)五点法作y Asin( x) 的简图,设t x,取0、、、3、2来求相应x22的值以及对应的y 值再描点作图。
三角函数章节复习(基础)
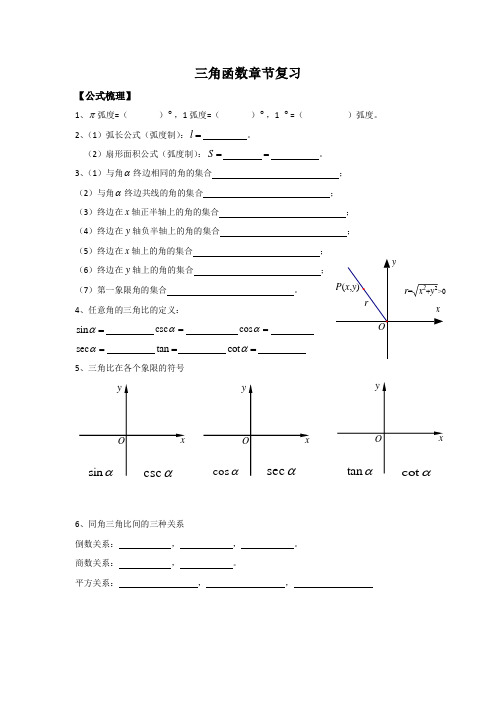
三角函数章节复习【公式梳理】1、π弧度=( )︒,1弧度=( )︒,1 ︒=( )弧度。
2、(1)弧长公式(弧度制):l = 。
(2)扇形面积公式(弧度制):S = = 。
3、(1)与角α终边相同的角的集合 ; (2)与角α终边共线的角的集合 ; (3)终边在x 轴正半轴上的角的集合 ; (4)终边在y 轴负半轴上的角的集合 ; (5)终边在x 轴上的角的集合 ; (6)终边在y 轴上的角的集合 ; (7)第一象限角的集合 。
4、任意角的三角比的定义:sin α= csc α= cos α=sec α= tan = cot α=5、三角比在各个象限的符号6、同角三角比间的三种关系倒数关系: , , 。
商数关系: , 。
平方关系: , ,sin αcsc αOxy cos αsec αOx yOtan αcot αxy7、8组诱导公式口诀:奇变偶不变,符号看象限偶不变:k 为偶数时,即终边在x 轴上的角α±,则函数名f 不变 奇变: k 为奇数时,即终边在y 轴上的角α±,则函数名变成其余函数g符号看象限:把α看成锐角,判断左边括号内的角属于第几象限,再判断出f 在该象限内的符号,从而确定右边三角比的符号补充:)(cot )cot(tan )tan(Z k k k ∈=+=+ααπααπ8、特殊角的三角比值:9、两角和与差的三角比sin()αβ+= sin()αβ-= cos()αβ+= cos()αβ-= tan()αβ+= tan()αβ-=10、倍角公式sin 2α=cos2α= = = tan 2α=11、降幂和升幂公式(1)降幂:2sin α= ,2cos α= 。
(2)升幂:1cos2α+=1cos2α-= 1sin 2α+=1sin 2α-=12、半角公式:sin2α= cos2α= ,tan2α= = =13、万能公式sin α= ,cos α= ,tan α= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数复习专题
一、知识框架:
二、复习要点:
1.主要内容:同角三角函数的基本关系式,诱导公式,和角(差角)公式,倍角公式;
正弦、余弦、正切函数的图象和性质(定义域、值域、周期、奇偶性、单调区间),函数()
sin y A x ωϕ=+的图象和图象变换,已知三角函数值求角。
2.主要题型:化简、求值、证明;求三角函数的定义域、值域、周期,判断奇偶性,求单调区间,利用单调性比较大小,图象的平移和伸缩,图象的对称轴和对称中心,利用图象解题,根据图象求解析式,已知三角函数值求角。
3.常用方法:化简、求值、证明常涉及三个方面的变形:角、函数名称、运算方式,关键是角的处理。
常用的变形措施有:负角化正,大角化小,切割化弦,化异为同,降高为低,引进辅助角,“1”的变换,和差配凑等。
对于给式求值的问题,要针对目标运用条件;对于证明问题,消除条件和结论的差异。
求三角函数的值域、最值:利用正弦、余弦函数的有界性,通过变换转化为代数最值问题; 求周期:将函数式化为一个三角函数的一次方的形式,再利用公式,利用图象判断。
三、重要数学方法:
(1)化归的思想方法:化难为易,化生为熟,画繁为简,化未知为已知。
例题1:求函数sin (0)2cos x y x x
π=
<<+的最大值。
练习:求函数sin 3cos 4
x y x +=-的最值。
(2)数形结合思想:
例题2:定义在R 上的函数()f x 满足()(2)f x f x =+,当[
3,5]x ∈时,()24f x x =--,则( )
A .(sin )(cos
)6
6f f π
π<
B .(sin 1)(cos1)f f >
C .(sin 2)(cos 2)f f < D.22(sin )(cos )3
3
f f ππ>
(3)换元的思想方法:求函数的定义域,周期,单调取间时,都可能用到整体换元的思想。
例题3:求函数(43sin )(43cos )16y x x =---的最值。
练习:求函数sin cos 2sin cos 2y x x x x =+++的最值。
又若[0,]2
x π∈呢?
(4)分类讨论的思想方法:当涉及字母取值时,往往引起分类讨论,要弄明白为什么分类讨论,怎样讨论。
例题4:已知函数()2sin(2)3
f x a x b π=-
+的定义域为[0,]2
π,函数的最大值为1,最小值为-5,
求a 和b 的值。
(5)函数方程思想:在解决数学问题时,先设定一些未知数,根据题设各量之间的关系列出方程,求得未知数;或者如果变量间的数量关系是用解析式给出的,那么把解析式看作是一个方程,通过解方程或对方程的研究,使问题得到解决。
例题5:是否存在两个锐角α和β
,使得22;tan tan 23
2
πααββ+=⋅=-
若存在,求出α,β的值,若不存在,请说明理由。
(6)巧用2
2
sin cos 1αα+=解题。
例题6:已知1sin cos ,(0,)5
θθθπ+=
∈,求cot θ的值。
练习:已知3
3
sin cos 1x x +=,求2009
2009
(sin )(cos )x x +的值。
(7)利用单位圆中的三角函数线解题。
例题7:若22
sin cos αα>,则α的取值范围是多少?
四、高考题:
1.(06四川)下列函数中,图象的一部分如右图所示的是 (A )
sin 6y x π⎛
⎫=+ ⎪
⎝
⎭ (B )
sin 26y x π⎛
⎫=- ⎪
⎝
⎭
(C )cos 43y x π⎛⎫=- ⎪
⎝
⎭ (D )cos 26y
x π⎛
⎫=- ⎪
⎝
⎭ 2.(06
北京)已知函数1)
4()cos x f x x
π
--=
,
(Ⅰ)求()f x 的定义域;(Ⅱ)设α是第四象限的角,且4tan 3
α=-
,求()f α的值.
3.(06
重庆)设函数2
()sin cos f x x x x a ωωω=
++(其中0,a R ω>∈)
,且()f x 的图象在y 轴右侧的第一个最高点的横坐标为
6
π。
(I )求ω的值;(II )如果()f x 在区间5,36ππ⎡⎤-⎢⎥⎣⎦
a 的值。
4.(07天津)已知函数()2cos (sin cos )1,f x x x x x R =-+∈。
(1) 求函数()f x 的最小正周期;(2)求函数()f x 在区间3[
,
]8
4
π
π的最大值和最小值。
五、练习与应用:
1.函数()sin cos f x a x b x =-图象的一条对称轴是直线4
x π
=
,则常数a 与b 满足 ( )
A .0a b +=
B .0a b -= C
.0a += D .
0a -=
2. 函数)2
52sin(π+=x y 的图象的一条对称轴方程是
( )
A .2
π-
=x B .4
π
-=x
C .8
π=x D .π4
5=x
3.要得到sin
2x
y =的图象,只需将函数cos 24x y π
⎛⎫=-
⎪⎝⎭
的图象
( )
A .向左平移
4
π
个单位 B .向右平移
4
π
个单位C .向左平移
2
π
个单位 D .向右平移
2
π
个单位
4.若()sin f
x x 是周期为π
的奇函数,则()f
x 可以是 ( )
A .sin x
B .cos x
C .sin 2x
D . cos 2x
5.函数sin 2sin 23y x x π⎛⎫=-- ⎪
⎝
⎭
的一个单调递增区间是 ( )
A .,
6
3π
π⎡⎤
-⎢
⎥
⎣
⎦
B .5,3
6ππ⎡⎤⎢⎥⎣⎦
C .513,12
12ππ⎡⎤⎢⎥⎣⎦
D . 7,1212ππ⎡⎤⎢⎥⎣⎦
6.已知)2cos()(),2sin()(ππ-=+=x x g x x f ,则下列结论中正确的是 ( ) A 函数)(x g x f y ⋅=)(的周期为π2 B 函数)()(x g x f y ⋅=的最大值为1
C 将)(x f 的图像向左平移2
π单位后得)(x g 的图像 D 将)(x f 的图像向右平移2
π单位后得)(x g 的图像
7.函数])32,6[)(8cos(πππ∈-=x x y 的最小值是 。
8.函数3sin 34cos 344y x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪
⎝
⎭
⎝
⎭
的最小正周期是 。
9. 函数)
4
2sin(log
2
1π+
=x y 的单调减区间为 。
10、要得到函数)3
2cos(2π+=x y 的图像。
可以由诱导公式先把它变成sin 2=y ( ) 然后由
x y sin =的图像先向 平移 个单位,再把各点的纵坐标不变,横坐标变为原来的 倍,最后
把各点的横坐标不变,纵坐标变为原来的 倍, 就可以得到)32cos(2π+=x y 的图像。
11.求函数]2)3
2[sin(log 3
++
=πx y 的定义域、值域、单调性、周期性、最值。
12.已知函数()sin()(0,0,)f x A x A x R ωϕω=+>>∈
在一个周期内的图象如图所示。
求直线y =
与函数()f x 图象的所有交点的坐标。
