Gaps Between Almost-Primes
孪生素数猜想证明

Bounded gaps between primesYitang ZhangAbstractIt is proved that(p n+1−p n)<7×107,lim infn→∞where p n is the n-th prime.Our method is a refinement of the recent work of Goldston,Pintz and Yildirim on the small gaps between consecutive primes.A major ingredient of the proof is a stronger version of the Bombieri-Vinogradov theorem that is applicable when the moduli are free from large prime divisors only(see Theorem2below),but it is adequate for our purpose.Contents1.Introduction22.Notation and sketch of the proof33.Lemmas74.Upper bound for S1165.Lower bound for S222binatorial arguments247.The dispersion method278.Evaluation of S3(r,a)299.Evaluation of S2(r,a)3010.A truncation of the sum of S1(r,a)3411.Estimation of R1(r,a;k):The Type I case3912.Estimation of R1(r,a;k):The Type II case4213.The Type III estimate:Initial steps4414.The Type III estimate:Completion48References5511.IntroductionLet p n denote the n-th prime.It is conjectured thatlim infn→∞(p n+1−p n)=2.While a proof of this conjecture seems to be out of reach by present methods,recently Goldston,Pintz and Yildirim[6]have made significant progress toward the weaker con-jecturelim infn→∞(p n+1−p n)<∞.(1.1) In particular,they prove that if the primes have level of distributionϑ=1/2+ for an (arbitrarily small) >0,then(1.1)will be valid(see[6,Theorem1]).Since the result ϑ=1/2is known(the Bombieri-Vinogradov theorem),the gap between their result and (1.1)would appear to be,as said in[6],within a hair’s breadth.Until very recently,the best result on the small gaps between consecutive primes was due to Goldston,Pintz andYildirim[7]that giveslim infn→∞p n+1−p n√log p n(log log p n)2<∞.(1.2)One may ask whether the methods in[6],combined with the ideas in Bombieri,Fried-lander and Iwaniec[1]-[3]which are employed to derive some stronger versions of the Bombieri-Vinogradov theorem,would be good enough for proving(1.1)(see Question1 on[6,p.822]).In this paper we give an affirmative answer to the above question.We adopt the following notation of[6].LetH={h1,h2,...,h k}(1.3) be a set composed of distinct non-negative integers.We say that H is admissible if νp(H)<p for every prime p,whereνp(H)denotes the number of distinct residue classes modulo p occupied by the h i.Theorem 1.Suppose that H is admissible with k0≥3.5×106.Then there are infinitely many positive integers n such that the k0-tuple{n+h1,n+h2,...,n+h k}(1.4) contains at least two primes.Consequently,we havelim infn→∞(p n+1−p n)<7×107.(1.5) The bound(1.5)results from the fact that the set H is admissible if it is composed of k0distinct primes,each of which is greater than k0,and the inequalityπ(7×107)−π(3.5×106)>3.5×106.2This result is,of course,not optimal.The condition k 0≥3.5×106is also crude and there are certain ways to relax it.To replace the right side of (1.5)by a value as small as possible is an open problem that will not be discussed in this paper.2.Notation and sketch of the proofNotationp −a prime number.a ,b ,c ,h ,k ,l ,m −integers.d ,n ,q ,r −positive integers.Λ(q )−the von Mangoldt function.τj (q )−the divisor function,τ2(q )=τ(q ).ϕ(q )−the Euler function.µ(q )−the M¨o bius function.x −a large number.L =log x .y,z −real variables.e (y )=exp {2πiy }.e q (y )=e (y/q ).||y ||−the distance from y to the nearest integer.m ≡a (q )−means m ≡a (mod q ).¯c /d −means a/d (mod 1)where ac ≡1(mod d ).q ∼Q −means Q ≤q <2Q .ε−any sufficiently small,positive constant,not necessarily the same in each occur-rence.B −some positive constant,not necessarily the same in each occurrence.A −any sufficiently large,positive constant,not necessarily the same in each occur-rence.η=1+L −2A .κN −the characteristic function of [N,ηN )∩Z . ∗l (mod q )−a summation over reduced residue classes l (mod q ).C q (a )−the Ramanujan sum∗l (mod q )e q (la ).We adopt the following conventions throughout our presentation.The set H given by(1.3)is assumed to be admissible and fixed.We write νp for νp (H );similar abbreviations will be used in the sequel.Every quantity depending on H alone is regarded as a constant.For example,the absolutely convergent productS = p1−νp p 1−1p −k 03is a constant.A statement is valid for any sufficiently smallεand for any sufficiently large A whenever they are involved.The meanings of“sufficiently small”and“sufficiently large”may vary from one line to the next.Constants implied in O or ,unless specified,will depend on H,εand A at most.Wefirst recall the underlying idea in the proof of[6,Theorem1]which consists in evaluating and comparing the sumsS1=n∼xλ(n)2(2.1)andS2=n∼x k0i=1θ(n+h i)λ(n)2,(2.2)whereλ(n)is a real function depending on H and x,andθ(n)=log n if n is prime, 0otherwise.The key point is to prove,with an appropriate choice ofλ,thatS2−(log3x)S1>0.(2.3) This implies,for sufficiently large x,that there is a n∼x such that the tuple(1.4) contains at least two primes.In[6]the functionλ(n)mainly takes the formλ(n)=1(k0+l0)!d|P(n)d≤Dµ(d)logDdk0+l0,l0>0,(2.4)where D is a power of x andP(n)=k0j=1(n+h j).Let∆(γ;d,c)=n∼xn≡c(d)γ(n)−1ϕ(d)n∼x(n,d)=1γ(n)for(d,c)=1,andC i(d)={c:1≤c≤d,(c,d)=1,P(c−h i)≡0(mod d)}for1≤i≤k0.4The evaluations of S1and S2lead to a relation of the formS2−(log3x)S1=(k0T∗2−LT∗1)x+O(x L k0+2l0)+O(E)for D<x1/2−ε,where T∗1and T∗2are certain arithmetic sums(see Lemma1below),andE=1≤i≤k0d<D2|µ(d)|τ3(d)τk0−1(d)c∈C i(d)|∆(θ;d,c)|.Let >0be a small constant.IfD=x1/4+ (2.5) and k0is sufficiently large in terms of ,then,with an appropriate choice of l0,one can prove thatk0T∗2−LT∗1L k0+2l0+1.(2.6)In this situation the error E can be efficiently bounded if the primes have level of distri-butionϑ>1/2+2 ,but one is unable to prove it by present methods.On the other hand,for D=x1/4−ε,the Bombieri-Vinogradov theorem is good enough for bounding E, but the relation(2.6)can not be valid,even if a more general form ofλ(n)is considered (see Soundararajan[12]).Ourfirst observation is that,in the sums T∗1and T∗2,the contributions from the termswith d having a large prime divisor are relatively small.Thus,if we impose the constraint d|P in(2.4),where P is the product of the primes less than a small power of x,the resulting main term is still L k0+2l0+1with D given by(2.5).Our second observation,which is the most novel part of the proof,is that with D given by(2.5)and with the constraint d|P imposed in(2.4),the resulting error1≤i≤k0d<D2d|Pτ3(d)τk0−1(d)c∈C i(d)|∆(θ;d,c)|(2.7)can be efficiently bounded.This is originally due to the simple fact that if d|P and d is not too small,say d>x1/2−ε,then d can be factored asd=rq(2.8) with the range for rflexibly chosen(see Lemma4below).Thus,roughly speaking,the characteristic function of the set{d:x1/2−ε<d<D2,d|P}may be treated as a well factorable function(see Iwaniec[10]).The factorization(2.8)is crucial for bounding the error terms.It suffices to prove Theorem1withk0=3.5×1065which is henceforth assumed.Let D be as in(2.5)with=1 1168.Let g(y)be given byg(y)=1(k0+l0)!logDyk0+l0if y<D,andg(y)=0if y≥D,wherel0=180.WriteD1=x ,P=p<D1p,(2.9)D0=exp{L1/k0},P0=p≤D0p.(2.10)In the case d|P and d is not too small,the factor q in(2.8)may be chosen such that (q,P0)=1.This will considerably simplify the argument.We chooseλ(n)=d|(P(n),P)µ(d)g(d).(2.11)In the proof of Theorem1,the main terms are not difficult to handle,since we deal with afixed H.This is quite different from[6]and[7],in which various sets H are involved in the argument to derive results like(1.2).By Cauchy’s inequality,the error(2.7)is efficiently bounded via the followingTheorem2.For1≤i≤k0we haved<D2 d|Pc∈C i(d)|∆(θ;d,c)| x L−A.(2.12)The proof of Theorem2is described as follows.First,applying combinatorial argu-ments(see Lemma6below),we reduce the proof to estimating the sum of|∆(γ;d,c)| with certain Dirichlet convolutionsγ.There are three types of the convolutions involved in the argument.Writex1=x3/8+8 ,x2=x1/2−4 .(2.13) In thefirst two types the functionγis of the formγ=α∗βsuch that the following hold.(A1)α=(α(m))is supported on[M,ηj1M),j1≤19,α(m) τj1(m)L.6(A2)β=(β(n))is supported on[N,ηj2N),j2≤19,β(n) τj2(n)L,x1<N<2x1/2.For any q,r and a satisfying(a,r)=1,the following”Siegel-Walfisz”assumption is satisfied.n≡a(r) (n,q)=1β(n)−1ϕ(r)(n,qr)=1β(n) τ20(q)N L−200A.(A3)j1+j2≤20,[MN,η20MN)⊂[x,2x).We say thatγis of Type I if x1<N≤x2;we say thatγis of Type II if x2<N<2x1/2.In the Type I and II estimates we combine the dispersion method in[1]with the factorization(2.8)(here r is close to N in the logarithmic scale).Due to the fact that the modulo d is at most slightly greater than x1/2in the logarithmic scale,after reducing the problem to estimating certain incomplete Kloosterman sums,we need only to save a small power of x from the trivial estimates;a variant of Weil’s bound for Kloosterman sums(see Lemma11below)will fulfill it.Here the condition N>x1,which may be slightly relaxed,is essential.We say thatγis of Type III if it is of the formγ=α∗κN1∗κN2∗κN3such thatαsatisfies(A1)with j1≤17,and such that the following hold.(A4)N3≤N2≤N1,MN1≤x1.(A5)[MN1N2N3,η20MN1N2N3)⊂[x,2x).The Type III estimate essentially relies on the Birch-Bombieri result in the appendix to[5](see Lemma12below),which is employed by Friedlander and Iwaniec[5]and by Heath-Brown[9]to study the distribution ofτ3(n)in arithmetic progressions.This result in turn relies on Deligne’s proof of the Riemann Hypothesis for varieties overfinitefields (the Weil Conjecture)[4].We estimate each∆(γ;d,c)directly.However,if one applies the method in[5]alone,efficient estimates will be valid only for MN1 x3/8−5 /2−ε. Our argument is carried out by combining the method in[5]with the factorization(2.8) (here r is relatively small);the latter will allow us to save a factor r1/2.In our presentation,all theα(m)andβ(n)are real numbers.3.LemmasIn this section we introduce a number of prerequisite results,some of which are quoted from the literature directly.Results given here may not be in the strongest forms,but they are adequate for the proofs of Theorem1and Theorem2.Lemma1.Let 1(d)and 2(d)be the multiplicative functions supported on square-free integers such that1(p)=νp, 2(p)=νp−1.7LetT∗1=d0d1d2µ(d1d2) 1(d0d1d2)d0d1d2g(d0d1)g(d0d2)andT∗2=d0d1d2µ(d1d2) 2(d0d1d2)ϕ(d0d1d2)g(d0d1)g(d0d2).We haveT∗1=1(k0+2l0)!2l0l0S(log D)k0+2l0+o(L k0+2l0)(3.1)andT∗2=1(k0+2l0+1)!2l0+2l0+1S(log D)k0+2l0+1+o(L k0+2l0+1).(3.2)Proof.The sum T∗1is the same as the sum T R(l1,l2;H1,H2)in[6,(7.6)]with H1=H2=H(k1=k2=k0),l1=l2=l0,R=D,so(3.1)follows from[6,Lemma3];the sum T∗2is the same as the sum˜T R(l1,l2;H1,H2,h0)in[6,(9.12)]withH1=H2=H,l1=l2=l0,h0∈H,R=D, so(3.2)also follows from[6,Lemma3].2Remark.A generalization of this lemma can be found in[12].Lemma2.LetA1(d)=(r,d)=1µ(r) 1(r)rg(dr)andA2(d)=(r,d)=1µ(r) 2(r)ϕ(r)g(dr).Suppose that d<D and|µ(d)|=1.Then we haveA1(d)=ϑ1(d)l0!SlogDdl0+O(L l0−1+ε)(3.3)andA2(d)=ϑ2(d)(l0+1)!SlogDdl0+1+O(L l0+ε),(3.4)whereϑ1(d)andϑ2(d)are the multiplicative functions supported on square-free integerssuch thatϑ1(p)=1−νpp−1,ϑ2(p)=1−νp−1p−1−1.8Proof.Recall that D 0is given by (2.10).Since 1(r )≤τk 0(r ),we have triviallyA 1(d ) 1+ log(D/d ) 2k 0+l 0,so we may assume D/d >exp {(log D 0)2}without loss of generality.Write s =σ+it .Forσ>0we have(r,d )=1µ(r ) 1(r )r1+s =ϑ1(d,s )G 1(s )ζ(1+s )−k 0whereϑ1(d,s )=p |d1−νpp 1+s−1,G 1(s )= p 1−νpp 1+s1−1p 1+s −k 0.It follows thatA 1(d )=12πi(1/L )ϑ1(d,s )G 1(s )ζ(1+s )k 0(D/d )s dss k 0+l 0+1.Note that G 1(s )is analytic and bounded for σ≥−1/3.We split the line of integration into two parts according to |t |≤D 0and |t |>D 0.By a well-known result on the zero-free region for ζ(s ),we can move the line segment {σ=1/L ,|t |≤D 0}toσ=−κ(log D 0)−1,|t |≤D 0 ,where κ>0is a certain constant,and apply some standard estimates to deduce thatA 1(d )=12πi |s |=1/L ϑ1(d,s )G 1(s )ζ(1+s )k 0(D/d )s ds s k 0+l 0+1+O (L −A).Note that ϑ1(d,0)=ϑ1(d )andϑ1(d,s )−ϑ1(d )=ϑ1(d,s )ϑ1(d )l |dµ(l ) 1(l )l(1−l −s ).If |s |≤1/L ,then ϑ1(d,s ) (log L )B ,so that,by trivial estimation,ϑ1(d,s )−ϑ1(d ) L ε−1.On the other hand,by Cauchy’s integral formula,for |s |≤1/L we haveG 1(s )−S 1/L .It follows that12πi |s |=1/L ϑ1(d,s )G 1(s )ζ(1+s )k 0(D/d )s ds s k 0+l 0+1−12πi ϑ1(d )S|s |=1/L(D/d )s ds s l 0+1 L l 0−1+ε.9This leads to(3.3).The proof of(3.4)is analogous.We have only to note thatA2(d)=12πi(1/L)ϑ2(d,s)G2(s)ζ(1+s)k0−1(D/d)s dss k0+l0+1withϑ2(d,s)=p|d1−νp−1(p−1)p s−1,G2(s)=p1−νp−1(p−1)p s1−1p1+s1−k0,and G2(0)=S.2Lemma3.We haved<x1/4 1(d)ϑ1(d)d=(1+4 )−k0k0!S−1(log D)k0+O(L k0−1)(3.5)andd<x1/4 2(d)ϑ2(d)ϕ(d)=(1+4 )1−k0(k0−1)!S−1(log D)k0−1+O(L k0−2),(3.6)Proof.Noting thatϑ1(p)/p=1/(p−νp),forσ>0we have∞ d=1 1(d)ϑ1(d)d1+s=B1(s)ζ(1+s)k0,whereB1(s)=p1+νp(p−νp)p s1−1p1+sk0.Hence,by Perron’s formula,d<x1/4 1(d)ϑ1(d)d=12πi1/L+iD01/L−iD0B1(s)ζ(1+s)k0x s/4sds+O(D−1L B).Note that B1(s)is analytic and bounded forσ≥−1/3.Moving the path of integration to[−1/3−iD0,−1/3+iD0],we see that the right side above is equal to1 2πi|s|=1/LB1(s)ζ(1+s)k0x s/4sds+O(D−1L B).Since,by Cauchy’s integral formula,B1(s)−B1(0) 1/L for|s|=1/L,andB1(0)=ppp−νp1−1pk0=S−1,10it follows thatd<x1/4 1(d)ϑ1(d)d=1k0!S−1L4k0+O(L k0−1).This leads to(3.5)since L/4=(1+4 )−1log D by(2.5).The proof of(3.6)is analogous.We have only to note that,forσ>0,∞ d=1 2(d)ϑ2(d)ϕ(d)p s=B2(s)ζ(1+s)k0−1withB2(s)=p1+νp−1(p−νp)p s1−1p1+sk0−1,and B2(0)=S−1.2Recall that D1and P are given by(2.9),and P0is given by(2.10).Lemma4.Suppose that d>D21,d|P and(d,P0)<D1.For any R∗satisfyingD21<R∗<d,(3.7)there is a factorization d=rq such that D−11R∗<r<R∗and(q,P0)=1.Proof.Since d is square-free and d/(d,P0)>D1,we may write d/(d,P0)asd (d,P0)=nj=1p j with D0<p1<p2<...<p n<D1,n≥2.By(3.7),there is a n <n such that(d,P0)nj=1p j<R∗and(d,P0)n +1j=1p j≥R∗.The assertion follows by choosingr=(d,P0)nj=1p j,q=nj=n +1p j,and noting that r≥(1/p n +1)R∗.2Lemma5.Suppose that1≤i≤k0and|µ(qr)|=1.There is a bijectionC i(qr)→C i(r)×C i(q),c→(a,b)11such that c(mod qr)is a common solution to c≡a(mod r)and c≡b(mod q).Proof.By the Chinese remainder theorem.2The next lemma is a special case of the combinatorial identity due to Heath-Brown[8].Lemma6Suppose that x1/10≤x∗<ηx1/10.For n<2x we haveΛ(n)=10j=1(−1)j−110jm1,...,m j≤x∗µ(m1)...µ(m j)n1...n j m1...m j=nlog n1.The next lemma is a truncated Poisson formula.Lemma7Suppose thatη≤η∗≤η19and x1/4<M<x2/3.Let f be a function of C∞(−∞,∞)class such that0≤f(y)≤1,f(y)=1if M≤y≤η∗M,f(y)=0if y/∈[(1−M−ε)M,(1+M−ε)η∗M],andf(j)(y) M−j(1−ε),j≥1,the implied constant depending onεand j at most.Then we havem≡a(d)f(m)=1d|h|<Hˆf(h/d)ed(−ah)+O(x−2)for any H≥dM−1+2ε,whereˆf is the Fourier transform of f,i.e.,ˆf(z)=∞−∞f(y)e(yz)dy.Lemma8.Suppose that1≤N<N <2x,N −N>xεd and(c,d)=1.Then for j,ν≥1we haveN≤n≤N n≡c(d)τj(n)νN −Nϕ(d)L jν−1,the implied constant depending onε,j andνat most.Proof.See[11,Theorem1].2The next lemma is(essentially)contained in the proof of[5,Theorem4].Lemma9Suppose that H,N≥2,d>H and(c,d)=1.Then we haven≤N (n,d)=1minH,||c¯n/d||−1(dN)ε(H+N).(3.8)12Proof.We may assume N≥H without loss of generality.Write{y}=y−[y]and assumeξ∈[1/H,1/2].Note that{c¯n/d}≤ξif and only if bn≡c(mod d)for some b∈(0,dξ],and1−ξ≤{c¯n/d}if and only if bn≡−c(mod d)for some b∈(0,dξ],Thus, the number of the n satisfying n≤N,(n,d)=1and||c¯n/d||≤ξis bounded byq≤dNξq≡±c(d)τ(q) dεN1+εξ.Hence,for any interval I of the formI=(0,1/H],I=[1−1/H,1),I=[ξ,ξ ]or I=[1−ξ ,1−ξ]with1/H≤ξ<ξ ≤1/2,ξ ≤2ξ,the contribution from the terms on the left side of (3.8)with{c¯n/d}∈I is dεN1+ε.This completes the proof.2Lemma10.Suppose thatβ=(β(n))satisfies(A2)and R≤x−εN.Then for any q we haver∼R 2(r)∗l(mod r)n≡l(r)(n,q)=1β(n)−1ϕ(r)(n,qr)=1β(n)2 τ(q)B N2L−100A.Proof.Since the inner sum is ϕ(r)−1N2L B by Lemma8,the assertion follows by Cauchy’s inequality and[1,Theorem0].2Lemma11Suppose that N≥1,d1d2>10and|µ(d1)|=|µ(d2)|=1.Then we have, for any c1,c2and l,n≤N (n,d1)=1 (n+l,d2)=1ec1¯nd1+c2(n+l)d2(d1d2)1/2+ε+(c1,d1)(c2,d2)(d1,d2)2Nd1d2.(3.9)Proof.Write d0=(d1,d2),t1=d1/d0,t2=d2/d0and d=d0t1t2.LetK(d1,c1;d2,c2;l,m)=n≤d(n,d1)=1(n+l,d2)=1ec1¯nd1+c2(n+l)d2+mnd.We claim that|K(d1,c1;d2,c2;l,m)|≤d0|S(m,b1;t1)S(m,b2;t2)|(3.10) for some b1and b2satisfying(b i,t i)≤(c i,d i),(3.11)13where S(m,b;t)denotes the ordinary Kloosterman sum.Note that d0,t1and t2are pairwise coprime.Assume thatn≡t1t2n0+d0t2n1+d0t1n2(mod d)andl≡t1t2l0+d0t1l2(mod d2).The conditions(n,d1)=1and(n+l,d2)=1are equivalent to(n0,d0)=(n1,t1)=1and(n0+l0,d0)=(n2+l2,t2)=1 respectively.Letting a i(mod d0),b i(mod t i),i=1,2be given bya1t21t2≡c1(mod d0),a2t1t22≡c2(mod d0),b1d20t2≡c1(mod t1),b2d2t1≡c2(mod t2),so that(3.11)holds,by the relation1 d i ≡¯tid0+¯dt i(mod1)we havec1¯n d1+c2(n+l)d2≡a1¯n0+a2(n0+l0)d0+b1¯n1t1+b2(n2+l2)t2(mod1).Hence,c1¯n d1+c2(n+l)d2+mnd≡a1¯n0+a2(n0+l0)+mn0d0+b1¯n1+mn1t1+b2(n2+l2)+m(n2+l2)t2−ml2t2(mod1).From this we deduce,by the Chinese remainder theorem,thatK(d1,c1;d2,c2;l,m)=e t2(−ml2)S(m,b1;t1)S(m,b2;t2)n≤d0(n,d0)=1(n+l0,d0)=1e da1¯n+a2(n+l0)+mn,whence(3.10)follows.By(3.10)with m=0and(3.11),for any k>0we havek≤n<k+d(n,d1=1 (n+l,d2)=1ec1¯nd1+c2d2≤(c1,d1)(c2,d2)d0.14It now suffices to prove(3.9)on assuming N≤d−1.By standard Fourier techniques, the left side of(3.9)may be rewritten as−∞<m<∞u(m)K(d1,c1;d2,c2;l,m)withu(m) minNd,1|m|,dm2.(3.12)By(3.10)and Weil’s bound for Kloosterman sums,wefind that the left side of(3.9)isd0|u(0)|(b1,t1)(b2,t2)+(t1t2)1/2+εm=0|u(m)|(m,b1,t1)1/2(m,b2,t2)1/2.This leads to(3.9)by(3.12)and(3.11).2 Remark.In the case d2=1,(3.9)becomesn≤N (n,d1)=1e d1(c1¯n) d1/2+ε1+(c1,d1)Nd1.(3.13)This estimate is well-known(see[2,Lemma6],for example),and it willfind application somewhere.Lemma12.LetT(k;m1,m2;q)=l(mod q)∗t1(mod q)∗t2(mod q)e q¯lt1−(l+k)t2+m1¯t1−m2¯t2,whereis restriction to(l(l+k),q)=1.Suppose that q is square-free.Then we haveT(k;m1,m2;q) (k,q)1/2q3/2+ε.Proof.By[5,(1.26)],it suffices to show thatT(k;m1,m2;p) (k,p)1/2p3/2.In the case k≡0(mod p),this follows from the Birch-Bombieri result in the appendix to[5](the proof is straightforward if m1m2≡0(mod p));in the case k≡0(mod p),this follows from Weil’s bound for Kloosterman sums.2154.Upper bound for S1Recall that S1is given by(2.1)andλ(n)is given by(2.11).The aim of this section is to establish an upper bound for S1(see(4.20)below).Changing the order of summation we obtainS1=d1|Pd2|Pµ(d1)g(d1)µ(d2)g(d2)n∼xP(n)≡0([d1,d2])1.By the Chinese remainder theorem,for any square-free d,there are exactly 1(d)distinct residue classes(mod d)such that P(n)≡0(mod d)if and only if n lies in one of these classes,so the innermost sum above is equal to1([d1,d2])[d1,d2]x+O( 1([d1,d2])).It follows thatS1=T1x+O(D2+ε),(4.1)whereT1=d1|Pd2|Pµ(d1)g(d1)µ(d2)g(d2)[d1,d2]1([d1,d2]).Note that 1(d)is supported on square-free integers.Substituting d0=(d1,d2)and rewriting d1and d2for d1/d0and d2/d0respectively,we deduce thatT1=d0|Pd1|Pd2|Pµ(d1d2) 1(d0d1d2)d0d1d2g(d0d1)g(d0d2).(4.2)We need to estimate the difference T1−T∗1.We haveT∗1=Σ1+Σ31,whereΣ1=d0≤x1/4d1d2µ(d1d2) 1(d0d1d2)d0d1d2g(d0d1)g(d0d2),Σ31=x1/4<d0<Dd1d2µ(d1d2) 1(d0d1d2)d0d1d2g(d0d1)g(d0d2).In the case d0>x1/4,d0d1<D,d0d2<D and|µ(d1d2)|=1,the conditions d i|P,i=1,2 are redundant.Hence,T1=Σ2+Σ32,16whereΣ2=d0≤x1/4d0|Pd1|Pd2|Pµ(d1d2) 1(d0d1d2)d0d1d2g(d0d1)g(d0d2),Σ32=x1/4<d0<Dd0|Pd1d2µ(d1d2) 1(d0d1d2)d0d1d2g(d0d1)g(d0d2).It follows that|T1−T∗1|≤|Σ1|+|Σ2|+|Σ3|,(4.3)whereΣ3=x1/4<d0<Dd0 Pd1d2µ(d1d2) 1(d0d1d2)d0d1d2g(d0d1)g(d0d2).First we estimateΣ1.By M¨o bius inversion,the inner sum over d1and d2inΣ1is equal to1(d0) d0(d1,d0)=1(d2,d0)=1µ(d1) 1(d1)µ(d2) 1(d2)d1d2g(d0d1)g(d0d2)q|(d1,d2)µ(q)=1(d0)d0(q,d0)=1µ(q) 1(q)2q2A1(d0q)2.It follows thatΣ1=d0≤x1/4(q,d0)=11(d0)µ(q) 1(q)2d0q2A1(d0q)2.(4.4)The contribution from the terms with q≥D0above is D−10L B.Thus,substitutingd0q=d,we deduce thatΣ1=d<x1/4D0 1(d)ϑ∗(d)dA1(d)2+O(D−1L B),(4.5)whereϑ∗(d)=d0q=dd0<x1/4q<D0µ(q) 1(q)q.By the simple boundsA1(d) L l0(log L)B(4.6) which follows from(3.3),ϑ∗(d) (log L)B17andx1/4≤d<x1/4D0 1(d)dL k0+1/k0−1,(4.7)the contribution from the terms on the right side of(4.5)with x1/4≤d<x1/4D0is o(L k0+2l0).On the other hand,assuming|µ(d)|=1and noting thatq|d µ(q) 1(q)q=ϑ1(d)−1,(4.8)for d<x1/4we haveϑ∗(d)=ϑ1(d)−1+Oτk0+1(d)D−1,so that,by(3.3),ϑ∗(d)A1(d)2=1(l0!)2S2ϑ1(d)logDd2l0+Oτk0+1(d)D−1L B+O(L2l0−1+ε).Inserting this into(4.5)we obtainΣ1=1(l0!)2S2d≤x1/41(d)ϑ1(d)dlogDd2l0+o(L k0+2l0).(4.9)Together with(3.5),this yields|Σ1|≤δ1k0!(l0!)2S(log D)k0+2l0+o(L k0+2l0),(4.10)whereδ1=(1+4 )−k0.Next we estimateΣ2.Similar to(4.4),we haveΣ2=d0≤x1/4d0|P(q,d0)=1q|P1(d0)µ(q) 1(q)2d0q2A∗1(d0q)2.whereA∗1(d)=(r,d)=1r|Pµ(r) 1(r)g(dr)r.In a way similar to the proof of(4.5),we deduce thatΣ2=d<x1/4D0d|P 1(d)ϑ∗(d)dA∗1(d)2+O(D−1L B).(4.11) 18Assume d|P.By M¨o bius inversion we haveA∗1(d)=(r,d)=1µ(r) 1(r)g(dr)rq|(r,P∗)µ(q)=q|P∗1(q)qA1(dq),whereP∗=D1≤p<Dp.Noting thatϑ1(q)=1+O(D−11)if q|P∗and q<D,(4.12) by(3.3)we deduce that|A∗1(d)|≤1l0!Sϑ1(d)logDdl0q|P∗q<D1(q)q+O(L l0−1+ε).(4.13)If q|P∗and q<D,then q has at most292prime factors.In addition,by the prime number theorem we haveD1≤p<D 1p=log293+O(L−A).(4.14)It follows thatq|P∗q<D 1(q)q≤1+292ν=1((log293)k0)νν!+O(L−A)=δ2+O(L−A),say.Inserting this into(4.13)we obtain|A∗1(d)|≤δ2l0!Sϑ1(d)logDdl0+O(L l0−1+ε).Combining this with(4.11),in a way similar to the proof of(4.9)we deduce that|Σ2|≤δ22(l0!)2S2d<x1/41(d)ϑ1(d)dlogDd2l0+o(L k0+2l0).Together with(3.5),this yields|Σ2|≤δ1δ22k0!(l0!)2S(log D)k0+2l0+o(L k0+2l0).(4.15) 19We now turn toΣ3.In a way similar to the proof of(4.5),we deduce thatΣ3=x1/4<d<D 1(d)˜ϑ(d)dA1(d)2,(4.16)where˜ϑ(d)=d0q=dx1/4<d0d0 P µ(q) 1(q)q.By(4.6)and(4.7),wefind that the contribution from the terms with x1/4<d≤x1/4D0 in(4.16)is o(L k0+2l0).Now assume that x1/4D0<d<D,|µ(d)|=1and d P.Noting that the conditions d0|d and x1/4<d0together imply d0 P,by(4.8)we obtain˜ϑ(d)=d0q=dx1/4<d0µ(q) 1(q)q=ϑ1(d)−1+Oτk0+1(d)D−1.Together with(3.3),this yields˜ϑ(d)A1(d)2=1(l0!)2S2ϑ1(d)logDd2l0+Oτk0+1(d)D−1L B+O(L2l0−1+ε).Combining these results with(4.16)we obtainΣ3=1(l0!)2S2x1/4D0<d<Dd P1(d)ϑ1(d)dlogDd2l0+o(L k0+2l0).(4.17)By(4.12),(4.14)and(3.5)we havex1/4<d<Dd P 1(d)ϑ1(d)d≤d<D1(d)ϑ1(d)dp|(d,P∗)1≤D1≤p<D1(p)ϑ1(p)pd<D/p1(d)ϑ1(d)d≤(log293)δ1(k0−1)!S−1(log D)k0+o(L k0)Together with(4.17),this yields|Σ3|≤(log293)δ1(k0−1)!(l0!)2S(log D)k0+2l0+o(L k0+2l0).(4.18)20Since1k0!(l0!)2=1(k0+2l0)!k0+2l0k02l0l0,it follows from(4.3),(4.10),(4.15)and(4.18)that|T1−T∗1|≤κ1(k0+2l0)!2l0l0S(log D)k0+2l0+o(L k0+2l0),(4.19)whereκ1=δ1(1+δ22+(log293)k0)k0+2l0k0.Together with(3.1),this implies thatT1≤1+κ1(k0+2l0)!2l0l0S(log D)k0+2l0+o(L k0+2l0).Combining this with(4.1),we deduce thatS1≤1+κ1(k0+2l0)!2l0l0S x(log D)k0+2l0+o(x L k0+2l0).(4.20)We conclude this section by giving an upper bound forκ1.By the inequalityn!>(2πn)1/2n n e−nand simple computation we have1+δ22+(log293)k0<2((log293)k0)292292!2<1292π(185100)584andk0+2l0k0<2k2l0(2l0)!<1√180π(26500)360.It follows thatlogκ1<−3500000log 293292+584log(185100)+360log(26500)<−1200.This givesκ1<exp{−1200}.(4.21)21。
孪生素数证明

孪生素数证明1. 引言孪生素数是指相差为2的两个素数,例如(3, 5)、(11, 13)等。
孪生素数一直以来都是数学研究中的一个重要课题,其性质和分布一直备受关注。
本文将从孪生素数的定义、性质以及存在性进行详细阐述,并给出相应的证明过程。
2. 孪生素数的定义首先我们需要明确什么是素数。
素数是指除了1和自身外没有其他正因子的自然数。
根据这个定义,我们可以得到孪生素数的定义:相差为2且都是素数的两个自然数。
3. 孪生素数的性质性质1:无穷性孪生素数有无穷多个。
这一结论最早由法国大学教授Alphonse de Polignac在1846年提出,并被后来人证明。
性质2:存在性对于任意大于等于5的自然数n,必然存在一个孪生素对(p, p+2),其中p为不小于n且为奇数的最小素数。
性质3:距离限制孪生素对中较大的那个数字必定小于等于某个特定的界限。
这个界限被称为孪生素数距离界限,通常记作C2。
4. 孪生素数证明证明1:无穷性假设只存在有限个孪生素数,我们可以将它们依次记作(p1, p1+2), (p2,p2+2), …, (pn, p n+2)。
我们构造一个新的自然数N = p1 * p2 * … * pn + 1。
显然,N大于所有已知的孪生素数中较大的那个数字。
现在我们来观察N和N+2: - 如果N是一个素数,那么(N, N+2)就是一个新的孪生素对,与我们假设只存在有限个孪生素数相矛盾。
- 如果N不是一个素数,那么根据整除关系可知,存在一个大于1且小于等于n的因子d能够整除N。
由于d也能够整除p1 * p2 * … * pn,所以d不能是p1, p2, …, pn中任何一个。
因此d必然比这些已知的孪生素对中较大的那个数字还要大。
而N = p1 * p2 * …* pn + 1又比这些已知的孪生素对中较大的那个数字还要大,所以d不能整除N+2。
综上所述,无论N是素数还是合数,都能够得出结论:存在一个大于已知孪生素对中较大的那个数字的新的孪生素对。
[精华]寂寞的数学家和不孤独的素数华裔数学家张益唐
![[精华]寂寞的数学家和不孤独的素数华裔数学家张益唐](https://img.taocdn.com/s3/m/968f89cc0342a8956bec0975f46527d3240ca689.png)
[精华]寂寞的数学家和不孤独的素数华裔数学家张益唐这又是一个关于数学家的传奇故事。
5月13日下午,新坎布尔大学讲师、华裔数学家张益唐在哈佛大学做了关于自己一项研究的报告,关于素数的报告。
素数,也就是质数,是那些只能被1和自身整除的数。
根据经验,我们认为素数的分布会越来越稀少,然而,也有数学家指出,素数们没那么孤独——对大于1的整数n,在n和2n之间必然存在一个素数,这就是“伯特兰-切比雪夫”定理。
素数们的亲密关系还不止于此,也许是上世纪最伟大数学家的大卫?希尔伯特在1900年的国际数学家大会上提出了著名的23个重要数学难题和猜想,其中的一个问题提到:应该存在无穷多个相差为2的素数对,希尔伯特把这些素数对称为孪生素数,这些素数在数轴上相互偎依着,是这种神奇的数字展现在世界上的一种奇特的存在形式。
数学家们相信这个猜想是成立的,但没人能够证明它。
张益唐所做的是,证明了存在无穷多个素数对,它们的差小于7000万。
虽然7000万与2之间尚存距离,但正如美国数学家多利安?戈德菲尔的评论:从7000万到2的距离相比从无穷到7000万的距离来说是微不足道的。
今年4月,张益唐向《数学年刊》(Annuals of Mathematics)杂志提交了题为“素数间的有界距离”(Bounded gaps between primes)的文章。
5月21日,文章被接受——这几乎创了这个顶级数学期刊的一个纪录,根据常规,要在这本数学界最受敬仰的期刊上发文,必须解决很难的问题,文章要很长,更长的是审稿人苛刻以及漫长的审稿过程,这个审稿过程耗费的时间往往以年计。
张益唐文章发表后,一位审稿人、数论专家伊万尼克(Henryk Iwaniec)称,这个结论经过了自己的严格检查,这位波兰裔美国数学家是公认的当今最顶级数论专家之一,而且,这种审稿人自称身份的做法在数学界并不多见。
5月14日,《自然》杂志以“第一个无穷组素数成对出现的证明”报道了张益唐的研究,那篇文章的开头说,“这真是个只有数学家才爱得起来的结论”。
DNAWorks_全基因合成介绍共41页文档

Codon Bias
E. coli H. sapiens
R:AGG R:AGA
I:ATA G:GGA P:CCC R:CGA L:CTA R:CGG T:ACA L:TTA S:AGT S:TCA L:CTG S:TCG R:CGC R:CGT A:GCG P:CCG
Synthetic Genes
Commerical Sources
Typical costs: • $0.79 - $3.60 / bp • Complexities? • Intellectual property?
• 800 bp = $1000 (Gene Script)
Genes From Scratch
• oligos ~ $0.20 / nt (NIH discount) • PCR reagents ~ $2 / reaction • sequencing ~ $20 / 600 bp • electrophoresis ~ $3 / gel • labor ~ $20 / hr
Protein/Structure Dependent Factors: • folding and aggregation • proteolysis and degradation • secretion and localization
90.0% 80.0% 70.0% 60.0% 50.0% 40.0% 30.0% 20.0% 10.0%
Benefits: • Codon use optimized for host • Flexibility in subcloning • Ease of complex mutagenesis
Problems: • Time consuming • Complicated • Error-prone
Finding prime pairs with particular gaps

PAMELA A. CUTTER
Abstract. By a prime gap of size g , we mean that there are primes p and p + g such that the g − 1 numbers between p and p + g are all composite. It is widely believed that infinitely many prime gaps of size g exist for all even integers g . However, it had not previously been known whether a prime gap of size 1000 existed. The objective of this article was to be the first to find a prime gap of size 1000, by using a systematic method that would also apply to finding prime gaps of any size. By this method, we find prime gaps for all even integers from 746 to 1000, and some beyond. What we find are not necessarily the first occurrences of these gaps, but, being examples, they give an upper bound on the first such occurrences. The prime gaps of size 1000 listed in this article were first announced on the Number Theory Listing to the World Wide Web on Tuesday, April 8, 1997. Since then, others, including Sol Weintraub and A.O.L. Atkin, have found prime gaps of size 1000 with smaller integers, using more ad hoc methods. At the end of the article, related computations to find prime triples of the form 6m + 1, 12m − 1, 12m + 1 and their application to divisibility of binomial coefficients by a square will also be discussed.
chapter 28-DNA replication
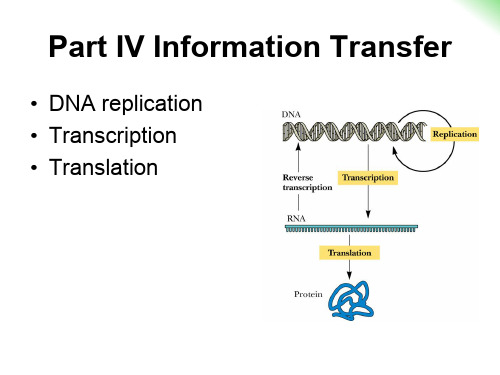
28.1 How is DNA replicated?
1. DNA replication is semiconservative 2. DNA replication is bidirectional 3. DNA replication is semidiscontinuous
How is DNA replicated?-I
site through base-pairing with the corresponding base in the template strand 2. Chain growth is in the 5->3 direction antiparallel to the template strand 3. DNA polymerases cannot initiate DNA synthesis de novo —all require a primer with a free 3-OH to build upon.
In prokaryotes, replicons are usually closed circles of DNA that have no ends. In most bacteria, linear molecules of DNA are degraded by exonucleases. Consequently, linear segments of DNA that enter a bacterial cell during conjugation or transformation will eventually be degraded.
E.coli DNA polymerase III holoenzyme-replicates chromosome
孪生素数 已证明的最小间隔
孪生素数的已证明最小间隔1. 引言孪生素数是指相差为2的两个素数,例如(3, 5), (11, 13), (17, 19)等。
孪生素数问题一直以来都吸引着数学家们的兴趣。
其中一个重要的研究方向是确定孪生素数之间的最小间隔。
本文将介绍已经证明的最小间隔,并讨论相关的研究成果和方法。
2. 已证明的最小间隔在过去几十年里,数学家们通过不断努力,已经证明了一些最小间隔。
2.1 最小间隔为6早在18世纪末,法国数学家Legendre就证明了存在无穷多对相差为6的孪生素数。
这个结果被称为Legendre猜想,并被后来的Erdős改进和推广。
2.2 最小间隔为161974年,美国数学家Helfgott通过计算机程序验证了存在无穷多对相差为16的孪生素数。
这一发现引起了广泛关注,并激发了更多研究。
2.3 最小间隔为70万亿2013年,由于技术和计算能力的进步,一支由Yitang Zhang领导的研究团队证明了存在无穷多对相差为70万亿的孪生素数。
这个突破性的结果震惊了整个数学界,被誉为“孪生素数间隔领域的重大突破”。
2.4 最小间隔为2462014年,由于前述成果的鼓舞和启发,由Tao和Maynard等人组成的合作团队证明了存在无穷多对相差为246的孪生素数。
这一结果进一步推动了孪生素数间隔研究的发展。
3. 研究方法和思路为了证明最小间隔问题,数学家们采用了不同的方法和思路。
3.1 基于筛法筛法是一种常见且有效的寻找素数的方法。
通过排除所有非素数,可以得到一系列素数。
在寻找孪生素数时,数学家们结合筛法来确定最小间隔。
3.2 基于整除性质另一个常用的方法是利用整除性质来推导最小间隔。
通过分析素数与其相邻数字之间可能存在的整除关系,可以得出最小间隔。
3.3 基于数论方法数论是研究整数性质的一个分支,对于最小间隔问题的研究也起到了重要作用。
数学家们运用数论中的定理和方法,通过分析素数的性质和规律来推导最小间隔。
4. 研究进展和展望孪生素数间隔问题是一个复杂而困难的研究领域。
CONGRUENCES WITH INTERVALS AND SUBGROUPS MODULO A PRIME
Here we consider the congruence (1) in the special case when m = p is prime. Furthermore, we are mostly interesting in the solvability of (1) for rather small intervals and subgroups. Since we consider congruences modulo primes, it is convenient to use the language of finite fields. For a prime p use Fp to denote the finite field of p elements, which we assume to represented by the set {0, 1, . . . , p − 1}. We say that a set I ⊆ Fp is an interval of length H if it contains H consecutive elements of Fp , assuming that p − 1 is followed by 0. Furthermore we say that I is an initial interval if I = {1, . . . , H } (we note that it is convenient to exclude 0 from initial intervals). Furthermore, instead of subgroups we consider a more general class sets, which also contain sets of N consecutive powers {g, . . . , g N } of a fixed element g ∈ F∗ p. Namely, as usual for a set U ⊆ Fp we use U (m) to denote its m-fold product set U (m) = {u1 . . . um : u1 , . . . , um ∈ U}.
Linear gaps between degrees for the polynomial calculus modulo distinct primes
Linear Gaps Between Degrees for the Polynomial Calculus Modulo Distinct PrimesAbstract1Sam Buss2,3 Department of Mathematics Univ.of Calif.,San Diego La Jolla,CA92093-0112sbuss@Dima GrigorievIMR Universite Rennes-1Beaulieu35042Rennes,Francedima@maths.univ-rennes1.frRussell Impagliazzo2,4 Computer Science and Engineering Univ.of Calif.,San DiegoLa Jolla,CA92093-0114russell@Toniann Pitassi2,5Computer Science University of Arizona Tucson,AZ85721-0077 toni@Two important algebraic proof systems are the Null-stellensatz system[1]and the polynomial calculus[2](also called the Gr¨o bner system).The Nullstellensatzsystem is a propositional proof system based on Hilbert’sNullstellensatz,and the polynomial calculus(PC)is aproof system which allows derivations of polynomials,over some£eld.The complexity of a proof in these systemsis measured in terms of the degree of the polynomials usedin the proof.The mod p counting principle can be formulated as aset MOD n p of constant-degree polynomials expressing thenegation of the counting principle.The Tseitin mod pprinciples,TS n(p),are translations of the MOD n p into the Fourier basis[3].The present paper gives linear lower bounds on thedegree of polynomial calculus refutations of MOD n p over£elds of characteristic q=p and over rings Z q with q,prelatively prime.These are the£rst linear lower boundsfor the polynomial calculus.As it is well-known tobe easy to give constant degree polynomial calculus(andeven Nullstellensatz)refutations of the MOD n p polynomials 1This paper was presented jointly to the14th Annual IEEE Conference on Computational Complexity and the31st Annual ACM Symposium on Theory of Computer Science.The complete version is in the latter’s proceedings volume.2Supported in part by international grant INT-9600919/ME-103from the NSF(USA)and the M³SMT(Czech republic)3Supported in part by NSF grant DMS-98035154Supported in part by NSF grant CCR-9734911,Sloan Research Fellowship BR-3311,and US-Israel BSF grant97-00188.5Supported in part by NSF grant CCR-9457783and US-Israel BSF grant95-00238.over F p,our results imply that the MOD n p polynomials have a linear gap between proof complexity for the polynomial calculus over F p and over F q.We also obtaina linear gap for the polynomial calculus over rings Z p andZ q where p,q do not have identical prime factors.Theorem1Let F be a£eld of characteristic q,and letG n be an r-regular graph with expansion .Then,for alld< n/8,there is no degree d PC refutation of TS n(p) over F.Theorem2Let q≥2be a prime such that q p and let F be a£eld of characteristic q.Any PC-refutation of the MOD n p polynomials requires degree>δn,for some constantδ>0.References[1]P.Beame,R.Impagliazzo,J.Kraj´ı³c ek,T.Pitassi,andP.Pudl´a k.Lower bounds on Hilbert’s Nullstellensatzand propositional proofs.Proceedings of the LondonMathematical Society,73:1–26,1996.[2]M.Clegg,J.Edmonds,and ing theGroebner basis algorithm to£nd proofs of unsatis£ability.InProceedings of the Twenty-eighth Annual ACM Symposiumon the Theory of Computing,pages174–183,1996.[3] D.Grigoriev.Nullstellensatz lower bounds for Tseitintautologies.In Proceedings of the39th Annual IEEESymposium on Foundations of Computer Science,pages648–652.IEEE Computer Society Press,1998.1。
The spectral gap of the REM under Metropolis dynamics
L. R. G. Fontes Universidade de S~o Paulo a M. Isopi Universita di Roma 1 Y. Kohayakawa Universidade de S~o Paulo a P. Picco CPT, CNRS, Marseille April 25, 1997
ZN
ZN ( ) =
X
e?
HREM (
)
(1.3)
the nite volume partition function and by 1 FN ( ) = N log ZN ( ) (1.4) the nite volume free energy. It was proved in 4] that for all 0, the limit limN !1 FN ( ) = F ( ) exists IP -almost surely and in Lp(E ; IP ) for 1 p < 1. F ( ) is ap random function non which is di erentiable in but the second derivative has a jump at c = 2 log 2. In fact, F ( ) is equal to 2=2 + c2=2 for < c and c for c , as expected from the results of 1]. This is called in the physics literature a third order phase transition. The point is, depending if we are in a high temperature regime ( < c) or in a low temperature one ( c ), not only that the free energy changes from a quadratic function of to a linear one but that the di erence between the nite volume free energy and its in nite volume limit is exponential in the high temperature case and this occurs almost surely, whereas in the low temperature regime this di erence behaves as C (!; ; N ) log N for some random N function C (!; ; N ). This function converges in IP -probability to a non-random limit but does 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a rXiv:152.1693v1[math.CO ]29Jan215Gaps Between Almost-Primes and a Construction of Almost-Ramanujan Graphs Adrian Dudek Mathematical Sciences Institute The Australian National University adrian.dudek@.au Abstract For all k ≥3,we show how one can explicitly construct an infinite family of k -regular graphs all of which have second largest eigenvalue satisfying the bound O (k 1/2).This resolves an open problem of Rein-gold,Vadhan and Wigderson.1Introduction In this note,we will consider a graph X with vertex set V .By a family of graphs,we mean a sequence {X m }of graphs with |V m |→∞as m →∞.We list the eigenvalues of the adjacency matrix of a graph X as λ1(X )≥λ2(X )≥···≥λ|V |(X ).Given a finite,connected,k -regular graph,it is a straightforward exercise to show that λ1=k .It is,however,of more interest to obtain upper bounds on λ2;the following theorem of Alon and Boppana [1]gives a limit on this asymptotically.Theorem 1.1.Let {X m}be a family of finite,connected,k -regulargraphs.Then lim inf m →∞λ2(X m )≥2√Thus,asymptotically,the spectral gapλ1−λ2is bounded above by k−√2k−1.The central problem in the theory,given an integer k≥3,is to construct a k-regular family of Ramanujan graphs, more precisely a sequence{X m}offinite,connected,k-regular graphs with √λ2(X m)≤2log k)In an earlier paper,the author[6]showed how one could improve on this slightly assuming the truth of the Riemann hypothesis.One starts with the explicit construction of a family of d-regular Ramanujan graphs where d is one more than a prime,and then uses the Cartesian graph product to produce a(d+1)-regular family of graphs with at least the same spectral gap.The reader should note that the new family is not necessarily Ramanujan,as we should expect an increase in the spectral gap with respect to an increase in d. We can iterate this procedure to furnish a family of k-regular graphs for any k.On the Riemann hypothesis,Cram´e r[5]proved that one can bound the difference between consecutive primes p n,p n+1withp n+1−p n=O(√In this note we resolve,without any condition,the open problem of Rein-gold,Vadhan and Wigderson viz.the following theorem.Theorem1.2.For all sufficiently large integers k,one can explicitly construct a k-regular family{X m}of graphs such that√λ2(X m)≤4qfor all m≥1,where d(n)denotes the number of divisors of n.The well-known divisor bound states thatd(n)≤n O(1/log log n),and so one immediately has the explicit construction of a(q+1)-regular family {X m}of graphs such thatλ2(X m)≤q1/2+O(1/log log q)for all m≥1.This,however,falls short of the result of Ben-Aroya and Ta-Shma.We will also need the following result of Wu[12]on almost-primes in short intervals.3Lemma2.2.Let x be sufficiently large.Then there exists an integer n in the interval(x−x101/232,x]such that the number of prime factors of n counted with multiplicity does not exceed two.The proof proceeds as follows.Given two graphs X and Y,the Cartesian product X Y is a natural way to obtain a new graph whose properties reflectthose of the original graphs.We will not need to see the general definition of this,for we are using one specific instance of the product.Consider K2,the complete graph on two vertices,that is,the graph consist-ing of two vertices connected by a single edge.Given afinite k-regular graph X,we note that X K2is obtained simply by taking X and a duplicate ofX,and connecting each vertex in X with its duplicate vertex.We will denote this particular Cartesian product by X′and note that this is a(k+1)-regular graph with twice as many vertices as X.The following result can be found in an earlier paper by the author[6]. Theorem2.3.Let X be afinite,connected k-regular graph and let X′= X K2.Thenλ2(X′)≤λ2(X)+1.(1) Therefore,one may take a k-regular family{X m}of graphs and get a (k+1)-regular family{X′m}with the same upper bound on the second largest eigenvalue.Iterating this process will give families of all degrees.Now,let k be sufficiently large,so that we can define q to be such that qhas at most two prime factors andk−k101/232<q≤k(2) where p and q are both prime numbers.By Lemma2.1,it follows that we can construct a family{X m}of q-regular graphs such thatλ2(X m)≤4√q−1+(k−q)<4References[1]N.Alon.Eigenvalues and binatorica,2(6):83–96,1986.[2]A.Ben-Aroya and A.Ta-Shma.A combinatorial construction of almost-Ramanujan graphs using the zig-zag product.STOC’08Proceedings of the40th annual ACM symposium on the theory of computing,2008.[3]A.Brouwer and W.Haemers.Spectra of graphs.Springer,2012.[4]P.Chiu.Cubic Ramanujan binatorica,(12):275–285,1992.[5]H.Cram´e r.Some theorems concerning prime numbers.Arkiv Mathematik,5:1–33,1920.[6]A.W.Dudek.Almost-Ramanujan graphs and prime gaps.European J.Combin.,43:204–209,2015.[7]A.Lubotzky,R.Phillips,and P.Sarnak.Ramanujan bina-torica,pages261–267,1988.[8]G.Margulis.Explicit group-theoretical constructions of combinatorialschemes and their application to the design of expanders and concentra-tors.Probl.Peredachi Inf.,24:51–60,1988.[9]M.Morgenstern.Existence and explicit constructions of q+1regularRamanujan graphs for every prime power b.Theory,(Ser B(62)):44–62,1994.[10]A.K.Pizer.Ramanujan graphs and Hecke operators.Bull.Amer.Math.Soc.(N.S.),23(1):127–137,1990.[11]O.Reingold,S.Vadhan,and A.Wigderson.Entropy waves,the zig-zag graph product,and new constant degree expanders.Ann.of Math, 2(155(1)):157–187,2002.[12]J.Wu.Almost primes in short intervals.Sci.China Math.,53(9):2511–2524,2010.5。
