哈工大课件机械系统动力学Dynamics of Mechanical System-ch1
合集下载
哈工大 机械系统设计 第四章传动系统设计_课件

13
传动链
传动链
外联传动链
内联传动链
内联传动:两执行件间的传动精度
外联传动:执行件的速度(转速)和传递动力
14
4.1.1 传动系统的类型
电机驱动 1.动力源 内燃机驱动
① 交流异步电动机 ② 直流并激电动机 ③ 交流调速主轴电动机 ④ 交、直流伺服电动机 ⑤ 步进电动机
机械无级变速 无级变速 液压无级变速 电气无级变速 交换齿轮变速 转速可变 2.输出速度 滑移齿轮变速 有级变速 离合器变速 上述的组合 啮合器变速 转速不可变(固定传动比传动系统)
2
典型驱动和传动方式的功率、精度关系
3
1. 多介质多形式高效驱动与传动
多介质:机、电、液、气、磁、声、光等介质; 多形式:机械、机电、机液、电液、电气、光电 、功能材料等两种或多种能量转换与传 递形式集成化;
高效:低摩擦损耗、高效率、工况和环境变化适 应性强的空间运动和功率传递方式
核心问题:高效能量转换与传递特性作用机理
作用:
(1) 齿轮—摩擦离合器换向机构
齿轮Z1、Z3均空套在轴Ⅰ上,摩擦离合器向左接合时,通过
Z1、Z2、传动轴Ⅱ实现正转;摩擦离合器向右接合时,通过Z3、 Z0、Z4、传动轴Ⅱ实现反转,摩擦离合器处于中间位置时,轴Ⅱ 不转。从而实现了轴Ⅱ的起停和换向。
34
(2) 齿轮换向机构
运动从轴Ⅰ传入,轴Ⅲ传出。当轴Ⅲ上的滑移齿轮向右移动时, 运动由轴Ⅰ经齿轮1(Z30)的右半部和齿轮2(Z56)传出,带动轴Ⅲ转动。 当滑移齿轮在图示位置时,运动由轴Ⅰ经齿轮1(Z30)的左半部及其常 啮合的惰轮3(Z30)传动轴Ⅲ上的齿轮2(Z56)从而带动轴Ⅲ转动,经过 一惰轮3,使轴Ⅲ反向运转。由于齿轮1与惰轮3的齿数相等,故输出 的转速正反向相等。
传动链
传动链
外联传动链
内联传动链
内联传动:两执行件间的传动精度
外联传动:执行件的速度(转速)和传递动力
14
4.1.1 传动系统的类型
电机驱动 1.动力源 内燃机驱动
① 交流异步电动机 ② 直流并激电动机 ③ 交流调速主轴电动机 ④ 交、直流伺服电动机 ⑤ 步进电动机
机械无级变速 无级变速 液压无级变速 电气无级变速 交换齿轮变速 转速可变 2.输出速度 滑移齿轮变速 有级变速 离合器变速 上述的组合 啮合器变速 转速不可变(固定传动比传动系统)
2
典型驱动和传动方式的功率、精度关系
3
1. 多介质多形式高效驱动与传动
多介质:机、电、液、气、磁、声、光等介质; 多形式:机械、机电、机液、电液、电气、光电 、功能材料等两种或多种能量转换与传 递形式集成化;
高效:低摩擦损耗、高效率、工况和环境变化适 应性强的空间运动和功率传递方式
核心问题:高效能量转换与传递特性作用机理
作用:
(1) 齿轮—摩擦离合器换向机构
齿轮Z1、Z3均空套在轴Ⅰ上,摩擦离合器向左接合时,通过
Z1、Z2、传动轴Ⅱ实现正转;摩擦离合器向右接合时,通过Z3、 Z0、Z4、传动轴Ⅱ实现反转,摩擦离合器处于中间位置时,轴Ⅱ 不转。从而实现了轴Ⅱ的起停和换向。
34
(2) 齿轮换向机构
运动从轴Ⅰ传入,轴Ⅲ传出。当轴Ⅲ上的滑移齿轮向右移动时, 运动由轴Ⅰ经齿轮1(Z30)的右半部和齿轮2(Z56)传出,带动轴Ⅲ转动。 当滑移齿轮在图示位置时,运动由轴Ⅰ经齿轮1(Z30)的左半部及其常 啮合的惰轮3(Z30)传动轴Ⅲ上的齿轮2(Z56)从而带动轴Ⅲ转动,经过 一惰轮3,使轴Ⅲ反向运转。由于齿轮1与惰轮3的齿数相等,故输出 的转速正反向相等。
哈工程机械原理课件第十二章

2
取 Jea≈ Jeb
令
Je
从而
d
DWmax 2 wm J e
或
Je
DWmax
2 w md
2.飞轮转动惯量的近似计算 当 d > [d] 时, 可增加一个转动惯量为 JF 的大质量的圆盘 — 飞轮.
DWmax [d ] 并使 d 2 wm ( J e J F ) DWmax [d ] 一般, JF 》Je 故. d 2 wm J F
d
最大盈亏功的求取
1. 分析: DWmax 为 wmin 到 wmax 区间的外力功. DWmax = Emax - Emin 按
DWmax JF≥——— 2 wm [d]
w
wmax
wmin
a
b
f
w2 dJF Me = Med - Mec = J e + — —— JF = 常 J e e F 2 dt
只要 Wd ≠ Wc ,
§2 机械系统运动方程和等效量
一、机械系统运动方程
M1
B
A 1
F2 2
C
S2 4
(力与运动关系的方程)
3
F3
dE = dW
或 dE = Pdt
dt 瞬间内 系统总动能的增量 = 系统各外力作的元功之和
1 m v 2 + — J w 2)= S(F v cosa + M w )dt 1 dS(— i Si 2 Si i i i i i i 2
+25
-50
f
a b c d e f g h
3.
= 575 (Nm) DWmax JF = ——— [d] wm2
DWmax = 2pnm 2 [d]( ——) 60 900 DWmax = [d]p2 nm2 =
取 Jea≈ Jeb
令
Je
从而
d
DWmax 2 wm J e
或
Je
DWmax
2 w md
2.飞轮转动惯量的近似计算 当 d > [d] 时, 可增加一个转动惯量为 JF 的大质量的圆盘 — 飞轮.
DWmax [d ] 并使 d 2 wm ( J e J F ) DWmax [d ] 一般, JF 》Je 故. d 2 wm J F
d
最大盈亏功的求取
1. 分析: DWmax 为 wmin 到 wmax 区间的外力功. DWmax = Emax - Emin 按
DWmax JF≥——— 2 wm [d]
w
wmax
wmin
a
b
f
w2 dJF Me = Med - Mec = J e + — —— JF = 常 J e e F 2 dt
只要 Wd ≠ Wc ,
§2 机械系统运动方程和等效量
一、机械系统运动方程
M1
B
A 1
F2 2
C
S2 4
(力与运动关系的方程)
3
F3
dE = dW
或 dE = Pdt
dt 瞬间内 系统总动能的增量 = 系统各外力作的元功之和
1 m v 2 + — J w 2)= S(F v cosa + M w )dt 1 dS(— i Si 2 Si i i i i i i 2
+25
-50
f
a b c d e f g h
3.
= 575 (Nm) DWmax JF = ——— [d] wm2
DWmax = 2pnm 2 [d]( ——) 60 900 DWmax = [d]p2 nm2 =
《机械系统动力学》课件

04
数值模拟法的缺点是计算量大,计算时间长,且需要较高的数学建模 和数值计算能力。
解析法
01 02 03 04
解析法是通过数学解析的方法来求解机械系统动力学问题的方法。
解析法需要建立系统的数学模型,利用数学解析的方法求解模型的微 分方程或差分方程,以获得系统的解析解。
解析法的优点是能够获得系统的精确解,具有较高的理论价值。
实验研究法的优点是能够直接获取系统的实际动 力学行为,具有较高的真实性和可靠性。
数值模拟法
01
数值模拟法是通过计算机数值计算来模拟机械系统的动态行为的方法 。
02
数值模拟法需要建立系统的数学模型,利用数值计算方法求解模型的 微分方程或差分方程,以获得系统的动态响应。
03
数值模拟法的优点是能够模拟复杂系统的动态行为,具有较高的灵活 性和可重复性。
动能定理
总结词
描述物体动能变化的定理
详细描述
动能定理指出,一个物体动能的改变等于作用力对物体所做的功。这个定理是能 量守恒定律在动力学中的表现,是分析机械系统运动状态的重要工具。
势能定理
总结词
描述物体势能变化的定理
详细描述
势能定理指出,一个物体势能的改变等于作用力对物体所做的负功。这个定理可以帮助我们分析机械系统的运动 状态,特别是当物体受到重力的作用时。
CHAPTER 04
机械系统动力学的研究方法
实验研究法
实验研究法需要设计和搭建实验装置,对系统 施加激励并采集响应数据,通过分析数据来揭
示系统的动态特性。
实验研究法的缺点是实验成本较高,实验条件难以控 制,且实验结果可能受到实验误差和环境因素的影响
。
实验研究法是通过实验测试和观察机械系统的 动态行为,以获取系统的动力学特性和性能参 数的方法。
数值模拟法的缺点是计算量大,计算时间长,且需要较高的数学建模 和数值计算能力。
解析法
01 02 03 04
解析法是通过数学解析的方法来求解机械系统动力学问题的方法。
解析法需要建立系统的数学模型,利用数学解析的方法求解模型的微 分方程或差分方程,以获得系统的解析解。
解析法的优点是能够获得系统的精确解,具有较高的理论价值。
实验研究法的优点是能够直接获取系统的实际动 力学行为,具有较高的真实性和可靠性。
数值模拟法
01
数值模拟法是通过计算机数值计算来模拟机械系统的动态行为的方法 。
02
数值模拟法需要建立系统的数学模型,利用数值计算方法求解模型的 微分方程或差分方程,以获得系统的动态响应。
03
数值模拟法的优点是能够模拟复杂系统的动态行为,具有较高的灵活 性和可重复性。
动能定理
总结词
描述物体动能变化的定理
详细描述
动能定理指出,一个物体动能的改变等于作用力对物体所做的功。这个定理是能 量守恒定律在动力学中的表现,是分析机械系统运动状态的重要工具。
势能定理
总结词
描述物体势能变化的定理
详细描述
势能定理指出,一个物体势能的改变等于作用力对物体所做的负功。这个定理可以帮助我们分析机械系统的运动 状态,特别是当物体受到重力的作用时。
CHAPTER 04
机械系统动力学的研究方法
实验研究法
实验研究法需要设计和搭建实验装置,对系统 施加激励并采集响应数据,通过分析数据来揭
示系统的动态特性。
实验研究法的缺点是实验成本较高,实验条件难以控 制,且实验结果可能受到实验误差和环境因素的影响
。
实验研究法是通过实验测试和观察机械系统的 动态行为,以获取系统的动力学特性和性能参 数的方法。
高等机构学第十一章-机械系统动力学课件.ppt

i 1
n
n
Pi
等效构件作转动
M e Pi ,
i 1
Me
i 1
n
n
Pi
等效构件作移动 Fev Pi , i 1
Fe
i 1
v
n
Pi 机构中所有构件在运动过程的瞬时功率之和
i 1
Me
Je
Fe
me
v
注意: M e M ed M er
等效构件的力矩或力的运动方程的微分形式为:
d 2 dJ M d M r J dt 2 d
d
2 d f (,)
d
J
将其代入下面的欧拉公式,则:
i1
i
(
d d
)
i
i
M
(
i
,
i
)
2
2
J ii
(
dJ
d
)
i
用差商 Ji1 Ji Ji1 Ji
i1 i
代替
(
dJ
d
)
i
则上式变换为:
i1
3J i J i1 2Ji
i
M (i ,i ) J i i
的近似值约为:
1 2
(i
i1)t
F1
m
( F jx
j 1
x j q1
F jy
y j q1
M
j
j
q1
)
F2
m
( F jx
j 1
x j q2
F jy
y j q2
Mj
j )
q2
……
Fn
m
( F jx
j 1
x j qn
F jy
y j qn
n
n
Pi
等效构件作转动
M e Pi ,
i 1
Me
i 1
n
n
Pi
等效构件作移动 Fev Pi , i 1
Fe
i 1
v
n
Pi 机构中所有构件在运动过程的瞬时功率之和
i 1
Me
Je
Fe
me
v
注意: M e M ed M er
等效构件的力矩或力的运动方程的微分形式为:
d 2 dJ M d M r J dt 2 d
d
2 d f (,)
d
J
将其代入下面的欧拉公式,则:
i1
i
(
d d
)
i
i
M
(
i
,
i
)
2
2
J ii
(
dJ
d
)
i
用差商 Ji1 Ji Ji1 Ji
i1 i
代替
(
dJ
d
)
i
则上式变换为:
i1
3J i J i1 2Ji
i
M (i ,i ) J i i
的近似值约为:
1 2
(i
i1)t
F1
m
( F jx
j 1
x j q1
F jy
y j q1
M
j
j
q1
)
F2
m
( F jx
j 1
x j q2
F jy
y j q2
Mj
j )
q2
……
Fn
m
( F jx
j 1
x j qn
F jy
y j qn
机械系统动力学
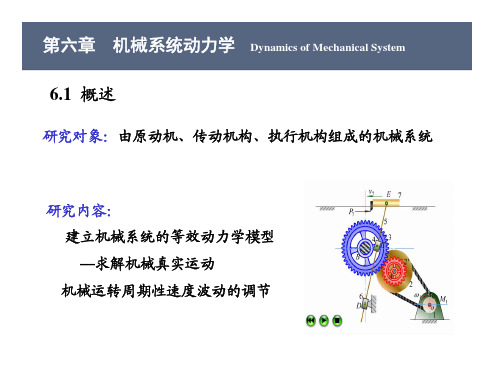
M e 2 M 1 1 P4 V4
V4 1 M e M1 P4 2 2 z2 l AB M1 P4 z1 cos 30
机械系统的等效动力学模型
小结 机械真实运动求解
建立机械系统的等效动力学模型
1 2 M e 2dt d( J e 2 ) 2
Me M1 z2 l P4 AB M e ( ) z1 cos 30
V3 M e M 1 P3 1
机械系统的等效动力学模型
等效构件为移动构件
1 2 Pe Vdt d m e V 2
Pe:等效驱动力 me:等效质量
2 VSi 2 i m e m i J Si i 1 V n
Vi i Pe Pi cos i M i V i 1
2 2 2
1
机械系统的等效动力学模型
等效力矩一般表达式
等效原则:动能相等 功率相等
M e Pi Vi cos i M i i
i 1
n
vi i M e Pi cos i M i i 1
n
机械系统的等效动力学模型
等效力矩 等效原则:动能相等 功率相等
M e 1 M 11 P3 v 3
2. 若构件2为等效构件 求解的飞轮转动惯量 是否为安装在齿轮1 上的飞轮转动惯量
机械运转周期性速度波动的调节
例:某用电动机作原动件剪床机械系统中,电动机转速 nm=1500 r/min.已知在一个稳定运转周期中电机轴 等效阻力矩MR变化规律如图,电动机驱动力矩MD 为常值.给定[]=0.05,机械系统各构件的转动惯量 忽略不计. 试求:安装在电机轴上飞轮所需转动惯量JF
小结
900W JF 2 2 Je n
周期性速度波动原因 周期性速度波动指标 周期性速度波动调节原理 飞轮转动惯量的确定
01-机械系统动力学ppt

目的 驱动功大于阻力功时飞轮积蓄能量而只使主轴的角速度略增;
驱动功小于阻力功时飞轮释放能量而只使主轴速度略降。
ω
02
2 Jv
0
M
vd
和两个位置间的运行时间: dt d
ω
1
t t0 ω d 0
(2)等效力矩为等效构件角速度的函数,等效转动惯量为常数 由电动机驱动的鼓风机、离心泵、起重机等
用力矩方程
M
v
M
va
M
vc
Jv
dω dt
求解达到某角速度ω的时间:
ω
dω
1 t dtt0 t
ω 0 M va M vc Jv t0
转化方法:
将整个机械系统的动力学问题转化为系统中 某一运动构件的动力学问题,该运动构件称 为等效构件,通常等效构件取为原动件。
转化
等效构件 作 直线移动 或作 定轴转动,用牛顿第二定律计算方便。
转化内容:
为使等效构件与系统中该构件的真实运动一致,需将作 用于原机械系统的所有外力与外力矩、所有运动构件的质量 与转动惯量都向等效构件转化。
直线移动:
Fv
v2 2
dm v ds
m
vv
dv/dt ds/dt
v2 2
dm v ds
m
v
dv dt
定轴转动:
M
v
ω 2 dJv
2 d
Jvω
dω /dt ω 2
d/dt 2
dJv
d
Jv
dω dt
当系统的速比为常数时,Jv、mv为常数,有:
直线移动:力形式的运动方程 dv
Fv Fva Fvc m v dt
1 2
(m
哈工大机械原理课件

I
5
IV
2
II
4
V
1
III
3
移 动 副
V
1
IV
2
螺 旋 副
V
1
2、根据组成运动副的两个运动副元素的接触情况分类 运动副元素以点或线接触的运动副称为高副 。
球面高副
柱面高副
运动副元素以面接触的运动副称为低副 。
球面低副
移动副
转动副
3、根据组成运动副的两个构件的相对运动形式分类
空间运动副
球销副
螺旋副
只是为了表明机构的运动状态或各构件的 相互关系,也可以不按比例来绘制运动简图, 通常把这样的简图称为机构示意图。
常用机构构件、运动副代表符号
绘制机构运动简图的步骤
1. 在绘制机构运动简图时,首先确定机构的原动件 和执行件,两者之间为传动部份,由此确定出组成机 构的所有构件,然后确定构件间运动副的类型。 2. 为将机构运动简图表示清楚,恰当地选择投影面。一 般选择与多数构件的运动平面相平行的面为投影面,必要 时也可以就机械的不同部分选择两个或两个以上的投影面 ,然后展开到同一平面上。总之,绘制机构运动简图要以 正确、简单、清晰为原则。 3. 选择适当的比例尺,根据机构的运动尺寸定出各运动 副之间的相对位置,然后用规定的符号画出各类运动副,并 将同一构件上的运动副符号用简单线条连接起来,这样便可 绘制出机构的运动简图。
30米/分
500
二、创新
◆自然科学领域的最高成就是发现
◆应用技术领域的最高成就是发明
发明:
◆基础理论知识
◆应用技术知识 ◆实践经验
◆强烈的创新意识 ◆勤奋的工作
两用折叠椅
外环
双曲面滚柱加载器
哈尔滨工业大学结构动力学PPT课件

x0 x0 , x0 x0 xt c1n cosnt c2n sinnt
c1 x0 n , c2 x0
第36页/共42页
x
t
x0
n
sin nt
x0
cos nt
令
x0 cos n
, x0 sin
则可化为
其中:
xt sinnt
2
x02
x0
n
tg x0n arctg x0n
T1
1 2
l 0
d
l
2
x2
1 2
(1 3
l)x2
1 m1 23
x2TΒιβλιοθήκη T1Tm1 2
m1 3
m
x2
1 2
meq x2
又因为: 弹簧的势能与弹簧质量无关, 则
V 1 kx2 2
由能量法,可得
meq x kx 0 弹性元件质量不能忽略时,利用等
效质量,将质量折算到质量块上, 弹性元件仍看作无质量的。
• 18世纪线性振动理论成熟期。
第11页/共42页
• 19世纪非线性振动理论,各种工程实际结构振动的近似 求解方法。
• 20世纪50年代初由于航空航天工程的发展,原本确定性 理论无法解释包含随机变化的工程问题,发展了随机振 动理论。
• 20世纪后期计算机技术的飞速发展,数值计算方法和理 论成为主要研究方法之一。
第7页/共42页
三、结构动力学研究的内容
结构动力学就是研究结构系统在激励力作用下产生的响 应规律的科学,研究激励力、结构和响应三者关系的科 学。
现代结构动力学主要研究以下三个方面的内容 第一类问题:响应分析(结构动力计算)
输入 (动力荷载)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2
x0 n tan v0
1
Undamped free response
Adding Damping
Damping
Damping is some form of friction! In solids, friction between molecules result in damping In fluids, viscosity is the form of damping that is most observed In this course, we will use the viscous damping model; i.e. damping proportional
Undamped Spring-Mass System
L
Unloaded Spring
k st m x
At equilibrium, kst = mg
Body in equilibrium (at rest)
m
Body in motion
Free Body Diagram
x
k( st + x )
Prerequisites: The most important prerequisite is ordinary differential equations. You should be prepared to review undergraduate differential equations if necessary.
………
考核办法—累加式
1. 大作业1 10%
2. 大作业2
3. 平时表现 4. 期终考试
10%
10% 70%
Preface
What is dynamics?
Dynamics focuses on understanding why objects move the way they do.
Dynamics = Kinematics + Kinetics
x(t ) ae
2
t
Into ODE you get the characteristic equation:
k t ae ae 0 m
t
Giving:
k m
2
k j m
The proposed solution becomes:
x(t ) a1e
机械系统动力学
机电工程学院 机械设计系
Chen Zhaobo (陈照波)
Tel: 86412057 E-mail: chenzb@ 机械楼一楼1020室
参考书
1. 闻邦椿等《机械振动理论及应用》 高等教育出版社
2. 胡海岩 《机械振动基础》 北京航空航天大学出版社
3. 师汉民 《机械振动系统》 华中科技大学出版社 4. W. T. Thomson 《振动理论及应用》 清华大学出版社
Critical Damping
No oscillation occurs.
2) 1, called over-damping two distinct real roots:
1,2 n n 2 1
x(t ) e
n t
(a1e
n t 2 1
Why to study dynamics of mechanical system? Higher speed Higher precision More flexible More complicated
Resonance
When a forcing frequency is equal to a natural frequency
x(t ) a1e jnt a2e- jnt
Note!
Natural frequency
In the previously obtained solution:
x(t ) A sin(nt ) The frequency of vibration is n
Three possibilities:
1)
1
Roots are repeated & equal.
Called critically damped
1 c ccr 2 mk 2m n
x(t ) a1e nt a2te nt Using the initial conditions: a1 x0 a2 v0 n x0
Chapter 1 Single degree of freedom systems
Objectives Recognize a SDOF system Be able to solve the free vibration equation of a SDOF system with and without damping Understand the effect of damping on the system vibration Apply numerical tools to obtain the time response of SDOF system
It depends only on the characteristics of the vibration system. That is why it is called the natural frequency of vibration.
k n m
Natural frequency
sin( ) sin( )cos( ) cos( )sin( )
Manipulating the solution
Solution we have: Rewriting:
x(t ) a1e
jnt
a2e
- jnt
Байду номын сангаас
x(t ) a1 (cos nt j sin nt ) +a2 (cos nt j sin nt ) (a1 a2 ) cos nt j (a1 - a2 )sin nt
=
mg
.. mx
Equations of motion
Sum forces:
F : mg - kst x m x
Rearrange to yield the familiar equation of motion:
Physical model
Spring Damping element
natural frequency from static deflection.
n
g
st
natural frequency from energy method.
Recall: Initial Conditions
Amplitude & phase from ICs
x0 A sin( n 0 ) A sin v0 A n cos( n 0 ) A n cos Solving yield v0 A x0 n
to velocity
Spring-mass-damper systems
From Newton’s Law:
mx(t ) cx(t ) kx(t ) 0 x(0) x0 x(0) v0
Solution (dates to 1743 by Euler)
Divide the equation of motion by m
COURSE GOALS:
1. To become proficient at modeling vibrating mechanical systems. 2. To perform dynamic analysis such as free and forced response of SDOF and MDOF systems. 3. To understand concepts of modal analysis. 4. To understand concepts in passive and active vibration control systems.
j
k t m
a2e
-j
k t m
For simplicity, let’s define:
k n m
jnt
Giving:
x(t ) a1e
a2e
- jnt
Let’s manipulate the solution
Recall
e
j
cos( ) j sin( )
Giving:
x(t ) A1 cos nt A2 sin nt
Further manipulation
Solution we have: Let:
x(t ) A1 cos nt A2 sin nt
A
A
2 A12 A2
A2
A1
cos A2 / A
sin A1 / A
2 x(t ) 2n x(t ) n x(t ) 0
Where the damping Ratio is given by: (dimensionless)
c 2 mk
Let x(t ) aet & substitute into equation of motion
a2 e
n t 2 1
)
where a1 a2 v0 ( 2 1) n x0 2 n 2 1 v0 ( 2 1) n x0 2 n 2 1
x0 n tan v0
1
Undamped free response
Adding Damping
Damping
Damping is some form of friction! In solids, friction between molecules result in damping In fluids, viscosity is the form of damping that is most observed In this course, we will use the viscous damping model; i.e. damping proportional
Undamped Spring-Mass System
L
Unloaded Spring
k st m x
At equilibrium, kst = mg
Body in equilibrium (at rest)
m
Body in motion
Free Body Diagram
x
k( st + x )
Prerequisites: The most important prerequisite is ordinary differential equations. You should be prepared to review undergraduate differential equations if necessary.
………
考核办法—累加式
1. 大作业1 10%
2. 大作业2
3. 平时表现 4. 期终考试
10%
10% 70%
Preface
What is dynamics?
Dynamics focuses on understanding why objects move the way they do.
Dynamics = Kinematics + Kinetics
x(t ) ae
2
t
Into ODE you get the characteristic equation:
k t ae ae 0 m
t
Giving:
k m
2
k j m
The proposed solution becomes:
x(t ) a1e
机械系统动力学
机电工程学院 机械设计系
Chen Zhaobo (陈照波)
Tel: 86412057 E-mail: chenzb@ 机械楼一楼1020室
参考书
1. 闻邦椿等《机械振动理论及应用》 高等教育出版社
2. 胡海岩 《机械振动基础》 北京航空航天大学出版社
3. 师汉民 《机械振动系统》 华中科技大学出版社 4. W. T. Thomson 《振动理论及应用》 清华大学出版社
Critical Damping
No oscillation occurs.
2) 1, called over-damping two distinct real roots:
1,2 n n 2 1
x(t ) e
n t
(a1e
n t 2 1
Why to study dynamics of mechanical system? Higher speed Higher precision More flexible More complicated
Resonance
When a forcing frequency is equal to a natural frequency
x(t ) a1e jnt a2e- jnt
Note!
Natural frequency
In the previously obtained solution:
x(t ) A sin(nt ) The frequency of vibration is n
Three possibilities:
1)
1
Roots are repeated & equal.
Called critically damped
1 c ccr 2 mk 2m n
x(t ) a1e nt a2te nt Using the initial conditions: a1 x0 a2 v0 n x0
Chapter 1 Single degree of freedom systems
Objectives Recognize a SDOF system Be able to solve the free vibration equation of a SDOF system with and without damping Understand the effect of damping on the system vibration Apply numerical tools to obtain the time response of SDOF system
It depends only on the characteristics of the vibration system. That is why it is called the natural frequency of vibration.
k n m
Natural frequency
sin( ) sin( )cos( ) cos( )sin( )
Manipulating the solution
Solution we have: Rewriting:
x(t ) a1e
jnt
a2e
- jnt
Байду номын сангаас
x(t ) a1 (cos nt j sin nt ) +a2 (cos nt j sin nt ) (a1 a2 ) cos nt j (a1 - a2 )sin nt
=
mg
.. mx
Equations of motion
Sum forces:
F : mg - kst x m x
Rearrange to yield the familiar equation of motion:
Physical model
Spring Damping element
natural frequency from static deflection.
n
g
st
natural frequency from energy method.
Recall: Initial Conditions
Amplitude & phase from ICs
x0 A sin( n 0 ) A sin v0 A n cos( n 0 ) A n cos Solving yield v0 A x0 n
to velocity
Spring-mass-damper systems
From Newton’s Law:
mx(t ) cx(t ) kx(t ) 0 x(0) x0 x(0) v0
Solution (dates to 1743 by Euler)
Divide the equation of motion by m
COURSE GOALS:
1. To become proficient at modeling vibrating mechanical systems. 2. To perform dynamic analysis such as free and forced response of SDOF and MDOF systems. 3. To understand concepts of modal analysis. 4. To understand concepts in passive and active vibration control systems.
j
k t m
a2e
-j
k t m
For simplicity, let’s define:
k n m
jnt
Giving:
x(t ) a1e
a2e
- jnt
Let’s manipulate the solution
Recall
e
j
cos( ) j sin( )
Giving:
x(t ) A1 cos nt A2 sin nt
Further manipulation
Solution we have: Let:
x(t ) A1 cos nt A2 sin nt
A
A
2 A12 A2
A2
A1
cos A2 / A
sin A1 / A
2 x(t ) 2n x(t ) n x(t ) 0
Where the damping Ratio is given by: (dimensionless)
c 2 mk
Let x(t ) aet & substitute into equation of motion
a2 e
n t 2 1
)
where a1 a2 v0 ( 2 1) n x0 2 n 2 1 v0 ( 2 1) n x0 2 n 2 1
