计算方法作业
北科大研究生计算方法作业

计算方法姓名:学号:班级:指导教师:目录作业1 (1)作业2 (5)作业3 (8)作业4 (10)作业5 (14)作业6 (16)作业7 (17)作业11、分别用不动点迭代与Newton 法求解方程 -+=x 2x e 30的正根与负根。
解:(1)不动点迭代a.原理:将 230x x e -+=变型为1()k k x g x +=进行迭代,直到 为止变型后为有两种形式: 和 b.程序:初值为1形式: x=zeros(100,1); tol=1; i=1; x(1)=1;while tol>=10e-6; disp(x(i))x(i+1)=log(2*x(i)+3); tol=abs(x(i+1)-x(i)); i=i+1; enddisp(i-1); 形式:x=zeros(100,1); tol=1; i=1; x(1)=1;while tol>=10e-6; disp(x(i))x(i+1)=(exp(x(i))-3)/2; tol=abs(x(i+1)-x(i)); i=i+1; end disp(i-1);c.运行结果:初值为1(23)1lnk x k x ++=6110k k x x -+-<132k x k e x +-=(23)1ln k x k x ++=132k xk e x +-=迭代次数:11迭代次数:9(2)Nexton法a.原理:令()()1'kk kkf xx xf x+=-得到迭代公式为:()1232kkxkk k xx ex xe+-+=--b.程序:初值为0x=zeros(100,1);tol=1;i=1;x(1)=0;while tol>=10e-6;disp(x(i))x(i+1)=x(i)-((2*x(i)-exp(x(i))+3)/(2-exp(x(i))));tol=abs(x(i+1)-x(i));i=i+1;enddisp(i-1);初值为1x=zeros(100,1);tol=1;i=1;x(1)=1;while tol>=10e-6;disp(x(i))x(i+1)=x(i)-((2*x(i)-exp(x(i))+3)/(2-exp(x(i))));tol=abs(x(i+1)-x(i));i=i+1;enddisp(i-1)a=x(i-1);b=2*a-exp(a)+3;disp(b);c.运行结果:初值为0迭代次数:5初值为1迭代次数:8 -1.6171e -006结果分析:不动点迭代会因为迭代公式选取的不同得出不同的迭代结果,而牛顿法迭代会因为初值选取的不同而得到不同的结果。
计算方法作业集及答案

计算方法作业集及答案第一章数值计算基本常识一.填空题1.用四舍五入得到的近似数0.628,有_____位有效数字,其绝对误差限是____________。
2.用四舍五入得到的近似数0.586,有_____位有效数字,其绝对误差限是____________。
3.用四舍五入得到的近似数0.69,其绝对误差是__________,由此计算出的相对误差限是__________。
4.用四舍五入得到的近似数0.7960,其绝对误差是__________,由此计算出的相对误差限是__________。
5.设0.484是0.4900的近似值,那么0.484具有____位有效数字。
6.设某某=0.231是真值某=0.229的近似值,则某某有_____位有效数字。
7.设某某=0.23是真值某=0.229的近似值,则某某有_____位有效数字。
8.设某=2.3149541,取5位有效数字,则所得的近似值某某=_____。
9.设某=2.3149541,取4位有效数字,则所得的近似值某某=_____。
10.若近似数0.1100有4位有效数字,由有效数字计算出的相对误差是____________。
11.若近似数76.82有4位有效数字,由有效数字计算出的相对误差是____________。
12.若近似数576.00有5位有效数字,由有效数字计算出的相对误差是____________。
13.用3.15作为π的近似值有_____位有效数字。
14.用3.14作为π的近似值有_____位有效数字。
15.用3.1416作为π的近似值有_____位有效数字。
解答:1.3、0.5某10-32.3、0.5某10-33.0.5某10-2、0.725%4.0.5某10-4、0.00628%5.16.27.28.2.31509.2.31510.0.05%11.0.007%12.0.001%13.214.315.5二.选择题1.3.141580是π的近似值,有()位有效数字。
计算方法平时作业

《计算方法》课程平时作业(2010-2011学年第一学期)作业(考试前交, 给出证明或计算过程、计算程序及计算结果)1. 对向量()12Tn x x x x = 定义1211,max ,nk k k nk x x xx x ∞≤≤====∑设A 是n n ⨯矩阵,规定1111max x A Ax ==,1max x A Ax∞∞∞==,2221max x A Ax ==证明111112max (),max (),.nnkj jk j nj nk k T A a Aa A A A λ∞≤≤≤≤=====∑∑列范数行范数是最大特征值2. 用简单迭代法(即不动点迭代法)求方程32210200x x x ++-=在1x =附近的根. 要求给出不动点方程、程序和运行结果. 3. 用Newton 迭代法求方程32210200x x x ++-=的一个正根,计算结果精确到7位有效数字. 要求给出程序和运行结果. 4. 用牛顿迭代法求方程310x x --=在01x =附近的根. 要求给出程序和运行结果.5. 证明迭代格式()21233k k k k x x a x x a++=+, 00,0a x >>.6. 编写用全主元Gauss 消去法解线性方程组的程序,并求解12345123451234512345123450.024*******4233433241634418x x x x x x x x x x x x x x x x x x x x x x x x x -+-+=⎧⎪-++++=⎪⎪+++-=⎨⎪-++++=⎪⎪+-++=⎩ 7. 用追赶法解线性方程组12345210001121000012100001210000120x x x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ 要求给出程序和运行结果. 8.给定线性方程组12122132x x x x +=-⎧⎨+=⎩ 问用雅可比迭代法和Gauss-Seidel 迭代法求解是否收敛? 9. 设有线性方程组123521121422023103x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ (1)考察用Jacobi 迭代法和Gauss-Seidel 迭代法解此方程组的收敛性; (2)分别用Jacobi 迭代法和Gauss-Seidel 迭代法解此方程组,要求当(1)()410k k x x +--<时迭代终止. 给出求解程序和迭代次数及结果.10.编写幂法程序求矩阵422251216A ⎛⎫⎪= ⎪ ⎪⎝⎭按模最大的特征值1λ和对应的特征向量1x 。
计算方法大作业

计算方法大作业
1、试探法证明方程0128423=++-x x x 有三个实根,并确定三个根所在区间(区间长度不超过1).
2、方程0123=--x x 在5.10=x 附近有根, 将方程作三种改写,可得三种迭代式: (1) 21211,11k
k x x x x +=+=+; (2) 321231,1k k x x x x +=+=+; (3) 11,1112-=-=+x x x x k .
判断各迭代式在5.10=x 附近的收敛性;选一种收敛最快的迭代式,计算5.10=x 附近的根,准确的4位小数.
3、用牛顿法于方程0n x a -=和1/0n a x -=
的迭代公式。
已知0 1.3x ≈=,问用这种迭代公式迭代一、二次能得几位小数准确的近似值(已
1.31607401=⋅⋅⋅)?
4、用雅可比迭代法与赛德尔迭代法解方程组 ⎪⎩⎪⎨⎧=-+=+-=++-7416518321
321321x x x x x x x x x ,取初值T x )0,0,0()0(=,准确到两位小数。
5、设有方程组
⎪⎩⎪⎨⎧=++=++=++.251084,118104,134410321
321321x x x x x x x x x ,写出雅可比迭代、赛德尔、2.1=ω的SOR 迭代算式。
三种迭代是否收敛?为什么?
6、设有方程组1231231231.25 3.6912.370.58,10.019.050.12 1.43,1.22 4.33 2.76 3.22.x x x x x x x x x --=⎧⎪-++=⎨⎪-+=⎩
写出收敛的迭代格式,说明收敛的理由。
计算方法第二章作业答案参考
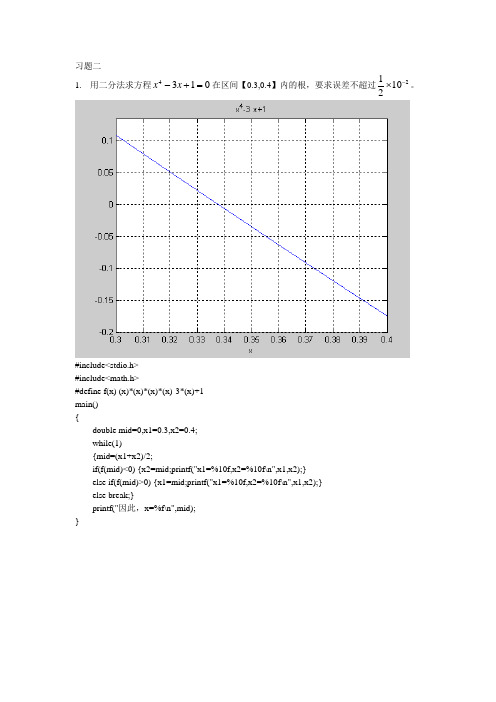
{
double mid=0,x1=0.3,x2=0.4;
while(1)
{mid=(x1+x2)/2;
if(f(mid)<0) {x2=mid;printf("x1=%10f,x2=%10f\n",x1,x2);}
else if(f(mid)>0) {x1=mid;printf("x1=%10f,x2=%10f\n",x1,x2);}
main()
{
float x1=1.5,a=0,b=0;
int i;
for(i=0;i<20;i++)
{
b=x1;
a=f(x1);
x1=f(a);
x1=(x1*b-a*a)/(x1-2*a+b);
printf("%10f",x1);
}
printf("\n因此,x=%.4f\n",x1);
}
9.用牛顿法求方程 在 附近的根,要求准确到小数点后第3位
main()
{
float x1=1.3;
int i;
for(i=0;i<20;i++)
{
x1=f(x1);
printf("%10f",x1);
}
printf("\n因此,x=%f\n",x1);
}
(3) ,
#include<stdio.h>
#include<math.h>
#define f(x) pow(x-1,-1*1.0/2)
main()
{
float x1=1.3;
22春“计算机科学与技术”专业《计算方法》离线作业-满分答案9

22春“计算机科学与技术”专业《计算方法》离线作业-满分答案1. 线性插值虽然只利用了两个节点上的信息,但是精度却比较高。
( )线性插值虽然只利用了两个节点上的信息,但是精度却比较高。
( )A、错误B、正确参考答案:A2. 雅可比方法的主要特点是什么( )A.精度高B.算法稳定C.稀疏性D.求得的特征向量正交性好参考答案:ABD3. 议程的近似方法有( )A.迭代法B.牛顿法C.弦截法D.二分法参考答案:ABCD4. 通过点(x₀,y₀),(x₁,y₁)的拉格朗日插值基函数l₀(x₀),l₁(x₁)满足( )。
通过点(x₀,y₀),(x₁,y₁)的拉格朗日插值基函数l₀(x₀),l₁(x₁)满足( )。
A、l₀(x₀)=0,l₁(x₁)=0B、l₀(x₀)=0,l₁(x₁)=1C、l₀(x₀)=1,l₁(x₁)=0D、l₀(x₀)=1,l₁(x₁)=1参考答案:D5. 十进制算术表达式:3*512+7*64+4*8+5的运算结果,用二进制表示为( )。
A.10111100101B.11111100101C.11110100101D.11111101101参考答案:B6. 构造拟合曲线不可以采用下列哪种准则?( )构造拟合曲线不可以采用下列哪种准则?( )A、使残差的最大绝对值为最小B、使残差的绝对值之和为最小C、使残差的平方和为最小D、是残差的绝对值之差为最小参考答案:D7. 下列叙述中正确的是( )。
A.线性表的链式存储结构与顺序存储结构所需要的存储空间是相同的B.线性表的链式存储结构所需要的存储空间一般要多于顺序存储结构C.线性表的链式存储结构所需要的存储空间一般要少于顺序存储结构D.上述三种说法都不对参考答案:B8. 列主元素消元法不是直接法中常用的方法。
( )A.正确B.错误参考答案:B9. 穷举法,也称辗转法,是一种针对于密码的破译方法,即将密码进行逐个推算直到找出真正的密码为止。
( )A.错误B.正确参考答案:A10. 任意一棵具有n个结点的二叉树,若它有m个叶子,则该二叉树上度数为1的结点为n-2m+1个。
计算方法作业参考答案(不断更新)

第一次作业1.下列各数都是经过四舍五入得到的近似数,指出他们有几位有效数字,并写出绝对误差限。
9800107480.566.385031.01021.1*65*5*4*3*2*1=⨯=====x x x x x x解: ,有5位有效数字,绝对误差限为; ,有2位有效数字,绝对误差限为; ;有4位有效数字,绝对误差限为; ;有5位有效数字,绝对误差限为; ;有1位有效数字,绝对误差限为; ;有4位有效数字,绝对误差限为。
2.要使的近似值的相对误差限小于,要取几位有效数字?解:由于,设要取位有效数字,则根据定理1.1.1,有()()%1.010811021111<⨯=⨯≤----n n r x ε,解得4≥n ,即要取4位有效数字。
3.序列满足递推关系若,计算到时误差有多大?这个计算过程数值稳定吗?解:,由于有3位有效数字,且,所以的绝对误差限为,因此的绝对误差限为。
很明显这个计算过程不是数值稳定的。
作业中出现的问题:第一题:主要是第五个数5*5107⨯=x ,不知道它有几位有效数字,很多同学认为有5或者6位有效数字,这是不对的,进而算错绝对误差限。
另外有个别同学分不清有效数字的概念,六个数的有效数字都弄错了。
第二题:主要是算错n ,不知道该取3还是4。
第三题:没有什么大的问题。
有个别同学一个数一个数的算出来了,这是不可取的。
直接迭代误差就行了。
附:地物1301班和1302班有几个同学花名册上没有名单,我添加上去了。
第二次作业1*11011021.01021.1⨯==x 4-5-1105.0105.0⨯=⨯1-*21031.0031.0⨯==x 3-2-1-105.0105.0⨯=⨯3*3103856.06.385⨯==x -14-3105.0105.0⨯=⨯2*41056480.0480.56⨯==x 3-5-2105.0105.0⨯=⨯65*5107.0107⨯=⨯=x 51-6105.0105.0⨯=⨯4*6109800.09800⨯==x 5.0105.04-4=⨯20%1.0110447213595.047213595.420⨯⋯=⋯=n {}n y ,,2,1,1101⋯=-=-n y y n n 41.120≈=y 10y ()()()*00*222*11*101010y y y y y y y y n n n n n n n -=⋯=-=-=-----*0y 1*010141.041.1⨯==y *0y 2-105.0⨯*10y 72-10105105.010⨯=⨯⨯1.利用二分法求方程在[2,3]内根的近似值,并指出误差。
计算方法作业

1. 利用函数y=x 在x 1=100,x 2=121处的值,计算115 的近似值,并估计误差。
解:y 1=100 =10, y 2=121 =11.取x 1和x 2为节点作一次插值,得L 1(x)=x-121100-121 ×10 + x-100121-100×11 则 L 1(115)= 115-121100-121 ×10 + 115-100121-100×11 = -6-21 ×10 + 1521×11 = 27 ×10 + 57×11 = 257=10.7142857 ≈115误差:y=x ,y ′=12 x -0.5, y ″=- 12 × 12 x -1.5=- 14x -1.5, 115 - L 1(115)= 12 ×(- 14 ξ-1.5)×(115-100)×(115-121) 100<ξ<121所以|115 - L 1(115)|≤12 ×|(- 14×100-1.5)|×|(115-100)×(115-121)| = 18 ×11000×15×6 =0.011252. 给出函数表 x 0 1 2 4 5y 0 16 46 88 0 试求各阶差商,并写出牛顿插值多项式。
解:差商表k x k f[x k ] f[x k ,x k+1] f[x k ,x k+1,x k+2] f[x k ,x k+1,x k+2,x k+3] f[x k ,x k+1,x k+2,x k+3,x k+4]0 0 0 16 7 - 52 - 761 1 16 30 -3 - 2532 2 46 21 -10933 4 88 -884 5 0所以N 4=0+16(x-0)+7(x-0)(x-1) - 52 (x-0)(x-1)(x-2) - 76(x-0)(x-1)(x-2)(x-4) =16x+7x(x-1) - 52 x(x-1)(x-2) - 76x(x-1)(x-2)(x-4) 3. 给定数据表x 0.125 0.250 0.375 0.500 0.625 0.750 f(x) 0.79618 0.77334 0.74371 0.70413 0.65632 0.60228使用三次牛顿差分插值公式计算f(0.1581)及f(0.636).解:x k f kΔf kΔ2f kΔ3f kΔ4f kΔ5f k 0.125 0.79618 -0.02284 -0.00679 -0.00316 0.00488 -0.00460 0.250 0.77334 -0.02963 -0.00995 0.00172 0.000280.375 0.74371 -0.03958 -0.00823 0.002000.500 0.70413 -0.04781 -0.006230.625 0.65632 -0.054040.750 0.60228N3(0.125+0.125t)=0.79618-0.02284t-0.00679t(t-1)-0.00316t(t-1)(t-2)N3(0.1581)= N3(0.125+0.125×0.2648)= 0.79618-0.02284×0.2648-0.00679×0.2648×(0.2648-1)-0.00316×0.2648×(0.2648-1)×(0.2648-2)=0.790N3(0,636)=N3(0.125+0.125×4.088)=0.79618-0.02284×4.088-0.00679×4.088×(4.088-1)-0.00316×4.088×(4.088-1)×(4.088-2)=0.534上机作业例1:已知函数表:xi 0.56160 0.56280 0.56401 0.56521yi 0.82741 0.82659 0.82577 0.82495用三次拉格朗日插值多项式求x=0.5635时的函数近似值C语言程序设计:# include<stdio.h>float Lagrange(float x[],float y[],float xx,int n){int i,j;float *a,yy=0;a=new float[n];for(i=0;i<=n-1;i++){a[i]=y[i];for(j=0;j<=n-1;j++)if(j!=i) a[i]*=(xx-x[j])/(x[i]-x[j]);yy+=a[i];}delete a;return yy;}void main(){float x[4]={0.56160,0.56280,0.56401,0.56521};float y[4]={0.82741,0.82659,0.82577,0.82495};float xx=0.5635,yy;yy=Lagrange(x,y,xx,4);printf("x=%f,y=%f\n",xx,yy);}运行结果:x=0.563500y=0.826116例2:已知函数表xi 0.4 0.55 0.65 0.8 0.9 yi 0.41075 0.57815 0.69675 0.88811 1.02652 用牛顿插值多项式求N n(0.596)和N n(0.895)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ch1 插值
1. 已知函数的观测数据为:,试求以
为节点的Lagrange插值多项式,并求的值.
2. 已知函数值,试用线性插
值和抛物线插值计算的近似值,并比较误差。
3. 在上给出的等距节点函数表,若用二次插值多项式求
的近似值,要使截断误差不超过,问该函数表的步长h应取多少?
4. 已知的函数值,求Newton
插值多项式以及的近似值。
5. 已知的函数值,求Newton插值多项式。
再增加,求。
6. 已知函数的观测数据为,分别求出三次Newton前插和后插多项式,并求和的近似值。
7. 求满足条件的Hermite插值多项式:
8. 求一个次数不高于4次的多项式,使其满足
并估计误差。
9. 已知数据表
求在区间[0,3]上的三次样条插值函数。
Ch2 线性方程组的直接解法和迭代解法1. 对方程组
(1)用Gauss 消去法求解(保留5位有效数字);
(2) 用列主元消去法求解,并与(1)比较。
2. 用追赶法求解三对角方程组,其中
3. 用分解法求解方程组:
4. 对于方程组
试建立解此方程组的Jacobi迭代格式和Gauss-Seidel迭代格式,写出对应的迭代矩阵并判别格式的收敛性。
CH3 非线性方程求根
1. 用简单迭代法求解方程, 并验证收敛性,结果精确至4位有效数字。
2. 分别用简单迭代法和Newton法解方程,并比较两种方法的收敛速度。
