最优化问题的数学模型
数学建模第二讲简单的优化模型

数学建模第二讲简单的优化模型数学建模是利用数学方法对实际问题进行建模、分析和求解的过程。
在实际问题中,常常需要针对一些指标进行优化,以达到最优的效果。
本讲将介绍一些简单的优化模型。
一、线性规划模型线性规划是一种重要的数学优化方法,广泛应用于工程、经济、管理等领域。
其数学模型可以表示为:\begin{aligned}&\text{max} \quad c^Tx \\&\text{s.t.} \quad Ax \leq b, \quad x \geq 0\end{aligned}\]其中,$x$为决策变量,$c$为目标函数系数,$A$为约束条件系数矩阵,$b$为约束条件右端向量。
线性规划模型指的是目标函数和约束条件都是线性的情况。
通过线性规划模型,可以求解出使得目标函数取得最大(或最小)值时的决策变量取值。
二、非线性规划模型非线性规划模型指的是目标函数或约束条件中存在非线性部分的情况。
非线性规划模型相对于线性规划模型更为复杂,但在实际问题中更为常见。
对于非线性规划问题,通常采用数值优化方法进行求解,如梯度下降法、牛顿法等。
这些方法通过迭代的方式逐步靠近最优解。
三、整数规划模型整数规划模型是指决策变量必须为整数的规划模型。
整数规划在实际问题中应用广泛,如物流配送问题、工程调度问题等。
整数规划模型通常难以求解,因为整数规划问题是一个NP难问题。
针对整数规划问题,常用的求解方法有枚举法、分支定界法、遗传算法等。
四、动态规划模型动态规划模型是指将问题划分为子问题,并通过求解子问题最优解来求解原问题最优解的方法。
动态规划通常用于求解具有重叠子问题和最优子结构性质的问题。
动态规划模型具有递推性质,通过递归或迭代的方式求解子问题的最优解,并保存中间结果,以提高求解效率。
五、模拟退火模型模拟退火是一种用来求解组合优化问题的随机优化算法。
模拟退火算法基于固体退火过程的模拟,通过温度的控制和随机跳出来避免陷入局部最优解。
最优化问题的建模与解法

最优化问题的建模与解法最优化问题(optimization problem)是指在一组可能的解中寻找最优解的问题。
最优化问题在实际生活中有广泛的应用,例如在工程、经济学、物流等领域中,我们经常需要通过数学模型来描述问题,并利用优化算法来求解最优解。
本文将介绍最优化问题的建模和解法,并通过几个实例来说明具体的应用。
一、最优化问题的数学建模最优化问题的数学建模包括目标函数的定义、约束条件的确定以及变量范围的设定。
1. 目标函数的定义目标函数是一个表达式,用来衡量问题的解的优劣。
例如,对于一个最大化问题,我们可以定义目标函数为:max f(x)其中,f(x)是一个关于变量x的函数,表示问题的解与x的关系。
类似地,对于最小化问题,我们可以定义目标函数为:min f(x)2. 约束条件的确定约束条件是对变量x的一组限制条件,用来定义问题的可行解集合。
约束条件可以是等式或不等式,通常表示为:g(x) ≤ 0h(x) = 0其中,g(x)和h(x)分别表示不等式约束和等式约束。
最优化问题的解必须满足所有的约束条件,即:g(x) ≤ 0, h(x) = 03. 变量范围的设定对于某些变量,可能需要限定其取值的范围。
例如,对于一个实数变量x,可能需要设定其上下界限。
变量范围的设定可以通过添加额外的不等式约束来实现。
二、最优化问题的解法最优化问题的解法包括数学方法和计算方法两种,常见的数学方法有最优性条件、拉格朗日乘子法等,而计算方法主要是通过计算机来求解。
1. 数学方法数学方法是通过数学分析来求解最优化问题。
其中,常见的数学方法包括:(1)最优性条件:例如,对于一些特殊的最优化问题,可以通过最优性条件来判断最优解的存在性和性质。
最优性条件包括可导条件、凸性条件等。
(2)拉格朗日乘子法:对于带有约束条件的最优化问题,可以通过拉格朗日乘子法将原问题转化为无约束最优化问题,从而求解最优解。
2. 计算方法计算方法是通过计算机来求解最优化问题。
优化问题数学表示方法

优化问题数学表示方法优化问题是指在一定约束下,寻找一个最优解的问题。
在实际应用中,我们经常遇到需要优化的情况,例如寻找最短路径、最大化利润、最小化损失等。
为了解决优化问题,我们需要对问题进行数学建模,将问题转化为数学表达形式。
常用的数学表示方法包括线性规划、整数规划、非线性规划、动态规划等。
首先,我们来介绍线性规划。
线性规划是一种数学优化方法,其目标是在一组线性约束条件下,最大化或最小化一个线性目标函数。
线性规划的数学表示形式如下:max/min c^T * xsubject to Ax <= bx >= 0其中,c是一个列向量,表示目标函数的系数;x是要优化的变量;A是一个矩阵,用于表示约束条件的系数;b是一个列向量,表示约束条件的右边界。
例如,假设我们需要在给定的预算下购买商品,使得商品的总价值最大化。
假设有三种商品,其价格分别为p1、p2、p3,我们可以定义目标函数为:max p1*x1 + p2*x2 + p3*x3其中,x1、x2、x3分别表示购买商品1、商品2、商品3的数量。
还需考虑约束条件,例如预算上限为B,每种商品的购买数量不能为负数,则有以下约束条件:p1*x1 + p2*x2 + p3*x3 <= Bx1 >= 0, x2 >= 0, x3 >= 0将这些问题表示为线性规划模型后,我们可以使用常见的线性规划算法,如单纯形法、内点法等,来求解最优解。
接下来,我们介绍整数规划。
整数规划是限制解向量的每个分量为整数的线性规划问题。
整数规划常用于离散决策问题,例如在作业安排中,每个作业有预计的完成时间和紧急程度,我们需要决定如何安排作业,使得总完成时间最短,且满足每个作业的紧急程度。
整数规划的数学表示形式与线性规划类似,只需要将变量的取值限制为整数。
假设有n个作业,每个作业需要的时间为t1、t2、…、tn,紧急程度为e1、e2、…、en,我们可以将优化问题表示为以下整数规划模型:min t1*x1 + t2*x2 + ... + tn*xnsubject to e1*x1 + e2*x2 + ... + en*xn <= Dx1, x2, ..., xn是整数其中,D是总紧急程度限制,xi表示第i个作业是否被安排。
典型优化问题的模型与算法

典型优化问题的模型与算法一、引言优化问题在各种领域中都有着广泛的应用,如生产管理、物流配送、资源分配、财务预算等。
为了解决这些实际问题,我们需要建立合适的数学模型,并设计有效的算法来求解。
本文将介绍一些典型的优化问题的模型与算法。
二、线性规划问题线性规划问题是一种常见的优化问题,用于求解一组线性目标函数和线性约束条件的最优解。
常用的算法包括单纯形法、分支定界法等。
模型:设有n个变量,其中n≥1,要求找到一组变量x的值,使得目标函数的值最大(或最小),同时满足一系列线性不等式约束条件。
算法:根据目标函数和约束条件,构建线性规划问题的数学模型;采用合适的算法(如单纯形法)求解该模型,得到最优解。
三、整数规划问题整数规划问题是一种特殊的优化问题,要求变量必须是整数。
常用的算法包括分支定界法、割平面法等。
模型:设有n个变量,其中n≥1,要求找到一组变量的整数值,使得目标函数的值最大(或最小),同时满足一系列不等式约束条件,且某些变量必须取整数值。
算法:根据目标函数和约束条件,构建整数规划问题的数学模型;采用分支定界法等算法,将整数规划问题分解为一系列子问题,并逐步求解,最终得到最优解。
四、非线性优化问题非线性优化问题是最常见的优化问题之一,要求目标函数和约束条件均为非线性形式。
常用的算法包括梯度下降法、牛顿法、共轭梯度法等。
模型:设有n个变量,其中n≥1,要求找到一组变量的值,使得目标函数的值最小(或最大),同时满足一系列非线性不等式约束条件。
算法:根据目标函数和约束条件,构建非线性优化问题的数学模型;采用梯度下降法、牛顿法等算法,逐步迭代优化目标函数,直到满足终止条件(如迭代次数或误差阈值)为止。
五、动态规划问题动态规划问题是一种特殊的优化问题,用于求解一系列决策过程中的最优解。
常用的算法包括记忆化搜索、最优子结构等。
模型:在给定的决策过程中,要求根据当前状态和可选动作选择最优动作,以最大化(或最小化)某一指标的值。
最优化问题数学模型

• 进入该区域的飞机在到达区域边缘时,与区域内 飞机的距离应在60km以上;
根据当年竞赛题目给出的数据,可以验证 新进入的飞机与区域内的飞机的距离超过 60公里。
• 最多需考虑六架飞机;
cij xij 表示该队员的成 目标函数:当队员i入选泳姿j时, 绩,否则 cij xij 0 。于是接力队的成绩可表示为
f cij xij .
j 1 i 1
4
5
约束条件:根据接力队要求, xij 满足约束条件
a. 每人最多只能入选4种泳姿之一,即
x
j 1
4
ij
1.
b. 每种泳姿必须有1人而且只能有一人入选,即
分析,对实际问题进行合理的假设、简化,首先考虑用
线性规划模型,若线性近似误差较大时,则考虑用非线 性规划.
例题讲解
例1 1995年全国数学建模A题:飞行管理问题 在约1万米的高空的某边长为160km的正方 形区域内,经常有若干架飞机作水平飞行,区 域内每架飞机的位置和速度向量均由计算机记 录其数据,以便进行飞行管理。当一架欲进入 该区域的飞机到达区域边缘时,计算机记录其 数据后,要立即计算并判断是否会发生碰撞。 若会发生碰撞,则应计算如何调整各架飞机 (包括新进入的飞机)飞行的方向角,以避免 碰撞,且使飞机的调整的幅度尽量小,
目标:求函数极值或最值,求取得极值时变量的取值。
x
1.线性规划
问题:某工厂在计划期内要安排生产I、II两种产品,已 知生产单位产品所需的设备台时及A、B两种原材料的消 耗,如下表所示
I 设备 1 II 2 8台时
最优化问题的数学模型一般可以用约束集X和目标函数f进行表示.集合X

n n
) (UP)
.
在后面的章节中, 我们将研究 X 是
n
的子集的优化问题, 其中 X 可由等式和 f 是一个连续可微的函数, 并且是二阶连续可微的, f 的 一阶和二阶导数在最优解的特征, 即充分必要条件中发挥了重要作用, 这是 1.1 节的主要 内容. 一阶和二阶导数对于计算近似最优解也是非常重要的,1.2 节~ 1.8 节将讨论这方 面的若干算法和理论.1.9 节将前几节的方法运用到了求解含有离散时间动态系统的最优 控制问题中. 虽然本章主要研究的是无约束优化问题, 但是本章的内容的很多思想也是全 书其余内容的重要基础.
况. 即 x 是 f 在 X 上的一个局部最小点值,如果 x ∈ X 并且存在 ε > 0,对于所有满 足 x − x∗ < ε 的 x ∈ X ,都有 f (x∗ ) 小值点的定义可以类似地给出. 局部和全局的 最大值点 的定义也是类似的,即如果 x∗ 是 −f 的无约束局部 (全局) 最小值点,那么 x∗ 是 f 的无约束局部 (全局) 最大值点. 最优性的必要条件 如果目标函数可微, 那么就可利用梯度和泰勒展开去比较某个向量的函数值及其邻域 内的向量函数值的大小关系. 特别地, 我们考虑在给定向量 x∗ 上给予一个微小扰动 ∆x, 从而利用一阶近似得到目标函数的变化量为
最优化问题的数学模型一般可以用 约束集X 和 目标函数f 进行表示. 集合 X 包含 所有可用的决策 x,函数 f (x) 将 X 的元素映射到实数集上,表示决策 x 带来的成本损 失. 我们试图寻找一个最优的决策,即 x∗ ∈ X ,并且满足
f (x∗ ) f (x), ∀ x ∈ X.
本书假定 x 是一个 n 维向量,即 x 是一个由实数构成的 n 元数组 (x1 , · · · , xn ),因此约 束集 X 是 n 维欧氏空间
数学建模最优化模型
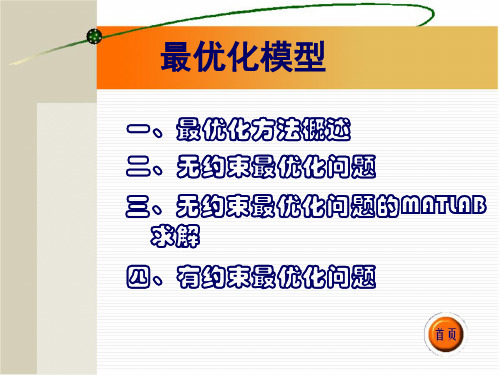
或[x,fval]= fminsearch(...) (4)[x,fval,exitflag]= fminunc(...);
或[x,fval,exitflag]= fminsearch (5)[x,fval,exitflag,output]= fminunc(...);
41m外点法sutm内点法障碍罚函数法1罚函数法2近似规划法罚函数法罚函数法基本思想是通过构造罚函数把约束问题转化为一系列无约束最优化问题进而用无约束最优化方法去求解这类方法称为序列无约束最小化方法简称为sumt法其一为sumt外点法其二为sumt内点法其中txm称为罚函数m称为罚因子带m的项称为罚项这里的罚函数只对不满足约束条件的点实行惩罚
曲线不一定通过那m个测量点,而要产生“偏差”.
将测量点沿垂线方向到曲线的距离的
y
平方和作为这种“偏差”的度量.即
2
x
S
m i 1
yi
a1
1 a3
a2 ln 1 exp
xi a4 a5
显然偏差S越小,曲线就拟合得越好,说明参数值就选择得越好,从而 我们的问题就转化为5维无约束最优化问题。即:
一下是否达到了最优。 (比如基金人投资)
• 在各种科学问题、工程问题、生产管理、社会 经济问题中,人们总是希望在有限的资源条件 下,用尽可能小的代价,获得最大的收获。
(比如保险)
数学家对最优化问题的研究已经有很多年的 历史。
以前解决最优化问题的数学方法只限于古典 求导方法和变分法(求无约束极值问题),拉格 朗日(Lagrange)乘数法解决等式约束下的条件 极值问题。
最优化问题数学模型

最优化问题数学模型在我们的日常生活和各种实际应用中,最优化问题无处不在。
从生产线上的资源分配,到物流运输中的路径规划,从金融投资中的资产配置,到工程设计中的参数选择,都需要找到最优的解决方案,以实现效率最高、成本最低、效益最大等目标。
而数学模型就是帮助我们解决这些最优化问题的有力工具。
那么,什么是最优化问题数学模型呢?简单来说,它是将实际问题转化为数学语言和表达式的一种方式,通过建立数学关系式,来描述问题中的各种约束条件和目标函数,然后运用数学方法和算法求解,找到最优的决策变量取值。
举个简单的例子,假设一家工厂要生产两种产品 A 和 B,生产 A 产品每件需要消耗 2 个单位的原材料和 3 个小时的工时,生产 B 产品每件需要消耗 3 个单位的原材料和 2 个小时的工时。
工厂共有 100 个单位的原材料和 80 个小时的工时可用,每件 A 产品的利润是 5 元,每件 B 产品的利润是 4 元。
那么,如何安排生产才能使工厂的总利润最大呢?为了建立这个问题的数学模型,我们首先定义决策变量:设生产 A 产品的数量为 x 件,生产 B 产品的数量为 y 件。
然后,我们确定目标函数,即要最大化的总利润:Z = 5x + 4y 。
接下来,考虑约束条件。
原材料的限制可以表示为:2x +3y ≤ 100 ;工时的限制可以表示为:3x +2y ≤ 80 ;还有非负约束:x ≥ 0 ,y ≥ 0 。
这样,我们就建立了一个简单的最优化问题数学模型。
通过求解这个模型,就可以得到最优的生产方案,即 x 和 y 的取值,使得总利润Z 最大。
最优化问题数学模型的类型多种多样,常见的有线性规划、非线性规划、整数规划、动态规划等。
线性规划是最简单也是应用最广泛的一种模型。
它的目标函数和约束条件都是线性的,就像我们上面的例子。
线性规划问题可以通过单纯形法等有效的算法在较短的时间内求解。
非线性规划则是目标函数或约束条件中至少有一个是非线性的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为凸集.
1,
0 证明: x , y 为超球中的任意两点, 设
则有:
x 1 y
r ???
x 1 y
r r r 1
即点 x 1 y 属于超球
所以超球为凸集.
注: 常见的凸集:空集,整个欧氏空间 超平面: H
T
aR
n
和实数
,
使得: T x a
a y , x D ,
xR a x
n T
即存在超平面 H y 与凸集 D .
严格分离点
注: 点与闭凸集的分离定理。
y.
D
定理
(点与凸集的分离定理)
是非空凸集,x D, 则存在 非零向量 a R n 使成立
DR
n
目标函数
R ( i 1, 2 , , p )
1
• 根据实际问题的不同要求,最优化模型有不同的形式, 但经过适当的变换都可以转换成上述一般形式.
最优化问题的分类
最优化问题
根据约束条件 分类
m in f ( x ), x R .
n
无约束最优化问题 约束最优化问题 等式约束最优化问题 不等式约束最优化问题 混合约束优化问题
设
a xa x
T T
x D . ( D代 表 D 的 闭 包 )
_ _
定理
(两个凸集的分离定理)
n
x
x
设 D1 , D2 是
且 R 的两个非空凸集, D1 D2 ,
则存在超平面分离 D1 和 D2 , 即存在非零向量 n a R 使得 aT x aT y , x D , y D . 1 2
f(x)
f ( x (1 ) y )
f(y)
x
y
例: 设 f x x 1 上是严格凸函数. 证明: 设
x, y R,
2
,
试证明 f x 在 ,
且x
y , 0,1 都有:
f x y f x f y 1 1
m in f ( x ), s.t. c i ( x ) 0, i 1, , m
m in f ( x ), s.t. c i ( x ) 0, i 1, , m
最优化问题的分类
最优化问题
连续最优化:决策变量取值连续
根据决策变 量的取值 光滑最优化:函数连续可微 线性规划 非线性最优化 非光滑最优化:有一个非光滑 离散最优化:决策变量取值离散
也是 D 上的凸函数.
n
f i ( x )( i 1, ..., m ) 是凸集 D R n (3) 设
f ( x ) m ax 1 i m f i ( x )
上的凸函数,
f i ( x )( i 1, ..., m )
m i i i 1
则 f (x)
是凸集 D R 上的凸函数, f ( x ) 也是 D 上的凸函数,其中 0. i
n
凸集的性质
(1) 有限个凸集的交集为凸集. (2) 设 (3) 设
D 是凸集,
是一实数, 则 是凸集. 的和(差)集
D y y x , x D
D1 , D2是凸集, 则 D1 , D2
D1 D2 y y x z , x D1 , z D2 是凸集.
f 都有: x 1 y f x 1 f y
则称函数 f x 为凸集 定义 严格凸函数
D 上的凸函数.
x y , , (0,1)
注:将上述定义中的不等式反向,可以得到 凹函数的定义.
f ( x ) (1 ) f ( y )
例:二次函数 f ( x) G是正定矩阵. 证明:
f (x) 1 2
1 2
x Gx b x 是Rn上的严格凸函数当且仅当
T T
x Gx b x
T T
严格凸
x , y R , x y , 0 1,
n
都 有 f ( x (1 ) y ) f ( x ) (1 ) f ( y )
T证明: 设Fra bibliotekx, y R , [0,1], 则
n
f x 1 y c x 1 y
T
c x 1 c y f x 1 f y
T T
所以 c T x 是凸函数. 类似可以证明 c T x 是凹函数.
R
n
x R a1 x1 a2 x2 an xn b
n
H 开半空间: x R n
H 闭半空间: 0 x R
n
a1 x1 a2 x2 an xn b ( H )
a1 x1 a2 x2 an xn b ( H 0 )
凸函数的判定定理
闭包:D的闭包是所有包含D的闭凸集的交.
投影定理 设
DR
n
是非空闭凸集, y R
x D,
n
但 到点
y D,
则: 使得集合
inf
(1) 存在唯一的点
y
D
的距离最小, x y 即:
xD
x y , x D.
(2)
是点
y
到集合 D的最短距离点的
T
充要条件为:
x x x y 0
T
d bi 0, i 1, , l ',
T
d a0 0
T
无解当且仅当存在实数 i ( i 使得
l
1, , l ) 和 非 负 实 数 i ( i 1, , l ')
l'
a0
a b .
i i i i i 1 i 1
凸函数
定义 设函数 f x 定义在凸集 D R n 上, 若对任意的 x, y D , 及任意的 0,1
a21 x1 a22 x2 a2 n xn b2 am1 x1 am 2 x2 amn xn bm
D { x R | A x b , x 0}
n
是多面集吗?
yes
D { x R | A x b , x 0}
n
{ x R | A x b , x 0}
定义 可行域是凸集,目标函数是凸函数的最优 化问题称为凸规划问题 定理 设
x 是凸规划问题的一个局部最优解,则
凸规划
(1) 局部最优解
x
也是全局最优解.
(2) 如果目标函数是严格凸的,则 x 是唯一的全局最优解.
F {x | ci ( x) 0, i 1, 2,..., m}.
n
若对于任意两点
1,
及实数 0
都有:
x 1 y D 则称集合 D 为凸集.
换句话说,如果任意两点 x , y D , 则连接x与y的直线段上的所有点都在D内。
定义: 设
n xi R , i 1,2, , k , 实数 i 0 ,
i 1,
(1) (2)
m
A y b,y 0,
T
其中
xR , yR
n
.
Farkas引理在最优化理论研究中起重要作用
Farkas引理的另一种形式 设l. l’是两个非负整数,a0,ai (i=1,…,l)和bi (i=1,…,l’)
是Rn中的向量,则线性方程组和不等式组
d a i 0, i 1, , l ,
整数规划,资源配 置,邮路问题生产 安排等
最优化问题
无约束最优化问题
线性搜索
约束最优化问题
单纯形法
线性规划
对偶单纯形法
最速下降法,牛顿法, 拟牛顿法,共轭方向法
( k 1)
d
二次规划 有效约束集法 可行方向法 二次罚函数 最小二乘法
x
x
(k )
dk
定义 设集合
x, y D,
DR ,
由有限个闭半空间的交组成的集合
D { x | p i x i , i 1, ..., m } ,
T
叫多面集,其中 p i 是非零向量, i 是数。 多面集是一个闭凸集。
D { x R | A x b , x 0} 是多面集吗? yes
n
a11 x1 a12 x2 a1n xn b1
最优化问题的数学模型
• 一般形式
决策变量
m in f ( x ) s.t. c i ( x ) 0, i 1, 2, , m , 约束 (1) c i ( x ) 0, i m 1, , p , 函数 其中 x x1 , x 2 , , x n T R n , f : R n R 1 , c i : R n 为连续函数,通常还要求连续可微.
注: 和集和并集有很大的区别,凸集的并集 未必是凸集,而凸集的和集是凸集.
定义 设 D1 , D2 R n 为两非空凸集,若存在 非零向量 a R n 和实数 , 使得:
D1 H D2 H
xR a x ,
n T n T
则称超平面 H x R a
n
R x
2 2
0??
2
x 1 y 1 x 1 1 y 1
1 x y
