向量加法的运算律
2020年高中数学新教材同步必修第二册 第6章 6.2.1 向量的加法运算

6.2平面向量的运算6.2.1向量的加法运算学习目标1.理解并掌握向量加法的概念.2.掌握向量加法的三角形法则和平行四边形法则,并能熟练地运用这两个法则作两个向量的加法运算.3.了解向量加法的交换律和结合律,并能作图解释向量加法运算律的合理性.知识点一向量加法的定义及其运算法则1.向量加法的定义求两个向量和的运算,叫做向量的加法.2.向量求和的法则向量和的方法叫做向量加法的平行四边形法则位移的合成可以看作向量加法的三角形法则的物理模型,力的合成可以看作向量加法的平行四边形法则的物理模型.思考 |a +b |与|a |,|b |有什么关系?答案 (1)当向量a 与b 不共线时,a +b 的方向与a ,b 不同,且|a +b |<|a |+|b |.(2)当a 与b 同向时,a +b ,a ,b 同向,且|a +b |=|a |+|b |.(3)当a 与b 反向时,若|a |>|b |,则a +b 的方向与a 相同,且|a +b |=|a |-|b |;若|a |<|b |,则a +b 的方向与b 相同,且|a +b |=|b |-|a |. 知识点二 向量加法的运算律 向量加法的运算律交换律 a +b =b +a 结合律(a +b )+c =a +(b +c )1.0+a =a +0=a .( √ )2.AB →+BC →=AC →.( √ ) 3.AB →+BA →=0.( √ ) 4.AB →+BC →>AC →.( × ) 5.|AB →|+|BC →|=|AC →|.( × )一、向量加法法则例1(1)如图①所示,求作向量a+b.(2)如图②所示,求作向量a+b+c.→=a,然后作向量AB→=b,则向量OB→=a+b.如图③所示. 解(1)首先作向量OA(2)方法一(三角形法则)如图④所示,首先在平面内任取一点O,作向量OA→=a,再作向量AB→=b,则得向量OB→=a+b,然后作向量BC→=c,则向量OC→=(a+b)+c=a+b+c即为所求.方法二(平行四边形法则)如图⑤所示,首先在平面内任取一点O,作向量OA→=a,OB→=b,OC→=c,以OA,OB为邻边作▱OADB,连接OD,则OD→=OA→+OB→=a+b.再以OD,OC为邻边作▱ODEC,连接OE,则OE→=OD→+OC→=a+b+c即为所求.反思感悟向量加法的平行四边形法则和三角形法则的区别和联系跟踪训练1如图所示,O为正六边形ABCDEF的中心,化简下列向量.(1)OA →+OC →=________;(2)BC →+FE →=________;(3)OA →+FE →=________. 答案 (1)OB → (2)AD →(3)0解析 (1)因为四边形OABC 是以OA ,OC 为邻边的平行四边形,OB 是其对角线,故OA →+OC →=OB →.(2)因为BC →=FE →,故BC →+FE →与BC →方向相同,长度为BC →的长度的2倍,故BC →+FE →=AD →. (3)因为OD →=FE →,故OA →+FE →=OA →+OD →=0. 二、向量加法运算律的应用 例2 化简:(1)BC →+AB →;(2)DB →+CD →+BC →;(3)AB →+DF →+CD →+BC →+F A →. 解 (1)BC →+AB →=AB →+BC →=AC →. (2)DB →+CD →+BC →=BC →+CD →+DB → =(BC →+CD →)+DB →=BD →+DB →=0. (3)AB →+DF →+CD →+BC →+F A → =AB →+BC →+CD →+DF →+F A → =AC →+CD →+DF →+F A → =AD →+DF →+F A →=AF →+F A →=0.反思感悟 向量加法运算律的意义和应用原则(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.(2)应用原则:通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.跟踪训练2 已知正方形ABCD 的边长等于1,则|AB →+AD →+BC →+DC →|=________. 答案 2 2解析 |AB →+AD →+BC →+DC →|=|AB →+BC →+AD →+DC →|=|AC →+AC →|=2|AC →|=2 2. 三、向量加法的实际应用例3 河水自西向东流动的速度为10 km/h ,小船自南岸沿正北方向航行,小船在静水中的速度为10 3 km/h ,求小船的实际航行速度.解 设a ,b 分别表示水流的速度和小船在静水中的速度,过平面内一点O 作OA →=a ,OB →=b ,以OA →,OB →为邻边作矩形OACB ,连接OC →,如图,则OC →=a +b ,并且OC →即为小船的实际航行速度.∴|OC →|=|a +b |2=|a |2+|b |2=20(km/h),tan ∠AOC =10310=3,∴∠AOC =60°,∴小船的实际航行速度为20 km/h ,沿北偏东30°的方向航行. 反思感悟 应用向量解决实际问题的基本步骤(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.(3)还原:根据向量的运算结果,结合向量共线、相等等概念回答原问题.跟踪训练3 如图,用两根绳子把重10 N 的物体W 吊在水平杆子AB 上,∠ACW =150°,∠BCW =120°,求A 和B 处所受力的大小.(绳子的重量忽略不计)解 如图所示,设CE →,CF →分别表示A ,B 所受的力,10 N 的重力用CG →表示,则CE →+CF →=CG →.由题意可得∠ECG =180°-150°=30°,∠FCG =180°-120°=60°. ∴|CE →|=|CG →|cos 30° =10×32=53(N), |CF →|=|CG →|cos 60° =10×12=5(N).∴A 处所受的力为5 3 N ,B 处所受的力为5 N.1.化简CB →+AD →+BA →等于( ) A.DB → B.CA → C.CD → D.DC → 答案 C解析 根据平面向量的加法运算,得CB →+AD →+BA →=(CB →+BA →)+AD →=CA →+AD →=CD →. 2.下列等式不正确的是( ) ①a +(b +c )=(a +c )+b ; ②AB →+BA →=0; ③AC →=DC →+AB →+BD →. A.②③ B.② C.① D.③ 答案 B解析 ②错误,AB →+BA →=0,①③正确. 3.在四边形ABCD 中,AC →=AB →+AD →,则( ) A.四边形ABCD 一定是矩形 B.四边形ABCD 一定是菱形 C.四边形ABCD 一定是正方形 D.四边形ABCD 一定是平行四边形 答案 D解析 由AC →=AB →+AD →知,A ,B ,C ,D 构成的四边形一定是平行四边形.4.如图,四边形ABCD 是梯形,AD ∥BC ,对角线AC 与BD 相交于点O ,则OA →+BC →+AB →+DO →等于( )A.CD →B.DC →C.DA →D.DO → 答案 B→+BC→+AB→+DO→=DO→+OA→+AB→+BC→=DA→+AB→+BC→=DB→+BC→=DC→.解析OA5.已知向量a表示“向东航行3 km”,b表示“向南航行3 km”,则a+b表示_________. 答案向东南航行3 2 km解析根据题意由于向量a表示“向东航行3 km”,向量b表示“向南航行3 km”,那么可知a+b表示向东南航行3 2 km.1.知识清单:(1)向量加法的三角形法则.(2)向量加法的平行四边形法则.(3)向量加法的运算律.2.方法归纳:数形结合.3.常见误区:向量加法的三角形法则要注意向量首尾相接,平行四边形法则要注意把向量移到共同起点.1.化简AE →+EB →+BC →等于( ) A.AB → B.BA → C.0 D.AC → 答案 D解析 AE →+EB →+BC →=AB →+BC →=AC →.2.如图,在正六边形ABCDEF 中,BA →+CD →+EF →等于( )A.0B.BE →C.AD →D.CF →答案 D解析 BA →+CD →+EF →=DE →+CD →+EF →=CE →+EF →=CF →. 3.若正方形ABCD 的边长为1,则|AB →+AD →|等于( )A.1B. 2C.3D.2 2答案 B解析 在正方形ABCD 中,AB =1,可知AC =2, 所以|AB →+AD →|=|AC →|=AC = 2.4.已知四边形ABCD 为菱形,则下列等式中成立的是( ) A.AB →+BC →=CA → B.AB →+AC →=BC →C.AC →+BA →=AD →D.AC →+AD →=DC →答案 C5.(多选)下列说法错误的有( )A.如果非零向量a 与b 的方向相同或相反,那么a +b 的方向必与a 或b 的方向相同B.在△ABC 中,必有AB →+BC →+CA →=0C.若AB →+BC →+CA →=0,则A ,B ,C 一定为一个三角形的三个顶点 D.若a ,b 均为非零向量,则|a +b |=|a |+|b | 答案 ACD解析 A 错,若a +b =0,则a +b 的方向是任意的;B 正确;C 错,当A ,B ,C 三点共线时,也满足AB →+BC →+CA →=0;D 错,|a +b |≤|a |+|b |. 6.已知AB →=a ,BC →=b ,CD →=c ,DE →=d ,AE →=e ,则a +b +c +d =________. 答案 e解析 a +b +c +d =AB →+BC →+CD →+DE →=AE →=e .7.在菱形ABCD 中,∠BAD =60°,|AB →|=1,则|BC →+CD →|=________. 答案 1解析 如图,由题意知△ABD 为等边三角形,所以|BC →+CD →|=|BD →|=|AB →|=1.8.如图,在平行四边形ABCD 中,O 是AC 和BD 的交点.(1)AB →+AD →+CD →=________; (2)AC →+BA →+DA →=________. 答案 (1)AD →(2)09.如图,已知在▱ABCD 中,O 是两条对角线的交点,E 是CD 的一个三等分点(靠近D 点),求作:(1)AO →+AC →;(2)DE →+BA →.解 (1)延长AC ,在延长线上截取CF =AO ,则向量AF →即为所求.(2)在AB 上取点G ,使AG =13AB ,则向量BG →即为所求.10.在静水中船的速度为20 m /min ,水流的速度为10 m/min ,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向. 解 作出图形,如图所示.设船速v 船与岸的方向成α角, 由图可知v 水+v 船=v 实际,结合已知条件,四边形ABCD 为平行四边形, 在Rt △ACD 中,|CD →|=|AB →|=|v 水|=10 m/min , |AD →|=|v 船|=20 m/min , ∴cos α=|CD →||AD →|=1020=12,∴α=60°,从而船行进的方向与水流方向成120°角. ∴船是沿与水流方向成120°角的方向行进.11.在矩形ABCD 中,|AB →|=4,|BC →|=2,则向量AB →+AD →+AC →的长度为( ) A.2 5 B.4 5 C.12 D.6 答案 B解析 因为AB →+AD →=AC →,所以AB →+AD →+AC →的长度为AC →的模的2倍. 又|AC →|=42+22=25,所以向量AB →+AD →+AC →的长度为4 5.12.若在△ABC 中,AB =AC =1,|AB →+AC →|=2,则△ABC 的形状是( ) A.正三角形 B.锐角三角形 C.斜三角形 D.等腰直角三角形答案 D解析 以AB ,AC 为邻边作平行四边形ABDC ,∵AB =AC =1,AD =2,∴∠ABD 为直角,该四边形为正方形,∴∠BAC =90°,△ABC 为等腰直角三角形. 13.已知点G 是△ABC 的重心,则GA →+GB →+GC →=______. 答案 0解析 如图所示,连接AG 并延长交BC 于点E ,点E 为BC 的中点,延长AE 到点D ,使GE =ED ,则GB →+GC →=GD →,GD →+GA →=0,∴GA →+GB →+GC →=0.14.如图所示,已知电线AO 与天花板的夹角为60°,电线AO 所受拉力|F 1|=24 N ,绳BO 与墙壁垂直,所受拉力|F 2|=12 N.则F 1和F 2的合力为________ N.答案 12 3解析 如图,根据向量加法的平行四边形法则,得到合力F =F 1+F 2=OC →.在△OCA 中,|OA →|=24, |AC →|=12,∠OAC =60°, ∴∠OCA =90°,∴|OC →|=12 3.∴F 1与F 2的合力大小为12 3 N ,方向为与F 2成90°角,竖直向上.15.如图所示,P ,Q 是△ABC 的边BC 上两点,且BP =QC .求证:AB →+AC →=AP →+AQ →.证明 AB →=AP →+PB →,AC →=AQ →+QC →,∴AB →+AC →=AP →+PB →+AQ →+QC →.∵PB →与QC →大小相等,方向相反,∴PB →+QC →=0,故AB →+AC →=AP →+AQ →+0=AP →+AQ →.16.如图,已知D ,E ,F 分别为△ABC 的三边BC ,AC ,AB 的中点,求证:AD →+BE →+CF →=0.证明 由题意知,AD →=AC →+CD →,BE →=BC →+CE →,CF →=CB →+BF →.由平面几何知识可知,EF→=CD→,BF→=F A→,所以AD→+BE→+CF→=(AC→+CD→)+(BC→+CE→)+(CB→+BF→) =(AC→+CD→+CE→+BF→)+(BC→+CB→)=(AE→+EC→+CD→+CE→+BF→)+0=AE→+CD→+BF→=AE→+EF→+F A→=0.。
向量的加法运算及其几何意义

向量加法的性质
结合律
向量加法满足结合律,即(a+b)+c=a+(b+c), 表明向量的加法不依赖于其组合的顺序。
交换律
向量加法满足交换律,即a+b=b+a,表明向量加法 的结果与元素的组合顺序无关。
分配律
向量加法不满足分配律,即a×(b+c)不等于 a×b+a×c。
02
向量加法的几何意义
向量加法的平行四边形法则
总结词
向量加法的平行四边形法则是向量的基本加法规则之一,它 表示将两个向量首尾相接,并连接它们的起点和终点,所形 成的平行四边形的对角线向量即为这两个向量的和。
详细描述
根据平行四边形法则,向量加法满足交换律和结合律,即不 论向量的顺序如何,也不论如何分组,向量加法的结果都相 同。
向量加法的三角形法则
分配律
总结词
向量加法的分配律是指向量加法满足分配性 ,即向量加法可以分配到括号内的各个向量 上。
详细描述
分配律是向量加法的另一个重要运算律。根 据分配律,对于任意两个向量$vec{a}$和任
意标量$k$,有$k(vec{a} + vec{b}) = kvec{a} + kvec{b}$。这意味着标量可以与括
总结词
向量加法的三角形法则是向量的另一种加法规则,它表示将一个向量的起点平 移到另一个向量的终点,所形成的向量即为这两个向量的和。
详细描述
三角形法则在几何中常用于表示力的合成或速度的合成等物理现象。通过三角 形法则,可以直观地理解向量加法的几何意义,并用于解决实际问题。
向量加法的向量场意义
总结词
向量加法的向量场意义是指向量加法可以看作是向量场中点的运动变化。在向量场中,任意两点之间 的连线可以表示为向量,而这个向量的加法运算则反映了这两点之间的相对运动关系。
向量运算律

向量运算律向量是一种有方向和大小的几何对象,广泛用于数学、物理和工程等领域。
向量运算律是向量代数中的基本概念,也是进行向量运算的基础。
本文将详细介绍向量的运算律,包括交换律、结合律、分配律、加法单位元、减法单位元、数乘单位元、数乘结合律、加法逆元、数量积、平行四边形法则、三角形法则、反向量、向量的模和向量夹角。
1.交换律交换律是指对任意两个向量a和b,有a+b=b+a。
这个定律表明,向量的加法运算满足交换性质,即不依赖于其运算顺序。
2.结合律结合律是指对任意三个向量a、b和c,有(a+b)+c=a+(b+c)。
这个定律表明,向量的加法运算满足结合性质,即不依赖于其运算顺序。
3.分配律分配律是指对任意实数r和任意两个向量a和b,有(r+a)+b=r+a+b=(r+b)+a。
这个定律表明,实数与向量的加法运算满足分配性质,即实数可以分配到向量的两边。
4.加法单位元加法单位元是指对任意向量a,有u+a=a+u=a,其中u是加法单位元。
这个概念表明,加法单位元是一个与任意向量相加都保持不变的向量。
5.减法单位元减法单位元是指对任意向量a,有v-a=-a+v=a,其中v是减法单位元。
这个概念表明,减法单位元是一个与任意向量相减都保持不变的向量。
6.数乘单位元数乘单位元是指对任意实数r和任意向量a,有ra=ar=r。
这个概念表明,实数与向量的数乘运算满足数乘单位性质,即实数可以分配到向量的两边并保持不变。
7.数乘结合律数乘结合律是指对任意实数r、s和任意向量a,有(rs)a=r(sa)=s(ra)。
这个定律表明,实数的乘积可以分配到向量的两边,并且不依赖于其运算顺序。
8.加法逆元加法逆元是指对任意向量a,有-a+b=b-a。
这个概念表明,加法逆元是一个与任意向量相加都等于另一个向量的向量。
9.数量积数量积是指对任意两个向量a和b,有a·b=|a||b|cosθ,其中θ是两个向量的夹角。
这个概念表明,两个向量的数量积等于它们的模长乘积与它们夹角的余弦值之积。
【课件】向量的加法运算课件高一下学期数学人教A版(2019)必修第二册

E
C
B
c
b
D
a+b
O
乙
法二:平行四边形法则
a
A
首先在平面内任取一点O,作向量=a,=b,=c,
以OA,OB为邻边作▱OADB,连接OD,则=+=a+b.
再以OD,OC为邻边作▱ODEC,连接OE,则= + =a+b+c即为所求.
多维探究
变式1 在本例(1)条件下,求+.
1 2 +2 3 +3 4 +…+−1
= 1
[例1]
(1)如图,在△ABC中,D,E分别是AB,AC上的点,F
为线段DE延长线上一点,DE∥BC,AB∥CF,连接CD,那么
(在横线上只填一个向量):
①+=________;
+=+=
②+=________;
(3)向量加法的运算律有哪两条?
(4)|a+b|,|a|+|b|,|a|-|b|三者之间的大小有何关系?
课前小测
1.下列各式不一定成立的是( D )
A.a+b=b+a
B.0+a=a
C.+=
D.|a+b|=|a|+|b|
2. + +等于(
A.
C)
B.
C.
D.
(1) + ;
+=
(2) + ;
= = =
+ =+ =
本课小结
1.三角形法则和平行四边形法则都是求向量和的基本方法,两个法则是
统一的,当两个向量首尾相连时,常选用三角形法则;当两个向量共起点
时,常选用平行四边形法则.
2.向量的加法满足交换律,因此在进行多个向量的加法运算时,可以按照
行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.
中职数学8.2.1向量的加法

2.向量加法的运算律:
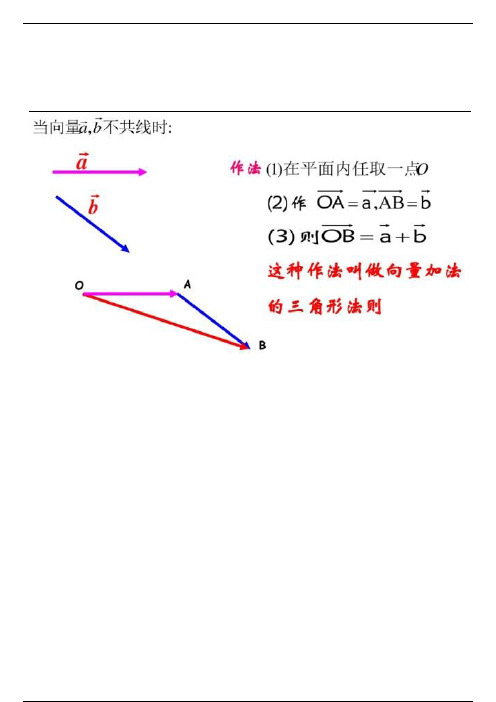
(1)证明:当 a , b 不平行时,
BC b ,则 作 AB a ,
ab ba (2)加法结合律 : (a b) c a (b c)
(1)加法交换律 :
D
a
ab
C
AC a b. 再作AD b ,连结 DC,
则四边形 ABCD 是平行四边形,
3.向量加法的平行四边形法则 :
AC AB BC a b
教材P52,练习 第 1 ,2题.
1km B 北
OA a,
AB b,
O
ab
b
OB OA AB a b,
| OB | 32 32 3 2 (km),
a
A
又 OA 与 OB的夹角是45°,所以a b 表示向 东北走 3 2km.
1.向量加法的三角形法则 :
多个向量求和
D
d
C
c
O
B
b
a
A
OD a b c d
b
A
b
b
a
B
a
于是 DC a .
因此 AD DC b a AC, 即 a b b a.
3.向量加法的平行四边形法则 :
若点A,B,D不共线,
AD b, 设 AB a ,
D
a
a b
C
以 AB, AD 为邻边作平行
A
b
四边形ABCD,
a
b
B
则对角线上的向量 AC AB BC a b
如图,填空:
(1) AB BC AC ; (2) AC CD DO AO ; (3) AC CD DA 0 .
向量加法运算及其几何意义 课件

【核心素养培优区】 【易错案例】向量的加法在向量化简中的应用 【典例】如图,在正六边形ABCDEF中, BA CD EF=( B )
A.0 B.BE C.AD D.CF
【失误案例】BA CD EF (BA AF) EF BF EF BE.
【错解分析】分析解题过程,请找出错误之处. 提示:本题错误的原因是未能结合正六边形边的关系, 得到 EF CB, 在化简的过程中代入.
【点拨】 (1)对向量加法三角形法则的两点说明 ①适用范围:任意向量. ②注意事项:(ⅰ)两个向量一定首尾相连. (ⅱ)和向量的始点是第一个向量的始点,终点是第二个 向量的终点. (ⅲ)当多个向量相加时,可以使用三角形法则.
(2)对向量加法的平行四边形法则的三点说明 ①适用范围:任意两个非零向量,且不共线. ②注意事项:(ⅰ)两个非零向量一定要有相同的始点; (ⅱ)平行四边形中的一个对角线所对应的向量为和向 量.
【变式训练】(荆州高一检测)设正六边形
ABCDEF,AB m,AE n, 则AD =________. 【解析】如图,
ED AB所 m以, 答案:n+m
AD AE ED n m.
类型三 向量加法的实际应用 【典例】长江两岸之间没有大桥的地方,常常通过轮渡 进行运输。现有一艘船从长江南岸A点出发,以5km/h的 速度向垂直于对岸的方向行驶,同时江水的速度为向东 2km/h.
列结论中,正确的是 ( ) ①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|; ⑤|a+b|=|a|+|b|. A.①② B.①③ C.①③⑤ D.③④⑤
3.如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中 点,化简下列各式:
平面向量加减法口诀
向量的加法口诀: 首尾相连,首连尾,方向指向末向量。
以第一个向量的起点为起点,以第二个向量的终点为终点的向量是两向量的和向量。
二、向量的减法两向量做减法运算,图像如下图所示:向量的减法口诀: 首首相连,尾连尾,方向指向被减向量。
以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量。
向量的学习是高一数学必修四第二章的内容,要求同学们会向量的基本运算,其中就包括加法、减法、数乘。
要求大家能根据运算法则解决基本的向量运算,学会运用图像解决向量加减法,向量的数乘等问题。
向量的相关题目难度也不是很大,只要大家认真学习,认真做好笔记,认真做做题目,总结做题规律,那么当我们遇到类似题目时就会似曾相识,做起来也很顺手,再细心点的话,得满分也没有问题。
学习方法很多,重要的事找到适合自己的方法,当然适合自己方法就是最好的方法。
附一;三角形定则解决向量加减的方法将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点。
注:两个向量相减,则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。
平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣>1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的λ∣倍;当∣λ∣<1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律:(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.数乘向量的消去律:① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义:已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义:两个向量的数量积(内积、点积)是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉;若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示:a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a(交换律);(λa)·b=λ(a·b)(关于数乘法的结合律);(a+b)·c=a·c+b·c(分配律);向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即:由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义:两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b.若a、b不共线,则a×b的模是:∣a×b∣=|a|·|b|·sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质:∣a×b∣是以a和b为边的平行四边形面积.。
向量的加减法及数乘运算

o·
A 的三角形法则
B
AB BC AC
ab ba (a b) c a (b c)
1. 相反向量:
与 做 记作
a长aa度的相相等反,向方量向相反的向量,叫
规定:零向量的相反向量仍是零向量。
注:(1) a a
((32))如任即 那果意: 么,向:量aaa与, b它互a相为b,反相b向反a量向a的量a, a和,0是b零向0量. 。
a
b
D
b
由作向量差的方法,
知
DB
AB
AD
a
A b
a
C B
练习u.A如uBur图,ar ,平uAuDu行r 四br边,形你A能B用CD的、ar 两br来条表对示角线Mu相uuAr交、uM于uuBr点、uMMuuCur,和且uMuuD。ur
D
C
M
b
A
r a
B
另:(1) a b a b a b
(2)若b // a(a 0),则b a是否成立?
成立
向量共线定理:
rr r r
向量a(a 0)与b共线,当且仅当有唯一一个实数,
rr
使b a.
rr
r rr r
即a与b共线
b a (a 0)
思考:1)
r a
为什么要是非零向量?
r 2) b 可以是零向量吗?
总结:
证明三点共线的方法:
AB=λBC
uuur r r uuur r r
OB a 2b,OC a 3b. 你能判断A、B、C三点之
间的位置关系吗?为什么?
C
r
r
a
b
r 3b
B
r
2b
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A5 A2 A4 A3
F
弹簧所受的拉力的合力 ?
F1 F1
F
(二)向量加法的平行四边形法则
b 已知:如图非零向量 a ,
B
a+b
C
a
a
b
A
b
D
作法: 在平面内任取一点A,作 AB= a, AD =b,以AB , AD为邻边 作平行四边形,则 AC = a + b 。 这种求向量和的方法称为向量加法的平行四边形法则。
2.2.1向量的加法
南溪中学李辉
复习
1、向量的定义 既有大小又有方母表示;
3、零向量和单位向量 长度为 0 的向量;长度为单位1的向量 4、平行向量(共线向量) 方向相同或相反的非零向量叫做平行向量. 5、相等向量 长度相等且方向相同的向量
提出问题:
a
b
A AC = a + b B C
2、方向相反
a b
A
B
C
AC = a + b
问题探究
问题1:你能说出实数运算有哪些运算律吗? 问题2:定义了一种新运算,自然要研究其运 算律问题.请类比数的加法的运算律,思考向 量的加法是否也有运算律?有哪些运算律?
(1) 交换律:
ab ba
作法: 作平行四边形ABCD ,使AB a, AD b 则 BC b,DC a ,则: AC AB BC a b
AB +(BC + CD ) = AD
练习2:求下列向量的和
(1)AB+BC+CD+DE+EF+FG= AG (2)CD+BC+AB= AD
例1、轮船从A港沿东偏北30°方向行驶了 40 n mile(海里)到达B处,再由B处沿 正北方向行驶 40 n mile到达C处,求此时轮 船与A港的相对位置 C 解:如图, 北
AB BC
AC
由此得出什么结论?
A
AB BC AC
一、向量的加法定义: 求向量和的运算,叫做向量 的 加法。
(一)向量加法的三角形法则:
b 已知:如图非零向量 a, a
b
A
C
a+b
a
b
B
作法: 在平面内任取一点A, 作 AB = a ,BC = 则向量 AC 叫做
b
a与 b
的和,即
AC AD DC b a
D
a b
C
b a
A
b a
B
(2) 结合律:
b
A
B
a
c O
C
OC OB BC (a+b)+c=_____+____=____ AC a+(b+c)=OA+_____=___ OC
向量加法的运算律
交换律: a b b a 结合律:(a b) c a (b c) 想一想
F1
1、向量加法的定义
(1)三角形法则及其推广
首尾相接 (适用于任意向量的加法)
(2)平行四边形法则
起点相同 (适用于不共线向量的加法)
2、共线向量的加法 3、向量加法的运算律
|| a | | b ||| a b || a | | b |
练习: 3、4
a+b = AB
+ BC = AC。
这种求向量和的方法称为向量加法的三角形法则。
说明:
1、向量的和仍是一个向量 2、首尾相接,由头指尾 3、不仅适用任何两个向量,而且可以推广到任 意多个向量(如下面例题)
推广:
A1 由若干条有向线段首尾相接组成的封闭的折线, 则它们的和向量为
0
如:
A 1A 2 A 2A 3 A 3A 4 A 4A 5 A 5A 1 0
答:略
B )30° D
东
A
2 | AC | | AD |2 | DC |2 (20 3) 602 40 3
例2、两个力F1、F2同时作用在一个物 体上,其中F1= 40N,方向向东, F2=30N,方向向北,求它们的合力
解:如图,
B
F2 O
C
OA表示F1, OB表示F2,以OA、OB为 邻边作平行四边形OACB,则OC表 示合力F.在Rt OAC中
2、方向相反
a
b
A
B
C AC = a + b
由此可见
ab
=
ab
=
ab
综上: a b ≤
ab
≤
ab
练习1:如图:已知平行四边形ABCD,填空
(1) (2) (3)
AB + BC =
AB + AD =
AC AC AC
AD
A
D
C
BC + AB =
B
(4) ( AB + BC)+ CD = (5)
数能进行运算,向量是否也能进行运算 呢?类比数的加法,猜想向量的加法,应 怎样定义向量的加法?
我们来看以下几个问题
1.一人从A到B,再从B按原方向到C,则两次的位移之和AB BC 是
AC
A
B
C
2.飞机从A到B,再改变方向从B到C,则两次的位移的和 AB BC 是: C A B
AC
3.船的速度为 AB ,水流的速度为 ,则两个速度的和 BC B C 是:
向量加 法
(三)方法特征
1、向量加法的三角形法则:
(1)将向量平移使得它们首尾相连 (2)和向量即是第一个向量的首指向第二个向量的尾
2、向量加法的平行四边形法则:
(1)将向量平移到同一起点 (2)和向量即以它们作为邻边平行四边形的共起点的对角线
a b
向量加 法
二、共线向量的加法: 三角形法则 1、方向相同
设 AB、 BC分别表示轮船的两次位移, 则 AC表示轮船的合位移, AC AB BC 在ADB中,ADB 90,DAB 30
| AB | 40 | DB | 20, | AD | 20 3 | DC | 20 40 60 | AC | 2 | AD | CAD 60
A | OA | F1 40 N | AC || OB | F2 30 N F合 | OC | 50 N
| AC | F2 3 设F合与F1的夹角为 , 则tan = 0.75 37 | OA | F1 4 答 : 合力大小为50 N , 方向为东偏北37
1.零向量和任一向量 a 的和为什么? 2.a b , a b 和 a b 的大小关系如何 ?
ab
a0 0a a
≤
ab
≤
ab
何时取得等号?
b 已知:如图非零向量 a, a
b
A
C
a+b
a
AC = a + b
b
B
由此可见
ab
<
ab
<
ab
1、方向相同
a
b
A AC = a + b B C
