上海大学数据库选修上机练习5
上海大学数据库选修上机练习5

《数据库系统与应用》上机习题*************************************************************************************************第五部分、SQL高级应用要求掌握:熟练掌握T-SQL语言,了解异常处理的相关语句,学会用游标方式对数据库进行操作。
一、做书上第十章的例题二、写出书上198页练习题10中第7、8、9、11题的结果,并上机验证。
完成第12、13、14题7、数据库中没有stud表8、9、重复插入ID的值11、12、编写一个程序,采用游标的方式输出所有课程的平均分use schoolgoset nocount ondeclare @s_cj int,@s_name char(8)declare c_cursor cursor forselect score、课程号,AVG(score、分数)from scoregroup by score、课程号order by score、课程号open c_cursorfetch next from c_cursor into @s_cj,@s_namewhile@@FETCH_STATUS=0beginprint CAST(@s_cj as char(8))+@s_namefetch next from c_cursor into @s_cj,@s_nameendclose c_cursordeallocate c_cursorgo13、编写一个程序,使用游标的方式输出所有学号,课程号,成绩等级use schooldeclare @s_xh int,@c_name char(8),@s_cj float,@dj char(1) declare c_cursor cursor forselect student、学号,score、课程号,score、分数from score,studentwhere score、学号=student、学号group by student、学号,score、课程号,score、分数order by student、学号beginset @dj=CASEwhen @s_cj>=90 then'A'when @s_cj>=80 then'B'when @s_cj>=70 then'C'when @s_cj>=60 then'D'else'E'endopen cfetch next from c_cursor into @s_xh,@c_name,@s_cjprint'学号课程号等级'print'---------------------------'while@@FETCH_STATUS=0beginprint @s_xh+' '+@c_name+' '+@s_cjfetch next from c_cursor into @s_xh,@c_name,@s_cjendclose c_cursordeallocate c_cursor14、编写一个程序,输出各班各课程的平均分use schoolgoset nocount ondeclare @s_cj int,@s_name char(8),@s_bj char(8)declare c_cursor cursor forselect student、班级,score、课程号,AVG(score、分数)from score,studentgroup by score、课程号,student、班级order by score、课程号,student、班级open c_cursorfetch next from c_cursor into @s_cj,@s_name,@s_bjprint'学号班级成绩'print'-------------------'while@@FETCH_STATUS=0beginprint CAST(@s_cj as char(8))+@s_name+@s_bjfetch next from c_cursor into @s_cj,@s_name,@s_bjendclose c_cursordeallocate c_cursorgo三、完成书上394页上机实验题3(1)对各出版社的图书比例情况进行分析,即图书比例高于50%为“很高”,图书比例高于30%为“'较高”,图书比例高于10%为“一般”。
数据库上机实验题目和答案

试用SQL的查询语句表达下列查询:1.检索王丽同学所学课程的课程号和课程名。
select Cno ,Cname from c where Cno in(select cno from sc where sno in (select sno from s where sname='王丽' ))2.检索年龄大于23岁的男学生的学号和姓名。
select sno,sname from swhere sex='男' and age>233.检索‘c01’课程中一门课程的女学生姓名select sname from swhere sex='女' and sno in(select sno from sc where cno='c01')4.检索s01同学不学的课程的课程号。
select cno from cwhere cno not in (select cno from sc where sno ='s01')5.检索至少选修两门课程的学生学号。
select sc.sno from s,scwhere s.sno=sc.snogroup by sc.snohaving count(o)>=26.每个学生选修的课程门数。
解法一:select so.sno sno,ount,s.snamefrom(select sc.sno sno,count(sc.sno) ccountfrom sc,swhere s.sno=sc.snogroup by sc.sno ) so,swhere s.sno=so.sno解法二:select sc.sno sno,s.sname,count(sc.sno) ccountfrom sc,swhere s.sno=sc.snogroup by sc.sno,sname7.求选修C4课程的学生的平均分。
数据库系统基础教程第五章答案
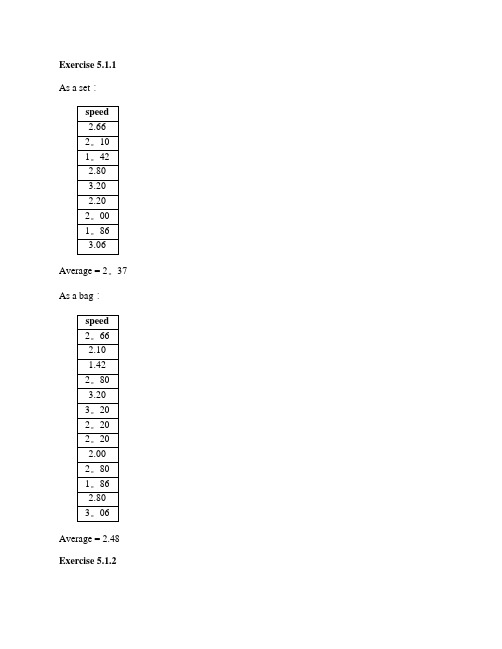
Exercise 5.1.1 As a set:Average = 2。
37 As a bag:Average = 2.48 Exercise 5.1.2Average = 218 As a bag:Average = 215 Exercise 5.1.3a As a set:18As a bag:bore1516141615151418Exercise 5。
1。
3bπbore(Ships Classes)Exercise 5.1.4aFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively, the union of bags R and S will have tuple t appear n + m times。
The further union of bag T with the tuple t appearing o times will have tuple t appear n + m + o times in the final result.On the right—hand side:Given bags S and T where a tuple t appears m and o times respectively, the union ofbags R and S will have tuple t appear m + o times. The further union of bag R with thetuple t appearing n times will have tuple t appear m + o + n times in the final result.For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set。
《数据库技术与应用》上机大作业

《数据库技术与应⽤》上机⼤作业数据库⼤作业1、查询XS表中的所有列。
use XSCJselect *from XS;2、查询XS表中计算机专业同学的学号、姓名和总学分。
use XSCJselect 学号,姓名,总学分from XSwhere 专业名= '计算机';3、查询XS表中计算机专业同学的学号、姓名和总学分,结果中各列的标题分别指定为number、name和mark。
use XSCJselect 学号as number , 姓名as name , 总学分as markfrom XSwhere 专业名= '计算机';4、查询XS表中通信⼯程专业总学分⼤于等于42的学⽣情况。
use XSCJselect *from XSwhere 专业名= '通信⼯程' and 总学分>= 42;5、查询XS表中姓“王”且单名的学⽣情况。
use XSCJselect *from XSwhere 姓名like '王_';6、查询XS表中不在1979年出⽣的学⽣情况。
use XSCJselect *from XSwhere 出⽣时间not between '1979-01-01' and '1979-12-31';7、查询选修了课程号为101的学⽣情况。
use XSCJselect *from XSwhere 学号in ( select 学号from XS_KCwhere 课程号= '101');8、查询未选修离散数学的学⽣情况。
use XSCJselect *from XSwhere 学号not in ( select 学号from XS_KC where 课程号in ( select 课程号from KC where 课程名= '离散数学'));9、查询⽐所有计算机系的学⽣年龄都⼤的学⽣情况。
上海大学数据库上机作业上机练习5作业

上大学数据库上机作业《数据库系统与应用》上机习题*************************************************************************************************第五部分、SQL高级应用一、做书上第十章的例题二、利用上次上机的学生_课程数据库1. 求选修了高等数学的学生学号和姓名。
USE学生课程SELECT学生.学号,姓名,选课.课程号FROM学生,选课,课程WHERE学生.学号=选课.学号AND课程.课程号=选课.课程号AND课程名='高等数学'2.求C1课程的成绩高于张三的学生学号和成绩。
USE学生课程SELECT x.学号,x.成绩FROM选课x,选课yWHERE x.课程号='C1'AND x.成绩>y.成绩AND y.学号='S4'AND y.课程号='C1'ORDER BY x.学号DESC第二种:USE学生课程SELECT学号,成绩FROM选课WHERE课程号='C1'AND成绩>(SELECT成绩FROM选课,学生WHERE课程号='C1'AND姓名='张三'AND选课.学号=学生.学号)3.求其他系中比自动化学院某一学生年龄小的学生。
USE学生课程SELECT学号,姓名,年龄,单位FROM学生WHERE年龄<(SELECT MAX(年龄)FROM学生WHERE单位='自动化学院')AND单位!='自动化学院'ORDER BY学号DESC4.求其他系中比自动化学院学生年龄都小的学生。
USE学生课程SELECT学号,姓名,年龄,单位FROM学生WHERE年龄<(SELECT MIN(年龄)FROM学生WHERE单位='自动化学院')AND单位!='自动化学院'ORDER BY学号DESC5.求选修了C2课程的学生的姓名。
上海大学数据库上机作业上机练习4作业(最新整理)

上大学数据库上机作业《数据库系统与应用》上机习题*************************************************************************************************第四部分、SQL查询━━嵌套和组合统计查询要求掌握:利用SQL查询语言表达嵌套查询语句以及数据查询中的统计计算和组合操作。
1、做书上第九章余下的例题,并完成书上练习题9中第11、12、13、14题11.if exists(SELECT*FROM sys.objects WHERE name=student)12.二、利用图书_读者数据库1. 求机械工业出版社出版的各类图书的平均价。
USE图书读者SELECT类别,AVG(定价)AS平均价FROM图书WHERE出版社='机械工业出版社'GROUP BY类别2. 求各类图书的最高价、最低价、图书的数量。
USE图书读者SELECT类别,MAX(定价)AS最高价,MIN(定价)AS最低价,COUNT(*)AS数量FROM图书GROUP BY类别3. 查找图书类别,要求类别中最高的图书定价不低于全部按类别分组的图书平均定价的1.5倍。
USE图书读者SELECT类别FROM图书WHERE定价=ALL(SELECT MAX(定价)FROM图书WHERE定价<=ALL(SELECT AVG(定价)*1.5FROM图书))4.计算机类和机械工业出版社出版的图书。
USE图书读者SELECT*FROM图书WHERE出版社='机械工业出版社'AND类别='计算机'5.查询所有读者借阅过的书,要求按读者姓名、书名来排序。
USE图书读者SELECT读者.编号,借阅.读者编号,姓名,书名FROM图书,读者,借阅WHERE读者.编号=借阅.读者编号AND借阅.书号=图书.书号ORDER BY姓名6. 查询所有在2008.11.15日以后被借阅过的图书名及借阅者。
(完整版)数据库系统基础教程第五章答案
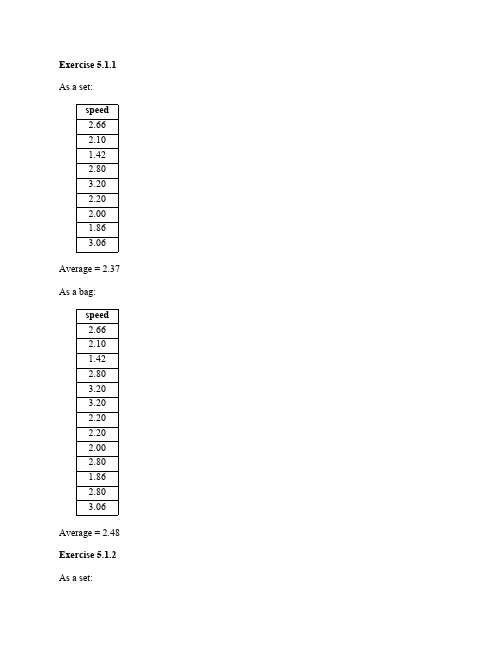
Exercise 5.1.1 As a set:speed2.662.101.422.803.202.202.001.863.06 Average = 2.37 As a bag:speed2.662.101.422.803.203.202.202.202.002.801.862.803.06 Average = 2.48 Exercise 5.1.2 As a set:hd25080320200300160 Average = 218 As a bag:hd2502508025025032020025025030016016080 Average = 215 Exercise 5.1.3a As a set:bore15161418As a bag:bore1516141615151418Exercise 5.1.3bπbore(Ships Classes)Exercise 5.1.4aFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively, the union of bags R and S will have tuple t appear n + m times. The further union of bag T with the tuple t appearing o times will have tuple t appear n + m + o times in the final result.On the right-hand side:Given bags S and T where a tuple t appears m and o times respectively, the union of bags R and S will have tuple t appear m + o times. The further union of bag R with the tuple t appearing n times will have tuple t appear m + o + n times in the final result.For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set. The tuple t only appears in the result if all the sets have the tuple t. Otherwise, the tuple t will not appear in the result. Since we cannot have duplicates, the result only has at most one copy of the tuple t.Exercise 5.1.4bFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively, the intersectionof bags R and S will have tuple t appear min( n, m ) times. The further intersection of bag T with the tuple t appearing o times will produce tuple t min( o, min( n, m ) ) times in the final result.On the right-hand side:Given bags S and T where a tuple t appears m and o times respectively, the intersection of bags R and S will have tuple t appear min( m, o ) times. The further intersection of bag R with the tuple t appearing n times will produce tuple t min( n, min( m, o ) ) times in thefinal result.The intersection of bags R,S and T will yield a result where tuple t appears min( n,m,o ) times. For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set. The tuple t only appears in the result if all the sets have the tuple t. Otherwise, the tuple t will not appear in the result.Exercise 5.1.4cFor bags:On the left-hand side:Given that tuple r in R, which appears m times, can successfully join with tuple s in S,which appears n times, we expect the result to contain mn copies. Also given that tuple tin T, which appears o times, can successfully join with the joined tuples of r and s, weexpect the final result to have mno copies.On the right-hand side:Given that tuple s in S, which appears n times, can successfully join with tuple t in T,which appears o times, we expect the result to contain no copies. Also given that tuple rin R, which appears m times, can successfully join with the joined tuples of s and t, weexpect the final result to have nom copies.The order in which we perform the natural join does not matter for bags.For sets:This is a similar case when dealing with bags except the joined tuples can only appear at most once in each result. If there are tuples r,s,t in relations R,S,T that can successfully join, then the result will contain a tuple with the schema of their joined attributes.Exercise 5.1.4dFor bags:Suppose a tuple t occurs n and m times in bags R and S respectively. In the union of these two bags R ⋃ S, tuple t would appear n + m times. Likewise, in the union of these two bags S ⋃ R, tuple t would appear m + n times. Both sides of the relation yield the same result.For sets:A tuple t can only appear at most one time. Tuple t might appear each in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t appears in both sets R and S will the union R ⋃ S have the tuple t. The same reasoning holds when we take the union S ⋃ R.Therefore the commutative law for union holds.Exercise 5.1.4eFor bags:Suppose a tuple t occurs n and m times in bags R and S respectively. In the intersection of these two bags R ∩ S, tuple t would appear min( n,m ) times. Likewise in the intersection of these two bags S ∩ R, tuple t would appear min( m,n ) times. Both sides of the relation yield the same result.For sets:A tuple t can only appear at most one time. Tuple t might appear each in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t appears in at least one of the sets R and S will the intersection R ∩ S have the tuple t. The same reasoning holds when we take the intersection S ∩R.Therefore the commutative law for intersection holds.Exercise 5.1.4fFor bags:Suppose a tuple t occurs n times in bag R and tuple u occurs m times in bag S. Suppose also that the two tuples t,u can successfully join. Then in the natural join of these two bags R S, the joined tuple would appear nm times. Likewise in the natural join of these two bags S R, the joined tuple would appear mn times. Both sides of the relation yield the same result.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuples u,v might appear respectively in sets R and S one or zero times. The combinations of number of occurrences for tuples u,v in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple u exists in Rand tuple v exists in S will the natural join R S have the joined tuple. The same reasoning holds when we take the natural join S R.Therefore the commutative law for natural join holds.Exercise 5.1.4gFor bags:Suppose tuple t appears m times in R and n times in S. If we take the union of R and S first, we will get a relation where tuple t appears m + n times. Taking the projection of a list of attributes L will yield a resulting relation where the projected attributes from tuple t appear m + n times. If we take the projection of the attributes in list L first, then the projected attributes from tuple t would appear m times from R and n times from S. The union of these resulting relations would have the projected attributes of tuple t appear m + n times.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuple t might appear in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t exists in R or S (or both R and S) will the projected attributes of tuple t appear in the result.Therefore the law holds.Exercise 5.1.4hFor bags:Suppose tuple t appears u times in R, v times in S and w times in T. On the left hand side, the intersection of S and T would produce a result where tuple t would appear min(v , w) times. With the addition of the union of R, the overall result would have u + min(v , w) copies of tuple t. On the right hand side, we would get a result of min(u + v, u + w) copies of tuple t. The expressions on both the left and right sides are equivalent.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuple t might appear in sets R,S and T one or zero times. The combinations of number of occurrences for tuple t in R, S and T respectively are (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0) and (1,1,1). Only when tuple t appears in R or in both S and T will the result have tuple t.Therefore the distributive law of union over intersection holds.Exercise 5.1.4iSuppose that in relation R, u tuples satisfy condition C and v tuples satisfy condition D. Suppose also that w tuples satisfy both conditions C and D where w≤ min(v , w). Then the left hand side will return those w tuples. On the right hand side, σC(R) produces u tuples and σD(R) produces v tuples. However, we know the intersection will produce the same w tuples in the result.When considering bags and sets, the only difference is bags allow duplicate tuples while sets only allow one copy of the tuple. The example above applies to both cases.Therefore the law holds.Exercise 5.1.5aFor sets, an arbitrary tuple t appears on the left hand side if it appears in both R,S and not in T. The same is true for the right hand side.As an example for bags, suppose that tuple t appears one time each in both R,T and two times in S. The result of the left hand side would have zero copies of tuple t while the right hand side would have one copy of tuple t.Therefore the law holds for sets but not for bags.Exercise 5.1.5bFor sets, an arbitrary tuple t appears on the left hand side if it appears in R and either S or T. This is equivalent to saying tuple t only appears when it is in at least R and S or in R and T. The equivalence is exactly the right side’s expression.As an example for bags, suppose that tuple t appears one time in R and two times each in S and T. Then the left hand side would have one copy of tuple t in the result while the right hand side would have two copies of tuple t.Therefore the law holds for sets but not for bags.Exercise 5.1.5cFor sets, an arbitrary tuple t appears on the left hand side if it satisfies condition C, condition D or both condition C and D. On the right hand side, σC(R) selects those tuples that satisfy condition C while σD(R) selects those tuples that satisfy condition D. However, the union operator will eliminate duplicate tuples, namely those tuples that satisfy both condition C and D. Thus we are ensured that both sides are equivalent.As an example for bags, we only need to look at the union operator. If there are indeed tuples that satisfy both conditions C and D, then the right hand side will contain duplicate copies of those tuples. The left hand side, however, will only have one copy for each tuple of the original set of tuples.A+B A2B210154910164167916 Exercise 5.2.1bB+1C-1103334431143 Exercise 5.2.1cA B0101232434 Exercise 5.2.1dB C010224253434A B01232434 Exercise 5.2.1fB C0124253402 Exercise 5.2.1gA SUM(B)022734 Exercise 5.2.1hB AVG(C)0 1.52 4.534 Exercise 5.2.1iA23Exercise 5.2.1jA MAX(C)24 Exercise 5.2.1kA B C23423401┴01┴24┴34┴Exercise 5.2.1lA B C234234┴01┴24┴25┴02 Exercise 5.2.1mA B C23423401┴01┴24┴34┴┴01┴24┴25┴02Exercise 5.2.1nA R.B S.B C0124012501340134012401250134013423┴┴24┴┴34┴┴┴┴01┴┴02Exercise 5.2.2aApplying the δ operator on a relation with no duplicates will yield the same relation. Thus δ is idempotent.Exercise 5.2.2bThe result of πL is a relation over the list of attributes L. Performing the projection again will return the same relation because the relation only contains the list of attributes L. Thus πL is idempotent.Exercise 5.2.2cThe result of σC is a relation where condition C is satisfied by every tuple. Performing the selection again will return the same relation because the relation only contains tuples that satisfy the condition C. Thus σC is idempotent.Exercise 5.2.2dThe result of γL is a relation whose schema consists of the grouping attributes and the aggregated attributes. If we perform the same grouping operation, there is no guarantee that the expression would make sense. The grouping attributes will still appear in the new result. However, the aggregated attributes may or may not appear correctly. If the aggregated attribute is given a different name than the original attribute, then performing γL would not make sense because it contains an aggregation for an attribute name that does not exist. In this case, the resultingrelation would, according to the definition, only contain the grouping attributes. Thus, γL is not idempotent.Exercise 5.2.2eThe result of τ is a sorted list of tuples based on some attributes L. If L is not the entire schema of relation R, then there are attributes that are not sorted on. If in relation R there are two tuples that agree in all attributes L and disagree in some of the remaining attributes not in L, then it is arbitrary as to which order these two tuples appear in the result. Thus, performing the operation τmultiple times can yield a different relation where these two tuples are swapped. Thus, τ is not idempotent.Exercise 5.2.3If we only consider sets, then it is possible. We can take πA(R) and do a product with itself. From this product, we take the tuples where the two columns are equal to each other.If we consider bags as well, then it is not possible. Take the case where we have the two tuples (1,0) and (1,0). We wish to produce a relation that contains tuples (1,1) and (1,1). If we use the classical operations of relational algebra, we can either get a result where there are no tuples or four copies of the tuple (1,1). It is not possible to get the desired relation because no operation can distinguish between the original tuples and the duplicated tuples. Thus it is not possible to get the relation with the two tuples (1,1) and (1,1).Exercise 5.3.1a)Answer(model) ← PC(model,speed,_,_,_) AND speed ≥ 3.00b)Answer(maker) ← Laptop(model,_,_,hd,_,_) AND Product(maker,model,_) AND hd ≥100c)Answer(model,price) ← PC(model,_,_,_,price) AND Product(maker,model,_) ANDmaker=’B’Answer(model,price) ← Laptop(model,_,_,_,_,price) AND Product(maker,model,_)AND maker=’B’Answer(model,price) ← Printer(model,_,_,price) AND Product(maker,model,_) ANDmaker=’B’d)Answer(model) ← Printer(model,color,type,_) AND color=’true’ AND type=’laser’e)PCMaker(maker) ← Product(maker,_,type) AND type=’pc’LaptopMaker(maker) ← Product(maker,_,type) AND type=’laptop’Answer(maker) ← LaptopMaker(maker) AND NOT PCMaker(maker)f)Answer(hd) ← PC(model1,_,_,hd,_) AND PC(model2,_,_,hd,_) AND model1 <>model2g)Answer(model1,model2) ← PC(model1,speed, ram,_,_) ANDPC(model2,_speed,ram,_,_) AND model1 < model2h)FastComputer(model) ← PC(model,speed,_,_,_) AND speed ≥ 2.80FastComputer(model) ← Laptop(model,speed,_,_,_,_) AND speed ≥ 2.80Answer(maker) ← Product(maker,model1,_) AND Product(maker,model2,_) ANDFastComputer(model1) AND FastComputer(model2) AND model1 <> model2i)Computers(model,speed) ← PC(model,speed,_,_,_)Computers(model,speed) ← Laptop(model,speed,_,_,_,_)SlowComputers(model) ← Computers(model,speed) AND Computers(model1,speed1) AND speed < speed1FastestComputers(model) ← Computers(model,_) AND NOT SlowComputers(model)Answer(maker) ← FastestComputers(model) AND Product(maker,model,_) j)PCs(maker,speed) ← PC(model,speed,_,_,_) AND Product(maker,model,_) Answer(maker) ← PCs(maker,speed) AND PCs(maker,speed1) ANDPCs(maker,speed2) AND speed <> speed1 AND speed <> speed2 AND speed1 <>speed2k)PCs(maker,model) ← Product(maker,model,type) AND type=’pc’Answer(maker) ← PCs(maker,model) AND PCs(maker,model1) ANDPCs(maker,model2) AND PCs(maker,model3) AND model <> model1 AND model <> model2 AND model1 <> model2 AND (model3 = model OR model3 = model1 ORmodel3 = model2)Exercise 5.3.2a)Answer(class,country) ← Classes(class,_,country,_,bore,_) AND bore ≥ 16b)Answer(name) ← Ships(name,_,launched) AND launched < 1921c)Answer(ship) ← Outcomes(ship,battle,result) AND battle=’Denmark Strait’ AND result= ‘sunk’d)Answer(name) ← Classes(class,_,_,_,_,displacement) AND Ships(name,class,launched)AND displacement > 35000 AND launched > 1921e)Answer(name,displacement,numGuns) ← Classes(class,_,_,numGuns,_,displacement)AND Ships(name,class,_) AND Outcomes (ship,battle,_) AND battle=’Guadalcanal’AND ship=namef)Answer(name) ← Ships(name,_,_)Answer(name) ← Outcomes(name,_,_) AND NOT Answer(name)g)MoreThanOne(class) ← Ships(name,class,_) AND Ships(name1,class,_) AND name <>name1Answer(class) ← Classes(class,_,_,_,_,_) AND NOT MoreThanOne(class)h)Battleship(country) ← Classes(_,type,country,_,_,_) AND type=’bb’Battlecruiser(country) ← Classes(_,type,country,_,_,_) AND type=’bc’Answer(country) ← Battleship(country) AND Battlecruiser(country)i)Results(ship,result,date) ← Battles(name,date) AND Outcomes(ship,battle,result) ANDbattle=nameAnswer(ship) ← Results(ship,result,date) AND Results(ship,_,date1) ANDresult=’damaged’ AND date < date1Exercise 5.3.3Answer(x,y) ← R(x,y) AND z = zExercise 5.4.1aAnswer(a,b,c) ← R(a,b,c)Answer(a,b,c) ← S(a,b,c)Exercise 5.4.1bAnswer(a,b,c) ← R(a,b,c) AND S(a,b,c)Exercise 5.4.1cAnswer(a,b,c) ← R(a,b,c) AND NOT S(a,b,c)Exercise 5.4.1dUnion(a,b,c) ← R(a,b,c)Union(a,b,c) ← S(a,b,c)Answer(a,b,c) ← Union(a,b,c) AND NOT T(a,b,c)Exercise 5.4.1eJ(a,b,c) ← R(a,b,c) AND NOT S(a,b,c)K(a,b,c) ← R(,a,b,c) AND NOT T(a,b,c)Answer(a,b,c) ← J(a,b,c) AND K(a,b,c)Exercise 5.4.1fAnswer(a,b) ← R(a,b,_)Exercise 5.4.1gJ(a,b) ← R(a,b,_)K(a,b) ← S(_,a,b)Answer(a,b) ← J(a,b) AND K(a,b)Exercise 5.4.2aAnswer(x,y,z) ← R(x,y,z) AND x = yExercise 5.4.2bAnswer(x,y,z) ← R(x,y,z) AND x < y AND y < z Exercise 5.4.2cAnswer(x,y,z) ← R(x,y,z) AND x < yAnswer(x,y,z) ← R(x,y,z) AND y < zExercise 5.4.2dChange:NOT(x < y OR x > y)To:x ≥ y AND x ≤ yThe above simplifies to x = yAnswer(x,y,z) ← R(x,y,z) AND x = yExercise 5.4.2eChange:NOT((x < y OR x > y) AND y < z)NOT(x < y OR x > y) OR y ≥ z(x ≥ y AND x ≤ y) OR y ≥ zTo:x = y OR y ≥ zAnswer(x,y,z) ← R(x,y,z) AND x = yAnswer(x,y,z) ← R(x,y,z) AND y ≥ zExercise 5.4.2fChange:NOT((x < y OR x < z) AND y < z)NOT(x < y OR x < z) OR y ≥ z To:(x ≥ y AND x ≥ z) OR y ≥ zAnswer(x,y,z) ← R(x,y,z) AND x ≥ y AND x ≥ zAnswer(x,y,z) ← R(x,y,z) AND y ≥zExercise 5.4.3aAnswer(a,b,c,d) ← R(a,b,c) AND S(b,c,d)Exercise 5.4.3bAnswer(b,c,d,e) ← S(b,c,d) AND T(d,e)Exercise 5.4.3cAnswer(a,b,c,d,e) ← R(a,b,c) AND S(b,c,d) AND T(d,e)Exercise 5.4.4a)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = syb)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx < sy AND ry < szc)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx < syAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry < szd)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = sye)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = syAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry ≥ szf)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx ≥ sy AND rx ≥ szAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry ≥ szExercise 5.4.5aR1 := πx,y(Q R)Exercise 5.4.5bR1 := ρR1(x,z)(Q)R2 := ρR2(z,y)(Q)R3 := πx,y(R1 (R1.z = R2.z) R2)Exercise 5.4.5cR1 := πx,y(Q R)R2 := σx < y(R1)。
数据库上机习题及答案

数据库上机习题及答案 Revised by Liu Jing on January 12, 2021数据库及应用复习题一、设计题有一个[学生课程]数据库,数据库中包括三个表:学生表Student由学号(Sno)、姓名(Sname)、性别(Ssex)、年龄(Sage)、所在系(Sdept)五个属性组成,记为:Student(Sno,Sname,Ssex,Sage,Sdept) ,Sno 为关键字。
课程表Course由课程号(Cno)、课程名(Cname)、先修课号(Cpno)、学分(Ccredit)四个属性组成,记为:Course(Cno,Cname,Cpno,Ccredit) Cno为关键字。
成绩表SG由学号(Sno)、课程号(Cno)、成绩(Grade)三个属性组成,记为: SG(Sno,Cno,Grade) (SNO, CNO)为关键字。
用SQL语言实现下列功能:1.建立学生表Student,其中学号属性不能为空,并且其值是唯一的。
2.向Student表增加“入学时间(Scome)”列,其数据类型为日期型。
3.查询选修了3号课程的学生的学号及其成绩,查询结果按分数的降序排列。
4.查询学习1号课程的学生最高分数、平均成绩。
5.查询与“李洋”在同一个系学习的学生。
6.将计算机系全体学生的成绩置零。
7.删除学号为05019的学生记录。
8.删除计算机系所有学生的成绩记录。
1.CREATETABLE Student(Sno CHAR(5) NOT NULL UNIQUE,Sname CHAR(20),Ssex CHAR(2),Sage INT,Sdept CHAR(15))2.ALTER TABLE Student ADD Scome DATETIME 3.SELECT Sno, GradeFROM SGWHERE Cno='3'ORDER BY Grade DESC4.SELECT MAX(Grade), AVG(Grade)FROM SCWHERE Cno='1'5.SELECT Sno, Sname, SdeptFROM StudentWHERE Sdept IN(SELECT Sdept FROM StudentWHERE Sname='李洋')6. UPDATE SGSET Grade=0WHERE Sno in( SELECT Sno FROM StudentWHERE Sdept = '计算机系')7.DELETE FROM StudentWHERE Sno='05019'8. DELETE FROM SGWHERE Sno in( SELECT Sno FROM StudentWHERE Sdept = '计算机系')二、设计题现有关系数据库如下:数据库名:教师数据库教师表(编号 char(6),姓名,性别,民族,职称,身份证号)课程表(课号 char(6),名称)任课表(ID,教师编号,课号,课时数)用SQL语言实现下列功能的sql语句代码:1. 创建上述三表的建库、建表代码(14分);要求使用:主键(教师表.编号,课程表.课号)、外键(任课表.教师编号,任课表.课号)、默认(民族)、非空(民族,姓名)、唯一(身份证号)、检查(性别、课时数),自动编号(ID)2. 将下列课程信息添加到课程表的代码(6分)课号课程名称100001 SQL Server数据库100002 数据结构100003 VB程序设计修改课号为100003的课程名称:Visual Basic程序设计删除课号为100003的课程信息3. 写出创建[任课表视图](教师编号,姓名,课号,课程名称,课时数)的代码;(4分)4. 写出创建[某门课任课教师]内嵌表值函数以及检索的代码;(6分)检索:所有代'SQL Server数据库'这门课程的老师姓名;5. 写出创建[统计课时数]:输出最大课时数、最低课时数、平均课时的存储过程以及执行代码;(6分)6.写出创建:计算某教师代课总课时,并将值返回的存储过程以及执行代码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数据库系统与应用》上机习题*************************************************************************************************第五部分、SQL高级应用要求掌握:熟练掌握T-SQL语言,了解异常处理的相关语句,学会用游标方式对数据库进行操作。
一、做书上第十章的例题二、写出书上198页练习题10中第7、8、9、11题的结果,并上机验证。
完成第12、13、14题7、数据库中没有stud表8、9、重复插入ID的值11、12、编写一个程序,采用游标的方式输出所有课程的平均分use schoolgoset nocount ondeclare @s_cj int,@s_name char(8)declare c_cursor cursor forselect score、课程号,AVG(score、分数)from scoregroup by score、课程号order by score、课程号open c_cursorfetch next from c_cursor into @s_cj,@s_namewhile@@FETCH_STATUS=0beginprint CAST(@s_cj as char(8))+@s_namefetch next from c_cursor into @s_cj,@s_nameendclose c_cursordeallocate c_cursorgo13、编写一个程序,使用游标的方式输出所有学号,课程号,成绩等级use schooldeclare @s_xh int,@c_name char(8),@s_cj float,@dj char(1) declare c_cursor cursor forselect student、学号,score、课程号,score、分数from score,studentwhere score、学号=student、学号group by student、学号,score、课程号,score、分数order by student、学号beginset @dj=CASEwhen @s_cj>=90 then'A'when @s_cj>=80 then'B'when @s_cj>=70 then'C'when @s_cj>=60 then'D'else'E'endopen cfetch next from c_cursor into @s_xh,@c_name,@s_cjprint'学号课程号等级'print'---------------------------'while@@FETCH_STATUS=0beginprint @s_xh+' '+@c_name+' '+@s_cjfetch next from c_cursor into @s_xh,@c_name,@s_cjendclose c_cursordeallocate c_cursor14、编写一个程序,输出各班各课程的平均分use schoolgoset nocount ondeclare @s_cj int,@s_name char(8),@s_bj char(8)declare c_cursor cursor forselect student、班级,score、课程号,AVG(score、分数)from score,studentgroup by score、课程号,student、班级order by score、课程号,student、班级open c_cursorfetch next from c_cursor into @s_cj,@s_name,@s_bjprint'学号班级成绩'print'-------------------'while@@FETCH_STATUS=0beginprint CAST(@s_cj as char(8))+@s_name+@s_bjfetch next from c_cursor into @s_cj,@s_name,@s_bjendclose c_cursordeallocate c_cursorgo三、完成书上394页上机实验题3(1)对各出版社的图书比例情况进行分析,即图书比例高于50%为“很高”,图书比例高于30%为“'较高”,图书比例高于10%为“一般”。
并按图书比例递增排列。
USE LibraryDECLARE @num intSELECT @num=(SELECT COUNT(*)FROM book)--图书总数SELECT a、出版社AS'出版社',CASEWHEN a、rate>50、0 THEN'很高'WHEN a、rate>30、0 THEN'较高'WHEN a、rate>10、0 THEN'一般'ELSE'较低'END AS'图书比例情况'FROM (SELECT出版社AS'出版社',CAST(ROUND(COUNT(*)*100、0/@num,1)AS decimal(5,1))AS'rate'FROM bookGROUP BY出版社) aORDER BY a、rate(2)对各系学生借书比例情况进行分析,即借书比例高于50%为“很高”,借书比例高于30%为“较高”,借书比例高于10%为“一般”。
并按借书比例递减排列。
USE LibraryDECLARE @num intSELECT @num=(SELECT COUNT(*)FROM borrow)--借书总数SELECT a、系名AS'系名',CASEWHEN a、rate>50、0 THEN'很高'WHEN a、rate>30、0 THEN'较高'WHEN a、rate>10、0 THEN'一般'ELSE'较低'END AS'借书情况'FROM (SELECT depart、系名,CAST(ROUND(COUNT(*)*100、0/@num,1)AS decimal(5,1))AS'rate' FROM borrow,student,departWHERE borrow、学号=student、学号AND student、班号=depart、班号GROUP BY depart、系名) aORDER BY a、rate DESC(3)采用游标方式对图书价格进行评价。
USE LibraryGODECLARE b_cur CURSORFOR SELECT DISTINCT(图书名),定价FROM bookDECLARE @bn char(20),@dj decimal(4,1),@pr char(10)OPEN b_curFETCH NEXT FROM b_cur INTO @bn,@djWHILE@@FETCH_STATUS= 0BEGINSET @pr=CASEWHEN @dj>=50 THEN'价格太高'WHEN @dj>=30 THEN'价格偏高'WHEN @dj>=20 THEN'价格适中'WHEN @dj>=10 THEN'价格偏低'ELSE'价格太低了'ENDPRINT @bn+CAST(@dj AS char(5))+@prFETCH NEXT FROM b_cur INTO @bn,@djENDCLOSE b_curDEALLOCATE b_cur(4)GO采用游标方式统计每个出版社图书的借出率。
USE LibraryGODECLARE A CURSORFORSELECT a、出版社,CAST(csum*100、0/bsum AS decimal(4,1))As'rate'FROM (SELECT出版社,COUNT(*)AS'bsum'FROM bookGROUP BY出版社) a,(SELECT b、出版社,COUNT(bor、图书编号)AS'csum'FROM book b,borrow borWHERE b、图书编号=bor、图书编号GROUP BY b、出版社) bWHERE a、出版社=b、出版社DECLARE @name char(16),@num decimal(4,1)OPEN AFETCH NEXT FROM A INTO @name,@numWHILE@@FETCH_STATUS= 0BEGINPRINT'"'+RTRIM(@name)+'"图书借出率为'+RTRIM(CAST(@num AS char(5)))+'%'FETCH NEXT FROM A INTO @name,@numENDCLOSE ADEALLOCATE A GO。
