数字图像处理作业 直方图均衡
数字图像处理实验报告直方图均衡化

数字图像处理实验报告实验名称:直方图均衡化姓名:班级:学号:专业:电子信息工程(2+2)指导教师:陈华华实验日期:2012年5月24日直方图均衡化图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。
直方图均衡化是最常见的间接对比度增强方法。
直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。
直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。
直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。
缺点:1)变换后图像的灰度级减少,某些细节消失;2)某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。
这种方法通常用来增加许多图像的局部对比度,尤其是当图像的有用数据的对比度相当接近的时候。
通过这种方法,亮度可以更好地在直方图上分布。
这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
直方图均衡化的基本思想是把原始图的直方图变换为均匀分布的形式,这样就增加了象素灰度值的动态范围从而可达到增强图像整体对比度的效果。
设原始图像在(x,y)处的灰度为f,而改变后的图像为g,则对图像增强的方法可表述为将在(x,y)处的灰度f映射为g。
在灰度直方图均衡化处理中对图像的映射函数可定义为:g = EQ (f),这个映射函数EQ(f)必须满足两个条件(其中L为图像的灰度级数):(1)EQ(f)在0≤f≤L-1范围内是一个单值单增函数。
这是为了保证增强处理没有打乱原始图像的灰度排列次序,原图各灰度级在变换后仍保持从黑到白(或从白到黑)的排列。
(2)对于0≤f≤L-1有0≤g≤L-1,这个条件保证了变换前后灰度值动态范围的一致性。
数字图像处理第四章作业

第四章图像增强1.简述直方图均衡化处理的原理和目的。
拍摄一幅较暗的图像,用直方图均衡化方法处理,分析结果。
原理:直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
也就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。
把给定图像的直方图分布改变成“均匀”分布直方图分布目的:直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。
它通常用来增加许多图像的局部对比度,尤其是当图像的有用数据的对比度相当接近的时候。
通过直方图均衡化,亮度可以更好地在直方图上分布。
这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
Matlab程序如下:clc;RGB=imread('wxf.jpg'); %输入彩色图像,得到三维数组R=RGB(:,:,1); %分别取三维数组的一维,得到红绿蓝三个分量G=RGB(:,:,2); %为R G B。
B=RGB(:,:,3);figure(1)imshow(RGB); %绘制各分量的图像及其直方图title('原始真彩色图像');figure(2)subplot(3,2,1),imshow(R);title('真彩色图像的红色分量');subplot(3,2,2), imhist(R);title('真彩色图像的红色分量直方图');subplot(3,2,3),imshow(G);title('真彩色图像的绿色分量');subplot(3,2,4), imhist(G);title(' 的绿色分量直方图');subplot(3,2,5),imshow(B);title('真彩色图像的蓝色分量');subplot(3,2,6), imhist(B);title('真彩色图像的蓝色分量直方图');r=histeq(R); %对个分量直方图均衡化,得到个分量均衡化图像g=histeq(G);b=histeq(B);figure(3),subplot(3,2,1),imshow(r);title('红色分量均衡化后图像');subplot(3,2,2), imhist(r);title('红色分量均衡化后图像直方图');subplot(3,2,3),imshow(g);title('绿色分量均衡化后图像');subplot(3,2,4), imhist(g);title('绿色分量均衡化后图像直方图');subplot(3,2,5), imshow(b);title('蓝色分量均衡化后图像');subplot(3,2,6), imhist(b);title('蓝色分量均衡化后图像直方图');figure(4), %通过均衡化后的图像还原输出原图像newimg = cat(3,r,g,b); %imshow(newimg,[]);title('均衡化后分量图像还原输出原图');程序运行结果:原始真彩色图像均衡化后分量图像还原输出原图图1.1 原始图像与均衡化后还原输出图像对比通过matlab仿真,由图1.1比较均衡化后的还原图像与输入原始真彩色图像,输出图像轮廓更清晰,亮度明显增强。
python数字图像处理实现直方图与均衡化

python数字图像处理实现直⽅图与均衡化在图像处理中,直⽅图是⾮常重要,也是⾮常有⽤的⼀个处理要素。
在skimage库中对直⽅图的处理,是放在exposure这个模块中。
1、计算直⽅图函数:skimage.exposure.histogram(image,nbins=256)在numpy包中,也提供了⼀个计算直⽅图的函数histogram(),两者⼤同⼩义。
返回⼀个tuple(hist, bins_center), 前⼀个数组是直⽅图的统计量,后⼀个数组是每个bin的中间值import numpy as npfrom skimage import exposure,dataimage =data.camera()*1.0hist1=np.histogram(image, bins=2) #⽤numpy包计算直⽅图hist2=exposure.histogram(image, nbins=2) #⽤skimage计算直⽅图print(hist1)print(hist2)输出:(array([107432, 154712], dtype=int64), array([ 0. , 127.5, 255. ]))(array([107432, 154712], dtype=int64), array([ 63.75, 191.25]))分成两个bin,每个bin的统计量是⼀样的,但numpy返回的是每个bin的两端的范围值,⽽skimage返回的是每个bin的中间值2、绘制直⽅图绘图都可以调⽤matplotlib.pyplot库来进⾏,其中的hist函数可以直接绘制直⽅图。
调⽤⽅式:复制代码代码如下:n, bins, patches = plt.hist(arr, bins=10, normed=0, facecolor='black', edgecolor='black',alpha=1,histtype='bar')hist的参数⾮常多,但常⽤的就这六个,只有第⼀个是必须的,后⾯四个可选arr: 需要计算直⽅图的⼀维数组bins: 直⽅图的柱数,可选项,默认为10normed: 是否将得到的直⽅图向量归⼀化。
数字图像处理3-直方图均衡,直方图匹配,空间滤波相关等

Timg(原图) im_1(MATLAB均衡处理) im_2(ps均衡处理)原图的rgb直方图r通道直方图(原图)g通道直方图(原图)b通道直方图(原图)r通道直方图(im_1)g通道直方图(im_1)b通道直方图(im_1)r通道直方图(im_2)g通道直方图(im_2)b通道直方图(im_2)这里找到了一张对比度较低的图像timg,其原本的对比度很低。
之后分别用MATLAB和ps对其进行了直方图均衡,生成了im_1与im_2,可见其处理的效果是有区别的。
MATLAB处理的结果色彩更加艳丽但是相对于原图来说其每个区域的颜色和旁边的区域颜色差别会很巨大,就是使得边界更明显,同时对比度提高了很多。
而ps处理的结果可以看出新的直方图和原直方图相比产生了很多形状上的差别,可见ps的直方图均衡采用了更为复杂的算法。
同时图像对比度以及颜色艳丽的程度得到了提升,但是没有MATLAB处理的效果明显,保持了原图的色调以及部分颜色关系。
Ps中直方图均衡可以一键实现,因此在此不做重点描写,我们来看如何用MATLAB实现这种操作。
MATLAB代码如下:主程序:im=imread('timg.jpg');im_r=change(im(:,:,1));im_g=change(im(:,:,2));im_b=change(im(:,:,3));im1(:,:,1)=im_r;im1(:,:,2)=im_g;im1(:,:,3)=im_b;figure;imshow(im1);imwrite(im1,'im1.jpg');Change函数:function [n] = change(m)n=m;sum=0;for i=0:255for j=1:407for k=1:500if(m(j,k)==i)sum=sum+1;endendendchan=sum/(407*500);chan1=fix(chan*255+0.5);for j=1:407for k=1:500if(m(j,k)==i)n(j,k)=chan1;endendendend[x,xout] = hist(n(:), 0:255);figure;bar(xout, x); xlim([0 255]);MATLAB其实本身有实现直方图均衡效果的函数,这里为了理解算法自己做了这个函数。
数字图像处理 实验 直方图均衡化实现图像增强

XXXXXXXX大学(数字图形处理)实验报告实验名称直方图均衡化实现图像增强实验时间年月日专业姓名学号预习操作座位号教师签名总评一、实验目的:掌握直方图均衡化的原理。
掌握直方图均衡化实现图像增强的实现方法。
二、实验原理:直方图是统计像数统计图,如设一张灰度图或一个通道,值0~255。
直方图如果按。
255个区分的话。
统计出来的就是,值为。
0的有几个像数,值为1的有机个像数,这样的一张表。
那么均衡化的意思就是。
这样表要均衡。
不直不于。
0有上万个像数,1只有1 个。
正常,直方图本身可以用小于255个区。
比如10个,那么这样相对图中的点就有一个映射,这时值0-9统计落在第一个区,值为10-19落第二个区。
这样的结果就会出来,10个区,10个统计数区。
这时。
你均衡就是让10区的统计数据都不会差很多。
表现出来的就是一张图上的颜色分布相对均衡。
总的来说直方图均衡化是通过灰度变换将一幅图像转换为另一幅具有均衡直方图,即在每个灰度级上都具有相同的象素点数的过程。
三、实验内容:利用直方图均衡化实现图像增强。
在资源编辑器中,在主菜单下添加一名为“直方图均衡化”的菜单步骤如前面实验。
实验代码如下:if(m_DibHead->biBitCount!=8){MessageBox("当前版本仅支持256色位图的操作!","系统提示!",MB_ICONINFORMA TION|MB_OK);return;}zftjh(m_Image,m_DibHead->biWidth,m_DibHead->biHeight);Invalidate();其中函数zftjh的实现代码如下:zftjh(unsigned char *lpDib,long lWidth,long lHeight){unsigned char *lpsrc;long lresult(0);long i,j;unsigned char bMap[256];long lCount[256];for(i=0;i<256;i++)lCount[i]=0;for(i=0;i<lHeight;i++)for(j=0;j<lWidth;j++){lpsrc=lpDib+i*lWidth+j;lCount[*lpsrc]++;}for(i=0;i<256;i++){lresult=0;for(j=0;j<=i;j++)lresult+=lCount[j];bMap[i]=(lresult*255)/lHeight/lWidth;}for(i=0;i<lHeight;i++)for(j=0;j<lWidth;j++){lpsrc=lpDib+i*lWidth+j;*lpsrc=bMap[*lpsrc];}}原图为下图的左边部分,均值化以后的图为右边的部分:。
【数字图像处理】直方图的均衡与规定化
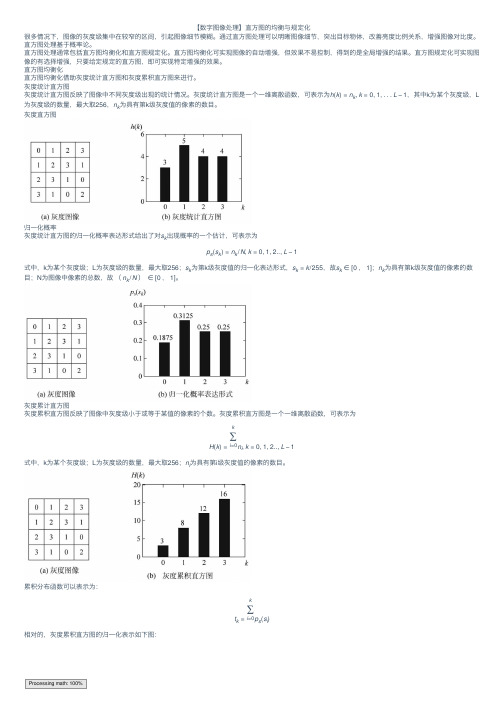
【数字图像处理】直⽅图的均衡与规定化很多情况下,图像的灰度级集中在较窄的区间,引起图像细节模糊。
通过直⽅图处理可以明晰图像细节,突出⽬标物体,改善亮度⽐例关系,增强图像对⽐度。
直⽅图处理基于概率论。
直⽅图处理通常包括直⽅图均衡化和直⽅图规定化。
直⽅图均衡化可实现图像的⾃动增强,但效果不易控制,得到的是全局增强的结果。
直⽅图规定化可实现图像的有选择增强,只要给定规定的直⽅图,即可实现特定增强的效果。
直⽅图均衡化直⽅图均衡化借助灰度统计直⽅图和灰度累积直⽅图来进⾏。
灰度统计直⽅图灰度统计直⽅图反映了图像中不同灰度级出现的统计情况。
灰度统计直⽅图是⼀个⼀维离散函数,可表⽰为h (k )=n k ,k =0,1,...L −1,其中k 为某个灰度级,L 为灰度级的数量,最⼤取256,n k 为具有第k 级灰度值的像素的数⽬。
灰度直⽅图归⼀化概率灰度统计直⽅图的归⼀化概率表达形式给出了对s k 出现概率的⼀个估计,可表⽰为p s (s k )=n k /N ,k =0,1,2..,L −1式中,k 为某个灰度级;L 为灰度级的数量,最⼤取256;s k 为第k 级灰度值的归⼀化表达形式,s k =k /255,故s k ∈[0,1];n k 为具有第k 级灰度值的像素的数⽬;N 为图像中像素的总数,故(n k /N )∈[0,1]。
灰度累计直⽅图灰度累积直⽅图反映了图像中灰度级⼩于或等于某值的像素的个数。
灰度累积直⽅图是⼀个⼀维离散函数,可表⽰为H (k )=k ∑i =0n i ,k =0,1,2..,L −1式中,k 为某个灰度级;L 为灰度级的数量,最⼤取256;n i 为具有第i 级灰度值的像素的数⽬。
累积分布函数可以表⽰为:t k =k ∑i =0p s (s i )相对的,灰度累积直⽅图的归⼀化表⽰如下图:Processing math: 100%原理步骤直⽅图均衡化主要⽤于增强动态范围偏⼩的图像的反差。
数字图像处理灰度化直方图均衡化灰度拉伸

数字图像处理与模式识别实验目的打开一幅图像,进行直方图均衡化。
并将其灰度线性变化,将灰度线性拉伸。
实验准备实验之前,收集数字图像处理编程的相关资料,查阅C或Java关于本实验图像处理的相关类库和编程核心。
经过C和Java相关资料编程的比较,Java将图像处理的类封装的较完整,运用起来比C灵活方便。
以下是相关类库和实现操作的方法:import java.awt.image.*;import javax.imageio.*; //相关的图像处理类库和方法封装在两个包中//Java读取图像的方法BufferedImage newImage = ImageIO.read(new File(filePath));int width = newImage.getWidth(); //获得图像的像素宽度int height = newImage.getHeight(); //获得图像像素的长度//获得图像的色彩模型RGB分量ColorModel colorModel = ColorModel.getRGBdefault();int r = colorModel.getRed(currPixArray[k]);int g = colorModel.getGreen(currPixArray[k]);int b = colorModel.getBlue(currPixArray[k]); //分别获得图像的rgb分量PixelGrabber p = new PixelGrabber(image, 0, 0, width, height, array, 0, width); //将image图像像素值读入一位矩阵实验步骤算法实现RGB图像转灰度图由于数字图像的直方图均衡化和灰度的线性拉伸都是基于灰度图的算法实现,本框架中增加了由彩色图转灰度图的功能。
简单讲述下算法思想:将存储图像的一维矩阵像素点彩色分量用ColorModel类中的getRed(),getGreen()和getBlue()方法读取,按照(r * 0.3 + g * 0.59 + b * 0.11)公式计算灰度值。
数字图像处理中的直方图均衡化使用注意事项

数字图像处理中的直方图均衡化使用注意事项直方图均衡化是一种通过分布调整来改善图像对比度的方法。
它通过重新分布图像的像素值以增强其视觉效果。
在数字图像处理中,直方图均衡化是一项常用的技术,但在使用过程中需要注意以下几个方面。
首先,直方图均衡化可能会导致图像细节丢失的问题。
因为直方图均衡化会根据像素值的分布进行调整,从而扩展像素值的范围,使得亮度范围更广。
但这也可能导致低对比度区域的细节消失,从而影响图像细节。
因此,在进行直方图均衡化时,应该密切关注图像的细节信息,尽量避免过度调整图像的对比度。
其次,直方图均衡化可能引起噪声的增加。
在直方图均衡化的过程中,图像的亮度分布被调整,可能会增加图像的噪声。
这是因为噪声通常与图像的低亮度区域有关,当低亮度区域被调整时,噪声也可能被放大。
为了减少噪声的影响,可以在均衡化之前对图像进行去噪处理,或者采用自适应的直方图均衡化方法,以避免过度增加图像噪声。
另外,直方图均衡化也可能导致图像的颜色失真问题。
因为直方图均衡化是基于像素值的灰度分布进行调整,对彩色图像来说,它可能会改变图像的颜色分布,从而造成颜色失真。
为了避免这种情况,可以在进行直方图均衡化前将图像转换为HSV颜色空间,并只对亮度(Value)通道进行均衡化,这样可以避免颜色的偏移。
此外,直方图均衡化的效果可能受到图像的动态范围限制。
在某些情况下,图像的动态范围可能不足以支持完整的直方图均衡化。
比如,当图像的某些区域非常亮或非常暗时,直方图可能会在动态范围两端产生剧烈的波动,从而导致图像的细节丢失或噪声增加。
为了解决这个问题,可以采用自适应的直方图均衡化方法,以根据图像的局部动态范围来进行调整,减少对整体图像的影响。
最后,直方图均衡化的选择需要根据具体的应用需求来确定。
直方图均衡化可以改善图像的对比度,使图像更加清晰和易于处理。
但对于一些特定的图像处理任务,如目标检测、图像识别等,直方图均衡化可能并不适用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业3:直方图均衡
1.选取一张对比度不明显的彩色图像,编写MATLAB代码对RGB通道独立地进行直方图
均衡,同时用PHOTOSHOP软件对其进行均衡,比较两种处理方法在效果上的差异。
使用R/G/B=image(:,:,1/2/3);提取图像的三个通道,imshow(R);显示三个通道的图像,imhist(R);显示对应颜色分量的直方图,r=histeq(R);分别对三个通道进行直方图均衡化,equated = cat(3,r,g,b);联合RGB三个数组,得到均衡化后的图像。
原图与matlab直方图均衡化后的图像
原图的RGB分量
均衡后的RGB分量
在photoshop中处理图像后得到下图的结果。
Ps中得到的图像RGB通道独立直方图均衡得到的图像比较:选取的原图是逆光拍摄,颜色很暗,暗部细节很多。
经过matlab处理后,灰度级部分合并,灰度级较低的间隔变大,灰度级较高的间隔变小。
但对真彩色图像的直方图均衡化时,通过单纯地对RGB三个分量图像分别均衡、合并, 会使均衡后的图像出现轻微的色彩失真现象, 而且原图中灰度级较高的地方的细节部分缺失。
但是经过ps处理后的图像,原本灰度值较低的地方明显变亮,同时原本灰度值较高的地方仍然很好保留了,并没有出现matlab处理后的问题。
Ps处理后的图像色彩也很正常,没有出现失真的问题。
数字图像直方图的算法步骤:
①列出原始图像的灰度级f j,j=0,1,…,L-1,
②统计各灰度级的像素数目n j,j=0,1,…,L-1,
③计算原始图像直方图各灰度级的频数p(f j)= n j/N,j=0,1,…,L-1,
④计算累计分布函数C(j)=Σp(f k), j=0,1,…,L-1,
⑤g i= INT[(g max-g min)C(f)+g min+0.5]
2.阅读"Exact Hitogram Specification"这篇英文文献第二部分和第三部分,结合压缩包中
MATLAB源代码,理解精确直方图均衡的算法原理,重点是借助空间滤波实现像素排序的算法原理,用(1)中图片,比较精确直方图均衡和PHOTOSHOP均衡的效果差异。
精确直方图均衡的算法原理:由于数字图像是离散的,所以直方图均衡化后并不能产生具有理想均衡直方图的图像,而如果定义一种新的排序关系,在对像素进行排序时应用严格的排序就可以得到一个精确均衡的直方图。
步骤:
①f是离散N*M图像的灰度级,H是直方图;
②定义<一种严格排序;
③让像素按照这个顺序排序;
④在灰度级中从左到右将③中的排序分割,类似j组有hj个像素;
⑤对于j组里的所有像素,都设为j灰度级。
排序判定规则:
严格排序可以由一对一映射和一组整数构成,比如:O:[1,N]×[1,M]→[1,M×N],那么如果在整数集中按通常的排序O(x1,y1)>O(x2,y2),那么诱导排序f(x1,y1)>f(x2,y2)。
总共这些映射的数量是(MN)!,但它们中的大部分对于精确直方图均衡都是无用的。
为了得到一个有用的严格排序,诱导排序必须与正常排序一致,即在正常排序时,一个像素的灰度值大于另一个像素的灰度值,在新排序中也应该是这样的。
而且,新的排序应当细化正常排序,细化程度在一定程度上应与人类对亮度的感知相一致。
这种排序要考虑像素邻域。
在有些改善直方图均衡的方法中,会考虑水平和垂直方向4个相邻像素的灰度值,但是4个像素的平均灰度值并不能完全区分,所以在这里考虑每个像素周围的一片区域。
K是一个整数,w1,w2,…w k是关系为w1⊂w2⊂…⊂wk的集合。
对于每个像素f(x,y),m i(x,y)是f(x,y)在w i集合中灰度值的平均值。
M(x,y)表示k元组,考虑定义在k元组上的字典顺序。
当M(x1,y1)<M(x2,y2)时,f(x1,y1)<f(x2,y2)。
在这种排序下,如果一个像素的局部灰度均值远大于另一个像素的局部灰度均值,经过排序后它的亮度将会高于另一个像素。
通过k取不同值,调整直方图均衡的程度。
原图
Ps处理后精确直方图均衡化后
比较:精确直方图均衡后的图像不仅在灰度值低的部分提高了亮度,灰度级经过严格排序后变得非常平均。
图像的对比度也增强很多,而暗部的细节变得更加清晰。
Ps处理后,图像也有明显的亮度和对比度的增强,但是整体灰度级没有精确直方图均衡后的图像更加平均。
总体来说,两种处理得到的图像差不多。
源代码:
1.histeq1
image=imread('original.jpg');
R=image(:,:,1);%%提取图片的RGB三种颜色
G=image(:,:,2);
B=image(:,:,3);
subplot(3,2,1),imshow(R);
title('红色分量');
subplot(3,2,2), imhist(R);
title('红色分量直方图');
subplot(3,2,3),imshow(G);
title('绿色分量');
subplot(3,2,4), imhist(G);
title('绿色分量直方图');
subplot(3,2,5),imshow(B);
title('蓝色分量');
subplot(3,2,6), imhist(B);
title('蓝色分量直方图');
r=histeq(R);%%分别对RGB通道进行直方图均衡
g=histeq(G);
b=histeq(B);
figure,
subplot(3,2,1),imshow(r);
title('红色分量均衡');
subplot(3,2,2), imhist(r);
title('红色分量均衡直方图');
subplot(3,2,3),imshow(g);
title('绿色分量均衡');
subplot(3,2,4), imhist(g);
title('绿色分量均衡直方图');
subplot(3,2,5), imshow(b);
title('蓝色分量均衡');
subplot(3,2,6), imhist(b);
title('蓝色分量均衡直方图');
figure,
equated = cat(3,r,g,b);%%联合RGB三个数组,维数为3
subplot(1,2,1),imshow(image);
title('original');
subplot(1,2,2),imshow(equated);
title('均衡化后的图像');
2.exact_histogram1
image=imread('grey.jpg');
output=exact_histogram(image);
imshow(output);。
