柏拉图直方图控制图制作方法
EXCEL柏拉图制作方法

他
累计百分
数量
比
0%
534 65.52%
218 92.27%
29 95.83%
16 97.79%
10 99.02%
8 100.00%
800 700 600
534 500 400 300 200 100
0 0% 粘砂
65.52% 218 冷疤
缺陷分布
92.27%
95.83%
97.79%
29 缺肉
16 砂眼
10 变形
99.02%
8 其他
100% 90% 80% 70% 60% 50% 40% 30% 20% 10% 0%
100% 90% 80% 70% 60% 50% 40% 30% 20% 10%
1、在统计表的最后一列插入累计百分比 2、标题栏下插入0% 3、0%以下表格制作直方图 4、系列2改为折线图 5、选中折线右击-设置数据系列格式-系列选项-次坐标轴 6、双击右侧纵坐标轴区域出现设置坐标轴格式-将最大值改为1,最小 值0. 7、选中整个图形:布局-坐标轴-次要横坐标轴-显示从左到右坐标轴 8、双击次摇号横坐标轴区域:主要刻度线类型(无)、坐标轴标签 (无)、位置坐标轴(在刻度线上)
柏拉图制作步骤
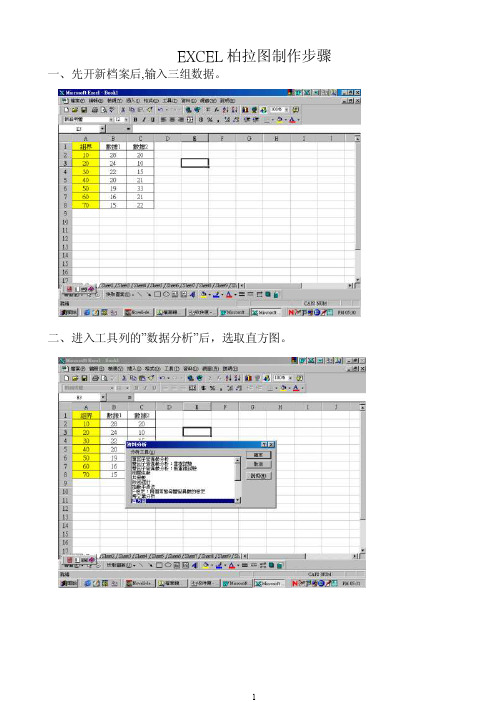
EXCEL柏拉图制作步骤一、先开新档案后,输入三组数据。
二、进入工具列的”数据分析”后,选取直方图。
三、选择数据范围,如下图所示。
四、选择完成后按确认,会出现图表、累计百分率及柏拉图,如下图。
五、依以下步骤删除不必要储存格。
六、删除储存格
七、删除以下三栏储存格。
八、得到下列结果。
九、更改自己所要之表头项目,如下例。
十、选取数据范围后依需求作计算。
十一、选取储存格数据范围后按鼠标右键,选取数据范围
十二、将累计%中的数值消除,重新输入累加百分率公式。
十三、如下图。
十四、输入完成后如下。
十五、依个人喜好调整柏拉图刻度。
十七、如下例。
十八、调整后如下。
十九、订正坐标轴名称。
二十、更改数列宽度。
二十一、调整间距。
二十二、完成后可依需要输入实验名称、日期时间、作业者等,或做改善前后比较。
11。
QC七大手法

品管知识培训-----数据的处理如果报表所呈现的结果,是一大堆的文字叙述或繁杂的数字,随着时间的推移,势将很难掌握问题的整体概念。
图表的运用,可以将繁杂的数字作情报转化,以最简单的方式表达出来,易看易懂,一目了然。
QC七大手法:统计方法数据与图表、检查表、层别法、柏拉图法、特性要因图法、散布图、直方图、控制图QC七大手法之使用情形,可归纳如下:1. 根据事实、数据发言——图表(Graph)、查检表(Check List)、散布图(Scatter Diagram)。
2. 整理原因与结果之关系,以探讨潜伏性之问题——特性要因图(Characteristic Diagram)。
3. 凡事物不能完全单用平均数来考虑,应了解事物均有变异存在,须从平均数与变异性来考虑——直方图、管制图。
4. 所有数据不可仅止于平均,须根据数据之来龙去脉,考虑适当分层——层别法(Stratification)。
5. 并非对所有原因采取处置,而是先从影响较大的2~3项采取措施,即所谓管理重点——柏拉图(Pareto Diagram)。
QC七大手法之运用一、数据与图表1、图表的种类1 依使用目的分(1)解析用图表:将过去的数据或现状,作成图表加以解析,从中发现问题点来加以改善。
适于工厂作业分析或研究之用。
如推移图、柏拉图、管制图、工程分析图……。
(2)管理用图表:加上目标或所定管理之处置界限,在进行管理时的使用。
如年度计划表。
(3)计划用图表:于拟定计划时使用,如甘特图(Gantt Chart)或称进度图。
(4)统计用图表:如柱形图(棒形图)、折线图。
(5)计算用图表:反覆做同一计算时,最好能将此计算做成图表,如此可节省计算时间,并减少错误。
如二项机率纸。
(6)说明用图表:描述事物之组织与流程等。
其优点为易理解,适合表示复杂的相互关系。
如组织图、制程流程图。
2、图表制作的原则1 制作前考虑事项(1)先确定目的何在?(2)要掌握的资料为何?(3)有哪些可用的情报数据?(4)制作图表及阅读的对象是谁?(5)以后用起来是否方便?是否经久可用?(6)实用性及时间性如何?使用起来方便?(7)符合正确、简洁、清楚的原则?2 制作应遵守的原则(1)目的要明确。
柏拉图(Pareto Diagram)

(6)每一不合格项目所引起的损失金额不同时,纵轴应以损失金额来表示。
(7)改善前后的比较时: a. 改善后,横轴项目别依照出现大小顺序由高而低排列。 b.前后比较基准应一致,且刻度应相同。 c.各项目别以颜色来区分,则更易于比较。
顿耍换聘乾床畅株谈蚀耳推酉志庇喘挽甸体玖汾提琳盆蒂嗅城党一奠脊弗包禄植颤涌罢攻掷殖渡蜕簿戍陨侵冰窟颂锤宣蓬戌雷猪柬熏畴贾援取狠烤不良项目不良数不良率累计数影响比率累计影响比率收敛不良5739357335335几何失真3423491200535白平衡不良2819311916570017117136100800无画面1409715082882画面倾斜1309016376958048170421000总检查数1450不良率各项不良数总检查数100柏拉图paretodiagram柏拉图paretodiagram前言由生产现场所收集到的数据有效的加以分析运用才能成为有价值的数据
80 品管七大手法
不良项目 不良数 不良率% 累计数 影响比率% 累计影响比率%
1 收敛不良
57
3.93
57
33.5
33.5
2 几何失真
34
2.34
91
20.0
53.5
3 白平衡不良 28
1.93
119
16.5
70.0
4敲 闪
17
1.17
136
10.0
80.0
5 无画面
14
0.97
150
8.2
直方图、正态分布、柏拉图

2.5 6
直方图、正态分布、柏拉图
2.6 正态分布应用
确定医学参考值范围 质量控制图
直方图、正态分布、柏拉图
2.6.1确定医学参考值范围
概念:医学参考值范围,又称参考值范围或正常值范围,是指特定 健康人群的解剖、生理、生化等各种数据的波动范围。习惯上是确 定包括95%的人的界值。
单双侧: 根据指标的实际用途, 有的指标有上下界值(双侧); 某些指标只需确定上限(单); 某些指标只需确定下限(单)。
直方图(Histogram)又称质量分布图。是一种统计报告图,由一系列高 度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类 型,纵轴表示分布情况。
1.2 直方图绘制
收集数据(n≥50)
确定数据极差R 确定组数 确定组距
数据N 组数K
50-100 6-10
组距=极差R/组数
100-250 7-12
的概率 • 对称区域面积相等。
2.4 3原则
区间 (-, +] (-2, +2] (-3, +3]
取值概率 68.3% 95.4% 99.7%
我们从上图看到,正态总体在 2,2以外取值的概率
只有4.6%,在 3,3以外取值的概率只有0.3 %。
当 a 3 时正态总体的 X 取值几乎总取值于区间 ( 3 , 3 ) 之内,其他区间取值几乎不可能.在实 际运用中就只考虑这个区间,称为 3 原则.
直方图、正态分布、柏拉图
3.3 柏拉图作用
1、作为降低不良依据。
1、80%的问题由20%的原因引起;
2、决定改善的攻击目标。
2、80%的索赔发生在20%的生产线上;
3、确认改善效果。
3、80%的销售额由20%的产品带来;
柏拉图及直方图和正态分布图绘制方法

正态图
40% 35% 30% 25% 20% 15% 10% 5% 0%
图9 为0
设置柱形图的“分类间距”
图10 直方图和正态分布图
准备绘制图表所需的数据。如图所示1,A3:B8单元格区域为消费支出的数 据,并按支出金额的大小排列,其中表格的第2行设计成累计值为0的空白 项目。 C3:C8单元格区域为每项支出占全部支出的比例,D3:D8单元格区域为每项 支出的累计比例,E3:E8单元格区域为绘制累计比例的XY散点图系列所对 应的x坐标值。 各列公式的设置方法如下:分别选取C3:C8、D3:D8和E3:E8单元格区域, 然后输入下列公式,按<Ctrl+Enter>组合键完成公式的编辑。
标准柏拉图(Pareto chart)
100% 80% 60% 40% 20% 0% 娱乐 租金 食物 衣服 交通 其它 17% 54% 100% 80% 60% 40% 20% 5% 3% 0%
12%
9%
图10 标准柏拉图
直方图及正态分布图绘制方法介绍
定义:直方图是通过对数据的加工整理,从而分析和掌握质量数据的分布 状况和估算工序不合格品率的一种方法。 用途:常用于分析质量原因,测量工序能力,估计工序不合格品率等。 作直方图的三大步骤:(1)作频数分布表 (2)画直方图 (3)进行相关计算 常见的几种典型形状:(1)正常型 (2)孤岛型 (3)偏向型 (4)平顶型 定量表示直方图的主要统计特征值: (1)平均值--表示数据的分布中心位置, (2)标准偏差--表示数据的分散程度 。 直方图和正态分布图是统计中使用最为频繁的图表。直方图是先按分组区 间计算出数据的发生频数,再以柱形表示频数的图表。正态分布图则描述数 据在分组区间内出现的概率,在图表中表现为一条单峰,对称的钟形曲线。 具体的绘制步骤如下: 原始数据:
柏拉图及直方图和正态分布图绘制方法共26页

பைடு நூலகம் 66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
柏拉图及直方图和正态分布图绘制方法
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
品管 七大手法

手法四 直方图
定义:
直方图又称柱状图,它是表示数据变化情况的一种主要工具。用直 方图可以将杂乱无章的资料,解析出规则性,比较直观地看出产品质量 特性的分布状态,对于资料中心值或分布状况一目了然,便于判断其总 体质量分布情况 ,
内容:
1、计算数据,数据总数以N表示 2、求最大值(L)与最小值(S) 3、求L与S之差后除以组数 4、决定组距(h) 5、决定各组之组界 6、作次数分配表 7、绘制直方图
1、明确要查核的项目及具体的要求; 2、根据项目和要求的性质设计窗体; 3、实施查核,将结果填在窗体上; 4、分析和总结记录的查核结果; 5、针对结果实施改进。
手法二 检查表(运用)
成品部七区七月各组长出现严重质量事故检查表:
责任组长 欧春妹 潘美珍 黄春兰 曾庆红 李水妹 陈玉珍 其它
漏合版
√√√√
内容:
包括纵轴、横轴、中心线CL,上管制界限UCL,下管制界限LCL, 如果点都在上管制界限和下管制界限之间,如此则即表示是在控制状态 下;如果点有连续往上或往下延伸或突出上下管制界限之外,这种情形 就表示必须深入调查原因。
受控制的過程的極差
6
不受控制的過程的極差(有超過控制界限 的點)
7 6
5
不良品個數
手法五 柏拉图
定义: 柏拉图又称为排列图,由此图的发明者19世纪意大利经 济学家柏拉(Pareto)的名字而得名。它是分析和寻找影响 质量主原因素的一种工具,是质量控制最主要、最常用的手 法。 用途: 1、作为决定降低不良的依据; 2、作为分析问题,决定改善目标之依据;
3、运用柏拉图从事管理;
4、作为QCC(品管圈)活动成果比较用
制程品质状况图
5 4 4 3 2 2 1 1 0 0 成品一区 成品二区 成品三区 成品四区 成品五区 成品六区 成品七区 1 1 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录
第一章柏拉图制作方法 (2)
1.1、制作方法 (2)
1.2、举例说明 (2)
第二章直方图制作方法 (6)
2.1、直方图的制作步骤 (6)
2.2、举例说明 (6)
第三章管制图制作说明 (10)
3.1、各个管制图界限一览表 (10)
3.2、符号说明 (10)
3.3、绘制管制图的步骤 (11)
3.4、管制图使用时之注意事项 (11)
3.5、举例说明 (12)
第一章柏拉图制作方法
1.1、制作方法
1、收集制作柏拉图需要的数据,分类输入表格。
2、将数据按照由小到大的顺序排列
3、以此计算出这些数据的累积数目和累积百分率。
4、选择需要的数据生成柱状图。
5、选择累积百分比,将图表类型变为折线形式。
6、更改两个纵坐标值将累积百分比的的最大值改为1;将发生数据的最大值改为发生数据
的累计最大值,或大于等于累计最大值。
7、调整图之间的间隙,美化图形生成柏拉图。
1.2、举例说明
第一步:收集整理数据。
收集不良数量,以此计算累计不良数,百分比,累计百分比。
第三步:在图上选择累计百分比图形,点击鼠标右键,选择更改图标类型,以此选择带标记的折线图。
将累计百分比的柱状图变为折线图。
第四步:更改成折线图后,选中折线图,在右键里面选择“设置数据系列格式”随后选择“次坐标轴”得到如下图像。
第五步:选择累积百分比的坐标轴,点击右键选择“设置坐标轴格式”。
在里面将最大值改为1,最小值为0,其他可按照需求或选择默认设置。
选择数量坐标轴,点击右键选择“设置坐标轴格式”在里面将最大值设置为大于或
等于累计不良数的最大值。
最小值和间隔可按照需要选择。
得到如下图形。
第六步:选中图形点击右键选择“设置数据系列格式”在里面将“分类间隔”调整为零。
双击每个柱子选择不同的颜色可以改变每个柱子的颜色。
最后调整后得到如下图形。
第七步:如果要清晰的表达数据,可点击右键在图形上面添加数据标签。
第二章直方图制作方法
直方图主要用来统计一组数据在某个范围内出现的次数,显示数据在各个区间的分布。
2.1、直方图的制作步骤
1.收集数据并且记录在纸上.
2.找出数据中的最大值与最小值.
3.计算全距.
4.决定组数与组距.
5.决定各组的上组界与下组界.
6.决定组的中心点.
7.制作次数分配表.
8.制作直方图.
2.2、举例说明
第一步:收集所需要的数据,并整理。
将不良的数据剔除。
下表收集了A,B两种数据的不良。
第二步:计算上述数据的最大值最小值:【=max(数组范围),=min(数组范围)】
,但却失去次数分配的本质;组数过过多,虽然表列详尽,但无法达到简化的目的.(异常值应先除
去再分组).分组不宜过多,也不宜过少,一般用数学家史特吉斯提出的公式计算组
数,其公式为:K=1+3.32 Lg n
一般对数据之分组可参考下表:
表三
第四步:确定分组的组解值;组距。
组距计算方法为:组距=(最大值−最小值)/分组数按照此公式本组的组距为
7.5,便于计算取8
第一组的下届值确定方法为:本组数据最小值−测定值最小位数
;测定值的最小位数如
2
果为整数则为1,小数的话可以取小数所精确到的最后一位(0.1;0.01;0.001……)。
所
以第一组的下届值为118.5。
第五步:确定每组的数值范围:第一组的上界值=下届值+组距;第二组的下届值就等于第一组的上界值。
以此类推计算每组的上下界线。
得到如下所示的数据:
表四
第六步:计算表一中的数据在各个组中出现的次数,得到的数据见表四。
EXCEL可用下面的公式查找。
【=COUNTIF(搜索数值范围,">=该组的下界值")-COUNTIF(搜索数值范围,"> 该组的下界值")】第七步:选择各组的“中间值”和“出现的次数”,“A出现的次数”,“B出现的次数”制作直方图。
图一:出现的次数
图二:A组出现的次数
图三:B组出现的次数
第三章 管制图制作说明
3.1、各个管制图界限一览表
表一
3.2、符号说明
X ̅:样本平均数;X =−∑x
i n
i=1n
X ̿:样本组平均数;X ̿=∑x ̅k i=1k
R :样本全距;
R :样本组全距平均值;R =
∑R k i=1K
R si :相邻两个样本距差的绝对值;R si =|R i −R i+1|
R s :样本距差的绝对值的平均数;R s ̅̅̅=R s1+R s2+⋯⋯+R s(k−1)
k−1
P :每个样本组的不良率; P :平均不良率;P =
样本组中总不良数
抽样总数
P n : P n 管制图的总体不良数;P n =
样本中总不良数样本组数
3.3、绘制管制图的步骤
第一步:收集数据,对数据进行处理。
第二步:按照表一所给的数据,分别计算管制图的管制界限。
第三步:绘制管制图。
一、管制图参数表
表二
N:代表每个样本里面的个体数。
3.4、管制图使用时之注意事项
1、管制图使用前,现场作业应予标准化作业完成;
2、管制图使用前,应先决定管制项目,包括品质特性之选择与取样数量之决定;
3、管制界限千万不可用规格值代替。
4、管制图种类之选择应配合管制项目之决定时搭配之。
5、抽样方法以能取得合理样组为原则。
6、点子超出界限或有不正常之状态,必须利用各种措施研究改善或配合统计方法,把异常
原因找了,同时加以消除。
7、X-R管制图里组的大小(n),一般采n=4-5最适合。
8、R管制图没有管制下限,系因R值是由同组数据据之最大值减最小值而得,因之LCL取
负值没有意义。
9、管制图一定要与制程管制的配置结合。
10、P管制图如果有点逸出管制下限,亦应采取对策,不能认为不良率低而不必采取对策,
因其异常原因可能来自:
⑴、量具的失灵,须予更新量具,并检讨以前之量测值影响度。
⑵、良品的判定方法有误,应予立即修正。
⑶、真正有不良率变小的原因,若能掌握原因,则有且国于日后大幅降低不良率。
11、制程管制做得不好,管制图形同虚设,要使管制图发挥效用,应使产品制程能力中之
Cp值(制程精密度)大于1以上。
3.5、举例说明
X-R管制图绘制:
第一步:测定不良品收集到如下的数据。
第二步:计算各个样本组的平均数,全距。
表五:平均数管制图界限
第四步:根据数据得到平均数管制图如下:
图一:平均数管制图
图二:全距管制图。
