沪科版八年级数学上册第十四章 全等三角形的概念和性质复习讲义(含练习答案)
沪科版八年级上册数学第14章 全等三角形 全等三角形

12.【芜湖繁昌期末】已知△ABC≌△DEF,AB=5 cm, BC=6 cm,且△ABC 的面积为 12 cm2,则 EF 边上的高是 __4_c_m____.
13.【合肥包河区期末】如图,在△ABC 中,∠ACB=90°,点 D 在边 AB 上,连接 CD,将△BCD 沿 CD 翻折得到△ECD, 使 DE∥AC,CE 交 AB 于点 F,若∠B=α,则∠ADC= ________(用含 α 的代数式表示).
解:对应边为 AB 和 AC,AE 和 AD, BE 和 CD; 其他的对应角为∠BAE 和∠CAD.
7.【中考·厦门】如图,点 E,F 在线段 BC 上,△ABF 与△DCE
全等,点 A 与点 D,点 B 与点 C 是对应顶点,AF 与 DE 交
于点 M,则∠DCE 等于( A )
A.∠B
B.∠A
(2)判断 AC 与 BD 的位置关系,并说明理由.
解:AC⊥BD. 理由如下:∵△ABD≌△EBC,∴∠ABD=∠EBC. 又∵∠ABD+∠EBC=180°, ∴∠ABD=∠EBC=90°,∴AC⊥BD.
16.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°, ∠EAB=120°,求∠DFB 和∠DGB 的度数.
1.能够__完__全__重__合____的两个图形,叫做全等形. 2.能够__完__全__重__合____的两个三角形叫全等三角形.互相重合的
顶点叫对应顶点,互相重合的边叫对应边,互相重合的角叫 对应角.在写两个三角形全等时,通常把表示对应顶点的字 母写在对应的位置上. 3.全等三角形的对应边相等,__对__应__角__相等.
(1)∠1 的度数;
解:∵△ADF≌△BCE,∠F=28°, ∴∠E=∠F=28°,∴∠1=∠B+∠E=32°+28°=60°.
沪科版八年级数学上册第14章 全等形和全等三角形 专题复习(解析版)
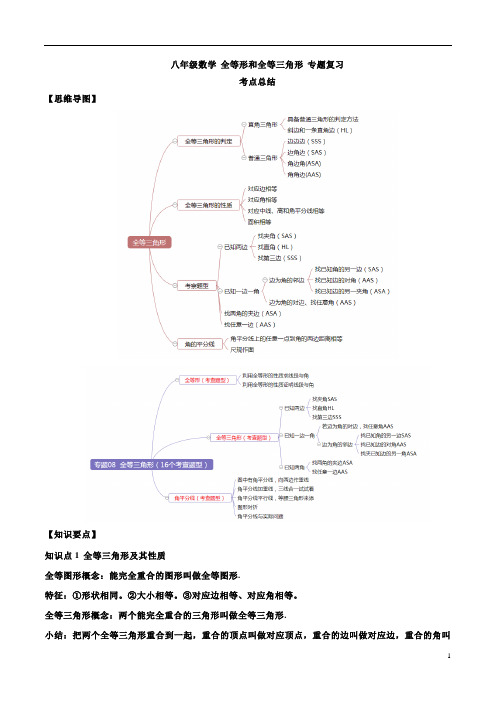
八年级数学全等形和全等三角形专题复习考点总结【思维导图】【知识要点】知识点1全等三角形及其性质全等图形概念:能完全重合的图形叫做全等图形.特征:①形状相同。
②大小相等。
③对应边相等、对应角相等。
全等三角形概念:两个能完全重合的三角形叫做全等三角形.小结:把两个全等三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.表示方法:全等用符号“≌”,读作“全等于”。
书写三角形全等时,要注意对应顶点字母要写在对应位置上。
全等变换定义:只改变图形的位置,而不改变图形的形状和大小的变换。
变换方式(常见):平移、翻折、旋转。
全等三角形的性质:对应边相等,对应角相等。
1.(2017·四川中考模拟)已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为()A.3 B.5 C.6 D.10【答案】D【详解】∵四边形OPEF≌四边形ABCD∴PE=BC=10,故选D.2.(2019·福建中考模拟)如图,若△MNP≌△MEQ,则点Q应是图中的()A.点A B.点B C.点C D.点D【答案】D【详解】∵△MNP≌△MEQ,∴点Q应是图中的D点,如图,故选:D.3.(2018·广西中考模拟)下列说法中不正确的是()A.全等三角形的周长相等B.全等三角形的面积相等C.全等三角形能重合D.全等三角形一定是等边三角形【答案】D【详解】根据全等三角形的性质可知A,B,C命题均正确,故选项均错误;D.错误,全等三角也可能是直角三角,故选项正确.故选D.考查题型一利用全等三角形性质求线段与角1.(2019·武冈市第七中学中考模拟)如图,三角形纸片ABC,AB=10CM,BC=7CM,AC=6CM,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为()A.9CM B.13CM C.16CM D.10CM【答案】A【解析】解:由折叠的性质知,CD=DE,BC=BE=7CM.∵AB=10CM,BC=7CM,∴AE=AB﹣BE=3CM.△AED的周长=AD+DE+AE=AC+AE=6+3=9(CM).故选A.2.(2017·江苏南京溧水孔镇中学中考模拟)如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5CM,BF=7CM,则EC长为()A.1CM B.2CM C.3CM D.4CM【答案】C【详解】解:∵△ABC≌△BAD,∴EF=BC=5CM,∵BF=7CM,BC=5CM,∴CF=EF-CF=3 CM,故选C.3.(2016·广东中考模拟)如图,△ACB≌△A′CB′,∠ACA′=30°,则∠BCB′的度数为()A.20°B.30°C.35°D.40°【答案】B【详解】∵△ACB≌△A′CB′,∴∠ACB=∠A′C′B′,∴∠ACB-∠A′CB=∠A′C′B′-∠A′CB,即∠BCB′=∠ACA′,又∠ACA′=30°,∴∠BCB′=30°,故选:B.4.(2019·沂源县中庄中学初一月考)如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.(1)求△ABC的周长;(2)求△ACE的面积.【答案】(1)24;(2)50【详解】解:(1))∵△ABC≌△CDE∴AC=CE∴△ABC的周长=AB+BC+AC=24(2)∵△ABC≌△CDE∴AC=CE,∠ACB=∠CED,∠BAC=∠DCE又∠B=90°∴∠ACB+∠BAC=90°∴∠ACB+∠DCE=90°∴∠ACE=180°-(∠ACB+∠DCE)=90°×AC×CE=50∴△ACE的面积=12考查题型二利用全等三角形性质证明线段、角相等1.(2019·湖北黄石十四中初二期中)如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.【答案】见解析【详解】∵△ABC≌△DEC,∴∠B=∠DEC,BC=EC,∴∠B=∠BEC,∴∠BEC=∠DEC,∴CE平分∠BED.2.(2018·颍上县第五中学初二期中)若△ABC≌△DCB,求证:∠ABE=∠DCE.【答案】见解析【详解】证明:∵△ABC≌△DCB∴∠ABC=∠DCB,∠ACB=∠DBC∴∠ABC-∠DBC=∠DCB-∠ACB即∠ABE=∠DCE知识点2:全等三角形的判定(重点)注:①判定两个三角形全等必须有一组边对应相等;②全等三角形周长、面积相等.证题的思路(重点):考查题型三 已知一边一角(若边为角的对边,找任意角AAS )1.(2018·四川中考模拟)如图,AB=AE ,∠1=∠2,∠C=∠D .求证:AC=AD .【答案】见解析【解析】详解:∵∠1=∠2∴∠1+∠EAC=∠2+∠EAC∴∠BAC=∠EAD在ΔABC 和ΔAED 中{∠BAC =∠EAD∠C =∠D AB =AE∴ΔABC ≌ΔAED (AAS)∴AC=AD2.(2014·北京中考模拟)已知:如图,E 是AC 上一点,AB=CE ,AB ∥CD ,∠ACB =∠D .求证:BC =ED .【答案】证明见解析.【详解】∵AB∥CD,∴∠A=∠ECD.在△ABC和△ECD中,∵∠A=∠ECD,∠ACB=∠D,AB=CE,∴△ABC≌△ECD(AAS).∴BC=DE.3.(2018·四川中考模拟)已知,如图,E、F分别为□ABCD的边BC、AD上的点,且∠1=∠2,.求证:AE=CF.【答案】详见解析【详解】∵四边形ABCD为平行四边形∴∠B=∠D,AB=CD在△ABE与△CDF中,∠1=∠2,∠B=∠D,AB=CD∴△ABE≌△CDF∴AE=CF4.(2016·福建中考模拟)如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.【答案】证明详见解析.【详解】∵AD⊥CE,BE⊥CE,∴∠ADC=∠E=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∵∠B+∠BCE=90°,∴∠B=∠ACD,在△BEC和△CDA中,∠ADC=∠E=90°,∠B=∠ACD,AC=BC,∴△ACD≌△CBE(AAS).考查题型四已知一边一角(边为角的邻边(找已知角的另一边SAS))1.(2016·四川中考真题)如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.【答案】见解析【详解】∵C是线段AB的中点,∴AC=CB,∵CD∥BE,∴∠ACD=∠B,在△ACD和△CBE中,∵AC=CB,∠ACD=∠B,CD=BE,∴△ACD≌△CBE(SAS),∴∠D=∠E.2.(2018·云南中考模拟)如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:∠C=∠D.【答案】证明见解析【详解】证明:∵AE=BF,∴AE+EF =BF+EF ,∴AF =BE ,在△ADF 与△BCE 中,AD BC A B AF BE =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△BCE (SAS ),∴∠C =∠D .3.(2019·辽宁中考真题)如图,点E ,F 在BC 上,BE =CF ,AB =DC ,∠B =∠C ,求证:AF =DE .【答案】见解析;【详解】证明:∵BE =CF ,∴BE +EF =CF +EF ,即BF =CE ,在ΔABF 和ΔDCE 中,{AB =DC∠B =∠C BF =CE,∴ΔABF ≌ΔDCE (SAS)∴AF =DE .考查题型五 已知一边一角(边为角的邻边(找已知边的对角AAS ))1.(2013·浙江中考真题)如图,△ABC 与△DCB 中,AC 与BD 交于点E ,且∠A=∠D ,AB=DC .(1)求证:△ABE ≌DCE ;(2)当∠AEB=50°,求∠EBC 的度数。
沪科版八年级上册数学第14章 全等三角形含答案精编

沪科版八年级上册数学第14章全等三角形含答案一、单选题(共15题,共计45分)1、下列说法:①一个底角和一条边分别相等的两个等腰三角形全等;②底边及底边上的高分别相等的两个等腰三角形全等;③两边分别相等的两个直角三角形全等;④一个锐角和一条边分别相等的两个直角三角形全等,其中正确的个数是()A.1B.2C.3D.42、如图,在和中,AB=DC , AC与BD相交于点E ,若不再添加任何字母与辅助线,要使,则还需增加的一个条件是()A. AC=BDB. AC=BCC. BE=CED. AE=DE3、如图,在Rt△ABC中,∠BAC=90°,AB=AC,直角∠EPF的顶点P是BC的中点,将∠EPF绕顶点P旋转,两边PE,PF分别交AB,AC于点E,F.下列四个结论:①AE=CF;②△PEF是等腰直角三角形;③EF=AP;④S四边形AEPF =S△ABC.在∠EPF旋转过程中,上述四个结论始终正确的有()A.①②③B.②③④C.①③④D.①②④4、下列说法中,其中正确的是()A.对于给定的一组数据,它的众数可以不只一个B.有两边相等且一角为30 的两个等腰三角形全等 C.为了防止流感的传染,学校对学生测量体温,应采用抽样调查法 D.直棱柱的面数、棱数和顶点数之间的关系是面数+顶点数=棱数-25、在下列给出的四组条件中,能判定△ABC≌△DEF的是()A.AB=DE,BC=EF,∠A=∠DB.∠A=∠D,∠C=∠F,AC=EF C.∠A=∠D,∠B=∠E,∠C=∠F D.AB=DE,BC=EF,△ABC的周长等于△DEF的周长6、如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是()A.POB.PQC.MOD.MQ7、如图,AD是△ABC的高,AD=BD,DE=DC,∠BAC=75°,则∠ABE的度数是()A.10°B.15°C.30°D.45°8、如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE=()A.1B.2C.3D.49、如图,一扇窗户打开后,用窗钩 AB 可将其固定,这里所运用的几何原理是( )A.垂线段最短B.两点之间线段最短C.两点确定一条直线D.三角形的稳定性10、如图,在中,是AC上一点,于点E,连接BD,若AC=8cm,则等于()A.6cmB.7cmC.8cmD.9cm11、下列说法正确的是()A.全等三角形是指形状相同的三角形B.全等三角形是指面积相等的两个三角形C.全等三角形的周长和面积相等D.所有等边三角形是全等三角形12、如图,在△ABC中,AB=AC,D为BC上一点,连接AD,点E在AD上,过点E作EM⊥AB,EN⊥AC,垂足分别为M,N.下面四个结论:①如果AD⊥BC,那么EM=EN;②如果EM=EN,那么∠BAD=∠CAD;③如果EM=EN,那么AM=AN;④如果EM=EN,那么∠AEM=∠AEN.其中正确有( )A.1个B.2个C.3个D.4个13、根据下列条件,能唯一地确定的是()A. ,,B. ,,C. ,,D. ,14、如图,平行四边形ABCD中,对角线AC、BD相交于O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=GF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确是()A. B. C. D.15、下面的两个三角形一定全等的是()A.腰相等的两个等腰三角形B.一个角对应相等的两个等腰三角形C.斜边对应相等的两个直角三角形D.底边相等的两个等腰直角三角形二、填空题(共10题,共计30分)16、如图,在△PAB中,∠A=∠B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为________.17、如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE,若AD=10,AB=6,则tan∠EDF的值是________.18、如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为________.19、如图,△ABC≌△DEF,BE=3,AE=2,则DE的长是________.20、在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________.21、如图,△ABC中,∠ACB=90 ,BC=3cm,CD⊥AB于D,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=________cm.22、撑上支撑后的自行车能稳稳地停在地上,是因为三角形具有________ 性.23、如图,已知以点A(0,1)、C(1,0)为顶点的△ABC中,∠BAC=60°,∠ACB=90°,在坐标系内有一动点P(不与A重合),以P、B、C为顶点的三角形和△ABC全等,则P点坐标为________.24、如图所示,抛物线与x轴交于A、B两点,过点B的直线与抛物线交于点C(点C在x轴上方),过ABC三点的⊙M满足∠MBC=45°,则点C的坐标为________.25、在△ABC中,AD为∠BAC的角平分线.若添加一个条件:________,则△ABD≌△ACD.三、解答题(共5题,共计25分)26、如图,∠C=∠D=90°,DA=CB,∠CBA=28°,求∠DAC.27、如图,在△ABC 中,点 D、E 分别在 BC、AC 上且 BD=CE,AD=DE,∠C =∠ADE,则∠B =∠C,试填写说理过程.解因为∠EDB =∠C+∠DEC(▲)即∠ADB+∠ADE =∠C+∠DEC因为∠C =∠ADE(▲)所以∠▲=∠▲(等式性质)在△ABD 与△DCE 中,所以△ABD ≌ △DCE(▲)所以∠B =∠C(▲)28、如图,. 求证:29、在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,BD=DF.求证:CF=EB30、风筝起源于中国,至今已有2300多年的历史.如图,在小明设计的“风筝”图案中,已知,,.求证:.参考答案一、单选题(共15题,共计45分)1、A3、D4、A5、B6、B7、B8、B9、D10、C11、C12、D13、C14、B15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、29、30、。
数学沪科版八年级(上册)14.1全等三角形(共32张PPT)

(全等三角形对应边相等).
5.如图,△ABC≌△AED,AB是△ABC的最大边,AE是 △AED的最大边, ∠BAC 与∠ EAD是对应角,且 ∠BAC=25°,∠B= 35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度.
解:∵ △ABC≌△AED,(已知)
A
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
例2 如图,已知△ABC≌△DCB,AB=3,DB=4, ∠A=60°. (1)写出△ABC和△DCB的对应边和对应角; (2)求AC,DC的长及∠D的度数. 解:(1)AB与DC,AC与DB,
BC与CB是对应边; ∠A与∠D,∠ABC与∠DCB, ∠ACB与∠DBC是对应角;
A
B
3.如图,已知△ABC≌△BAD 边 请指出图中的对应边和对应角. 边
AB= BA AC= BD
D
A
边 BC= AD
角 ∠BAC= ∠ABD
B
C
角 ∠ABC= ∠BAD
角 ∠C= ∠D
归纳 有公共边的,公共边一定是对应边.
变式:
D E
B
如图:平移后△ABC≌△ EFD, 若AB=6,AE=2.你能说出AF的 F 长吗?说说你的理由.
∴ ∠E=∠N. ∴ EF∥NM.
当堂练习
1.如图,△ABC≌△BAD,如果AB=5cm, BD=
4cm,AD=6cm,那么BC的长是 ( A )
A.6cm B.5cm C.4cm D.无法确定
2.在上题中,∠CAB的对应角是 ( B )
A.∠DAB B.∠DBA C.∠DBC D.∠CAD
C
D
O
∠A= ∠A ∠B= ∠E ∠ACB= ∠ADE
沪科版八年级上册数学第14章 全等三角形含答案

沪科版八年级上册数学第14章全等三角形含答案一、单选题(共15题,共计45分)1、如图,若,,则的度数为()A. B. C. D.2、如图,在四边形中,,对角线、相交于点O,于点E,于点F,连接、,若,则下列结论不一定正确的是()A. B. C. 为直角三角形 D.四边形是平行四边形3、下列说法正确的是()A.全等三角形是指形状相同的三角形B.全等三角形是指面积相等的三角形C.全等三角形的周长和面积都相等D.所有的等边三角形都全等4、如图,边长为24的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN则在点M运动过程中,线段HN长度的最小值是()A.12B.6C.3D.15、如图,用直尺和圆规作射线OC,使它平分∠AOB,则△ODC≌△OEC的理由是()A. SSSB. SASC. AASD. HL6、已知△ABC≌△DEF,且S△ABC =4,则S△DEF=( )A.8B.5C.4D.27、下列说法不正确的是()A.有斜边和一条直角边对应相等的两个直角三角形全等B.有斜边和一个锐角对应相等的两个直角三角形全等C.二条直角边对应相等的两个直角三角形全等D.有斜边对应相等的两个直角三角形全等8、如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连按PQ.下列结论:①AD=BE;②AP=BQ;③PQ∥AE;④∠AOB=60°;⑤DE=DP.其中正确的有()A.2个B.3个C.4个D.5个9、下列语句正确的是()A.三角形的三条高都在三角形内部B.三角形不一定具有稳定性C.三角形的三条中线交于一点D.三角形的角平分线可能在三角形的内部或外部10、如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD =1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S=;四边形BDEF④S=.其中正确的有()△AEFA.1个B.2个C.3个D.4个11、下列两个三角形的对应元素中,不能判断两个三角形全等的是()A.SSAB.AASC.SASD.ASA12、下列说法中不正确的是()A.平行四边形是中心对称图形B.斜边及一锐角分别相等的两直角三角形全等C.两个锐角分别相等的两直角三角形全等D.一直角边及斜边分别相等的两直角三角形全等13、下列说法中:①法国数学家笛卡尔首先建立了坐标思想;②全等三角形对应边上的中线长相等;③若则④有两边和其中一条边所对的一个角对应相等的两个三角形一定全等.说法正确的为()A.①③④B.②④C.①②D.②③④14、如图所示,在下列条件中,能判断△ARD △BAC的条件是( )①∠D=∠C,∠BAD=∠ABC;②∠BAD=∠ABC,AD=BC;③BD=AC,∠BAD=∠ABC;④AD=BC,BD=AC.A.4个B.3个C.2个D.1个15、如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A 1C1D1,连结AD1, BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B②当x=1时,四边形ABC1D1是菱形③当x=2时,△BDD1为等边三角形④s= (x﹣2)2(0<x<2),其中正确的有()A.1 个B.2 个C.3 个D.4 个二、填空题(共10题,共计30分)16、如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.已知CD=2,则AB的长度等于________.17、如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:①△ABE≌△ACF;②BC=DF;③S△ABC =S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是________.(填写所有正确结论的序号)18、如图,C、D是半圆O上两点,AB是直径,若AD=CD=2,CB=4,则半圆的半径为________.19、已知△ABC中,AB=6cm,AC=8cm,AD为边BC上的中线,则中线AD的取值范围是________20、如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为________.21、如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系、已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处,若在y轴上存在点P,且满足FE=FP,则P点坐标为________.22、如图,平面内4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线l1、l4上,该正方形的面积是________平方单位.23、如图,△OAD≌△OBC,且∠O=58°,∠C=20°,则∠OAD=________°.24、如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是________.25、在等边三角形ABC中,点F是线段AC上一点,点E是线段BC上一点,BF 与AE交于点H,∠BAE=∠FBC,AG⊥BF,∠GAF:∠BEA=1:10,则∠BAE=________°.三、解答题(共5题,共计25分)26、如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.27、如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=16,AB=CD=34.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长.28、已知:如图,BE=CF,AC=DE,∠ACB=∠DEF,求证:AB=DF29、如图,在▱ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.30、(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到Rt△ABC的两边AC、BC的距离相等,并且点O到A、B两点的距离也相等.(不写作法,但需保留作图痕迹)(2)在(1)中,作OM⊥AC于M,ON⊥BC于N,连结AO、BO.求证:△OMA≌△ONB.参考答案一、单选题(共15题,共计45分)1、B2、C3、C4、B5、A6、C7、D8、C9、C10、C11、A12、C13、C14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题,共计25分)26、29、。
沪科版数学八年级上册14.1全等三角形课件(共19张PPT)

全等形定义:能够完全重合的两个图形,叫做全等形.
全等形性质:如果两个图形全等,它们的形状相同,大小相等.
1.与下左图所示图形全等的是 .
①、④
2.下列说法:①用一张底片冲洗出来的2张1寸相片是全等的; ②所有正三角形是全等形; ③面积相等的图形一定是全等形.其中正确的是 .
两个三角形全等是通过什么方法验证的?
平移
解:对应边是:__________________________________
对应角是:__________________________________
AC与DF,AB与DE,BC与EF
∠A与∠D,∠B与∠E,∠C与∠F
A
C
B
如图△AOC≌△BOD
1.对应边是:________________________
2.∠AOC的对应角是________
∠A的对应角是________
OC与OD,AC与BD
∠BOD
∠B
O
D
小结:有对顶角的,对顶角也是对应角.
想一想: 有什么办法判断两个三角形全等?用数学式子表示两个三角形全等,并指出对应角、对应边.
旋转
A
B
C
D
A
A
B
B
D
C
如图△ABD≌△ABC
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
同学们再见!
授课老师:
时间:2024年9月1日
第十四章 全等三角形
14.1 全等三角形
学习目标
学习重难点
重点
难点
1.了解全等形,明确全等三角形的概念.2.掌握全等三角形的性质,识别全等三角形的对应边和对应角.
沪科版八年级数学上册第13—14章 三角形与全等三角形知识点复习讲义(含答案)

三角形与全等三角形知识点复习讲义一、选择题(本大题共6道小题)1. 若a、b、c为△ABC的三边长,且满足|a-4|+b-2=0,则c的值可以为()A. 5B. 6C. 7D. 82. 如图,在Rt△ABC中,AB=10,AC=8,BC=6,DE是AC的垂直平分线,DE交AB于点D,连接CD,则CD=()A. 3B. 4C. 4.8D. 53. 如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为()A. 1B. 2C. 3D. 1+ 34. 如图,在△ABC中,AB=4,BC=6,DE、DF是△ABC的中位线,则四边形BEDF 的周长是()A. 5B. 7C. 8D. 105. 如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC 的长为()A. 5B. 6C. 8D. 106. 已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为()A.32B.332C.32D. 不能确定二、填空题(本大题共7道小题)7. 如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线.若∠B=71°,则∠BAC=________.8. 如图,在Rt△ABC中,E是斜边AB的中点,若∠A=40°,则∠BCE=________.9. 如图,在△ABC中,AB=BC,∠ABC=110°.AB的垂直平分线DE交AC于点D,连接BD,则∠ABD=________度.10. 如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8.分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F.过点E,F作直线EF,交AB于点D,连接CD,则CD的长是________.11. 在等腰直角三角形ABC中,∠ACB=90°,AC=3,点P为边BC的三等分点,连接AP,则AP的长为________.12. 如图,已知直线a∥b,△ABC的顶点B在直线b上,∠C=90°,∠1=36°,则∠2=________.13. 如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点.当△APB为直角三角形时,AP=________.三、解答题(本大题共4道小题)14. 如图,四边形ABCD是平行四边形,延长BA至E,延长DC至F,使得AE=CF,连接EF交AD于G,交BC于H.求证:△AEG≌△CFH.15. 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;(2)指出图中所有平行的线段,并说明理由.16. 如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.17. 如图,已知AD=BC,AC=BD.(1)求证:△ADB≌△BCA;(2)OA与OB相等吗?若相等,请说明理由.参考答案一、选择题(本大题共6道小题)1. 【答案】A 【解析】∵|a -4|≥0,b -2≥0,∴a =4,b =2,∵三角形的两边之和大于第三边,两边之差小于第三边,故c 的取值范围为:2<c <6,故本题选A .2. 【答案】D 【解析】∵DE 垂直平分AC ,∴∠AED =90°,AE =CE =4,在Rt △ABC中,∠ACB =90°,∴DE ∥BC ,∴DE 是△ABC 的中位线,∴DE =12BC =3.在Rt △CED 中,CD =CE 2+DE 2=5.3. 【答案】A 【解析】∵在Rt △ABC 中,∠A =30°,BC =1,∴AB =2BC =2×1=2,∵D 、E 分别是AB 、AC 的中点,∴DE 是△ABC 的中位线,∴DE =12AB =12×2=1.4. 【答案】D 【解析】∵DE 、DF 是△ABC 的中位线,∴DE ∥AB ,DF ∥BC ,DE =12AB ,DF =12BC ,∴四边形BEDF 是平行四边形,∵AB =4,BC =6,∴DE =BF =2,DF =BE =3,∴四边形BEDF 的周长为:2(DE +DF )=10.5. 【答案】C 【解析】∵AB =AC ,AD 平分∠BAC ,∴根据等腰三角形三线合一性质可知AD ⊥BC ,BD =CD ,在Rt △ABD 中,AB =5,AD =3,由勾股定理得BD =4,∴BC =2BD =8.6. 【答案】B 【解析】如解图,△ABC 是等边三角形,AB =3,点P 是三角形内任意一点,过点P 分别向三边AB ,BC ,CA 作垂线,垂足依次为D ,E ,F ,过点A 作AH ⊥BC 于点H ,则BH =32,AH =AB 2-BH 2=332.连接P A ,PB ,PC ,则S △P AB +S △PBC +S △PCA =S△ABC,∴12AB ·PD +12BC ·PE +12CA ·PF =12BC ·AH ,∴PD +PE +PF =AH =332.二、填空题(本大题共7道小题)7. 【答案】38° 【解析】∵AD ∥BC ,∠B =71°,∴∠EAD =∠B =71°.∵AD 是∠EAC的平分线,∴∠EAC =2∠EAD =142°,∴∠BAC =180°-∠EAC =180°-142°=38°.8. 【答案】50° 【解析】∵E 是Rt △ABC 斜边AB 的中点,∴EC =AB2=AE ,∴∠ECA =∠A =40°,∴∠BCE =90°-40°=50°.9. 【答案】35 【解析】∵AB =BC ,∠ABC =110°,∴∠A =∠C =35°,∵DE 垂直平分AB ,∴DA =DB ,∴∠ABD =∠A =35°.10. 【答案】5 【解析】由题意知EF 垂直平分AB ,∴点D 是AB 的中点,∵∠ACB=90°,∴CD 为斜边AB 的中线,∴CD =12AB .∵BC =6,AC =8,∴AB =AC 2+BC 2=82+62=10,∴CD =5.11. 【答案】13 或10 【解析】(1)如解图①所示,当P 点靠近B 点时,∵AC =BC=3,∴CP =2,在Rt △ACP 中,由勾股定理得AP =13;(2)如解图②所示,当P 点靠近C 点时,∵AC =BC =3,∴CP =1,在Rt △ACP 中,由勾股定理得AP =10.综上可得:AP 长为13 或10.12. 【答案】54° 【解析】如解图,过点C 作直线CE ∥a ,则a ∥b ∥CE ,则∠1=∠ACE ,∠2=∠BCE ,∵∠ACE +∠BCE =90°,∴∠1+∠2=90°,∵∠1=36°,∴∠2=54°.13. 【答案】3或3 3 或37 【解析】如解图,∵点O 是AB 的中点,AB =6,∴AO=BO =3.①当点P 为直角顶点,且P 在AB 上方时,∵∠1=120°,∴∠AOP 1=60°,∴△AOP 1是等边三角形,∴AP 1=OA =3;②当点P 为直角顶点,且P 在AB 下方时,AP 2=BP 1=62-32=33;③当点A 为直角顶点时,AP 3=AO ·tan ∠AOP 3=3×3=33;④当点B 为直角顶点时,AP 4=BP 3=62+(33)2=37.综上,当△APB 为直角三角形时,AP 的值为3或3 3 或37.三、解答题(本大题共4道小题)14. 【答案】证明:∵在▱ABCD 中,∠BAD =∠BCD ,AB ∥CD ,∴∠E =∠F ,180°-∠BAD =180°-∠BCD ,即∠EAG =∠FCH ,(5分) 在△AEG 和△CFH 中, ⎩⎪⎨⎪⎧∠E =∠F AE =CF ∠EAG =∠FCH, ∴△AEG ≌△CFH (ASA ).(7分)15. 【答案】(1)证明:∵BF =EC ,∴BF +FC =EC +CF ,即BC =EF .(3分) 在△ABC 与△DEF 中, ⎩⎪⎨⎪⎧BC =EF AB =DE AC =DF, ∴△ABC ≌△DEF (SSS ).(5分) (2)解:AB ∥DE ,AC ∥DF .(7分) 理由如下:∵△ABC ≌△DEF ,∴∠ABC =∠DEF ,∠ACB =∠DFE , ∴AB ∥DE ,AC ∥DF .(9分)16. 【答案】证明:∵AB ∥CD , ∴∠B =∠DEF ,(1分) 在△AFB 和△DFE 中,⎩⎪⎨⎪⎧∠B =∠DEF BF =EF ∠BFA =∠EFD,(3分) ∴△AFB ≌△DFE (ASA ),(5分) ∴AF =DF .(6分)17. 【答案】(1)证明:在△ADB 和△BCA 中, ⎩⎪⎨⎪⎧AD =BC BD =AC AB =BA, ∴△ADB ≌△BCA (SSS ).(4分) (2)解:相等.理由如下: 由(1)得△ADB ≌△BCA ,∴∠DBA =∠CAB ,即∠OBA =∠OAB ,(6分) ∴OA =OB .(8分)。
沪科版八年级数学上册第14章-全等三角形知识例题讲解与练习

第14章 全等三角形【知识剖析】一、全等形:能够完全重合的两个图形,叫做全等形. 二、全等三角形的有关概念1、全等三角形的定义:能够完全重合的两个三角形,叫做全等三角形.2、全等三角形的对应元素:全等三角形中,互相重合的边叫做对应边;互相重合的角叫做对应角;互相重合的顶点叫做对应顶点.3、全等三角形的性质:全等三角形的对应边相等,对应角相等.注:用全等符号“≌”表示两个全等三角形时,通常把表示对应顶点的字母写在对应位置上.[例1] 如图,将△ABC 绕其顶点B 顺时针旋转一定角度后得到△DBE ,请说出图中两个全等三角形的对应边和对应角.[例2] (1)如图,△ABE 与△CED 是全等三角形,可表示为△ABE ≌_______,其中∠A=30°,∠B=70°,AB=3cm ,则∠D=_____,∠DEC =_____,CD=_____.(2)如图,△ABC ≌△DCB ,若CD=4cm ,∠A=28°,∠DBC=35°,则AB=_____,∠D=_____,∠ABC=_______.(3)如图,△AOB ≌△COD ,若CD=2cm ,∠B=45°,则AB=_____,∠D=______.[例3] 如图,△ACB ≌△A /CB /,∠A /CB=30°,∠ACB/=110°,则∠ACA/=______.[例4] 如图,在Rt △ABC 中,∠ACB=90°,且AC=BC=4cm ,已知△BCD ≌△ACE ,则四边形AECD 的面积是_________.[例5] 如图,将△ABC 沿直线DE 折叠后,使得点B 与点A 重合,已知AC=5cm ,△ADC 的周长为17cm ,则BC 的长为_______.[例6] 如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C /处,折痕为EF ,若∠EFC /=125°,那么∠ABE 的度数为________.三、全等三角形的判定 1、“边角边”定理:两边和它们的夹角对应相等的两个三角形全等.(SAS )ABC 和△DEF 中,AB DEB E BC EF =⎧⎪∠=∠⎨⎪=⎩ABC ≌△DEF 2、.(ASA ) 在△ABC 和△DEF 中,∵ B EBC EF C F ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEF 3、“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等.(AAS ) 在△ABC 和△DEF 中,∵B EC F AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF4、“边边边”定理:三边对应相等的两个三角形全等.(SSS)在△ABC和△DEF中,∵AB DE BC EF AC DF=⎧⎪=⎨⎪=⎩∴△ABC≌△DEF另外,判定两个直角三角形全等还有另一种方法.:斜边和一条直角边对应相等的两个直角三角形全等.(HL)在Rt△ABC和Rt△DEF中,∵AB DEAC DF=⎧⎨=⎩∴ Rt△ABC≌Rt△DEF四、全等三角形的证明思路:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧)找任意一边()找两角的夹边(已知两角)找夹已知边的另一角()找已知边的对角()找已知角的另一边(边为角的邻边)任意角(若边为角的对边,则找已知一边一角)找第三边()找直角()找夹角(已知两边AASASAASAAASSASAASSSSHLSAS[例7]如图,已知AB=AE,∠1=∠2,∠B=∠E,求证:BC=ED.[例8]如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.求证:∠ACE=∠DBF.[例9]如图,在Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.[例10] 如图,AC=DF,AD=BE,BC=EF.求证:AC∥DF.[例11]如图,AD是△ABC中BC边上的中线,求证:1()2AD AB AC<+[例12]如图,AB∥CD,EC、EB分别平分∠BCD和∠CBA,点E在AD上,求证:BC=AB+CD.[例13]如图,已知△ABC中,AC=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF 的直角顶点D放在AC的中点上(直角三角形的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.(1)在图(1)中,DE交AB于M,DF交BC于N.①证明DM=DN;②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的.若不发生变化,求出其面积. (2)继续旋转至图(2)的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)继续旋转至图(3)的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?请写出结论,不用证明.【综合练习】一、选择题1、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等.其中真命题的个数有( )A、3个B、2个C、1个D、0个2、下列说法正确的是()A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两角和其中一角的对边对应相等的两个三角形全等3、如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是()A. 相等B. 不相等C. 互余或相等D. 互补或相等4、已知△ABC≌△DEF,若∠A=50°,∠C=30°,则∠E等于()A. 30°B. 50°C.60°D.100°5、已知△ABC和△DEF中,∠B=∠E,∠C=∠F,若要△ABC≌△DEF,只要满足下列条件中的()A. AB=DFB.BC=DFC. AC=DED.BC=EF6、如图,AB=AC,EB=EC,那么图中的全等三角形共有()A. 1对B. 2对C.3对D.4对7、某同学不小心把一块三角形玻璃打碎,变成了如图所示的三块,现在要到玻璃店去配一块完全一样的玻璃,那么应带()去,才能配好.A. ①B.②C.③D.任意一块8、已知:的三边分别为,的三边分别为,且有,则与().A.一定全等 B.不一定全等 C.一定不全等 D.无法确定9、如图,已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AC=AE,则有( )A、△ABD≌△AFDB、△AFE≌△ADCC、△AEF≌△DFCD、△ABC≌△ADE(第9题)(第10题)(第11题)10、如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有()A.1个 B.2个C.3个D.4个11、如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=64,且BD:CD=9:7,则点D到AB边的距离为( )A、18B、32C、28D、2412、如果D是△ABC中BC边上一点,并且△ADB≌△ADC,则△ABC是()A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形二、填空题13、已知:△ABC ≌△A ′B ′C ′,∠A=∠A ′,∠B=∠B ′,∠C=70°,AB=15cm ,则∠C ′=_________,A ′B ′=__________.14、如图,在△ABC 和△FED ,AD=FC ,AB=FE ,当添加条件__________时,就可得到△ABC ≌△FED.(只需填写一个你认为正确的条件)(第14题) (第15题) (第16题)15、如图,BE ,CD 是△ABC 的高,且BD =EC ,判定△BCD ≌△CBE 的依据是 . 16、如图,在△ABC 中,AD=DE ,AB=BE ,∠A=80°,则∠CED=_____.17、如图,△ABC ≌△ADE ,BC 的延长线交DA 于点F ,交DE 于点G ,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB=_________.18、如图是重叠的两个直角三角形,将其中一个直角三角形沿BC 方向平移得到△DEF.如果AB=8cm ,BE=4cm ,DH=3cm ,那么图中阴影部分面积为_______cm 2. 三、解答题19、如图,在△ABC 中,F 为AC 的中点,E 为AB 上一点,D 为EF 延长线上一点,∠A=∠ACD.求证://CD AE .20、如图,在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E ,AD 、CE 交于点H ,已知EH=EB=3,AE=4,求CH 的长.21、如图,已知AD为△ABC的中线,试比较AB+AC与2AD的大小.22、如图,∠ABC=90°,AB=AC,D为AC上一点,分别过A、C作BD的垂线,垂足分别为E、F.求证:EF=CF-AE.23、(1)如图(1),A、E、F、C在同一条直线上,AE=CF,DE⊥AC,BF⊥AC,若AB=CD. 求证:BD平分EF;(2)若将图形变为图(2),其余条件不变,上述结论是否成立?请说明理由.24、如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B、C 在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:BD=DE+CE;(2)若直线AE绕点A旋转到图(2)的位置(BD<CE)时,其余条件不变,问BD与DE、CE 的关系如何?请给予证明;(3)若直线AE绕点A旋转到图(3)的位置(BD>CE)时,其余条件不变,问BD与DE、CE 的关系如何?请直接写出结果,不需证明.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的概念和性质(提高)【学习目标】1.理解全等三角形及其对应边、对应角的概念;能准确辨认全等三角形的对应元素. 2.掌握全等三角形的性质;会用全等三角形的性质进行简单的推理和计算,解决某些实际问题.【要点梳理】要点一、全等形形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.要点诠释:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.要点二、全等三角形能够完全重合的两个三角形叫全等三角形.要点三、对应顶点,对应边,对应角1. 对应顶点,对应边,对应角定义两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.要点诠释:在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.2. 找对应边、对应角的方法(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;(3)有公共边的,公共边是对应边;(4)有公共角的,公共角是对应角;(5)有对顶角的,对顶角一定是对应角;(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.要点四、全等三角形的性质全等三角形的对应边相等;全等三角形的对应角相等;要点诠释:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.【典型例题】类型一、全等形和全等三角形的概念1、请观察下图中的6组图案,其中是全等形的是__________.【答案】(1)(4)(5)(6);【解析】(1)(5)是由其中一个图形旋转一定角度得到另一个图形的,(4)是将其中一个图形翻折后得到另一个图形的,(6)是将其中一个图形旋转180°再平移得到的,(2)(3)形状相同,但大小不等.【总结升华】是不是全等形,既要看形状是否相同,还要看大小是否相等.举一反三:【变式1】全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1),若运动方向相反,则称它们是镜面合同三角形(如图2),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°,下列各组合同三角形中,是镜面合同三角形的是( )【答案】B;提示:抓住关键语句,两个镜面合同三角形要重合,则必须将其中一个翻转180°,B答案中的两个三角形经过翻转180°就可以重合,故选B;其它三个选项都需要通过平移或旋转使它们重合.类型二、全等三角形的对应边,对应角2、如图,△ABD≌△CDB,若AB∥CD,则AB的对应边是()A.DB B. BC C. CD D. AD【答案】C【解析】因为AB∥CD,所以∠CDB=∠ABD,这两个角为对应角,对应角所对的边为对应边,所以,BC和DA为对应边,所以AB的对应边为CD.【总结升华】公共边是对应边,对应角所对的边是对应边.类型三、全等三角形性质3、(2014秋•盐城期中)如图,△ABD≌△EBC,AB=3cm,BC=6cm,(1)求DE的长.(2)若A、B、C在一条直线上,则DB与AC垂直吗?为什么?【思路点拨】(1)根据全等三角形对应边相等可得BD=BC=6cm,BE=AB=3cm,然后根据DE=BD ﹣BE代入数据进行计算即可得解;(2)DB⊥AC.根据全等三角形对应角相等可得∠ABD=∠EBC,又A、B、C在一条直线上,根据平角的定义得出∠ABD+∠EBC=180°,所以∠ABD=∠EBC=90°,由垂直的定义即可得到DB⊥AC.【答案与解析】解:(1)∵△ABD≌△EBC,∴BD=BC=6cm,BE=AB=3cm,∴DE=BD﹣BE=3cm;(2)DB⊥AC.理由如下:∵△ABD≌△EBC,∴∠ABD=∠EBC,又∵∠ABD+∠EBC=180°,∴∠ABD=∠EBC=90°,∴DB⊥AC.【总结升华】本题主要考查了全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.也考查了平角的定义与垂直的定义,熟记性质与定义是解题的关键.举一反三:【变式】(2014春•吉州区期末)下列命题中:(1)形状相同的两个三角形是全等形;(2)在两个全等三角形中,相等的角是对应角,相等的边是对应边;(3)全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有()A.3个B.2个C.1个D.0个【答案】C;提示:(1)形状相同、大小相等的两个三角形是全等形,而原说法没有指出大小相等这一点,故(1)错误;(2)在两个全等三角形中,对应角相等,对应边相等,而非相等的角是对应角,相等的边是对应边,故(2)错误;(3)全等三角形对应边上的高、中线及对应角平分线分别相等,故(3)正确.综上可得只有(3)正确.故选C .4、 如图,△ABE 和△ADC 是△ABC 分别沿着AB ,AC 翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,∠α的度数是_________.【思路点拨】(1)由∠1,∠2,∠3之间的比例关系及利用三角形内角和可求出∠1,∠2,∠3的度数;(2)由全等三角形的性质求∠EBC ,∠BCD 的度数;(3)运用外角求∠α的度数.【答案】∠α=80°【解析】∵∠1∶∠2∶∠3=28∶5∶3,设∠1=28,∠2=5,∠3=3,∴28+5+3=36=180°,=5°即∠1=140°,∠2=25°,∠3=15°∵△ABE 和△ADC 是△ABC 分别沿着AB ,AC 翻折180°形成的,∴△ABE ≌△ADC ≌△ABC∴∠2=∠ABE ,∠3=∠ACD∴∠α=∠EBC +∠BCD =2∠2+2∠3=50°+30°=80°【总结升华】此题涉及到了三角形内角和,外角和定理,并且要运用全等三角形对应角相等的性质来解决问题.见“比例”设未知数是比较常用的解题思路.举一反三:【变式】如图,在△ABC 中,∠A :∠ABC:∠BCA =3:5:10,又△MNC≌△ABC,则∠BCM:∠BCN等于( )A .1:2B .1:3C .2:3D .1:4【答案】D ;提示:设∠A=3,∠ABC =5,∠BCA=10,则3+5+10=18x x x x x x x x x x x x x x x xx=180°,=10°. 又因为△MNC≌△ABC,所以∠N=∠B=50°,CN=CB,所以∠N=∠CBN=50°,∠ACB=∠MCN=100°,∠BCN=180°-50°-50°=80°,所以∠BCM:∠BCN=20°:80°=1:4.【巩固练习】一、选择题1.下列命题中,真命题的个数是()①全等三角形的周长相等②全等三角形的对应角相等③全等三角形的面积相等④面积相等的两个三角形全等A.4个 B.3个 C.2个 D.1个2. 如图,△ABC≌ΔADE,若∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为()A.40° B.35° C.30° D.25°3.下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有( )A.3个B.2个C.1个D.0个4.△ABC≌△DEF,且△ABC的周长为100,A、B分别与D、E对应,且AB=35,DF =30,则EF的长为()A.35 B.30 C.45 D.555.(2014秋•红塔区期末)如图,已知△ACE≌△DFB,下列结论中正确的个数是()①AC=DB;②AB=DC;③∠1=∠2;④AE∥DF;⑤S△ACE=S△DFB;⑥BC=AE;⑦BF∥EC.6.如图,△ABE≌△ACD,AB=AC, BE=CD, ∠B=50°,∠AEC=120°,则∠DAC的度数为()A.120°B.70 °C.60°D.50°二、填空题7. 如图,把△ABC绕C点顺时针旋转35°,得到△,交AC于点D,则.cm cm cmcm cm cm cm''A B C''A BAB'D =∠8. 如图,△ABC ≌△ADE ,如果AB =5,BC =7,AC =6,那么DE 的长是________.9. 如图,△ABC≌△ADE,则,AB = ,∠E =∠ ;若∠BAE=120°,∠BAD=40°,则∠BAC=___________.10.(2014•梅列区质检)如图,△ACB ≌△A ′CB ′,∠BCB ′=30°,则∠ACA ′的度数为__________.11. △ABC 中,∠A ∶∠C ∶∠B =4∶3∶2,且△ABC ≌△DEF ,则∠DEF =______12. 如图,AC 、BD 相交于点O ,△AOB≌△COD,则AB 与CD 的位置关系是 .三、解答题13. 如图,△ABC 中,∠ACB =90°,△ABC ≌△DFC ,你能判断DE 与AB 互相垂直吗?说出你的理由.cm cmcm14.(2014秋•无锡期中)如图,已知△ABC ≌△DEF ,∠A=30°,∠B=50°,BF=2,求∠DFE的度数和EC 的长.15.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,(1)写出图中一对全等的三角形,并写出它们的所有对应角;(2)设的度数为,∠的度数为,那么∠1,∠2的度数分别是多少?(用含有或的代数式表示)(3)∠A 与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.【答案与解析】一.选择题1. 【答案】 B ;【解析】①②③是正确的;2. 【答案】B ;【解析】∠EAC =∠BAD =180°-80°-30°-35°=35°;3. 【答案】C ;【解析】只有(3)是正确的命题;4. 【答案】A ;【解析】AC =DF =30,EF =BC =100-35-30=35;5. 【答案】C ;【解析】解:∵△ACE ≌△DFB ,∴AC=DB ,①正确;∠ECA=∠DBF ,∠A=∠D ,S △ACE=S △DFB ,⑤正确;∵AB+BC=CD+BC ,∴AB=CD ②正确;∵∠ECA=∠DBF ,∴BF ∥EC ,⑦正确;AED ∠x ADE y xy∠1=∠2,③正确;∵∠A=∠D ,∴AE ∥DF ,④正确.BC 与AE ,不是对应边,也没有办法证明二者相等,⑥不正确.故选C .6. 【答案】B ;【解析】由全等三角形的性质,易得∠BAD =∠CAE =10°,∠BAC =80°,所以∠DAC =70°.二.填空题7. 【答案】35° ;【解析】旋转得到的三角形和原三角形全等,所以,,所以,180°-∠-∠=180°-(∠ABC +∠)=∠=35°.8. 【答案】7;【解析】BC 与DE 是对应边;9.【答案】AD C 80°;【解析】∠BAC =∠DAE =120°-40°=80°;10.【答案】30°;【解析】解:∵△ACB≌△A′CB′,∴∠ACB=∠A′CB′,∵∠BCB′=∠A′CB′﹣∠A′CB,∴∠ACA′=∠ACB﹣∠A′CB,∴∠ACA′=∠BCB′=30°.故答案为:30°.11.【答案】40°;【解析】∠DEF =∠ABC =×180°=40°; 12.【答案】平行;【解析】由全等三角形性质可知∠B =∠D ,所以AB ∥CD.三.解答题13.【解析】DE 与AB 互相垂直.∵△ABC ≌△DFC∴∠A =∠D ,∠B =∠CFD ,又∵∠ACB =90°∴∠B +∠A =90°,而∠AFE =∠CFD∴∠AFE +∠A =90°,即DE ⊥AB.14.【解析】解:∵∠A=30°,∠B=50°,∴∠ACB=180°﹣∠A ﹣∠B=180°﹣30°﹣50°=100°,∵△ABC ≌△DEF ,∴∠DFE=∠ACB=100°,EF=BC ,∴EF ﹣CF=BC ﹣CF ,即EC=BF ,'B C BC =A B C=ABC ''∠∠AB D ='∠BB C 'A'B'C BB C 'BCB 'cm 2432++∵BF=2,∴EC=2.15.【解析】(1)△EAD ≌△,其中∠EAD =∠,;(2)∠1=180°-2,∠2=180°-2;(3)规律为:∠1+∠2=2∠A .EA D 'EA D 'AED A ED ADE A DE ''=∠=,∠∠∠x y。
