2012-2013学年度九年级(上)期末质检复习检测数学试卷
2012-2013学年江苏省徐州市九年级(上)期末数学试卷

2012-2013学年江苏省徐州市九年级(上)期末数学试卷一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填写在第3页相应的答题栏内,在卷Ⅰ上答题无效)1.(3分)﹣2的相反数是()A.2 B.﹣2 C.D.﹣2.(3分)计算(﹣1)(+1)的结果是()A.1 B.﹣1 C.+1 D.3+23.(3分)若等腰三角形的两边长分别为2和5,则它的周长为()A.9 B.7 C.12 D.9或124.(3分)下列坐标表示的点中,不在反比例函数y=的图象上的是()A.(﹣2,﹣3)B.(﹣1,﹣6)C.(﹣0.5,12)D.(1.5,4)5.(3分)若正方形的对角线长为,则它的面积为()A.1 B.C.2 D.26.(3分)已知x2﹣1=﹣x,则x﹣的值等于()A.0.382 B.0.618 C.1 D.﹣17.(3分)若实数a、b在数轴上对应点的位置如图所示,则可化简为()A.a+b B.a﹣b C.b﹣a D.﹣a﹣b8.(3分)如图,在⊙O中,∠AOB=120°,=2,则∠ADC等于()A.15°B.20°C.30°D.40°二、填空题(本大题共有8小题,每小题3分,共24分.请将答案填写在第3页相应的答题处,在卷Ⅰ上答题无效)9.(3分)若二次根式有意义,则x的取值范围是.10.(3分)我国“钓鱼岛”周围海域面积约为170 000km2,该数用科学记数法可记作km2.11.(3分)方程x2﹣2x=0的根是.12.(3分)如图为我市某周内的气温走势图,这七天中,温差最大的一天是.13.(3分)如图,半径为1的圆片与数轴相切于原点,将该圆片沿数轴向负方向滚动一周,点A从原点到达点A′的位置,则数轴上点A′对应的实数为.14.(3分)若将一根长为8m的绳子围成一个面积为3m2的矩形,则该矩形的长为m.15.(3分)若一次函数y=x+b的图象与两坐标围成的三角形面积为2,则b=.16.(3分)如图,扇形OAB的圆心角为90°,正方形OCDE的顶点C、E、D分别在OA、OB、上.AF⊥OA且与ED的延长线交于点F.若正方形的边长为1,则图中阴影部分的面积为.三、解答题(本大题共有9小题,共72分)17.(8分)(1)计算:(﹣1)2+()0﹣()﹣1;(2)解方程:x2﹣2x﹣3=0.18.(6分)甲、乙两人进行射击比赛,在相同条件下各射击10次,成绩如图:(1)填表(2)请从不同角度评价甲、乙两人的打靶成绩.19.(8分)如图,在△ABC中,D、E分别是AC、AB的中点,BD为角平分线.求证:(1)∠EBD=∠EDB;(2)BE=BC.20.(8分)如图,在⊙O中,直径AB⊥弦CD,垂足为P,OB=5,PB=2,求CD 的长.21.(8分)如图,在Rt△ABC中,∠ABC=90°,BC=5cm,AC﹣AB=1cm.(1)求AB、AC的长;(2)求△ABC内切圆的半径.22.(8分)某网店以每件40元的价格购进一批商品,若以单价60元销售,每月可售出300件.调查表明:单价每上涨1元,该商品每月的销量就减少10件.问:单价定为多少元时,每月销售该商品的利润最大?23.(8分)如图,抛物线为二次函数y=x2﹣4x的图象.(1)抛物线的顶点A的坐标是;(2)抛物线与x轴的交点的坐标是;(3)将抛物线绕原点O旋转180°,求所得图象对应二次函数的关系式.24.(8分)如图,在梯形ABCD中,AD∥BC,∠A=∠B=90°,BC=4AD.AB为⊙O 的直径,OA=2,CD与⊙O相切于点E,求CD的长.25.(10分)如图①.点C、B、E、F在直线l上,线段AB与DE重合.将等腰直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG平移,当C、F重合时停止运动.已知△ABC与正方形DEFG重叠部分的面积y(cm2)与运动时间x(s)的函数图象如图②所示.请根据图中信息解决下列问题:(1)填空:m=s;n=cm2;(2)分别写出0≤x≤4和4<x≤m时,y与x的函数关系式;(3)x为何值时,重叠部分的面积为 3.5cm2?2012-2013学年江苏省徐州市九年级(上)期末数学试卷参考答案与试题解析一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填写在第3页相应的答题栏内,在卷Ⅰ上答题无效)1.(3分)﹣2的相反数是()A.2 B.﹣2 C.D.﹣【解答】解:根据相反数的定义,﹣2的相反数是2.故选:A.2.(3分)计算(﹣1)(+1)的结果是()A.1 B.﹣1 C.+1 D.3+2【解答】解:原式=()2﹣1=2﹣1=1.故选A.3.(3分)若等腰三角形的两边长分别为2和5,则它的周长为()A.9 B.7 C.12 D.9或12【解答】解:(1)若2为腰长,5为底边长,由于2+2<5,则三角形不存在;(2)若5为腰长,则符合三角形的两边之和大于第三边.所以这个三角形的周长为5+5+2=12.故选C.4.(3分)下列坐标表示的点中,不在反比例函数y=的图象上的是()A.(﹣2,﹣3)B.(﹣1,﹣6)C.(﹣0.5,12)D.(1.5,4)【解答】解:A、把(﹣2,﹣3)代入y=得:左边=﹣3,右边=﹣3,左边=右边,即(﹣2,﹣3)在反比例函数图象上,故本选项错误;B、把(﹣1,﹣6)代入y=得:左边=﹣6,右边=﹣6,左边=右边,即(﹣1,﹣6)在反比例函数图象上,故本选项错误;C、把(﹣0.5,12)代入y=得:左边=12,右边=﹣12,左边≠右边,即(﹣0.5,12)不在反比例函数图象上,故本选项正确;D、把(1.5,4)代入y=得:左边=4,右边=4,左边=右边,即(1.5,4)在反比例函数图象上,故本选项错误;故选C.5.(3分)若正方形的对角线长为,则它的面积为()A.1 B.C.2 D.2【解答】解:∵四边形ABCD是正方形,∴AO=BO=AC=,∵∠AOB=90°,由勾股定理得,AB=1,S正方形ABCD=1×1=1.故选A.6.(3分)已知x2﹣1=﹣x,则x﹣的值等于()A.0.382 B.0.618 C.1 D.﹣1【解答】解:由x≠0,已知等式变形得:x﹣=﹣1.故选D7.(3分)若实数a、b在数轴上对应点的位置如图所示,则可化简为()A.a+b B.a﹣b C.b﹣a D.﹣a﹣b【解答】解:∵实数a、b在数轴上对应点的位置可知b>a,∴b﹣a>0.原式==b﹣a.故选:C.8.(3分)如图,在⊙O中,∠AOB=120°,=2,则∠ADC等于()A.15°B.20°C.30°D.40°【解答】解:连接OC,∵∠AOB=120°,∴=120°,∵=2,∴==×120°=40°,∴∠AOC=40°,∴∠ADC=∠AOC=×40°=20°.故选B.二、填空题(本大题共有8小题,每小题3分,共24分.请将答案填写在第3页相应的答题处,在卷Ⅰ上答题无效)9.(3分)若二次根式有意义,则x的取值范围是x≥1.【解答】解:根据二次根式有意义的条件,x﹣1≥0,∴x≥1.故答案为:x≥1.10.(3分)我国“钓鱼岛”周围海域面积约为170 000km2,该数用科学记数法可记作 1.7×105km2.【解答】解:170 000=1.7×105,故答案为:1.7×105.11.(3分)方程x2﹣2x=0的根是x1=0,x2=2.【解答】解:因式分解得x(x﹣2)=0,解得x1=0,x2=2.故答案为x1=0,x2=2.12.(3分)如图为我市某周内的气温走势图,这七天中,温差最大的一天是周六.【解答】解:这七天的温差分别是:昨天:﹣2﹣(﹣10)=8;今天:2﹣(﹣6)=8;周二:0﹣(﹣5)=5;周三:2﹣(﹣3)=5;周四:3﹣(﹣1)=4;周五:6﹣0=6;周六:4﹣(﹣5)=9;则温差最大的一天是周六.故答案为周六.13.(3分)如图,半径为1的圆片与数轴相切于原点,将该圆片沿数轴向负方向滚动一周,点A从原点到达点A′的位置,则数轴上点A′对应的实数为﹣2π.【解答】解:∵圆的半径为1,∴周长为2π,∴点A′对应的实数为﹣2π.故答案为:﹣2π.14.(3分)若将一根长为8m的绳子围成一个面积为3m2的矩形,则该矩形的长为3m.【解答】解:设该矩形的长为xm,则宽为(4﹣x)m,由题意,得x(8÷2﹣x)=3,解得:x1=3,x2=1.答:矩形的长为3m.15.(3分)若一次函数y=x+b的图象与两坐标围成的三角形面积为2,则b=±2.【解答】解:∵令x=0,则y=b;令y=0,则x=﹣b,∴一次函数y=x+b的图象与x、y轴的交点分别为(﹣b,0),(0,b),∴b2=2,解得b=±2.故答案为:±2.16.(3分)如图,扇形OAB的圆心角为90°,正方形OCDE的顶点C、E、D分别在OA、OB、上.AF⊥OA且与ED的延长线交于点F.若正方形的边长为1,则图中阴影部分的面积为﹣1.【解答】解:连接OD,∵正方形OCDE的面积为1,∴正方形OCDE的边长为1,∴OD=,∴AC=﹣1,∵DE=DC,BE=AC,=,∴S=长方形ACDF的面积=AC•CD=﹣1.阴故答案为:﹣1.三、解答题(本大题共有9小题,共72分)17.(8分)(1)计算:(﹣1)2+()0﹣()﹣1;(2)解方程:x2﹣2x﹣3=0.【解答】解:(1)原式=1+1﹣2=0;(2)由原方程,得(x﹣3)(x+1)=0,则x﹣3=0或x+1=0,解得,x1=3,x2=﹣1.18.(6分)甲、乙两人进行射击比赛,在相同条件下各射击10次,成绩如图:(1)填表(2)请从不同角度评价甲、乙两人的打靶成绩.【解答】解:(1)由图形可知,甲的最好成绩是9环,所以甲命中9环以上次数为0次;把乙运动员10次比赛成绩按从小到大的顺序排列为:2、4、6、7、7、8、8、9、9、10;位于中间的两个数是7、8,所以乙的中位数为:(7+8)÷2=7.5.填表如下:(2)①从平均数来看,两人成绩不相上下;②从中位数来看,乙的成绩较好;③从方差来看,甲的成绩比较稳定;④从成绩变化趋势看,乙的成绩越来越好.19.(8分)如图,在△ABC中,D、E分别是AC、AB的中点,BD为角平分线.求证:(1)∠EBD=∠EDB;(2)BE=BC.【解答】证明:(1)∵BD是角平分线,∴∠EBD=∠DBC,∵E、D是中点,∴ED是中位线,∴ED∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB;(2)由∠EBD=∠EDB得BE=DE,∵ED是中位线,∴ED=BC,∴BE=BC.20.(8分)如图,在⊙O中,直径AB⊥弦CD,垂足为P,OB=5,PB=2,求CD的长.【解答】解:连接OC,∵⊙O中,直径AB⊥弦CD,∴CD=2CP.在Rt△OPC中,∵PC2+PO2=OC2,且OP=OB﹣PB=5﹣2=3.∴PC===4,∴CD=2CP=8.21.(8分)如图,在Rt△ABC中,∠ABC=90°,BC=5cm,AC﹣AB=1cm.(1)求AB、AC的长;(2)求△ABC内切圆的半径.【解答】解:(1)设AB=xcm,则AC=(x+1)cm,∵在Rt△ABC中,由勾股定理得:AC2﹣AB2=BC2,∴((x+1)2﹣x2=52,解得:x=12,即AB=12cm,AC=13cm;(2)连接AO、BO、CO、OD、OE、OF,设内切圆的半径为y,根据题意,得S=×5×12=×5r+×12r+×13r,△ABC解得:r=2,即所求内切圆的半径为2cm.22.(8分)某网店以每件40元的价格购进一批商品,若以单价60元销售,每月可售出300件.调查表明:单价每上涨1元,该商品每月的销量就减少10件.问:单价定为多少元时,每月销售该商品的利润最大?【解答】解:根据题意得出:y=[300﹣10(x﹣60)](x﹣40)=﹣10(x﹣90)(x﹣40)=﹣10(x﹣65)2+6250.当x=65即单价为65元时,每月销售该商品的利润最大.23.(8分)如图,抛物线为二次函数y=x2﹣4x的图象.(1)抛物线的顶点A的坐标是(2,4);(2)抛物线与x轴的交点的坐标是(0,0),(4,0);(3)将抛物线绕原点O旋转180°,求所得图象对应二次函数的关系式.【解答】解:(1)y=x2﹣4x的顶点坐标是(2,﹣4);(2)当x2﹣4x=0时,解得x=4,x=0,即抛物线与x轴的交点坐标是(4,0),(0,0);(3)将抛物线绕原点O旋转180°,所得图象对应二次函数的关系式y=﹣x2+4x,故答案为:(2,﹣4),(4,0),(0,0).24.(8分)如图,在梯形ABCD中,AD∥BC,∠A=∠B=90°,BC=4AD.AB为⊙O 的直径,OA=2,CD与⊙O相切于点E,求CD的长.【解答】解:∵AB为⊙O的直径,∠A=∠B=90°,∴AD、BC均为⊙O的切线,又CD与⊙O相切于点E,∴DE=DA,CE=CB,∴CD=AD+BC,设AD=x,则BC=4AD=4x,CD=5x,如图所示,作梯形的高DF,在Rt△CDF中,DF=AB=2OA=4,CF=CB﹣BF=CB﹣AD=3x,CD=5x,由勾股定理得:DF2+FC2=CD2,得42+(3x)2=(5x)2,解得:x1=1,x2=﹣1(舍去),∴CD=5x=5.25.(10分)如图①.点C、B、E、F在直线l上,线段AB与DE重合.将等腰直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG平移,当C、F重合时停止运动.已知△ABC与正方形DEFG重叠部分的面积y(cm2)与运动时间x(s)的函数图象如图②所示.请根据图中信息解决下列问题:(1)填空:m=8s;n=8cm2;(2)分别写出0≤x≤4和4<x≤m时,y与x的函数关系式;(3)x为何值时,重叠部分的面积为 3.5cm2?【解答】解:(1)由题意可知,当点C与点E重合时,y有最大值,由图2知此时x=4s,∵等腰直角三角形ABC运动速度为1cm/s,∴CB=AB=1×4=4,=×4×4=8,即n=8cm2;∴S△ABC∵点C与点F重合时,面积达到最小值0,又EF=CB=4,∴t=8s,即m=8s.故答案为8,8;(2)当0≤x≤4时,如图,设DE与AC交于点H.∵BE=x,∴EH=CE=BC﹣BE=4﹣x,∴y=S=(EH+AB)•BE=(4﹣x+4)x=﹣x2+4x,梯形ABEH即y=﹣x2+4x;当4<x≤8时,如图,设GF与AC交于点I.∵BE=x,BC=4,∴CE=BE﹣BC=x﹣4,∴FI=CF=EF﹣EC=4﹣(x﹣4)=8﹣x,=CF2=(8﹣x)2=x2﹣8x+32,∴y=S△CFI即y=x2﹣8x+32;综上所述,y=;(3)当0≤x≤4时,令﹣x2+4x=3.5,整理,得x2﹣8x+7=0,解得x1=1,x2=7(不合题意,舍去);当4<x≤8时,令x2﹣8x+32=3.5,整理,得x2﹣16x+57=0,解得x1=8﹣,x2=8+(不合题意,舍去).综上所述,当x为1s或(8﹣)s时,重叠部分面积为3.5cm2.。
2012-2013九年级上学期期末试题

2012-2013学年度上学期期末考试题九年级数学、选择题(本大题有12小题,在下面的每小题的四个选项中,有且只有一个符合题意,把符合题意的选项代号填在题后括号内,每小题 3分,共5. 如图,O O 是厶ABC 的外接圆,/ BAC=60,若O O 的半径OC 为2,则 弦BC 的长为 A . 1B .、、3C. 2D. 2、36. 已知OA 平分/ BOC P 是OA 上任意一点,如果以 P 为圆心的圆与 OC 相 切,那么O P 与OB 的位置关系是( )A ・相离B •相切C •相交D •不能确定36 分.)1.下列各式中,正确的是( A ( 3)23 B •、. ( 3)22. 一兀一次方 程 x(x 2)2 A .— 1B . 2 3.关于x 的元- 一次方程x则m 的值是() A . 0B . 8)3 C •323 D . 32 3x 的根是()C . 1 和 2D . — 1 和 2(m 2)x m 1 0有两个相等的实数根,4.平面直角坐标系内一点M (-2A.(3,-2)B. (2,-3) CC • 4 .2D • 0 和 83)关于原点对称点的坐标是()• (-2,-3) D • (2,3)7. 以半径为2的圆内接正三角形、 正方形、正六边形的边心距为三边作三角 形,则( )8. 如图,在 Rt △ ABC 中,/ ACB=90,/ BAC=60 .把厶ABC 绕点A 按顺时 针方向旋转60°后得到△ ABC ,,若AB=4,则线段BC 在上述旋转过程中所 扫过部分(阴影部分)的面积是( )52A. 2 nB.n C.nD. 4n339. 已知三角形的两条边长分别是 7和3,第三边长为整数,则这个三角形的程x 2 6x n 0的一个解为洛1,则另一个解X 2=( )A.3B.4C.5D.612. 已知:M N 两点关于y 轴对称,且点 M 在双曲线尸占上,点N 在直线__ 2y=x+3上,设点 M 的坐标为(a , b ),则二次函数 y= - abx + (a+b ) x ( )A .有最大值,最大值为 -gB .有最大值,最大值为 書周长是偶数的概率是()A 1 m23 4 A .B .C.-555710.若二次函数y (x m)21 .当x w l 时, y 随x 的增大而减小,则m的取值是()A . m =l Bm >l CA.不能构成三角形B.这个三角形是等腰三角形 C.这个三角形是直角三角形D.这个三角形是钝角三角形m w l D . m > l C'11.二次函数y x 2 6x n 的部分图像如图所示,若关于 x 的一元二次方第5题图C.有最小值,最小值为2D.有最小值,最小值为-9冈1二、填空题(本题有6个小题,每小题3分,计15)13. 已知x =- 2是方程x2-ax + 6 = 0的一个根,则a = _____________ ,另一个根为_______ .14. (2,48 3.27).6= ________ .15. 如图,C是线段BD上一点,分别以BC CD为边在BD同侧作等边△ ABC和等边△ CDE,AD交CE于F, BE交AC于G,则图中可通过旋转而相互得到的三角形对数有____ 对.16. 如图,在Rt△ ABC中,/ C=90,/ A=60°, BC=4cm 以点C为圆心,以3cm长为半径作圆,则OC0 :②c>1;③2a- b<0 :④a+b+c<0.其中正确的命题是___________ .(只要求填写正确命题的序号)三、解答题(本题有9个小题,计69分.)其中x 3.F面四条信息:①b2 4ac18.(本题满分6分)先化简,再求值:1 x2 x 22 2x x x 2x 1 x 1与AB的位置关系是第15题图17.如图所示的二次函数19.(本题满分6分)一张桌子的桌面长6m宽4m台布面积是桌面面积的2倍,如果将台布铺在桌子上,各边垂下的长度相同,求这块台布的长和宽•20.(本题满分6分)一个不透明的布袋里装有3个球,其中2个红球,1 个白球,它们除颜色外其余都相同.⑴求摸出1个球是白球的概率;(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);⑶现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为 -,7 求n的值.21.(本题满分7分)如图,O 0的直径AB=10cm分线交O 0于D. (1 )求BC ADD BD的长; 弦AC=6cm / ACB的平(2 )求CD的长22.(本题满分7分)已知:关于x的方程ax2(1 )当a取何值时,二次函数y ax2 (1 3a)x(2)求证:a取任何实数时,方程ax2(1 3a)x (1 3a)x 2a 1 0 2a 1的对称轴是x=-2 ;2a 1 0总有实数根.23.(本题满分8分)某网店以每件60元的价格购进一批商品,若以单价80元销售.每月可售出300件调查表明:单价每上涨I元,该商品每月的销量就减少I0件。
2012~2013年人教版九年级上学期数学期末试卷40;含答案41;
17.解:
∴
18.解:由一元二次方程根与系数地关系可得: ,
∴ .
19.解:∵∠AOB=90°,∠B=30°,∴∠A=60°.由旋转性质得OA=OA′,∴△AOA′是等边三角形,
∴旋转角∠AOA′=∠α=60°.
20.解:由题意,得 解得- ≤k< 且k≠0.
21.解: (1)y1=-x2+2x+3,y2=3x+1.
∴AP是⊙O地切线;
(2) CD是⊙O地直径,连接AD,∴∠CAD=900,
∴AD=AC∙tan300= .
∵∠ADC=∠B=600,∴∠PAD=∠ADC-∠P=300,∴∠P=∠PAD,
∴PD=AD= .新课标第一网
24解:(1)由题意,得: =200+(80- )·20=-20 +1800,
∴销售量 件与销售单价 元之间地函数关系式为: =-20 +1800.
13.如图5,抛物线 =- 2+2 +m(m<0)与 轴相交于点A( 1,0)、B( 2,0),点A在点B地左侧.当 = 2-2时, 0(填“>”“=”或“<”号).__________________
14.抛物线y=﹣x2+bx+c地部分图象如图所示,若y>0,则x地取值范围是.
15、已知二次函数y=x2+bx-2地图象与x轴地一个交点为(1,0),则它与x轴地另一个交点坐标是_.
安徽省阜阳市第十中学2012~2013学年度九年级上期末考试数学试卷
参考答案
第一题:选择题(请把你认为正确地选项填到对应地空格里,每题只有一个正确答案)
题号
1
2
3
4
5
6
7
8
9
10
湖北省黄冈市启黄中学2012-2013学年九年级(上)期末数学试题(含答案)

黄冈市启黄中学2013届初三期末考试数 学 考 试 题命题:明元慧审稿:姚利霞校对:龙俊(满分:120分时间:120分钟)一、选择题(每小题3分,共24分) 1.在实数0,3-, 32-,2-中,最小的数是( ) A .32-B .3-C .0D .2-2.一种细胞的直径为0.00000156,将0.00000156用科学记数法表示应为( ) A .61056.1⨯B .61056.1-⨯C .51056.1-⨯ D .41056.1-⨯3.用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是()A. BC .D .4.下列运算正确的是( )A .1)1(+=+--x xB .459=-C .222)(b a b a -=-D .3)31(1=-5.如图,点A 是直线l 外一点,在l 上取两点B 、C ,分别以A 、C 为圆心,BC 、AB 为半径画弧,两弧交于点D ,分别连接AB 、AD 、CD ,则四边形ABCD 一定是( ) A .平行四边形 B .矩形 C .菱形D .梯形6.如图,AB 是O 的弦,半径OA =2,32sin =∠A ,则弦AB 的长为( ) A .352 B .132 C .4D .54BCAD 第5题图 第6题图第8题图7.已知:M 、N 两点关于y 轴对称,且点M 在双曲线xy 21=上,点N 在直线3+=x y 上,设点M 的坐标为),(b a ,则二次函数x b a abx y )(2++-=( ) A .有最大值,最大值为29-B .有最大值,最大值为29 C .有最小值,最小值为29D .有最小值,最小值为29-8.如图,A 、B 是双曲线)0(>=k xky 上的点,A 、B 两点的横坐标分别是a 、a 3,线段AB 的延长线交x 轴于点C ,若6=∆AOC S ,则k 的值为( ) A .2B .3C .4D .6二、填空题(每小题3分,共24分) 9.51-的倒数= . 10.分解因式:=-a ax 162.11.若线段CD 是由线段AB 平移得到的,点A (-2,3)的对应点为C (3,6),则点B (-5,-2)的对应点D的坐标是 . 12.若不等式组0122x a x x -≥⎧⎨->-⎩有解,则a 的取值范围是 .13.已知1O 与2O 的半径分别是方程0342=+-x x 的两实根,且221+=t O O ,若这两个圆相切,则t = .14.如图,已知AB 是O 的弦,30=∠B ,20=∠D ,C 是弦AB 上的任意一点(不与点A 、B 重合),连接CO 并延长,CO 交O 于点D ,连接AD ,则BOD ∠的度数为 .15.如图,已知矩形纸片ABCD ,2AD =,AB =A 为圆心,AD 长为半径画弧交BC 于点E ,将扇形AED 剪下围成一个圆锥,则该圆锥的底面半径为 . 16.如图,在ABC Rt ∆中,︒=∠90C ,︒=∠30B .P 是AB 上的动点(P 异于A 、B ),过点P 的直线截ABC Rt ∆,使截得的三角形与ABC Rt ∆相似,当=BA BP 时,截得的三角形面积为ABC Rt ∆面积的41.DBOC A第14题图第15题图DAB第16题图三、解答题(共计72分)17.(5分) 先化简代数式412)231(22-+-÷+-a a a a ,再从2-,2,0三个数中选一个恰当的数作为a 的值代入求值.18.(6分)某地为了了解当地推进“阳光体育”运动情况,就“中小学每天在校体育活动时间”的问题随机调查了300名中小学生.根据调查结果绘制成的统计图的一部分如图(其中分组情况见下表):请根据上述信息解答下列问题:(1)B 组的人数是 人;(2)本次调查数据(指体育活动时间)的中位数落在 组内;(3)若某地约有64000名中小学生,请你估计其中达到国家规定体育活动时间(不低于1小时)的人数约有多少?A B C D人数组别19.(6分)如图,在正方形ABCD 中,等边AEF ∆的顶点E 、F 分别在BC 和CD 上.(1)求证:CE =CF ;(2)若等边AEF ∆的边长为2,求正方形ABCD 的边长.20.(6分)如图所示,某海滨浴场东西走向的海岸线可近似看作直线l . 救生员甲在A 处的瞭望台上观察海面情况,发现其正北方向的B 处有人发出求救信号. 他立即沿AB 方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C 处入海,径直向B 处游去.甲在乙入海10秒后赶到海岸线上的D 处,再向B 处游去.若CD =40米,B 在C 的北偏东︒30方向,甲、乙的游泳速度均是2米/秒.问谁先到达B 处?请说明理由.D CEBA F瞭望台21.(8分)某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”、“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:(1)该顾客至少可得元购物券,至多可得元购物券;(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.22.(8分)某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍.若由一个工程队单独完成,C队比A队要多用10天.(1)求工程队A平均每天维修课桌的张数;(2)学校决定由三个工程队一齐施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,提高后,A、B的工作效率仍然相同,且都为C队的2倍.这样他们至少还需要3天才能完成整个维修任务.求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.23.(8分)如图,在ABC ∆中,AB =AC ,以AB 为直径的O 交BC 于点M ,AC MN ⊥于点N .(1)求证:MN 是O 的切线;(2)若︒=∠120BAC ,AB =2,求图中阴影部分的面积.24.(12分) 企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量1y (吨)与月份x (61≤≤x ,且x 取整数)之间满足的函数关系如下表:7至12月,该企业自身处理的污水量2y (吨)与月份x(127≤≤x ,且x 取整数)之间满足二次函数关系式c ax y +=22,其图象如图所示.1至6月,污水厂处理每吨污水的费用1z (元)与月份x 之间满足函数关系式x z 211=,该企业自身处理每吨污水的费用2z (元)与月份x 之间满足函数关系式2212143x x z -=;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.C(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出1y ,2y 与x 之间的函数关系式;(2)设该企业去年第x 月用于污水处理的费用为W (元),试求出W 与x 之间的函数关系式; (3)请你求出该企业去年哪个月用于污水处理的费用W (元)最多,并求出这个最多费用.25.(13分) 如图,已知抛物线c ax ax y +-=22与y 轴交于点C ,与x 轴交于A 、B 两点,点A 的坐标是(-1,0),O 是坐标原点,且OA OC 3=.点E 为线段BC 上的动点(点E 不与点B ,C 重合),以E 为顶点作︒=∠45OEF ,射线ET 交线段OB 于点F .(1) 求出此抛物线函数表达式,并直接写出直线BC 的解析式; (2)求证:COE BEF ∠=∠;(3)当EOF ∆为等腰三角形时,求此时点E 的坐标;(4)点P 为抛物线的对称轴与直线BC 的交点,点M 在x 轴上,点N 在抛物线上,是否存在以点A 、M 、N 、P 为顶点的平行四边形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.备用图2备用图1试数学答案一、选择题1、B2、B3、C4、D5、A6、D7、B8、B二、填空题9、-5 10、a (x +4)(x -4) 11、(0,1)12、a <113、2或014、100° 15、1316、13244三、解答题 17、解:21(2)(2)221(1)a a a a a a a -+--==+-- 原式,∵a ≠-2,2,∴取a =0,∴原式=2. 18、(1)30;(2)C ;(3)150906400051200()300+⨯=人19、解:(1)证明:在正方形ABCD 中,AB =AD ,∠B =∠D =90°.在等边△AEF 中,∵AE =AF ,∴Rt △ABE ≌Rt △ADF (HL ),∴BE =DF . 又∵BC =CD , ∴BC -BE =CD -DF ,即CE =CF .(2)在Rt △CEF 中,EF =2,CE =CF ,∴∠CEF =∠CFE =45°.cos 45CE EF ∴=︒=设AB =x,则BE x =Rt △ABE 中,AB 2+BE 2=AE 2,222212(210,220,x x x x x x x ABCD +=∴--=∴==>∴=∴ 即又正方形 20、解:乙先到达B 处,理由如下:由题可知:BD ⊥CD . ∠CBD =30°. ∴BC =2CD =80米,1010)28040()2BD t t ===+=+==甲乙秒秒 ∵t 甲>t 乙∴乙先到达B 处. 21、(1)10;80;(2)树状图如图所示:由树状图可知,本次实验共有12种等可能的结果,并且所获购物券的金额不低于50元有6种. ∴61(50)122P ==该顾客所获购物券的金额不低于元. 22、解:(1)设A 队平均每天维修课桌x 张,则600600102x x =+ ∴x =60.经检验:x =60是原分式方程的解,且符合题意. ∴工程队A 平均每天维修课桌60张. (2)设A 队提高效率后平均每天多维修a 张, 2天已修:2(60+60+30)=300(张) 还剩:600+360-300=660(张)3(606030)6604(606030)22553(150)6604(150)22a aa a a a a a++++++++++++≤≤即≤≤∴6≤a ≤28.23、解:(1)证明:连OM .∵AB =AC∴∠B =∠C∵OM =OB∴∠B =∠OMB∴∠C =∠OMB∴OM ∥AC∵MN ⊥AC∴MN ⊥OM又∵M 在⊙上且OM 为⊙O 的半径∴MN 是⊙O 的切线.(2)连AM .∵AB 是⊙O 的直径∴∠AMB =90°即AM ⊥BC又∵∠BAC =120°∴∠BAM =∠CAM =12∠BAC =60° ∴△AOM 为等边三角形112AM OA AB ∴===. 在Rt △AMN 中,∠AMN =30°,211,22111())2226013606.6ANMD AOM AOM AN AM MN S MN OM AN S S S S πππ∴===∴=+=+===∴=-=- 梯形扇形阴梯形扇形24、解:(1)112000y x=;y 2=x 2+10000 (2)当1≤x ≤6时,222120001200031(12000)()241260009000100090001000 1000100003000x W x x x x x x xx x =+--=+--+=-+- 当7≤x ≤12时,W =1.5(x 2+10000)+2(12000-x 2-10000)=1.5x 2+15000+4000-2x 2=-0.5x 2+19000221000100003000 (16)0.519000 (712)x x x W x x ⎧-+-⎪∴=⎨-+⎪⎩≤≤≤≤ (3)当1≤x ≤6时,W =-1000(x -5)2+22000∵-1000<0且1≤x ≤6∴当x =5时,W max =22000当7≤x ≤12时,W 随x 的增大而减小.∴当x =7时,W max =18975.5∵22000>18975.5∴当x =5时,W max =22000.∴第5个月,污水处理费用最大为22000元.25、解:(1)OC =3OA =3∴C 为(0,-3)∵抛物线过(-1,0)和(0,-3)20313a a c c a c ++=⎧∴⎨=-⎩=⎧∴⎨=-⎩ ∴y =x 2-x -3BC :y =x -3(2)∵OB =OC =3∴∠OCB =∠OBC =45°又∵∠OEF +∠BEF =∠COE +∠OCB且∠OEF =45°∴∠BEF =∠COE .(3)①∵∠OFE =∠BEF +∠OBC >45°∴∠OFE >∠OEF∴OE >OF 即OE ≠OF .②当OE =EF 时,∠BEF =∠COE ,∠OCE =∠EBF∴△COE ≌△BEF (AAS )∴BE =CO =3.过E 作ED ⊥x 轴于D .cos 453(3ED BD BE OD E ∴==︒=∴=-∴为③当OF =EF 时,则∠FOE =∠OEF =45°∴∠OFE =90°.∴EF ⊥OB .∴E 为BC 的中点,∴E 为33(,)22-.(4)对称轴为x =1,∴P 为(1,-2).①AP 为边,此时P 点纵坐标为2或-2,令x 2-2x -3=2即x 2-2x -5=01211(12)(12)(3(3x x N M ∴=+=∴+为或故为或令x 2-2x -3=-2即x 2-2x -1=01211(12)(12)(1(1x x N M ∴=+=-∴----+-为或故为或②AP 为对角线,设M 为(x ,0)则N 为(-x ,-2)∴x 2+2x -3=-2x 2+2x -1=01211(1(1x x M ∴=-+=-∴---为或综上所述:M为(1(1(3(3---或或或.。
2012-2013学年九年级数学上册期末试卷

2012-2013学年九年级数学上册期末试卷岳池县2012年秋季期末质量检测题九年级数学试卷(全卷满分120分,120分钟完卷)题号一二三四五总分总分人题分3018242820120得分得分评卷人一、选择题:(每小题3分,共30分)在下列各题中,每个题只有一个正确答案,请将正确答案的代号填在括号内。
()1.若是整数,则正整数n的最小值是A.2B.3C.4D.5()2.与的大小关系是A.>B.()3.若a(a-2)-8=0,则a3-1的值为A.63B.-9C.63或-9D.-63或9()4.一个图形无论经过平移还是旋转,有以下说法:①对应线段平行②对应线段相等③对应角相等④图形的形状和大小都没有发生变化其中说法正确的是A.①②③B.①②④C.①③④D.②③④()5.如图,从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60o,线段PA=10,那么弦AB的长是A.10B.12C.5D.10()6.在Rt△ABC中,∠C=90o,AB=13,AC=12,以B为圆心,6为半径的圆与直线AC的位置关系是A.相切B.相交C.相离D.不能确定()7.下列事件是必然事件的是A.打开电视机,任选一个频道,屏幕上正在播放天气预报B.到电影院任意买一张电影票,座位号是奇数C.在地球上,抛出去的篮球会下落D.掷一枚均匀的骰子,骰子停止转动后偶数点朝上()8.从连续的20个整数中,任意选取一个数,这个数是2的倍数的可能性和它是3的倍数的可能性相比A.3的倍数的可能性大B.2的倍数的可能性大C.两7的可能性相等D.不能确定()9.将抛物线y=4x2向上平移3个单位,再向右平移1个单位,那么得到的抛物线的解析式为A.y=4(x-1)2+3B.y=4(x-1)2-3C.y=4(x+1)2+3D.y=4(x+1)2-3()10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a、b同号;②当x=1时和x=3时,函数值相等;③4a+b=0;④当y=-2时,x的值只能取2;⑤当-1其中正确的有A.2个B.3个C.4个D.5个得分评卷人二、填空题:(每小题3分,共18分)11.在一个不透明袋中装有五个除数字外其它完全相同的小球,球面上分别写有0,1,2,3,4这5个数字,玲玲从袋中任意摸出一个小球,球面数字的平方根是有理数的概率是。
2012-2013九年级数学上册期末质量检测试卷(含二次函数、相似)
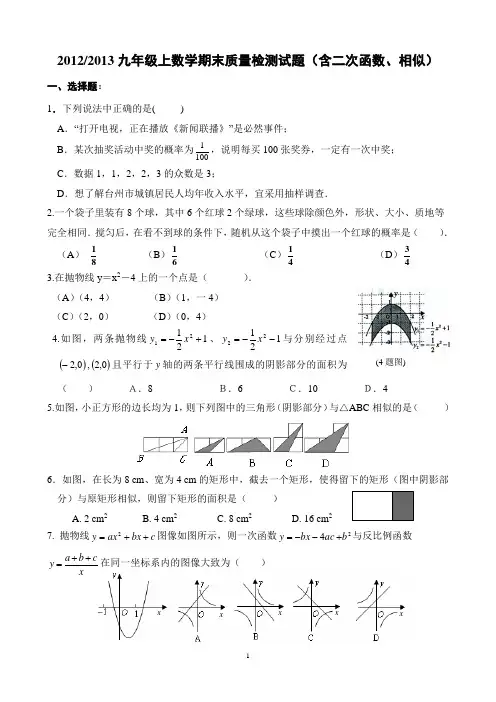
2012/2013九年级上数学期末质量检测试题(含二次函数、相似)一、选择题:1.下列说法中正确的是( )A .“打开电视,正在播放《新闻联播》”是必然事件;B .某次抽奖活动中奖的概率为1001,说明每买100张奖券,一定有一次中奖;C .数据1,1,2,2,3的众数是3;D .想了解台州市城镇居民人均年收入水平,宜采用抽样调查.2.一个袋子里装有8个球,其中6个红球2个绿球,这些球除颜色外,形状、大小、质地等 完全相同.搅匀后,在看不到球的条件下,随机从这个袋子中摸出一个红球的概率是( ). (A )81 (B )61 (C )41 (D )433.在抛物线y =x 2-4上的一个点是( ). (A )(4,4) (B )(1,一4) (C )(2,0) (D )(0,4)4.如图,两条抛物线12121+-=x y 、12122--=x y 与分别经过点()0,2-,()0,2且平行于y 轴的两条平行线围成的阴影部分的面积为( ) A.8 B.6 C.10 D.45.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC 相似的是( )6.如图,在长为8 cm 、宽为4 cm 的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )A. 2 cm 2B. 4 cm 2C. 8 cm 2D. 16 cm 27. 抛物线c bx ax y ++=2图像如图所示,则一次函数24b ac bx y +--=与反比例函数a b cy x++=在同一坐标系内的图像大致为( )(4题图)xxx x8.如图,已知正方形ABCD 的边长为4 ,E 是BC 边上的一个 动点,AE ⊥EF , EF 交DC 于F , 设BE =x ,FC =y ,则当 点E 从点B 运动到点C 时,y 关于x 的函数图象是( ).A .B .C .D .10.已知等于,那么yx y x 32=( )A.2B.3C.32 D.2311. 反比例函数xy 1=的图象在 ( )A.第一、三象限B.第二、四象限C.第一、二象限D.第三、四象限 12. 小明不慎把家里的一块圆形玻璃打碎了,其中四块碎片如图所示,为配到一块与 原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )A.第①块B.第②块C.第③块D.第④块13. 把抛物线22x y -=向上平移3个单位,所得新抛物线的解析式为( )A.322+-=x yB.322--=x yC.2)3(2+-=x y D.2)3(2--=x y14. 如图,△ABC 与△DEF 是位似图形,位似比为2:3, 已知AB=4, 则DE 的长等于( )A.4B.5C.6D.3815. 如图,冰淇淋蛋筒下部呈圆锥形,则此圆锥部分包装纸的面积(接缝面积忽略不计) 是( )A.15cm 2B.30cm2C.15πcm 2D.30πcm 216. 已知力F 所做的功是10焦,则力F 与物体在力的方向上通过的距离S (功=力×距离)的图象大致是ADBEF如下图中的( )17. 二次函数)0(2≠++=a c bx ax y 的图象如图所示,下列说法不正确...的是( ) A .0a > B .0c >C .02b a-< D .240b ac ->18. 你看过日出时的美丽景色吧!如图是一位同学从照片剪切下来的画面,“图上”太 阳与海平线交于A 、B 两点,他测得“图上”圆的半径是5cm ,AB=8cm ,若以目前 太阳所处的位置到太阳完全跳出海面的时间为16 min ,则“图上”太阳升起的速度为 ( )A.0.4cm/minB.0.5cm/minC.0.6cm/minD.0.7cm/min19. 一张等腰三角形纸片(如图),底边长为15cm ,底边上的高为22.5cm ,现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条,如图所示,已知剪得的纸条中有一张 是正方形,则这张正方形纸条是( ) A.第4张B.第5张C.第6张D.第7张二、填空题:20.抛物线y=x 2-2x-8的对称轴是直线 21.若双曲线xy 6-=经过点A (m, 1),则m 的值为____ __22.请写出一个开口向下,顶点坐标为(2,-3)的二次函数解析式(用顶点式表示), 如:____ _.23.如图,在△ABC 中,DE//BC ,DE 交AB 、AC 分别于点D 、E ,且AD :AB=1:2 ,若△ADE 的面积为2,则S △ABC =_____ ____.24.操场上有一棵树,数学兴趣小组的同学们想利用树影测量树高,在阳光下他们测得 一根长为1m 的直立竹竿的影长是1.5m ,此时,测得树的影长为16.5 m ,则树高为 ___ _ _m.25.如图,圆心角都是90°的扇形OAB 与扇形OCD 叠放在一起,OA=3, OC=1, 分别连结AC ,BD ,则图中阴影部分的面积为_____________26.. 如图,在反比例函数y=x4 (x>0)的图象上,有点P 1、P 2、P 3 、P 4 ,它们的横坐标依次是1、2、3、4,分别过这些点作x 轴 与y 轴的垂线,图中所构成的阴影部分面积从左到右依次为 S 1、S 2、S 3,则S 1+S 2+S 3=_____ ____.27.在一个袋中,装有五个除数字外其它完全相同的小球,球面上分别标有1、2、3、4、5这5个数字, 从中任摸一个球,球面数字是奇数的概率是 .28.花园中学举行以“保护环境,从我做起”为主题的演讲比赛.经预赛,七、八年级各有一名同学进入决 赛,九年级有两名同学进入决赛.前两名都是九年级同学的概率是 .29.已知A B C △与D EF △相似且面积比为4∶25,则A B C △与D EF △的相似比为 .30.如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A 处目测得点A 与甲、乙楼顶B C 、 刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是__________________米.第12题 第13题 31.将三角形纸片(△ABC )按如图所示的方式折叠,使点B 落在边AC 上,记为点B′,折痕为EF .已知 AB =AC =3,BC =4,若以点B′,F ,C 为顶点的三角形与△ABC 相似,那么BF 的长度是 . 32.若二次函数k x x y ++-=22的部分图象如图所示,则关于x 的一元二次方程022=++-k x x 的一个解31=x ,另一个解=2x ;33.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距 地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触 到绳子,则绳子的最低点距地面的距离为 米.第16题第15题xyOP 1P 2 P 3P 4yS 1S 2S 334.如图,是二次函数)0(2≠++=a c bx ax y 在平面直角坐标系中的图象,根据图形判断 ① c >0;② a +b +c <0;③ 2a -b <0; b 2+8a >4a c 中正确的是(填写序号) . 三、解答题:1.小刚参观上海世博会,由于仅有一天的时间,他上午从A —中国馆、B —日本馆、C —美国馆中任意选择一处参观,下午从D —韩国馆、E —英国馆、F —德国馆中任意选择一处参观.(1)请用画树状图或列表的方法,分析并写出小刚所有可能的参观方式(用字母表示即可); (2)求小刚上午和下午恰好都参观亚洲国家展馆的概率.2.如图7,△ABC 内接于⊙O ,AD 是△ABC 的边BC 上的高,AE 是⊙O 的直径,连接BE ,△ABE 与△ADC 相似吗?请证明你的结论.3.小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD =1.2m ,CE =0.8m ,CA =30m (点A 、E 、C 在同一直线上).已知小明的身高EF 是1.7m ,请你帮小明求出楼高AB (结果精确到0.1m ).4.如图,已知二次函数y =— 12 x 2+bx +c 的图象经过A (2,0)、B (0,—6)两点.(1)求这个二次函数的解析式;(2)设该二次函数图象的对称轴与x 轴交于点C ,连结BA 、BC ,求△ABC 的面积.5.如图,A B C △在方格纸中(1)请在方格纸上建立平面直角坐标系,使(23)(62)A C ,,,,并求出B 点坐标;(2)以原点O 为位似中心,相似比为2,在第一象限内将A B C △放大,画出放大后的图形A B C '''△; (3)计算A B C '''△的面积S .6.为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价 付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得 低于3500元/个.乙店一律按原价的80℅销售.现购买太阳能路灯x 个,如果全部在甲商家购买,则所需 金额为y 1元;如果全部在乙商家购买,则所需金额为y 2元. (1)分别求出y 1、y 2与x 之间的函数关系式;(2)若市政府投资140万元,最多能购买多少个太阳能路灯?A BC(第21题)7..如图,已知抛物线与x交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)。
(2021年整理)2012-2013学年度北师大版九年级数学上册期末试卷
2012-2013学年度北师大版九年级数学上册期末试卷(推荐完整)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2012-2013学年度北师大版九年级数学上册期末试卷(推荐完整))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2012-2013学年度北师大版九年级数学上册期末试卷(推荐完整)的全部内容。
2012—2013学年度北师大版九年级数学上册期末试卷(推荐完整)编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望 2012-2013学年度北师大版九年级数学上册期末试卷(推荐完整)这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为〈2012-2013学年度北师大版九年级数学上册期末试卷(推荐完整)〉这篇文档的全部内容.2012—2013学年九年级(上)期末试卷一、选择题(10小题,每题3分,共30分)。
1、下列三角形中,是正三角形的为( )①有一个角是60°的等腰三角形; ②有两个角是60°的三角形; ③底边与腰相等的等腰三角形; ④三边相等的三角形. A .①④B .②③C .③④D .①②③④2、如图1,在Rt △ACB 中,∠C=90°,BE 平分∠CBA 交AC 于点E ,过E 作ED ⊥AB 于D 点,当∠A=_____时,ED 恰为AB 的中垂线( )A .10°B .15°C .30°D .45°3、如图2,在平行四边形ABCD 中(AB >BC ),点E 、F 分别在AB 、CD 上移动,且AE=CF,则四边形BFDE 的形状不可能是( ) A .矩形B .菱形C .平行四边形D .梯形4、如图3,反比例函数y= xk(k >0)在第一象限内的图象如图,点M 是图象上一点,MP 垂直x 轴于点P ,如果△MOP 的面积为1,那么k 的值是( )A 、1B 、2C 、3D 、25、如图4,▱ABCD 的周长为16cm ,AC 与BD 相交于点O,OE⊥AC 交AD 于E ,则△DCE 的周长为( )A .4cmB .6cmC .8cmD .10cm6、下列三角形中,是正三角形的为( )①有一个角是60°的等腰三角形; ②有两个角是60°的三角形; ③底边与腰相等的等腰三角形; ④三边相等的三角形. A .①④B .②③C .③④D .①②③④7、下列四个命题中,假命题的是( )A .有三个角是直角的四边形是矩形B .对角线互相垂直平分且相等的四边形是正方形C .四条边都相等的四边形是菱形 D .顺次连接一个四边形各边中点,得到一个菱形,那么这个四边形是等腰梯形8、电影院呈阶梯或下坡形状的主要原因是( ) A .为了美观B .减小盲区C .增大盲区D .盲区不变9、面积为20平方厘米的矩形,其长宽分别为x 厘米和y 厘米,则y 与x 之间的函数关系式的图象为( )A .B .C .D .10、x 1,x 2是方程2x 2—4x+1=0的两根,则x 1+x 2=( ) A .2B .—2C 、21D 、31二、填空题(6小题,每题4分,共24分)11、请写出一个根为x=1,另一根满足-1<x <1的一元二次方程_____。
香坊区2012~2013学年度上学期期末调研测试九年级数学试卷及答案(扫描版)
香坊区2012——2013学年度上学期九年级期末调研测试数学试卷答案一、选择题:1.D 2.A 3.B 4.B 5.D 6.A 7.C 8.A 9.D 10.C 二、填空题: 11.(-2,3) 12.14-13.2 14.6 15.291832+-x x 16.3 17.-1219.2或220.5三、解答题: 21.原式=11(1)(1)1x x x x x x +=+-- …………3分 当x=2tan60°+1=1时…………………………………………1分原式6==…………………………………………………2分22.图形规范正确每题3分.23.证明:连接OA 、OB ,∵OA=OB ,∴∠OAB=∠OBA……………………………………1分在△OAE 和△OBF 中O A O B O AE O BF AE BF =⎧⎪=⎨⎪=⎩∠∠………………………………………………………2分 ∴△OAE ≌△OBF ……………………………………………………………1分 ∴OE=OF ……………………………………………………………………1分 ∵OC=OD∴OC-OE=OD-OF∴CE=DF ……………………………………………………………………1分 24.解:S=21102x x -+ …………………………………2分 ∵a=12-<0,∴S 有最大值∴当x=b 2a-=10时………2分,y 最大值=24ac b 4a-=214()01025014()2⨯-⨯-=⨯-………2分答:当x 为10米时,四边形ABCD 的面积最大,最大面积为50平方米.25.解:作CH ⊥AD 于H由题意得∠EAC=60°,∠FBC=30°, ∴∠CAB=30°, ∠CBD=60°……………………………1分∴所筹资金能将这块梯形空地植满草坪.……………………………1分27.(1) 设BD与y轴交点坐标为E,在Rt△BOE中,1163,22E O B O==⨯=∴E(0, 3), (1)分设直线BD的解析式为y=kx+b,603k bb-+=⎧⎨=⎩,∴123kb⎧=⎪⎨⎪=⎩,∴y=12x+3, ………………1分(2)15(0)52H E t=≤<,………………2分,1511)52H E t=-<≤ (2)分,(3)∵AP为直径,∴∠AQP=90°,过点Q作MN⊥BC.∵∠PQM+∠AQN=90°, ∠QAN+∠AQN=90°, ∴∠PQM=∠QAN,∵∠PMQ=∠ANQ,∴△ANQ∽△QPM, ∴12AQ AN QNPQ QM PM===,设AN=a,则QM=2a,OM=a,如图1,在Rt△BQM中,2162Q M aB M a==+,∴a=2, ………………1分∴NQ=MN-QM=113422-=,∴PM=2NQ=3, ∵PM=BM-BP=8-t, ∴8-t=3, ∴t1=5………………1分如图2,设AN1=b,则Q1M1=2b,OM1=b,在Rt△BQ1M1中,1112162Q M bBM b==-,∴b=65,………………1分∴N 1Q 1= M 1N 1- Q 1M 1=1112312510-=,∴P 1M 1=2N 1Q 1=315, ∵P 1M 1= BP 1-BM 1=24,5t -∴245t -=315,∴t 2=11 ………………1分28.(1)证明:∵∠BAC=60°,AB=AC, AD ⊥BC, DE ⊥AC,∴BD=DC, ∠DAC=∠EDC=30°,……………1分 ∴在Rt △DEC 中,2D C E C=,∴4B C E C=……………1分,在Rt △ADE 中, ∴2A D D E=,∴4A D D G=,……………1分∴B C E C=A D D G,∴B C A D=E C D G,……………1分,∵∠ADE=∠C,∴△ADG ∽△BCE, ……1分(2) ∵∠ADE+ ∠EDC =90°, ∠EDC+∠C=90°, ∴∠ADE=∠C, ∵∠DEC=∠AED=90°,∴△CDE ∽△DAE,∴C DD A =C ED E ,∴12B CD A=2C E D G ,∴B C C E =D A D G ,∠ADE=∠C, ∴△ADG ∽△BCE,∴4B E E C A G D G ==,∴22D G D E E C E C ==,∴tanC=12,……………1分 ∴∠DAG=∠EBC, ∠AMH=∠BMD, ∴∠AHE=∠ADB=90°, …………1分 设DG=a 5,则GE=a 5,EC=4a 5,DC=10a, ∴AD=5a, AE=a 5, ∴∠AGE=45°, ……………1分过E 作EF ⊥BC 于F ,∴EF=4a,FC=8a,BF=12a,∵MD ∥EF ,∴△BMD ∽△BEF, ∴M D B D E FB F=,∴31124===aa BFEF BDMD =tan ∠MBD= tan ∠DAG=13,在Rt △AHE 中,AH=a a 21025=,在Rt △AMH 中,AM=a 35=1∴53=a ,AD=3 (1)分,过点H 作HP ⊥AD 于点P,∴AH=10,AP=109,DP=1021,HP=103,∴22322=+=DPPHDH………1分(以上解答题如有不同解法并且正确,请按相应步骤给分)。
2012-2013学年九年级上期末数学试卷
A.
B.
C.
D.
考点: 简单组合体的三视图. 分析: 找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中. 解答: 解:先细心观察原立体图形的位置, 从正面看去,是一个矩形,矩形左上角缺一个角, 从左面看,是一个正方形, 从上面看,也是一个正方形, 故选 A. 点评: 本题考查了三视图的知识,主视图是从物体的正面看得到的视图. 5.(3 分)如图,在平行四边形 ABCD 中,AB=2,BC=3,∠ABC、∠BCD 的平分线分别 交 AD 于点 E、F,则 EF 的长是( )
.
A. 3
B.2
C.1.5
D. 1
考点: 平行四边形的性质;角平分线的定义;等腰三角形的判定与性质. 专题: 数形结合. 分析: 根据平行四边形的性质可知∠DFC=∠FCB,又因为 CF 平分∠BCD,所以∠DCF=∠FCB ,则∠DFC=∠DCF,则 DF=DC,同理可证 AE=AB,那么 EF 就可表示为 AE+FD﹣BC=2AB﹣BC,继而可得出答案. 解答: 解:∵平行四边形 ABCD, ∴∠DFC=∠FCB, 又 CF 平分∠BCD, ∴∠DCF=∠FCB,
A.△ACE
B.△ADF
C.△ABD
D.四边形 BCED
考点: 视点、视角和盲区. 分析: 根据盲区的定义,视线覆盖不到的地方即为该视点的盲区,由图知,E 是视点,找到 在 E 点处看不到的区域即可. 解答: 解:由图片可知,E 视点的盲区应该在△ABD 的区域内. 故选:C. 点评: 此题主要考查了视点、视角和盲区,解答此类问题,首先要确定视点,然后再根据盲 区的定义进行判断. 8.(3 分)若反比例函数图象经过点(﹣1,6),则下列点也在此函数上的是( )
2012-2013九上数学参考答案2013.1.10
九上数学期末试卷(参考答案)2013.01(本试卷满分150分 考试时间120分钟)一、选择题(本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一二、填空题(本大题共10个小题,每小题3分,共30分.)9. 1>x 10. 3 11. )2,1( 12. 能13. 6 14. 4 15. 5 16. 03017. 2 18. F三、解答题(本大题共10个小题,共96分,解答时应写出文字说明、证明过程或演算步骤) 19.(本题满分10分)计算: (1)原式=23 (2)原式=332 20.(本题满分10分)解方程:(1)2)1(1x x -=- (2)0222=-+x x解:2,121==x x 解:4171,417121--=+-=x x 21.(本题满分8分)(每小题2分)(1)画图(略) (2)(﹣3,﹣2) (3)(﹣2,3) (4)π21022.(本题满分8分) (1)9;9. (2)s 2甲=32 s 2乙=34. (每个2分) (3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.23.(本题满分8分)解:由题意可知:012=+++b a 1,2-=-=∴b a ………………………3分 此时一元二次方程为:0122=--x kx 有两个不等实根, ………………………4分 有:04442>+=-k ac b 且0≠k ………………………6分 所以实数k 的范围为:01≠->k k 且。
………………………8分24.(本题满分8分) 解:(1)设每年平均增长的百分率为x .6000(1+x )2=8640, ………………………3分 (1+x )2=1.44, ∵1+x >0,∴1+x=1.2,x=20%. ………………………5分答:每年平均增长的百分率为20%; ………………………6分 (2)按20%的平均增长率2013年该区教育经费为 8640×(1+20%)=10368(万元)>9500万元.故不能保持前两年的平均增长率. ………………………8分 25.(本题满分10分) 证明:①∵CN ∥AB ,∴∠DAC=∠NCA ,在△AMD 和△CMN 中,∵,∴△AMD ≌△CMN (ASA ), ∴AD=CN , 又∵AD ∥CN ,∴四边形ADCN 是平行四边形,∴CD=AN ; ………………………5分②∵∠AMD=2∠MCD ∠AMD=∠MCD+∠MDC , ∴∠MCD=∠MDC , ∴MD=MC ,由①知四边形ADCN 是平行四边形, ∴MD=MN=MA=MC , ∴AC=DN ,∴四边形ADCN 是矩形. ………………………10分 26.(本题满分10分)解:(I) 如图①,连接OC ,则OC=4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
2012-2013学年度九年级(上)期末质检复习检测
数 学 试 卷
一、选择:(每小题3分,共21分) 1
、下列是最简二次根式的是 A.
C.
b
a 2
D.7.0
2、下列图形中既是轴对称又是中心对称图形的是( )
A 、三角形
B 、平行四边形
C 、圆
D 、正五边形
3、十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒.当你抬头看信号灯时,是黄灯的概率是( ) A .
1 3 B .51
2 C .112 D .1 2
4、在一个不透明的塑料袋中装有红色、白色球共40,除 颜色外其它都相同,小明通过多次摸球试验后发现,其 中摸到红色球的频率稳定在15%左右,则口袋中红色球 可能有( ) A 、4个 B 、6个 C 、34个 D 、36个
5、时钟的时针在不停的旋转,时针从上午的6时到9时,时针旋转的旋转角是 ( )
A 、30°
B 、60°
C 、90°
D 、9° 6、如图:在⊙O 中∠A=25°,∠E=30°,∠BOD 的度数为( )
A. 55°
B. 110°
C. 125°
D. 150° 7、如图,正方形ABCD 的边长为2,动点P 从C 出发, 在正方形的边上沿着C ⇒B ⇒A 的方向运动(点P 与A 不重合).设P 的 运动路程为x ,则下列图象中△ADP 的面积y 关于
x 的函数关系( )
A B C D
二、填空:(每空4分,共40分)
8、二次根式x -在实数范围内有意义,则x 的取值 。
9、“氢气在氧气中燃烧生成水”,这是 事件(填“随机”“不可能”“必然”) 10、方程(x -2)(2x +1)=x 2+2化为一般形式为_____________________ 11、已知方程x 2+(k-1)x-3=0的一个根为1,则k 的值为 12、⊙O 的半径为5,圆心O 到直线l 的距离为3,则直线l 与⊙O 的位置 。
13、如图,点A,B,C 都在⊙O 上,∠A =∠B =20º,则∠AOB 等于 14、有四条线段,分别为3,4,5,6,从中任取三条,能够成直角三角形
的概率是 D A B
C
E
O
15、3-x +(y-4)2=0,则xy=
16、m 是关于x 的方程02=++m nx x 的根,且0≠m ,则n m +的值是__________ 17、如图3,在平行四边形ABCD 中,O 是线段BD 的中点,G 是线段BC 的中点, 点F 在BC 的延长线上,OF 交DC 于点E .
若AB =6,CF =2,EC =1,则BC = .
三、解答题(本大题有9小题,共89分) 18、 (本题18分) (1)计算:0
4
27
)2(75|23|-++
+-π
(2)解方程: 02322=--x x (3)解方程: 2670x x -+=
19、(本题8分)如图,在边长为1的小正方形组成的网格中,AO B △的三个顶点均 在格点上,点
A 、
B 的坐标分别为(23)31.A B
--,、(,). (1)在图1中画出AO B △绕点O 顺时针...
旋转90°后的11A OB △; (2)若点P (a ,b )是AB 边上一点,平移AO B △后,点P 的对应点的坐标是'(3,2)P a b +-,在图2中画出平移后的△'''A O B .
图1 图2
20、(本题8分)在分别写有整数1到15的15张小卡片中,随机抽取1张卡片,求: (1)该卡片上的数字恰好是偶数的概率; (2)该卡片上的数字不能被5整除的概率. G O F
图3
E
D C B
A A
B
O
A
B
O
21、(本题10分)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)、写出你所学过的特殊四边形中是勾股四边形的一种图形的名称 , (2)、 如图(1),已知格点(小正方形的顶点)O(0,0),A (3,0),B(0,4),请你画出以格点为顶点,OA 、OB 为勾股边且对角线相等的勾股四边形OAMB 。
(3)、若点在(图1)中的坐标为(1,2),那么在图中所有格点中是否能找到一点D ,使以CA 、CB 为勾股边的四边形ACBD 是勾股四边形。
如果能找到,请写出D 点的坐标(不需要证明)。
(4)、在(图2)中连结CE ,4)、如图(2),将△ABC 绕顶点B 按顺时针方向旋转60°,得到△DBE ,连结AD 、DC ,∠DCB=30°。
求证:DC2+BC2=AC2,即四边形ABCD 是勾股四边形.
22、(本题8分) 已知:在⊙O 中,AB 是直径,AC 是弦,OE ⊥AC 于点E ,过点C 作直线FC ,使∠FCA =∠AOE ,交AB 的延长线于点D.
(1)求证:FD 是⊙O 的切线;
(2)若⊙O 半径的长为6,CA=CD,求图中阴影部分的面积。
23、(本题8分)已知:关于x 的一元二次方程01)2(2
=+++-m x m x (1)求证:方程有两个实数根.
(2)设m<0,且方程的两个实数根分别为21x x 、(其中21x x <),若y 是关于m 的函数,且
12
13x x y -=
,当y ≥2时,求m 的取值范围.
24、(本题8分)如图所示,利用22米长的墙为一边,用篱笆围成一个长方形养鸡场,中间用篱笆分割出两个小长方形,总共用去篱笆36米,为了使这个长方形ABCD 的面积为96平方米,问AB 和BC 边各应是多少?
A E D
B F
C 25、(本题9分)已知:如图8,⊙O 是△ABC 的外接圆,AB 为⊙O 的直径,弦C
D 交AB 于
E ,∠BCD
=∠BAC .
(1)求证:AC =AD ;
(2)过点C 作直线CF ,交AB 的延长线于点F ,
若∠BCF =30°,则结论“CF 一定是⊙O
26、(本题12分)已知直线y=x +b 交x 轴于点A ,交y 轴于点B ,交双曲线x
k y =
(k >0,x >0
于点C ,过点C 作CD ⊥x 轴并交x 轴于点D 。
(1) 若b=-2,且四边形OBDC 是平行四边形,请根据题意画出示意图,并求k 的值。
(2) 若OC=2OB 且BC ·AC=4,求b 的值。
图8
A。
