数电第1章习题解答
数电课后答案解析康华光第五版(完整)

第一章数字逻辑习题1.1数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制2 1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127 (4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章 逻辑代数 习题解答2.1.1 用真值表证明下列恒等式 (3)A B AB AB ⊕=+(A ⊕B )=AB+AB 解:真值表如下A B A B ⊕ABAB A B ⊕AB +AB0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 11111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
数电习题解(1-2章)

数电习题解答(1,2章)第一章数制与码制(教材p17)题1.2 将下列二进制整数转换为等值的十进制数。
(3)(10010111)2=1×27+1×24+1×22+1×21+1×20=151题1.4 将下列二进制数转换为等值的十进制数。
(2)(110.101)2=1×22+1×21+1×2-1+1×2-3=6.625题1.4 将下列二进制数转换为等值的八进制数和十六进制数。
(3)(101100.110011)2=(54.63)8, (101100.110011)2=()16题1.6 将下列十六进制数转换为等值的二进制数。
(2)(3D.BE)16=(111101.10111110)2题1.8将下列十进制数转换为等值的二进制数和十六进制数。
要求二进制数保留小数点以后8位有效数字。
(2) (0.251)10≈(0.01000000)2=(0.40)16题1.9将下列十进制数转换为等值的二进制数和十六进制数。
要求二进制数保留小数点以后4位有效数字。
(1) (25.7)10≈(11001.1011)2=(19.B)16题1.10 写出下列二进制数的原码、反码和补码。
(2) (+00110)2(+00110)原=000110, (+00110)反=000110, (+00110)补=000110.(3) (-1101)2(-1101)原=11101, (-1101)反=10010, (-1101)补=10011.题1.11 写出下列带符号位二进制数(最高位为符号位)的反码和补码。
(2) (001010)2(3) (111011)2(001010)2反码: 001010 , (001010)2补码: 001010(111011)2反码:100100, (111011)2补码:100101题1.12 用8位的二进制数补码表示下列十进制数。
数字电子技术答案 第1章 逻辑代数基础习题解答

X Y Z
F
图1.28 习题1-2(1)逻辑图
解:
X Y Z
00001111 00110011 01010101
00001111 11001100
11001111 01000101 01010101 00100000 01100101 F
11110000 00110011 10101010
真值表 X 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 F 0 1 1 0 0 1 0 1
CD AB 00 01 11 10 00 1 0 0 1 01 0 0 0 0 11 0 0 1 1 10 1 0 0 1
1-5 以卡诺图法化简下列函数,写成或-与表达式的形式。 (1) F AB (C D) A B DC 解: F (C D)( A C )( A D)( B D)( B C )
图1.29 习题1-2(6)的卡诺图
真值表 A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 0
(2) F
A, B , C
m(1,2,5,7)
真值表 A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 F 0 1 1 0 0 1 0 1
(3) F
W , X ,Y , Z
M (2,3,6,7,10,12)
真值表 W 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 X 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 1 0 0 1 1 0 0 1 1 0 1 0 1 1 1
数字电路与数字电子技术 课后答案第一章
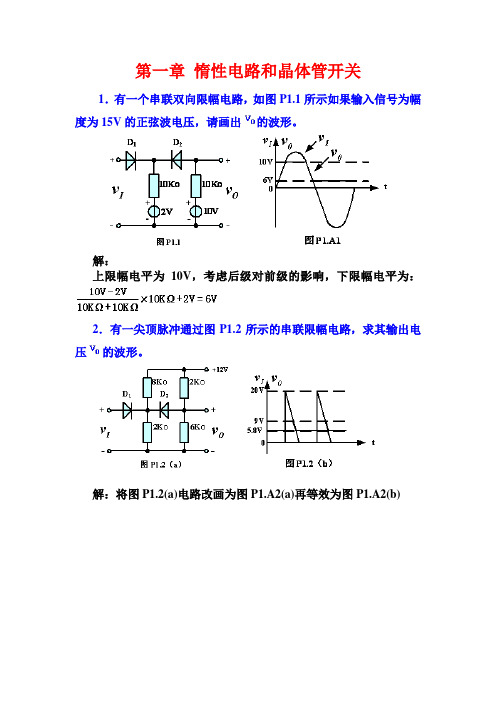
第一章惰性电路和晶体管开关1.有一个串联双向限幅电路,如图P1.1所示如果输入信号为幅度为15V的正弦波电压,请画出的波形。
解:上限幅电平为10V,考虑后级对前级的影响,下限幅电平为:2.有一尖顶脉冲通过图P1.2所示的串联限幅电路,求其输出电压的波形。
解:将图P1.2(a)电路改画为图P1.A2(a)再等效为图P1.A2(b)根据图P1. A2(a)可求出上限幅电平为=9V由图P1. A2(b)可求出下限幅电平为3.有一幅度为10V的正弦波电压通过如图P1.3所示的限幅电路,画出其输出电压的波形。
解:4.幅度为5V,周期为2ms的方波通过P1.4所示的电路,画出其输出波形()。
满足钳位条件为钳位电平为2V的顶部钳位。
5.在图P1.5所示电路中,设,V=10V 试对应输入电压画出电压的波形。
解:当二极管D导电时,当D截止时6.在图P1.6所示电路中,设,画出下列两种情况下的输出波形。
(1)的幅度(2)的幅度解:(1)的幅度这种情况电路为钳位电压为的顶部钳位,画出波形为(2)的幅度这种情况二极管始终处于截止状态,本电路相当于RC耦合电路,画出波形为过渡过程结束后为稳态波形。
7.试判断图P1.7所示的电路中,晶体管工作在什么状态。
图 P1.7解:(a)晶体管工作在放大状态(b)晶体管饱和条件晶体管处于饱和状态(c)晶体管处于截止状态(d)×晶体管处于饱和状态(e)晶体管处于截止状态×(f)设T截止所以三极管应导电,设T饱和晶体管处于饱和状态(g)设T饱和导电T饱和8.电路如图P1.8所示,设二极管正向电压降为0.7伏(忽略其内阻),分别计算开关K接通和断开两种情况下,A点的电位,以及二极管×中流过的电流。
解:(1)开关K接通,设均截止接上二极管后,导电,截止所以.(2)开关K断开后,这时导电,截止9.核算图P1.9所示反相器在输入信号作用下晶体三极管的工作状态,并画出输出波形。
数字电子技术基础第一章习题答案

(1)(+1011) 的原码和补码都是01011(最高位的0是符号位)。
(2)(+00110) 的原码和补码都是(最高位的0是符号位)。
(3)(-1101) 的原码是11101(最高位的1是符号位),补码是10011
(4)(-) 的原码是(最高位的1是符号位),补码是
[题1.5] [解]
[题1.15]解答如下
(4)用卡诺图证明。画出表示左式的卡诺图。将图中的0合并后求反,应与右式相等。将0合并后求反得到
,故成立。
(5)用卡诺图证明。画出左式的卡诺图,化简后得到
卡诺图如下:
[题1.16]解答如下
[题1.17]解答如下
[题1.18]参见教材第1. 8. 1节。
[题1.19]解答如下
根据题意可知,m 到m 均为约束项,而约束项的值恒为0,故
(2) (3D.BE) =(.) =(61. )
(3)(8F.FF) =(.) =( 143.)
(4)(10.00) =(10000.) =(16. )
[题1. 3][解]
(17) =(10001) =(11) (127) =() =(7F)
(0.39) =(0.0110) =(0.6) (25.7) =(11001.1011) =(19.B)
同理,由题意可知m9~m15,m34~m31也都是约束项,故得到, 余类推。
[题1.20]解答如下
[题1.21]
〔解〕设两个逻辑பைடு நூலகம்数分别为
(1)证明
因为任何两个不同的最小项之积均为0,而两个相同的最小项之积仍等于此最小项,所以Y 和Y 的乘积仅为它们的共同的最小项之和,即
因此,可以通过将Y 和Y 卡诺图上对应的最小项相乘,得到Y Y 卡诺图上对应的最小项。
数字电路第1章习题解答

第1章 数字逻辑基础1-1 将下列二进制数转换为十进制数。
(1) 2(1101) (2) 2(10110110) (3) 2(0.1101) (4) 2(11011011.101) 解(1)3210210(1101)12120212(13)=⨯+⨯+⨯+⨯=(2)75421210(10110110)1212121212(182)=⨯+⨯+⨯+⨯+⨯= (3) 124210(0.1101)1212120.50.250.0625(0.8125)---=⨯+⨯+⨯=++= (4)76431013210(11011011.101)22222222 12864168210.50.125 (219.625)--=+++++++=+++++++= 1-2 将下列十进制数转换为二进制数和十六进制数(1) 10(39) (2) 10(0.625) (3) 10(0.24) (4) 10(237.375) 解(1)10216(39)(100111)(27)== (2) 10216(0.625)(0.101)(0.A)==(3)近似结果: 16210)3.0()00111101.0()24.0(D =≈ (4) 10216(237.375)(1110'1101.011)(0ED.6)== 1-3 将下列十六进制数转换为二进制数和十进制数(1) 16(6F.8) (2) 16(10A.C) (3) 16(0C.24) (4) 16(37.4) 解(1) 16210(6F.8)(1101111.1)(111.5)== (2) 16210(10A.C)(1'0000'1010.11)(266.75)== (3) 16210(0C.24)(1100.0010'01)(12.140625)== (4) 16210(37.4)(11'0111.01)(55.25)== 1-4 求出下列各数的8位二进制原码和补码(1) 10(39)- (2) 10(0.625) (3) 16(5B) (4) 2(0.10011)- 解(1)10(39)(1'0100111)(1'1011001)-==原码补码 (2) (0.1010000)(0.1010000)==10原码补码(0.625)(3) 16(5B)(01011011)(01011011)==原码补码(4) 2(0.10011)(1.1001100)(1.0110100)-==原码补码1-5 已知10X (92)=-,10Y (42)=,利用补码计算X +Y 和X -Y 的数值。
(完整版)《数字电子技术基础》第一章习题答案

第一章 逻辑代数及逻辑函数的化简1。
1、用布尔代数的基本公社和规则证明下列等式. 1、D B A DC D A BD B A +=+++证:左边=D B A DC D BD B A DC D A AD BD B A +=+++=++++=右边 2、C AB D A C AB D B A D AB +=++证:左边=C AB D A C AB B B D A +=++)(=右边 3、D B B DA C B D D BC +=++++))((证:左边=D B C B C DA B DA D BC B DA C B D BC +=++++=++++))((=右边 4、D B C B BC D A D C A ACD +=++++ 证:左边=B D B D A AD +=++=右边 5、))()((A C C B B A CA BC AB +++=++证:右边=AB BC AC A C B AC A C BC B AC AB ++=++=++++))(())((=左边 6、A C C B B A C B A ABC ++=+证:右边=C B A ABC A C BC C A B A A C C B B A A C C B B A +=+++=+++=))(())()(( 7、A C C B B A A C C B B A ++=++证:左边=A C C B B A C B B A A C A C C B B A ++=+++++=右边 8、)())()()((X W YZ Z Y Z Y X W Z Y +=++++证:左边=)())()((X W YZ Z Y X W Y Z YZ +=+++=右边 9、0))()()((=++++B A B A B A B A证:左边=0))((==++++A A B A B A A AB B A A =右边10、A D D C C B B A D C CD C B BC B A AB +++=+++))()(( 证:左边=D C B A ABCD D C CD C B A ABC +=++))((右边=))()()((A D D C C B B A A D D C C B B A ++++==D C B A ABCD AD C A D C BC C A B A +=++++))((=左边11、=⊕⊕C B A A ⊙B ⊙C证:左边=C B A ABC C B A C B A C B A AB C B A B A +++=+++)()( ==+++)()(C B C B A C B BC A A ⊙B ⊙C =右边 12、如果Y B X A BY AX B A +=+=⊕,证明0证:AB B A Y X X B Y A B A Y B X A BY AX +++++=++=+))((=X A Y B AB Y X X B Y A B A ++++++ =X A Y B X A Y B AB B A +=+++=右边1.2、求下列函数的反函数.1、B A AB F += 解:))((B A B A F ++=2、C B A C B A C AB ABC F +++=解:))()()((C B A C B A C B A C B A F ++++++++=3、)(D A C C B B A F +++= 解:))()((D A C C B B A F +++=4、))()((B A D C C D A B F +++= 解:B A D C C D A B F ++++=)(5、RST T S R T S R F ++= 解:))()((T S R T S R T S R F ++++++= 1.3、写出下列函数的对偶式.1、E DE C C A B A F ++++=))()(( 解:E E D C C A AB F )](['+++=2、B A D B C AB F = 解:B A D B C B A F ++++++='3、C B C A C B B A F +++++++= 解:BC C A BC B A F ='4、Z Y X Z XY F += 解:Z Y X Z Y X F ++++=' 1.4、证明函数F 为自对偶函数。
习题数电参考答案(终)

习题数电参考答案(终)第⼀章数字逻辑概论1.1 数字电路与数制信号1.1.1 试以表1.1.1所列的数字集成电路的分类为依据,指出下列IC器件属于何种集成度器件:(1)微处理器;(2)计数器;(3)加法器;(4)逻辑门;(5)4兆位存储器。
解:依照表1.1.1所⽰的分类,所列的五种器件:(1)、(5)属于⼤规模;(2)、(3)属于中规模;(4)属于⼩规模。
1.1.2⼀数字信号波形如图题1.1.2所⽰,试问该波形所代表的⼆进制数是什么?解:图题1.1.2所⽰的数字信号波形的左边为最⾼位(MSB),右边为最低位(LSB),低电平表⽰0,⾼电平表⽰1。
该波形所代表的⼆进制数为010110100。
1.1.3 试绘出下列⼆进制数的数字波形,设逻辑1的电压为5V,逻辑0的电压为0V。
(1)001100110011(2)0111010 (3)1111011101解:⽤低电平表⽰0,⾼电平表⽰1,左边为最⾼位,右边为最低位,题中所给的3个⼆进制数字的波形分别如图题1.1.3(a)、(b)、(c)所⽰,其中低电平为0V,⾼电平为5V。
1.1.4⼀周期性数字波形如图1.1.4所⽰,试计算:(1)周期;(2)频率;(3)占空⽐。
解:因为图题1.1.4所⽰为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms。
频率为周期的倒数,f=1/T=1/0.01s=100Hz。
占空⽐为⾼电平脉冲宽度与周期的百分⽐,q=1ms/10ms×100%=10%。
1.2 数制1.2.1 ⼀数字波形如图1.2.1所⽰,时钟频率为4kHz,试确定:(1)它所表⽰的⼆进制数;(2)串⾏⽅式传送8位数据所需要的时间;(3)以8位并⾏⽅式传送的数据时需要的时间。
解:该波形所代表的⼆进制数为00101100。
时钟周期T=1/f=1/4kHz=0.25ms。
串⾏⽅式传送数据时,每个时钟周期传送1位数据,因此,传送8位数据所需要的时间t=0.25ms×8=2ms。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.11 试写出下列十进制数的二进制原码、补码、反码(码长为 8) 。 (1)+48; 解: (1)+48=(000)原码=(00110000)反码=(00110000)补码 (2)-96=(11100000)原码=(10011111)反码=(10100000)补码 (3)+9.75=(001001.11)原码=(001001.11)反码=(001001.11)补码 (4)-36=(10100100)原码=(11011011)反码=(11011100)补码 1.12 试用反码和补码完成下列运算,设字长为 8 位。 (1)33-17; 解: (33)10=(00100001)2 (17)10=(00010001)2 (-33)10=(11011110)反码=(11011111)补码 (-17) 10=(11101110)反码=(11101111)补码 (1)33-17=16 (-17) 10=(11101110)反码=(11101111)补码
3
(2)432-379。
0101 1000 0010 0111 ( 1) 0111 1111 + 0110 1000 0101
0100 0011 0010 - 0011 0111 1001 ( 2) 0000 1011 1001 0110 0110 0101 0011
4
00010001 11011111 011110000
补码:
00010001 11011110 反码: 011101111 0 011101111
( 3) 、 (4)略 1.13 分别用 8421BCD 码、余三码表示下列各数。 (1)(378.625)10; 解: (1)(378.625)10=(0011 0111 1000.0110 0010 0101)8421BCD =(0110 1010 1011.1001 0101 1000)余三码 (2)(1001110)2=(78)10=(0111 1000)8421BCD=(1010 1011)余三码 (3)(2EF)16 (4)(27.6)8 =(751)10=(0111 0101 0001)8421BCD=(1010 1000 0100)余三码 =(23.75)10=(0010 0011.0111 0101)8421BCD =(0101 0110.1010 1000)余三码 1.14 将下列 8421 BCD 码转换成二进制数。 (1)1001 0101; 解: ( 1) (1001 0101)8421BCD=(95)10=(1011111)2 ( 2) (0101 1000 1001)8421BCD=(589)10=(1001001101)2 ( 3) (0111 0110.0011)8421BCD=(76.3)10=(1001100.0101)2 1.15 将下列各数转换成 8421 BCD 码。 (2)(00111001)余 3 码 (3)(11000101)5421BCD (2)0101 1000 1001; (3)0111 0110.0011。 (2)(1001110)2; (3)(2EF)16; (4)(27.6)8。
第一章习题解答
1.1 转换下列二进制数为等值的十进制数、八进制数、十六进制数。 (1)1011001; 解: ( 1) (1011001)2=(89)10=(131)8=(59)16 ( 2) (0.10110)2=(0.6875)10=(0.54)8=(0.B)16 ( 4) (1001.10101)2=(9.65625)10=(11.52)8=(9.A8)16 1.2 转换下列十进制数为等值的二进制数、八进制数、十六进制数。 (1)76; 解: ( 1) ( 2) 1.3 (76)10=(1001100)2=(114)8=(4C)16 (0.4375)10=(0.0111)2=(0.34)8=(0.7)16 (3)0.4375。 (2)0.10110; (4)1001.10101。
00100001
(2)-96;
(3)+9.75;
(4)-36。
(2)17-33;
(3)33+17;
(4)-33-17。
补码:
11101111 000010000
00100001 11101110 反码: 100001111 1 00010000
(2)17-33= -16
2
(-33)10=(11011110)反码=(11011111)补码
完成下列二进制数的加法、减法运算,并转换成十进制数进行检查。 (1)0101.01+1001.11; (2)1011.1-101.11。
解: (1)0101.01+1001.11=1111.00 1.7 以二进制数完成下列运算。 (2)36.5+28.625; 解: (2) 36.5+28.625=(1000001.001)2 (3) 116-78=(0100110)2
(1)(10101101)2421BCD 解:
(1)(1010 1101)2421BCD=(47)10=(0100 0111)8421BCD (2)(0011 1001)余 3 码=(0000 0110)8421BCD (3)(1100 0101)5421BCD =(95)10=(1001 0101)8421BCD 1.16 试用 8421BCD 码完成下列十进制数的运算。 (1)58+27; 解:
1
( 2)
1011.1-101.11=101.11
(3)116-78。
1.9
将下列自然二进制数转换成格雷码。 (1) 011010; (2) 10011001。
解: (1) (011010)2=(010111)gray 1.10 将下列格雷码转换成自然二进制数。 (1) 001101; 解: ( 1) (0011001)gray=(0010001)2 (2) (10010)gray=(11100)2 (2) 10010。 (2) (10011001)2=(11010101)gray
把下列十进制数转换为二进制数,小数点后保留 4 位。 (3)0.57; (4)1.375。
解: (3) (0.57)10=(0.1001)2 ; 1.5 转换下列十六进制数为二进制数。 (1)10A; 解: (1) (10A)16=(1 0000 1010)2 1.6 (2) (0.521)16=(0.0101 0010 0001)2 (2)0.521。 (4) (1.375)10=(1.0110)2
