多变量分析
统计学中的多变量分析方法

统计学中的多变量分析方法统计学是一门重要的科学领域,它致力于研究如何收集、组织、分析和解释数据。
在统计学中,多变量分析方法是一种常用的技术,用于探究多个变量之间的关系和模式。
本文将介绍多变量分析方法的概念和应用场景。
一、多变量分析方法的概述在统计学中,多变量分析方法是一种通过同时考虑多个变量来研究数据集的方法。
相比传统的单变量分析方法,多变量分析方法可以更全面地探究各个变量之间的关联和影响。
为了帮助研究者更好地理解数据集中变量之间的关系,多变量分析方法提供了多种技术和模型。
其中最常用的方法包括主成分分析、因子分析、聚类分析、判别分析和回归分析。
二、主成分分析主成分分析是一种常见的多变量分析方法,用于减少数据集的维度并提取潜在的主要变量。
通过主成分分析,可以将原始数据转化为一组无关的主成分,这些主成分可以解释数据中大部分的方差。
主成分分析可用于降维、特征选择和数据可视化。
它广泛应用于生物医学、工程学、金融和市场研究等领域,有助于简化复杂数据集的分析过程。
三、因子分析因子分析是一种用于研究多个变量之间关联模式的方法。
它通过将一组观测变量转化为一组潜在的无关因子,来揭示观测变量背后的潜在结构。
因子分析可以用于探究样本中隐藏的潜在因子,如人格特征、消费者满意度和员工工作满意度等。
通过因子分析,研究者可以了解到不同变量之间的潜在关系,并进一步洞察潜在因子对观测变量的解释贡献。
四、聚类分析聚类分析是一种将样本或变量分组成类别的方法。
通过聚类分析,可以根据样本间的相似性或变量间的相关性,将数据集划分为不同的群组。
聚类分析在市场研究、社会科学和生物学等领域得到广泛应用。
它可以用于发现数据集中的隐藏模式和群组,帮助研究者识别并理解不同群体之间的相似性和差异。
五、判别分析判别分析是一种用于解释组间差异和评估变量重要性的统计方法。
它可以帮助研究者确定哪些变量对于区分不同组别的样本最具有预测性。
判别分析在医学研究、社会科学和商业决策等领域得到广泛应用。
资料的统计分析——双变量及多变量分析

资料的统计分析——双变量及多变量分析双变量及多变量分析是指在统计分析中,同时考察两个或多个变量之间的关系。
通过对多个变量进行综合分析,可以更全面地了解变量之间的相互作用和影响。
双变量分析是指考察两个变量之间的关系,常用的方法包括相关分析和回归分析。
相关分析是用来评价两个变量之间的线性关系的强度和方向。
常用的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。
皮尔逊相关系数适用于两个变量都为连续型变量的情况,而斯皮尔曼相关系数适用于至少一个变量为有序分类变量或者两个变量都为有序分类变量的情况。
回归分析是用来探究一个变量(因变量)与一个或多个变量(自变量)之间的关系的强度和方向。
常用的回归分析方法有简单线性回归分析和多元线性回归分析。
简单线性回归分析是用来研究一个自变量与一个因变量之间的线性关系的情况,而多元线性回归分析则可以同时研究多个自变量与一个因变量之间的关系。
在进行双变量分析之前,需要先进行数据的描述性分析。
描述性分析是对数据的基本特征进行总结和描述,包括样本数量、均值、方差、最小值、最大值等。
多变量分析是指同时考虑多个变量之间的关系。
常用的方法包括多元方差分析、聚类分析和因子分析。
多元方差分析是用来比较多个因素对于一个或多个因变量的影响的强度和方向。
聚类分析是用来将样本按照其中一种相似度划分为不同的群组,从而研究变量之间的内部关系。
因子分析是用来探究多个变量之间的潜在结构,从而找出变量之间的共性和差异。
除了以上方法,还可以采用交叉表分析、卡方检验和回归分析等方法来研究多个变量之间的关系。
在进行双变量及多变量分析时,需要注意以下几个问题:首先,需要选择合适的统计方法,根据变量的类型和变量之间的关系特点来选择合适的分析方法。
其次,需要注意变量之间的相关性,避免多重共线性的问题。
此外,还需要注意样本的选择和样本量的大小,以及结果的解释和推断的注意事项。
总之,双变量及多变量分析是一种重要的统计方法,可以帮助我们更全面地了解变量之间的相互作用和影响。
常用多变量统计分析方法简介

表 14-5 对例 14.1 回归分析的部分中间结果
回归方程中包含的
平方和(变异)
自变量
SS回归
SS剩余
① X1 , X2 , X3 , X4 ② X2 , X3 , X4 ③ X1 , X3 , X4 ④ X1 , X2 , , X4 ⑤ X1 , X2 , X3
133.7107 133.0978 121.7480 113.6472 105.9168
2
多变量统计分析方法概述
对于多变量医学问题,如果用单变量统计方法就要对 多方面分别进行分析,而一次分析一个方面,同时忽视了各 方面之间存在的相关性,这样会丢失很多信息,分析的结果 不能客观全面地反映情况。
多变量统计方法不仅能够研究多个变量之间的相互关 系以及揭示这些变量之间内在的变化规律,而且能够使复 杂的指标简单化,并对研究对象进行分类和简化。
partial
regression
coefficient)。标准偏回归系数
b
' i
与
注 意
偏回归系数之间的关系为:
b
' i
=
bi
lii l yy
= bi
si sy
标准偏回归系数绝对值的大小,可用以衡量自变量对
因变量贡献的大小,即说明各自变量在多元回归方程
中的重要性。
27
3、标准化偏回归系数
变量
回归系数bj
b1l21
b2l22
bml2m
l2y
b1lm1 b2lm2 bmlmm lmy
方程组中: lij l ji (Xi Xi )(X j X j ) Xi X j [(Xi )(X j )]/ n liy (Xi Xi )(Y Y ) XiY [(Xi )(Y)]/ n
多变量统计分析在社会科学研究中的应用与解读

多变量统计分析在社会科学研究中的应用与解读多变量统计分析是社会科学研究中常用的方法之一,可以用于研究多个自变量对一个因变量的影响,同时控制其他可能影响因素的干扰。
这种方法可以帮助研究者更全面和准确地理解社会现象,提高研究结论的可靠性和可解释性。
在社会科学研究中,多变量统计分析可以用于解决诸如以下问题:1.探索因果关系:在社会科学研究中,我们往往需要确定一个自变量对一个因变量的影响是否具有因果关系。
多变量统计分析可以通过控制其他可能的影响因素,仅仅关注自变量与因变量之间的关系,从而更准确地判断两者之间的因果关系。
2.解释复杂现象:社会现象往往是由多个变量相互作用形成的,而多变量统计分析可以通过考察多个变量之间的关系,帮助解释复杂现象。
例如,在分析犯罪现象时,我们可以考察诸如社会经济地位、教育程度、家庭环境等多个因素对犯罪率的影响,从而更全面和准确地理解犯罪行为的成因。
3.预测和建模:多变量统计分析可以用于建立预测模型,比如通过多个自变量对一些因变量进行预测。
这种方法可以帮助研究者预测未来的社会现象,提供决策支持。
例如,在经济学中,我们可以通过探究多个因素对经济增长率的影响,建立经济增长模型,从而预测未来的经济走势。
在进行多变量统计分析时,需要注意以下几个方面:1.变量选择和测量:在进行多变量统计分析之前,需要仔细选择并测量相关变量。
合理的变量选择和准确的测量可以提高研究结论的可靠性和可解释性。
同时,还需要关注变量之间的相关性和多重共线性问题,避免过度解读变量之间的关系。
2.统计方法选择:多变量统计分析涉及多种统计方法,如线性回归、逻辑回归、主成分分析等。
在选择统计方法时,需要根据研究设计和研究问题的特点,选择适合的方法。
同时,还需要关注模型的拟合度和解释能力,确保模型的可靠性和有效性。
3.解释和解读:在进行多变量统计分析之后,需要对结果进行解释和解读。
研究者需要注意结果的显著性和效应的大小,并结合相关理论和背景知识,解释变量之间的关系及其对因变量的影响。
统计学中的多变量分析方法

统计学中的多变量分析方法多变量分析是统计学中一个重要的分析方法,用于研究多个变量之间的关系以及它们对观察结果的影响。
多变量分析可以帮助我们从多个维度来解释数据,揭示隐藏在数据背后的规律和结构。
在统计学中,常见的多变量分析方法主要包括回归分析、主成分分析、聚类分析和因子分析等。
下面将对这些方法进行详细介绍。
回归分析是一种用于研究因变量和自变量之间关系的方法。
它通过建立一个数学模型来描述这种关系,并根据数据推断模型的参数。
回归分析可以用于预测因变量的取值,也可以用于确定自变量对因变量的影响程度。
常见的回归分析方法有线性回归、多元线性回归、逻辑回归等。
主成分分析(PCA)是一种通过线性组合将多个相关变量转换为少数几个无关变量的方法。
它可以帮助我们发现数据中的主要结构和模式。
主成分分析的输出是一组新的变量,称为主成分,它们是原始变量的线性组合。
主成分分析可以用于数据降维、数据压缩和特征提取等。
聚类分析是一种将相似的个体或对象归类为一组的方法。
聚类分析基于样本之间的相似性或距离度量,将样本划分为不同的簇。
聚类分析可以用于数据分类、观察群体相似性和发现群组之间的关系等。
常用的聚类分析方法有层次聚类和k均值聚类等。
因子分析是一种用于解释变量之间关系的方法。
它通过将多个观测变量解释为少数几个潜在因子,来揭示数据背后的结构。
因子分析可以帮助我们压缩数据信息、发现共性因子和解释观测变量之间的关系。
常见的因子分析方法有主成分分析和最大似然法等。
此外,还有其他一些多变量分析方法,比如判别分析、典型相关分析、结构方程模型等,它们也在统计学的研究中得到广泛应用。
这些方法在实际研究中可以结合使用,以更全面地分析数据和解释现象。
总结来说,多变量分析是统计学中重要的分析手段,用于研究多个变量之间的关系。
常见的多变量分析方法包括回归分析、主成分分析、聚类分析和因子分析等。
这些方法可以帮助我们从多个维度来理解数据,揭示数据背后的规律和结构。
(整理)因子分析方法——多变量分析
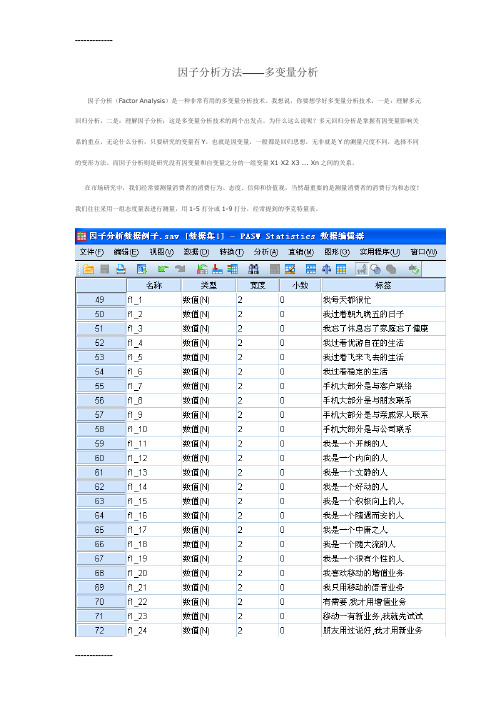
因子分析方法——多变量分析因子分析(Factor Analysis)是一种非常有用的多变量分析技术。
我想说,你要想学好多变量分析技术,一是:理解多元回归分析,二是:理解因子分析;这是多变量分析技术的两个出发点。
为什么这么说呢?多元回归分析是掌握有因变量影响关系的重点,无论什么分析,只要研究的变量有Y,也就是因变量,一般都是回归思想,无非就是Y的测量尺度不同,选择不同的变形方法。
而因子分析则是研究没有因变量和自变量之分的一组变量X1 X2 X3 ... Xn之间的关系。
在市场研究中,我们经常要测量消费者的消费行为、态度、信仰和价值观,当然最重要的是测量消费者的消费行为和态度!我们往往采用一组态度量表进行测量,用1-5打分或1-9打分,经常提到的李克特量表。
上面的数据是我们为了测量消费者的生活方式或者价值观什么的,选择了24个语句,让消费者进行评估,同意还是不同意,像我还是不像,赞成还是不赞成等等,用1-9打分;因子分析有探索性因子分析和证实性因子分析之分,这里我们主要讨论探索性因子分析!证实性因子分析主要采用SEM结构方程式来解决。
从探索性因子分析角度看:∙一种非常实用的多元统计分析方法;∙∙一种探索性变量分析技术;∙∙分析多变量相互依赖关系的方法;∙∙数据和变量的消减技术;∙∙其它细分技术的预处理过程;我们为什么要用因子分析呢?首先,24个可测量的观测变量之间的存在相互依赖关系,并且我们确信某些观测变量指示了潜在的结构-因子,也就是存在潜在的因子;而潜在的因子是不可观测的,例如:真实的满意度水平,购买的倾向性、收获、态度、经济地位、忠诚度、促销、广告效果、品牌形象等,所以,我们必须从多个角度或维度去测量,比如多维度测量购买产品的动机、消费习惯、生活态度和方式等;这样,一组量表,有太多的变量,我们希望能够消减变量,用一个新的、更小的由原始变量集组合成的新变量集作进一步分析。
这就是因子分析的本质,所以在SPSS软件中,因子分析方法归类在消减变量菜单下。
多变量相关性分析

spss多变量相关性分析
1、首先我们打开电脑里的spss软件打开整理好的数据文件。
2、选择面板上方“分析”选项,点击“相关”,这时会弹出三个选项,如果只需要进行两个变量的相关分析就选择“双变量”,多个变量交叉分析则选择“偏相关“,在这里示范“双变量”分析的方法。
3、进入页面后,将需要分析的两个变量转换到右边变量框中,点击确定。
4、确定后得出的结果,呈显著相关。
5、如果需要所有变量的两两相关分析数据,则将所有变量转移到变量框中,点击确定。
6、这样就能得出所有变量间两两相关是否显著的结果了。
自变量之间存在共线性,说明自变量所提供的信息是重叠的,可以删除不重要的自变量减少重复信息。
但从模型中删去自变量时应该注意:
从实际经济分析确定为相对不重要并从偏相关系数检验证实为共线性原因的那些变量中删除。
如果删除不当,会产生模型设定误差,造成参数估计严重有偏的后果。
多重共线性问题的实质是样本信息的不充分而导致模
型参数的不能精确估计,因此追加样本信息是解决该问题的一条有效途径。
但是,由于资料收集及调查的困难,要追加样本信息在实践中有时并不容易。
扩展资料:
多元线性回归的基本原理和基本计算过程与一元线性回归相同,但由于自变量个数多,计算相当麻烦,一般在实际中应用时都要借助统计软件。
这里只介绍多元线性回归的一些基本问题。
但由于各个自变量的单位可能不一样,比如说一个消费水平的关系式中,工资水平、受教育程度、职业、地区、家庭负担等等因素都会影响到消费水平,而这些影响因素(自变量)的单位显然是不同的,因此自变量前系数的大小并不能说明该因素的重要程度。
多变量分析技术

多变量分析技术多变量分析技术是一种基于统计学原理和数学模型的数据分析方法,广泛应用于各个领域,包括社会科学、生物科学、医学、市场营销等。
通过对多个变量之间的关系进行综合分析,可以揭示出隐藏在数据背后的规律和趋势,为决策提供科学依据。
本文将介绍多变量分析的一些常用技术和应用领域。
一、主成分分析(Principal Component Analysis)主成分分析是一种用于降维的数据分析方法,通过创建新的变量来代替原始变量,使得新变量间相互独立,尽量包含原始信息的大部分方差。
主成分分析在数据可视化和数据压缩方面具有重要应用。
例如,在市场调研中,研究人员可以通过主成分分析确定最能代表顾客喜好的几个主要特征,进而制定相应的市场策略。
二、聚类分析(Cluster Analysis)聚类分析是一种将样本或变量进行分组的技术。
通过计算样本或变量间的相似性,聚类分析可以将相似的样本或变量归为一类。
聚类分析在市场细分、社交网络分析等领域得到广泛应用。
例如,在客户细分中,企业可以通过聚类分析将具有相似购买行为的顾客划分为不同的群体,为不同群体设计专属的营销策略。
三、判别分析(Discriminant Analysis)判别分析是一种通过构建分类函数将样本分为不同类别的技术。
判别分析根据变量的值来判别样本所属类别,广泛应用于模式识别、生物统计学等领域。
例如,在医学诊断中,医生可以通过判别分析将患者的症状与疾病进行关联,辅助诊断和治疗决策。
四、回归分析(Regression Analysis)回归分析是一种用于建立变量之间关系的统计技术。
回归分析可以确定自变量对因变量的影响程度,并通过建立数学模型进行预测。
回归分析在经济学、金融学、社会学等领域具有广泛应用。
例如,在金融领域,研究人员可以使用回归分析来探究经济因素对股票价格的影响,并进行风险评估和资产配置。
五、因子分析(Factor Analysis)因子分析是一种用于研究变量间的潜在结构和因果关系的技术。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
❖ 抽樣方法 (Sampling Techniques) ❖ 類別資料分析 (Categorical Data Analysis) ❖ 無母數方法 (Nonparametric Methods) ❖ 時間序列模式 (Time Series Models)
(AR, MA, ARMA, ARIMA) ❖ 存活分析 (Survival Analysis) ❖ 可靠度分析 (Reliability Analysis)
❖ 蒙地卡羅模擬 (Monte Carlo Simulation)
在管理實證研究上的應用舉證
一. 實證程序:
1. 建立研究假設 ↓
2. 收集樣本資料 ↓
3. 評估信度效度(針對問卷資料) ↓
4. 檢驗研究假設
在 2. 收集樣本資料、 3. 評估信度效度、 4. 檢驗研究假設
等各階段,均需應用統計方法!
❖ 修畢 楊老師的課,保證厚植統計實力,滿 載而歸!
❖ 傳道、授業、解惑是 楊老師對學生春風化 雨四十載一貫的付出!
❖ 老師榮獲全校特優及傑出教學獎,是教學成 就最崇高的肯定,實至名歸!學生們皆與有 榮焉。
❖ 謝謝 老師對歷屆學生們辛勞的教導,老師 教導之恩,學生們皆謹記在心,也謝謝 老 師對母系以及對母校無私的奉獻與卓越的貢 獻!
e. 人力資源管理 Journal of Applied Psychology (3.769)
f. 資訊管理 MIS Quarterly (5.183)
g. 管理研究方法 Psychological Methods (5.140) Organizational Research Methods (3.019) Structural Equation Modeling (4.351)
F12
F13
F21
F22
F23
F24
F25
F26
F27
F31
F32
F33
F34
F 2 F1
1
F1F2
F2
F2F3
F3
1
2
❖ 欲檢驗上圖中 latent factors F1, F2 以及 F3 之 量測信度與效度,需使用 CFA,所涉及之統 計概念包括:
變異數、共變數、相關、多變量常態、最 大概似法、信賴區間、模型配適度、t 檢定、 卡方檢定、大樣本理論等。
❖多變量分析 (Multivariate Analysis) 多變量變異數分析 (MANOVA) 多變量迴歸 (Multivariate Regression) 重複測度變異數分析 (RepeatedMeasures ANOVA) 因素分析 (Factor Analysis) 區別分析 (Discriminant Analysis) 典型相關 (Canonical Correlation) 多變量時間序列 (Multivariate Time Series)
祝福 老師 健康、如意!
二. 與統計緊密連結之管理類主流期刊:
(括弧內數字為 2008年之 impact factors)
a. 組織、策略管理 Academy of Management Journal (6.079) Strategic Management Journal (3.344) Journal of Management (3.080)
❖ 結構方程模式 (Structural Equation Modeling, SEM) 驗證性因素分析 (Confirmatory Factor Analysis, CFA)
❖ 多層次模式 (Multi-Level Models) 混合效果模式 (Mixed-Effects Models)
❖ 一般化自我迴歸條件異質變異數模型 (GARCH)
b. 生產與作業管理 Management Science (2.354)
c. 財務金融 Journal of Finance (4.018) Journal of Financial Economics (3.542) Econometrica (3.865)
d. 行銷、消費者行為 Journal of Marketing (3.598) Journal of Marketing Research (2.574) Journal of Consumer Research (1.592)
❖ 以上各期刊皆為所屬管理功能領域頂尖 學術期刊。
❖ 以上各期刊所刊登文章涉及統計方法之 應用與發展所佔比例,少則六成,多達 十成。
❖ 同一篇文章所使用之統計方法愈趨精緻 且多樣。
三. 範例:
a Mediation Model with a Common Method Factor
M
M11
M12
❖ 欲檢驗上圖之中介模型內 γF1F2 以及 βF2F3 兩路徑之顯著性 (即研究假設是否成立), 需使用 SEM,所涉及之統計概念包括:
變異數、共變數、相關、多變量常態、 最大概似法、模型配適度、t 檢定、卡方 檢定、R2、大樣本理論等。
結語
❖ 統計的發展與應用蓬勃,是當今顯學, 更 是明日之星!其重要基礎概念在 楊老師所 開授之初統、數統以及統計問題等課程, 皆有完整且循序漸進的授課綱要、授課內 涵與授課秘訣。
統計重要基礎概念
機率原理 機率分配 平均數、變異數、共變數、相關係數 隨機樣本 統計量與抽樣分配 大樣本理論 估計 檢定 貝氏理論
在管理領域應用與發展之統計方法
❖ 相關分析 (Correlation Analysis) ❖ 迴歸分析 (Regression Analysis) ❖ 變異數分析 (ANOVA) ❖ 共變數分析 (ANCOVA) ❖ 實驗設計 (Experimental Designs)
M13
M21
M 22
M23
Mபைடு நூலகம்24
M 25
M26
M 27
M31
M 32
M 33
M 34
11 x11 12 x12 13 x13
21 x21 22 x22 23 x23 24 x24 x 25 25 26 x26 27 x27
31 x31 32 x32 x 33 33 34 x34
F11
