第四章 齿 轮 机 构答案
机械知识习题册答案4-2

第四章齿轮传动§4-2 标准直齿圆柱齿轮传动一、填空题1.2.3.4. 有一标准直齿圆柱齿轮其模数m = 2mm,齿数z = 26,则分度圆直径距5.二、判断题(X)1. 有一对传动齿轮,已知主动轮的转速n1=960 r/min,齿数z1=20,从动轮的齿数z2=50,则这对齿轮的传动比i12=2.5,从动轮的转速为n2=2400 r/min。
(X)2. 不同齿数和模数的标准渐开线齿轮,其分度圆上的齿形角不同。
(√)3. 分度圆可定义为齿轮上具有标准模数和标准齿形角的圆。
(X)4. 模数m表示齿轮齿形的大小,它是没有单位的。
(√)5. 模数m越大,轮齿的承载能力越强。
(X)6. 标准直齿圆柱齿轮传动,其主动轮的转速与从动轮的转速之比等于主动轮分度圆直径与从动轮分度圆直径之比。
(X)7. 大小齿轮的齿数分别为84和42,当两齿轮啮合传东时,大齿轮转速高,小齿轮转速低。
三、选择题1. 标准直齿圆柱齿轮分度圆上的内齿厚( C )槽宽。
A.大于 B. 小于 C. 等于2. 渐开线齿廓上各点的齿形角角( B )。
A.相等 B. 不相等 C. 基本相等3. 我国齿轮的标准齿形角为( A )。
A.20° B.15° C. 14°30′4. 对于模数相同的齿轮,如果齿数增加,齿轮的几何尺寸( A )。
A. 增大B. 减小C.没有变化5. 下列关于模数m的说法正确的是( B )A.模数m等于齿距除以 所得到的商,是一个无单位的量。
B.模数m是齿轮几何尺寸计算中最基本的一个参数。
C.模数一定时,齿轮的几何尺寸与齿数无关。
D.模数一定时,齿轮的齿距p不变,不同齿数的齿轮的基圆半径不变,轮齿的齿形相同。
6. 已知下列各标准直齿圆柱齿轮的参数:齿轮1:z1=72,d a1=222 mm;齿轮2:z2=72,h2=22.5 mm;齿轮3: z3=22,d f3=156mm;齿轮4:z4=22,d a4=240mm ,则可正确啮合的一对齿轮是( C )。
机械课后习题答案第4章习题及解答

第4章习题4.1典型棘轮机构由哪些构件组成?在棘轮机构中为保证棘爪能顺利进入棘轮轮齿的齿根,应满足的条件是什么?答:典型的棘轮机构由棘轮、驱动棘爪、摆杆和止回棘爪。
为保证棘爪能顺利进入棘轮轮齿的齿根,应满足的条件是齿面的偏斜角大于齿面摩擦角。
4.2为什么棘爪与棘轮轮齿接触处的公法线要位于棘轮与棘爪的转动中心之间?答:为了使棘爪能顺利受到棘轮轮齿金轮的齿底面而不致从棘轮轮齿尚滑脱出来。
4.3槽轮机构有什么特点?何谓运动系数τ,为什么τ必须大于零而必须小于1?答:槽轮机构的结构简单,外形尺寸小,其机械效率高,并能较平稳地、间歇地进行转位。
但因传动时尚存在柔性冲击,故常用于速度不太高的场合。
槽轮机构的运动系数是指在一个运动循环内,槽轮的运动时间与转臂的运动时间之比。
槽轮机构是间歇运动,因此运动系数必须大于零而小于1。
4.4槽轮机构的槽数z 和圆销数n 的关系如何?答:22-<z zK 4.5如何避免不完全齿轮机构在啮合开始和终止时产生的冲击?从动轮停歇期间,如何防止其运动?答:可在两轮的端面分别装上瞬心线附加杆,使从动件的角速度由零逐渐增加到某一数值从而避免冲击。
为了防止从动轮在停歇期间游动,两轮轮缘上各装有锁住弧。
4.6如图4.36示为一偏置直动从动件盘形凸轮机构。
已知AB 段为凸轮的推程廓线,试在图上标注推程运动角δt 。
图4.36解:见图。
4.7图4.37所示为一偏置直动从动件盘形凸轮机构。
已知凸轮为一以C为中心的圆盘,问轮廓上D点与尖顶接触时其压力角为多少?试作图加以表示。
图4.37解:4.8已知一凸轮以等角速度ω=10rad/s顺时针转动,直动推杆的运动规律及其对应的凸轮转角如表所示。
要求:(1)作出s-δ、v-δ和a-δ线图;(2)求出当δ为90︒、180︒和270︒时,推杆的s、v和a值。
δ/︒h/mm推杆运动规律0~12040等加速等减速运动120~1500休止150~210-20简谐运动210~2400休止240~300-20等速运动300~3600休止解:取比例尺:μs=1mm/mm、μv=1mm/s/mm、μa=1mm/s2/mm、μδ=3︒/mm、4.9图4.38示为一对心尖顶推杆单元弧凸轮(偏心轮),其几何中心O’与凸轮转轴O的距离为L O’O=15mm,偏心轮半径R=30mm,凸轮以等角速度ω顺时针转动,试作出推杆的位移线图s-δ。
(整理)第4章习题及解答

第4章习题4.1 典型棘轮机构由哪些构件组成?在棘轮机构中为保证棘爪能顺利进入棘轮轮齿的齿根,应满足的条件是什么?答:典型的棘轮机构由棘轮、驱动棘爪、摆杆和止回棘爪。
为保证棘爪能顺利进入棘轮轮齿的齿根,应满足的条件是齿面的偏斜角大于齿面摩擦角。
4.2 为什么棘爪与棘轮轮齿接触处的公法线要位于棘轮与棘爪的转动中心之间?答:为了使棘爪能顺利受到棘轮轮齿金轮的齿底面而不致从棘轮轮齿尚滑脱出来。
4.3 槽轮机构有什么特点?何谓运动系数τ,为什么τ必须大于零而必须小于1?答:槽轮机构的结构简单,外形尺寸小,其机械效率高,并能较平稳地、间歇地进行转位。
但因传动时尚存在柔性冲击,故常用于速度不太高的场合。
槽轮机构的运动系数是指在一个运动循环内,槽轮的运动时间与转臂的运动时间之比。
槽轮机构是间歇运动,因此运动系数必须大于零而小于1。
4.4 槽轮机构的槽数z 和圆销数n 的关系如何? 答:22-<z zK4.5 如何避免不完全齿轮机构在啮合开始和终止时产生的冲击?从动轮停歇期间,如何防止其运动?答:可在两轮的端面分别装上瞬心线附加杆,使从动件的角速度由零逐渐增加到某一数值从而避免冲击。
为了防止从动轮在停歇期间游动,两轮轮缘上各装有锁住弧。
4.6 如图4.36示为一偏置直动从动件盘形凸轮机构。
已知AB 段为凸轮的推程廓线,试在图上标注推程运动角δt 。
解:见图。
轮廓上D点与尖顶接触时其压力角为多少?试作图加以表示。
解:4.8已知一凸轮以等角速度ω=10 rad/s顺时针转动,直动推杆的运动规律及其对应的凸轮转角如表所示。
要求:(1)作出s-δ、v-δ和a-δ线图;(2)求出当δ为90︒、180︒和270︒时,推杆的s、v和a值。
解:取比例尺:μs v a、μδ=3︒/mm、4.9图4.38示为一对心尖顶推杆单元弧凸轮(偏心轮),其几何中心O’与凸轮转轴O的距离为L O’O =15mm,偏心轮半径R=30mm,凸轮以等角速度ω顺时针转动,试作出推杆的位移线图s-δ。
第四章齿轮机构

(5)、在任意圆上dk 齿槽宽ek 齿厚SK 齿距PK= ek+SK
基节 Pb
基节—基圆上的齿距
周节 P
周节—分度圆上的齿距
P=s+e=2s=2e
总之,齿轮与齿条啮合时,不论是否标准安装,齿轮分度圆与节 圆总是重合的,啮合角 恒等于分度圆压力角 。只是在非标准安装 时,齿条的节线与其分度线不再重合。
§4-6 渐开线齿轮的加工方法及根切现象
齿轮加 工方法
铸造法 热轧法
冲压法 粉末冶金法 模锻法 成形法
铣削 拉削
切制法 (最常用)
插齿
范成法 滚齿 (展成法 共轭法 剃齿 包络法)
轮齿廓上由齿顶 向齿根移动;
终止啮合点:主动轮的齿顶点与从动轮的齿根处某点
接触,在啮合线N1N2上为主动轮的齿顶 圆与啮合线N1N2的交点B1。
——实际啮合线 齿廓工作段,齿廓非工作段
——理论啮合线
2、连续传动条件
要求:前一对轮齿脱离啮合时,后一对轮齿必须已经进入啮合 或刚刚进入啮合
B1B2 Pb 或
磨齿
一、齿轮轮齿的加工方法 1.成形法(仿形法)
成形法是在普通铣床上用轴向剖面形状与被切齿轮齿 槽形状完全相同的铣刀切制齿轮的方法,如图所示。铣完 一个齿槽后,分度头将齿坯转过3600/z,再铣下一个齿槽 ,直到铣出所有的齿槽。
成形法加工方便易行,但精度难以保证。由于渐开线齿廓形状取 决于基圆的大小,而基圆半径rb=(mzcosα)/2,故齿廓形状与m、z 、α有关。欲加工精确齿廓,对模数和压力角相同的、齿数不同的 齿轮,应采用不同的刀具,而这在实际中是不可能的。生产中通常 用同一号铣刀切制同模数、不同齿数的齿轮,故齿形通常是近似的 。表中列出了1-8号圆盘铣刀加工齿轮的齿数范围。
《机械设计基础》答案
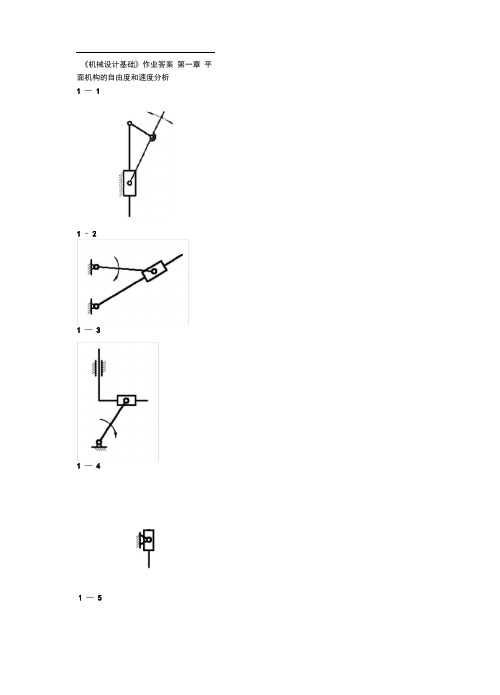
《机械设计基础》作业答案第一章平面机构的自由度和速度分析1 —11 - 21 —31 —41 —5自由度为:F 3n (2P L P H P') F'3 7 (2 9 1 0) 121 19 11或:F 3n 2P L P H3 6 2 8 111-6自由度为F 3n (2P L P H P') F'3 9 (2 12 1 0) 11或:F 3n 2P L F H3 8 2 11 124 22 111 —10自由度为:F 3n (2P L P H P') F'3 10 (2 14 1 2 2) 130 28 11或:F 3n 2P L P H3 9 2 12 1 227 24 211 —11F 3n 2P L P H3 4 2 4 221 —13:求出题1-13图导杆机构的全部瞬心和构件1 R4R3 3 卩34只31、3的角速度比。
1 - 14:求出题1-14图正切机构的全部瞬心。
设1 10rad/s,求构件3的速度v3。
100v3v P13 1P14P310 200 2000mm/s1- 15:题1-15图所示为摩擦行星传动机构,设行星轮2与构件1、4保持纯滚动接触,试1 R4p2 2 B4R2IP 24R 2I 2r 2IR 4P 12I r 11 10rad /s ,求机构全部瞬心、滑块速度 g 和连杆角速度1 P 4P 3I 10 AC tan BCA 916.565mm/sR 4R2 1 _100_10_ 2.9rad P 24R22 AC 1001 — 17:题1-17图所示平底摆动从动件凸轮 1为半径r 20的圆盘,圆盘中心 C 与凸轮回 转中心的距离l AC 15mm , l AB 90mm ,1 10rad /s ,求 00和 1800时,从动件角速度 2的数值和方向。
1 — 16 :题1-16图所示曲柄滑块机构,已知:1AB 100mm /s , I BC 250mm/s,在三角形ABC 中, BC sin 45°AB ------------- ,sin sin BCA BCA —, 5 cos BCA AC sin ABCBC sin 45° ,AC 310.7mm V 3 V p131 R4p 22 P24 P 2〔|P12 R3I|p2 P23I15 1090 152rad / s 方向如图中所示1 R2p3 2p2P23当1800时P2R3IP12P23IV——1.43rad / s90 15方向如图中所示第二章平面连杆机构2-1试根据题2-1图所注明的尺寸判断下列铰链四杆机构是曲柄摇杆机构、双摇杆机构。
机械原理部分试题及解答

第一章机构的组成和结构1-1 试画出图示平面机构的运动简图,并计算其自由度。
F=3×3-2×4=1 F=3×3-2×4=1F=3×3-2×4=1 F=3×3-2×4=11-2 计算图示平面机构的自由度。
将其中高副化为低副。
确定机构所含杆组的数目和级别,以及机构的级别。
(机构中的原动件用圆弧箭头表示。
)F=3×7-2×10=1 F=3×7-2×10=1 含3个Ⅱ级杆组:6-7,4-5,2-3。
含3个Ⅱ级杆组:6-7,4-5,2-3。
该机构为Ⅱ级机构构件2、3、4连接处为复合铰链。
该机构为Ⅱ级机构F=3×4-2×5-1=1 F=3×3-2×3-2=1F=3×5-2×7=1(高副低代后)F=3×5-2×7=1(高副低代后)含1个Ⅲ级杆组:2-3-4-5。
含2个Ⅱ级杆组:4-5,2-3。
该机构为Ⅲ级机构构件2、3、4连接处为复合铰链。
该机构为Ⅱ级机构F=3×8-2×11-1=1 F=3×6-2×8-1=1F=3×9-2×13=1(高副低代后)F=3×7-2×10=1(高副低代后)含4个Ⅱ级杆组:8-6,5-7,4-3,2-11。
含1个Ⅱ级杆组6-7。
该机构为Ⅱ级机构含1个Ⅲ级杆组2-3-4-5。
第二章 连 杆 机 构2-1 在左下图所示凸轮机构中,已知r = 50mm ,l OA =22mm ,l AC =80mm,︒=901ϕ,凸轮1的等角速度ω1=10rad/s ,逆时针方向转动。
试用瞬心法求从动件2的角速度ω2。
解:如右图,先观察得出瞬心P 13和P 23为两个铰链中心。
再求瞬心P 12:根据三心定理,P 12应在P 13与P 23的连线上,另外根据瞬心法,P 12应在过B 点垂直于构件2的直线上,过B 点和凸轮中心O 作直线并延长,与P 13、P 23连线的交点即为P 12。
齿轮及凸轮机构试题和答案

齿轮机构及其设计答案渐开线直齿圆柱齿轮正确啮合的条件是: 两齿轮的模数相等和压力角相等。
一对平行轴斜齿圆柱齿轮的正确啮合条件是:两轮法面上的模数和压力角分别相等,螺旋角大小相等,方向相反(外啮合)或相同(内啮合),一对直齿圆锥齿轮传动的正确啮合条件是两轮大端的模数和压力角相等。
3.蜗杆蜗轮传动的正确啮合条件是 : 其中间平面内蜗轮与蜗杆的模数和压力角分别相等, 当两轴交错为90度时,还应使蜗杆的导程角等于涡轮螺旋角。
标准渐开线直齿圆锥齿轮的标准模数和压力角定义在大端。
一对渐开线直齿圆柱齿轮啮合传动时,两轮的节圆总是相切并相互作纯滚动的,而两轮的中心距不一定总等于两轮的分度圆半径之和。
7.共轭齿廓是指一对能满足齿廓啮合基本定律的齿廓。
8. 用齿条刀具加工标准齿轮时,齿轮分度圆与齿条中线相切,加工变位齿轮时,中线与分度圆不相切。
被加工的齿轮与齿条刀具相"啮合"时,齿轮节圆与分度圆重合。
9. 有两个模数、压力角、齿顶高系数及齿数相等的直齿圆柱齿轮,一个为标准齿轮1,另一个为正变位齿轮2,试比较这两个齿轮的下列尺寸,哪一个较大、较小或相等:db1 = db2;da1 < da2;d1=d2;df1 < df2;sa1 > sa2;s1 > s2。
10. 标准齿轮除模数和压力角为标准值外,还应当满足的条件是分度圆上齿厚等于齿槽宽,即s=e 。
11. 斜齿轮在法面上具有标准模数和标准压力角。
12. 若两轴夹角为90度的渐开线直齿圆锥齿轮的齿数为Z1=25, Z2=40,则两轮的分度圆锥角= 32度 ; = 58度。
13. 一对直齿圆锥齿轮传动时的分度圆锥角应根据齿轮齿数和两轴交角来决定。
14. 如图所示两对蜗杆传动中,(a)图蜗轮的转向为逆时针;(b)图蜗杆的螺旋方向为右旋。
15. 用标准齿条型刀具加工标准齿轮时,其刀具的中线与轮坯分度圆之间做纯滚动.第二章答案:1)平面运动副的最大约束数为 2 ,最小约束数为 1 。
机械设计基础习题集及参考答案

机械设计基础习题集及参考答案机械设计基础习题集及参考答案Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】机械设计基础习题集及参考答案⼀、判断题(正确 T,错误 F)1. 构件是机械中独⽴制造的单元。
()2. 能实现确定的相对运动,⼜能做有⽤功或完成能量形式转换的机械称为机器。
()3. 机构是由构件组成的,构件是机构中每个作整体相对运动的单元体。
()4. 所有构件⼀定都是由两个以上零件组成的。
()⼆、单项选择题1. 如图所⽰,内燃机连杆中的连杆体1是()。
A 机构B 零件C 部件D 构件2. ⼀部机器⼀般由原动机、传动部分、⼯作机及控制部分组成,本课程主要研究()。
A 原动机B 传动部分C ⼯作机D 控制部分三、填空题1. 构件是机械的运动单元体,零件是机械的______单元体。
2. 机械是______和______的总称。
参考答案⼀、判断题(正确 T,错误 F)1. F2. T3. T4. F⼆、单项选择题1. B2. B三、填空题1. 制造2. 机构机器第⼀章平⾯机构的⾃由度⼀、判断题(正确 T,错误 F)1. 两构件通过点或线接触组成的运动副为低副。
()2. 机械运动简图是⽤来表⽰机械结构的简单图形。
()3. 两构件⽤平⾯低副联接时相对⾃由度为1。
()4. 将构件⽤运动副联接成具有确定运动的机构的条件是⾃由度数为1。
()5. 运动副是两构件之间具有相对运动的联接。
()6. 对独⽴运动所加的限制称为约束。
()7. 由于虚约束在计算机构⾃由度时应将其去掉,故设计机构时应尽量避免出现虚约束()8. 在⼀个确定运动的机构中,计算⾃由度时主动件只能有⼀个。
()⼆、单项选择题1. 两构件通过()接触组成的运动副称为⾼副。
A ⾯B 点或线C 点或⾯D ⾯或线2. ⼀般情况下,门与门框之间存在两个铰链,这属于()。
A 复合铰链B 局部⾃由度C 虚约束D 机构⾃由度3. 平⾯机构具有确定运动的条件是其⾃由度数等于()数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 齿 轮 机 构4-1有一对使用日久磨损严重的标准齿轮需要修复。
按磨损情况,拟将小齿轮报废,修复大齿轮,修复后的大齿轮的齿顶圆要减小8mm 。
已知Z 1=24,Z 2=96,m=4mm ,α=20°,ha *=1及c *=0.25。
试求这两个齿轮的几何尺寸。
解:根据题意要求中心距不变,修复大齿轮,即大齿轮负变位,小齿轮正变位。
根据大齿轮的磨损情况,通过对大齿轮进行负变位,把磨损部分切掉。
原齿轮2的齿顶圆直径为:mz 2+2h a *m=4×96+2×1×4=392 现齿轮2的齿顶圆直径为:d a2=392-8=384 齿轮负变位后:d a2=mz 2+2(h a *+x 2)m即:11429643842*222-=-⨯⨯-=--=a a h m mz d x 为了保持中心距不变,可对新设计的小齿轮进行正变位,x 1=-x 2=1 几何尺寸计算如下:分度圆直径:d 1=mz 1=4×24=96mmd 2=mz 2=4×96=384mm齿顶圆直径:d a1=mz 1+2(h a *+x 1)m=4×24+2×(1+1)×4=112mmd a2=mz 2+2(h a *+x 2)m=4×96+2×(1-1)×4=384mm齿根圆直径:d f1=mz 1-2(h a *+c *-x 1)m=4×24-2×(1+0.25-1)×4=94mmd f2=mz 2-2(h a *+c *-x 2)m=4×96-2×(1+0.25+1)×4=366mm4-2 已知一对外啮合变位齿轮的齿数Z 1=10,Z 2=12,ha *=1,C *=0.25,α=20°,m=10mm ,求相应的最小变位系数,计算两轮的齿顶圆直径d a 。
(inv 26.985°=0.038264,inv20°=0.014904)解:因为两齿轮的齿数都小于不产生根切的最小齿数(z min =17),故应采用正变位,最小变位系数为x 1=(17-z 1)/17=(17-10)/17=0.412 x 2=(17-z 2)/17=(17-12)/17=0.294038264.020121020)294.0412.0(2tan )(22121=︒++︒+=+++='inv tg inv z z x x inv ααα得:︒='985.26αααcos cos a a ='' 其中a=m(z 1+z 2)/2=10(10+12)/2=110 得:995.115985.26cos 20cos 110cos cos =︒︒⨯='='ααa a中心距变动系数 5995.010110995.115=-=-'=m a a y齿高变动系数 △y=x 1+x 2-y=0.412+0.294-0.5995=0.1065齿顶高 h a1=(h a *+x 1-△y)m=(1+0.412-0.1065)×10=13.055mm h a2=(h a *+x 2-△y)m=(1+0.294-0.1065)×10=11.875mm 齿顶圆直径 d a1=d 1+2h a1=mz 1+2×13.055=126.11mm d a2=d 2+2h a2=mz 2+2×11.875=143.75mm4-3已知两个直齿圆柱齿轮的齿数分别为Z 1=12,Z 2=15,用α=20°,m=4mm 的滚刀切制。
如两齿轮按最小变位系数切制,试求无侧隙传动的中心距。
(inv αˊ=0.026,则αˊ=23°54′,inv20°=0.014904)解:因为两齿轮的齿数都小于不产生根切的最少齿数(z min =17),故应采取正变位,其最小变位系数为:x 1=(17-z 1)/17=(17-12)/17=0.294 x 2=(17-z 2)/17=(17-15)/17=0.1176 根据无侧隙啮合方程式得:026.020151220tan )1176.0294.0(2tan )(22121=︒++︒+=+++='inv inv z z x x inv ααα查P140渐开线函数表得:α′=23°54′无侧隙传动的中心距为: mm z z m a a 53.554523cos 20cos )1512(24cos cos )(2cos cos 21='︒︒+⨯='+='='αααα4-4 某球磨机上有一对标准直齿圆柱齿轮,已测知m=16mm ,Z 1=27,Z 2=245,中心距a=2176mm 。
两齿轮齿面磨损严重需要修复。
为了节约材料和降低制造成本,决定只更换小齿轮,而通过变位切削修复大齿轮。
检测后知大齿轮分度圆上齿厚的磨损量为5.61mm 。
试求小齿轮的齿顶圆直径以及修复大齿轮时的大齿轮齿顶圆直径。
解:(1)根据分度圆齿厚的磨损量,首先对大齿轮进行负变位切削,把齿面磨损部分全部切掉。
由磨损量等于齿厚减薄量条件得:2x 2mtg α=-5.61 则482.02016261.5261.52-=︒⨯⨯-=-=tg mtg x α取x 2=-0.5,则能保证将磨损部分全部切掉。
(2)为了保持无侧隙啮合中心距不变,应采用高度变位传动,故小齿轮为正变位,即x 1=-x 2=0.5(3) 在高度变位齿轮传动中,齿高变动系数△y=0 h a = (h a *+x-△y)m d a =d+2(h a *+x-△y)md a1=mz 1+2(h a *+x 1)m=480mm d a2=mz 2+2(h a *+x 1)m=3936mm而标准齿轮的大齿轮z 2=245,d a2=3952,其齿顶圆相应车小到d a2=3936mm4-5已知:一对正常齿渐开线标准斜齿圆柱齿轮的中心距a=250mm ,齿数Z 1=23,Z 2=98,法向模数m n =4mm ,试计算其螺旋角、端面模数、端面压力角、当量齿数、分度圆直径、齿顶圆直径和齿根圆直径。
解:)(cos 2)(212121z z m z z m a n t +=+=β968.02502)9823(42)(cos 21=⨯+=+=a z z m n β 得:螺旋角 β=14.53°端面模数 m t =m n /cos β=4/0.968=4.13 端面压力角 ︒=︒︒==6.2053.14cos 20cos tg tg arctgn t βαα 当量齿数 β3cos zz v =36.25968.023cos 3311===βz z v 04.108968.098cos 322===βz z v 分度圆直径(按端面参数计算) mm z m z m d n t 04.9523968.04cos 111=⨯===βmm z m z m d n t 96.40498968.04cos 222=⨯===β 齿顶圆直径(按端面参数计算)d a1=d 1+2h at *m t =95.04+2×h an *×cos14.53°×4.13=103.04mm d a2=d 2+2h at *m=404.96+2×h an *×cos14.53°×4.13=412.96mm 齿根圆直径(按端面参数计算)d f1=d 1-2(h at *+c t *)m t =95.04-2(1+0.25) ×cos14.53°×4.13=85.04mm d f2=d 2-2(h at *+c t *)m t =404.96-2(1+0.25) ×cos14.53°×4.13=394.96mm4-6一对标准斜齿圆柱齿轮,已知传动比i=3.5,法向模数m n =2mm ,中心距a=90mm ,初设螺旋角β=15°。
试确定这对齿轮的实际螺旋角β和齿数,计算分度圆直径、齿顶圆直径、齿根圆直径和当量齿数。
解:因为传动比i=z 2/z 1=3.5 则:z 2=3.5z 1βcos 2)(21z z m a n +=93.86215cos 290cos 221=︒⨯⨯=⨯=+n m a z z β 即z 1+3.5z 1=86.93 z 1=19.32 z 2=67.61 若取 z 1=20 则 z 2=70βcos 2)(21z z m a n +=1902)7020(22)(cos 21=⨯+⨯=+=a z z m n β显然cos β不可能大于等于1若取z 1=19,根据传动比i=3.5,则 z 2=66.5,显然齿数不能为小数,取z 2=67。
将z 1=19 则 z 2=67,代入上式得出实际β=17.2°(在8°-20°之间)mm m m nt 093.2cos ==βh at *=h an *cos β c t *=c n *cos β 计算分度圆直径:mm z m d t 77.3911== mm z m d t 23.14022== 计算齿顶圆直径:d a1=d 1+2h at *m t =43.77mm d a2=d 2+2h at *m t =144.23mm 计算齿根圆直径 d f1=d 1-2(h at *+c t *)m=34.77mm d f2=d 2-2(h at *+c t *)m=135.23mm 计算当量齿数 8.21cos 311==βz z v 8.76cos 322==βz z v 4-7有一对蜗杆蜗轮的参数为Z 1=1,Z 2=40,α=20°,h a *=1,C *=0.2,m=5mm ,d 1=50mm 。
试计算其几何尺寸和传动比。
解:分度圆直径:d 1=50mm d 2=mz 2=5×40=200mm中心距: a=(d 1+d 2)/2=125mm齿顶圆直径:d a1=d 1+2h a *m=50+2×1×5=60mmd a2=d 2+2h a *m=200+2×1×5=210mm齿根圆直径:d f1=d 1-2(h a *+c *)m=50-2×(1+0.2)×5=38d f2=d 2-2(h a *+c *)m=200-2×(1+0.2)×5=188蜗杆导程角:γ=arctg(z 1m/d 1)=arctg(1×5/50)=5.7° 蜗轮螺旋角:β2=γ=5.7° 传动比: i 12=z 2/z 1=40/1=40。
