材料力学第四版课后习题
第四版单辉祖材料力学课后答案

第四版单辉祖材料力学课后答案引言《材料力学》是材料科学与工程专业的一门基础课程,主要介绍了材料的力学性质和力学行为。
本文以《材料力学》第四版的单辉祖所编写的课后习题为题,给出了相应的答案。
通过对这些习题的解答,帮助学生巩固课堂所学的知识,并提供了一些解题思路和方法。
目录•第一章引言•第二章物质的内部力和应力•第三章弹性和塑性力学基础第一章引言1. 什么是材料力学?答案:材料力学是研究物质响应外力作用下的变形和破坏行为的科学。
2. 材料力学的主要内容有哪些?答案:材料力学的主要内容包括静力学、动力学、弹性力学、塑性力学、断裂力学等。
第二章物质的内部力和应力1. 什么是内力?答案:内力是物质内部分子间相互作用所产生的力。
2. 什么是应力?答案:应力是单位面积上的力,表示为单位面积上的力的矢量。
3. 应力的分类有哪些?答案:应力可分为法向应力和切应力两种,法向应力垂直于截面,切应力与截面垂直。
4. 弹性应力-应变关系有哪些?答案:弹性应力-应变关系有胡克定律,即应力与应变成正比。
第三章弹性和塑性力学基础1. 弹性和塑性的区别是什么?答案:弹性是指物体在受到外力作用下发生变形后,外力去除后恢复原状的能力;塑性是指物体在受到外力作用下发生变形后,即使外力去除,物体也不能恢复原状。
2. 什么是弹性模量?答案:弹性模量是描述物质抵抗压缩和拉伸变形能力的指标,表示为物质单位应力与应变的比值。
3. 什么是屈服强度?答案:屈服强度是材料在拉伸过程中,在产生明显塑性变形或显著应力减小时的应力值。
4. 什么是塑性应变?答案:塑性应变是指材料在超过屈服点后产生的应变。
结论本文为《材料力学》第四版单辉祖所编写的课后习题的答案,涵盖了材料力学的部分基础知识。
通过对这些习题的解答,希望能够帮助学生深入理解材料力学的概念和原理,并提供一些解题思路和方法。
通过不断练习,学生能够对材料力学有更深入和全面的认识,为日后的学习和研究打下坚实的基础。
工程力学材料力学第四版(北京科技大学与东北大学)习题答案

(北京科技大学与东 北大学)
第 一意轴向拉伸和压缩
, 1-1 lfJ截 Illi法 求 下列各轩指 定的 lii fl'J 内 )J
2
f
2
F 2k N
I
(a 1
2
f
(bl
3P
11
(d 1
2kN P
2
2
(e 1
题 1 ) [fI
解
P
({)
P rlp|p
iE
『
e-
I Iz Il
F
5,
为 20 俐 , 许用应力 I δ]=50 Mpa . 试
根据吊钩螺纹部分的强主确定吊钩的阵 111 起重盐 1 解 P= 119kN
P
3m
B
P
E
题1-1 8 固
lIlí l - l ~ 罔
1 - 1 9 如入所示结构的 ABH 为钢轩,其帧故而积 -4.:::6 cm2 • 咛用阻力 ( σ 1=140 MPa ; BC
<.l
(bl
题 1-3 归
且ø 1 -4 因
1-4 : 桩杆起lli:机如 l 国所示,起lli:忏 AB 为钢管 , J[外径 。=2ûrnm , 内径 d= 1 8mrn;制绳
CB 的棋极而而积为 01cnEZe 己知l起重证
P=2脱lO N ,
试计fI起重机轩;归 钢丝绳的应 )J.
解 受力分析得
解
E = GPa . v = 0.3 17
1- 10: i主杆端部与的如1I相迹 , 其构应如罔 ,谊作用在连杆的轴向 jJ P=l28KN , 蝉挟处的内
径 d = 3.7cm , 螺栓材料的冉川剧
工程力学材料力学第四版(北京科技大学和东北大学)习题答案解析

工程力学材料力学(科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力 解:(a):N 1=0,N 2=N 3=P (b):N 1=N 2=2kN(c):N 1=P,N 2=2P,N 3= -P (d):N 1=-2P,N 2=P(e):N 1= -50N,N 2= -90N (f):N 1=0.896P,N 2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a 所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b 所示;拉杆上端螺纹的内径d=175mm 。
以知作用于拉杆上的静拉力P=850kN ,试计算大钟拉杆的最大静应力。
解:σ1= 2118504P kN S d π==35.3Mpaσ2=2228504P kNS d π==30.4MPa∴σmax =35.3Mpa1-3:试计算图a 所示钢水包吊杆的最大应力。
以知钢水包与其所盛钢水共重90kN ,吊杆的尺寸如图b 所示。
解:下端螺孔截面:σ1=19020.065*0.045P S ==15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa上端双螺孔截面:σ3=3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB 为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm 2。
已知起重量P=2000N ,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F 1*sin15=F 2*sin45 F 1*cos15=P+F 2*sin45∴σAB = 11F S =-47.7MPa σBC =22F S =103.5 MPa1-5:图a 所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c 所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力. 解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S=38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形. (2)AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm (2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:AC AC ACLNL EA EA σε===1.59*104,CB CB CBLNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧 制压力.压头材料的弹性模量E=200Gpa. 解:1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
材料力学第四版课后习题答案

材料力学第四版课后习题答案1. 引言。
材料力学是材料科学与工程中的重要基础课程,通过学习材料力学,可以帮助我们更好地理解材料的性能和行为。
本文档将针对材料力学第四版的课后习题进行答案解析,帮助学习者更好地掌握课程内容。
2. 第一章。
2.1 课后习题1。
答,根据受力分析,可以得到杆件的受力情况。
然后利用杆件的受力平衡条件,可以得到杆件的应力状态。
最后,根据应力状态计算应变和变形。
2.2 课后习题2。
答,利用受力分析,可以得到杆件的受力情况。
然后利用杆件的受力平衡条件,可以得到杆件的应力状态。
最后,根据应力状态计算应变和变形。
3. 第二章。
3.1 课后习题1。
答,利用受力分析,可以得到梁的受力情况。
然后利用梁的受力平衡条件,可以得到梁的应力状态。
最后,根据应力状态计算应变和变形。
3.2 课后习题2。
答,利用受力分析,可以得到梁的受力情况。
然后利用梁的受力平衡条件,可以得到梁的应力状态。
最后,根据应力状态计算应变和变形。
4. 第三章。
4.1 课后习题1。
答,利用受力分析,可以得到薄壁压力容器的受力情况。
然后利用薄壁压力容器的受力平衡条件,可以得到薄壁压力容器的应力状态。
最后,根据应力状态计算应变和变形。
4.2 课后习题2。
答,利用受力分析,可以得到薄壁压力容器的受力情况。
然后利用薄壁压力容器的受力平衡条件,可以得到薄壁压力容器的应力状态。
最后,根据应力状态计算应变和变形。
5. 结论。
通过对材料力学第四版课后习题的答案解析,我们可以更好地掌握材料力学的基本原理和方法。
希望本文档能够对学习者有所帮助,促进大家对材料力学的深入理解和应用。
材料力学答案第四版单辉祖课后答案
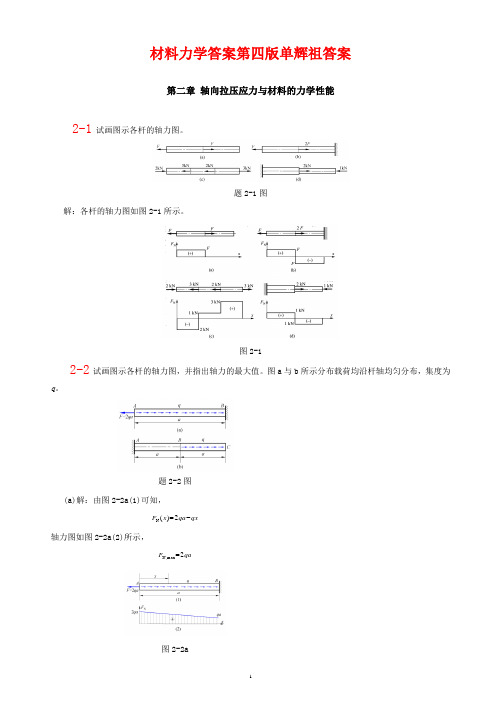
材料力学答案第四版单辉祖答案第二章 轴向拉压应力与材料的力学性能2-1 试画图示各杆的轴力图。
题2-1图解:各杆的轴力图如图2-1所示。
图2-12-2试画图示各杆的轴力图,并指出轴力的最大值。
图a 与b 所示分布载荷均沿杆轴均匀分布,集度为q 。
题2-2图(a)解:由图2-2a(1)可知,qx qa x F -=2)(N轴力图如图2-2a(2)所示,qa F 2m ax ,N =图2-2a(b)解:由图2-2b(2)可知, qa F =R qa F x F ==R 1N )(22R 2N 2)()(qx qa a x q F x F -=--=轴力图如图2-2b(2)所示,qa F =m ax N,图2-2b2-3 图示轴向受拉等截面杆,横截面面积A =500mm 2,载荷F =50kN 。
试求图示斜截面m -m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
题2-3图解:该拉杆横截面上的正应力为100MPa Pa 1000.1m10500N 10508263=⨯=⨯⨯==-A F σ 斜截面m -m 的方位角, 50-=α故有 MPa 3.41)50(cos MPa 100cos 22=-⋅== ασσαMPa 2.49)100sin(MPa 502sin 2-=-⋅== αστα 杆内的最大正应力与最大切应力分别为 MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示,图中还同时画出了低应变区的详图。
试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
题2-5解:由题图可以近似确定所求各量。
220GPa Pa 102200.001Pa 10220ΔΔ96=⨯=⨯≈=εσE MPa 220p ≈σ, MPa 240s ≈σMPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。
材料力学ppt(刘鸿文第四版含课后答案)

l1
A' l3
(3) 物理关系
A
l1
N1l
E1A1 cos
l1 l2 A' l3
(1) 静平衡方程
N1 N2
(1)
N3 2N1 cos P 0 (2)
(2) 变形协调方程 l1 l源自 l3 cos (3)(3) 物理关系
l1
N1l
E1A1 cos
0.52 104 (m)
AB杆的变形
lAB lBD lCD lAC 1.05104(m)
例 2 (书例2. 7) 已知: BC杆: d=20mm, BD杆: 8号槽钢。[]= 160 MPa, E=200GPa, P=60kN。 求:校核强度及B点位移。 解:(1) 求轴力
Al
l Nl Pl 胡克定律的
EA EA
另一种形式
EA 抗拉(或抗压)刚度
注意:上式只在应力不超过比例极限时成立。
推广: (1) 阶梯轴
l Nili
Ei Ai
(2) 变截面轴
l
l
N ( x) EA(x)
dx
l1
l2
l3
A1
A2
A3
x
N(x)+dN(x)
N(X)
应力 A2 1024.8106 m2
1
N1 A1
143MPa
[ ] 160MPa
2
N2 A2
73.2 MPa
[ ] 160MPa
(3) 计算杆的变形
BC杆变形
l1
BB1
N1l1 EA1
材料力学ppt(刘鸿文第四版含课后答案)

应力分布均匀 均匀时 应力分布均匀时
N Al N l U = uV = V = = 2 2E 2EA 2EA
Nl 推广到多杆系统 U = ∑ i=1 2E A i i
1 由能量守恒原理 U =W= P∆l 2 2 n 有 1 Ni li P∆l = ∑ 2 i=1 2E A i i
n 2 i i
关于静不定的基本概念
静定问题
静不定问题 —— 静不定次数 —— 多余约束 ——
求解静不定问题的基本方法
力的平衡关系。 静力平衡方程 -力的平衡关系。 变形与约束的协调关系。 变形协调方程 - 变形与约束的协调关系。 力与变形的关系。 物理关系 - 力与变形的关系。
例 1 (书p.50) 书 已知:1、2杆相同,抗拉 杆相同, 已知: 、 杆相同 刚度为E 刚度为 1A1 , 3杆的抗拉 杆的抗拉 长为l 角 刚度为E 刚度为 3A3 , 长为 , α角。 各杆的内力。 求:各杆的内力。 解: 静不定的次数? 静不定的次数?
(2) 变形协调方程 (3) 物理关系
∆l1 = ∆l2 = ∆l3 cosα (3) N1l N3l ∆l1 = ∆l3 = E1A cosα E3 A 1 3
(4)
物理关系代入变形协调方程
N1l N3l = cosα E A cosα E3 A 1 1 3
与平衡方程联立,可解出 与平衡方程联立,可解出:
D
C
B
2 l N2
3
1
αα
A P y N3
αα
∑X = 0 N1 sin α − N2 sinα = 0 N1 = N2 ∑Y = 0 N3 +2N1 cosα − P = 0
N1
x
P
工程力学(静力学材料力学)第四版习题答案

静力学部分第一章基本概念受力图工程力学(静力学与材料力学)第四版习题答案全解由新疆大学&东华大学汤2-1 解:由解析法,23co s 80R X F X P P Nθ==+=∑12sin 140R Y F YP P Nθ==+=∑故:161.2R F N==1(,)a rc c o s 2944R Y R RF F P F '∠==工程力学(静力学与材料力学)第四版习题答案全解由新疆大学&东华大学 汤2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123co s 45co s 453R X F X P P P K N==++=∑13sin 45sin 450R Y F YP P ==-=∑故:3R F K N== 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:X =∑sin 300A C AB F F -=Y=∑co s 300A C F W -=0.577A B F W=(拉力)1.155A C F W=(压力)(b ) 由平衡方程有:X =∑co s 700A C AB F F -=Y=∑sin 700A B F W -=1.064A B F W=(拉力)0.364A CF W=(压力)(c ) 由平衡方程有:X =∑co s 60co s 300A C AB F F -=Y=∑sin 30sin 600A B A C F F W +-=0.5A B F W= (拉力)0.866A C F W=(压力)(d ) 由平衡方程有:X =∑sin 30sin 300A B A C F F -=Y=∑co s 30co s 300A B A C F F W +-=0.577A B F W= (拉力)0.577A C F W= (拉力)工程力学(静力学与材料力学)第四版习题答案全解由新疆大学&东华大学 汤2-4 解:(a )受力分析如图所示:由x =∑4c o s 450R A F P ⋅-=15.8R A F K N∴=由0Y =∑s in 450R A R B F F P ⋅+-=7.1R B F K N∴=(b)解:受力分析如图所示:由x =∑c o s 45c o s 450R A R B F F P ⋅--=Y=∑s in 45s in 450R A R B F F P ⋅+-=联立上二式,得:22.410R A R B F K N F K N==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5R A F K N= (压力)5R B F K N=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2A C F G =由x =∑c o s 0A C r F F α-=12c o s G G α∴=由0Y =∑s in 0A C N F F W α+-=工程力学(静力学与材料力学)第四版习题答案全解由新疆大学&东华大学 汤2s in N F W G W α∴=-⋅=-2-7解:受力分析如图所示,取左半部分为研究对象由x =∑co s 45co s 450R A C B P F F --=Y=∑sin 45sin 450C B R A F F '-=联立后,解得:0.707R A F P=0.707R B F P=由二力平衡定理0.707R B C B C B F F F P'===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑co s 60co s 300A C AB F F W ⋅--=Y=∑sin 30sin 600A B A C F F W +-=联立上二式,解得: 7.32A BF K N=-(受压)27.3A CF K N=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑s in c o s 0D B T W αα-=D B T W c tg α∴==(2)取B 点列平衡方程:由Y=∑s in c o s 0B D T T αα'-=230B D T T ctg W ctg K Nαα'∴===2-10解:取B 为研究对象:工程力学(静力学与材料力学)第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理由Y=∑s in 0B C F P α-=sin B C P F α∴=取C 为研究对象:由x =∑c o s s in s in 0B C D C C E F F F ααα'--=由0Y =∑s in c o s c o s 0B C D C C E F F F ααα--+=联立上二式,且有B C B CF F '= 解得:2c o s 12s in c o s C E P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象:由0Y =∑c o s 0N H C E F F α'-=C E C EF F '= 故有:22c o s 1c o s 2s in c o s 2s in N H P P F ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750A B A D F F -=Y=∑co s 75co s 750A B A D F F P +-=联立后可得: 2c o s 75A D AB P F F ==取D 点平衡,取如图坐标系:x =∑co s 5co s 800AD N D F F '-=c o s 5c o s 80N D A DF F '=⋅由对称性及A D A DF F '=工程力学(静力学与材料力学)第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理c o s 5c o s 5222166.2c o s 80c o s 802c o s 75N N D A D P F F F K N'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑co s co s 300R A D C F F P α+-=Y=∑sin sin 300R A F P α-=联立上二式得:2.92R A F K N=1.33D C F K N=(压力)列C 点平衡x =∑405D C A C F F -⋅=Y=∑305B C A C F F +⋅=联立上二式得:1.67A C F K N=(拉力)1.0B CF K N=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑R D R E F F '=Y =∑R D F Q =联立方程后解得:R D F =2R E F Q'=(2)取ABCE 部分,对C 点列平衡x =∑co s 450R E R A F F -=Y=∑sin 450R B R A F F P --=工程力学(静力学与材料力学)第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理且 R ER EF F '=联立上面各式得:R AF =2R B F Q P=+(3)取BCE 部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
满足强度条件。
ppt课件
2-9
FRA
FRB
以整个桁架为研究对象: FRAFRBF
用截面法求杆CD内力:
ME0, FCD 2mFRA 2m
FRA
FCD F
E
F FNAB
x
FNBC 125kN(受压)
FNAB 75kN(受拉) ppt课件
2-5 (2)求各杆应力。 根据公式: FN 得: A
AB杆应力:AB FN AAB371 5 1 033 0 m N 22M 5 (P拉a应力) ABCC杆杆应应力力:: A BC C F F N A N AA B C C 1 3 1 3 0 1 2 1 1 1 0 0 3 5 0 3m 3 m 3 0 0 N N 22 34..37 1M M ((P 拉P 压应应aa力力)) CD杆应力:CD FN AC D371 5 1 033 0 m N 22M 5 (P压a应力)
F2
E2A2 E1A1E2A2
F(压力)
2
F2 A2
E2F E1A1E2A2
(压应力)
1A F11 E1A1E2FE2A2A pA pt课12件(拉应力)
习题 第3章
3-2
FFSbA
解题关键是求受剪 面面积A。
ppt课件
习题 第3章
3-3
剪切强度 挤压强度 板抗拉强度
搭接接头。
F 60kN Fs n 3 20kN
ppt课件
FCD
2-10 解(1)先求出两杆内力
FNAB 2F FNBC F
(2)先让杆AB充分发挥作用, 相应最大轴力为:
[FN]ABA161 060P a14
3.14 (20 1 03m)25.02kN FAB
FBC
F1
[FN]AB35.5kN 2
F
ppt课件
2-10
(2) 让杆BC充分发挥作用,相 应最大轴力为:
ppt课件
2-6
ppt课件
2-7
解:首先根据公式 FN 求横截面上的应力:
A
F N A1
0 22 0 0 10 3 1 N 00 6 0 m 16P 0 a1M
P
a
(1)分别代入公式
co2s
、
1sin2 2
得斜截面m-m上的应力为:
ppt课件
习题 第2章
( ( 6 ) 6) 1 2 (sci 6 2 o n )2 6 s ()1 M 1 21 M P 4 3 a0 .P 72 3 M 5 a 0.4 P3 M a3P
Fy 0, F 1 c4 o 5 s F 2 c3 o 0 s F 0 F1 F2
联立求解得: F120.7kN F2 29.3kN(受拉)
F
ppt课件
2-8 则由公式 FN 得两杆正应力分别为: A
1A F 1 13 .1 4 2 4 1.7 2 0 6 1 17 6 N 0 0 m 2 1M 03 P a 1M 60
习题 第3章
3-4
解:先由杆的强度条件确定所 需的直径,直径确定后,再按
杆的刚度条件校核刚度。
因t<2t1,由铆钉的强度条件:
maxA FNS
F 2
14d2
得:
d
2
2F
2 24p6pt0 课01件103N 06Pm a20.6mm
习题 第3章
3-4 校核挤压强度: 将d=20.6mm代入公式 b A F b b t F d 2 1 0 3 m 0 4 1 2 0 m 3 .N 6 0 0 1 3 m 0 9 m .1 M 7 P b s1 aM 20 满足挤压强度。
习题 第2章
2-1
(1)
ppt课件
2-3 A1=400mm2,A2=300mm2,试求1-1、2-2截面
上的应力。
2-5
ppt课件
2-5
(1)求各杆内力。以结点
B为研究对象受力分析如图
所示:
α
建立直角坐标系,因受力 平衡可列平衡方程:
Fx 0, FFNB cCo s0 FNBC y
Fy 0, F NB sCi nF NA B 0
△l1
(2)分析两者变形关系。
△l3
l2l3l1
△l2
式中,△l1-F作用下钢筋的总伸长; △l2-F1、F2作用下
钢筋及混凝土的伸长; △l3p-p混t课件凝土反力对钢筋造成的伸 长量。
习题 第2章
2-25
△l1
△l3
l2l3l1 △l2
F2l F2l Fl E 2A 2 E 1A 1 E 1A 1
(1)根据公式
co2s、
1sin2知: 2
当 0时,正应力最大,此时,
当ma x c时o,2切0s 应1力M最P大a,此时,
41Leabharlann max2sin 2(4pp)t课 件 0.5MPa
2-8
解:取结点A为脱离体,受力 分析如图所示,求出两杆内力 与F关系为:
Fx 0, F 2s3 in 0 F 1si4n 5 0 A
Fb
FF20kN n3
A s 1 4 3 .1 ( 4 1 1 6 ppt课 3 件m 0)2 0 .2m 0 2 1
习题 第3章
3-3 A b d 1 t 1 6 3 m 0 1 1 2 3 m 0 0 .1m 9 2 2
A t ( b d ) 1 1 2 3 m ( 0 8 1 0 3 m 0 1 1 6 3 m ) 0 0 . 7 m 2 6
DE
静力方面
几何方面
ppt课件
物理方面
习题 第2章
2-22 P225 附录A
A钢3.086cm2
l钢 l木
l FN l EA
ppt课件
习题 第2章
2-25
(1)假设卸载后钢筋受力
FI,混凝土F2,现分析两者 关系。
因卸载后无外力,所以FI、 F2应为一对相互作用力,即:
F1 F2 而且,F2一定是压力。
F S6 0 130 N9.5 9M P a 14 M 0Pa
A S 0.20 m 21
b s A F b b2 0.1 0 19 m 3N 0 22 10 .2M 4 P ba s30 M 0Pa A F6 0.7 0 16 m 3N 0 28 7.1 8 Mpp t课P 件 a 16 M 0Pa
[FN]BCA16010 6P a14
3.14(2010 3m)25.02kN
F 2 F N B C3.5 5 kN F M (F 1 i,F n 2 )
FAB
FBC
F
ppt课件
2-17
ppt课件
2-20
l FN l EA
关键: l1l2l3
ppt课件
静力方面 几何方面 物理方面
2-21
C
