菱形的判定证明题(5篇)
菱形的判定(含答案)

菱形的判定一、选择题1.下列四边形中不一定为菱形的是()A.对角线相等的平行四边形 B.每条对角线平分一组对角的四边形C.对角线互相垂直的平行四边形 D.用两个全等的等边三角形拼成的四边形2.四个点A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD= BC; ⑤AD∥BC.这5个条件中任选三个,能使四边形ABCD是菱形的选法有().A.1种 B.2种 C.3种 D.4种3.菱形的周长为32cm,一个内角的度数是60°,则两条对角线的长分别是()A.8cm和43cm B.4cm和83cm C.8cm和83cm D.4cm和43cm二、填空题4.如图1所示,已知□ABCD,AC,BD相交于点O,•添加一个条件使平行四边形为菱形,添加的条件为________.(只写出符合要求的一个即可)图1 图25.如图2所示,D,E,F分别是△ABC的边BC,CA,AB上的点,且DE∥AB,DF∥CA,要使四边形AFDE 是菱形,则要增加的条件是________.(只写出符合要求的一个即可)6.菱形ABCD的周长为48cm,∠BAD: ∠ABC= 1:•2,•则BD=•_____,•菱形的面积是______.7.在菱形ABCD中,AB=4,AB边上的高DE垂直平分边AB,则BD=_____,AC=_____.四、思考题9.如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD,PC相交于点P,四边形PCOD是菱形吗?试说明理由.]2、如图ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.3如图所示,四边形ABCD、DEBF都是矩形,AB=BF,AD、BE相交于M,BC、DF交于N,求证:四边形BMDN是菱形.1、用两个边长为a的等边三角形纸片拼成的四边形是___________2、有一组邻边相等的四边形是菱形()3、对角线互相垂直的四边形是菱形()4、对角线互相平分垂直的四边形是菱形()5、如图,△ABC中,AD平分∠BAC,DE∥AC,与AB相交于点E,DF∥AB,与AC相交于点F,试说明四边形AEDF是菱形。
专题16 菱形的判定与性质(含答案)

专题16 菱形的判定与性质知识解读菱形是一个特殊的平行四边形,理解菱形的定义,可从菱形的共性和特性两个方面来理解.共性:菱形是一个特殊的平行四边形,它具有平行四边形的一切性质,如对边平行且相等,对角相等,邻角互补,对角线互相平分等。
菱形的特性主要体现在两个方面:①邻边相等;②对角线互相垂直判断一个四边形是菱形有三种方法方法1:有一组邻边相等的平行四边形是菱形方法2:对角线互相垂直的平行四边形是菱形方法3:四条边相等的四边形是菱形。
如果把一组邻边相等和对角线互相垂直看作菱形的特征,前两种判断方法可以理解为“平行四边形+菱形特征=菱形”,也就是说,要证明一个四边形是菱形,可先证明这个四边形是一个平行四边形,然后再添加一个菱形的特征。
培优学案典例示范一、菱形四边相等为全等提供了可能例1如图4-16-1①,在菱形ABCD中,点E,F分别为AB,AD的中点,连接CE,CF.(1)求证:CE=CF;(2)如图4-16-1②,若H为AB上一点,连接CH,使∠CHB=2∠ECB,求证:CH=AH+AB.BA EBAEHCFFCDD①②图4-16-1【提示】(1)由菱形ABCD中,点E,F分别为AB,AD的中点,易证得△BCE2A△DCF(SAS),则可得CE=CF;(2)延长BA与CF,交于点G,由平行线的性质,可得AG=AB,∠G=∠FCD,由全等三角形的对应角相等,可得∠BCE=∠DCF,然后由∠CHB=2∠ECB,易证得∠G=∠HCG,则可得CH=GH,则可证的结果。
【解答】【技巧点评】菱形的四条边相等、对角相等,这就为全等三角形提供了条件,因此菱形问题常常与全等三角形联系在一起.【跟踪训练】1.如图4-16-2,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:①△AED≌△DFB;②S四边形BCDG=34CG2;③若AF=2DF,则BG=6GF.其中正确的结论()A.只有①②B.只有①③C.只有②③D.①②③二、菱形被两条对角线分成四个直角三角形例2已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是()A.12cm2B.24cm2C.48cm2D.96cm2【提示】菱形的周长是20cm,故边长为5cm,又两条对角线的比是4:3,不妨设两条对角线长为4k,3k,因菱形的对角线互相垂直平分,同勾股定理可得(4k)2+(3k)=100,可求出k的值,即可求出菱形的两条对角线的长,代入菱形的面积公式,可求出菱形的面积.【技巧点评】菱形的一边和两条对角线的一半构成直角三角形,在直角三角形中,应用勾股定理,是解决这个问题的基本思路,本题在计算菱形的面积的时候,应用了菱形的面积等于对角线之积的一半.【跟踪训练】1.如图4-16-3,菱形ABCD的周长为40cm,AC,BD相交于O,且BD:AC=3:4.求AC,BD的长及菱形ABCD的面积.【解答】三、含60°角的菱形常与等边三角形结合在一起例3如图4-16-4,菱形ABCD的边长为2,BD=2,E,F分别是边AD,CD上的两个动点,且满足AE+CF=2.(1)求证:△BDE≌△BCF;(2)判断△BEF的形状,并说明理由;【提示】(1)由于菱形ABCD的边长为2,BD=2,所以△ABD和△BCD是等边三角形,则∠BDE=∠BCF=60°,BC=BD,又由于AE+CF=2,AE+ED=2可得DE=CF,即可证明△BDE≌△BCF;(2)由△BDE≌△BCF可证BE=BF,∠DBE=∠CBF,由于∠CBF+∠DBF=60°,即可证明∠FBE=60°,根据有一个角是60°的等腰三角形是等边三角形证得△DEF是等边三角形.【解答】【技巧点评】如果一个菱形有一个内角等于60°,那么这个菱形较短的对角线会把菱形分成两个等边三角形,此时常需要用等边三角形知识解决问题.【跟踪训练】3.如图4-16-5,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是.四、菱形的判定思路,平行四边形+菱形特性=菱形由于菱形是一个特殊的平行四边形,因此判定一个四边形是菱形时,可考虑先证明这个四边形是平行四边形,然后再证明这个平行四边形具有菱形特征(如邻边相等或对角线互相垂直).当然如果能直接证明四条边相等,就不需要先证明它是平行四边形.例4如图4-16-6,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D.交AB于E,F在DE上,且AF=CE=AE.(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形?并说明理由.【提示】(1)用两组对边平行且相等,可以证明四边形ACEF是平行四边形.(2)通过探究得出当∠B=30°时,四边形ACEF是菱形,可以用一组对边相等的平行四边形来证明.【解答】【技巧点评】要证明一个四边形是菱形,应尽可能先证明这个四边形是平行四边形,然后再证明一组邻边相等或者证明对角线互相垂直.【跟踪训练】4.如图4-16-7,在□ABCD中,对角线AC,BD相交于点O,过点O作直线EF⊥BD,分别交AD,BC 于点E 和点F ,求证:四边形BEDF 是菱形.【解答】例5 如图4-16-8,在四边形ABCD 中,AD ∥BC ,AB =CD ,点E ,F ,G ,H 分别是AD ,BD ,BC ,AC 的中点.试说明:四边形EFGH 是菱形.【提示】由于“点E ,F ,G ,H 分别是AD ,BD ,BC ,AC 的中点”,我们可联想到三角形中位线定理,EH ,HG ,GF ,FE 分别是△ACD ,△ABC ,△BCD ,△ABD 的中位线,EH ,HG ,GF ,FE 分别等于12CD ,12AB ,12CD ,12A B .由于AB =CD ,所以EH =HG =GF =FE ,根据“四条边相等的四边形是菱形”可得四边形EFGH 是菱形.【解答】【技巧点评】当题目不容易证明两直线平行时,我们可考虑通过证明四条边相等来证明这个四边形是菱形. 【跟踪训练】5.如图4-16-9,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB,BC,CD,DA的中点分别为P,Q,M,N,试判断四边形PQMN为怎样的四边形,并证明你的结论.【解答】五、从对称的角度考虑菱形问题,可以为解决问题提供帮助例6如图4-16-10,在菱形ABCD中,对角线AC=6,BD=8,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是()A.3B.4C.5D.6【提示】找到点F关于AC的对称点(即CD的中点),连接CD的中点与点E交AC于点B P,则点P为AC 与BD的交点,此时PE+PF的和最短,即等于AD的长,由于菱形的对角线互相垂直,由勾股定理可得AD =5,所以PE+PF的长为5.【技巧点评】本题是把轴对称变换与菱形的轴对称性结合在一起的综合题,解决问题的方法是作出F点的对称点F',线段EF'的长就是PE+PF的最小值,同样道理,也可以作E点的对称点E’.菱形既是中心对称图形,又是轴对称图形,许多题目正是从对称的角度展开对问题的讨论,因此从对称的角度思考问题,常常会给解决问题带来便利.【跟踪训练】6.如图4-16-11,在平行四边形ABCD中,AB⊥AC,AB=1,BC=.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;(2)试说明在旋转过程中,线段AF与EC总保持相等;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.【解答】【拓展延伸】例7如图4-16-12,在Rt△ABC中,∠B=90°,BC=5,∠C=30o.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(3)当t为何值时,△DEF为直角三角形?请说明理由.【提示】(1)在△DFC中,∠DFC=90°,∠C=30°,由已知条件求证;(2)求得四边形AEFD为平行四边形,若使口AEFD为菱形则还需要满足一组邻边相等;(3)①∠EDF=90°时,四边形EBFD为矩形.在直角三角形AED中利用AD=2AE即求得.②∠DEF=90°时,由(2)知EF//AD,则得∠ADE=∠DEF=90°,求得AD=AE·cos60°列式得.③∠EFD=90°时,此种情况不存在.【解答】【跟踪训练】7.如图4-16-13,菱形ABCD的边长为24厘米,∠A=60°,质点P从点A出发沿着AB-BD-DA作匀速运动,质点Q从点D同时出发沿着线路DC-CB-BD作匀速运动.(1)求BD的长;(2)已知质点P,Q运动的速度分别为4cm/s、5cm/s,经过12秒后,P,Q分别到达M,N两点,若按角的大小进行分类,请问△AMN是哪一类三角形?并说明理由.【解答】【竞赛连接】例8(希望杯全国数学邀请赛试题)若某一个内角为30°的菱形中有一个点到四边的距离分别为1、2、3、4,则这个菱形的面积等于.【提示】菱形内的点到对边的距离之和为菱形的高线,故菱形的高为1+4=2+3=5,根据直角三角形中30°角的特殊性可以证明AB=2AE,根据边长和高即可求菱形ABCD的面积.【跟踪练习】8.(湖北初中数学竞赛试题)如图4-16-14,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=()A.35°B.45°C.50°D.55°培优训练1.如图4-16-15,菱形ABCD的对角线AC,BD相交于O,△AOB的周长为3+,∠ABC=60°,则菱形ABCD的面积为.2.如图4-16-16,在菱形ABCD中,∠BCD=120°,点F是BD上一点,EF⊥CF,AE⊥EF,AE=3,EF=4,求AB长.3.如图4-16-17,在△ABC 中,∠BAC =90°,AD ⊥BC 于D ,CE 平分∠ACB ,交AD 于G ,交AB 于E ,EF ⊥BC 于F . 求证:四边形AEFG 是菱形.G DFECB A图4-16-174.如图4-16-18,在△ABC 中,∠BAC =90°,AD ⊥BC 于点D ,BE 平分∠ABC ,交AD 于点M ,AN 平分∠DAC ,交BC 于点N . 求证:四边形AMNE 是菱形.OENMD ACB图4-16-185.如图4-16-19,在菱形ABCD 中,E ,F 分别为BC ,CD 上的点,且CE =CF .试说明:AE =AF .F DABC图4-16-196.如图4-16-20,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF . (1)求证:AF =DC ;(2)若AB ⊥AC ,试判断四边形ADCF 的形状,并证明你的结论.FED图4-16-207.如图4-16-21,在平行四边形ABCD 中,E 为BC 边上的一点,连接AE ,BD 且AE =AB . (1)求证:∠ABE =∠EAD ;(2)若∠AEB =2∠ADB , 求证:四边形ABCD 是菱形.ECBA图4-16-218.如图4-16-22,在四边形ABCD 中,AB =AC =AD ,BC =CD ,锐角∠BAC 的角平分线AE 交BC 于点E ,AF 是CD 边上的中线,且PC ⊥CD 与AE 交于点P ,QC ⊥BC 与AF 交于点Q . 求证:四边形APCQ 是菱形.QPEFACB图4-16-229.如图4-16-23,在△ABC 中,∠ABC =90°,BD 为AC 边的中线,过点C 作CE ⊥BD 于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG =BD ,连接BG 、DF .若AG =13,CF =6,求四边形BDFG 的周长.EFDBC图4-16-2310.如图4-16-24,点D 是等腰Rt △ABC 的直角边BC 上一点,AD 的垂直平分线EF 分别交AC ,AD ,AB 于E ,O ,F ,且BC =2. (1)当CD =2时,求AE ;(2)当CD =2(21) 时,试证明四边形AEDF 是菱形.FE OACD图4-16-24直击中考11.★★(2017·湖北十堰)如图4-16-25,在菱形ABCD 中,AC 交BD 于点O ,DE ⊥BC 于点E ,连接OE ,若∠ABC =140°,则∠OED =________.O EDCABE D ABCP ADBC图4-16-25图4-16-26图4-16-2712.★★(2017·山东东营)如图4-16-26,已知菱形ABCD 的周长为16,面积为83,E 为AB 的中点,若P 为对角线BD 上一动点,则EP +AP 的最小值为________.13.★★★★(2017·湖南怀化)如图4-16-27,在菱形ABCD 中,∠ABC =120°,AB =10cm ,点P 是这个菱形内部或边上的一点。
实用文档之菱形的判定证明题练习

实用文档之" 菱形的判定证明题练习"1如图,梯形ABCD 中,AB ∥CD ,AC 平分∠BAD ,CE ∥AD 交AB 于点E .求证:四边形AECD 是菱形.2 已知:如图,在ABCD 中,AE 是BC 边上的高,将ABE △沿BC 方向平移,使点E 与点C 重合,得GFC △. (1)求证:BE DG =; (2)若60B ∠=°,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.3如图,在四边形ABCD 中,点E ,F 分别是AD BC ,的中点,G H ,分别是BD AC ,的中点,AB CD ,满足什么条件时,四边形EGFH 是菱形?请证明你的结论.4如图,在□ABCD 中,EF ∥BD ,分别交BC 、CD 于点P 、Q ,分别交AB 、AD 的延长线于点E 、F .已知BE=BP . 求证:(1)∠E=∠F .(2)□ABCD 是菱形.A B C D E ADG CBFEA B DEG HDC BAOE5. 如图,在平行四边形ABCD 中,BE 平分ABC ∠交AD 于点E ,DF 平分∠ADC 交BC 于点F . 求证:(1)ABE CDF △≌;(2)若BD EF ⊥,则判断四边形EBFD 是什么特殊四边形,请证明你的结论.6. 如图,在△ABC 中,D 是BC 边的中点,E 、F 分别在AD 及其延长线上,CE ∥BF ,连接BE 、CF .(1)求证:△BDF ≌△CDE ;(2)若AB =AC ,求证:四边形BFCE 是菱形.7. 如图,O 为矩形ABCD 对角线的交点,DE ∥AC ,CE ∥BD .(1)试判断四边形OCED 的形状,并说明理由; (2)若AB =6,BC =8,求四边形OCED 的面积.8. 已知:如图,在梯形ABCD 中,AB CD ∥,BC CD =,AD BD ⊥,E 为F D ECA BAB 中点.求证:四边形BCDE 是菱形.9. 如图,矩形ABCD 的对角线相交于点O ,DE CA AE BD ∥,∥. (1)求证:四边形AODE 是菱形;(2)若将题设中“矩形ABCD ”这一条件改为“菱形ABCD ”,其余条件不变,则四边形AODE 是_____________.10. 如图,在△ABC 中,∠ACB =90°,BC 的垂直平分线DE 交BC 于D ,交AB 于E ,F 在DE 上,且AF =CE =AE .(1)说明四边形ACEF 是平行四边形;(2)当∠B 满足什么条件时,四边形ACEF 是菱形,并说明理由.11. 如图,在平行四边形ABCD 中,E F 、分别为边AB CD 、的中点,BD 是对角线,过A 点作AG DB ∥交CB 的延长线于点.G (1)求证:DE BF ∥; (2)若90G ∠=°,求证:四边形DEBF 是菱形.12.如图,在平面直角坐标系中,点O 为原点,反比例函数ky x=的图像经过点(1,4),菱形OABC 的顶点A 在函数的图像上,对角线OB 在x 轴上. (1)求反比例函数的关系式; (2)直接写出菱形OABC 的面积.13.如图,在平行四边形ABCD 中,点P 是对角线AC 上一点,PE ⊥AB ,PF ⊥AD ,垂足分别为点E 、F ,且PE =PF ,平行四边形ABCD 是菱形吗?为什么?14. (2011 山东省济宁市) 如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作直线EF BD ⊥,分别交AD 、BC 于点E 和F .求证:四边形BEDF 是菱形.15. (2011 山东省临沂市) 如图,ABC △中,AB AC =,AD 、CD 分别是ABC △两个外角的平分线. (1)求证:AC AD =;(2)若60B ∠=°,求证:四边形ABCD 是菱形.FD EACPBAE DCFBOAF ECB16. (2011 山东省青岛市) 已知:□ABCD 中,E 、F 分别是AB 、CD 的中点,连接AF 、CE .(1)求证:△BEC ≌△DF A ;(2)连接AC ,当CA =CB 时,判断四边形AECF 是什么特殊四边形?并证明你的结论.A E BCF D。
数学菱形判定

数学菱形判定全文共四篇示例,供读者参考第一篇示例:数学中的菱形判定是一个重要的几何学概念,它涉及到平面几何中的图形判断和证明。
一个菱形是一个有四个相等边长的四边形,同时每两个相邻边之间的夹角是直角。
在实际生活和数学题目中,我们经常需要判断一个给定的四边形是否为菱形,这就需要运用一些基本的几何学知识和推理能力。
菱形判定的主要原理是根据菱形的定义来判断一个四边形是否满足菱形的性质。
也就是说,要判断一个四边形是否为菱形,就需要证明它有相等的四条边和四个直角。
我们来看一个简单的例子。
如图所示,有一个四边形ABCD,我们要判断它是否为菱形。
[图]我们需要证明四边形ABCD的四条边相等。
根据几何学知识,如果一个四边形的对边相等,那么这个四边形就是平行四边形。
所以我们可以先证明AB平行于CD,同时AD平行于BC。
如果AB平行于CD,我们可以用平行线的性质来证明AB等于CD。
同理,如果AD平行于BC,我们可以用同样的方法证明AD等于BC。
经过以上步骤,我们可以得出结论:四边形ABCD是一个菱形,因为它有四个相等的边长和四个直角。
除了上述方法,我们还可以通过另一种方法来判断一个四边形是否为菱形。
这种方法利用了菱形的特殊性质:对角线相互垂直且相等。
我们需要绘制对角线AC和BD。
接着,我们可以利用直角的定义和垂直线的性质来判断对角线AC和BD是否相互垂直。
如果AC和BD 相互垂直,那么我们可以通过勾股定理来证明AC等于BD。
同理,如果AC和BD相互垂直,那么我们可以通过同样的方法证明BD等于AC。
菱形判定是一个基础且重要的几何学概念,它需要我们熟练掌握几何学知识和推理能力。
在实际生活和数学题目中,要判断一个四边形是否为菱形,我们可以通过证明它有相等的四条边和四个直角,或者证明它有对角线相互垂直且相等来判断。
通过不断练习和思考,我们可以提高自己的数学水平和解题能力。
【这篇文章总结了数学中菱形判定的原理和方法,希望对读者有所帮助。
菱形的判定(含答案)
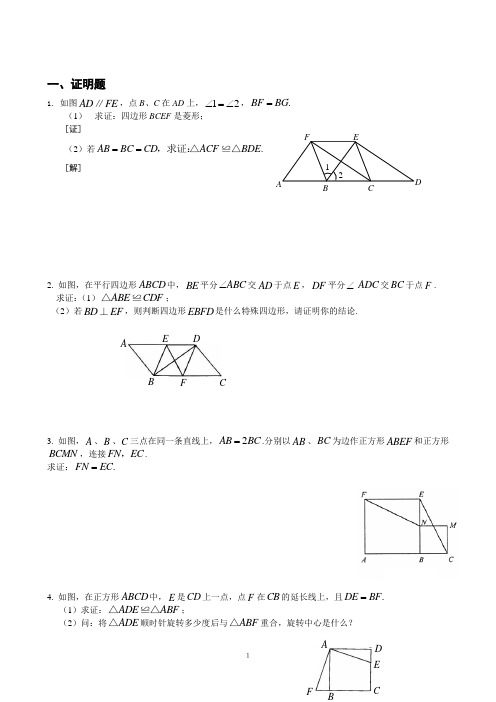
1一、证明题1. 如图AD FE ∥,点B 、C 在AD 上,12∠=∠,.BF BG =(1) 求证:四边形BCEF 是菱形; [证](2)若.AB BC CD ACF BDE ==,求证:△≌△ [解]2. 如图,在平行四边形ABCD 中,BE 平分ABC ∠交AD 于点E ,DF 平分∠ADC 交BC 于点F . 求证:(1)ABE CDF △≌;(2)若BD EF ⊥,则判断四边形EBFD 是什么特殊四边形,请证明你的结论.3. 如图,A 、B 、C 三点在同一条直线上,2AB BC =.分别以AB 、BC 为边作正方形ABEF 和正方形BCMN ,连接FN EC ,. 求证:.FN EC =4. 如图,在正方形ABCD 中,E 是CD 上一点,点F 在CB 的延长线上,且.DE BF = (1)求证:ADE ABF △≌△;(2)问:将ADE △顺时针旋转多少度后与ABF △重合,旋转中心是什么?FEB ACD12FDEC AB ADB CE BBF25. 如图,在正方形ABCD 中,G 是BC 上的任意一点(G 与B C 、两点不重合),E F 、是AG 上的两点(E F 、与A G 、两点都不重合),若AF BF EF =+,12∠=∠,请判断线段DE 与BF 有怎样的位置关系,并证明你的结论.6. 如图,四边形ABCD 是平行四边形,AC 、BD 交于点O ,∠1 =∠2.(1)求证:四边形ABCD 是矩形;(2)若∠BOC =120°,AB = 4cm ,求四边形ABCD 的面积.2 ABCDEF G 1D37. 如图,在ABC △中,AB AC ,D 为BC 中点.四边形ABDE 是平行四边形. 求证:四边形ADCE 是矩形.8. 如图,菱形ABCD 的对角线AC 与BD 相交于点O ,点E 、F 分别为边AB 、AD 的中点,连接EF 、OE 、OF .求证:四边形AEOF 是菱形.9. 在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED . (1)求证:△BEC ≌△DEC ;(2)延长BE 交AD 于F ,当∠BED =120°时,求∠A F DB E O4CD10. 已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF .(1)求证:BE = DF ;(2)连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM .判断四边形AEMF 是什么特殊四边形?并证明你的结论.证明:(1)(2)11. 如图,四边形ABCD 是边长为a 的正方形,点G ,E 分别是边AB ,BC 的中点,∠AEF =90o ,且EF 交正方形外角的平分线CF 于点F . (1)证明:∠BAE =∠FEC ; (2)证明:△AGE ≌△ECF ; (3)求△AEF 的面积.12. 如图, 已知四边形ABCD 是菱形, DE ⊥AB ,DF ⊥BC . 求证:△ADE ≌△CDF .A DB E FO C513. 已知梯形ABCD 中,BC AD //,AD AB = (如图所示).BAD ∠的平分线AE 交BC 于点E ,联结DE . (1) 在图中,用尺规作BAD ∠的平分线AE (保留作图痕迹,不写作法),并证明四边形ABED 是菱形;(2) 若︒=∠60ABC ,BE EC 2=,求证:DC ED ⊥.14. 如图,正方形ABCD 中,E F 、分别是AB BC 、边上的点,且.AE BF =求证.AF DE ⊥15. 如图,将矩形纸片ABCD 沿EF 折叠,使点A 与点C 重合,点D 落在点G 处,EF 为折痕. (1)求证:FGC EBC △≌△;(2)若84AB AD ==,,求四边形ECGF (阴影部分)的面积.A BC D D C F B E A616. 如图,在△ABC 中,D 是BC 边的中点,E 、F 分别在AD 及其延长线上,CE ∥BF ,连接BE 、CF . (1)求证:△BDF ≌△CDE ;(2)若AB =AC ,求证:四边形BFCE 是菱形.一、证明题1. (1)证:2.AD FE FEB ∴∠=∠∥,12 1.FEB ∠=∠∴∠=∠,..BF BC BC EF BF EF =∴=∴=,∴四边形BCEF 是平行四边形.BF BC =,∴四边形BCEF 是菱形. (5分) (2)证:EF BC AB BC CD AD FE ===,,∥,∴四边形ABEF 、四边形CDEF 均为平行四边形,AF BE FC ED ∴==,.(8分) 又2AC BC BD ==,.ACF BDE ∴△≌△ (10分)2. 证明:(1)∵四边形ABCD 是平行四边形,∴A C AB CD ABC ADC ∠=∠=∠=∠,,∵BE 平分ABC ∠,DF 平分ADC ∠,∴ABE CDF ∠=∠ 2′ ∴()ABE CDF ASA △≌△4′ (2)由ABE CDF △≌△,得AE CF =5′在平行四边形ABCD 中,AD BC AD BC =∥,7∴DE BF DE BF =∥,∴四边形EBFD 是平行四边形 6′ 若BD EF ⊥,则四边形EBFD 是菱形 8′3. 证明:在正方形ABEF 和正方形BCMN 中,90AB BE EF BC BN FEN EBC ===∠=∠=,,°. (2分) 2AB BC =, .EN BC ∴=(4分) FEN EBC ∴△≌△. (5分).FN EC ∴= (6分)4. (1)证明:在正方形ABCD 中, 90D ABC AD AB ∠=∠==°,, (1分) 90ABF D ABF ∴∠=∴∠=∠°,, (3分) 又DE BF =,4分)ADE ABF ∴△≌△;5分)(2)将ADE △顺时针旋转90度后与ABF △重合, (7分) 旋转中心是A 点.(9分)5. 根据题目条件可判断.DE BF ∥证明如下:∵四边形ABCD 为正方形,∴ 290AB AD BAF ∠+∠==,°. ∵,AF AE EF =+又,AF BF EF =+ ∴AE BF =,∵12,∠=∠∴().ABF DAE SAS △≌△5分∴AFB DEA ∠=∠,BAF ADE ∠=∠. ∴290ADE ∠+∠=°.∴90AED BFA ∠=∠=°. ∴.DE BF ∥ 9分6. (1)∵∠1 =∠2,∴BO=CO 即2 BO=2CO (1分) ∵四边形ABCD 是平行四边形∴ AO=CO ,BO=OD (2分) 即AC=2CO ,BD= 2 BO ∴AC= BD (3分)∵四边形ABCD 是平行四边形 ∴四边形ABCD 是矩形 (4分)(2)在△BOC 中,∠BOC =120°, ∴ ∠1 =∠2 =(180°—120°)÷2 = 30° (5分) ∴在Rt △ABC 中,AC=2AB=2⨯4=8(cm ),D8∴BC=344822=-(cm ) (6分) ∴四边形ABCD 的面积=24)= (7分)7. 证明:四边形ABDE 是平行四边形, AE BC ∴∥,AB DE =,.AE BD = 2分 D 为BC 中点, ∴.CD BD =3分.CD AE CD AE ∴=∥∴四边形ADCE 是平行四边形.5分AB AC =, ∴.AC DE =∴平行四边形ADCE 是矩形.7分8. 证明:点E F 、分别为AB AD 、的中点,1122AE AB AF AD ∴=,=. 2分又四边形ABCD 是菱形, AB AD ∴=. AE AF ∴=.4分又菱形ABCD 的对角线AC 与BD 相交于点O , O ∴为BD 的中点.OE OF ∴、是ABD △的中位线. 6分 OE AD OF AB ∴∥,∥.∴四边形AEOF 是菱形. 10分9. (1)证明:∵四边形ABCD 是正方形∴BC =CD ,∠ECB =∠ECD =45°又EC =EC …………………………2分 ∴△ABE ≌△ADE ……………………3分 (2)∵△ABE ≌△ADE∴∠BEC =∠DEC =12∠BED …………4分 ∵∠BED =120°∴∠BEC =60°=∠AEF ……………5分 ∴∠EFD =60°+45°=105° …………………………6分10. 证明:(1)∵四边形ABCD 是正方形,AF DBEO9∴AB =AD ,∠B = ∠D = 90°. ∵AE = AF ,∴Rt Rt ABE ADF △≌△. ∴BE =DF .4分(2)四边形AEMF 是菱形.∵四边形ABCD 是正方形, ∴∠BCA = ∠DCA = 45°,BC = DC .∵BE =DF ,∴BC -BE = DC -DF . 即CE CF =. ∴OE OF =. ∵OM = OA ,∴四边形AEMF 是平行四边形. ∵AE = AF ,∴平行四边形AEMF 是菱形.8分11. (1)证明:∵∠AEF =90°,∴∠FEC +∠AEB =90°.………………………………………1分 在Rt △ABE 中,∠AEB +∠BAE =90°,∴∠BAE =∠FEC ;……………………………………………3分 (2)证明:∵G ,E 分别是正方形ABCD 的边AB ,BC 的中点,∴AG=GB=BE=EC ,且∠AGE =180°-45°=135°. 又∵CF 是∠DCH 的平分线,∴∠ECF =90°+45°=135°.………………………………………4分在△AGE 和△ECF 中,135AG EC AGE ECF GAE FEC =⎧⎪∠=∠=⎨⎪∠=∠⎩,,AD BEF O C10∴△AGE ≌△ECF ; …………………………………………6分 (3)解:由△AGE ≌△ECF ,得AE=EF .又∵∠AEF =90°,∴△AEF 是等腰直角三角形.………………………………7分由AB=a ,BE =21a ,知AE =25a , ∴S △AEF =85a 2.…………………………9分12. 证明:在△ADE 和△CDF 中,∵四边形ABCD 是菱形,∴∠A =∠C ,AD =CD .……………………2分又DE ⊥AB ,DF ⊥BC ,∴∠AED =∠CFD =900.……………………4分∴△ADE ≌△CDF . ……………………6分13. (1) 图略(有作图痕迹,且正确).证明:∵AE 为BAD ∠的平分线,∴DAE BAE ∠=∠. 又∵BC AD //,∴AEB DAE ∠=∠.∴AEB BAE ∠=∠.∴BE AB =. ∵AB AD =,∴BE AD =.∵BE AD //,∴四边形ABED 是平行四边形. ∵AB AD =,∴四边形ABED 是菱形.(2)证明:由(1) 知,四边形ABED 是菱形,∴AB DE //,BE DE =. ∴︒=∠=∠60ABC DEC .(方法一)设线段EC 中点为F ,联结DF ,则FC EF =. ∵BE EC 2=,BE DE =.∴FC EF DE ==. ∵︒=∠60DEF ,∴△DEF 为等边三角形.∴︒=∠=∠60EFD EDF ,FC EF DF ==.∴FCD FDC ∠=∠.∴FDC FCD FDC DFE ∠=∠+∠=∠2.∴︒=∠30FDC .∴︒=∠+∠=∠90FDC EDF EDC ,即DC DE ⊥.(方法二)作EC DH ⊥,垂足为H ,则︒=∠30EDH .∴在Rt △DEH 中,ED EH 21=,ED DH 23=. ∵BE DE =,BE EC 2=,∴ED HC 23=.在Rt △DCH 中,3tan ==∠DHHCCDH .∴︒=∠60CDH .∴︒=∠+∠=∠90EDH CDH EDC ,即DC DE ⊥.14. 证明:四边形ABCD 为正方形90DA ABDAE ABF ∴=∠=∠=° 又AE BF =DAE ABF ∴△≌△ADE BAF ∴∠=∠(4分)90ADE AED ∠+∠=°90BAF AED ∴∠+∠=°AF DE ∴⊥ (3分)15. (1)证明:四边形ABCD 是矩形, 90A B BCD D AD BC ∴∠=∠=∠=∠==°,. ······························································ 1分 将矩形纸片ABCD 沿EF 折叠,点A 与点C 重合,点D 落在点G 处,90G D ∴∠=∠=°,90ECG A CG AD ∠=∠==°,, ·················································· 2分 9090G B CG BC ECG BCD ∴∠=∠==∠=∠=°,,°,90GCF BCE FCE ∴∠=∠=∠°-, ·················································································· 3分 FGC EBC ∴△≌△. ·········································································································· 4分(2)解:由(1)得FGC EBC △≌△,EBCF ECGF AEFD S S S ∴==四边形四边形四边形,2ABCD ECGF AEFD EBCF S S S S ∴=+=矩形四边形四边形四边形,11841222ABCD ECGF S S ∴==⨯⨯=矩形四边形. ······································································· 6分16. (1)证明:∵ D 是BC 的中点,∴BD =CD .………………………………1分 ∵CE ∥BF ∴∠DBF=∠DCE . ………………………………………………2分又∵∠BDF=∠CDE , …………………………………………………………3分 ∴△BDF ≌△CDE . ……………………………………………………………4分(2)证明:∵△CDE ≌△BDF ,∴DE =DF .………………………………5分 ∵BD =CD ,∴四边形BFCE 是平行四边形.…………………………………6分 在△ABC 中,∵AB =AC ,BD =CD . ∴AD ⊥BC ,即EF ⊥BC .……………7分 ∴平行四边形BFCE 是菱形. …………………………………………………8分 (另解)∵△CDE ≌△BDF ,∴CE =BF . ……………………………………5分 ∵CE ∥BF ,∴四边形BFCE 是平行四边形.……………………………………6分 ∴BE =CF .在△ABC 中,∵AB =AC ,BD =CD .∴AD ⊥BC ,即AD 垂直平分BC ,∴BE =CE .…………………………………7分 ∴平行四边形BFCE 是菱形. ……………………………………………………8分。
菱形的判定证明题练习

菱形的判定
(1)有一组邻边相等的平行四边形是菱形。
(2)对角线互相垂直的平行四边形是菱形。
(3)四条边都相等的四边形是菱形。
(4)每条对角线平分一组对角的四边形是菱形。
1如图,梯形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.求证:四边形AECD是菱形.
2已知:如图,在 中,AE是BC边上的高,将 沿 方向平移,使点E与点C重合,得 .
(1)求证: ;
(2)若 ,求证:四边形 是菱形.
16. (2011 山东省青岛市)已知:□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
8.如图所示,在四边形ABCD中,AB∥CD,AB=CD=BC,四边形ABCD是菱形吗? 说明理由.
(2)若AB=AC,求证:四边形BFCE是菱形.
7.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
8.已知:如图,在梯形 中, , , , 为 中点.
求证:四边形 是菱形.
9.如图,矩形 的对角线相交于点 , .
11.(科内交叉题)如图所示,已知△ABC中,AB=AC,D是BC的中点,过点D 作DE⊥AB,DF⊥AC,垂足分别为E,F,再过E,F作EG⊥AC,FH⊥AB,垂足分别为G,H,且EG, FH相交于点K,试说明EF和DK之间的关系.
12.菱形以其特殊的对 称美而备受人们喜爱,在生产生活中有极其广泛的应用.如图所示是一块长30cm,宽20cm的长方形的瓷砖,E,F,G,H分别是边BC ,CD,DA, AB的中点,涂黑部分为淡蓝色花纹,中间部分为白色.现有一面长4.2m,宽2.8m的墙壁准备贴这种瓷砖,试问:
经典特殊的菱形证明题

经典特殊的菱形证明题
问题描述
给定一个菱形,我们要证明:菱形的对角线互相垂直。
证明过程
首先,设菱形的四个顶点为A、B、C和D。
由于菱形的定义,四边相等且两两相交于90度角。
我们先证明线段AC和线段BD相等,即证明ABCD是一个菱形。
假设ABCD是一个菱形,则有以下两个等式成立:
AB = BC (菱形的定义)
AC ⊥ BD (菱形的性质)
接下来,我们可以利用勾股定理进行证明。
根据勾股定理,直
角三角形的对角线满足以下关系:
AC^2 + BD^2 = AB^2
由于AB = BC,我们可以将AB代入上式,得到:
AC^2 + BD^2 = BC^2
由菱形的定义可知,BC = CD,代入上式得到:
AC^2 + BD^2 = CD^2
我们再次利用勾股定理,将另一个直角三角形的对角线代入上式:
AD^2 + BD^2 = CD^2
由于AD = AC,代入上式得到:
AC^2 + BD^2 = AD^2 + BD^2
化简后可得:
AC^2 = AD^2
通过化简发现,AC = AD,即菱形的对角线AC和BD相等。
由于两条对角线互相垂直的定义是:两条线段交于一个直角,则我
们可以得出结论:经典特殊的菱形证明题中,菱形的对角线互相垂直。
总结
经典特殊的菱形证明题是一种富有挑战性和创造性的数学问题。
通过运用勾股定理和菱形的性质,我们可以证明菱形的对角线互相
垂直。
这个证明过程展示了数学中的推理和逻辑思维,让我们更好
地理解了菱形的性质和特点。
菱形的判定证明题 经典
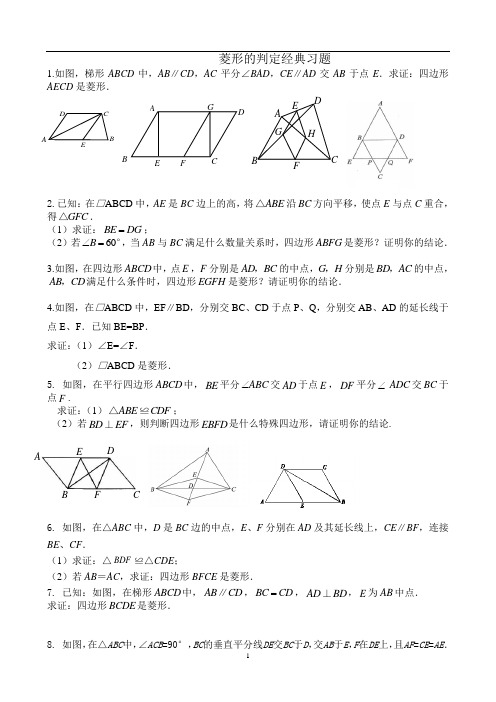
菱形的判定经典习题 1.如图,梯形ABCD 中,AB ∥CD ,AC 平分∠BAD ,CE ∥AD 交AB 于点E .求证:四边形AECD 是菱形.2.已知:在□ABCD 中,AE 是BC 边上的高,将ABE △沿BC 方向平移,使点E 与点C 重合,得GFC △.(1)求证:BE DG =;(2)若60B ∠=°,当AB 与BC 满足什么数量关系时,四边形ABFG 是菱形?证明你的结论.3.如图,在四边形ABCD 中,点E ,F 分别是AD BC ,的中点,G H ,分别是BD AC ,的中点,AB CD ,满足什么条件时,四边形EGFH 是菱形?请证明你的结论.4.如图,在□ABCD 中,EF ∥BD ,分别交BC 、CD 于点P 、Q ,分别交AB 、AD 的延长线于点E 、F .已知BE=BP .求证:(1)∠E=∠F .(2)□ABCD 是菱形.5. 如图,在平行四边形ABCD 中,BE 平分ABC ∠交AD 于点E ,DF 平分∠ADC 交BC 于点F .求证:(1)ABE CDF △≌;(2)若BD EF ⊥,则判断四边形EBFD 是什么特殊四边形,请证明你的结论.6. 如图,在△ABC 中,D 是BC 边的中点,E 、F 分别在AD 及其延长线上,CE ∥BF ,连接BE 、CF .(1)求证:△BDF ≌△CDE ;(2)若AB =AC ,求证:四边形BFCE 是菱形.7. 已知:如图,在梯形ABCD 中,AB CD ∥,BC CD =,AD BD ⊥,E 为AB 中点. 求证:四边形BCDE 是菱形.8. 如图,在△ABC 中,∠ACB =90°,BC 的垂直平分线DE 交BC 于D ,交AB 于E ,F 在DE 上,且AF =CE =AE . A B C D E A D G C B F E A B C D E F G H F D E C A B(1)说明四边形ACEF 是平行四边形;(2)当∠B 满足什么条件时,四边形ACEF 是菱形,并说明理由.9. 如图,在平行四边形ABCD 中,E F 、分别为边AB CD 、的中点,BD 是对角线,过A 点作AG DB ∥交CB 的延长线于点.G(1)求证:DE BF ∥;(2)若90G ∠=°,求证:四边形DEBF 是菱形.10.如图,在平行四边形ABCD 中,点P 是对角线AC 上一点,PE ⊥AB ,PF ⊥AD ,垂足分别为点E 、F ,且PE =PF ,平行四边形ABCD 是菱形吗?为什么?11. (济宁) 如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作直线EF BD ⊥,分别交AD 、BC 于点E 和F .求证:四边形BEDF 是菱形.12. (临沂) 如图,ABC △中,AB AC =,AD 、CD 分别是ABC △两个外角的平分线.(1)求证:AC AD =;(2)若60B ∠=°,求证:四边形ABCD 是菱形.13. (青岛) 已知:□ABCD 中,E 、F 分别是AB 、CD 的中点,连接AF 、CE .(1)求证:△BEC ≌△DF A ;(2)连接AC ,当CA =CB 时,判断四边形AECF 是什么特殊四边形?并证明你的结论. F D EA CP B A E D C F B O A F E C BA EBC F D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
菱形的判定证明题(5篇)第一篇:菱形的判定证明题菱形的判定证明题练习1如图,梯形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB 于点E.求证:四边形AECD是菱形.CBAE已知:如图,在ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.(1)求证:BE=DG;(2)若∠B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论. DBEF3如图,在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,AB,CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.4如图,在□ABCD中,EF∥BD,分别交BC、CD于点P、Q,分别交AB、AD的延长线于点E、F.已知BE=BP.求证:(1)∠E=∠F.(2)□ABCD是菱形.BE平分∠ABC交AD于点E,DF平分∠ADC5.如图,在平行四边形ABCD中,交BC于点F.求证:(1)△ABE≌CDF;(2)若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.DEABCF6.如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.(1)求证:△BDF≌△CDE;(2)若AB=AC,求证:四边形BFCE是菱形.7.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)试判断四边形OCED的形状,并说明理由;(2)若AB=6,BC=8,求四边形OCED的面积.AOEB8.已知:如图,在梯形ABCD中,AB∥CD,BC=CD,AD⊥BD,E为AB中点.求证:四边形BCDE是菱形.9.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.11.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.(1)求证:DE∥BF;(2)若∠G=90°,求证:四边形DEBF是菱形.k的图像经过点(1,x4),菱形OABC的顶点A在函数的图像上,对角线OB在x轴上.(1)求反比例函数的关系式;(2)直接写出菱形OABC的面积.12.如图,在平面直角坐标系中,点O为原点,反比例函数y=13.如图,在平行四边形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥AD,垂足分别为点E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?F A B C E14.(2011 山东省济宁市)如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O作直线EF⊥BD,分别交AD、BC于点E 和F.求证:四边形BEDF是菱形.DC F15.(2011 山东省临沂市)如图,△ABC中,AB=AC,AD、CD分别是△ABC两个外角的平分线. F(1)求证:AC=AD;(2)若∠B=60°,求证:四边形ABCD是菱形.AB E C16.(2011 山东省青岛市)已知:□ABCD中,E、F分别是AB、CD 的中点,连接AF、CE.(1)求证:△BEC≌△DFA;(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.DEFC第二篇:菱形的判定证明题练习姓名1、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O作直线EF⊥BD,分别交AD、BC于点E和F.求证:四边形BEDF是菱形.DFC2.已知:□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.(1)求证:△BEC≌△DFA;(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.ED F C3、已知:如图,在ABCD中,AE是BC边上的高,将△ABE 沿BC方向平移,使点E与点C重合,得△GFC.(1)求证:BE=DG;(2)若∠B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论.DBEF4.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.5.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.(1)求证:DE∥BF;,(2)若∠G=90°求证:四边形DEBF是菱形.(提示:直角三角形斜边上的中线等于斜边的一半)第三篇:菱形的判定证明题练习菱形的判定证明题练习1如图,梯形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB 于点E.求证:四边形AECD是菱形.CBA E已知:如图,在ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.(1)求证:BE=DG;(2)若∠B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论. DψB EF3如图,在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,AB,CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.4如图,在□ABCD中,EF∥BD,分别交BC、CD于点P、Q,分别交AB、AD的延长线于点E、F.已知BE=BP.求证:(1)∠E=∠F.(2)□ABCD是菱形.5.如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于点F.求证:(1)△ABE≌CDF;(2)若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论.接BE、CF.(1)求证:△BDF≌△CDE;(2)若AB=AC,求证:四边形BFCE是菱形.7.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.AEDBFC6.如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连(1)试判断四边形OCED的形状,并说明理由;(2)若AB=6,BC=8,求四边形OCED的面积.求证:四边形BCDE是菱形.AOBE8.已知:如图,在梯形ABCD中,AB∥CD,BC=CD,AD⊥BD,E为AB中点.9.如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.(1)求证:四边形AODE是菱形;(2)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE是_____________.10.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC 于D,交AB于E,F在DE上,且AF=CE=AE.(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.11.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.(1)求证:DE∥BF;,(2)若∠G=90°求证:四边形DEBF是菱形.12.如图,在平面直角坐标系中,点O为原点,反比例函数y=k的图像经过点(1,4),菱形xOABC的顶点A在函数的图像上,对角线OB在x轴上.(1)求反比例函数的关系式;(2)直接写出菱形OABC的面积.13.如图,在平行四边形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥AD,垂足分别为点E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?FABCEAC、BD相交于点O,过14.(2011 山东省济宁市)如图,在平行四边形ABCD中,对角线点O作直线EF⊥BD,分别交AD、BC于点E和F.求证:四边形BEDF是菱形.角的平分线.(1)求证:AC=AD;(2)若∠B=60°,求证:四边形ABCD是菱形.(1)求证:△BEC≌△DFA;DFC15.(2011 山东省临沂市)如图,△ABC中,AB=AC,AD、CD分别是△ABC两个外F ABCE16.(2011 山东省青岛市)已知:□ABCD中,E、F分别是AB、CD 的中点,连接AF、CE.(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.ED FC第四篇:证明题(旋转得到菱形)64363811、平行四边形ABCD中,AB⊥AC,AB=1,BC= 根号5,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形。
(2)试说明在旋转过程中,线段AF与EC总保持相等。
(3)在旋转过程中,四边形BEDF可能是菱形?如果不能,请说明理由;如果能,说明理由1、平行四边形ABCD中,AB⊥AC,AB=1,BC= 根号5,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形。
(2)试说明在旋转过程中,线段AF与EC总保持相等。
(3)在旋转过程中,四边形BEDF可能是菱形?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转地度数。
如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=5.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;(2)试说明在旋转过程中,线段AF与EC总保持相等;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.分析:(1)当旋转角为90°时,∠AOF=90°,由AB⊥AC,可得AB∥EF,即可证明四边形ABEF为平行四边形;(2)证明△AOF≌△COE即可;(3)EF⊥BD时,四边形BEDF为菱形,可根据勾股定理求得AC=2,∴OA=1=AB,又AB⊥AC,∴∠AOB=45°.证明:(1)当∠AOF=90°时,AB∥EF,又∵AF∥BE,∴四边形ABEF为平行四边形.(2)证明:∵四边形ABCD为平行四边形,∴AO=CO,∠FAO=∠ECO,∠AOF=∠COE.∴△AOF≌△COE.∴AF=EC.(3)四边形BEDF可以是菱形.理由:如图,连接BF,DE由(2)知△AOF≌△COE,得OE=OF,∴EF与BD互相平分.∴当EF⊥BD时,四边形BEDF为菱形.在Rt△ABC中,AC=,∴OA=1=AB,又AB⊥AC,∴∠AOB=45°,∴∠AOF=45°,∴AC绕点O顺时针旋转45°时,四边形BEDF为菱形.第五篇:菱形的判定教学设计《菱形的判定(1)》的教学设计一、教学目标:知识技能: 经历菱形的判定方法的探究过程,掌握菱形的两种判定方法.数学思考:1、经历利用菱形的定义探究菱形其他判定方法的过程,培养学生的动手实验、观察、推理意识,发展学生的形象思维和逻辑推理能力.2、根据菱形的判定定理进行简单的证明,培养学生的逻辑推理能力和演绎能力.解决问题:1、尝试从不同角度寻求菱形的判定方法,并能有效的解决问题,尝试评价不同判定方法之间的差异.2、通过对菱形判定过程的反思,获得灵活判定四边形是菱形的经验.情感态度: 在探究菱形的判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心.二、教学重点: 菱形判定方法的探究.三、教学难点: 菱形判定方法的探究及灵活运用.四、教学过程: 【活动1、引入新课,激发兴趣】1、复习:教师提问:菱形的定义式什么?学生答:菱形的定义:一组邻边相等的平行四边形是菱形。
