渠道梯形应用经济断面计算
梯形类渠道水力最佳断面统一公式的推求

梯形类渠道水力最佳断面统一公式的推求
荣丰涛
【期刊名称】《山西水利科技》
【年(卷),期】2003(000)004
【摘要】文中导出了梯形类渠道(包括梯形渠道、弧形底梯形渠道、弧形坡脚梯形渠道)的水力最佳断面统一计算公式.
【总页数】3页(P5-7)
【作者】荣丰涛
【作者单位】山西省水利科学研究所
【正文语种】中文
【中图分类】TV131.4
【相关文献】
1.梯形渠道水力最佳断面的一种计算方法 [J], 张显辉;吕宏兴
2.梯形渠道水力最佳断面边坡系数推求 [J], 王开民
3.梯形渠道水力最佳断面参数的快速确定方法 [J], 孔庆迎
4.平底抛物线形复合渠道水力最佳断面及实用经济断面统一设计方法 [J], 王正中;陈柏儒;王羿;赵延风
5.抛物线类渠道水力最佳及实用经济断面统一设计方法 [J], 陈柏儒;王羿;赵延风;王正中
因版权原因,仅展示原文概要,查看原文内容请购买。
弧底渠道梯形应用经济断面计算

弧底渠道梯形应用经济断面计算弧底渠道是一种在水利工程中常见的渠道形式,其横截面呈梯形状。
弧底渠道梯形应用经济断面计算是指通过一定的计算方法和公式,确定出适合工程需要的渠道横截面的尺寸和形状。
弧底渠道的横断面形状是按照一定的经济性和实用性要求设计的。
通常,弧底渠道的经济横断面是在一定的条件下,使其渠底斜坡的下坡率最小、渠底宽度最小、渠脊高度最小的渠槽形式。
首先,我们可以使用经验公式法进行初步的计算。
经验公式法是通过经验公式提供的参数,结合实际的工程要求和地理条件,计算出最初的横断面尺寸。
例如,对于给定的流量和坡度,可以使用曼宁公式计算出渠底的速度和水深。
根据曼宁公式,流速与水深和坡度有关。
然后,可以使用渠道横断面积和湿周的关系,计算出渠底的宽度。
根据经验公式计算出的初步参数,可以进行理论分析法的计算。
理论分析法是基于渠道水流力学原理,通过计算流量、底坡和阻力系数等参数,进一步优化渠道横断面形状。
利用伯努利方程和欧拉方程,可以得到渠道的水力坡度、流速和水深等关系。
根据这些关系,可以计算出渠底的宽度、渠脊高度等参数,以满足流量和坡度要求。
最后,可以使用模型试验法进行验证。
模型试验法是通过建立几何模型和流体力学模型,通过测量和观察渠道的水流情况,验证理论计算结果的准确性和可靠性。
在模型试验中,可以使用透水模型和非透水模型进行实验。
通过模型试验可以得到渠道的水面高度、流速和水深等实际观测数据,与理论计算值进行比较,从而确定是否需要对横断面进行调整。
综合运用经验公式法、理论分析法和模型试验法,可以确定弧底渠道的梯形应用经济断面。
这种断面形状在满足工程要求的前提下,可以使渠底的斜坡最小,渠底宽度最小,渠脊高度最小,以达到经济和实用性最优化的设计目标。
总结起来,弧底渠道梯形应用经济断面计算涉及到多种方法和公式的运用,需要考虑到流量、坡度、流速等因素,并通过经验公式法、理论分析法和模型试验法不断优化和调整渠道断面形状,以满足工程要求和经济效益。
第一节灌溉渠道流量确定和设计(3)

弄虚作假要不得,踏实肯干第一名。19:30:4219:30: 4219:3012/1/ 2020 7:30:42 PM
安全象只弓,不拉它就松,要想保安 全,常 把弓弦 绷。20.12.119: 30:4219:30Dec-201- Dec-20
重于泰山,轻于鸿毛。19:30:4219:30: 4219:30Tuesday, December 01, 2020
(4) 梯形渠道水力最佳断面的计算公式: 在渠道比降和渠床糙率一 定的条件下,通过设计流量所需要的最小过水断面称为水力最佳断 面,梯形渠道水力最佳断面的水力要素按下表计算。
表3-16 梯形渠道水力最佳断面参数计算公式
梯型渠道水力最优断面常为窄深式,这种渠施工困难, 特别是大型渠道,当地形条件复杂时施工就更加困难, 因此在实际应用中,水力最优断面不一定是经济断面。 但水力最优断面具有工程量最小的优点,小型渠道和 石方渠道可以采用。在工程实践中为了经济合理,常 常放弃水力最优断面,而选用实用经济断面。实际过 程中存在一组宽浅式的梯形断面,其水深和底宽有一 个较广的选择范围,以适应各种具体情况的需要,而 在此范围内又能基本上满足水力最优断面的要求(即
(2) 续灌渠道设计流量的计算: 续灌渠道一般为干、支渠道,流量较大,上、 下游流量相差悬殊,这就要求分段推算设计 流量,各渠段可采用不同的断面。各级续灌 渠道的输水时间都等于灌区灌水延续时间, 可以直接由下级渠道的毛流量推算上级渠道 的毛流量。所以续灌渠道设计流量的推算方 法是自下而上逐级、逐段进行推算。生产实 际中一般用经验公式估算续灌渠道分段设计 流量。
土质渠道不冲流速
渠床土质 轻壤土 中壤土 重壤土 粘土
不冲流速(m s-1)
备注
0.6~0.8 0.65~0.85 0.70~0.95 0.75~1.00
梯形渠道断面挖填土方量计算方法总结

挖填土方量计算方法土方量计算是工程设计中经常遇到的问题。
如渠道设计、防洪堤设计、水库坝堤设计等,都需要精确计算其土方量。
土方量计算是这些工程设计的一个重要组成部分,也是其设计中最关键最烦琐的一道工序。
土方量直接关系到工程造价,所以计算起来一定要准确、符合实际。
一般工程土方量主要包括挖方、填方等。
按照施工设计的精度要求,一般沿其纵断面每50m(或25m,具体数值根据不同的设计精度要求而定)计算一个土方量(包括挖方、填方等)。
对于一条十几公里乃至几十公里的渠道来说,按这种方法计算无疑工作量是非常大的。
特别是一个断面一个断面地用手算,不但工作量大,而且误差大,工作效率极低。
难道就没有一种计算误差小而工作效率又高的计算方法吗?下面我们就以新建土渠为例把自己在实际工作中摸索出的一种计算方法作一简介,以供参考。
1.计算原理大家都知道Excel是具有强大的数据计算与分析功能电子表格软件,其计算精度远远可以满足设计需要。
只要在当前工作表的活动单元格里输入正确的计算公式,就会立即在该单元格中显示计算结果,并在编辑栏里显示当前单元格的具体公式,且可供编辑与修改。
公式是在工作表中对数据进行分析计算的等式,它可以对工作表数值进行加、减、乘、除等运算。
公式可以引用同一工作表的单元格、同一工作薄不同工作表中的单元格或者其它工作薄的工作表中的单元格。
在一个公式中可以包含有各种运算符、常量、变量、函数、以及单元格引用等。
在单元格中输入公式类似于输入文字,不同之处在于输入公式时是以等号(=)作为开头。
在等号(=)后输入公式的内容,然后按回车键或者单击编辑栏的“输入”按钮,则表明公式输入完毕。
这里我们就是利用Excel软件来计算新建土渠的工程量。
对于新建土渠其每个横断面上的地面线在设计精度要求范围内可以近似看作一条直线。
整个渠道近似可以分段看作一个个不规则的棱柱体,其挖方、填方等均可用棱柱体的体积公式来求。
我们知道棱柱体的体积公式为:体积= (上底面面积+下底面面积)×高÷2 式⑴2计算步骤现设定渠道每50米一个桩号,相邻两桩号间的渠段(即50米长的渠道)为一个计算单位,也就是说每50米有一个计算断面。
渠道水力计算类型

渠道水力计算类型在水利工程中,梯形渠道应用最为广泛,因而后面以梯形断面为代表,讨论渠道的水力计算方法。
因明渠流量计算公式32352132==x A n i i R n A Q ,将梯形的面积h mh b A )(+=、湿周212m h b ++=χ代入上式得[][]32235+12++=mh b h mh b n i Q )( (6-17) 则),,,,(=i n m h b f Q ,这说明,梯形断面水力计算存在着(Q 、b 、h 、m 、n 、i )六个变量。
通常渠道的边坡系数m 和糙率系数n ,可由渠的地质情况、施工条件、护面材料等实测确定,或由经验查表确定。
则渠道的水力计算主要是流量计算、正常水深计算、渠宽度计算及渠底坡度计算。
明渠均匀流的水力计算问题,可分为两大类:一类是对已建成的渠道进行计算,如校核流速、流量、糙率和底坡;另一类是按要求设计新渠道,如确定底宽、水深、底坡、边坡系数或超高等。
一、已成渠道的水力计算已成渠道的水力计算任务是校核过水能力及流速,或由实测过水断面的流量反推粗糙系数和底坡。
下面以例题形式来说明。
1. 流量和流速的校核【例6-3】 某灌溉工程粘土渠道,总干渠全长70km ,糙率n =0.028,断面为梯形,底宽为8m ,边坡系数m = 1.5,底坡i=1/8000,设计流量Q 为40m 3/s 。
试校核当水深为4m 时,能否满足通过设计流量的要求。
解: (1) 流量校核由于渠道较长,断面规则,底坡和糙率固定,故可按明渠均匀流计算。
因: 4)45.18()(⨯⨯+=+=h mh b A = 56(m 2)42.22=5.1+1×4×2+8=+12+=22m h b x (m )水力半径: 42.2256==x A R = 2.498 m 谢才系数: 6161498.2028.011⨯==R n C = 41.6 m 1/2 / s流 量 =)8000/1(×498.2×6.41×56==Ri AC Q 41.17 m 3 /s(2) 流速较核:74.0=5617.41==A Q v (m/s )>不淤v =0.5m/s查表6-4粘土渠道,不冲流速允许值为(0.75~0.85)m/s,水力半径为2.498m, 则实际允许流速为()=498.2×)85.0~75.0(==41αR 表不冲v v 0.942~1.07m/s因计算流量大于设计流量,则满足能过设计流量的要求;实际流速满足不冲、不淤允许流速要求。
梯形类渠道断面计算软件的开发与使用

Xo
其 中 :r rH; K =/
m =
流 量 下 , 渠道 的 宽深 比可 以有 更 多 可供 选 择 的 方 其 案, 以满 足 不 同工 程 条 件 的 需 求。 按 水 力最 佳 断面
设计 的渠 道 宽 深 比 不 够 理 想 时 , 假 设 不 同 的 可
 ̄ + / m; 1
6一 最 佳 断面直 线 段 底 宽 ( 弧 底 梯 形 的 弧底 。 或
弦长 ) m: 渠 底 圆 弧 半 径 , 日一断 面 水 深 , , m; m; 渠 底圆弧 的 圆心角 ( 每边 圆 弧的 圆 心 角 为 O2 , / )
值, 计算 出相 应 的水 力要 素 , 并从 中选 择合 适 的 断面
维普资讯
l O
东 北水利 水 电
20 0 8年第 5期 ( 2 第 6卷第 26期 ) 8 合, 清楚 、 便 、 捷。 方 快 ( ) 用 加载 了宏 的按 钮进 行 数据 输 入 、 算 、 2采 计
( %…0 )
= =
维普资讯
20 0 8年 第 5期 ( 2 第 26期 ) 第 6卷 8
[ 章 编 号 ]0 2— 64 2 0 ) 5 0 9—0 文 10 0 2 (道断面计算软件的开发与使用
徐 文 秀
( 山西水 利职 业技 术学 院 , 山西 运城 0 4 0 4 0 4)
() 2
。 =
弧形 坡 脚 梯 形和 弧 底梯 形 实 用 经 济 断 面 计 算 公 式
复 杂 , 算 工作 量 相 当大 , 发 一 个 简 单 实 用 的计 计 开 算软 件 是 十 分 必要 的。
丢 删
Xo =no M
其 中 M =( m 一 m 一0 ( r ) 4 4 ) K 一1 +0 2 + m。
Q-1 梯形断面渠道土石方工程量计算程序
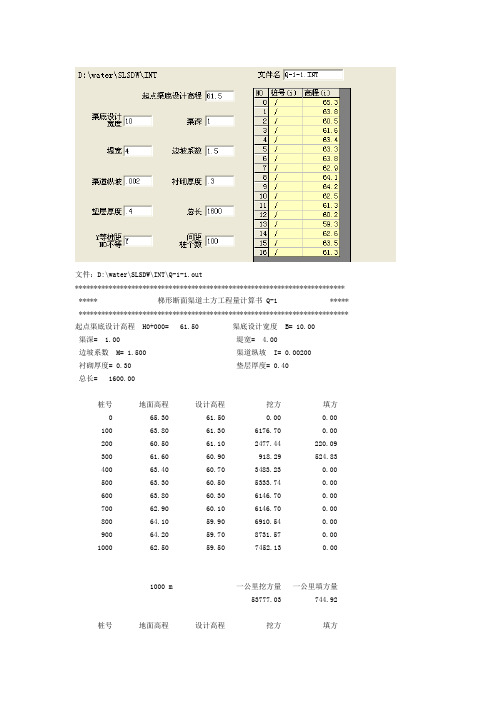
文件:D:\water\SLSDW\INT\Q-1-1.out************************************************************************ ***** 梯形断面渠道土方工程量计算书 Q-1 ***** ************************************************************************ 起点渠底设计高程 H0+000= 61.50 渠底设计宽度 B= 10.00渠深= 1.00 堤宽= 4.00边坡系数 M= 1.500 渠道纵坡 I= 0.00200衬砌厚度= 0.30 垫层厚度= 0.40总长= 1600.00桩号地面高程设计高程挖方填方0 65.30 61.50 0.00 0.00100 63.80 61.30 6176.70 0.00200 60.50 61.10 2477.44 220.09300 61.60 60.90 918.29 524.83400 63.40 60.70 3483.23 0.00500 63.30 60.50 5333.74 0.00600 63.80 60.30 6146.70 0.00700 62.90 60.10 6146.70 0.00800 64.10 59.90 6910.54 0.00900 64.20 59.70 8731.57 0.001000 62.50 59.50 7452.13 0.001000 m 一公里挖方量一公里填方量53777.03 744.92 桩号地面高程设计高程挖方填方1100 61.30 59.30 4874.15 0.00 1200 60.20 59.10 3142.88 0.00 1300 59.30 58.90 1820.97 0.00 1400 62.60 58.70 4498.31 0.00 1500 63.50 58.50 8988.81 0.00 1600 61.30 58.30 8042.73 0.00 1600m 渠道 总挖方量 总填方量 85144.86 744.92总衬砌方 总垫层方 6705.06 9095.11Q-1 梯形断面渠道土石方工程量计算程序作者 潘乐平(新疆和田地区水电勘测设计队)一、程序功能已知渠道起始断面渠底设计高程、底宽、渠深、堤顶宽、边坡系数、纵坡、衬砌厚度、垫层厚度、总长、桩号及地面高程,计算各断面渠底设计高程和渠道土石方工程量:每两个桩号之间的挖、填方;每公里累计挖、填方;全线累计总挖、填方和衬砌方量、垫层方量。
梯形灌溉渠道横断面设计分析

1 水 力 最 佳 断 面
按 照水力 学 理论 , 从 均 匀 流 的公 式 可 以看 出 , 明 渠 的输 水 能力 取决 于 过水 断面 积 形状 、 尺寸 、 底 坡 和 粗 糙 系数 的大小 ¨ J 。
式 中: 为 平均 流 速 ( 米/ 秒) ; Q为 设 计 流 量 , I n / s ; 为过水 断 面 面积 , m ; R为水力 半径 , m; i 为水 面坡
A 为实用 经济 断面 的 过水 断面的设 计 中 , 根据 《 灌 排 与排 水 T 程设 计 规 济断 面湿周 , m; R为 实用 经济 断 面的水 力半 径 , m; b
范》 ( G B 5 0 2 8 8 - - - 9 9 ) , 渠 道 水 力 最 佳 断 面 计 算 方 为实 用 经济 断 面 底 宽 , i n ; / 3 为 实 用 经济 断 面 底 宽 与 法( 参 照附 录 H) 如下 : 1 ) 梯 形 渠 道 水 力 最 佳 断 面 水 力 要 素 计 算 公
Q=
t I
i  ̄ / 2 R
2 / 3
=
t I
…
( 3 )
工, 不 能达 到经 济 的 目的 , 在实 际 应用 中有 很 大 的局
限性。
[ 收 稿 日期 ] 2 0 1 3—0 3—1 2 [ 作 者 简介 】 周春 霞 ( 1 9 6 3一) , 女, 黑龙 江 克 山人 , 高级 工程 师 , 主要从 事水利 工程 设计 工作 。
降; C为 谢 才系数 ; n为糙 率 ; X为湿周 , i n 。
2 在 渠 道 设 计 中水 力最 佳 断 面 和 实 用 经 济
