梯形断面渠道流量计算
梯形明渠水力最优断面尺寸计算书

梯形明渠水力最优断面尺寸计算书项目名称_____________日期_____________设计者_____________校对者_____________一、基本资料:1.参考书目:武汉水利电力学院编《水力计算手册》中国水利水电出版社《工程流体力学》2.输入参数:设计流量:Q = 3.000m3/s边坡系数:m1 = 1.00边坡系数:m2 = 1.00糙率系数:n = 0.0225渠底坡度:i = 0.00500二、计算过程:水力最优断面的宽深比:β= (1+m1×m1)0.5+(1+m2×m2)0.5-m1-m2 = 0.828 程序采用试算法求解,正常水深h从0.1米开始以0.01米的步长递增取值。
通过程序试算,当h = 0.930m时,计算流量Q1 = 2.983m3/s计算流量Q1与设计流量Q比较接近,此时的正常水深h就是所求的渠道水深。
具体计算过程如下:渠道底部宽度b = β×h = 0.828×0.930 = 0.770m断面面积:A = b×h+(m1+m2)/2.0×h×h= 0.770×0.930+(1.00+1.00)/2.0×0.930×0.930 = 1.581m2渠道湿周:X = b+h×[(1+m1×m1)0.5+(1+m2×m2)0.5]= 0.770+0.930×[(1+1.00×1.00)0.5+(1+1.00×1.00)0.5] = 3.401m 水力半径:R = A/X = 1.581/3.401 = 0.465m谢才系数:C = 1/n×R1/6 (曼宁公式)代入上式:C = 1/0.0225×0.4651/6 = 39.119计算流量:Q1 = A×C×(R×i)0.5= 1.581×39.119×(0.465×0.00500)0.5 = 2.983m3/s三、计算结果:所以,正常水深计算值h = 0.930m渠道底部宽度b = β×h = 0.828×0.930 = 0.770m平均流速:v = Q1/A = 2.983/1.581 = 1.886m/s。
Excel水力计算展示—明渠均匀流断面尺寸计算演示(精)

水利水电建筑工程
水力分析与计算
二 用excel求解正常水深
2.Excel计算程序编制
需要用到的公式和需要注意的问题: ①基本变量的单元格符号应加“$”加以固定; ②常用的excel计算符号: 求和 sum函数; 求差 “—”号; 求积 “ * ”号; 求商 “ / ”号; 平均数 average 函数; 开方 “sqrt”或“power(a,0.5)”函数; 幂函数 “^”或 power(a,b)=ab 三角函数 相应的三角函数(注意:默认的格 式是弧度制)。
b 2h 1 m2
R A
1 1/6 C R n
谢才公式:
Q CA Ri
水力分析与计算
A 2/3 1/2 i R i n n (b 2h 1 m2 ) 2/3
水利水电建筑工程
(b mh)h
5/3
水力分析与计算
以此为例进行说明
已知Q,i,m,b,n 明渠均匀流梯 形断面水力计 算任务 已知Q,i,m,h0,n 已知Q,i,m,n 已知Q,i,m,n,宽深比
水力分析与计算
水利水电建筑工程
水力分析与计算
二 用excel求解正常水深
2.Excel计算程序编制
(1)确定基本参数 基本参数是题目中给定的或者通过题目中的条件可以推测的参数。 在编制计算程序时,应注意这些参数在计算过程中始终不变,应当使 用“$”符号加以控制。 以该工程任务为例,题目中给定的基本参数设计流量Q0、渠道底 宽b、边坡系数m、渠道底坡 i 和糙率n 。 将以上参数一一列入计算表格的“基本参数”项。 (2)编制试算程序 依次列清试算过程中所需的全部中间变量和目标变量,并按照试算 的思路逐一编写各个变量的计算程序。
渠道水力计算
0.068611328 9.12
8.476 0.929386 47.19416011 14.398045 3.806583286
0.068611328 9.12
8.476 0.929386 47.19416011 14.398045 3.806583286
综合糙率(n)
nmax/nmin<1.5 nmax/nmin>
定了渠底宽度b,设一系列h,做出K=f(h)曲线图,再由已知流量Q和底坡i算出相应的流量模数K已知,在曲线图上查出
湿周(χ)
水力半径 (R)
谢才系数 流量模数 已知流量模数
(C)
(K)
(K已知)
6.52 0.693251534 37.6306567 141.620346 18.76091434 1.453306673 47.3017302 1554.77278 23.41640786 2.049844719 50.0923003 3442.49006 27.88854382 2.58170525 52.055736 6022.18949 32.36067977 3.090169944 53.6390663 9429.14667
相对稳定断面 (β)
水深 (h)
底宽
(b)
38
0.007
0 0.0209 7.448471389 1.162294654 8.657318479
(3)实用经济断面宽深比
计算方法: (1)拟定偏离系数α:α=A经/A优(一般取α=1.01~1.4) (2)计算γ: γ=h经/h优 γ=α5/2-(α*(α4-1))1/2 (3)计算宽深比β:β=(α*(2(1+m2)1/2-m)-m)/r2
0.0225 0.020932018 0.020932018
梯形、矩形渠道水力计算表 ——有用(算出流速和流量)
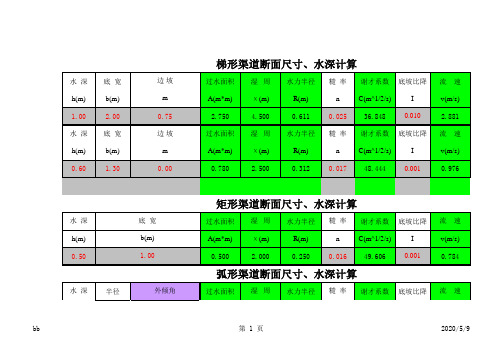
A(m*m) 0.151 0.392 0.280
χ (m) 1.244 1.568 1.453
R(m) 0.121 0.250 0.193
n 0.016 0.016 0.016
C(m^1/2/s) 43.975 49.606 47.499
I 0.001 0.001 0.001
v(m/s) 0.484 0.784 0.659
bb
第 2 页
2017/11/25
bb
第 3 页
2017/11/25
bb
第 4 页
2017/11/25
流
量
Q(m^3/s) 7.921 流 量
Q(m^3/s) 0.761
流
量
Q(m^3/s) 0.392 1.69 流 量 适用条件
bb
第 5 页
2017/11/25
适用条件 Q(m^3/s) 0.073 0.307 0.185 r≤0.2 r<1.0 r≥1.0 水深h 在圆弧 段以上 -1.32
bb
第 9 页
2017/11/25
bb
第 10 页
2017/11/25
bb
第 11 页
2017/11/25
bb
第 12 页
2017/11/25
bb
第 13 页
2017/11/25
水力半径 R(m) 0.428 R(m) 0.308
糙 率 n 0.017 n 0.017
谢才系数 底坡比降 C(m^1/2/s) 51.068 C(m^1/2/s) 48.344 I 0.001 I 0.00/s) 0.968
Q(m^3/s) 1.723 Q(m^3/s) 0.702
梯形渠道断面尺寸、水深计算
梯形渠道水力最优断面分析计算的一种方法

R=o x 2 1 2 一m]22 2 1 2 一m] :h2 a :[ ( +m ) / h/ 1 ( +m ) h /
() 7
将 () ( ) 5 、7 代入( ) , : 3式 得
Q a' R : e . n
解得
:[( +m) —m h n(/ )3以 21 2 ]2 .h22] / /
-
在 般的水力学教科书中, 所给出的梯形水力最优断面
应满 足的几何条件是 : b= [ 1 ) 一m] 2 (+ h
在中小渠道设 计 的取 值范 围 内, 出各 出始 变 量 的座 标 点 算 局, 绘制 出求解水深 的诺模 图( 1 。 图 ) .
式中: 为断面底宽; 为断面水深; b h m为边坡系数。
t b m , = 21 m) 二 ]2 . o =( + hh [( + 2 ) mh
x +2 ( +m ) =22 1 2 =b h 1 2 [ ( +m )
,
。
mh ] ‘
() 5
() 6
一
于是 , 可求 得水 力半 径 R为 :
[ 日期 ] 0 — 6 2 收稿 2 5 0 —0 0
BQ( , 拳 秒J
[ 作者简介] 周开元( 7 一 , 上海人 , 1 3 ) 男, 9 工程师; 君( 6 一)男, 宿良 1 8 , 山东掖县人 , 9 工程师。
一
2 9 —
维普资讯
20 06年
第 i 期 ( 3卷) 第 4
黑
龙
江
水
利
科
技
No 12 o . .o 6
J
式 中: 为渠道糙率 。 n
・
将 () 2 代入 () , 1式 得
U形渠道

H
b
U 形渠道的K r 值 m(a) θ Kr 0(0° ) 180° 0.65-0.72 2) 0.1(5.7° ) 168.6° 0.62-0.68 0.2(11.3° ) 157.4° 0.56-0.63 0.3(16.7° ) 146.6° 0.49-0.56 0.4(21.8° ) 136.4° 0.39-0.47
U 形、弧形底梯形断面设计 1. 流量计算 Q = C × A × Ri 式中: A = K A × H2 X = KX × H KA = (
θ 2
+ 2m − 2m′) × K 2 r + 2×
θ 2
m′ − m × K r + m
K X = 2 × (m + H 为水深,m;
θ 2
− m′) × K r + 2m′
2 θ
(4) 过水断面面积 A: 已知:r、m(a) 、H2 , A=
r2 2
π × 1−
a 90°
− sin 2a + H2 × 2r × cos a + H2 tan a
(5) 湿周 X: 已知:B、r、m(a) 、H2 , X=π r× 1−
a 90°
+
2H 2 cos a
或:X = (6) 水力半径 R: 已知:A、X, R=
A X
B m
× 1 + m2 -
2r m× 1 −m cot −1 m
(7) 弧段水深H1 : 已知:H、H2 , H1 = H − H2 湿周中 2 cot −1 m为弧度值,弧度为 57.32484° 5. U 形渠道计算实例 已知:K r =0.8,m=0.3,H=0.6m,i=0.008 求:U 形渠道过流量 解:1.计算半径 r: r = K r × H = 0.8 × 0.6 = 0.48m 2.计算圆心角θ : θ = 2 × cot −1 m = 2 × cot −1 0.3 = 2 × 90° − 16.7° = 146.6° 3.计算K A KA =
梯形明渠水力最优断面尺寸计算书

具体计算过程如下:
渠道底部宽度b =β×h = 0.828×0.930 = 0.770m
断面面积:ห้องสมุดไป่ตู้
A = b×h+(m1+m2)/2.0×h×h
= 0.770×0.930+(1.00+1.00)/2.0×0.930×0.930 = 1.581m2
= 1.581×39.119×(0.465×0.00500)0.5= 2.983m3/s
三、计算结果:
所以,正常水深计算值h = 0.930m
渠道底部宽度b =β×h = 0.828×0.930 = 0.770m
平均流速:
渠道湿xx:
X = b+h×[(1+m1×m1)0.5+(1+m2×m2)0.5]
= 0.770+0.930×[(1+1.00×1.00)0.5+(1+1.00×1.00)0.5] = 3.401m
水力半径:
xx系数:
C = 1/n×R(xx公式)
代入上式:
×0.465= 39.119
计算流量:
Q1 = A×C×(R×i)0.5
渠底坡度:
i = 0.00500
二、计算过程:
水力最优断面的宽深比:
β= (1+m1×m1)0.5+(1+m2×m2)0.5-m1-m2 = 0.828程序采用试算法求解,正常水深h从0.1米开始以0.01米的步长递增取值。
通过程序试算,当h = 0.930m时,计算流量Q1 = 2.983m3/s
梯形
项目名称_______日期_______
水力学教材习题解答习题解答7

第 七 章 习 题 解 答7-1 梯形断面壤土渠道,已知通过流量Q = 10.5 m 3/s ,底宽b = 8.9 m ,边坡系数m = 1.5,正常水深h 0= 1.25 m ,糙率 n = 0.025,求底坡i 和流速v 。
解: A = 1.25×(8.9+1.5×1.25) = 13.47 m 2,χ= 8.9+2×1.25×25.11+= 13.41 m , R = A /χ=1.005 m ,C = 1.0051/6/0.025 = 40.03 m 1/2·s , K = ACR 1/2=540.57 m/3si = (Q /K )2 = 0.000377,v = Q /A = 0.78 m/s7-2 有一灌溉干渠,断面为梯形,底宽b = 2.2 m ,边坡系数m = 1.5,实测得流量Q = 8.11 m 3/s 时,均匀流水深h 0 = 2 m ,在1800m 长的顺直渠段水面落差Δh = 0.5 m ,求渠道的糙率n 。
解:i = J = J P = △h /L =1/3600,A = 2×(2.2+1.5×2 ) = 10.4 m 2, χ= 2.2+2×2×25.11+= 9.41 m , R = A /χ= 1.105 mn = AR 2/3i 1/2/Q = 0.02287-3 一石渠的边坡系数m = 0.1,糙率n = 0.020,底宽b = 4.3 m ,水深h = 2.75 m ,底坡i = 1/2000,求流量和流速。
解:A = 2.75×(4.3+0.1×2.75 ) = 12.58 m 2,χ= 4.3+2×2.75×21.01+= 9.83 m R = A /χ= 1.28 m ,v = n i R 32=1.318 m/s , Q = vA =16.58 m 3/s7-4 直径为d 的圆形管道中的明槽均匀流动,试根据式(7-2-5)导出Q/Q 1~h/d 的关系式(Q 1为h/d = 1时的流量),并论证当充满度h/d 为多大时Q/Q 1达到最大值。
