第51讲 导数的应用(解析版)
(完整版)导数及其应用最全教案(含答案),推荐文档

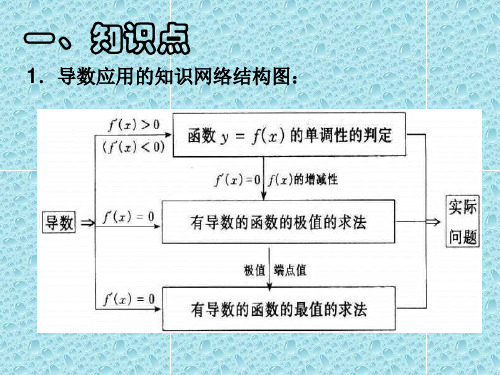
一、知识点梳理
1.导数:当x 趋近于零时, f (x0 x) f (x0 ) 趋近于常数 c。可用符号“ ”记作: x
当x 0 时, f (x0 x) f (x0 ) c 或记作 lim f (x0 x) f (x0 ) c ,符号
x
x0
x
“ ”读作“趋近于”。函数在 x0 的瞬时变化率,通常称作 f (x) 在 x x0 处的导数,并
例3:设函数f(x)= 2x3 3(a 1)x2 1, 其中a 1. (Ⅰ)求f(x)的单调区间;(Ⅱ)讨论
f(x)的极值。
解:由已知得 f ' (x) 6x x (a 1),令 f ' (x) 0 ,解得
x 0, x a 1。
1
2
(Ⅰ)当 a 1 时, f ' (x) 6x2 , f (x) 在(, ) 上单调递增;
注意:(1)在求函数的极值时,应注意:使导函数 f (x) 取值为 0 的点可能是它的极值点, 也可能不是极值点。例如函数 f (x) x3 的导数 f (x) 3x2 ,在点 x 0 处有 f (0) 0 ,
即点 x 0 是 f (x) x3 的驻点,但从 f (x) 在 ,上为增函数可知,点 x 0 不是
当 a 1时, f ' (x) 6x x a 1 , f ' (x), f (x) 随 x 的变化情况如下表:
x f ' (x) f (x)
(, 0) + A
0 0 极大值
(0, a 1) A
a 1
0 极小值
(a 1, ) A
从上表可知,函数 f (x) 在(, 0) 上单调递增;在(0, a 1) 上单调递减;在(a 1, ) 上 单调递增。 (Ⅱ)由(Ⅰ)知,当 a 1 时,函数 f (x) 没有极值;
导数的应用(第1课时)利用导数研究函数的单调性(课件)高二数学(沪教版2020选择性必修第二册)

图 ( 1 ) 中的曲线越来越 “ 陡峭 ”, 在区间 ( 0 , 1 ) 上各点处 的切线斜率始终大于 1 ; 图 ( 2 ) 中的曲线由 “ 陡峭 ” 变得 “ 平缓 ”, 在区间 ( 0 , 1 ) 的右半段的切线斜率小于 1 ; 图 ( 3 ) 中的曲线由 “ 平缓 ” 变得 “ 陡峭 ”, 在区间 ( 0 , 1 ) 的左半段的切线斜率小于 1 ; 图 ( 4 ) 中的曲线越来越 “ 平缓 ”, 在区间 ( 0 , 1 ) 上各点处 的切线斜率始终小于 1. 因此 , 只有图 5-3-1 ( 1 ) 中的图像有可能表示函数 y = f( 可能成为严格递增区间与严格 递减区间的分界点 .
例4.确定函数(f x)=x2的单调区间 .
解函数在x 0处没有定义 .当x 0时,f (x)=-2x3,
方程f′( x )=0 无解 , 所以函数 f( x )没有驻点 . 但当 x >0 时 ,f′( x ) <0 ,f( x ) 单调递减 ; 当 x <0 时 ,f′( x) >0 , f( x ) 单调递增 . 可 见 , 函数 f ( x ) 的严格递增区间为 (-∞,0), 严格 递减区间为(0,+∞)
课本练习 宋老师数学精品工作室
1. 利用导数研究下列函数的单调性 , 并说明所得结果与你 之前的认识是否一致 :
宋老师数学精品工作室 2. 确定下列函数的单调区间 :
随堂检测 宋老师数学精品工作室
1、函数y=x2cos 2x的导数为( )
A.y′=2xcos 2x-x2sin 2x
B.y′=2xcos 2x-2x2sin 2x
上面我们用导数值的正负判断函数在某区间的单调性 . 但导数值还可 以进一步用以判断函数变化速度的快慢 : 导数f′( x 0 ) 是函数 f( x ) 在点 x 0 的切线的斜率 , 所以它描述了曲线 y=f( x ) 在点 x0 附近相 对于x轴的倾斜程度 : 当f′( x 0 ) >0 时 ,f′( x0 ) 越大 , 曲线 y = f ( x ) 在点 x 0 附近相对于 x 轴倾斜得越厉害 ,f( x ) 递增得 越快 ; 而当f′( x 0 ) <0 时 ,f′( x 0 ) 越小 , 曲线y = f ( x ) 在点 x0 附近相对于x轴倾斜得越厉害 , f ( x ) 递减得越快 . 综合这 两个方面 , 导数的绝对值越大 , 函数图像就越 “ 陡峭 ”, 也就是 函数值变化速度越快 .
导数及其应用课件PPT

又因为函数在(0,+∞)上只有一个极大值点,所以函数在x=9处取得最大值.
解析答案
12345
4.某公司生产某种产品,固定成本为 20 000 元,每生产一单位产品,成本增
加 100 元,已知总收益 r 与年产量 x 的关系是 r=400x-21x2,0≤x≤400, 80 000, x>400,
则总利润最大时,年产量是( )
即当x为2.343 m,y为2.828 m时,用料最省.
解析答案
题型二 面积、容积的最值问题 例2 如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形 栏目(即图中阴影部分),这两栏的面积之和为18 000 cm2,四周空白的宽 度为10 cm,两栏之间的中缝空白的宽度为5 cm.怎样确定广告的高与宽的 尺寸(单位:cm),能使矩形广告面积最小?
反思与感悟
解析答案
跟踪训练1 某单位用木料制作如图所示的框架,框架的下部是边长分别为
x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架的总面积为8 m2,
问:x,y分别是多少时用料最省?(精确到0.001 m)
解 依题意,有 xy+12·x·2x=8,∴y=8-x x42=8x-4x(0<x<4 2),
即当x为2.343 m,y为2.828 m时,用料最省.
解析答案
题型二 面积、容积的最值问题 例2 如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形 栏目(即图中阴影部分),这两栏的面积之和为18 000 cm2,四周空白的宽 度为10 cm,两栏之间的中缝空白的宽度为5 cm.怎样确定广告的高与宽的 尺寸(单位:cm),能使矩形广告面积最小?
S′(x)=6x2-24x+16,
令
S′(x)=0,得
《导数的应用》ppt课件
设 x 1 cos , y 1 sin ,由x,y为正实数得: 0 .
xy
1
(1
2
cos
)si n
.
2
设 f ( ) 1 (1 cos )sin .
2
f
(
)
1
[
s i n2
(1
cos
) co s
]
(cos
1)(cos
1 ).
2
2
令 f ( ) 0,得 cos 1,cos 1 ;又0 , .
从而当x>0时,f(x)≥1恒成立,即:
2
1
2 3
(1
x)3
成立.
令 Y
x6
3
0
1 2x
,得
4.
x
1.
当x<-1时, Y 0,则Y单调减小;当-1<x<0时, Y 0,则
Y单调增加;当0<x<1时,Y 0,则Y单调减小;当x>1
时,Y 0 ,则Y单调增加. 故当x 1时,Y有最小值5/6,此时点 (1, 1 )为所求.
3
例4: 如图,在二次函数f(x)=
2 ( x 1)3( x 3
0).
则
f
( x)
1 x
1 x2
( x 1)
2( x 1)2
(x
1)3
2x 1 x2 ,
令f (x) 0 ,结合x>0得x=1.
而0<x<1时, f (x) 0;x>1时,f (x) 0 ,所以x=1是f(x)的 极小值点.
所以当x=1时,f(x)取最小值f(1)=1.
令
S(
x)
0
导数的应用教学课件ppt

对于两个函数f(x)和g(x),其导数分别为f'(x)和g'(x),则两函数积的导数为(fg)'(x)=f'(x)g(x)+f(x)g'(x)。
幂法则
对于一个函数f(x),其导数为f'(x),则(x^n)'=nx^(n-1)。
导数计算的常见问题与解决方案
常见问题
在导数计算中,容易出现一些错误,如符号错误、运算错误 、化简错误等。
导数可以用来求函数的极值、单调区间、凹凸区间等
导数在其他领域中的应用
导数可以用来解决物理、经济、工程等领域中的一些问题,如物体运动时的加速 度、经济学中的边际效应、工程中的曲率等等
02
导数的计算
极限与导数
极限的定义
极限是函数在某一变化过程中, 某个变量的变化趋势,通常用符 号lim表示。
导数的定义
与其他学生或老师交流讨论,及时解决学习中遇 到的问题。
THANKS
导数的深入研究
1
深入理解导数的定义和计算方法,包括高阶导 数和复合函数的导数。
2
研究导数在函数性质、曲线形状、极值等方面 的应用,以及在实际问题中的应用。
3
探讨导数在数学中的地位和作用,以及与其他 数学分支的联系。
导数在未来的应用前景
分析导数在金融、经济、工程等领域 的应用前景,例如最优化问题、供应 链管理、计算机图形学等。
导数的应用教学课件ppt
xx年xx月xx日Biblioteka contents目录
• 导数的概念及背景 • 导数的计算 • 导数在函数性质研究中的应用 • 导数在几何中的应用 • 导数在实际问题中的应用 • 导数的进一步探讨与展望
01
导数及其应用课件

个数便是确定的了,它除了不依赖于定义
中的区间分法和 的取法外,也不依赖
于符号 b
= f (t)dt
ab,f (x因)dx此中,的定积积分分变记量号x中,的即积分ab f (变x)dx
a
量可以用任何字母来表示.此外,对于定
a x b 积分符号
化范围是
b
a f (x)dx
,意味着积分变量
(五)求函数 y = f ( x )在点x 。处的导数有两 种方法,即导数定义法和导函数的函数值法.
(六)导数的应用
1利用导数判断函数的单调性
2 函数的极值
(l )设函数 f ( x )在点 x 。的附近有定义,如果对附 近所有的点都有:
(2 )可导函数 f ( x )在极值点处的导数为0,但 导数为0的点不一定是极值点。
由于定积分反映的是函数在一个区间上的整体性质,所以 不能用它来研究函数的局部性质,例如有两个在 [ a ,b]上 可积的函数 f (x)和 g ( x ) ,若
则由定积分的性质知道
• 奇函数或偶函数在对称区间上的定积分的结论也是 很有用的,但要求被积函数是奇函数或偶函数,积 分区间是对称区间 [- a , a ] .不过在解题时可以活 用,例知:
(1)在闭区间[a ,b]上连续的函数 f ( x ) ,在 [ a ,b]上必有最大值和最 小值. (2 )利用导数求最值的步骤:
① 求 f (x )在( a , b )内的极值;
② 将 f ( x )的各极值与 f ( a ) , f (b )比较, 确定 f (x )的最大值和最小值.
(七)定积分的概念
1关于定积分的定义
在定 f (x )在 [a , b ]上连续或可导的条件 相比是最弱的条件,即 f (x )在[ a ,b] 上有以下关系:
专题4.4 导数的综合应用 (讲)解析版

专题4.4 导数的综合应用【考纲解读与核心素养】1. 了解函数极值的概念及函数在某点取到极值的条件,会用导数求函数的极大值、极小值,会求闭区间上函数的最大值、最小值,会用导数解决某些实际问题.2.培养学生的数学抽象、数学运算、数学建模、逻辑推理、直观想象等核心数学素养. 3. 高考预测:(1)导数是研究函数性质的重要工具,它的突出作用是用于研究函数的单调性、极值与最值、函数的零点等.解答题难度较大,常与不等式的证明、方程等结合考查,且有综合化更强的趋势; (2)适度关注生活中的优化问题. 4.备考重点:(1)熟练掌握导数公式及导数的四则运算法则是基础;(2)熟练掌握利用导数研究函数的单调性、极值(最值)的基本方法,灵活运用数形结合思想、分类讨论思想、函数方程思想等,分析问题解决问题.【知识清单】1.利用导数研究函数的图象与性质函数图象的识别主要利用函数的定义域、值域、奇偶性、单调性以及函数值的符号等.解决此类问题应先观察选项的不同之处,然后根据不同之处研究函数的相关性质,进而得到正确的选项.如该题中函数解析式虽然比较复杂,但借助函数的定义域与函数的单调性很容易利用排除法得到正确选项. 2.与函数零点有关的参数范围问题 (1)方程()0f x =有实根函数()y f x =的图象与x 轴有交点函数()y f x =有零点.(2)求极值的步骤:①先求'()0f x =的根0x (定义域内的或者定义域端点的根舍去);②分析0x 两侧导数'()f x 的符号:若左侧导数负右侧导数正,则0x 为极小值点;若左侧导数正右侧导数负,则0x 为极大值点.(3)求函数的单调区间、极值、最值是统一的,极值是函数的拐点,也是单调区间的划分点,而求函数的最值是在求极值的基础上,通过判断函数的大致图象,从而得到最值,大前提是要考虑函数的定义域.(4)函数()y f x =的零点就是()0f x =的根,所以可通过解方程得零点,或者通过变形转化为两个熟悉函数图象的交点横坐标.3.与不等式恒成立、有解、无解等问题有关的参数范围问题不等式的恒成立问题和有解问题、无解问题是联系函数、方程、不等式的纽带和桥梁,也是高考的重点和热点问题,往往用到的方法是依据不等式的特点,等价变形,构造函数,借助图象观察,或参变分离,转化为求函数的最值问题来处理.()f x a >:min max max ()()()f x a f x a f x a⇔>⎧⎪⇔>⎨⎪⇔≤⎩恒成立有解无解4.利用导数证明、解不等式问题无论不等式的证明还是解不等式,构造函数,运用函数的思想,利用导数研究函数的性质(单调性和最值),达到解题的目的,是一成不变的思路,合理构思,善于从不同角度分析问题,是解题的法宝.【典例剖析】高频考点一 :利用导数研究函数的零点或零点个数【典例1】(2020届山东省菏泽一中高三2月月考)已知函数()ln 2sin f x x x x =-+,()f x '为()f x 的导函数.(1)求证:()f x '在()0π,上存在唯一零点; (2)求证:()f x 有且仅有两个不同的零点. 【答案】(1)证明见解析;(2)证明见解析. 【解析】(1)设()()112cos g x f x x x'==-+, 当()0,x π∈时,()212sin 0g x x x'=--<,所以()g x 在()0,π上单调递减,又因为31103g ππ⎛⎫=-+>⎪⎝⎭,2102g ππ⎛⎫=-< ⎪⎝⎭所以()g x 在,32ππ⎛⎫⎪⎝⎭上有唯一的零点α,所以命题得证.(2) ①由(1)知:当()0,x α∈时,()0f x '>,()f x 在()0,α上单调递增; 当(),x απ∈时,()0f x '<,()f x 在(),απ上单调递减; 所以()f x 在()0,π上存在唯一的极大值点32ππαα⎛⎫<<⎪⎝⎭所以()ln 2202222f f ππππα⎛⎫>=-+>->⎪⎝⎭又因为2222111122sin 220f e e e e ⎛⎫=--+<--+<⎪⎝⎭所以()f x 在()0,α上恰有一个零点. 又因为()ln 20fππππ=-<-<所以()f x 在(),απ上也恰有一个零点.②当[),2x ππ∈时,sin 0x ≤,()ln f x x x ≤- 设()ln h x x x =-,()110h x x'=-< 所以()h x 在[),2ππ上单调递减,所以()()0h x h π≤< 所以当[),2x ππ∈时,()()()0f x h x h π≤≤<恒成立 所以()f x 在[),2ππ上没有零点. ③当[)2,x π∈+∞时,()ln 2f x x x ≤-+ 设()ln 2x x x ϕ=-+,()110x xϕ'=-< 所以()x ϕ在[)2,π+∞上单调递减,所以()()20x ϕϕπ≤< 所以当[)2,x π∈+∞时,()()()20f x x ϕϕπ≤≤<恒成立 所以()f x 在[)2,π+∞上没有零点. 综上,()f x 有且仅有两个零点.【典例2】(2019·全国高考真题(理))已知函数()sin ln(1)f x x x =-+,()f x '为()f x 的导数.证明:(1)()f x '在区间(1,)2π-存在唯一极大值点;(2)()f x 有且仅有2个零点. 【答案】(1)见解析;(2)见解析 【解析】(1)由题意知:()f x 定义域为:()1,-+∞且()1cos 1f x x x '=-+ 令()1cos 1g x x x =-+,1,2x π⎛⎫∈- ⎪⎝⎭ ()()21sin 1g x x x '∴=-++,1,2x π⎛⎫∈- ⎪⎝⎭()211x +在1,2π⎛⎫- ⎪⎝⎭上单调递减,sin x -,在1,2π⎛⎫- ⎪⎝⎭上单调递减 ()g x '∴在1,2π⎛⎫- ⎪⎝⎭上单调递减又()0sin0110g '=-+=>,()()2244sin 102222g ππππ⎛⎫'=-+=-< ⎪⎝⎭++00,2x π⎛⎫∴∃∈ ⎪⎝⎭,使得()00g x '=∴当()01,x x ∈-时,()0g x '>;0,2x x π⎛⎫∈ ⎪⎝⎭时,()0g x '<即()g x 在()01,x -上单调递增;在0,2x π⎛⎫⎪⎝⎭上单调递减 则0x x =为()g x 唯一的极大值点即:()f x '在区间1,2π⎛⎫- ⎪⎝⎭上存在唯一的极大值点0x .(2)由(1)知:()1cos 1f x x x '=-+,()1,x ∈-+∞ ①当(]1,0x ∈-时,由(1)可知()f x '在(]1,0-上单调递增()()00f x f ''∴≤= ()f x ∴在(]1,0-上单调递减又()00f =0x ∴=为()f x 在(]1,0-上的唯一零点②当0,2x π⎛⎤∈ ⎥⎝⎦时,()f x '在()00,x 上单调递增,在0,2x π⎛⎫⎪⎝⎭上单调递减 又()00f '= ()00f x '∴>()f x ∴在()00,x 上单调递增,此时()()00f x f >=,不存在零点又22cos 02222f ππππ⎛⎫'=-=-<⎪++⎝⎭10,2x x π⎛⎫∴∃∈ ⎪⎝⎭,使得()10f x '=()f x ∴在()01,x x 上单调递增,在1,2x π⎛⎫⎪⎝⎭上单调递减又()()000f x f >=,2sin ln 1ln ln102222e f ππππ⎛⎫⎛⎫=-+=>= ⎪ ⎪+⎝⎭⎝⎭()0f x ∴>在0,2x π⎛⎫⎪⎝⎭上恒成立,此时不存在零点③当,2x ππ⎡⎤∈⎢⎥⎣⎦时,sin x 单调递减,()ln 1x -+单调递减 ()f x ∴在,2ππ⎡⎤⎢⎥⎣⎦上单调递减又02f π⎛⎫>⎪⎝⎭,()()()sin ln 1ln 10f ππππ=-+=-+< 即()02ff ππ⎛⎫⋅<⎪⎝⎭,又()f x 在,2ππ⎡⎤⎢⎥⎣⎦上单调递减 ∴()f x 在,2ππ⎡⎤⎢⎥⎣⎦上存在唯一零点④当(),x π∈+∞时,[]sin 1,1x ∈-,()()ln1ln 1ln 1x e π+>+>=()sin ln 10x x ∴-+<即()f x 在(),π+∞上不存在零点综上所述:()f x 有且仅有2个零点 【方法技巧】利用导数研究函数零点或方程根的方法 (1)通过最值(极值)判断零点个数的方法.借助导数研究函数的单调性、极值后,通过极值的正负,函数单调性判断函数图象走势,从而判断零点个数或者通过零点个数求参数范围. (2)数形结合法求解零点.对于方程解的个数(或函数零点个数)问题,可利用函数的值域或最值,结合函数的单调性,画出草图数形结合确定其中参数的范围. (3)构造函数法研究函数零点.①根据条件构造某个函数,利用导数确定函数的单调区间及极值点,根据函数零点的个数寻找函数在给定区间的极值以及区间端点的函数值与0的关系,从而求解.②解决此类问题的关键是将函数零点、方程的根、曲线交点相互转化,突出导数的工具作用,体现转化与化归的思想方法. 【变式探究】1.(2020届山东省枣庄市高三上学期统考)【多选题】关于函数()2ln f x x x=+,下列判断正确的是( ) A .2x =是()f x 的极大值点B .函数()y f x x =-有且只有1个零点C .存在正实数k ,使得()f x kx >恒成立D .对任意两个正实数1x ,2x ,且21x x >,若()()12f x f x =,则124x x +> 【答案】BD 【解析】(1)()f x 的定义域为()0,∞+,()'22x f x x-=,所以()f x 在()0,2上递减,在()2,+∞上递增,所以2x =是()f x 的极小值点.故A 选项错误.(2)构造函数()()()2ln 0g x f x x x x x x =-=+->,()()2'22x x g x x--+=2217240x x ⎡⎤⎛⎫--+⎢⎥⎪⎝⎭⎢⎥⎣⎦=<,所以()g x 在()0,∞+上递减.而()1ln 210g =+>,()2ln 210g =-<,()()120g g ⋅<.所以()g x 有且只有一个零点.故B 选项正确.(3)构造函数()()()2ln 0,0h x f x kx x kx x k x =-=+->>.()2'22kx x h x x-+-=,由于0k -<,22y kx x =-+-开口向下,0x →和x →+∞时,220y kx x =-+-<,即()2'220kx x h x x-+-=<,x →+∞时()0h x <,故不存在正实数k ,使得()f x kx >恒成立,C 选项错误.(4)由(1)知,()f x 在()0,2上递减,在()2,+∞上递增, 2x =是()f x 的极小值点.由于任意两个正实数1x ,2x ,且21x x >,()()12f x f x =,故1202x x <<<.令211x t x =>,21x tx =.由()()12f x f x =得121222ln ln x x x x +=+,即2121212ln x x x x x x -⋅=,即()11112ln t x t x tx -⋅=⋅,解得()121ln t x t t-=⋅,则()2121ln t t x tx t t -==⋅.所以21222ln t x x t t-+=⋅.要证124x x +>,即证1240x x +->,即证2222224ln 40ln ln t t t t t t t t----=>⋅⋅,由于1t >,所以ln 0t t >,故即证()2224ln 01t t t t -->>①.构造函数()()2224ln 1h t t t t t =--≥(先取1t ≥),()10h =;()'44ln 4h t t t =--,()'10h =;()()''41440t h t t t-=-=>.所以()'h t 在[)1,+∞上为增函数,所以()()''10h t h ≥=,所以()h t 在[)1,+∞上为增函数,所以()()10h t h ≥=.故当1t >时,()0h t >.即证得①成立,故D 选项正确. 故选:BD.2.(2019·浙江高三期末)已知()ln af x x x=+,()x g x e -=,其中a R ∈, 2.718e =⋯为自然对数的底数.()I 若函数()g x 的切线l 经过()1,0点,求l 的方程;(Ⅱ)若函数()f x 在20,e ⎛⎫⎪⎝⎭为递减函数,试判断()()()x f x g x ϕ=-函数零点的个数,并证明你的结论.【答案】(Ⅰ)?1y x =-+;(Ⅱ)见解析 【解析】(Ⅰ)设l 和()g x 的切点是()00,x x e -,()g x 在该点处的导数()00'x g x e -=-,它是切线l 的斜率, l 经过()1,0,也过切点()00,x x e -,l ∴的斜率又可写为01x e x --, 故001x x e e x --=--,故011x -=-,解得:00x =, 故直线l 的斜率为()00'1x g x e -=-=-,故l 的方程是:1y x =-+;(Ⅱ)判断:函数的零点个数是0,下面证明()()f x g x >恒成立,()20x af x x -'=≤,故x a ≤, 若()f x 在20,e ⎛⎫ ⎪⎝⎭递减,则2a e≥, 因此,要证明()()ln x af x xg x e x-=+>=对0x >恒成立, 只需证明2ln x x e e x -+>⋅对0x >恒成立, 考虑2ln x x e e x -+>⋅等价于2ln x x x xe e->-, 记()ln u x x x =,()2xv x x e e-=⋅-,先看()u x ,()'ln 1u x x =+,令()'0u x >,解得:1x e >, 令()'0u x <,解得:10x e<<,故()u x 在10,e ⎛⎫ ⎪⎝⎭递减,在1,e ⎛⎫+∞ ⎪⎝⎭递增,()11min u x u e e ⎛⎫==- ⎪⎝⎭,再看()2xv x x ee-=⋅-,()()'1x v x x e -=-⋅. 令()'0v x >,解得:01x <<, 令()'0v x <,解得:1x >,故()u x 在()0,1递增,在1,e ⎛⎫+∞ ⎪⎝⎭递减,()()11max v x v e==-.()()min max u x v x =,且两个函数的极值点不在同一个x 处,故()()u x v x >对0x >恒成立, 综上,()()f x g x >对0x >恒成立, 故函数()()()x f x g x ϕ=-函数零点是0个. 高频考点二:与函数零点有关的参数范围问题【典例3】(2017课标3)已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则a =A .12-B .13C .12D .1【答案】C 【解析】函数的零点满足()2112x x x x a e e --+-=-+,设()11x x g x ee--+=+,则()()211111111x x x x x x e g x eeee e ---+----'=-=-=,当()0g x '=时,1x =,当1x <时,()0g x '<,函数()g x 单调递减, 当1x >时,()0g x '>,函数()g x 单调递增, 当1x =时,函数取得最小值()12g =,设()22h x x x =- ,当1x =时,函数取得最小值1- ,【典例4】(2020·全国高考真题(文))已知函数32()f x x kx k =-+. (1)讨论()f x 的单调性;(2)若()f x 有三个零点,求k 的取值范围. 【答案】(1)详见解析;(2)4(0,)27. 【解析】(1)由题,'2()3f x x k =-,当0k ≤时,'()0f x ≥恒成立,所以()f x 在(,)-∞+∞上单调递增;当0k >时,令'()0f x =,得3k x ='()0f x <,得33k kx << 令'()0f x >,得3k x <3k x >()f x 在(,)33k k -上单调递减,在 (,)3k -∞,,)3k+∞上单调递增.(2)由(1)知,()f x 有三个零点,则0k >,且(00f f ⎧>⎪⎪⎨⎪<⎪⎩即22203203k k ⎧+>⎪⎪⎨⎪-<⎪⎩,解得4027k <<, 当4027k <<>20f k =>, 所以()f x在上有唯一一个零点,同理1k --<32(1)(1)0f k k k --=--+<, 所以()f x在(1,k --上有唯一一个零点, 又()f x在(上有唯一一个零点,所以()f x 有三个零点, 综上可知k 的取值范围为4(0,)27. 【变式探究】(2019·江西临川一中高考模拟(文))已知函数22()()x f x e ax x a =++存在极大值与极小值,且在1x =-处取得极小值. (1)求实数a 的值;(2)若函数()()2g x f x x m =--有两个零点,求实数m 的取值范围.(参考数据: 2.236e ≈≈) 【答案】(1)1(2)()1,+∞ 【解析】(1)函数()22()xf x eaxx a =++存在极大值与极小值,且在1x =-处取得极小值,()22()211x f x e ax a x a '++⎡⎤∴=++⎣⎦,依题意知(1)0f '-=,解得0a =或1a =, 当0a =时,()()1xf x ex '=+,1x <-时,()0f x '<,()f x 单调递减;1x >-时,()0f x '>,()f x 单调递增,此时,()f x 只有极小值,不符合题意. 当1a =时,()(1)(2)xf x e x x '=++,2x <-或1x >-时,()0f x '>,()f x 单调递增;21x -<<-时,()0f x '<,()f x 单调递减,符合在1x =-处取得极小值的题意, 综上,实数a 的值为1. (2)()2()12xg x exx x m =+--+,()(1)(2)2x g x e x x '=++-,当0x >时,()0g x '>,故()g x 在()0,∞+上单调递增, 当0x <时,令()(1)(2)2xh x e x x =++-, 则()2()55xh x exx '=++,()0,()h x x x h x '><>单调递增,55()0,,()22h x x h x '--+<<<单调递减,5(0)0,202h h ⎛⎫=-=< ⎪ ⎪⎝⎭,0x <时,()0g x '>,故()g x 在(),0-∞上单调递减,()g x 在R 上有两个零点,(0)10,1g m m ∴=-<∴>,此时当0x <时,02m g ⎛⎫-> ⎪⎝⎭,()g x ∴在,02m ⎛⎫- ⎪⎝⎭有一个零点,当0x >时,2m ()120x g x x x >++--=,令012x +=()00g x ∴>,()g x 在()00,x 有一个零点,综上,实数m 的取值范围是()1,+∞. 【易错提醒】极值点处的导数为0,而导数为0的点不一定是极值点,要检验极值点两侧导数是否异号. 高频考点三:与不等式恒成立、有解、无解等问题有关的参数范围问题【典例5】(2020·安徽屯溪一中高二期中(理))已知不等式()1ln xxe a x x -+≥对任意正数x 恒成立,则实数a 的最大值是( ) A .12B .1 CD .2e 【答案】B 【解析】0x >时,不等式(1)x xe a x lnx -+可化为(1)x a x xe lnx +-,所以1x xe lnxa x -+,设()1x xe lnxf x x -=+,其中0x >,则221(1)1()(1)x x x e lnxx f x x ++--+'=+, 设21()(1)1xg x x x e lnx x =++--+,其中0x >,则21()(1)[(2)]0xg x x x e x'=+++>恒成立,则()g x 在(0,)+∞上单调递增,2211())(1)1(1)1x x x g x x x e lnx x e xe lnx x x==++--+=+---+,令()0o g x =,得1ox oex =, 所以()f x 在(0,)o x 单调递减,(o x ,)+∞单调递增,1()111o x o o omino o ox e lnx x f f x x x -+====++,对任意正数x 恒成立,即()1min a f x =, 故选:B .【典例6】(2020·全国高考真题(理))已知函数2()e xf x ax x =+-. (1)当a =1时,讨论f (x )的单调性; (2)当x ≥0时,f (x )≥12x 3+1,求a 的取值范围. 【答案】(1)当(),0x ∈-∞时,()()'0,f x f x <单调递减,当()0,x ∈+∞时,()()'0,f x f x >单调递增.(2)27,4e ⎡⎫-+∞⎪⎢⎣⎭【解析】(1)当1a =时,()2x x x e f x =+-,()21x f x e x '=+-,由于()20xf x e ''=+>,故()'f x 单调递增,注意到()00f '=,故:当(),0x ∈-∞时,()()0,f x f x '<单调递减, 当()0,x ∈+∞时,()()0,f x f x '>单调递增. (2)由()3112f x x ≥+得,23112x e ax x x +-+,其中0x ≥, ①.当x =0时,不等式为:11≥,显然成立,符合题意;②.当0x >时,分离参数a 得,32112x e x x a x ----, 记()32112x e x x g x x ---=-,()()231212x x e x x g x x ⎛⎫---- ⎪⎝⎭'=-,令()()21102xe x x h x x ---≥=, 则()1xh x e x '=--,()10xh x e ''=-≥,故()'h x 单调递增,()()00h x h ''≥=, 故函数()h x 单调递增,()()00h x h ≥=, 由()0h x ≥可得:21102xe x x ---恒成立, 故当()0,2x ∈时,0g x ,()g x 单调递增; 当()2,x ∈+∞时,0g x ,()g x 单调递减;因此,()()2max724e g x g -⎡⎤==⎣⎦, 综上可得,实数a 的取值范围是27,4e ⎡⎫-+∞⎪⎢⎣⎭. 【规律方法】1.一般地,若不等式a ≥f (x )恒成立,a 的取值范围是a ≥[f (x )]max ;若不等式a ≤f (x )恒成立,则a 的取值范围是a ≤[f (x )]min .2.含参数的不等式()()f x g x >恒成立、有解、无解的处理方法:①()y f x =的图象和()y g x =图象特点考考虑;②构造函数法,一般构造()()()F x f x g x =-,转化为()F x 的最值处理;③参变分离法,将不等式等价变形为()a h x >,或()a h x <,进而转化为求函数()h x 的最值. 【变式探究】1.(2020·湖南长郡中学高三其他(文))已知函数()()()1xf x e x a a R =-∈-.(1)讨论()f x 在区间[]1,2上的单调性; (2)若()af x e≥恒成立,求实数a 的最大值.(e 为自然对数的底) 【答案】(1)见解析;(2)1-. 【解析】(1)由已知()()xf x ex a '=-,(),x a ∈-∞时,()0f x '<﹔(),x a ∈+∞时,()0f x '>,①当1a ≤时,()f x 在[]1,2上单调递增; ②当12a <<时,()f x 在[]1,a 上单调递减,(],2a 上单调递增;③当2a ≥时,()f x 在[]1,2的单调递减; (2)由已知()10xae x a e---≥恒成立, 令()()1xag x ex a e=---,则()min 0g x ≥, 由(1)知:()g x 在(),x a ∈-∞上单调递减,在(),x a ∈+∞上单调递增,则()()min 0g x g a =≥,即()10aae a a e---≥ 整理得10a e a ++≤, 令()1x h x ex +=+,()110x h x e +'=+>恒成立,即()1x h x e x +=+在R 上单调递增, 而()11110h e-+-=-=,()()101a h a e a h +=+≤=-,所以1a ≤-,即a 的最大值为1-.2.(2019·全国高考真题(文))已知函数f (x )=2sin x -x cos x -x ,f′(x )为f (x )的导数. (1)证明:f′(x )在区间(0,π)存在唯一零点; (2)若x ∈[0,π]时,f (x )≥ax ,求a 的取值范围. 【答案】(1)见解析;(2)(],0a ∈-∞. 【解析】(1)()2cos cos sin 1cos sin 1f x x x x x x x x '=-+-=+-令()cos sin 1g x x x x =+-,则()sin sin cos cos g x x x x x x x '=-++= 当()0,x π∈时,令()0g x '=,解得:2x π=∴当0,2x 时,()0g x '>;当,2x ππ⎛⎫∈⎪⎝⎭时,()0g x '< g x 在0,2π⎛⎫⎪⎝⎭上单调递增;在,2ππ⎛⎫ ⎪⎝⎭上单调递减又()0110g =-=,1022g ππ⎛⎫=-> ⎪⎝⎭,()112g π=--=- 即当0,2x时,()0g x >,此时()g x 无零点,即()f x '无零点()02g g ππ⎛⎫⋅< ⎪⎝⎭ 0,2x ππ⎛⎫∴∃∈ ⎪⎝⎭,使得()00g x = 又()g x 在,2ππ⎛⎫⎪⎝⎭上单调递减 0x x ∴=为()g x ,即()f x '在,2ππ⎛⎫⎪⎝⎭上的唯一零点 综上所述:()f x '在区间()0,π存在唯一零点(2)若[]0,x π∈时,()f x ax ≥,即()0f x ax -≥恒成立 令()()()2sin cos 1h x f x ax x x x a x =-=--+ 则()cos sin 1h x x x x a '=+--,()()cos h x x x g x '''== 由(1)可知,()h x '在0,2π⎛⎫⎪⎝⎭上单调递增;在,2ππ⎛⎫⎪⎝⎭上单调递减 且()0h a '=-,222h a ππ-⎛⎫'=- ⎪⎝⎭,()2h a π'=-- ()()min 2h x h a π''∴==--,()max 222h x h a ππ-⎛⎫''==- ⎪⎝⎭①当2a ≤-时,()()min 20h x h a π''==--≥,即()0h x '≥在[]0,π上恒成立()h x ∴在[]0,π上单调递增 00h xh ,即()0f x ax -≥,此时()f x ax ≥恒成立②当20a -<≤时,()00h '≥,02h π⎛⎫'>⎪⎝⎭,()0h π'< 1,2x ππ⎛⎫∴∃∈ ⎪⎝⎭,使得()10h x '=()h x ∴在[)10,x 上单调递增,在(]1,x π上单调递减又()00h =,()()2sin cos 10h a a ππππππ=--+=-≥()0h x ∴≥在[]0,π上恒成立,即()f x ax ≥恒成立③当202a π-<<时,()00h '<,2022h a ππ-⎛⎫'=->⎪⎝⎭20,2x π⎛⎫∴∃∈ ⎪⎝⎭,使得()20h x '=()h x ∴在[)20,x 上单调递减,在2,2x π⎛⎫⎪⎝⎭上单调递增()20,x x ∴∈时,()()00h x h <=,可知()f x ax ≥不恒成立④当22a π-≥时,()max 2022h x h a ππ-⎛⎫''==-≤⎪⎝⎭()h x ∴在0,2π⎛⎫⎪⎝⎭上单调递减 00h xh可知()f x ax ≥不恒成立 综上所述:(],0a ∈-∞高频考点四:利用导数证明、解不等式问题【典例7】(2019·山东高考模拟(文))已知函数35791131()135791113x x x x x x f x x =+-+-+-+,则使不等式(1)0f x ->成立的x 的最小整数为( ) A .-3 B .-2C .-1D .0【答案】D 【解析】根据题意,函数35791131()135791113x x x x x x f x x =+-+-+-+,其导数24681012()1f x x x x x x x '=-+-+-+,0x ≠时,()f x '可以看成是1为首项,2x -为公比的等比数列,则有24681012()1f x x x x x x x '=-+-+-+142101x x+=>+, 函数()f x 在R 上为增函数,又由111111(1)1(1)()()()035791113f -=+-+-+-+->, 35791113222222(2)1(2)035791113f ⎛⎫⎛⎫⎛⎫-=+-+-+-+-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则函数()f x 在(2,1)--上存在唯一的零点,设其零点为t ,(1)011f x x t x t ->⇒->⇒>+,又由21t -<<-,则110t -<+<,故不等式(1)0f x ->成立的x 的最小整数为0; 故选:D .【典例8】(2019·北京高考真题(文))已知函数321()4f x x x x =-+. (Ⅰ)求曲线()y f x =的斜率为1的切线方程; (Ⅱ)当[2,4]x ∈-时,求证:6()x f x x -≤≤;(Ⅲ)设()|()()|()F x f x x a a =-+∈R ,记()F x 在区间[2,4]-上的最大值为M (a ),当M (a )最小时,求a 的值. 【答案】(Ⅰ)0x y -=和2727640x y --=.(Ⅱ)见解析; (Ⅲ)3a =-. 【解析】 (Ⅰ)23()214f x x x '=-+,令23()2114f x x x '=-+=得0x =或者83x =. 当0x =时,(0)0f =,此时切线方程为y x =,即0x y -=;当83x =时,88()327f =,此时切线方程为6427y x =-,即2727640x y --=; 综上可得所求切线方程为0x y -=和2727640x y --=.(Ⅱ)设321()()4g x f x x x x =-=-,23()24g x x x '=-,令23()204g x x x '=-=得0x =或者83x =,所以当[2,0]x ∈-时,()0g x '≥,()g x 为增函数;当8(0,)3x ∈时,()0g x '<,()g x 为减函数;当8[,4]3x ∈时,()0g x '≥,()g x 为增函数;而(0)(4)0g g ==,所以()0g x ≤,即()f x x ≤; 同理令321()()664h x f x x x x =-+=-+,可求其最小值为(2)0h -=,所以()0h x ≥,即()6f x x ≥-,综上可得6()x f x x -≤≤.(Ⅲ)由(Ⅱ)知6()0f x x -≤-≤, 所以()M a 是,6a a +中的较大者,若6a a ≥+,即3a -≤时,()3M a a a ==-≥; 若6a a <+,即3a >-时,()663M a a a =+=+>; 所以当()M a 最小时,()3M a =,此时3π. 【规律方法】利用导数证明不等式f (x )>g (x )的基本方法(1)若f (x )与g (x )的最值易求出,可直接转化为证明f (x )min >g (x )max ;(2)若f (x )与g (x )的最值不易求出,可构造函数h (x )=f (x )-g (x ),然后根据函数h (x )的单调性或最值,证明h (x )>0. 【变式探究】1.(2018·全国高考真题(理))已知函数.(1)讨论的单调性;(2)若存在两个极值点,证明:.【答案】(1)见解析;(2)见解析 【解析】(1)的定义域为,. (i )若,则,当且仅当,时,所以在单调递减.(ii )若,令得,或.当时,;当时,.所以在单调递减,在单调递增.(2)由(1)知,存在两个极值点当且仅当.由于的两个极值点满足,所以,不妨设,则.由于,所以等价于.设函数,由(1)知,在单调递减,又,从而当时,.所以,即.2.(2019·浙江高考模拟)设函数2()ln ()f x ax x a R =-∈. (1)讨论函数()f x 的单调性;(2)若()0f x ≥恒成立,求实数a 的取值范围. 【答案】(1)见解析;(2)1[,)2e+∞ 【解析】(1)由题意,2'21()(0)ax f x x x-=>.当0a ≤时,'()0f x <,函数()f x 在(0,)+∞上单调递减;当0a >时,令()0f x '=,解得2x a=. ∴当(0,)2x a ∈时,'()0f x <,当(,)2x a ∈+∞时,'()0f x >. ∴()f x 在(0,)2a 上单调递减,在(,)2a+∞上单调递增; (2)∵()0f x ≥恒成立,∴(e)0f ≥,可得21a e≥. 由(1)可得,()f x 在(0,)2a 上单调递减,在(,)2a+∞上单调递增, ∴()f x 的最小值为1()ln()222f a a =-.∴1ln 022a -≥,解得12a e≥.因此,实数a 的取值范围为1[,)2e+∞. 高频考点五:利用导数解决生活中的最优化问题【典例9】(2020届山东省济宁市高三3月月考)如图所示,某几何体由底面半径和高均为1的圆柱与半径为1的半球对接而成,在该封闭几何体内部放入一个小圆柱体,且小圆柱体的上下底面均与外层圆柱的底面平行,则小圆柱体积的最大值为__________.【答案】3227π【解析】由题意,设小圆柱体底面半径为cos θ, 则高为1sin 0,2πθθ⎛⎫+∈ ⎪⎝⎭,, 小圆柱体体积()2cos1sin V πθθ=⋅⋅+,设()sin 0,1t t θ=∈,,则()()()232111V tt tt t ππ=⋅-+=⋅--++则()()()2321311V t t t t ππ'=⋅--+=⋅-++当13t =时,max 3227V π= 故答案为:3227π【典例10】(2020·江苏省高考真题)某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O 在水平线MN 上,桥AB 与MN 平行,OO '为铅垂线(O '在AB 上).经测量,左侧曲线AO 上任一点D 到MN 的距离1h (米)与D 到OO '的距离a (米)之间满足关系式21140h a =;右侧曲线BO 上任一点F 到MN 的距离2h (米)与F 到OO '的距离b (米)之间满足关系式3216800h b b =-+.已知点B 到OO '的距离为40米.(1)求桥AB 的长度;(2)计划在谷底两侧建造平行于OO '的桥墩CD 和EF ,且CE 为80米,其中C ,E 在AB 上(不包括端点).桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k >0).问O E '为多少米时,桥墩CD 与EF 的总造价最低?【答案】(1)120米(2)20O E '=米 【解析】 (1)由题意得2311||40640||8040800O A O A ''=-⨯+⨯∴= ||||||8040120AB O A O B ''∴=+=+=米(2)设总造价为()f x 万元,21||8016040O O '=⨯=,设||O E x '=, 32131()(1606)[160(80)],(040)800240f x k x x k x x =+-+--<<3221336()(160),()()0208008080080f x k x x f x k x x x '∴=+-∴=-=∴=(0舍去) 当020x<<时,()0f x '<;当2040x <<时,()0f x '>,因此当20x 时,()f x 取最小值, 答:当20O E '=米时,桥墩CD 与EF 的总造价最低. 【规律方法】1.常见生活最优化问题:(1)面积、体积(容积)最大,周长最短,距离最小等实际几何问题,求解时先设出恰当的变量,将待求解最值的问题表示为变量的函数,再按函数求最值的方法求解,最后检验.(2)利润最大、效率最高等实际问题,关键是弄清问题的实际背景,将实际问题用函数关系表达,再求解. (3)用料最省、费用最低问题出现的形式多与几何体有关,解题时根据题意明确哪一项指标最省(往往要从几何体的面积、体积入手),将这一指标表示为关于自变量x 的函数,利用导数或其他方法求出最值,但一定要注意自变量的取值范围. 2.利用导数解决生活中的优化问题的步骤第一步 分析实际问题中各量之间的关系,构建数学模型,写出实际问题中变量之间的函数关系式y =f (x )第二步 求函数f (x )的导数f ′(x ),解方程f ′(x )=0第三步 比较函数在区间端点和f ′(x )=0的点的函数值的大小,最大(小)者为最大(小)值 第四步回归实际问题,给出优化问题的答案3.以及等号成立的条件成立,否则易犯错误,注意f ′(x 0)=0的x 0是否在定义域内,从而进行分类讨论. 【变式探究】1.(2018·江苏高考真题)某农场有一块农田,如图所示,它的边界由圆的一段圆弧(为此圆弧的中点)和线段构成.已知圆的半径为40米,点到的距离为50米.现规划在此农田上修建两个温室大棚,大棚内的地块形状为矩形,大棚内的地块形状为,要求均在线段上,均在圆弧上.设与所成的角为.(1)用分别表示矩形和的面积,并确定的取值范围;(2)若大棚内种植甲种蔬菜,大棚内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为.求当为何值时,能使甲、乙两种蔬菜的年总产值最大.【答案】(1),;(2).【解析】解:(1)连结PO并延长交MN于H,则PH⊥MN,所以OH=10.过O作OE⊥BC于E,则OE∥MN,所以∠COE=θ,故OE=40cosθ,EC=40sinθ,则矩形ABCD的面积为2×40cosθ(40sinθ+10)=800(4sinθcosθ+cosθ),△CDP 的面积为×2×40cosθ(40–40sinθ)=1600(cosθ–sinθcosθ).过N作GN⊥MN,分别交圆弧和OE的延长线于G和K,则GK=KN=10.令∠GOK=θ0,则sinθ0=,θ0∈(0,).当θ∈[θ0,)时,才能作出满足条件的矩形ABCD,所以sinθ的取值范围是[,1).答:矩形ABCD的面积为800(4sinθcosθ+cosθ)平方米,△CDP的面积为1600(cosθ–sinθcosθ),sinθ的取值范围是[,1).(2)因为甲、乙两种蔬菜的单位面积年产值之比为4∶3,设甲的单位面积的年产值为4k,乙的单位面积的年产值为3k(k>0),则年总产值为4k×800(4sinθcosθ+cosθ)+3k×1600(cosθ–sinθcosθ)=8000k(sinθcosθ+cosθ),θ∈[θ0,).设f(θ)= sinθcosθ+cosθ,θ∈[θ0,),则.令,得θ=,当θ∈(θ0,)时,,所以f (θ)为增函数; 当θ∈(,)时,,所以f (θ)为减函数,因此,当θ=时,f (θ)取到最大值.答:当θ=时,能使甲、乙两种蔬菜的年总产值最大.2.(2020届山东省枣庄市高三上学期统考)2018年森林城市建设座谈会在深圳举行.会上宣读了国家森林城市称号批准决定,并举行授牌仪式,滕州市榜上有名,被正式批准为“国家森林城市”.为进一步推进国家森林城市建设,我市准备制定生态环境改造投资方案,该方案要求同时具备下列两个条件:①每年用于风景区改造的费用y 随每年改造生态环境总费用x 增加而增加;②每年用于风景区改造的费用y 不得低于每年改造生态环境总费用x 的15%,但不得高于每年改造生态环境总费用x 的25%.若每年改造生态环境的总费用至少1亿元,至多4亿元;请你分析能否采用函数模型()31416100y x x =++作为生态环境改造投资方案.【答案】能采用函数模型()31416100y x x =++作为生态环境改造投资方案,理由见解析 【解析】∵()21340100y x '=+>,[]1,4x ∈. ∴当[]1,4x ∈时,函数()31416100y x x =++是增函数,满足条件①. 设()21164100y g x x x x ⎛⎫==++ ⎪⎝⎭,[]1,4x ∈. 则()3221168210050x g x x x x-⎛⎫'=-= ⎪⎝⎭.令()0g x '=,得2x =.当x 变化时,()g x ',()g x 的变化情况,如下表:当2x =时,()g x 有最小值为16%15%>, 当4x =时,()24%25%g x =<,当1x =时,()21%25%g x =<,满足条件②. 所以能采用函数模型()31416100y x x =++作为生态环境改造投资方案.。
人教版高二《导数的应用》数学教案

人教版高二《导数的应用》数学教案【小编寄语】查字典数学网小编给大家整理了人教版高二«导数的运用»数学教案,希望能给大家带来协助!第三章导数运用3.1 函数的单调性与极值3.1.1 导数与函数的单调性学习目的:1、了解导数正、负与函数单调性之间的关系;2、能应用导函数确定函数的单调区间重点、难点:应用导函数求单调性自主学习(1) 对恣意,有,那么在区间内(2) 对恣意,有,那么在区间内协作探求资源网例1、确定函数在哪个区间上是增函数,哪个区间上是减函数?例2、确定函数在哪些区间上是增函数。
例3、确定函数的单调区间。
例4、证明:当时,有。
练习反应1、确定以下函数的单调区间(1) (2)2、讨论函数的单调性:(1)(2)(3)3、用导数证明:(1) 在区间上是增函数;3.1.2 函数的极值学习目的:1、掌握函数极值点的定义与求解步骤;2、体会导数方法在研讨函数性质中的普通性与有效性。
重点、难点:应用导数求极大、极小值自主学习1、极大值2、极小值3、极值与导数之间的关系:(1)极大值与导数的关系:左侧右侧增加(2)极小值与导数的关系:左侧增加极小值添加例1、求函数的极值。
例2、求函数的极值。
练习反应1、求以下函数的极值:2、设函数有极小值、极大值,一定小于吗?试作图说明。
3、作出契合以下条件的函数图像(1) 时,时, ;3.2 导数在实践效果中的运用3.2.1 实践效果中导数的意义学习目的:1、掌握解运用题的思绪与方法,能剖析出变量间的关系,树立起函数模型,确定自变量的定义域。
2、能用导数的知识对实践效果求解。
重点、难点:1、树立起函数模型,确定自变量的定义域。
2、用导数的知识对实践效果求解自主学习解运用题的思绪与方法:1、审题:了解题意,剖析效果的主要关系2、建模:3、求解:求得数学效果的解4、反应:例1、在边长为60厘米的正方形铁皮的四角切去边长相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底铁皮箱,箱底边长为多少时,箱子容积最大?最大容积是多少?例2、某种圆柱形的饮料罐的容积一定时,如何确定它的高与底半径,使得所用资料最省?例3、在平面直角坐标系内,过点(1,4)引不时线,使它与两坐标轴上的截距都为正,且两截距之和最小,求这条直线的方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中等已测:2438次正确率:74.8 %1.若是函数的极值点,则的极⼩值为( )A.B.C.D.考点:函数在某点取得极值的条件知识点:函数的极⼤值、极⼩值、函数极值与导数的关系答案:A解析:由题可得因为,所以,,故令,解得或,所以在上单调递增,在上单调递增,在单调递减所以极⼩值,故选.中等已测:2754次正确率:70.2 %2.函数的图象如图所⽰,则下列结论成⽴的是( )A.B.C.D.考点:利⽤导数研究函数的单调性、利⽤导数判断含参函数的单调性知识点:函数图象与导函数图象之间的关系、函数单调性和导数的关系答案:A解析:函数的图象在轴上的截距为正值,.,且函数在上单调递增,上单调递减,上单调递增,的解集为,,⼜均为正数,,,x =−2f (x )=(x +ax −1)e 2x −1f (x )−1−2e −35e −31f (x )=(2x +a )e +(x +ax −1)e =[x +(a +2)x +a −1]e ′x −12x −12x −1f (−2)=0′a =−1f (x )=(x −x −1)e 2x −1f (x )=(x +x −2)e ′2x −1f (x )>0′x <−2x >1f (x )(−∞,−2)(1,+∞)(−2,1)f (x )=f (1)=(1−1−1)e =−11−1A f (x )=ax +bx +cx +d 32a >0,b <0,c >0,d >0a >0,b <0,c <0,d >0a <0,b <0,c >0,d >0a >0,b >0,c >0,d <0∵f (x )y ∴d >0∵f (x )=3ax +2bx +c ′2f (x )=ax +bx +cx +d 32(−∞,x )1(x ,x )12(x ,+∞)2∴f (x )<0′(x ,x )12∴a >0x ,x 12∴ >03a c − >03a 2b可得.较难已测:1807次正确率:39.2 %3.已知函数有两个极值点,.若,则关于的⽅程的不同实根个数为( )A.B.C.D.考点:函数在某点取得极值的条件、利⽤导数研究函数的极值知识点:三次函数的极值与零点的关系答案:A 解析:,根据已知,得有两个不同的实根,,且,根据三次函数的性质可得是函数的极⼤值点,⽅程必然有或.由于且,如图,可知⽅程有两个实根,有⼀个实根,故⽅程共有个不同实根.⼀般已测:4239次正确率:69.7 %4.设函数,其中,存在使得成⽴,则实数的最⼩值为( )A.B.C.D.考点:利⽤导数研究曲线上某点的切线⽅程、利⽤分离变量求最值解决不等式存在性问题知识点:函数在某点处的切线、点到直线的距离答案:C解析:函数可以看作动点与点的距离的平⽅,点在曲线上,点在直线上,问题转化为直线上的点到曲线上的点的距离的最⼩值,由求导可得,令,解得,此时,则,c >0,b <0f (x )=x +ax +bx +c 32x 1x 2f (x )=x <x 112x 3(f (x ))+2af (x )+b =023456f (x )=3x +2ax +b ′23x +2ax +b =02x 1x 2x <x 12x 1f (x )3(f (x ))+2af (x )+b =02f (x )=x 1f (x )=x 2f (x )=x 1x <x 12f (x )=x 23(f (x ))+2af (x )+b =023f (x )=(x −a )+(lnx −2a )222x >0,a ∈R x 0f (x )≤b 0b 51 52 541f (x )P (x ,lnx )2Q (a ,2a )P y=2lnx Q y =2x y =2lnx y = ′x 2y =2′x =1y =2ln 1=0M (1,0)所以点到直线的距离,即为直线与曲线之间最⼩的距离,故。
由于存在使得,则,即,故选:.中等已测:3612次正确率:57.1 %5.如图所⽰的是函数的⼤致图象,则等于( )A.B.C.D.考点:求函数的零点、函数零点与⽅程根的关系知识点:函数的零点、函数零点具有的性质答案:C解析:由图象知的根为,..的两个根为和....为的两根,..中等已测:3430次正确率:72.3 %6.设函数(,为⾃然对数的底数).若曲线上存在点使得,则的取值范围是( )A.B.C.D.考点:利⽤导数研究函数的单调性知识点:函数单调性和导数的关系M (1,0)y=2x d == 2+(−1)22252 5f (x ) =d = min 254x 0f (x )≤b 0f (x ) ≤b min b ≥ 54C f (x )=x +bx +cx +d 32x +x 1222 3234 38 316f (x )=00,1,2∴d =0∴f (x )=x +bx +cx =x (x +bx +c )=0322∴x +bx +c =0212∴b =−3,c =2∴f (x )=x −3x +2x 32∴f (x )=3x −6x +2′2∵x ,x 123x −6x +2=02∴x +x =2,x x = 121232∴x +x =(x +x )−2x x =2−2× = 12221221223238f (x )=e +x −a x a ∈R e y =sinx (x ,y )00f (f (y ))=y 00a [1,e ][e −1,1]−1[1,e +1][e −1,e +1]−1答案:A 解析:因为,⽽,,所以,因为为单调增函数令则若,那么即,⽭盾同理,⽭盾,所以,①.所以在上有解,令,所以,设,则,所以当时,,当时,,所以.所以在上单调递增.所以原题中的⽅程有解必须⽅程①有解.所以.故选.中等已测:368次正确率:61.6 %7.若存在,使得不等式成⽴,则实数的取值范围是( )A.B.C.D.考点:利⽤导数研究函数的单调性、导数在最⼤值、最⼩值问题中的应⽤知识点:利⽤导数求函数的最值、利⽤最值解不等式恒成⽴问题答案:B 解析:在上有解,在上有解,令,,则.则,当时,,当时,,在上单调递减,在上单调递增,当时,取得最⼩值.y =sinx ∈[−1,1]00f (x )≥0f (f (y ))=y 00y ∈[0,1]0f (x )f (y )=t ,0f (t )=y0y >t 0f (t )=y ,0t >y 0y <t 0y =t0故 =x e +x −a x x ∈[0,1]e +x −x =a x 2x ∈[0,1]g (x )=e +x −x x 2g (x )=e +1−2x ′x h (x )=e +1−2x x h (x )=e −2′x x ∈(0,ln 2)h (x )<0′x∈(ln 2,1)h (x )>0′g (x )≥g (ln 2)=3−2ln 2>0′′g (x )[0,1]g (0)≤a ≤g (1)A x ∈(−1,1]e −ax <a 2x a (−∞, )e 2( ,+∞)e 2(−∞, )e 1( ,+∞)e1∵e −ax <a 2x(−1,1]∴a > x +1e 2x (−1,1]f (x )= x +1e 2xx ∈(−1,1]a >f (x )min f (x )= ′(x +1)2e (2x +1)2x ∴x ∈(−1,− )21f (x )<0′x ∈(− ,1]21f (x )>0′∴f (x )(−1,− ]21(− ,1]21∴x =− 21f (x )f (− )= 21e 2.故选:.⼀般已测:4365次正确率:93.7 %8.如果函数在区间上单调递减,那么的最⼤值为( )A.B.C.D.考点:已知单调区间求参数的取值范围、根据平⾯区域写出相应的不等式(组)知识点:函数单调性和导数的关系、线性规划问题的有关概念答案:B 解析:由已知得,⼜对任意的,所以 ,即.画出该不等式组表⽰的平⾯区域如图中阴影部分所⽰,令,则当时,,当时,.由线性规划的相关知识知,只有当直线与曲线相切时,取得最⼤值.由,解得,所以.较难已测:552次正确率:49.2 %9.设,其中均为实数.下列条件中,使得该三次⽅程仅有⼀个实根的是.(写出所有正确条件的编号)①;②;③;④;⑤.考点:转化为两个图象交点来处理函数零点问题、利⽤导数研究函数零点问题知识点:函数的零点、三次函数的极值与零点的关系答案:①③④⑤解析:令,则.对于①,由,得,,,,函数的图象与轴只有⼀个交点,∴a > e 2B f (x )= (m −2)x +(n −8)x +1(m ≥0,n ≥0)212[ ,2]21mn 161825281f (x )=(m −2)x +n −8′x ∈[ ,2],f (x )≤021′ {f ( )≤0′21f (2)≤0′ ⎩⎨⎧m ≥0,n ≥0m +2n ≤182m +n ≤12mn =t n =0t =0n ≠0m =n t 2m +n =12m =n t t {− =− n 2t 216− n = 21nt n =6,t =18(mn ) =18max x +ax +b=03a ,b a=−3,b =−3a =−3,b =2a =−3,b >2a =0,b =2a =1,b =2f (x )=x +ax +b 3f (x )=3x +a ′2a =b =−3f (x )=x −3x −33f (x )=3(x +1)(x −1)′f (x ) =f (−1)=−1<0极大值f (x ) =f (1)=−5<0极小值f (x )x故仅有⼀个实根;对于②,由,得,,,,函数的图象与轴有两个交点,故有两个实根;对于③,由,得,,,,函数的图象与轴只有⼀个交点,故仅有⼀个实根;对于④,由,得,,在上单调递增,函数的图象与轴只有⼀个交点,故仅有⼀个实根;对于⑤,由,得,,在上单调递增,函数的图象与轴只有⼀个交点,故仅有⼀个实根.⼀般已测:964次正确率:85.1 %10. 设,,若时恒有,则.考点:函数在某点取得极值的条件知识点:函数极值与导数的关系答案:解析:当时,,则,,令,则在时恒成⽴,,则应为极⼩值点,,故,,,.中等已测:4162次正确率:72.9 %11.若函数有零点,则的取值范围为.考点:利⽤导数研究函数的单调性、利⽤分离变量求最值解决不等式存在性问题知识点:利⽤导数求函数单调区间、利⽤导数求函数的最值答案:或解析:当时,可得,故不是函数的零点;x +ax +b =03a =−3,b =2f (x )=x −3x +23f (x )=3(x +1)(x −1)′f (x ) =f (−1)=4>0极大值f (x ) =f (1)=0极小值f (x )x x +ax +b =03a=−3,b >2f (x )=x −3x +b 3f (x )=3(x +1)(x −1)′f (x ) =f (−1)=2+b >0极大值f (x ) =f (1)=b −2>0极小值f (x )x x +ax +b =03a=0,b =2f (x )=x +23f (x )=3x ≥0′2f (x )R f (x )x x +ax +b =03a =1,b =2f (x )=x +x +23f (x )=3x +1>0′2f (x )R f (x )x x +ax +b=03a b ∈R x ≥00≤x −x +ax +b ≤(x −1)4322ab =−1x=10≤a +b ≤0a +b =0b =−a f (x )=(x −1)−(x −x +ax −a )=x −2x −ax +a +1224332f (x )≥0x ≥0f (1)=1−2−a +a +1=0x =1f (x )=3x −4x −a ′2f (1)=0′a =−1b =1ab =−1f (x )=kx −e x k k ≥e k <0x=0f (0)=−1x =0当时,由函数有零点可得有解,即,故的取值范围为函数的值域,,令可得,故函数在上单调递减,上单调递减,上单调递增,故当时,函数值,当时,为函数的最⼩值,且,故,综上可得的取值范围为或,故的取值范围为:或.故答案为:或.⼀般已测:1575次正确率:82.6 %12.某商场从⽣产⼚家以每件元购进⼀批商品,若该商品零售价定为元,则销售量(单位:件)与零售价(单位:元)有如下关系:.则该商品零售价定位元时⽑利润最⼤(⽑利润销售收⼊进货⽀出).考点:利⽤导数解决实际⽣活中的问题、求商品的最⼤利润知识点:利⽤导数求函数的最值、⽣活中优化问题答案:解析:由题意知:⽑利润等于销售额减去成本,即,所以.令,解得或(舍去).此时,.因为在附近的左侧,右侧.所以是极⼤值,根据实际问题的意义知,是最⼤值,故答案为:.中等已测:2671次正确率:67.1 %13.已知函数,其中为⾃然对数的底数,若存在实数使成⽴,则实数的值为.考点:利⽤导数求闭区间上函数的最值、利⽤导数解决存在性问题知识点:利⽤导数求函数的最值、基本不等式与最⼤(⼩)值答案:解析:令可得:,令,,则,令可得,即或(舍),当时,,当时,,在上单调递减,在上单调递增,,x ≠0f (x )=kx −e x kx =e x k = x e x k g (x )= ,(x ≠0)x e x∵y = =′x 2e ⋅x −e x x x 2e (x −1)x y <0′x <1g (x )(−∞,0)(0,1)(1,+∞)x <0g (x )<0x >0g (1)g (1)=e g (x )≥e g (x )g (x )<0g (x )≥e k k <0k ≥e k ≥e k <020p Q p Q =8300−170p −p 2=−30L (p )=pQ −20Q =Q (p −20)=(8300−170p −p )(p −20)=−p −150p +11700p −166000232L (p )=−3p −300p +11700′2L (p )=0′p =30p =−130L (30)=23000p=30L (p )>0′L (p )<0′L (30)L (30)30f (x )=2x −3x −lnx +e +4e 2x −a a −x e x 0f (x )=30a 1−ln 2f (x )=32x −3x −lnx −3=−e −4e 2x −a a −x g (x )=2x −3x −lnx −32h (x )=−e −4e x −a a −x g (x )=4x −3− = ′x 1x4x −3x −12g (x )=0′4x −3x −1=02x =1x =− 41∴0<x <1g (x )<0′x >1g (x )>0′∴g (x )(0,1)(1,+∞)∴g (x )≥g (1)=−4h (x )=−e −4e =−(e +4e )≤−2 =−4x −a a −x x −a a −x e ⋅4e x −a a −x(1)(2)(1)(2)(当且仅当即时取等号),,即,,.中等已测:4092次正确率:57.7 %14.已知函数.求曲线在点处的切线⽅程;求函数在区间上的最⼤值和最⼩值.考点:利⽤导数研究曲线上某点的切线⽅程、求导公式、求导法则的综合应⽤知识点:函数在某点处的切线、导数的运算法则(1)答案:解析:因为,所以,.⼜因为,所以曲线在点处的切线⽅程为.(2)答案:最⼤值,最⼩值.解析:设,则.当时,,所以在区间上单调递减.所以对任意有,即.所以函数在区间上单调递减.因此在区间上的最⼤值为,最⼩值为.中等已测:2454次正确率:78.8 %15.某村庄拟修建⼀个⽆盖的圆柱形蓄⽔池(不计厚度).设该蓄⽔池的底⾯半径为⽶,⾼为⽶,体积为⽴⽅⽶.假设建造成本仅与表⾯积有关,侧⾯积的建造成本为元/平⽅⽶,底⾯的建造成本为元/平⽅⽶,该蓄⽔池的总建造成本为元(为圆周率).将表⽰成的函数,并求该函数的定义域;讨论函数的单调性,并确定和为何值时该蓄⽔池的体积最⼤.考点:⼆次函数模型的应⽤、利⽤导数求闭区间上函数的最值知识点:常⻅的函数模型、利⽤导数求函数的最值(1)答案:解析:因为蓄⽔池的侧⾯积的建造成本为元,底⾯积成本为元,所以蓄⽔池的总建造成本为元.⼜据题意,所以,从⽽.因,⼜由可得,故函数的定义域为.(2)答案:,解析:因,故.令,解得,(因不在定义域内,舍去) .当时,,故在上为增函数;当时,,故在e =4e x −a a −x x =a +ln 2∵f (x )=30g (x )=h (x )00∴x =1=a +ln 20∴a =1−ln 2f x =e cos x −x ()x y =f x ()0,f 0(())f x ()0, [2π]y=1fx =e cos x −x ()x f x =e cos x −sin x −1′()x ()f 0=0′()f0=1()y =f x ()0,f 0(())y =11− 2πh x =e cos x −sin x −1()x ()h x =e cos x −sin x −sin x −cos x =−2e sin x ′()x ()x x∈0, (2π)h x <0′()h x ()0, [2π]x ∈0, [2π]h x <h 0=0()()f x <0′()f x ()0, [2π]f x ()0, [2π]f 0=1()f=− (2π)2πr h V 10016012000ππV r V (r )V (r )r h (0,5)3100⋅2πrh=200πrh 160πr 2(200πrh +160πr )2200πrh +160πr =12000π2h = (300−4r )5r 12V (r )=πr h = (300r −4r )25π3r >0h >00<r <5 3V (r )(0,5 )3r=5h =8V (r )= (300r −4r )5π3V (r )= (300−12r )′5π2V (r )=0′r =51r =−52r ∈(0,5)V (r )>0′V (r )(0,5)r ∈(5,5)3V (r )<0′V (r )(1)(2)(3)(1)(2)(3)上为减函数.由此可知,在处取得最⼤值,此时.即当,时,该蓄⽔池的体积最⼤.较难已测:4533次正确率:62.6 %16.已知函数求的单调区间;设曲线与轴正半轴的交点为,曲线在点处的切线⽅程为.求证:对于任意的实数,都有若⽅程(为实数)有两个实数根,且,求证:考点:利⽤导数研究曲线上某点的切线⽅程、利⽤导数研究函数的单调性知识点:函数在某点处的切线、函数单调性和导数的关系(1)答案:的单调递增区间为,单调递减区间为解析:由,可得.当,即时,函数单调递增;当,即时,函数单调递减.所以,的单调递增区间为,单调递减区间为.(2)答案:⻅解析解析:设点的坐标为,则,.曲线在点处的切线⽅程为即.令函数,即,则.由于在上单调递减,故在上单调递减.⼜因为,所以当时,,当时,,所以在上单调递增,在上单调递减,所以对于任意的实数,即对于任意的实数,都有(3)答案:⻅解析解析:由(2)知.设⽅程的根为,可得因为在上单调递减,⼜由(2)知,因此.类似地,设曲线在原点处的切线⽅程为,可得.对于任意的,有,即.设⽅程的根为,可得.因为在上单调递增,且,因此.由此可得较难已测:2126次正确率:36.9 %17.设,函数.求的单调区间证明:在上仅有⼀个零点;若曲线在点处的切线与x 轴平⾏,且在点处的切线与直线平⾏(是坐标原点),证明:.(5,5 )3V (r )r =5h =8r=5h =8f (x )=4x −x ,x ∈R .4f (x )y=f (x )x P P y =g (x )x f (x )≤g (x )f (x )=a a x ,x 12x <x 12x −x ≤−+4213a 31f (x )(−∞,1)(1,+∞)f (x )=4x −x 4f (x )=4−4x ′3f (x )>0′x <1f (x )f (x )<0′x >1f (x )f (x )(−∞,1)(1,+∞)P x ,0(0)x =4031f x =−12′(0)y =f (x )P y =f x x −x ,′(0)(0)g x =f x x −x ()′(0)(0)F (x )=f (x )−g (x )F x =f x −f x x −x ()()′(0)(0)F (x )=f (x )−f (x )′′′0f x =−4x +4′()3(−∞,+∞)F (x )′(−∞,+∞)F (x )=0′0x ∈(−∞,x )0F (x )>0′0x ∈(x ,+∞)0F (x )<0′0F (x )(−∞,x )0(x ,+∞)0x ,F (x )≤F x =0(0)x f (x )≤g (x )g (x )=−12(x −4) 31g (x )=a x 2′x = +42′12a 31g (x )(−∞,+∞)g x ≥f x =a =g x (2)(2)(2′)x ≤x 22′y=f (x )y =h (x )h (x )=4x x ∈(−∞,+∞)f (x )−h (x )=−x ≤04f (x )≤h (x )h (x )=a x 1′x =1′4a h (x )=4x (−∞,+∞)h (x )=a =f x ≤h (x )1′(1)1x ≤x 1′1x −x ≤x −x =− +4212′1′3a 31a >1f (x )=(1+x )e −a 2x f (x )f (x )(−∞,+∞)y=f (x )P M (m ,n )OP O m ≤−13a −e 2(1)(2)考点:利⽤导数研究曲线上某点的切线⽅程、利⽤导数研究函数零点问题知识点:函数零点存在性定理、函数在某点处的切线(1)答案:单调增区间是⽆单调减区间.解析:,故是上的单调递增函数,其单调增区间是⽆单调减区间.(2)答案:⻅解析.解析:因为,且,由零点存在性定理知,在上⾄少有⼀个零点.⼜由知,函数是上的单调递增函数,故函数在上仅有⼀个零点.(3)答案:⻅解析.解析:设点,由曲线在点处的切线与轴平⾏知,,即,即.由点处的切线与直线平⾏知,,即.由知,,即,即.较难已测:1959次正确率:63.1 %18.设函数.证明:在单调递减,在单调递增;若对于任意,都有,求的取值范围.考点:利⽤导数研究函数的单调性、转化思想在证明不等式中的应⽤知识点:利⽤导数求函数单调区间、利⽤导数求函数的最值(1)答案:证明⻅解析解析:.若,则当时,;当时,.若,则当时,,;当时,,.所以在单调递减,在单调递增.(2)答案:的取值范围是解析:由(1)知,对任意的在单调递减,在单调递增,故在处取得最⼩值.所以对于任意,的充要条件是:即①设函数,则。
