matlab如何绘制二维正态曲面
Matlab中二维图的绘制

Matlab中二维图的绘制
(1)准备图形数据
(2)选择图形的显示位置
(3)调用绘图指令并设置参数
(4)选择线性和标记属性
(5)设置坐标范围及网格线
(6)给图形加注释
(7)图形输出
网格图形是指连接相邻数据点形成的网状曲面,数据点是x-y平面的矩形网格上点的z轴坐标值。
网格图的绘制步骤如下:
(1)在x-y平面上指定一个矩形区域,采用与坐标轴平行的直线进行分格;
(2)计算矩形网格点的z轴坐标值,得到三维空间的数据点;(3)利用以上得到的数据点,将x-z平面或者y-z平面内,以及平行平面内的数据点连接,形成网格图。
数学2-用MATLAB绘制二维-三维图形(lq)

[i,j,v]=find(A) 返回矩阵A中非零元素所在的行i,
列j,和元素的值v(按所在位置先后 顺序输出)
A=[3 2 0; -5 0 7; 0 0 1]; [i,j,v]=find(A)
i= 1 2 1 2 3 j= 1 1 2 3 3 v = 3 -5 2 7 1
[X,Y]=meshgrid(x,y) 3)根据函数表达式生成全部网格节点出对应的函数值矩阵z: z=f(X,Y) 4)顺序连接已经产生的空间点(x,y,z)绘制相应曲面: mesh(X,Y,Z) surf(X,Y,Z) shading flat %去除网格线。
例2-7画出矩形域[-1,1]×[-1,1]旋转抛物面:z=x2+y2. x=linspace(-1,1,100); y=x; [X,Y]=meshgrid(x,y); %生成矩形区[-1,1]×[-1,1]的网格坐标矩阵 Z=X.^2+Y.^2; subplot(1,2,1) mesh(X,Y,Z); subplot(1,2,2) surf(X,Y,Z); shading flat; %对曲面z=x2现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
用matlab绘制二维、三维图形
2.1二维图形的绘制
2.1.1 二维绘图的基本命令 matlab中,最常用的二维绘图命令是plot。
使用该命令,软件将开辟一个图形窗口,并 画出连接坐标面上一系列点的连线。
例2-5 采用不同形式(直角坐标、参数、极坐标),画出 单位圆x2+y2=1的图形。
分析:对于直角坐标系方程,y= 1 x2,对于参数方 程x=cost,y=sint,t[0,2 pi] ,利用plot(x,y)命令可以实现。 而在极坐标系中单位圆为r=1(1+0t),利用polar(t,r)命 令实现。
MATLAB图形绘制-二维

MATLAB提供了一些绘图选项,用于确定所绘曲线的线型、 颜色和数据点标记符号。 例如,“b-.”表示蓝色点画线,“y:d”表示黄色虚线并用菱 形符标记数据点。当选项省略时,MATLAB规定,线型一 律用实线,颜色将根据曲线的先后顺序依次采用表3.2给 出的前7种颜色。
表 3.1 线型选项 选 项 : --. 线 型 实线(默认值) 虚线 双画线 点画线
二维统计分析图 MATLAB中提供了多个函数可绘制各种条形图,bar函数 绘制柱形图,barh函数绘制水平条形图,stem函数绘制杆 图,errorbar函数绘制误差条图。 下面以bar函数为例说明用法。 bar函数的调用格式为 bar(x,width,style) 当x是m × n阶的矩阵时,绘制的条形图以分组或堆积的 形式表现。矩阵中每一行元素绘制在一组中,每一列元素 绘制在每组中相对应的位置上。其中,width设置条形的 相对宽度和控制在一组内条形的间距,默认值为0.8, style指定条形的排列模式,类型有'group'(分组)和 'stack'(堆积),默认时采用&#图命令每执行一次就刷新当前图形窗口,原有图形 将不复存在。若希望在已存在的图形上再叠加新的图形, 可使用图形保持hold on/off命令控制是保持原有图形还是 刷新原有图形。 例如: x=0:pi/100:2*pi; y1=0.2*exp(-0.5*x).*cos(4*pi*x); plot(x,y1) hold on y2=1.5*exp(-0.5*x).*cos(pi*x); plot(x,y2); hold off
表 3.2 选 项 b( blue ) g( green ) r (red) c(cyan ) 颜色选项 颜 蓝色 绿色 红色 青色 色 选 项 颜 色 m (magenta) y (yellow) k (black ) w( white) 品红色 黄色 黑色 白色
第三讲 matlab二维绘图
>> pie(x,[0,0,0,1])
练习: 练习
1.在[-2,2]内,绘制幂函数 在 内 y=xa 的图象: 的图象: (1)当a=1/2,a=1/3,a=1,a=2,a=3; 当 (2)把上面函数图象绘制在一个图形窗口中 把上面函数图象绘制在一个图形窗口中 2.在[-1,1]内,绘制指数函数 在 内 y=ax 的图象: 的图象:
(1)当a=1/2,a=2,a=1/10,a=10; 当 (2)把上面函数图象绘制在一个图形窗口中 把上面函数图象绘制在一个图形窗口中
练习: 练习
3.在[-1,1]内,绘制指数函数 y=ax 的图象: 在 内 的图象: (1)当a=1/2,a=2,a=1/10,a=10; 当 (2)把上面函数图象绘制在一个图形窗口中 把上面函数图象绘制在一个图形窗口中 4.在[-1,1]内,绘制幂函数 在 内 y=xa 的图象: 的图象:
线型 X,Y是向量,分别表示点集的横坐标和纵坐标
•y •m •c -. + . 点 黄色 o 圈 洋红 x 蓝绿色 r 长短线 -加号 - 连线 : 短虚线 x-符号 符号 红色 长虚线
plot(X,Y)--画实线 plot(X,Y1,S1,X,Y2,S2,……,X,Yn,Sn) --将多条线画在一起
>> x=0:0.1:2*pi; >> y1=sin(x); >> y2=cos(x); >> plot(x,y1) >> x=0:0.1:2*pi; >> y1=sin(x); >> y2=cos(x); >> plot(x,y1,x,y2)
>> x=0:0.1:2*pi; >> y1=sin(x); >> y2=cos(x); >> plot(x,y2)
利用MATLAB 绘制二维图形

利用MATLAB 绘制二维图形
1. 显函数的图形绘制
MATLAB 中二维显函数的调用格式为: (1)plot (x,y,s) x为自变量,y为函数,两者均为同长度的向量,分别表示点的横坐标 和纵坐标. (2)plot (x1,y1,s1,x2,y2,s2 , ,xn,yn,sn) s1,s2 , ,sn是颜色、标记点和线型参数, 可叠加使用. 若不设置参数s ,则默认画实线.常用参数见表8-5所示 .
例2
解
x linspace0 ,2 pi ,50; %设置自变量的范围 y1 sin x; y2 cos x;
plot(x ,y1,k ,x,y2 ,m ) %取不同参数画两条曲线 运行结果如图8-5所示 .
图8-5
利用MATLAB 绘制二维图形
2. 隐函数的图形绘制
MATLAB中二维隐函数的调用格式为 : (1)ezplot(fun,[a ,b]) fun为隐函数表达式,需用单引号界定 . [a ,b]用来指定自变
利用MATLAB 绘制二维图形
表8-5
利用MATLAB 绘制二维图形
例1
解
x 2 :0 . 01:2 ; %定义数组变量x ,从 2开始到2为止 ,步长 0.01 y x.2 1; %计算对应的函数值 plot (x ,y) 运行结果如图8-4所示 .
图8-4
利用MATLAB 绘制二维图形
量的取值范围,默认范围为2π ,2π .
(2)ezplot(funx ,funy,[a ,b])funx ,funy是用单引号界定的x(t)和y(t)的表达
式 ,[a ,b]为参数的取值范围,默认范围为0 ,2π .
利用MATLAB 绘制二维图形
例3
Matlab绘制曲面

Matlab绘制曲⾯本⽂整理了⼀些三维绘图的内容,代码都⽐较简单1、surf、surfc、surfl之后可以试试shading interp2、绘制隐函数3、参数⽅程绘制曲⾯4、三维到平⾯:等⾼线+引⼒线5、快速绘制球⾯(椭球⾯)6、绘制旋转⾯7、绕轴旋转8、分段曲⾯1、surf、surfc、surfl之后可以试试shading interp>> [X Y]=meshgrid(linspace(-2,2),linspace(-2,2));>> Z=exp(-X.^2-Y.^2);>> subplot(2,1,1);surf(X,Y,Z);subplot(2,1,2);surf(X,Y,Z);shading interp2、绘制隐函数⼆维使⽤ezplot,三维使⽤ezimplot3(需安装)>> f1='x^2+(y-(x^2)^(1/3))^2-1';f2='x*sin(y+z^2)+y^2*cos(x+z)+z*x*cos(z+y^2)';>> subplot(1,2,1);ezplot(f1,[-1,1,-1,1.6]);subplot(1,2,2);ezimplot3(f2,[-1,1])3、参数⽅程绘制曲⾯莫⽐乌斯环,其中u、v是参数>> syms u v;>> x=cos(u)+v*cos(u)*cos(u/2);>> y=sin(u)+v*sin(u)*cos(u/2);>> z=v*sin(u/2);>> ezsurf(x,y,z,[0,2*pi,-0.5,0.5])4、三维到平⾯:等⾼线+引⼒线>> syms x y;z(x,y)=(x^2-2*x)*exp(-x^2-y^2-x*y);>> zx=diff(z,x);zy=diff(z,y);>> [X,Y]=meshgrid(-3:.1:2,-2:.1:2);Z=double(z(X,Y));>> ZX=double(zx(X,Y));ZY=double(zy(X,Y));>> subplot(1,2,1);surf(X,Y,Z);shading interp;zlim([-0.7 1.5]);>> subplot(1,2,2);contour(X,Y,Z,30);>> hold on;quiver(X,Y,-ZX,-ZY)5、快速绘制球⾯(椭球⾯)[x y z]=sphere(50);surf(x,y,z);%单位球⾯,50多⾯形数量(越多图越精确)%修改x、y、z可以作出任意位置的球、椭球%当然前⾯的隐函数也可以绘制6、绘制旋转⾯⽣成柱⾯的⽅程r1(z)=1,0<z<1r2(z)=e−z22sin z,−1<z<3r(z) 表⽰到曲⾯上z坐标的点到z轴的距离>> subplot(1,2,1);[x,y,z]=cylinder(1);surf(x,y,z) >> subplot(1,2,2);>> z0=-1:0.1:3;r=exp(-z0.^2/2).*sin(z0);>> [x,y,z]=cylinder(r);>> z=-1+4*z;surf(x,y,z);7、绕轴旋转以六中的图2为例>> z0=-1:0.1:3;r=exp(-z0.^2/2).*sin(z0);>> [x,y,z]=cylinder(r);z=-1+4*z;h=surf(x,y,z);>> r_ax=[0 0 1] %该点与坐标原点的连线为旋转轴>> axis tight; %保证尺度不变>> for i=0:360rotate(h,r_ax,1);pause(0.02),end%循环结构每0.02s转动1°,循环360次8、分段曲⾯p(x1,x2)={0.5457e−0.75x22−3.75x21−1.5x1,x1+x2>10.7575e−x22−6x21,−1<x1+x2⩽>> [x y]=meshgrid(-1:.04:1,-2:.04:2);>> z=0.5457*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1)+...0.7575*exp(-y.^2-6*x.^2)&((x+y>-1)&(x+y)<=1)+...0.5457*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<-1);>> surf(x,y,z);shading flat;Loading [MathJax]/jax/element/mml/optable/SuppMathOperators.js。
MATLAB二维三维曲面拟合程序
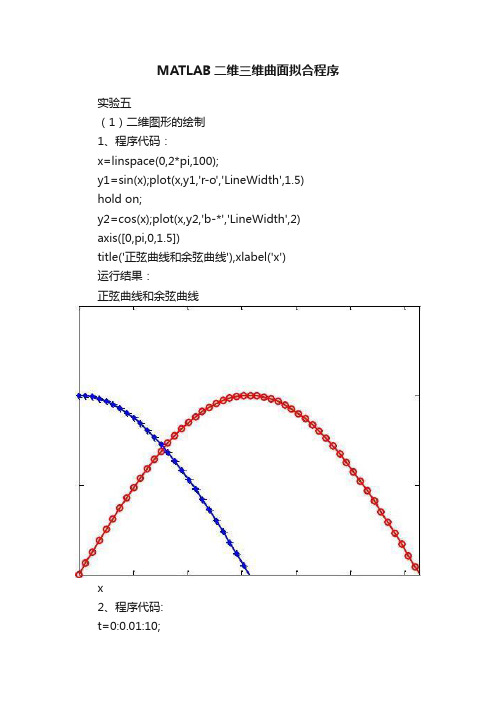
实验五
(1)二维图形的绘制
1、程序代码:
x=linspace(0,2*pi,100);
y1=sin(x);plot(x,y1,'r-o','LineWidth',1.5)
hold on;
y2=cos(x);plot(x,y2,'b-*','LineWidth',2)
axis([0,pi,0,1.5])
y=(t.^2)+1;
subplot(2,2,3),stairs(t,y)
t=0:pi/75:2*pi;
y=abs(cos(2*t));
subplot(2,2,4),polar(t,y)
(2)三维曲线和三维曲面的绘制
1、程序代码:
z=0:0.1:6*pi;x=cos(z);y=sin(z);plot3(x,y,z); view(90,90); view(90,0); view(0,0) 运行结果:
matlab二维三维曲面拟合程序 实验五 (1)二维图形的绘制 1,程序代码: x=linspace(0,2*pi,100); y1=sin(x);plot(x,y1,'r-o','linewidth',1.5) hold on; y2=cos(x);plot(x,y2,'b-*','linewidth',2) axis([0,pi,0,1.5]) title('正弦曲线和余弦曲线'),xlabel('x') 运行结果: 正弦曲线和余弦曲线 x 2,程序代码: t=0:0.01:10; y=exp(-t); subplot(2,2,1),bar(t,y) t=0:pi/20:2*pi; y=sin(t); subplot(2,2,2),stem(t,y) t=0:0.01:10; y=(t.^2)+1; subplot(2,2,3),stairs(t,y) t=0:pi/75:2*pi; y=abs(cos(2*t)); subplot(2,2,4),polar(t,y) (2)三维曲线和三维曲面的绘制 1,程序代码: z=0:0.1:6*pi;x=cos(z);y=sin(z);plot3(x,y,z); view(90,90); view(90,0); view(0,0)运行结果: -50 5 10 15 00.20.40.6 0.8 1 5 10 50 100 150 -1 1 左视图: 前视图: -1-0.8-0.6-0.4-0.2 00.20.40.60.81-1 -0.8 -0.6 -0.4 -0.2 0.2 0.4 0.6 0.8 1 02468101214161820 02468101214161820 2,程序代码; x=-2:0.1:2; y=x; [x,y]=meshgrid(x,y); z=(x.^2)*exp(-(x.^2+y.^2)); mesh(x,y,z); title('拱形抛物面网线图') figure(2);surf(x,y,z); title('拱形抛物面网面图') 拱形抛物面网线图 拱形抛物面网面图
MATLAB二维图形绘制的基本操作

6、坐标轴范围的设定
axis函数 x=0:pi/30:4*pi; plot(x,sin(x)); axis([0 4*pi -2 2])
‘hexagram’ 六角星
‘square’
□
2、离散序列图形的绘制
(1)stem(y) 以x=1,2,3,…为各个数据点的x坐标,以y向量的各个对 应元素为y坐标,在(x,y)坐标点画一个空心小圆圈,并连接 一条线段到X轴. x=[0,1,1,2,2,3,3,4,4] y=[1,1,0,0,1,1,0,0,1] stem(x,y)
其中包含了MATLAB的各种命令 M函数文件(functions)
M文件的编辑、保存、运行
M脚本文件(scripts)
theta=-pi:0.01:pi; rho(1,:)=2*sin(5*theta).^2;
rho(2,:)=cos(10*theta).^3;
rho(3,:)=sin(theta).^2; rho(4,:)=5*cos(3.5*theta).^3; for k=1:4 polar(theta, rho(k,:)) pause end
%axis([0 5 0 2])
2、离散序列图形的绘制
(2)stem(x,y,’option’) x=[0,1,1,2,2,3,3,4,4] y=[1,1,0,0,1,1,0,0,1]
stem(x,y,'r-.')
%axis([0 5 0 2])
2、离散序列图形的绘制
(3)stem(x,y) x=0:pi/30:3*pi; y=sin(x);
四、图形的绘制
1、二维图形的绘制
(1)plot(x)
当y为一向量时,以y的序号为X轴,按向量y的值绘制曲线.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二维连续随机变量(X,Y)的联合概率密度为:
2(,)21x y f x y r πσσ=-22222()()()()122(1)x y y x x y x y x y y x r r e μμμμσσσσ⎡⎤----⎢⎥--+-⎢⎥⎣⎦
记作(X ,Y )~()r N y x y x ,,,,σσμμ
下面我自己绘制一个(X ,Y )~()5.0,1,1,0,0N 的正态函数的图像(2013年1月8日) (,)23f x y π=
222x 3xy y e ⎡⎤--+⎣⎦
close all;
clear
clc
x=-4:.1:4;
y=x;
[x y]=meshgrid(x,y);
z=sqrt(3)/2/pi*exp(-2.*x.^2./3-2.*y.^2./3+x.*y);
mesh(x,y,z)
close all;
clear
clc
x=-4:.1:4;
y=x;
[x y]=meshgrid(x,y);
z=sqrt(3)/2/pi*exp(-2.*x.^2./3-2.*y.^2./3+x.*y); mesh(x,y,z)
hold on;
fill3([-4 -4 4 4],[0 0 0 0],[0.35 0 0 0.35],'r')
surf(1:2,[1 1],[0 0;1 1])
ezmesh('100-x-y')
ezplot('x=2')
高三数学图片 >> 二维正态分布的密度函数图像
资料名称:二维正态分布的密度函数图像
资料编号:100973
资源分类:图像素材
所属科目:数学
适用年级:高三
文件大小:12.55KB
文件类型:image/jpeg
资料简介:二维正态分布的密度函数图像正态分布,概率与统计, >> clf
>> x=2;
>> y=0;
>> z=0;
>> plot3(2,0,0,'m:p')
在matlab中绘制三维平面图
检举|2011-04-17 23:07 提问者:现在的博士|浏览次数:1186次
已知四个点的三坐标分别为(100,1030,500)、(340,1030,500)(340,280,500)(100,280,500),如何在三坐标系中绘制以上四点围成的矩形的曲面图,请高手给出具体程序。
这个程序的功能是任意给出四点就能生成三维平面图。
问题补充:
另外我还想知道matlab中可以实现机器人运动轨迹的仿真吗?意思是说能不能生成以下的轨迹图?如何实现?
我来帮他解答
满意回答
2011-04-17 23:18
fill3([100 340 340 100],[1030 1030 280 280],[500 500 500 500],'w')
fill3([100 340 340 100],[1030 1030 280 280],[500 500 500 500],'r')
fill3([-4 -4 4 4],[0 0 0 0],[0.35 0 0 0.35],'r') %%设平面方程为z=ax+by+c。
a=1;b=2;c=3;
y=0:0.01:1;
z=0:0.01:1;
[x y]=meshgrid(y,z);
x=2
surf(x,y,z)
%%设平面方程为z=ax+by+c。
a=1;b=2;c=3;
x=0:0.01:1;
y=0:0.01:1;
[x y]=meshgrid(x,y);
z=a*x+b*y+c;
surf(x,y,z)
x=[-2*pi:pi/10:2*pi];
y= exp(-4+2.*x-x.^2);
plot(x,y);
x=[-2*pi:pi/10:2*pi];
y= exp(-4+2*x-x^2);
plot(x,y);
同问 matlab 三维中画一个平面
检举|2012-05-31 11:54 提问者:匿名|浏览次数:255次知道了平面的向量,想在三维中画出这个平面
我来帮他解答
满意回答
2012-05-31 12:15
%%设平面方程为z=ax+by+c。
a=1;b=2;c=3;
x=0:0.01:1;
y=0:0.01:1;
[x y]=meshgrid(x,y);
z=a*x+b*y+c;
surf(x,y,z)。
