第三讲完全且完美信息动态博弈
合集下载
第3讲 完全信息动态博弈
q2 0
最优化的一阶条件意味着： s（q1） （a q1 c） =1 2 2
第3讲 完全信息动态博弈
假定q1 a c。这实际上是库诺特模型中企业2的反应函数，不同的 是，这里，s（q1）是当企业1选择q1时企业2的实际选择，而在库诺 2 特模型中，R2 q1）是企业2对于假设的q1的最优反应。 （ 因为企业1预测到企业2将根据s（q1）选择q 2，企业1在第一阶段的问 2 题是： max 1 = q1，s（q1）=q1 a q1 s（q1） c） （ 2 2
第3讲 完全信息动态博弈
• 这个例子也说明，在博弈中，拥有信息优势可能 使参与人处于劣势，而这在单人决策中是不可能 的。企业2在斯坦克尔伯格博弈中的利润之所以低 于库诺特博弈中的利润，是因为它在决策之前就 知道了企业1的产量。即使企业1先行动，但如果 企业2在决策之前不能观测到企业1的产量，我们 就回到了库诺特均衡，因为此时，企业1的先动优 势就不存在了。
第3讲 完全信息动态博弈
* 1 回忆一下，在上一讲得到的库诺特模型的纳什均衡是q1 =q* = （a c）， 2 3 3 比较这两个结果，发现斯坦克尔伯格均衡的总产量 （a c）大于库诺特 4 2 的总产量 （a c）。但是，企业1的斯坦克尔伯格均衡产量大于库诺特 3
均衡产量，而企业2的斯坦克尔伯格均衡产量小于库诺特均衡产量。 因为企业1本来可以选择库诺特均衡产量但它没有选择，说明企业1在斯坦 克尔伯格博弈中的利润大于库诺特博弈中的利润，而总产量上升意味着 总利润下降了从而企业2的利润一定下降了。这就是所谓的“先动优势”。
第3讲 完全信息动态博弈
• 宏观经济政策的动态一致性 宏观经济学上与子博弈精炼纳什均衡相对应的概 念是政府政策的动态一致性（dynamic consistency 或time consistency）。政府政策 的动态一致性指的是，一个政策不仅在制定阶段 应该是最优的（从政府的角度），而且在指定之 后的执行阶段也应该是最优的，假设没有任何新 的信息出现。如果一个政策只是在制定阶段是最 优的，而在执行阶段并不是最优的，这个政策就 是动态不一致的。说它是动态不一致的，是因为
最优化的一阶条件意味着： s（q1） （a q1 c） =1 2 2
第3讲 完全信息动态博弈
假定q1 a c。这实际上是库诺特模型中企业2的反应函数，不同的 是，这里，s（q1）是当企业1选择q1时企业2的实际选择，而在库诺 2 特模型中，R2 q1）是企业2对于假设的q1的最优反应。 （ 因为企业1预测到企业2将根据s（q1）选择q 2，企业1在第一阶段的问 2 题是： max 1 = q1，s（q1）=q1 a q1 s（q1） c） （ 2 2
第3讲 完全信息动态博弈
• 这个例子也说明，在博弈中，拥有信息优势可能 使参与人处于劣势，而这在单人决策中是不可能 的。企业2在斯坦克尔伯格博弈中的利润之所以低 于库诺特博弈中的利润，是因为它在决策之前就 知道了企业1的产量。即使企业1先行动，但如果 企业2在决策之前不能观测到企业1的产量，我们 就回到了库诺特均衡，因为此时，企业1的先动优 势就不存在了。
第3讲 完全信息动态博弈
* 1 回忆一下，在上一讲得到的库诺特模型的纳什均衡是q1 =q* = （a c）， 2 3 3 比较这两个结果，发现斯坦克尔伯格均衡的总产量 （a c）大于库诺特 4 2 的总产量 （a c）。但是，企业1的斯坦克尔伯格均衡产量大于库诺特 3
均衡产量，而企业2的斯坦克尔伯格均衡产量小于库诺特均衡产量。 因为企业1本来可以选择库诺特均衡产量但它没有选择，说明企业1在斯坦 克尔伯格博弈中的利润大于库诺特博弈中的利润，而总产量上升意味着 总利润下降了从而企业2的利润一定下降了。这就是所谓的“先动优势”。
第3讲 完全信息动态博弈
• 宏观经济政策的动态一致性 宏观经济学上与子博弈精炼纳什均衡相对应的概 念是政府政策的动态一致性（dynamic consistency 或time consistency）。政府政策 的动态一致性指的是，一个政策不仅在制定阶段 应该是最优的（从政府的角度），而且在指定之 后的执行阶段也应该是最优的，假设没有任何新 的信息出现。如果一个政策只是在制定阶段是最 优的，而在执行阶段并不是最优的，这个政策就 是动态不一致的。说它是动态不一致的，是因为
第三章 完全且完美信息动态博弈
以“开金矿博弈”为例对相机选择和可信性问
题 进行一些分析。 甲欲开采一价值4万元的金矿，缺1万元资金， 乙刚好有1万元资金。设甲对乙承诺，只要乙将这1 万元资金借给自己，采到金子后与乙对半分成。 乙
借 甲 分 （2，2） 不分 不借 （1，0）
乙是否该将钱借给甲呢？
（0，4）
开金矿博弈(单位:万元)
一个扩展式博弈由下列要素构成： 1、参与人集合 2、行动顺序 3、参与人行动时的可选行动方案及信息状 况 4、支付函数
扩展型表示
A 仿冒 B 制止 仿冒 （-2，5） 制止 B 不仿冒
不制止
A
（0，10）
不仿冒
不制止
（5，5）
（2，2）
（10，4）
对于一些比较复杂的博弈（比如存在许多选择或连续策 略），如果用博弈树表达就很麻烦，有时也不可能。
军事博弈
犯人
不犯人 (-3,-3)
B 犯 A 不犯
(2, -2) (-2, 2)
B
犯人 不犯人
(0, 0)
第二节 子博弈完美均衡与逆推归纳法
一、动态博弈中的相机选择问题与可信性 问题
动态博弈中博弈方的策略是预先设定的。这些策 略在博弈过程中究竟哪个会实施，博弈方会从自 身利益的角度出发，针对其他博弈方的策略选择 来选择，我们称这种策略选择行为为动态博弈中 的“相机选择”。 相机选择的存在使得博弈方的策略中所设定的各 个阶段、各种情况下所采取的行为的可信性有了 疑问。
不借！
可信的威胁！
如果乙在甲违背承诺时采取打官司的措施收回本 钱1万元，而甲被罚没全部收入，博弈为图所示。
乙
借 甲 分 （2，2） 打 （1，0） 不分 乙 不打 （0，4） 不借 （1，0）
第三讲非合作博弈的解：（4）
例子：斯坦伯尔伯模型。两个厂商垄断某个市场，其中厂商 1处于支配地位，它先行动，然后从属企业2后行动。假定 市场需求函数为p=a-Q。厂商的单位产品的成本c。这些是 企业1和2的公共知识。问：厂商1和2是如解。
假定厂商1和2所决定的产量分别为q1,q2。 企业2后行动，对于企业1的任何行动，即任意给定的产量，
• 例子：假定甲在开采一个价值4万元的金矿时需要1万元 资金，乙有1万元资金。甲向乙借钱来开金矿。在这个 博弈的第一阶段，甲向乙承诺: 如果乙借钱给他的话， 那么他就会将采到的金子与乙对半分成，即(2，3)—— 乙得到2万元的金子，同时收回自己的1万元投资。对于 甲的承诺，乙如果不借钱给甲的话，那么博弈到此为止， 双方收益为(0，1)。如果乙借钱给甲的话，那么博弈进 入第二个阶段。在第二阶段中，若甲遵守他的承诺，分 给乙一半的金子，这样两人的收益为(2，3)，其中1万 元为投资成本。然而，若甲违背自己的承诺，博弈就会 进入到第三个阶段: 如果乙同甲打官司，那么由于打官 司费时费力， 两个人的收益为(0，1)；若乙不打官司， 那么两个人的收益就为(5，0)。
安娜
2 1
鲍伯
1 4
安娜
4 3 蜈蚣博弈
鲍伯 2n+1
3 6
安娜 鲍伯
2n+2
2n 2n-1
2 n-1 2 n+2
• 这个博弈有两个参与人安娜和鲍伯。该博弈从安娜开始，她有两 个策略“合作”和“不合作”，若她选择“不合作”，博弈即刻 终止，安娜得到2，鲍伯得到1；若她选择“合作”，那么博弈继 续进行，由鲍伯开始选择。鲍伯同样有“合作”和“不合作”两 种策略。在这第二轮选择中，若鲍伯选择“不合作”，博弈终止， 选择“合作”，博弈继续进行……在这个博弈最后一轮，即第2n 轮，若鲍伯选择“不合作”，他所得2n+1，安娜得2n-1；若他选 择“合作”，鲍伯得2n+1安娜得2n+2。
第三讲 完全信息动态博弈
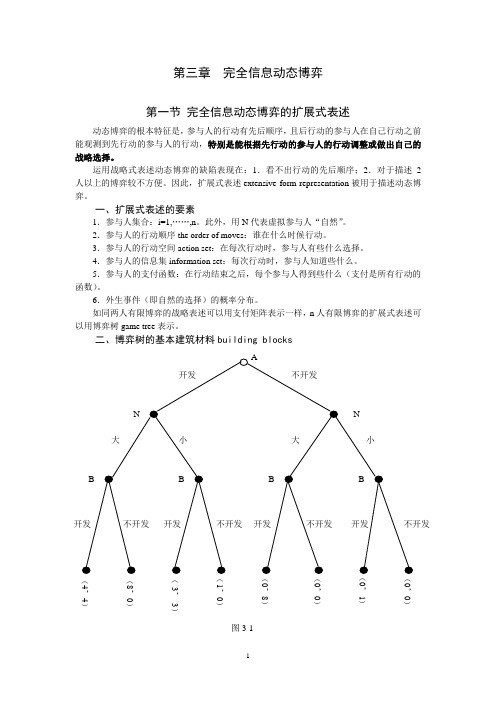
第三章完全信息动态博弈第一节完全信息动态博弈的扩展式表述动态博弈的根本特征是，参与人的行动有先后顺序，且后行动的参与人在自己行动之前能观测到先行动的参与人的行动，特别是能根据先行动的参与人的行动调整或做出自己的战略选择。
运用战略式表述动态博弈的缺陷表现在：1．看不出行动的先后顺序；2．对于描述2人以上的博弈较不方便。
因此，扩展式表述extensive form representation被用于描述动态博弈。
一、扩展式表述的要素1．参与人集合：i=1,……,n。
此外，用N代表虚拟参与人“自然”。
2．参与人的行动顺序the order of moves：谁在什么时候行动。
3．参与人的行动空间action set：在每次行动时，参与人有些什么选择。
4．参与人的信息集information set：每次行动时，参与人知道些什么。
5．参与人的支付函数：在行动结束之后，每个参与人得到些什么（支付是所有行动的函数）。
6．外生事件（即自然的选择）的概率分布。
如同两人有限博弈的战略表述可以用支付矩阵表示一样，n人有限博弈的扩展式表述可以用博弈树game tree表示。
二、博弈树的基本建筑材料building blocks（4，4）（8，）（-3，-3）1，），8），），1），）图3-1（一）结nodes1．结的分类（1）决策结decision nodes：参与人采取行动的时点。
包括：起点结——initial nodes非起点结——（2）终点结terminal nodes：博弈行动路径的终点。
2．结的顺序关系precedence relation用X表示所有结的集合，x∈X表示某个特定的结。
x≺x"表示“x在x"之前”≺3．前列集the set of predecessors和后续集the set of successors定义P(x)为在x之前的所有结的集合，简称为x的前列集；定义T(x)为x之后的所有结的集合，简称为x的后续集。
3 完全且完美信息动态博弈
完美信息perfect information
后行动者记得此前的全部博弈进程，称为完美信息 全部博弈进程包括
局中人的博弈顺序 每个局中人在各个阶段的行为选择
2011-12-8 魏光兴——重庆交通大学 3
3.3 动态博弈中的行为与战略I
事例1：中美战略博弈
解放初，美国总是寻找各种机会来侵犯我国。对此，毛主 席提出了“人不犯我、我不犯人，人若犯我、我必犯人” 的战略方针。
-2，-3 2，-5
-2，-3 0，0
1，-4 2，-5
1，-4 0，0
纳什均衡
美不犯我，我不犯美
2011-12-8
魏光兴——重庆交通大学
6
3.3 动态博弈中的行为与战略IV
事例2：产品开发博弈
两企业就是否开发某种新产品展开竞争。设A先决定是否开 发，B看到A的选择后再决定是否开发。如果只有一家企业 开发，开发者将获利1，不开发者收益不变。如果两家企业 都开发，各自将亏损3。如果都不开发，收益都不变。
3.9 承诺行动IV
绑架与劫持中的承诺行动
绑架与劫持
影视作品中的一种常见情节 现实生活中也时有发生
歹徒的威胁是空头的吗？
可能是，因为他们不想罪上加罪 可能不是，因为他们要树立自己言出必行的声誉
歹徒的承诺行动有哪些？
电话里人质的痛苦和呐喊声 照片、录像带、人质的衣物甚至器官
警方的威胁是空头的吗？
可能是，特别是不知道歹徒是谁的时候 可能不是，一旦知道歹徒是谁在哪
我站在未来的山坡上回头看 过去和现在如同不再有悬念的平静湖面 所有发生的一切都是如此清晰和必然
5.12汶川大地震
事前难以预测 事后却成必然
棋局、股价与政策
棋局：对弈的基本规则与原则 股价：事后判断什么时候买进什么时候卖出很容易 政策：其有效性取决于大众的反应
博弈论原理 第3讲 完全且完美信息动态博弈
引入一个“自然”的外部参与人，随机性 事件被假定为一个称为自然的参与人来控制
3.1动态博弈的表示法和特点
工商管理学院
School .Busi Admin
注意：支付向量的 顺序与博弈树上行 动顺序是对应的！
A
行动顺序：A——自然—— B在观察到A的行动和自然 的行动后进行决策
开发
N
不开发
N
“自然”：虚拟 参与人
若美国“犯我”，中国“犯人”，则支付向量为 (-2,-2)； 若美国“犯我”，中国“不犯人”，则支付向量为 (2,-4)； 若美国“不犯我”，中国“犯人”，则支付向量为 (3,-5)； 若美国“不犯我”，中国“不犯人”，则支付向量为 (1,1)。
6
3.1动态博弈的表示法和特点
7
工商管理学院
School .Busi Admin
不开发
x’ 不论A开发不开发，我 开发——{开发，开发} 追随策略：A开发我开发，A不开发 我不开发——{开发，不开发} ； 对抗策略：A开发我不开发，A不开 发我开发——{不开发，开发} ； 不开发策略:不论A开发不开发我不 开发）——{不开发，不开发}； {开发，开发}、{开发，不开发}
3.2 可信性和纳什均衡的问题
21
工商管理学院
School .Busi Admin
一、动态博弈中的可信性（Credibility）问题 “破釜沉舟” 秦朝末年，秦国大将章邯率领数10万人攻打赵国的都 城巨鹿。赵国向楚国求援，楚王派项羽率兵救赵。项 羽带领人马渡过漳河后，马上命令弄沉渡船，每人只 带三天的粮食。将士们知道后退的路没有了，个个奋 勇杀敌，终于解了赵国之危。
美中军事博弈
美国 犯我
3.1动态博弈的表示法和特点
工商管理学院
School .Busi Admin
注意：支付向量的 顺序与博弈树上行 动顺序是对应的！
A
行动顺序：A——自然—— B在观察到A的行动和自然 的行动后进行决策
开发
N
不开发
N
“自然”：虚拟 参与人
若美国“犯我”，中国“犯人”，则支付向量为 (-2,-2)； 若美国“犯我”，中国“不犯人”，则支付向量为 (2,-4)； 若美国“不犯我”，中国“犯人”，则支付向量为 (3,-5)； 若美国“不犯我”，中国“不犯人”，则支付向量为 (1,1)。
6
3.1动态博弈的表示法和特点
7
工商管理学院
School .Busi Admin
不开发
x’ 不论A开发不开发，我 开发——{开发，开发} 追随策略：A开发我开发，A不开发 我不开发——{开发，不开发} ； 对抗策略：A开发我不开发，A不开 发我开发——{不开发，开发} ； 不开发策略:不论A开发不开发我不 开发）——{不开发，不开发}； {开发，开发}、{开发，不开发}
3.2 可信性和纳什均衡的问题
21
工商管理学院
School .Busi Admin
一、动态博弈中的可信性（Credibility）问题 “破釜沉舟” 秦朝末年，秦国大将章邯率领数10万人攻打赵国的都 城巨鹿。赵国向楚国求援，楚王派项羽率兵救赵。项 羽带领人马渡过漳河后，马上命令弄沉渡船，每人只 带三天的粮食。将士们知道后退的路没有了，个个奋 勇杀敌，终于解了赵国之危。
美中军事博弈
美国 犯我
第三章完全且完美信息动态博弈
第三章完全且完美信息动态博弈在动态博弈中，参与者需要根据对手的行为和策略来调整自己的行动，以便达到最佳的结果。
动态博弈可以分为完全信息动态博弈和不完全信息动态博弈。
完全信息动态博弈是指所有参与者都知道其他参与者的策略和收益函数，而不完全信息动态博弈则是指参与者不知道其他参与者的策略和收益函数。
在完全信息动态博弈中，参与者可以通过观察对手的行为来推断出对手的策略和收益函数。
这种博弈可以通过逆向归纳法来求解，即从博弈的阶段开始，逐步向前推导出每个阶段的最佳策略。
逆向归纳法是一种有效的求解完全信息动态博弈的方法，它可以帮助参与者找到最佳策略，从而实现最佳的结果。
然而，在现实世界中，完全信息动态博弈并不常见。
大多数博弈都是不完全信息动态博弈，参与者无法知道其他参与者的策略和收益函数。
在这种情况下，参与者需要通过观察对手的行为和策略来推断出对手的类型和收益函数。
这种博弈可以通过贝叶斯纳什均衡来求解，即参与者根据对手的类型和收益函数来选择自己的策略，以达到最佳的结果。
完全且完美信息动态博弈是指所有参与者都知道其他参与者的策略和收益函数，并且参与者能够观察到其他参与者的行为和策略。
这种博弈可以通过逆向归纳法和贝叶斯纳什均衡来求解，从而帮助参与者找到最佳策略，实现最佳的结果。
在完全且完美信息动态博弈中，参与者可以通过观察对手的行为和策略来推断出对手的类型和收益函数，从而调整自己的策略，以实现最佳的结果。
在完全且完美信息动态博弈中，参与者之间的互动是基于透明和预知性的。
每个参与者不仅清楚自己的策略选择和可能的收益，同时也了解其他参与者将如何根据这些信息做出反应。
这种透明度使得参与者能够做出更加精确的决策，因为他们能够预测对手的行动并据此调整自己的策略。
这种博弈的一个关键特点是，参与者之间的信息是对称的。
这意味着没有参与者拥有其他参与者所不知道的信息优势。
这种信息对称性使得博弈变得更加公平，因为它消除了信息不对称带来的不确定性。
第三章 完全且完美信息动态博弈
3.3 子博弈完美纳什均衡分析
子博弈完美纳什均衡
如果在一个完全且完美信息动态博弈中， 各博弈方的策略构成的一个策略组合满足，在 整个动态博弈及它的所有子博弈中都构成纳什 均衡，那么这个策略组合称为该动态博弈的一 个“子博弈完美纳什均衡”。
3.1.1 动态博弈的扩展形表示 “仿冒和反仿冒”博弈 仿冒和反仿冒” 仿冒和反仿冒
设有一家企业的产品被另一家企业仿冒， 设有一家企业的产品被另一家企业仿冒，如果被 仿冒企业采取措施制止，那么仿冒企业就会停止仿冒； 仿冒企业采取措施制止，那么仿冒企业就会停止仿冒； 如果被仿冒企业不采取措施制止， 如果被仿冒企业不采取措施制止，那么仿冒企业就会 继续仿冒。对被仿冒企业来说， 继续仿冒。对被仿冒企业来说，被仿冒会造成经济损 因此采取措施制止仿冒是符合自身利益的， 失，因此采取措施制止仿冒是符合自身利益的，但问 题是制止仿冒是有成本（代价） 题是制止仿冒是有成本（代价）的，因此在遭遇仿冒 时是否应该制止是需要研究的问题。 时是否应该制止是需要研究的问题。对于仿冒企业来 仿冒不被制止就能够获得很大利益， 说，仿冒不被制止就能够获得很大利益，但如果被制 止就会“偷鸡不成反蚀一把米” 止就会“偷鸡不成反蚀一把米”，因此是否仿冒也要 仔细推敲。 仔细推敲。
3.1 .1动态博弈的扩展形表示法
注解
扩展形表示法形象的体现了动态博弈的 阶段” “阶段” ； 不是所有动态博弈都可以用扩展形表示。 不是所有动态博弈都可以用扩展形表示。 比如：下象棋、双寡头先头决策产量等 比如：下象棋、
3.1.2 动态博弈(DG)的特征
基本特征
博弈方依次选择行为(有时也称为序列博 博弈方依次选择行为 有时也称为序列博 弈,Sequential Games)； ； 每个博弈方的一次选择常称为一个阶段， 每个博弈方的一次选择常称为一个阶段，动态博弈 至少有两个阶段， 至少有两个阶段，所以也称为多阶段博弈 (Multistage Games); 在某个阶段， 在某个阶段，可能存在几个博弈方同时选择的情况
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
先来后到的启示 后进者信息多，但利润不如先进入者。
15
3.2.2 一个承诺可信性问题
开金矿
甲去开采一价值4万元的金矿，缺1万元，乙恰好有1万元 可以投资。甲向乙借1万元开金矿，并“许诺”成功后与 其对半分成
乙是否该借钱给甲呢？ 如果乙借钱给甲，甲是 否该分钱给乙呢？
16
3.2.2 一个承诺可信性问题
分 （2，2）
乙
借
不借
（1，0）
甲 不分
（0，4）
甲的承诺是否可信？
17
3.2.2 一个承诺可信性问题
根据自身利益最大化 原则，甲的选择是不分，
乙
借
不借
甲
（1，0）
分
不分
而乙清楚甲的行为准
（2，2）
（0，4）
则，则选择不借。对乙来讲，本博弈中甲有一个不可信的
承诺。
怎样使甲的承诺变为可信，既让乙能保住本钱，又能有 更多的收益呢？关键在于增加一些对甲行为的约束。
法律保障的开金矿博弈——分钱打官司都可信
19
3.2.2 一个承诺可信性问题
乙
借
不借
甲
分 （2，2）
打
（1，0） 不分
乙 不打
（1，0）
（0，4）
乙的策略：第一阶段 借，如甲在第二阶段选择不 分，则第三阶段选择打；甲 的策略：若乙第一阶段借， 则他在第二阶段就选择分。
在双方这样的策略组合 下，本博弈的路径是（借， 分），双方得益为（2， 2），实现有效率的理想结 果。
● (1000,5000)
● (-1000,3000)
经发生了，容忍并保持 高价是符合自己利益的。
容忍得5000万元，阻挠
得3000万元。
稳定的结果是（进入，容忍）
12
3.2.1一个威胁可信性问题
新的博弈格局：
Ⅱ 不进入 ● (0,7000) 设在位者现在（而
进
不是后），投资于万一
入
进入发生时增加产量和
经济博弈论
第三章 完全且完美信息动态博弈
苏兵
西安工业大学经济管理学院 2009年8-12月
3 完全且完美信息动态博弈
完全－对得益的完全了解 完美－对先行博弈过程的完全了解 动态－各博弈方先后，依次行动
2
3 完全且完美信息动态博弈
尝试考虑以下问题 （1）是不是信息越多越有利？ （2）过程是否重要？ （3）动态博弈与静态博弈有 哪些异同之处？ （4）人们对已经过去的博弈是更注重结果还 是更注重过程？其意义何在？
18
3.2.2 一个承诺可信性问题
若乙采取法律手段，
乙
借
不借
即打官司保护自己的利 益，则产生了一个新的
甲
分 （2，2）
打
（1，0） 不分
乙 不打
博弈过程如图所示。在 新的博弈中，乙的唯一 选择是打官司，对甲来 讲，乙打官司的威胁是
（1，0）
（0，4）
可信的，是肯定会信守 的，他最理智的选择就
是分。
6
3.1 动态博弈的表示法
每一种可能行动组合下的收益是共同知识 如果企图进入者不进入，则在位者独享10000万元 利润； 如果进入而在位者容忍，则在位者得5000万元,进 入者利润1000万元； 如果进入并且在位者阻挠，则在位者利润3000万 元而进入者-1000万元。
信息完全且完美
7
3.1 动态博弈的表示法
20
3.2.2 一个承诺可信性问题
乙
借
不借
甲
分 （2，2）
打
（1，0） 不分
乙 不打
（-1，0）
（0，4）
10
3.2.1一个威胁可信性问题
Ⅱ
进 入
Ⅰ
容忍
● (1000,5000)
不进入 ●(0,10000)
阻挠
● (-1000,3000)
在本例中 “只要进入就 阻挠”的威胁 是否可信？
11
3.2.1一个威胁可信性问题
Ⅱ 不进入 ●(0,10000)
进
入
事实上这个威胁是不可
Ⅰ
容忍
阻挠
信的，因为理性的在位 者知道（如同潜在进入 者所知），一旦进入已
入
资额外生产能力的决策
Ⅰ
的结果。（3000万元＞
2000万元）。潜在进入
容忍
阻挠
者现在知道进入的结果 是商战，所以不进入该
● (1000,2000)
● (-1000,3000)
行业是理智的。
20世纪70年代，美国杜邦公司在二氧化钛行业中阻止进 入，投资近4亿美元增加生产能力……
14
3.2.1一个威胁可信性问题
3
3 完全且完美信息动态博弈
主要内容 动态博弈的表示法 可信性问题 子博弈和逆推归纳法 有同时选择的两阶段动态博弈
3.1 动态博弈的表示法
动态博弈
行动有先后顺序，不同的参与人在不同时点行动，先 行动者的选择影响后行动者的选择空间，后行动者可 以观察到先行动者做了什么选择。
为了做出最优的行动选择，每个参与人都必须这样思 考问题： 如果我如此选择，对方将如何应对？如果我是他， 我将会如何行动？给定他的应对，什么是我的最优选 择？
信息集（information sets）：参与人在决策节 点选择行动时，需要有关信息；对此前博弈过程 的一个全部而明确的认识就构成一个信息集。
9
3.2 可信性问题
可信性 动态博弈中，先行为的博弈方是否应该相信后行为
博弈方会采取某种策略或行为 后行为博弈方的许诺是否可信呢？ 后行为博弈方的威胁是否可信呢？
如下棋
5
3.1 动态博弈的表示法
先来后到博弈 为了进入一行业，进入者必须付出4000万元的（沉
没）成本建一个工厂。 如果进入者不进入，在位者能继续定高价，享受垄断利
润10000万元。 如果进入者进入，在位者可以“容忍”，维持高价，此 时
在位者只能赚到5000万元，进入者将赚到1000万元的净 利润：在位者可以“阻挠”，把价格压低，这种商战导 致 双方的低润：在位者的利润下降到3000万元， 进入者将有1000万元的净损失。
Ⅰ
进行价格战所需要的额 外的生产能力，成本是
容忍
阻挠
3000万元。当然，如果 今后在位者保持高价
●
●
(1000,2000) (-1000,3000)
（不管是否有进入）， 这个额外成本将减少在 位者的得益。
13
3.2.1一个威胁可信性问题
Ⅱ 不进入 ● (0,7000) 阻挠的威胁是完全
进
可信的，它是在位者投
扩展形表示法(博弈树）
Ⅱ
进 入
不进入
●(0,10000)
Ⅰ
容忍
阻挠
● (1000,5000)
● (-1000,3000)
8
3.1 动态博弈的表示法
•扩展形表示法(博弈树)的构成： 决策节点（decision nodes）
节点（nodes） 终点节（terminal nodes）
树枝（branches）：每一条树枝代表一个行动
15
3.2.2 一个承诺可信性问题
开金矿
甲去开采一价值4万元的金矿，缺1万元，乙恰好有1万元 可以投资。甲向乙借1万元开金矿，并“许诺”成功后与 其对半分成
乙是否该借钱给甲呢？ 如果乙借钱给甲，甲是 否该分钱给乙呢？
16
3.2.2 一个承诺可信性问题
分 （2，2）
乙
借
不借
（1，0）
甲 不分
（0，4）
甲的承诺是否可信？
17
3.2.2 一个承诺可信性问题
根据自身利益最大化 原则，甲的选择是不分，
乙
借
不借
甲
（1，0）
分
不分
而乙清楚甲的行为准
（2，2）
（0，4）
则，则选择不借。对乙来讲，本博弈中甲有一个不可信的
承诺。
怎样使甲的承诺变为可信，既让乙能保住本钱，又能有 更多的收益呢？关键在于增加一些对甲行为的约束。
法律保障的开金矿博弈——分钱打官司都可信
19
3.2.2 一个承诺可信性问题
乙
借
不借
甲
分 （2，2）
打
（1，0） 不分
乙 不打
（1，0）
（0，4）
乙的策略：第一阶段 借，如甲在第二阶段选择不 分，则第三阶段选择打；甲 的策略：若乙第一阶段借， 则他在第二阶段就选择分。
在双方这样的策略组合 下，本博弈的路径是（借， 分），双方得益为（2， 2），实现有效率的理想结 果。
● (1000,5000)
● (-1000,3000)
经发生了，容忍并保持 高价是符合自己利益的。
容忍得5000万元，阻挠
得3000万元。
稳定的结果是（进入，容忍）
12
3.2.1一个威胁可信性问题
新的博弈格局：
Ⅱ 不进入 ● (0,7000) 设在位者现在（而
进
不是后），投资于万一
入
进入发生时增加产量和
经济博弈论
第三章 完全且完美信息动态博弈
苏兵
西安工业大学经济管理学院 2009年8-12月
3 完全且完美信息动态博弈
完全－对得益的完全了解 完美－对先行博弈过程的完全了解 动态－各博弈方先后，依次行动
2
3 完全且完美信息动态博弈
尝试考虑以下问题 （1）是不是信息越多越有利？ （2）过程是否重要？ （3）动态博弈与静态博弈有 哪些异同之处？ （4）人们对已经过去的博弈是更注重结果还 是更注重过程？其意义何在？
18
3.2.2 一个承诺可信性问题
若乙采取法律手段，
乙
借
不借
即打官司保护自己的利 益，则产生了一个新的
甲
分 （2，2）
打
（1，0） 不分
乙 不打
博弈过程如图所示。在 新的博弈中，乙的唯一 选择是打官司，对甲来 讲，乙打官司的威胁是
（1，0）
（0，4）
可信的，是肯定会信守 的，他最理智的选择就
是分。
6
3.1 动态博弈的表示法
每一种可能行动组合下的收益是共同知识 如果企图进入者不进入，则在位者独享10000万元 利润； 如果进入而在位者容忍，则在位者得5000万元,进 入者利润1000万元； 如果进入并且在位者阻挠，则在位者利润3000万 元而进入者-1000万元。
信息完全且完美
7
3.1 动态博弈的表示法
20
3.2.2 一个承诺可信性问题
乙
借
不借
甲
分 （2，2）
打
（1，0） 不分
乙 不打
（-1，0）
（0，4）
10
3.2.1一个威胁可信性问题
Ⅱ
进 入
Ⅰ
容忍
● (1000,5000)
不进入 ●(0,10000)
阻挠
● (-1000,3000)
在本例中 “只要进入就 阻挠”的威胁 是否可信？
11
3.2.1一个威胁可信性问题
Ⅱ 不进入 ●(0,10000)
进
入
事实上这个威胁是不可
Ⅰ
容忍
阻挠
信的，因为理性的在位 者知道（如同潜在进入 者所知），一旦进入已
入
资额外生产能力的决策
Ⅰ
的结果。（3000万元＞
2000万元）。潜在进入
容忍
阻挠
者现在知道进入的结果 是商战，所以不进入该
● (1000,2000)
● (-1000,3000)
行业是理智的。
20世纪70年代，美国杜邦公司在二氧化钛行业中阻止进 入，投资近4亿美元增加生产能力……
14
3.2.1一个威胁可信性问题
3
3 完全且完美信息动态博弈
主要内容 动态博弈的表示法 可信性问题 子博弈和逆推归纳法 有同时选择的两阶段动态博弈
3.1 动态博弈的表示法
动态博弈
行动有先后顺序，不同的参与人在不同时点行动，先 行动者的选择影响后行动者的选择空间，后行动者可 以观察到先行动者做了什么选择。
为了做出最优的行动选择，每个参与人都必须这样思 考问题： 如果我如此选择，对方将如何应对？如果我是他， 我将会如何行动？给定他的应对，什么是我的最优选 择？
信息集（information sets）：参与人在决策节 点选择行动时，需要有关信息；对此前博弈过程 的一个全部而明确的认识就构成一个信息集。
9
3.2 可信性问题
可信性 动态博弈中，先行为的博弈方是否应该相信后行为
博弈方会采取某种策略或行为 后行为博弈方的许诺是否可信呢？ 后行为博弈方的威胁是否可信呢？
如下棋
5
3.1 动态博弈的表示法
先来后到博弈 为了进入一行业，进入者必须付出4000万元的（沉
没）成本建一个工厂。 如果进入者不进入，在位者能继续定高价，享受垄断利
润10000万元。 如果进入者进入，在位者可以“容忍”，维持高价，此 时
在位者只能赚到5000万元，进入者将赚到1000万元的净 利润：在位者可以“阻挠”，把价格压低，这种商战导 致 双方的低润：在位者的利润下降到3000万元， 进入者将有1000万元的净损失。
Ⅰ
进行价格战所需要的额 外的生产能力，成本是
容忍
阻挠
3000万元。当然，如果 今后在位者保持高价
●
●
(1000,2000) (-1000,3000)
（不管是否有进入）， 这个额外成本将减少在 位者的得益。
13
3.2.1一个威胁可信性问题
Ⅱ 不进入 ● (0,7000) 阻挠的威胁是完全
进
可信的，它是在位者投
扩展形表示法(博弈树）
Ⅱ
进 入
不进入
●(0,10000)
Ⅰ
容忍
阻挠
● (1000,5000)
● (-1000,3000)
8
3.1 动态博弈的表示法
•扩展形表示法(博弈树)的构成： 决策节点（decision nodes）
节点（nodes） 终点节（terminal nodes）
树枝（branches）：每一条树枝代表一个行动