光程差的概念
相位传输与光程差的关系

相位传输与光程差的关系全文共四篇示例,供读者参考第一篇示例:相位传输与光程差的关系是光学中一个非常重要的概念。
在光学中,光波的传播可以采用波动模型来描述。
而相位传输和光程差则是描述光波在传播过程中的一个重要参数。
本文将从相位传输和光程差的概念入手,探讨它们之间的关系。
首先,我们来解释一下什么是相位传输和光程差。
在光学中,相位是用来描述波的状态的一个物理量,它是一个关于时间和空间的函数。
光波在传播过程中,相位传播就是描述波前的传播方向和速度,而光程差则是描述波在传播过程中经过的路径长度差异。
光程差和相位传输之间的关系可以通过波动方程来解释。
在光学中,光波的传播可以用亥姆霍兹方程来描述:∇²E + k²E = 0其中,E是电场的复振幅,∇是梯度算子,k是波数,其定义为k=2π/λ,λ是波长。
这个方程描述了光波在介质中的传播。
在自由空间中,k=k0=2π/λ0,λ0表示真空中的波长。
根据亥姆霍兹方程,我们可以得到波动方程:E(x,t) = Aexp(i(kx-ωt))其中,A是振幅,i是虚数单位,k是波数,ω是角频率。
这个方程描述了光波在空间和时间上的特性。
通过这个方程,我们可以看到,相位传输和光程差之间的关系是密切相关的。
假设光波在传播过程中经过了一段光程差ΔL。
光波的相位传输Δθ可以表示为:Δθ = kΔL根据光程差的定义,可以得到:ΔL = nΔd其中,n是介质的折射率,Δd是光波在介质中传播的路径长度。
将光程差代入相位传输的公式中,可以得到:Δθ = nkΔd这个公式表明了相位传输和光程差之间的关系。
可以看到,光程差越大,相位传输也会随之增大。
这是因为在光学中,路径长度的增加会导致相位的改变。
因此,相位传输和光程差之间存在着紧密的关联。
在实际的光学实验中,相位传输和光程差的关系可以用来解释一些光学现象。
例如,在干涉实验中,两路光波的相位差可以通过光程差来计算。
在多束干涉中,由于不同光束走过路径不同,因此相位传输和光程差之间的关系非常重要。
光谱傅里叶分辨率光程差公式

光谱傅里叶分辨率光程差公式光谱傅里叶分辨率是描述光谱分辨能力的重要参数,它反映了光谱中两个相邻波长之间最小可分辨的差异。
光谱分辨力的提高对于光谱分析和光谱影像技术都具有重要意义。
在光谱傅里叶分辨率公式的推导过程中,光程差是一个关键概念。
光谱傅里叶分辨率公式的推导基于干涉效应。
在干涉光谱仪中,通过将样品光与参比光进行干涉,产生干涉光谱。
在干涉路径不同的条件下,干涉谱线之间的间距将取决于样品光和参比光的波长差异。
光程差是描述干涉路径差异的一个重要参数。
光程差(OPD)定义为样品光和参比光之间的光学路径差,即:OPD=n2d2-n1d1其中,n1和n2分别为样品光和参比光的折射率,d1和d2分别为样品光和参比光通过的光学路径长度。
当光程差为整数倍的波长时,干涉结果为最大值;当光程差为半整数倍的波长时,干涉结果为最小值。
通过控制干涉条件,可以实现对样品光谱的解析。
光程差与波长的关系可以根据光的波动方程进行推导。
根据波动方程,光的传播速度为:v=c/n,其中v为光的传播速度,c为真空中的光速,n为光的折射率。
因此,光在单位时间内传播的距离为:v*Δt=c*Δt/n。
在平行的光学路径中,波长为λ的光在经过光程差OPD后的相位差为:Δφ=2π*OPD/λ。
根据上述推导可以得到一个重要结论:光程差OPD与相位差Δφ成正比,与波长λ成反比。
在光谱傅里叶分辨率的公式推导中,光谱分辨率(R)定义为波长差Δλ与光谱傅里叶变换的半峰全宽(FWHM)的比值,即:R=λ/Δλ根据上述推导可以得到光谱傅里叶分辨率的公式:R=λ/(2π*OPD/λ)化简后得到:R=λ²/(2π*OPD)光程差OPD可以通过光学路径和折射率进行计算,因此可以通过实验手段测量。
通过测量光程差和波长,可以计算光谱傅里叶分辨率,从而评估光谱分辨力的优劣。
光谱傅里叶分辨率公式的推导是光谱分析的基础,具有重要的理论和实用价值。
光谱傅里叶分辨率公式的应用可以帮助科学家和工程师实现对光谱信号的高分辨率解析,从而提高分析和测量的准确性和可信度。
恒星光程差

恒星光程差
恒星光程差是由地球公转引起的。
地球在绕太阳公转时,相对于恒星的位置也在不断变化。
这种变化会产生光线的光程差,从而使我们观察到的恒星位置发生变化。
英国学者布拉德利发现了这一现象,并成功解释了这一物理效应。
恒星光程差的原理是,恒星是不动的,而地球在绕太阳公转。
因此,对于一颗正在头顶上方的恒星,在地球上看来,光线并不是垂直照下来的,而是有一定的倾角。
这个角度被称为光行差常数,它与恒星的距离无关。
通过简单的合成原则,可以得出光行差常数的公式:k=v/c。
其中,c为光速,v是地球绕太阳公转的速度。
通过该公式,我们可以得出光行差常数的值,并进一步推算出恒星的位置变化。
总之,恒星光程差是由地球公转引起的光线变化现象。
通过理解这一现象,我们可以更好地理解天文学中的恒星观测和定位。
§14-2 光程、光程差

d2 n2
( r2 ( n2 1 )d 2 ) ( r1 ( n1 1 )d1 ) r2 r1 ( n2 1 )d 2 ( n1 1 )d1
P 点产生干涉加强的条件 k
(2k 1 ) P 点产生干涉减弱的条件 2
波长的整数倍
(k 0,1,2 )
半波长的奇数倍
A
o
F
B
A
F'
焦平面
B
各波束所走路程不等
∵焦点处各波叠加加强 ∴ 各波之间无波程差(光程相等)
f
结论:经透镜汇聚后的光束,不引起附加的光程差!
相干长度( l ):光波列在真空中的长度称为相干长度
t 相干时间( ):两波列到达干涉点所允许的最大时间差
例1 在相同时间内,一束波长为的单色光在空气 中和玻璃中传播的距离相同吗?走过的光程相同吗? 解:传播时间为 t 解:空气中传播的距离 玻璃中传播的距离 空气中传播的光程
r ct c rn vt t n
光程差: n r2 n0 r1
玻璃中光程 水中光程
n1r1
n2 r2
s
s1
玻璃
n1
r1
r2
p
光程差
n2r2 n1r1
k
s2
水 n2
2
2 2k
(2k 1 )
干涉减弱 2 将相位差的讨论化简为光程差的讨论
(2k 1 )
距离不同
L1 r ct
光程相同
玻璃中传播的光程
L2 nrn ct
例2 如图计算p点的光程差。
解:
L2 r2 d2 n2d2
17_03_光程与光程差

n2 r2
n1r1
)
—— 相位差与光程差的关系
r
光在介质中传播的距离 ct 引起的相位变化: 2 代入 ct nr 得到:
—— 在计算光在不同介质中传播到某一点所引起的相位变化时, 将光在介质中走过的路程折算为光 在真空中走过的距离 nr ,统一用光在真空的波长进行相位变化的计算。 —— 相位差表达式中 (1 2 ) 2
普通物理学_程守洙_第十七章 波的光学_20090921
17_03 光程和光程差 1 光程和光程差 —— 光在不同的介质中传播速度不同,在走过相同的距离时,引起的相差变化不同。 如图 XCH004_047 所示,两束光沿不同介质和路径在 P 点相遇。
2 r1 E E 1 ) 1 10 cos( t 1 两束光在 P 引起的振动: E E cos( t 2 r2 ) 2 20 2 2
2
附加光
2
附加光程差。
REVISED TIME: 09-10-7
-3-
CREATED BY XCH
在 P 点两束光的相差: (1 2 ) —— 应用 1 u1T
2 r2
2
2 r1
1
c T 和 2 n2 n1 n1
—— 真空中光的波长
得到 (1 2 ) 2 ( 引入光程: nr 光程差: n2 r2 n1r1 相位差: (1 2 ) 2 光程的意义 在相同时间 t 里,光在介质 n 中传播距离 r 引起的相位变化,与光在真空中传播距离 ct 所引起 的相位变化相同。 光在介质 n 中传播的距离 r 引起的相位变化: 2
12-3 光程与光程差
s1
S
r1 r2
∆ = r2 − r1 = 0 e 点为零 o 点为零级明纹位置 r1′ = ( r2′ − e ) + ne 有劈尖时 r < (r2 − e) + ne 零级明纹位置下移 1
第十二章 波动光学
r1 = r2
r1′
r2′Βιβλιοθήκη s2o o′§12-3 光程与光程差 12-
在杨氏双缝干涉实验中, 例 在杨氏双缝干涉实验中,用波长 λ = 550nm 的单色光垂直照射在双缝上. 的单色光垂直照射在双缝上.若用一折射率 = 1.58 、 n 的云母片覆盖在上方的狭缝上, 厚度为 = 6.6 × 10 −6 m 的云母片覆盖在上方的狭缝上, e 问(1)屏上干涉条纹有什么变化?(2)屏上中央o点 )屏上干涉条纹有什么变化? ) 现在是明纹还是暗纹? 现在是明纹还是暗纹? 解:(1)干涉条纹向 干涉条纹向 上平移 s1 (2) ( n − 1)e = kλ
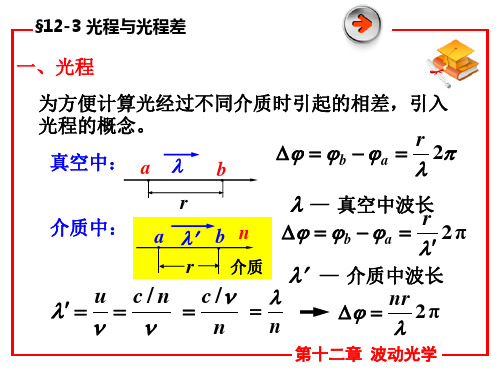
λ — 真空中波长
ν
c /ν λ = = n n
∆ϕ =
nr
λ
2π
第十二章 波动光学
§12-3 光程与光程差 12-
光程: 光程 媒质折射率与光的几何路程之积 =
nr
物理意义: 物理意义:光程就是光在媒质中通过的几何路 按波数相等折合到真空中的路程. 程 , 按波数相等折合到真空中的路程 二、光程差 光程差
s1 *
r1
P
δ = nr2 − r1
δ ∆ϕ = 2 π λ
s2*
r2
n
λ — 真空中波长
第十二章 波动光学
§12-3 光程与光程差 12-
三、物像之间的等光程性 在干涉和衍射装置中经常要用到透镜, 在干涉和衍射装置中经常要用到透镜,光线经过 透镜后并不附加光程差。 透镜后并不附加光程差。 A a 焦点 F、F′ 都是亮点,说明 、 都是亮点, F B b 各光线在此同相叠加。 各光线在此同相叠加。而 A、 、 · C c B、C 或 a、b、c都在同相 、 、 、 都在同相 面上。 面上。说明 A→F, B→F, → , → , F′ a · A C→F或 A→F′, B→F′,各 → 或 → → b B F 光线等光程。 光线等光程。 c C a 物点到象点( 亮点) 物点到象点 ( 亮点 ) 各光线 S′ S · 之间的光程差为零。 · b 之间的光程差为零。 c
迈克尔逊干涉 光程差公式

迈克尔逊干涉光程差公式摘要:1.迈克尔逊干涉仪的概述2.光程差的概念及计算公式3.迈克尔逊干涉仪的调节方法4.光程差近于零时干涉条纹的特点5.结论正文:一、迈克尔逊干涉仪的概述迈克尔逊干涉仪是一种用于测量光程差的光学仪器。
它主要由两个臂组成,一个叫静臂,不动;一个叫动臂,可以伸长缩短,移动其中的平面反射镜,从而改变这一条光路的光程。
在迈克尔逊干涉仪中,一束激光被分成两束,经过平面镜分别反射,再干涉,形成干涉环。
如果有材料的长度的变化,反映出光程差的变化,这样,原来干涉相消的位置可能就会干涉相长,看起来就像环溢出或者收回,通过数干涉环溢出或者收回的个数,就可以计算长度变化的多少。
二、光程差的概念及计算公式光程差是指两个光路之间的光程差异。
在迈克尔逊干涉仪中,光程差可以通过以下公式计算:光程差= 折射率变化的长度/ 激光波长相位差其中,折射率变化的长度指的是材料长度的变化导致的光程变化,激光波长相位差是指激光在两个光路中传播时,相位差的变化。
三、迈克尔逊干涉仪的调节方法为了获得清晰的干涉条纹,迈克尔逊干涉仪需要调节两个臂之间的光程差。
可以通过以下方法进行调节:1.调整动臂的长度:通过移动动臂中的平面反射镜,改变光程差。
2.调整激光器和反射镜的相对位置:通过调整激光器和反射镜的相对位置,使得激光束在静臂和动臂之间形成合适的光程差。
3.调整激光束的入射角度:通过调整激光束的入射角度,使得激光束在静臂和动臂之间形成合适的光程差。
四、光程差近于零时干涉条纹的特点当光程差接近零时,迈克尔逊干涉仪中的干涉条纹会发生变化,不再是同心圆,而是类似于双曲线。
这是因为两片镜子不是绝对平行的,且在相互比较接近的地方,光程差为0,导致左右两边提供的光程差刚好是相反的,从而形成了类似双曲线的干涉条纹。
五、结论总之,迈克尔逊干涉仪是一种测量光程差的精密仪器,它可以通过调整光程差来观察干涉条纹的变化,从而得到材料的长度变化。
光程差和相位差的计算

波长:不同波长 光的波长计算公 式
04
光程差和相位差的应用
在干涉现象中的应用
光程差和相位差是干涉现象中的重要概念 光程差和相位差的计算方法 光程差和相位差在干涉条纹形成中的作用 光程差和相位差在干涉测量中的应用
在光学仪器中的应用
光程差和相位差 在显微镜中的应 用
光程差和相位差 在望远镜中的应 用
Hale Waihona Puke 相位差:光程差会 导致光的相位发生 变化,这个变化量 称为相位差。
关系:光程差和相 位差之间存在正比 关系,即光程差越 大,相位差也越大 。
应用:光程差和相 位差的关系在光学 系统中非常重要, 例如在干涉仪、光 纤通信等领域都有 广泛应用。
02
光程差的计算方法
几何光程差的计算
光程差的定义:光在传播过程中, 由于介质的折射率不同,导致光 程发生变化的现象
迈克尔逊干涉仪中光程差和相位差的应用
迈克尔逊干涉仪的原理:利用光程差和相位差来测量光的波长 光程差的计算:通过计算两束光的传播路径长度之差 相位差的计算:通过计算两束光的相位之差 迈克尔逊干涉仪的应用:在光学测量、精密测量和科学研究等领域有着广泛的应用
薄膜干涉中光程差和相位差的应用
薄膜干涉:光在薄 膜表面反射和折射 时产生的干涉现象
单击此处添加副标题
光程差和相位差的计算
汇报人:
目录
01 02 03 04 05
光程差和相位差的基本概念 光程差的计算方法 相位差的计算方法
光程差和相位差的应用 光程差和相位差的实际案例分析
01
光程差和相位差的基本概念
光程差的定义
光程差:光在传 播过程中,由于 介质的折射率不 同,导致光程发 生变化的现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光程差的概念
光程差(Path Difference)是指光线通过两种不同介质时所经过的路径长度的差异。
在波动光学中,光程差是一个重要的概念,因为它决定了干涉、衍射和偏振等现象。
光程差对于理解光线如何通过介质以及如何与物质相互作用非常重要。
光程差的计算方法如下:
光程差= n1 ×Δd1 + n2 ×Δd2
其中:
n1 和n2 分别是两个介质的折射率
Δd1 和Δd2 分别是两个介质中光线所经过的路径长度差
当一个光波从一种介质传播到另一种介质时,它的速度发生变化,因为光的速度等于频率乘以波长,而波长与介质的折射率有关。
当光线从一个介质进入另一个介质时,折射率发生变化,从而导致光波波长的变化。
这种波长的变化导致了光程差的出现。
