方位角计算公式
日出日落的方位角度计算公式

计算日出日落的方位角度公式要计算任意一个地方在任意一天日出日落的方位角度,可以用下面的公式:方位角=90 - 0.5arccos[2(sinM/cosN)^2- 1]公式中,M表示的是某天太阳直射的纬度,N表示的是某地的纬度,^2表示平方。
例如,北京在北纬40度,则N=40,夏至这一天太阳在北纬23.5度(太阳直射北纬23.5度),即M=23.5,把N和M的值代入上式,可求得方位角=31度意思是,夏至这一天,在北京的人看来,太阳是从东偏北31度的方位升起的,是在西偏北31度的方位落下的。
说明:1本公式是在理想条件下推导出来的,即假设地球是个标准球体。
而实际上地球两极略扁,而且各地也有高山、洼地等,所以计算结果可能与实测结果有一点误差。
2 太阳围绕地球旋转的轨迹实际上是螺旋线(好象在地球外面套一根弹簧),所以实际上每天日出和日落的方位角稍微有点差别。
例如,在春分到夏至这段时间,日出方位角要略小于日落方位角。
昼夜长短的计算公式:Cost=-tgδ*tgφ太阳视位置太阳视位置指从地面上看到的太阳的位置,用太阳高度角和太阳方位角两个角度作为坐标表示。
太阳高度角指从太阳中心直射到当地的光线与当地水平面的夹角,其值在0°到90°之间变化,日出日落时为零,太阳在正天顶上为90°(本万年历中显示的高度角均已进行了蒙气差的订正,蒙气差值取自天文年历)。
太阳方位角即太阳所在的方位,指太阳光线在地平面上的投影与当地子午线的夹角,可近似地看作是竖立在地面上的直线在阳光下的阴影与正南方的夹角。
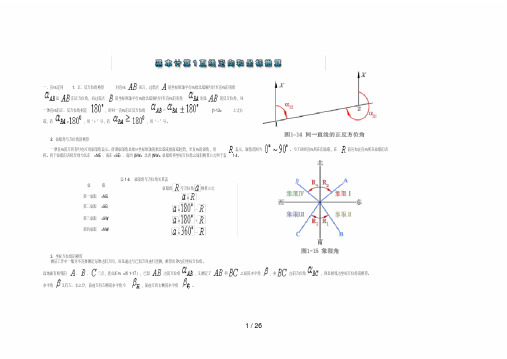
方位角以正南方向为零,由南向东向北为负,由南向西向北为正,如太阳在正东方,方位角为-90°,在正东北方时,方位为-135°,在正西方时方位角为90°,在正北方时为±180°。
实际上太阳并不总是东升西落,只有在春秋分两天,太阳是从正东方升,正西方落。
在北半球,从春分到秋分的夏半年中,太阳从东偏北的方向升(方位角为-90°到-180°之间),在西偏北的方向落(方位角为90°到180°之间);而从秋分到下一年春分的冬半年中,太阳从东偏南的方向升(方位角为-90°到0°之间),在西偏南的方向落(方位角为0°到90°之间)。
方位变化计算公式

方位变化计算公式
方位角计算公式是:坐标方位角=磁方位角+ (±磁坐偏角)。
原计算公式为:
S12=sqr( (x2-x1)2+(y2-y1)2)= sqr(△x221+△y221)
A12=arcsin((y2-y1)/S12)
S12为测站点1至放样点2的距离;A12为测站点1至放样点2的坐标方位角。
宽方位角勘探:
横纵比大于0.5的观测系统。
在宽方位角勘探发展的初期,也存在着明显的缺陷。
因为要满足横纵比大于0.5,炮检对的数量较窄方位勘探会大大增加,一定程度上大幅度的增加了勘探的经济成本。
但是,在采集技术迅猛发展的今天,宽方位角勘探技术也得到了大幅度的发展,随着万道地震仪和数字检波器的应用让宽方位角勘探成本大大降低了,裂缝性油气藏的客观需求也让宽方位角勘探推广开来。
方位角计算公式范文

方位角计算公式范文方位角是指从一个参考方向(通常是正北方向)起,按顺时针方向测量到其中一方向线的角度。
方位角通常用度数表示,范围从0度到360度。
下面介绍常见的方位角计算公式:1.方位角计算公式(两点坐标):假设已知起点坐标A(x1,y1)和终点坐标B(x2,y2),方位角θ的计算公式如下:θ = atan2(y2 - y1, x2 - x1)其中,atan2函数是一个双变量反正切函数,返回值为[-π, π]之间的角度值。
注意:上述公式计算得到的θ是以正北方向为参考的方位角。
如果要将方位角转换为以其他方向为参考的角度(如正东方向为0度),可以将θ减去相应的修正值。
2.方位角计算公式(两点经纬度):假设已知起点的经度(lon1)、纬度(lat1)和终点的经度(lon2)、纬度(lat2),方位角θ的计算公式如下:θ = atan2(sin(Δlon) * cos(lat2), cos(lat1) * sin(lat2) -sin(lat1) * cos(lat2) * cos(Δlon))其中,Δlon = lon2 - lon1是两点经度差。
注意:上述公式计算得到的θ是以正北方向为参考的方位角。
如果要将方位角转换为以其他方向为参考的角度(如正东方向为0度),可以将θ减去相应的修正值。
3.方位角计算公式(方向余弦矩阵):方向余弦矩阵(Direction Cosine Matrix)是一种将方位角和俯仰角等转化为三维空间坐标旋转的方式。
方向余弦矩阵的计算公式如下:D=[ cos(θ) * cos(φ), sin(θ) * cos(φ), -sin(φ) ][ -sin(θ), cos(θ), 0 ][ cos(θ) * sin(φ), sin(θ) * sin(φ), cos(φ) ]其中,θ是方位角,φ是俯仰角。
D是一个3行3列的矩阵,表示坐标变换矩阵。
上述是常见的方位角计算公式,根据不同的应用场景和问题,可能还会有其他的计算公式。
方位角计算公式.

一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13)上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东(NE)、南东(SE)、南西(SW)、北西(NW)。
象限角和坐标方位角之间的换算公式列于表1-4。
表1-4 象限角与方位角关系表象限象限角与方位角换算公式第一象限(NE)=第二象限(SE)=-第三象限(SW)=+第四象限(NW)=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线(图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17()所示,应有=++ (1-14)设三点相关位置如图1-17()所示,应有=++-=+- (1-15)若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16)显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=- (1-17)上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
如图1所示,设直线AB的边长DAB和一个端点A的坐标XA、YA为已知,则直线另一个端点B的坐标为:XB=XA+ΔXABYB=YA+ΔYAB式中,ΔXAB、ΔYAB称为坐标增量,也就是直线两端点A、B的坐标值之差。
结构设计常用计算公式

计算公式一、 方位角的计算公式 二、 平曲线转角点偏角计算公式 三、 平曲线直缓、缓直点的坐标计算公式 四、 平曲线上任意点的坐标计算公式 五、 竖曲线上点的高程计算公式 六、 超高计算公式 七、 地基承载力计算公式 八、 标准差计算公式一、 方位角的计算公式1. 字母所代表的意义:x 1:QD 的X 坐标 y 1:QD 的Y 坐标 x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg--+︒=α3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+Tcos(A+180°)Y ′=V+Tsin(A+180°)缓直(圆直)点的国家坐标:X ″=U+Tcos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角 L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C -T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号 K=H+L :缓直桩号2. 计算公式:1)当P<I 时中桩坐标:X m =U+(C -P)cos(A+180°) Y m =V+(C -P)sin(A+180°) 边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+=()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosO Y m =V+Tsin(A+180°)+GsinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW+90°) Y b =Y m +Bsin(A+MW+90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW+90°) Y b =Y m +Bsin(O+MW+90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++=()2390R P K P K G ---=中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD -MW+90°) Y b =Y m +Bsin(A+MD -MW+90°)5)当P>K 时中桩坐标:X m =U+(T+P -K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD+90°) Y b =Y m +Bsin(A+MD+90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;若要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
方位角的计算公式

计算公式一、 方位角的计算公式1. 字母所代表的意义:x 1:QD 的X 坐标 y 1:QD 的Y 坐标 x 2:ZD 的X 坐标 y 2:ZD 的Y 坐标 S :QD ~ZD 的距离 α:QD ~ZD 的方位角2. 计算公式:()()212212y y x x S -+-=1)当y 2- y 1>0,x 2- x 1>0时:1212x x y y arctg--=α2)当y 2- y 1<0,x 2- x 1>0时:1212360x x y y arctg --+︒=α 3)当x 2- x 1<0时:1212180x x y y arctg--+︒=α 二、 平曲线转角点偏角计算公式1. 字母所代表的意义:α1:QD ~JD 的方位角 α2:JD ~ZD 的方位角 β:JD 处的偏角2. 计算公式:β=α2-α1(负值为左偏、正值为右偏)三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义:U :JD 的X 坐标 V :JD 的Y 坐标 A :方位角(ZH ~JD )T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=D :JD 偏角,左偏为-、右偏为+2. 计算公式:直缓(直圆)点的国家坐标:X ′=U+Tcos(A+180°)Y ′=V+Tsin(A+180°)缓直(圆直)点的国家坐标:X ″=U+Tcos(A+D)Y ″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义:P :所求点的桩号B :所求边桩~中桩距离,左-、右+ M :左偏-1,右偏+1C :JD 桩号 D :JD 偏角 L s :缓和曲线长 A :方位角(ZH ~JD ) U :JD 的X 坐标 V :JD 的Y 坐标T :曲线的切线长,2322402224R L L D tg R L R T ss s -+⎪⎪⎭⎫ ⎝⎛+=I=C -T :直缓桩号 J=I+L :缓圆桩号s L DRJ H -+=180π:圆缓桩号K=H+L :缓直桩号2. 计算公式: 1)当P<I 时中桩坐标:X m =U+(C -P)cos(A+180°) Y m =V+(C -P)sin(A+180°) 边桩坐标:X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2)当I<P<J 时()s230RL I P MA O π-︒+= ()()2390R I P I P G ---=中桩坐标:X m =U+Tcos(A+180°)+GcosO Y m =V+Tsin(A+180°)+GsinO()s290RL I P W π-︒=边桩坐标:X b =X m +Bcos(A+MW+90°) Y b =Y m +Bsin(A+MW+90°)3)当J<P<H 时()()R J P L M A R J P R L M A O s s πππ-+︒+=⎪⎭⎫⎝⎛-︒+︒+=909090 ()RJ P R G π-︒=90sin2中桩坐标:()O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23+⎪⎭⎫⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23+⎪⎭⎫ ⎝⎛︒+⎪⎪⎭⎫ ⎝⎛-+︒++=π ()RJ P W π-︒=90边桩坐标:X b =X m +Bcos(O+MW+90°) Y b =Y m +Bsin(O+MW+90°)4)当H<P<K 时()sRL K P MMD A O π230180-︒-︒++= ()2390R P K P K G ---= 中桩坐标:X m =U+Tcos(A+MD)+GcosO Y m =V+Tsin(A+MD)+GsinO()s290RL K P W π-︒=边桩坐标:X b =X m +Bcos(A+MD -MW+90°) Y b =Y m +Bsin(A+MD -MW+90°)5)当P>K 时中桩坐标:X m =U+(T+P -K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标:X b =X m +Bcos(A+MD+90°) Y b =Y m +Bsin(A+MD+90°)注:计算公式中距离、长度、桩号单位:“米”;角度测量单位:“度”;假设要以“弧度”为角度测量单位,请将公式中带°的数字换算为弧度。
太阳高度角和方位角计算公式

太阳高度角和方位角计算公式太阳高度角和方位角计算是天文学和地理学中的一个重要问题,它们用来描述太阳在天空中的位置。
太阳高度角是太阳光线与水平面之间的夹角,而方位角则是从北方起算,指示太阳在水平面上的位置。
太阳高度角和方位角的计算可以通过以下公式进行修正:1.太阳高度角的计算公式(修正3):首先,我们需要知道太阳的赤纬(δ)和地球的纬度(φ),以及当前时间的时角(H)。
太阳赤纬是指太阳在黄道面上的纬度,范围从-23.45°到+23.45°之间。
赤纬的计算公式是一个复杂的数学模型,涉及到太阳的运动、地球的倾斜等因素,一般通过天文软件或表格查询得到。
地球的纬度是指地球表面其中一点与赤道平面之间的夹角,范围从-90°到+90°之间。
地球纬度可以通过GPS定位系统或地图查询得到。
当前时间的时角是指当前时间距离中午(太阳在最高点的时间)的时间差,范围从-12小时到+12小时之间。
在已知这些参数的情况下,太阳高度角的计算公式(修正3)为:sin(θ) = sin(δ) * sin(φ) + cos(δ) * cos(φ) * cos(H)其中,θ为太阳高度角,sin为正弦函数,cos为余弦函数。
2.方位角的计算公式(修正3):同样需要知道太阳的赤纬(δ)和地球的纬度(φ),以及当前时间的时角(H)。
方位角的计算公式(修正3)为:tan(A) = sin(H) / (cos(H) * sin(φ) - tan(δ) * cos(φ))其中,A为方位角,tan为正切函数。
需要注意的是,这些公式只适用于地球上的其中一点,并且在计算过程中可能还需要考虑修正项,如大气折射等。
此外,还需要选取适当的参考系统,如地心坐标系或大地坐标系,以确保计算结果的准确性。
总之,太阳高度角和方位角的计算是一个复杂而重要的问题,涉及到多个因素的考虑和修正。
需要掌握一定的天文学和地理学知识,并借助专业的软件或表格来进行计算。
方位角计算公式
辅助 计算
点名 2 BM1 1
2
3
BM2
测站数 3 8 3 4 5
20
表 2-2 附合水准路线计算
观测高差 /m
改正数 /m
改正后高差 /m
4
5
6
+8.364
- 0.014
+8.350
- 1.433
- 0.005
- 1.438
- 2.745
- 0.007
- 2.752
+4.661
- 0.008
+4.653
+ 8.847
- 0.034
一、直线定向
1、正、反方位角换算
对直线
而言,过始点
的坐标纵轴平行线指北端顺时针至直线的夹角
是
的正方位角,而过端点
的坐标纵轴平行线指北端顺时针至直线的夹角
则是
的反方位角,同
一条直线的正、反方位角相差
,即同一直线的正反方位角
=
(1-13>
上式右
端,若
<
,用“+”号,若
,用“-”号。
2、象限角与方位角的换算
算
各
待
定
点
的
高
程
。
如上 所述,闭 合水准 路线的 计算方法除高差 闭合差 的计算有 所区别 而外,其余与附 合路线 的计算 完全相 同。
二
、
举
例
1.
附
合
水
准
路
线
算
例
5 / 26
下图 2-18 所示附合水准路线为例,已知水准点 A 、 B 和待定点 1、2、3 将整个路线分为四个测段。
测段号 1 1 2 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13> 上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东<NE)、南东<SE)、南西(SW>、北西(NW>。
象限角和坐标方位角之间的换算公式列于表1-4。
表1-4 象限角与方位角关系表象限象限角与方位角换算公式第一象限<NE)=第二象限<SE)=-第三象限<SW)=+第四象限<NW)=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线<图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17(>所示,应有=++ (1-14>设三点相关位置如图1-17(>所示,应有=++-=+- (1-15>若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16>显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=- (1-17>上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
如图1所示,设直线AB的边长DAB和一个端点A的坐标XA、YA 为已知,则直线另一个端点B的坐标为:XB=XA+ΔXABYB=YA+ΔYAB式中,ΔXAB、ΔYAB称为坐标增量,也就是直线两端点A、B的坐标值之差。
由图1中,根据三角函数,可写出坐标增量的计算公式为:ΔXAB=DAB·cosαABΔYAB=DAB·sinαAB式中ΔX、ΔY均有正、负,其符号取决于直线的坐标方位角所在的象限,参见表1-5。
表1-5 不同象限坐标增量的符号坐标方位角及其所在象限之符号之符号<第一象限)<第二象限)<第三象限)<第四象限)+--+++--2、坐标的反算根据、两点的坐标、和、,推算直线的水平距离与坐标方位角,为坐标反算。
由图1可见,其计算公式为:= ( 1-20 >= ( 1-21 >注意,由<1-20)式计算时往往得到的是象限角的数值,必须参照表1-5表1-4,先根据、的正、负号,确定直线所在的象限,再将象限角化为坐标方位角。
例如、均为-1。
这时由<1-20)式计算得到的数值为,但根据、的符号判断,直线应在第三象限。
因此,最后得==,余类推。
表1-4 象限角与方位角关系表象限象限角与方位角换算公式第一象限<NE)=第二象限<SE)=-第三象限<SW)=+第四象限<NW)=-三、举例1、某导线12边方位角为45°,在导线上2点测得其左角为250°,求α32 ?解:1)23边的方位角:根据公式=+因α12=250°,α12 >180°,故计算公式中,前面应取“-”号:α23=α12+-=45°+250°-180°=115°2)求α23反方位角:根据公式=,本例α23<180°,故前面应取“+”号:α32=α23+=295°当前位置:首页-复习总结-基本计算2一、水准测量业的方法:水准测量的业即计算路线的高差闭合差,如其符合要求则予以调整,最终推算出待定点的高程。
1.高差闭合差的计算与检核附合水准路线高差闭合差为:=-(>(2-8> 闭合水准路线高差闭合差为:=(2-9> 为了检查高差闭合差是否符合要求,还应计算高差闭合差的容许值<即其限差)。
一般水准测量该容许值规定为平地=mm 山地=mm (2-11>式中,―水准路线全长,以km为单位;―路线测站总数。
2.高差闭合差的调整若高差闭合差小于容许值,说明观测成果符合要求,但应进行调整。
方法是将高差闭合差反符号,按与测段的长度(平地>或测站数(山地>成正比,即依下式计算各测段的高差改正数,加入到测段的高差观测值中:⊿= -(平地>⊿= -(山地> 式中,―路线总长;―第测段长度(km>(=1、2、3...>;―测站总数;―第测段测站数。
3.计算待定点的高程将高差观测值加上改正数即得各测段改正后高差:h i改=hi+⊿h i i=1,2,3,……据此,即可依次推算各待定点的高程。
如上所述,闭合水准路线的计算方法除高差闭合差的计算有所区别而外,其余与附合路线的计算完全相同。
二、举例1.附合水准路线算例下图2-18所示附合水准路线为例,已知水准点A、B和待定点1、2、3将整个路线分为四个测段。
测段号点名测站数观测高差/m 改正数 /m 改正后高差/m 高程/m 备注1 2 3 4 5 6 7 81 BM1 8 +8.364 -0.014+8.350 39.8331 48.1832 3 -1.433 -0.005 -1.4382 46.7453 4 -2.745 -0.007 -2.7523 43.9934 5 +4.661 -0.008 +4.653BM2 48.64620+ 8.847 -0.034 +8.813辅助计算=+ 0.034m== 54mm1)将点名、各测段测站数、各测段的观测高差、已知高程数填入表2-2相应栏目2、3、4、7(如系平地测量,则将测站数栏改为公里数栏,填入各测段公里数;表加粗字为已知数据>。
2)进行高差闭合差计算:=- (> =8.847-(48.646-39.833>=+ 0.034m由于图中标注了测段的测站数,说明是山地观测,因此依据总测站数计算高差闭合差的容许值为:=== 54mm计算的高差闭合差及其容许值填于表2-2下方的辅助计算栏。
3)高差闭合差的调整fh≤fh容,故其精度符合要求。
本例中,将高差闭合差反符号,按下式依次计算各测段的高差改正数:⊿= -< ―测站总数,―第测段测站数)第一测段的高差改正数为:⊿=-14mm同法算得其余各测段的高差改正数分别为-5、-7、-8mm,依次列入表2-2中第5栏。
注:1、所算得的高差改正数总和应与高差闭合差的数值相等,符号相反,以此对计算进行校核。
如因取整误差造成二者出现小的较差可对个别测段高差改正数的尾数适当取舍1mm,以满足改正数总和与闭合差数值相等的要求。
2、若为平地,高差改正数按各测段长度比例分配:用公式⊿=-计算,式中,―路线总长;―第测段长度 (km> (=1、2、3...>。
4)计算待定点的高程将高差观测值加上改正数即得各测段改正后高差:h i改=hi+⊿h i i=1,2,3,4据此,即可依次推算各待定点的高程。
<上例计算结果列入表2-2之第6、7栏)。
H1=HA+H1改H2=H1+H2改……HB<算)=HB(已知>注:改正后的高差代数和,应等于高差的理论值<HB-HA),即: ∑h改=HB-HA 。
如不相等,说明计算中有错误存在。
最后推出的终点高程应与已知的高程相等。
2 闭合水准路线算例闭合水准路线的计算方法除高差闭合差的计算有所区别而外,其余与附合路线的计算完全相同。
计算时应当注意高差闭合差的公式为:fh=∑h测。
如图2所示一闭合水准路线,A为已知水准点,A点高程为51.732m,,其观测成果如图中所示,计算1、2、3各点的高程。
将图中各数据按高程计算顺序列入表2进行计算:表2 水准测量成果计算表测段号点名测站数观测高差/m 改正数/mm 改正后高差/m高程/m1 2 3 4 5 6 71 BMA11 -1.352 0.006 -1.34651.732 1 50.3862 8 2.158 0.004 2.1622 52.5483 6 2.574 0.003 2.5773 55.1254 7 -3.397 0.004 -3.393BMB 51.73232 -0.017 0.017 0辅助计算=30mm=mm=±68mm计算步骤如下:⑴计算实测高差之和∑h测=3.766m= 3.766- 3.736=0.030m=30mm⑶计算容许闭合差fh容==±68mmfh≤fh容,故其精度符合要求,可做下一步计算。
⑷计算高差改正数高差闭合差的调整方法和原则与符合水准路线的方法一样。
本例各测段改正数vi计算如下:⊿=-(fh/∑n>×n1=-(-17/32>×11=6mm ⊿h2=-(fh/∑n>×n2=-(-17/32>×8=4mm……检核∑⊿h=-fh=-0.030m⑸计算改正后高差h改各测段观测高差hi分别加上相应的改正数后⊿hi,即得改正后高差:h1改=h1+⊿h 1=- 1.352+0.006=-1.346m h2改=h2+⊿h 2=2.158+0.004=2.162m……注:改正后的高差代数和,应等于高差的理论值0,即:∑h改=0 ,如不相等,说明计算中有错误存在。
⑹高程计算测段起点高程加测段改正后高差,即得测段终点高程,以此类推。
最后推出的终点高程应与起始点的高程相等。
即:H1=HA+h1改=51.732-1.346=50.386mH2=H1+h2改=50.386+2.162=52.548m……HA<算)=HA(已知>=51.732m 计算中应注意各项检核的正确性。
下一节:::当前位置:首页-复习总结-基本计算3一、经纬仪测回法测水平角1、基本数据:设、、为地面三点,为测定、两个方向之间的水平角,在O点安置经纬仪(图3-7>,采用测回法进行观测。
1)上半测回(盘左>水平度盘读数:目标:=0°02′06″,目标:=68°49′18″;2>下半测回(盘右>水平度盘读数:目标:=248″49′30″,目标:=180°02′24″。
