西电微波电子线路作业
西电微波电子线路大作业1教材

微波电子线路大作业姓名:班级:021014学号:一 肖特基势垒二极管与混频器1 肖特基势垒二极管利用金属与半导体接触形成肖特基势垒构成的微波二极管称为肖特基势垒二极管。
这种器件对外主要呈现非线性电阻特性,是构成微波混频器、检波器和微波开关等器件的核心元件。
目前绝大多数混频器都采用肖特基势垒二极管,因为肖特基势垒二极管的耗尽电容比PN 结电容小的多,因此肖特基势垒二极管更适合微波频率下工作。
肖特基势垒二极管的等效电路如右图所示:肖特基二极管作为非线性电阻应用时,除结电容之外,其他都是寄生参量,会对电路的性能造成影响,应尽量减小它们本身的值,或在微波电路设计时,充分考虑这些寄生参 量的影响。
一般地,肖特基势垒二极管的伏安特性可以表示为:对于理想的肖特基势垒,;当势垒不理想时,,点接触型二极管,面结合型二极管。
如下图是肖特基势垒二极管的伏安特性曲线:肖特基势垒二极管特性参量:1) 截止频率2) 噪声比(理想情况下) 3) 中频阻抗 4) 变频损耗2 混频器微波混频器的核心元件是肖特基势垒二极管。
混频机理是基于肖特基势垒二极管结电阻的非线性管子在偏压和本振的激励下,跨导随时间变化,加上信号电压后出现一系列频率成分的电流,用滤波器取出所需中频即可。
j R SR j C p C SL描述二极管混频器的混频过程,需要建立一个等效电路。
由于混频二极管是一个单向器件,不仅与和差拍产生新的频率,而其电流在一定的阻抗上所建立起的电压也会反过来加到二极管上该电压与和差拍,也产生新的频率。
混频器等效电路如右图所示:信频、中频和镜频电流的幅值为:由等效电路可以求出变频损耗。
微波混频器的作用是将微波信号转换为中频信,频率变换后的能量损耗即为变频损耗。
变频损耗主要包括三部分:(1) 由寄生频率产生的净变频损耗。
(2) 由混频二极管寄生参量引起的结损耗 。
(3) 混频器输入/输出端的失配损耗。
结论;混频器的变频损耗载镜频开路时变频损耗最低,镜频匹配时变频损耗最高。
微波电子线路大作业

题目:微波电子线路大作业授课老师:杨锐学院:电子工程学院专业:电子信息工程学生姓名:王静波学号:02111344微波二极管介绍微波领域内的各种二极管,包括变容二极管、阶跃二极管、PIN二极管、限幅二极管、电调变容二极管、固体噪声二极管和雪崩二极管等。
一.微波混频二极管和微波检波二极管基于金属-半导体相接触具有非线性电导原理制成的两端器件。
这种器件早在第二次世界大战期间就用于雷达接收机中,是半导体领域中最早出现的实用性器件。
1965年以前,这两种二极管均为点接触结构,即用微米级的金属触丝尖端与半导体锗或硅接触而产生高频整流特性。
1965年以后出现性能优越的肖特基势垒型混频和检波二极管(又称肖特基二极管),其工作频率从几百兆赫到 300吉赫,具有噪声低、频带宽、抗烧毁性能好等特点。
在整个微波频带内直接用二极管混频的微波接收机的噪声系数为4.0~70分贝。
梁式引线结构和四管堆具有多倍频程的性能。
检波二极管的工作频率范围为0~40吉赫,检波正切灵敏度为45~55分贝毫瓦。
二.变容二极管基于PN结结电容随反向偏压变化而制成的微波半导体器件。
大体可分两大类:低噪声参量放大器用变容管和电调谐用变容管。
前者用于微波参量放大器,噪声温度低达30K,已广泛用于卫星地球站。
后者主要用于频率调谐、压控振荡器、电子对抗和捷变频雷达快速调频等。
此外,变容管还可以用于移相、限幅等。
在制作上,两类器件有一定区别,参放变容管要有好的电容非线性和很高的优值;而电调谐变容管则要严格控制半导体外延层的掺杂浓度分布以便获得大的电容变化区,并且应具有较高的优值。
三.肖特基势垒二极管结构:肖特基势垒二极管在结构原理上与PN结二极管有很大区别,它的内部是由阳极金属(用钼或铝等材料制成的阻挡层)、二氧化硅(SiO2)电场消除材料、N-外延层(砷材料)、N型硅基片、N+阴极层及阴极金属等构成,如图所示。
在N型基片和阳极金属之间形成肖特基势垒。
当在肖特基势垒两端加上正向偏压(阳极金属接电源正极,N型基片接电源负极)时,肖特基势垒层变窄,其内阻变小;反之,若在肖特基势垒两端加上反向偏压时,肖特基势垒层则变宽,其内阻变大。
微波电子线路大作业

微波电子线路大作业姓名:哦呵呵 学号: 班级: 一、肖特基势垒二极管肖特基势垒二极管是利用金属与半导体接触形成肖特基势垒而构成的一种微波二极管,它对外主要体现出非线性电阻特性,是构成微波阻性混频器、检波器、低噪声参量放大 器、限幅器和微波开关等的核心元件。
1、结构:肖特基势垒二极管有两种管芯结构:点接触型和面接触型。
2、工作原理:肖特基势垒二极管工作的关键区域是金属和N 型半导体结形成的肖特基势垒区域,是金属和N 型半导体形成的肖特基势垒结区域。
在金属和N 型半导体中都存在导电载流子—电子。
它们的能级不同,逸出功也不同。
当金属和N 型半导体相结时,电子流从半导体一侧向金属一侧扩散,同时也存在金属中的少数能量大的电子跳跃到半导体中,称为热电子。
显然,扩散运动占据明显优势,于是界面上金属中形成电子堆积,在半导体中出现带正电的耗尽层。
在界面上形成由半导体指向金属的内建电场,它是阻止电子向金属一侧扩散的,而对热电子发射则没有影响。
随着扩散过程的继续,内建电场增强,扩散运动削弱。
于是在某一耗尽层厚度下,扩散和热电子发射处于平衡状态。
宏观上耗尽层稳定,两边的电子数也稳定。
界面上就形成一个对半导体一侧电子的稳定高度势垒GW eN D D S 22=φ,D N 是N 半导体的参杂浓度,D W 厚度存在于金属—半导体界面由扩散运动形成的势垒成为肖特基势垒,耗尽层和电子堆积区域成为金属—半导体结。
3、伏安特性:利用金属与半导体接触形成肖特基势垒构成的微波二极管称为肖特基势垒二极管。
这种器件对外主要呈现非线性电阻特性,是构成微波混频器、检波器和微波开关等的核心元件。
一般地,肖特基势垒二极管的伏安特性可以表示为半导外延点接半导外延面结氧化金属金 金两种肖特基势垒二极管结构 金属触欧姆接触]1)[exp(1)exp()(-=⎥⎦⎤⎢⎣⎡-==U I nkT qU I U f I S S α (1-1) 式中:nkTq =α。
微波电子线路大作业

微波电子线路大作业02091411范仕祥一.PIN 管微波开关按功能分有两种:通断开关和转换开关;按PIN 管与传输线的连接方式分为串联型、并联型和串并联型;从开关结构形式出发可分为反射式开关、谐振式开关、滤波器型开关、阵列式开关等。
单刀单掷开关基本原理如果PIN 管正、反偏时分别为理想短路和开路,则对上图(a )的串联型开关来说,PIN 管理想短路时,开关电路理想导通;PIN 管理想开路时,开关理想断开。
对(c )图的并联型开关来说,情况相反,PIN 管短路,对应开关断开;PIN 管开路,对应开关导通。
由于封装参数的影响,对于单管开关无论是串联型还是并联型,都只能在固定的某几个较窄的频率区间有开关作用,而实际的工作频率常常不在这些区域。
为了扩展开关的工作模区,改善开关性能,有的直接把管芯做在微波集成电路上;也有采用改进的开关电路,其中常用的有谐振式开关、阵列式开关和滤波器型开关。
单刀双掷开关开关指标开关时间:τ为载流子寿命,I0为正向电流,IR 为反 向电流,IR ↑,ts ↓, 则: 功率容量:并联开关:导通时 截止时串联开关:导通时 截止时00ln 's s f R I I T T I I ττ==、2010(2)4f dn dm f Z R P P Z R +=2302B dn V P Z =2020(2)4f dn dm f Z R P P Z R +=2308B dn V P Z =当频率升高时,串联或并联一只PIN 管的开关,其性能指标将恶化,因此,可采用多个二极管级联,以提高开关性能。
多管阵列型开关是在均匀传输线上等间隔的并联(或串联)若干个PIN 管而构成,根据微波网络理论可对阵列型开关进行分析。
单管开关级联就可做成阵列式开关,因此阵列式开关的分析可归结为级联网络分析,可用传递矩阵相乘的方法求出阵列开关的衰减特性。
采用多管串联的电路形式,可加大该通道开关的功率容量:而采用多管并联的形式,则可提高该通道开关的隔离度。
微波电子线路-西安电子科技大学3
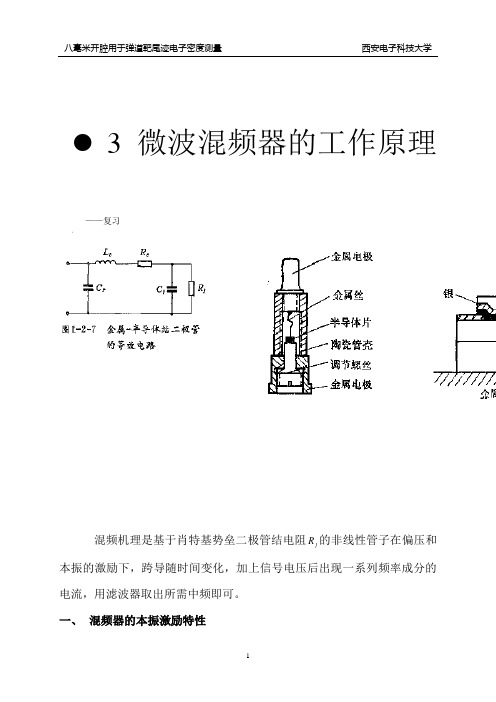
3 微波混频器的工作原理——复习混频机理是基于肖特基势垒二极管结电阻R的非线性管子在偏压和j本振的激励下,跨导随时间变化,加上信号电压后出现一系列频率成分的电流,用滤波器取出所需中频即可。
一、混频器的本振激励特性以单管混频器为例,输入:本振、偏压、信号、输出、中频()u f i =()au sa au Sa e I e I ≈-=1由图t V t V V u S S L L ωωcos cos 0++=S u 远小于L u ,故可视为微分增量u ∆ ()u u f i ∆+=∴()()+∆+'++=u t V V f t V V f L L L L ωωc o s c o s 00…...u ∆很小,忽略平方以后高次项,只取一阶导数项。
一阶导数表示了小信号电流与小信号电压之间的关系,即变频跨导()tL V V u dudiuu i i i ωcos 0+=∆+=∆+()()t ug u i ∆+= 式中 ()()t V V a Sa L L e aI dudit g ωcos 0+==现 ()t g 是t 的周期偶函数,可展成以下形式的级数 ()∑∞=+=10cos 2n L n n t g g t g ωn g 为n 阶变混频跨导,是t n L ωcos 的付利叶系数平均混频跨导()⎰=πωπ20021t d t g g L ()⎰+=πωπ20cos 021t V V a Sa L L e aI t d L ω()L aV Sa aV J e aI 00= n 阶变混频跨导1g ()⎰+=πωπ20cos 021t V V a Sa L L e aI tdt L ωcos()L aV Sa aV J e aI 10=……n g ()⎰+=πωπ20cos 021t V V a Sa L L e aI tdt L ωcos()L n aV Sa aV J e aI 0= J n (x),第一类贝赛尔函数本振电压作用下,混频器为一周期时变电导0g 为平均电导,n g 为n 次变频跨导(对本振n 次而言)与本振信号有关的电流 ()t V V f i L L ωcos 0+= ∑∞=+=10cos 2n L n t n I I ω平均电流 ()L aV Sa aV J e I I 000=基波电流 ()L aV Sa L aV J e I I J 11022==L aV 足够大 ,大宗量近似, ()LLn dV eaV J π2aV L ≈代入上两式 02I I L ≈本振激励功率为L L L L V I I V P 021== 本振电导 LL L L V I V I G 02==可通过0I 和L V 来调节L P L G ,测量L P 和0I 可以了解本振工作性质 ——具有工程意义,直流和本振大小使混频器特性好二、非线性电阻的电流频谱1、小信号一次混频结果。
西安电子科技大学射频微波电路实验

LS
=
XS 2πfC
,
CP
=
1 2πfC ⋅
XL
图 2-2(c) Ls-Cp低通式L型匹配电路
CS
=
1 2πfC ⋅
XS
,
LP
=
XL 2πfC
图 2-2(d) Cs-Lp高通式L型匹配电路
CP
=
1 2πfC ⋅
XS
,
LS
=
XL 2πfC
图 2-2(e) Cp-Ls低通式L型匹配电路
LP
=
XS 2πfC
Zs Vg
2-Port Network
a2
ZL
H参数 V1 = h11 I 1 + h12V 2 I 2 = h21 I 1 + h22V 2
Y参数 I 1 = y11V1 + y12V 2 I 2 = y 21V1 + y 22V 2
Z参数 V1 = z11 I 1 + z12 I 2 V 2 = z 21 I 1 + z 22 I 2
j
complex Γ plane
|Γ|=1
-1
1
-j 14
Smith Chart3
1.05
x=0.5
|Γ|=1
Smith Chart
x=1
Γr i( 0, θ )
+jx Γr i( 0.5, θ )
Γr i( 1, θ )
Γr i( 2, θ )
Γx i( 2, θ )
Γx i( 1, θ )
Γx i( 0.5, θ )
Frequency
Impedance
Analyzer
Scalar / Vector
微波电子线路大作业(3)讲诉

微波电子线路大作业(3)班级:姓名:学号:一、微波二极管负阻振荡器由砷化镓材料制成的体效应二极管呈现负阻效应的物理基础是能带结构的电子转移效应,而产生负阻效应的原理则是由于高场畴的形成。
典型的Gunn 二极管的结构如图所示.铜底座(接铜螺纹)提供一条外加散热器的低阻热通道,螺纹端拧在散热器上,它是接到直流电源的负极,陶瓷圆环起绝缘作用,它把正负极隔开。
若将耿氐二极管装在谐振腔的适当位置上,只要在它的两端加上适当的直流电压,就可以在谐振腔内产生微波振荡.这就构成了微波负阻振荡器。
由于谐振腔相当于集总电路的000L R L --并联谐振电路,它与耿氐二极管组合起来就形成了如图3-12(a)的等效电路,其中图(a)的左侧表示Gunn 二极管等效电路。
d C 和d R -是有源区参数,Cd 是Gunn 管电荷区域的电容参数,d R -是在电场超过阈值后所呈现的负阻特性,C 、L 是管壳及引线所呈现的分布参数;图(a)右侧表示谐振腔等效电路。
二极管具有负阻-Rd ,而负载则是正电阻R0,由于-Rd 与R0并联,它的电阻为00R R R R R d d t +=所以进一步简化后就变成如图(b)所示的等效电路。
当直流电源刚接通时,如工作点选择恰当且能满足Rd>R0的条件,则Rt 为负值。
在这种情况下,噪声足以触发振荡,使振幅随时间而增长。
但是,管阻-Rd 是非线性的,随着振幅的增大|-Rd|的数值逐渐减小。
当|-Rd|=R0时,从式不难看出,Rt=∞。
这就相当并联电阻Rt开路,变成Lt与Ct所组成的无损耗回路,因此产生等幅振荡。
谐振腔的作用是一方面可以调谐振荡波形使其接近正弦,另一方面把高频电磁能量收集在腔内,并通过耦合把高频能量送到负载上。
X波段波导耿氏振荡器的结构如图耿氏二极管横装在矩形波导中,并且由调节短路活塞改变腔的大小进行频率调谐。
振荡频率与腔体的长度有关,它的长度大体等于半个波导波长整数倍,腔体的长度是指从Gunn管的安装柱面到可调短路面之间的距离。
微波电子线路大作业(1)

微波电子线路大作业姓名:袁宁班级:020914学号:02091400一、肖特基势垒二极管利用金属与半导体接触形成肖特基势垒构成的微波二极管称为肖特基势垒二极管。
这种器件对外主要呈现非线性电阻特性,是构成微波混频器、检波器和微波开关等的核心元件。
一般地,肖特基势垒二极管的伏安特性可以表示为(1)如图是肖特基势垒二极管的伏安特性曲线假定二极管两端的电压由两部分构成:直流偏压和交流信号(t)=cos,即(2)代入式(1),求得时变电流为(3)定义二极管的时变电导g(t)为根据式(1)得对式(3)进行傅里叶级数展开:i(t)=交流偏压的基波电流幅度I1=I L:I n=2I S exp(αU dc)J1(αU L)根据贝塞尔函数的大宗量近似式,当αU L较大时,有I dcI L二极管对交流信号所呈现的电导为G L=交流偏压一定时,G L随I dc的增大而增大,借助于U dc来调节I dc 可以改变G L的值,使交流信号得到匹配。
二.变容二极管PN结的结电容(主要是势垒电容)随着外加电压的改变而改变,利用这一特性可以构成变容二极管(简称为变容管)。
变容管作为非线性可变电抗器件,可以构成参量放大器、参量变频器、参量倍频器(谐波发生器)、可变衰减或调制器等。
结电容可以表示为以下普遍形式:mj j U C U C ]1[)0()(Φ=— 式中:m 称为结电容非线性系数,取决于半导体中参杂浓度的分布状态。
给变容管加上直流负偏压dc U 和交流信号(泵浦电压) t U t u p p p ωcos )(=,即 t U U t u p p ωcos )(dc += 由上式得时变电容为m cos p 1)(]cos 1[)0()()—(—t U C tU U C t C p dc j mp p dc j j ωω=Φ+=式中:m dc j dc j U C U C ]1[)0()(Φ=—,dcU U p p—Φ=其中:)(dc j U C 为直流工作点dc U 处的结电容;p 为相对泵浦电压幅度(简称相对泵幅),表明泵浦激励的强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微波电子线路作业班级:020911姓名:张盎农学号:02091086一ADS混频器设计耦合器设计仿真结果低通滤波器设计仿真结果输出频谱仿真1按照文档所连错误提示2直接代入数值修改后端口1:P=dbmtow(-20),功率源输出信号功率为-20dBm Freq=,射频输入频率端口2:P=dbmtow(10),功率源输出信号功率为10dBm Freq=,本振输入频率谐波平衡仿真控制器设置如图所示本振与输出修改端口2重新设置:P=dbmtow(LO_pwr),即设置变量LO_pwr 增加变量设置VAR,设置如图所示仿真结果从图像结果可看出Vout输出与本振功率有关三阶交调分析将的端口1的单品功率源更换为多频功率源P_nTone,对其设置如图所示修改端口2 和VAR的设置,如图所示修改谐波平衡仿真控制器,设置如图所示插入测量方程控件Meas Eqn,并对其参数如图设置仿真结果二,理论分析微波混频器1、微波混频器的作用与用途微波混频器是通信、雷达、电子对抗等系统的微波接收机以及很多微波测量设备所不可缺少的组成部分。
它将微弱的微波信号和本地振荡信号同时加到非线性元件上,变换为频率较低的中频信号,进一步进行放大、解调和信号处理。
2,混频原理下图是微波混频器的原理图,对它的基本要求是小变频损耗和低噪声系数。
通常,微波混频器是一种非线性电阻频率变换电路。
微波混频器的核心元件是肖特基势垒二极管。
常见的微波混频器基本电路有三种类型:单端混频器使用一个混频二极管,是最简单的微波混频器;单平衡混频器使用两个混频二极管;双平衡混频器采用四个混频二极管。
本节以元件的特性为基础,分析非线性电阻微波混频器的工作原理及性能指标,包括电路时-频域关系、功率关系、变频损耗、噪声特性,并给出各种微波混频器的电路实现等。
本振激励特性——混频器的大信号参量如下图所示,在混频二极管上加大信号本振功率和直流偏置(或零偏压)时,流过混频二极管的电流由二极管的伏安特性来决定。
加在二极管上的电压是直流偏置与本振信号之和,二极管的伏安特性近似为指数函数,即则流过二极管的大信号电流为0L L sa ()cos ()evu t E U t i f v I αω=+=≈0L L 0L L (cos )0L L sa cos sa (cos )e e e E U t E U ti f E U t I I αωααωω+=+==混频二极管加直流偏压和本振功率时的原理图显然,流过二极管的大信号电流是本振功率ωL 的周期性函数,可用傅里叶级数表示为式中:直流分量n 次谐波电流幅值本振基波电流幅值当αU L 足够大时, 有故直流分量和本振基波电流幅值为0L 12cos n n i I I n tω∞==+∑00sa 0L e ()E I I J U αα=0sa L e ()E n n I I J U αα=0L11sa 1L 22e ()E I I I J U αα==L L Le ()2πU n J U U ααα≈L L1L 0L12P I U I U =≈即I L1≈2I 0 (3-4)则所需的本振激励功率为混频器对本振呈现的电导为可见,当U L一定时,G L值随直流电流的增大而增大,因而可以借助于调整E 0来调节I 0,从而改变G L 使本振口达到匹配。
在实际工作中,因为微波波段很难测量U L ,所以通常由测量P L 和I 0来测定U L 和G L 。
当混频二极管上只加直流偏压E 0和本振功率时,混频二极管呈现的电导为式(3-7)说明当本振电压随时间作周期性变化时,瞬时电导g (t )也随时间作周期性变化,故称为时变电导;同样g (t )也可以展成傅里叶级数:式中:g 0称为二极管的平均混频电导,g n 是对应本振n 次谐波的混频电导。
非线性电阻的混频原理二极管混频器的原理等效电路如图3-3所示,在肖特基势垒二极管上加有较小的直流偏压(或零偏压)、大信号本振功率(1 mW 以上)及接收到的0L ()sa 0Le2πE U I I U αα+≈0L L 0L L cos 0L L (cos )sa d |'(cos )d e ()u E U t E U t if E U t vI g t ωαωωα=++=+== 0L1L L L2I I G U U =≈0L 1()2cos n n g t g g tω∞==+∑微弱信号(微瓦(μW)量级以下)。
假设本振与信号分别表示为u L (t )=U L cos ωL tu S (t )=U S cos ωS t图 3-3 二极管混频器原理图由于U L >>U S ,可以认为二极管的工作点随本振电压变化,认为接收到的信号是一个微小电压增量,因此将回路电流在各个工作点展开为泰勒级数。
为了讨论方便,将Z L 、Z L0、Z S 短路,这时流过二极管的瞬时电流值为展开式中的第一项为本振激励下的流过二极管的大信号电流,它包含直流和本振基波其谐波项。
展开式中的其他各项为二极管中的小信号成分,当u S 很小时,可仅取第二项。
由式(3-9)可知,f ′(E 0+U L cos ωL t )是在本振激励下二极管所呈0L L S S 0L L 0L L S S 20L L S S ()(cos cos )(cos )'(cos )cos 1''(cos )(cos )2!i f u f E U t U t f E U t f E U t U t f E U t U t ωωωωωωω==++=++++++…现的时变电导g (t )。
由式(3-7)~式(3-9)可知,二极管中的小信号成分近似为混频器电流的主要频谱如图3-4所示,并用虚线画出了混频电流中的大信号成分,即直流、本振基波及本振各次谐波。
图 3-4 混频器电流的主要频谱(设ω0=ωS -ωL )从上分析可见:(1) 在混频器中产生了无数的组合频率分量,若负载Z L 采用中频带通滤波器,就可以取出所需的中频分量而将其他组合频率滤掉。
(2) 从式(3-10)可得中频分量振幅为I 0=g 1U S中频电流振幅与输入信号振幅U S 成比例,即在小信号时,混频输入端与输出端的分量振幅之间具有线性关系。
(3) 混频过程中,本振是强信号,它产生了无数的谐波,但其谐波功率大约随1/n 2变化(n 为谐波次数),因此混频电流的组合分量强度随n 的增加而很快地减少。
通常只有当本振基波ωL 和2次谐波2ωL 分量足够大时,0L L S S ()'(cos )cos i t f E U t U tωω=+01L 2L S S (2cos 2cos 2)cos g g t g t U tωωω=+++…0S S S L S 1cos cos()n n g U t g U n t ωωω∞==+±∑才会对变频效率的影响较大。
因此,我们只讨论几个特殊的频率分量:信号频率与本振频率产生的和频ω+=ωL +ωS 、差频ω0=ωS -ωL (当ωS >ωL 时)或ω0=ωL -ωS (当ωL >ωS 时),ωS 与2ωL 产生的镜像频率ωi =2ωL -ωS =ωL -ω0分量。
由图3-4可以看出,ωi 是信号相对于本振基频ωL 的“镜像”,故称之为镜频,其幅度由g 2U S 决定。
ωi 中包含部分有用信号功率,如果在输入电路中将其反射回二极管并重新与本振混频,即可再次产生中频ωL -ωi =ω0。
当相位选择合适时,就能“回收”信号能量,以减小变频损耗。
这是后面要讨论的“镜频回收问题”。
以上是假设接收信号较弱情况下的小信号分析,并设本振与信号初相位均为零。
实际中二者之间有相位差,而且信号可能较强,如雷达近距离目标的反射信号、附近电台的干扰信号等,在这种情况下,就不能将U 2S 以上的高次项忽略了。
此时混频电流的频谱分量大为增加。
下面定性分析信号较强情况下的电流频谱。
为了简便起见,用指数形式表达g (t )函数。
根据式(3-8),考虑初相位φL 和φS ,则有用指数形式可表示为0L L 1()2cos()n n g t g g n t n ωϕ∞==++∑L L L j j j *01()[ee]e n tn tn tn nnn n g t g y y yωωω∞∞-==-∞=++=∑∑式中: 。
如果定义g n =g -n ,则 ,并且y 0=g 0。
同样,信号电压可以表示为当U S 较大,不能忽略U 2S 以上各项时,则式(3-9)最终可写为式中: 是每个n ωL +m ωS 频率分量的复振幅。
因为i (t )是时间的实函数,所以有从式(3-14)中可得到实数中频电流为。
可见,当信号较强时,混频电流i (t )中包括信号(ωS )和本振(ωL )所有可能的各次谐波组合,它比小信号时的组合分量丰富得多,从而消耗更多的信号功率,使变频损耗增加,并产生各种变频干扰和失真。
因此,在设计混频电路时,应考虑如何抑制部分组合频率成分,以改善混频器的性能。
Lj e n n n y g ϕ=,L j en n n y g ϕ--=L j *e n n n ny g y ϕ-==-S S j j S S S S S 1cos()(e e )2t t u U t U ωωωϕ-=+=+L S L S .j()j()()||e e n m n m tn m n m i t I ϕϕωω∞∞++=-∞=-∞=∑∑L S .j()e n m tn m n m I ωω∞∞+=-∞=-∞=∑∑.1,10S L ()2||cos[()]i t I t ωωϕ-+=--.*,n m n mI I --=混频器等效网络上面求混频产生的小信号电流i(t)时,仅计算了接收信号v S(t)和本振的所谓“一次混频”,而未考虑混频产物的反作用。
在实际工作中,至少要考虑中频ω0和镜频ωi的反作用,实际的混频器电路可以等效为图3-5所示的简化电路。
加在二极管上的电压为本振电压:u L(t)=U L cosωL t信号电压:u S(t)=U S sinωS t中频电压:u0(t)=-U0 sinω0t镜频电压:u i(t)=-U i sinωi t图 3-5 加在混频二极管上的电压其中:u0(t)和u i(t)取负号是因为混频电流i在中频电阻R0和镜频电阻R i上产生的电压降反向加到二极管上。
在这些电压中,本振是大信号,其余幅值都很小,本振和直流偏压决定二极管的工作点,混频器的工作状态可看成是大信号u L上叠加了小信号u S、u0和u i。
这时流过二极管的电流为i=f (E0+u L+u S+u0+u i)=f (E0+u L+Δu)式中:Δu=u S+u0+u i,利用前面的分析方法,得到小信号电流为i D小= f′(E0+u L)Δu=g(t)·Δu= (g0+2g1 cosωL t+2g2 cos2ωL t+?)×(U S sinωS t-U0 sinω0t-U i sin ωi t)=g0U S sinωS t-g0U0 sinω0t-g0U i sinωi t+g1U S sin(ωL+ωS)t+g1U S sin(ωS-ωL)t-g1U0 sin(ωL+ω0)t+g1U0 sin(ωL-ω0)t+g1U i sin(ωL-ωi)t-g1U i sin(ωL+ωi)t+g2U S sin(2ωL+ωS)t-g2U S sin(2ωL-ωS)t-g2U0 sin(2ωL+ω0)t+g2U0 sin(2ωL-ω0)t-g2U i sin(2ωL+ωi)t+g2U i sin(2ωL-ωi)t(3-15)从式(3-15)中取出信频、中频和镜频电流,它们的幅值分别为I S=g0U S-g1U0+g2U iI0=g1U S-g0U0+g1U iI i=-g2U S+g1U0-g0U i式(3-16)是一个三端口网络的线性方程组。
