(完整版)勾股定理典型例题详解及练习(附答案)
勾股定理实际应用(习题及答案)

勾股定理实际应用(习题)例题示范例1:如图,这是一个供滑板爱好者使用的U 型池,该U 型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为2m 的半圆,其边缘AB =CD =10m ,点E 在CD 上,且CE =2m .若一滑行爱好者从点A 到点E ,则他滑行的最短距离是多少?(边缘部分的厚度忽略不计,π取整数3)思路分析:1.作侧面展开图2.找点,连线3.构造直角三角形,利用勾股定理进行计算①由已知得,AD 6≈,DE =8②在Rt △ADE 中,由勾股定理可得AE =10过程书写:解:如图,作出U 型池的侧面展开图由题意得,AD 2262π⋅=≈,DE =8在Rt △ADE 中,∠D =90°由勾股定理,得AD 2+DE 2=AE 2∴62+82=AE 2∴AE =10∴他滑行的最短距离是10m巩固练习1.如图,有两棵树,一棵高10米,一棵高5米,两树相距12米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行________米.第1题图第2题图2.如图,沿AC方向开山修建一条公路,为了加快施工进度,要在小山的另一边寻找点E同时施工,从AC上的一点B取∠ABD=150°,沿BD的方向前进,取∠BDE=60°,测得BD=520m,BC=80m,并且AC,BD和DE在同一平面内,那么公路CE段的长度为()A.180m B.2603mC.(260280)-m-m D.(260380)3.在一次课外实践中,王强想知道学校旗杆的高,但不能爬上旗杆也不能把绳子解下来,可是他发现旗杆上的绳子垂到地面上还多1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,则旗杆的高为()A.13m B.12m C.4m D.10m 4.11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题:小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高30肘尺(肘尺是古代的长度单位),另外一棵树高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻飞去抓鱼,并且同时到达目标.则这条鱼出现的地方与较高的棕榈树之间的距离为__________.5.如图,一个三级台阶的每一级的长、宽、高分别为50cm,30cm,10cm,A和B是这个台阶的两个相对的端点,A点处有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,需要爬行的最短路径长为__________.6.小明家新装修房子,其中有一段楼梯需要铺上地毯,楼梯高6米,斜面长10米,到底该买多长的地毯才能恰好把楼梯铺满呢(原则:铺满楼梯但不能浪费),小明爸妈也摸不着头脑.小明给爸妈的正确答案应是___________.第6题图第7题图7.如图,长方体的长、宽、高分别为4cm,2cm,5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为_________cm.8.如图,已知圆柱底面的周长为2cm,高为1cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为________.第8题图第9题图9.如图,圆柱体的高为10cm,底面圆的半径为4cm.在AA1上的点Q处有一只蚂蚁,QA=3cm;在BB1上的点P处有一滴蜂蜜,PB1=2cm.若蚂蚁想要沿圆柱体侧面爬到点P处吃蜂蜜,则爬行的最短路径长是___________.(π取整数3)10.长方体敞口玻璃罐,长、宽、高分别为10cm、4cm和4cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐内壁,在长方形ABCD中心正上方1cm的点H处,则蚂蚁到达饼干的最短距离是()cm.A.74B.8C.310D.34411.如图所示的一只玻璃杯,高为8cm,将一根筷子插入其中,若杯外最长4cm,最短2cm,则这只玻璃杯的底面直径是___________cm.第10题图第11题图12.如图,将一根长为24cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中.设筷子露在杯子外面的长为h cm,则h的取值范围是__________________.13.如图,某隧道的截面是一个半径为4.2米的半圆形,一辆高3.6米,宽3米的卡车能通过该隧道吗?【参考答案】巩固练习1.132.D3.B4.20肘尺5.130cm6.14米7.138.22cm9.13m10.A11.612.11≤h≤1213.卡车能通过该隧道,理由略。
(完整版)勾股定理典型例题详解及练习(附答案)

典型例题知识点一、直接应用勾股定理或勾股定理逆定理例1:如图,在单位正方形组成的网格图中标有AB CD EF、GH四条线段, 其中能构成一个直角三角形三边的线段是()A.CD、EF、GHC. AB、CD GHB.AB、EF、GHD. AB、CD EF愿路分乐屮1)題意分析’本题考查幻股定理及勾股定理的逆定理.亠2)解題思器;可利用勾脸定理直接求出各边长,再试行判断•』解答过整屮在取DEAF中,Af=l, AE=2,根据勾股定理,得昇EF = Q抡於十£尸° = Q +F二艮同理HE = 2百* QH. = 1 CD = 2^5计算发现W十◎血尸=(鸥31即血+曲=GH2,根据勾股定理的逆宦理得到UAAE、EF\ GH为辺的三角形是直毎三角形.故选B. *縮題后KJ思专:*1.勾股定理只适用于直角三角形,而不适用于说角三角形和钝角三角形・因此」辭题时一宦妾认真分析题目所蛤■条件■,看是否可用勾股定理来解口*2.在运用勾股左理时,要正确分析题目所给的条件,不要习惯性地认为就是斜迫而“固执”地运用公式川二/十就其实,同样是S6"不一罡就等于餌,疋不一罡就昱斜辺,KABC不一定就是直角三祐3.直角三第形的判定条件与勾股定理是互逆的.区别在于勾股定理的运用是一个从卅形s—个三角形是直角三角形)到懺 y =沖十沪)的过程,而直角三角形的判定是一①从嗦(一个三角形的三辺满足X二护+酹的条件)到偲个三角形是直角三角形)的过程.a4•在应用勾股定理解题叭聲全面地琴虑间题.注意m题中存在的多种可能性,遊免漏辭.初例玉如圏,有一块直角三角形®椀屈U,两直角迫4CM5沁丸m・现将直角边AC沿直绘AD折蠡便它落在斜边AB上.且点C落到点E处, 则切等于(、*C/) "禎B. 3cm G-Icnin題童分析,本题着查勾股定理的应用刎:)解龜思路;車题若直接在△MQ中运用勾股定理是无法求得仞的长的,因为貝知遒一条边卫0的长,由题意可知,AACD和心迓门关于直线KQ对称.因而^ACD^hAED ・进一歩则有应RUm CZAED ED 丄AB,设UD=E2>黄泱,则在Rt A ABO中,由勾股定理可得^=^(^+^=^83=100,得AB=10cm,在松迟DE 中,W ClO-fl)2= d驚解得尸九4解龜后的思琴尸勾股定理说到底是一个等式,而含有未知数的等式就是方程。
(完整版)勾股定理经典例题(含答案)

经典例题透析类型一:勾股定理的直接用法1、在Rt△ABC中,∠C=90°(1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a.思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
解析:(1) 在△ABC中,∠C=90°,a=6,c=10,b=(2) 在△ABC中,∠C=90°,a=40,b=9,c=(3) 在△ABC中,∠C=90°,c=25,b=15,a=举一反三【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?【答案】∵∠ACD=90°AD=13, CD=12∴AC2 =AD2-CD2=132-122=25∴AC=5又∵∠ABC=90°且BC=3∴由勾股定理可得AB2=AC2-BC2=52-32=16∴AB= 4∴AB的长是4.类型二:勾股定理的构造应用2、如图,已知:在中,,,. 求:BC的长.思路点拨:由条件,想到构造含角的直角三角形,为此作于D,则有,,再由勾股定理计算出AD、DC的长,进而求出BC的长.解析:作于D,则因,∴(的两个锐角互余)∴(在中,如果一个锐角等于,那么它所对的直角边等于斜边的一半).根据勾股定理,在中,.根据勾股定理,在中,.∴.举一反三【变式1】如图,已知:,,于P. 求证:.解析:连结BM,根据勾股定理,在中,.而在中,则根据勾股定理有.∴又∵(已知),∴.在中,根据勾股定理有,∴.【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的面积。
分析:如何构造直角三角形是解本题的关键,可以连结AC,或延长AB、DC交于F,或延长AD、BC交于点E,根据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。
勾股定理经典题型(后附答案)

勾股定理经典题型(后附答案)第 1 页共 5 页勾股定理经典题型(后附答案)⼀、经典例题精讲题型⼀:直接考查勾股定理例1.在ABC ?中,90C ∠=?.⑴已知6AC =,8BC =.求AB 的长. ⑵已知17AB =,15AC =,求BC 的长. 题型⼆:利⽤勾股定理测量长度例题1 如果梯⼦的底端离建筑物9⽶,那么15⽶长的梯⼦可以到达建筑物的⾼度是多少⽶?例题2 如图(8),⽔池中离岸边D 点1.5⽶的C 处,直⽴长着⼀根芦苇,出⽔部分BC 的长是0.5⽶,把芦苇拉到岸边,它的顶端B 恰好落到D 点,并求⽔池的深度AC.题型三:勾股定理和逆定理并⽤——例题3 如图3,正⽅形ABCD 中,E 是BC 边上的中点,F 是AB 上⼀点,且AB FB 41=那么△DEF 是直⾓三⾓形吗?为什么?题型四:利⽤勾股定理求线段长度——例题4 如图4,已知长⽅形ABCD 中AB=8cm,BC=10cm,在边CD 上取⼀点E ,将△ADE 折叠使点D 恰好落在BC 边上的点F ,求CE 的长.题型五:利⽤勾股定理逆定理判断垂直——例题5 如图5,王师傅想要检测桌⼦的表⾯AD 边是否垂直与AB 边和CD 边,他测得AD=80cm ,AB=60cm ,BD=100c m,AD 边与AB 边垂直吗?怎样去验证AD 边与CD 边是否垂直?例题6 有⼀个传感器控制的灯,安装在门上⽅,离地⾼4.5⽶的墙上,任何东西只要移⾄5⽶以内,灯就⾃动打开,⼀个⾝⾼1.5⽶的学⽣,要⾛到离门多远的地⽅灯刚好打开?第 2 页共 5 页题型六:旋转问题:例题7 如图,△ABC 是直⾓三⾓形,BC 是斜边,将△ABP 绕点A 逆时针旋转后,能与△ACP ′重合,若AP=3,求PP ′的长。
变式1: 如图,P 是等边三⾓形ABC 内⼀点,PA=2,PB=23,PC=4,求△ABC 的边长.变式2: 如图,△ABC 为等腰直⾓三⾓形,∠BAC=90°,E 、F 是BC 上的点,且∠EAF=45°,试探究222BE CF EF 、、间的关系,并说明理由.题型七:关于翻折问题例题8 如图,矩形纸⽚ABCD 的边AB=10cm ,BC=6cm ,E 为BC 上⼀点,将矩形纸⽚沿AE 折叠,点B 恰好落在CD 边上的点G 处,求BE 的长.变式:如图,AD 是△ABC 的中线,∠ADC=45°,把△ADC 沿直线AD 翻折,点C 落在点C ’的位置,BC=4,求BC ’的长.题型⼋:关于勾股定理在实际中的应⽤:例题9 如图,公路MN 和公路PQ 在P点处交汇,点A处有⼀所中学,AP=160⽶,点A 到公路MN 的距离为80⽶,假使拖拉机⾏驶时,周围100⽶以内会受到噪⾳影响,那么拖拉机在公路MN 上沿PN ⽅向⾏驶时,学校是否会受到影响,第 3 页共5页请说明理由;如果受到影响,已知拖拉机的速度是18千⽶/⼩时,那么学校受到影响的时间为多少?题型九:关于最短性问题例题10 如右图1-19,壁虎在⼀座底⾯半径为2⽶,⾼为4⽶的油罐的下底边沿A 处,它发现在⾃⼰的正上⽅油罐上边缘的B 处有⼀只害⾍,便决定捕捉这只害⾍,为了不引起害⾍的注意,它故意不⾛直线,⽽是绕着油罐,沿⼀条螺旋路线,从背后对害⾍进⾏突然袭击.结果,壁虎的偷袭得到成功,获得了⼀顿美餐.请问壁虎⾄少要爬⾏多少路程才能捕到害⾍?(π取3.14,结果保留1位⼩数,可以⽤计算器计算)变式:如图为⼀棱长为3cm 的正⽅体,把所有⾯都分为9个⼩正⽅形,其边长都是1cm ,假设⼀只蚂蚁每秒爬⾏2cm ,则它从下地⾯A 点沿表⾯爬⾏⾄右侧⾯的B 点,最少要花⼏秒钟?三、课后训练:⼀、填空题1.如图(1),在⾼2⽶,坡⾓为30°的楼梯表⾯铺地毯,地毯的长⾄少需________⽶. 2.种盛饮料的圆柱形杯(如图),测得内部底⾯半径为2.5㎝,⾼为12㎝,吸管放进杯⾥,杯⼝外⾯⾄少要露出 4.6㎝,问吸管要做㎝。
勾股定理经典题型(后附答案)
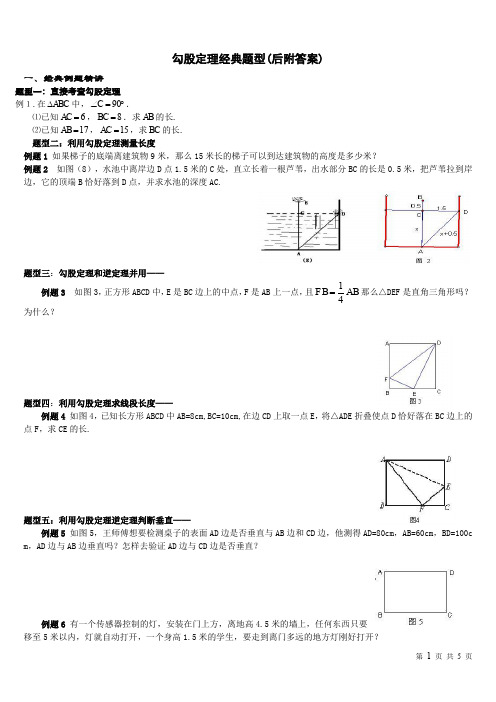
第 1 页 共 5 页勾股定理经典题型(后附答案)一、经典例题精讲题型一:直接考查勾股定理例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长. ⑵已知17AB =,15AC =,求BC 的长. 题型二:利用勾股定理测量长度例题1 如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是多少米?例题2 如图(8),水池中离岸边D 点1.5米的C 处,直立长着一根芦苇,出水部分BC 的长是0.5米,把芦苇拉到岸边,它的顶端B 恰好落到D 点,并求水池的深度AC.题型三:勾股定理和逆定理并用——例题3 如图3,正方形ABCD 中,E 是BC 边上的中点,F 是AB 上一点,且AB FB 41=那么△DEF 是直角三角形吗?为什么?题型四:利用勾股定理求线段长度——例题4 如图4,已知长方形ABCD 中AB=8cm,BC=10cm,在边CD 上取一点E ,将△ADE 折叠使点D 恰好落在BC 边上的点F ,求CE 的长.题型五:利用勾股定理逆定理判断垂直——例题5 如图5,王师傅想要检测桌子的表面AD 边是否垂直与AB 边和CD 边,他测得AD=80cm ,AB=60cm ,BD=100c m ,AD 边与AB 边垂直吗?怎样去验证AD 边与CD 边是否垂直?例题6 有一个传感器控制的灯,安装在门上方,离地高4.5米的墙上,任何东西只要移至5米以内,灯就自动打开,一个身高1.5米的学生,要走到离门多远的地方灯刚好打开?第 2 页 共 5 页题型六:旋转问题:例题7 如图,△ABC 是直角三角形,BC 是斜边,将△ABP 绕点A 逆时针旋转后,能与△ACP ′重合,若AP=3,求PP ′的长。
变式1: 如图,P 是等边三角形ABC 内一点,PA=2,PB=23,PC=4,求△ABC 的边长.变式2: 如图,△ABC 为等腰直角三角形,∠BAC=90°,E 、F 是BC 上的点,且∠EAF=45°,试探究222BE CF EF 、、间的关系,并说明理由.题型七:关于翻折问题例题8 如图,矩形纸片ABCD 的边AB=10cm ,BC=6cm ,E 为BC 上一点,将矩形纸片沿AE 折叠,点B 恰好落在CD 边上的点G 处,求BE 的长.变式:如图,AD 是△ABC 的中线,∠ADC=45°,把△ADC 沿直线AD 翻折,点C 落在点C ’的位置,BC=4,求BC ’的长.题型八:关于勾股定理在实际中的应用:例题9 如图,公路MN 和公路PQ 在P点处交汇,点A处有一所中学,AP=160米,点A 到公路MN 的距离为80米,假 使拖拉机行驶时,周围100米以内会受到噪音影响,那么拖拉机在公路MN 上沿PN 方向行驶时,学校是否会受到影响,第 3 页共5页请说明理由;如果受到影响,已知拖拉机的速度是18千米/小时,那么学校受到影响的时间为多少?题型九:关于最短性问题例题10 如右图1-19,壁虎在一座底面半径为2米,高为4米的油罐的下底边沿A 处,它发现在自己的正上方油罐 上边缘的B 处有一只害虫,便决定捕捉这只害虫,为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿一 条螺旋路线,从背后对害虫进行突然袭击.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问壁虎至少要爬行多少 路程才能捕到害虫?(π取3.14,结果保留1位小数,可以用计算器计算)变式:如图为一棱长为3cm 的正方体,把 所有面都分为9个小正方形,其边长都是1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下地面A 点沿表面爬行至右侧面 的B 点,最少要花几秒钟?三、课后训练: 一、填空题1.如图(1),在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需________米. 2.种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出 4.6㎝,问吸管要做 ㎝。
勾股定理练习题(含答案)

勾股定理练习题(含答案)1.下列说法正确的是:C.若a、b、c是Rt△ABC的三边,A=90°,则a+b=c。
2.根据勾股定理,应该选B.a+b>c。
3.根据勾股定理,斜边长为√(k-1)²+(2k)²,即√(5k²-4)。
4.根据(a-b)(a+b-c)=0,可得a=b或a+b=c,所以它的形状为等腰三角形或直角三角形。
5.设另一直角边为x,则根据勾股定理得x²+9²=(x+1)²,解得x=40/9,周长为9+40/9+41/9=120/9=40/3,选C。
6.根据勾股定理得BC=√(13²-12²)=5,所以周长为15+13+5=33,选D。
7.根据勾股定理和中线长度公式得周长为2d+2√(d²-S),选C。
8.根据勾股定理得OP的长度为√(3²+4²)=5,选C。
9.根据勾股定理和海伦公式得BC=√(26²-24²/25)=17,选A。
10.根据(a-6)+b-8+c-10²=0,可得a+b+c=24,所以它的形状为等边三角形。
11.根据勾股定理和面积公式得面积为(8*15)/2=60,选D。
12.根据等腰三角形的性质,顶角的平分线与底边中线重合,所以答案为底边中线,即6.5.13.根据勾股定理得斜边长为√200=10√2,选D。
14.根据三角形边长比的性质,10:8:6无法构成三角形,所以不是三角形。
15.一个三角形的三边比为5:12:13,周长为60,则其面积为多少?16.在直角三角形ABC中,斜边AB=4,则AB+BC+AC=多少?17.如图,已知直角三角形ABC中,∠C=90°,BA=15,AC=12,以直角边BC为直径作半圆,则该半圆的面积为多少?18.若三角形三个内角的比为1:2:3,最短边长为1cm,最长边长为2cm,则该三角形三个角度数分别为多少?另外一边的平方是多少?19.长方形的一边长为3cm,面积为12cm²,则其一条对角线长为多少?20.如图,一个高为4m、宽为3m的大门,需要在对角线的顶点间加固一个木条,求该木条的长度。
勾股定理综合应用题(包含答案)

勾股定理综合应用题(包含答案)勾股定理综合应用题及答案1.一艘船从A地出发,向东航行20海里到达B地,再向XXX15海里到达C地。
求AC的长度。
答案:25海里2.一块长方形的地,长60米,宽40米。
现在要在这块地上建造一个正方形的花坛,使剩下的土地面积最大。
问这个花坛的边长和剩余土地的面积。
答案:花坛边长为20米,剩余土地面积为2400平方米或者3987.5平方米。
3.一架飞机以每小时600千米的速度飞行,从A地飞往B 地,飞行时间是5小时。
飞机从B地返回A地的途中,由于风向的影响,飞机的速度变为每小时400千米,飞行时间是6小时。
求AB两地的距离。
答案:10千米。
4.一列货车从A地出发,以每小时50千米的速度行驶,3小时后到达B地,再以每小时40千米的速度行驶,2小时后到达C地。
求AC两地的距离。
答案:20km。
5.一辆汽车从A地出发,向东行驶30海里到达B地,再向北行驶40海里到达C地。
已知汽车的速度为60千米/小时,求(1)AB、BC两段路程所需的时间;(2)从C地返回A地的汽车速度为50千米/小时,求从C地返回A地所需的时间。
答案:(1)AB段需要0.5小时,BC段需要0.67小时;(2)从C地返回A地需要1小时。
6.一条长方形的草坪长12米,宽8米,现在要在这条草坪上建造一个半径为3米的圆形花坛,请问这个花坛占用的草坪面积是多少?答案:96平方米。
7.已知一条边长为4米的正方形,将这个正方形绕其中心旋转45度,求旋转后正方形所在的圆的周长。
答案:2√3–4.8.一座高度为8米的房子前有一座高度为6米的灯杆,灯杆顶部离房顶的最短距离为2米。
求灯杆离房子底部的最短距离。
答案:10米。
9.甲乙两人同时从A地出发,甲向B地行驶,乙向C地行驶,两人相遇于D地,甲行驶了8天,乙行驶了12天。
已知AB、DC两段路程长度相等,求AD的长度。
答案:10天。
10.一条直角三角形的斜边长为13米,一条直角边长为5米,求另一条直角边的长度。
(完整版)八年级勾股定理典型练习题含答案

八年级勾股定理典型练习题含答案一、选择题1、下列各组数中,能构成直角三角形的是A:4,5,B:1,1:6,8,11 D:5,12,22、在Rt△ABC中,∠C=90°,a=12,b=16,则c的长为 A:26B:1 C:20D:213、在平面直角坐标系中,已知点P的坐标是,则OP 的长为 A:3B:4C:5D:74、在Rt△ABC中,∠C=90°,∠B=45°,c=10,则a的长为 A: B:C:5D:、等边三角形的边长为2,则该三角形的面积为A、、、36、若等腰三角形的腰长为10,底边长为12,则底边上的高为A、 B、C、8D、9、已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为A、3cmC、6cm22B、4cm D、12cm228、若△ABC中,AB?13cm,AC?15cm,高AD=12,则BC 的长为 A、1 B、 C、14或4D、以上都不对二、填空题1、若一个三角形的三边满足c?a?b,则这个三角形是2、木工师傅要做一个长方形桌面,做好后量得长为80cm,宽为60cm,对角线为100cm,则这个桌面。
3、直角三角形两直角边长分别为3和4,则它斜边上的高为__________。
2224、如右图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为5,则正方形A,B,C,D的面积的和为。
5、如右图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=___________。
E6、一只蚂蚁从长为4cm、宽为cm,高是cm的FC长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是____________cm。
7、将一根长为15㎝的筷子置于底面直径为5㎝,高为12㎝的圆柱形水杯中,设筷子露在杯子外面的长为h㎝,则h的取值范围是________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
典型例题
知识点一、直接应用勾股定理或勾股定理逆定理
例1:如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是()
A. CD、EF、GH
B. AB、EF、GH
C. AB、CD、GH
D. AB、CD、EF
勾股定理说到底是一个等式,而含有未知数的等式就是方程。
所以,在利用勾股定理求线段的长时常通过解方程来解决。
勾股定理表达式中有三个量,如果条件中只有一个已知量,必须设法求出另一个量或求出另外两个量之间的关系,这一点是利用勾股定理求线段长时需要明确的思路。
方程的思想:通过列方程(组)解决问题,如:运用勾股定理及其逆定理求线段的长度或解决实际问题时,经常利用勾股定理中的等量关系列出方程来解
决问题等。
例3:一场罕见的大风过后,学校那棵老杨树折断在地,此刻,张老师正和占明、清华、绣亚、冠华在楼上凭栏远眺。
清华开口说道:“老师,那棵树看起来挺高的。
”
“是啊,有10米高呢,现在被风拦腰刮断,可惜呀!”
“但站立的一段似乎也不矮,有四五米高吧。
”冠华兴致勃勃地说。
张老师心有所动,他说:“刚才我跑过时用脚步量了一下,发现树尖距离树根恰好3米,你们能求出杨树站立的那一段的高度吗?”
占明想了想说:“树根、树尖、折断处三点依次相连后构成一个直角三角
形。
”
“勾股定理一定是要用的,而且不动笔墨恐怕是不行的。
”绣亚补充说。
几位男孩子走进教室,画图、计算,不一会就得出了答案。
同学们,你算
出来了吗?
思路分析:
1)题意分析:本题考查勾股定理的应用
2)解题思路:本题关键是认真审题抓住问题的本质进行分析才能得出正确
的解答
常通过作辅助线构造直角三角形将它们转化为直角三角形问题等。
解题后的思考:
分类讨论思想是解题时常用的一种思想方法,同学们如果掌握了这种方法,可以使思维的条理性、缜密性、灵活性得到培养,才能在解题中真正做到不重
不漏。
知识点三、勾股定理及其逆定理的正逆混用
例6:(1)图甲是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形。
若大正方形的面积为13,每个直角三角形两条直角边的和是5,求中
间小正方形的面积。
(2)现有一张长为6.5cm、宽为2cm的纸片,如图乙,请你将它分割成6
块,再拼合成一个正方形。
(要求:先在图乙中画出分割线,再画出拼成的正方形并标明相应数据)。
