运筹学第3版熊伟编著习题答案
熊伟编《运筹学》习题十详细解答

【解】模型 4。
D=50, A=40, H=10f 2HAD2一10一40一50 25200(元) 则每隔0.4月生产一次,每次生产量为20件。
10.2某化工厂每年需要甘油 100吨,订货的固定成本为 100元,甘油单价为7800元/吨,每 吨年保管费为32元,求:(1)最优订货批量;(2)年订货次数;(3)总成本。
【解】模型 4。
D=100 , A=100 , H=32 , C=7800小 J 2AD''2 100 100 冲Q上-上厂绚件)n D/Q 4(次) f . 2 HAD CD2一32一100一100 7800 100 780800(元)则(1)最优订货批量为 25件;(2)年订货4次;(3)总成本为780800元。
10.3工厂每月需要甲零件 3000件,每件零件120元,月存储费率为1.5%,每批订货费为 150元,求经济订货批量及订货周期。
【解】模型 4。
D=3000 , A=150 , H=120 X 0.015= 1.8, C=120Q 磐 FP 0707(件) t Q/D 0.24(月)f 2HAD CD 2 1.8 150 3000 120 3000 361272.79(元)则经济订货批量为 707件,订货周期为0.24月。
10.4某公司预计年销售计算机 2000台,每次订货费为 500元,存储费为32元/ (年台),缺货费为100元/年台。
试求:(1)提前期为零时的最优订货批量及最大缺货量; (2)提前期为10天时的订货点及最大存储量。
【解】模型 3。
D=2000 , A=500 , H=32 , B=100, L=0.0274(年)R = LD — S = 0.0274X 2000 — 69= 55-69 = — 14 (件)(1)最优订货批量为 287台,最大缺货量为 69台;⑵再订货点为—14台,最大存储量习题十10.1某产品每月用量为 优生产批量及生产周期。
熊伟编《运筹学》习题九详细解答

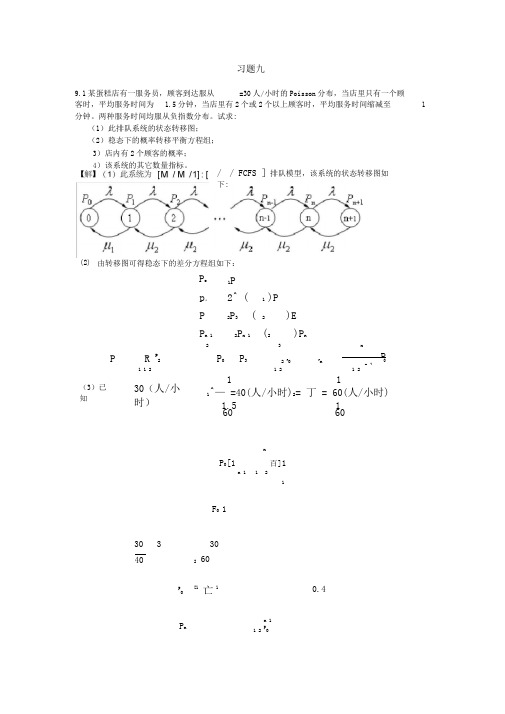
熊伟编《运筹学》习题九详细解答n 1 1 2 p习题九9.1某蛋糕店有一服务员,顾客到达服从=30人/小时的Poisson 分布,当店里只有一个顾客时,平均服务时间为1.5分钟,当店里有2个或2个以上顾客时,平均服务时间缩减至 1分钟。
两种服务时间均服从负指数分布。
试求: (1)此排队系统的状态转移图;(2)稳态下的概率转移平衡方程组;3)店内有2个顾客的概率; 4)该系统的其它数量指标。
(2) 由转移图可得稳态下的差分方程组如下: / / FCFS ]排队模型,该系统的状态转移图如下:1Pp 。
2^ ( 1)PP 2P 3( 2)EPn 1 2Pn 1(2)P n23 nP RP2 P 0 P3 2 PPnP n 11 1 21 21 2Po (3)已知 30(人/小时)1 11^— =40(人/小时)2= 丁 = 60(人/小时) 1.5 1 60 60 nP 0[1百]1n 11 21F 0 130 330 40260 p[1亡10.4P n3 10.4 0.15 4 2(4)系统中的平均顾客数(队长期望值)系统中顾客等待时间9.2某商店每天开10个小时,一天平均有90个顾客到达商店,商店的服务平均速度是每小时服务10个,若假定顾客到达的规律是服从Poisson 分布,商店服务时间服从负指数分布, 试求:(1)在商店前等待服务的顾客平均数。
(2)在队长中多于2个人的概率。
(3)在商店中平均有顾客的人数。
(4)若希望商店平均顾客只有2人,平均服务速度应提高到多少。
【解】此题是属于[M/M/1]:[ / /FCFS]系统,其中:=9 (个/小时) =10(个/小时)/ =9/10(1) L q2/(1)8.1 (个)(2) P(N 2)30.729⑶ L /(1 )9 (个)⑷L/( )22 9 1813.5(个/小时) 229.3为开办一个小型理发店,目前只招聘了一个服务员,需要决定等待理发的顾客的位子应设立多少。
运筹学版熊伟编著习题答案

运筹学(第3版)习题答案P36 P74 P88 P105 P142 P173 P195 P218 P248 P277 P304 品P343 P371全书420页第1章 线性规划工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.产品 资源 A B C 资源限量 材料(kg) 4 2500 设备(台时) 3 1400 利润(元/件)101412310和130.试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-24所示:型号A 型号B 每套窗架需要材料长度(m ) 数量(根)长度(m) 数量(根)A 1:2 2B 1: 2 A 2:3 B 2:23需要量(套)300400问怎样下料使得(1)用料最少;(2)余料最少. 【解 方案 一 二 三 四 五 六 七 八 九 十 需要量 B1 2 1 1 1 0 0 0 0 0 0 800 B2 2 0 1 0 0 2 1 1 0 0 0 1200 A1 2 0 0 1 0 0 1 0 2 1 0 600 A2120 2 3 900 余料(m) 0 1 1 1 01设x j (j =1,2,…,10)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为10112342567368947910min 28002120026002239000,1,2,,10jj j Z x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩∑ (2)余料最少数学模型为2345681012342567368947910min 0.50.50.52800212002*********0,1,2,,10j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩某企业需要制定1~6月份产品A 的生产与销售计划。
熊伟编《运筹学》习题九详细解答
n 1 1 2 p习题九9.1某蛋糕店有一服务员,顾客到达服从 =30人/小时的Poisson 分布,当店里只有一个顾 客时,平均服务时间为 1.5分钟,当店里有2个或2个以上顾客时,平均服务时间缩减至 1分钟。
两种服务时间均服从负指数分布。
试求: (1) 此排队系统的状态转移图; (2) 稳态下的概率转移平衡方程组; 3) 店内有2个顾客的概率; 4) 该系统的其它数量指标。
(2) 由转移图可得稳态下的差分方程组如下: / / FCFS ]排队模型,该系统的状态转移图如下:1Pp 。
2^ ( 1)PP 2P 3( 2)EPn 1 2Pn 1(2)P n23 nP RP2 P 0 P3 2 PPnP n 11 1 21 21 2Po (3)已知 30(人/小时)1 11^— =40(人/小时)2= 丁 = 60(人/小时) 1.5 1 60 60nP 0[1百]1n 11 21F 0 130 330 40260 p[1亡10.4P n3 10.4 0.15 4 2(4)系统中的平均顾客数(队长期望值)系统中顾客等待时间9.2某商店每天开10个小时,一天平均有 90个顾客到达商店,商店的服务平均速度是每小 时服务10个,若假定顾客到达的规律是服从 Poisson 分布,商店服务时间服从负指数分布, 试求:(1) 在商店前等待服务的顾客平均数。
(2) 在队长中多于2个人的概率。
(3) 在商店中平均有顾客的人数。
(4) 若希望商店平均顾客只有 2人,平均服务速度应提高到多少。
【解】此题是属于[M/M/1]:[ / /FCFS]系统,其中:=9 (个/小时) =10(个/小时)/ =9/10(1) L q2/(1)8.1 (个)(2) P(N 2)30.729⑶ L /(1 )9 (个)⑷L/( )22 9 1813.5(个/小时) 229.3为开办一个小型理发店,目前只招聘了一个服务员,需要决定等待理发的顾客的位子应 设立多少。
运筹学第三版课后习题答案 (2)

运筹学第三版课后习题答案第一章:引论1.1 课后习题习题1a)运筹学是一门应用数学的学科,旨在解决实际问题中的决策和优化问题。
它包括数学模型的建立、问题求解方法的设计等方面。
b)运筹学可以应用于各个领域,如物流管理、生产计划、流程优化等。
它可以帮助组织提高效率、降低成本、优化资源分配等。
c)运筹学主要包括线性规划、整数规划、指派问题等方法。
习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。
它可以帮助制定最佳的生产计划,优化供应链管理,提高运输效率等。
运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题,优化医疗资源分配等。
1.2 课后习题习题1运筹学方法可以应用于各个领域,如物流管理、生产计划、供应链管理、流程优化等。
在物流管理中,可以使用运筹学方法优化仓储和运输的布局,提高货物的运输效率。
在生产计划中,可以使用运筹学方法优化产品的生产数量和生产周期,降低生产成本。
在供应链管理中,可以使用运筹学方法优化订单配送和库存管理,提高供应链的效率。
在流程优化中,可以使用运筹学方法优化业务流程,提高整体效率。
习题2在物流管理中,可以使用运筹学方法优化车辆的调度和路线规划,以提高运输效率和降低成本。
在生产计划中,可以使用运筹学方法优化生产线的安排和产品的生产量,以降低生产成本和提高产能利用率。
在供应链管理中,可以使用运筹学方法优化供应链各个环节的协调和调度,以提高整体效率和减少库存成本。
在流程优化中,可以使用运筹学方法优化业务流程的排布和资源的分配,以提高流程效率和客户满意度。
第二章:线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法,用于解决包含线性约束和线性目标函数的优化问题。
其一般形式为:max c^T*xs.t. Ax <= bx >= 0其中,c是目标函数的系数向量,x是决策变量向量,A是约束矩阵,b是约束向量。
习题2使用线性规划方法可以解决许多实际问题,如生产计划、供应链管理、资源分配等。
熊伟编《运筹学》习题十一详细解答
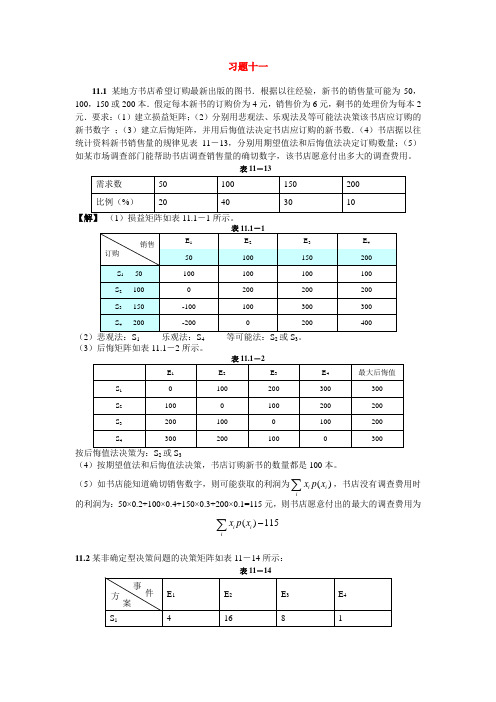
习题十一11.1 某地方书店希望订购最新出版的图书.根据以往经验,新书的销售量可能为50,100,150或200本.假定每本新书的订购价为4元,销售价为6元,剩书的处理价为每本2元.要求:(1)建立损益矩阵;(2)分别用悲观法、乐观法及等可能法决策该书店应订购的新书数字 ;(3)建立后悔矩阵,并用后悔值法决定书店应订购的新书数.(4)书店据以往统计资料新书销售量的规律见表11-13,分别用期望值法和后悔值法决定订购数量;(5)如某市场调查部门能帮助书店调查销售量的确切数字,该书店愿意付出多大的调查费用。
表11-13(21423(3)后悔矩阵如表11.1-2所示。
23(4)按期望值法和后悔值法决策,书店订购新书的数量都是100本。
(5)如书店能知道确切销售数字,则可能获取的利润为()iiix p x ∑,书店没有调查费用时的利润为:50×0.2+100×0.4+150×0.3+200×0.1=115元,则书店愿意付出的最大的调查费用为()115iiix p x -∑11.2某非确定型决策问题的决策矩阵如表11-14所示:表11-14(1定出相应的最优方案.(2)若表11-14中的数字为成本,问对应于上述决策准则所选择的方案有何变化?【解】(1)悲观主义准则:S3;乐观主义准则:S3;Lapalace准则:S3;Savage准则:S1;折衷主义准则:S3。
(2)悲观主义准则:S2;乐观主义准则:S3;Lapalace准则:S1;Savage准则:S1;折衷主义准则:S1或S2。
11.3在一台机器上加工制造一批零件共10 000个,如加工完后逐个进行修整,则全部可以合格,但需修整费300元.如不进行修理数据以往资料统计,次品率情况见表11-15.表11-15(1)用期望值决定这批零件要不要整修;(2)为了获得这批零件中次品率的正确资料,在刚加工完的一批10000件中随机抽取130个样品,发现其中有9件次品,试修正先验概率,并重新按期望值决定这批零件要不要整修.【解】(1)先列出损益矩阵见表11-19(2)修正先验概率见表11-2011.4某工厂正在考虑是现在还是明年扩大生产规模问题.由于可能出现的市场需求情况不一样,预期利润也不同.已知市场需求高(E1)、中(E2)、低(E3)的概率及不同方案时的预期利润,如表11-16所示.表11-16(单位:万元)事件概率方案E1E2E3P(E1)=0.2 P(E2)=0.5 P(E3)=0.3现在扩大10 8 -1明年扩大8 6 1①肯定得8万元或0.9概率得10万和0.1概率失去1万;②肯定得6万元或0.8概率得10万和0.2概率失去1万;③肯定得1万元或0.25概率得10万和0.75概率失去1万。
熊伟编《运筹学》习题九详细解答
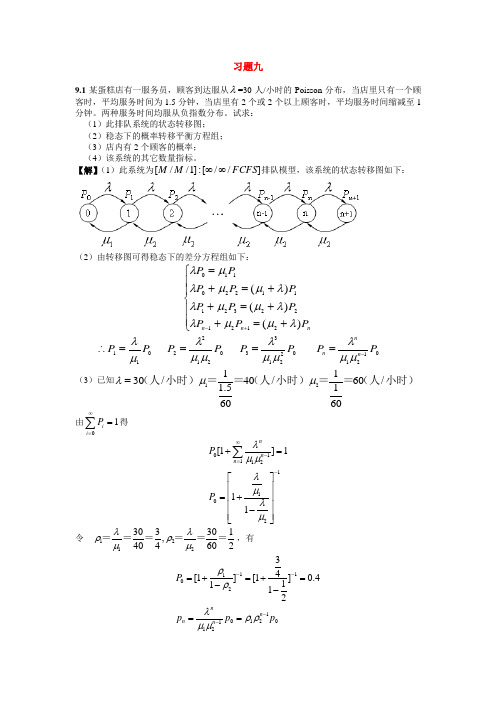
习题九9.1某蛋糕店有一服务员,顾客到达服从λ=30人/小时的Poisson 分布,当店里只有一个顾客时,平均服务时间为1.5分钟,当店里有2个或2个以上顾客时,平均服务时间缩减至1分钟。
两种服务时间均服从负指数分布。
试求: (1)此排队系统的状态转移图; (2)稳态下的概率转移平衡方程组; (3)店内有2个顾客的概率; (4)该系统的其它数量指标。
【解】(1)此系统为]//[:]1//[FCFS M M ∞∞排队模型,该系统的状态转移图如下:(2)由转移图可得稳态下的差分方程组如下:⎪⎪⎩⎪⎪⎨⎧+=++=++=+=+-nn n P P P P P P P P P P P )()()(21212232111220110λμμλλμμλλμμλμλ 011P P μλ=∴ 02122P P μμλ= 022133P P μμλ= 0121P P n n n -=μμλ (3)已知小时)(人==小时)(人==小时)(人/606011/40605.11/3021μμλ= 由1i i P ∞==∑得011121102[1]111n n n P P λμμλμλμ∞-=-+=⎡⎤⎢⎥⎢⎥=+⎢⎥-⎢⎥⎣⎦∑令 1212303301,404602λλρρμμ======,有111021012011234[1][1]0.41112n n n n P p p p ρρλρρμμ----=+=+=--==则 2120310.40.1542P P ρρ==⨯⨯= (4)系统中的平均顾客数(队长期望值))(2.1)5.01(14.043)1(1...)321(222010320101210人=-⨯⨯=-=+++===∑∑∞=-∞=ρρρρρρρP P P n nP L n n n n在队列中等待的平均顾客数(队列长期望值))(4.02114.0432.11...)...1()1(2011222201111人=-⨯-=--=+++++-=-=-=-∞=∞=∞=∑∑∑ρρρρρρp L P L P nP P n L n n nn n n n q 系统中顾客逗留时间1.20.04()30LW λ===小时 系统中顾客等待时间)(013.0304.0小时===λqq L W9.2某商店每天开10个小时,一天平均有90个顾客到达商店,商店的服务平均速度是每小时服务10个,若假定顾客到达的规律是服从Poisson 分布,商店服务时间服从负指数分布,试求:(1)在商店前等待服务的顾客平均数。
熊伟编《运筹学》习题十一详细解答

习题十11.1某地方书店希望订购最新出版的图书•根据以往经验,新书的销售量可能为 50,100, 150或200本.假定每本新书的订购价为4元,销售价为6元,剩书的处理价为每本 2元.要求:(1 )建立损益矩阵;(2)分别用悲观法、乐观法及等可能法决策该书店应订购的 新书数字;(3)建立后悔矩阵,并用后悔值法决定书店应订购的新书数. (4)书店据以往统计资料新书销售量的规律见表11 - 13,分别用期望值法和后悔值法决定订购数量;(5)如某市场调查部门能帮助书店调查销售量的确切数字,该书店愿意付出多大的调查费用。
表 11- 13表- (2) 1 4 23(3)后悔矩阵如表11.1-2所示。
表2 3(4) 按期望值法和后悔值法决策,书店订购新书的数量都是 100本。
(5) 如书店能知道确切销售数字,则可能获取的利润为X j p (x ),书店没有调查费用时i的利润为:50X0.2+100 >0.4+150 X0.3+200 X ).仁115元,则书店愿意付出的最大的调查费用为X i P (X j ) 115i11.2某非确定型决策冋题的决策矩阵如表 11 — 14所示:表 11- 14(1)若乐观系数a =0.4,矩阵中的数字是利润,请用非确定型决策的各种决策准则分别确定出相应的最优方案.(2)若表11 - 14中的数字为成本,问对应于上述决策准则所选择的方案有何变化?【解】(1)悲观主义准则:S3 ;乐观主义准则:S3 ; Lapalace准则:S3 ; Savage准则:3 ;折衷主义准则:S3。
(2 )悲观主义准则:S2 ;乐观主义准则:S3 ; Lapalace准则:S1 ; Savage准则: S1 ;折衷主义准则:S1或S2。
11.3在一台机器上加工制造一批零件共 10 000个,如加工完后逐个进行修整,则全部可以合格,但需修整费 300元.如不进行修理数据以往资料统计,次品率情况见表11- 15.(1 )用期望值决定这批零件要不要整修;(2)为了获得这批零件中次品率的正确资料,在刚加工完的一批10000件中随机抽取130个样品,发现其中有9件次品,试修正先验概率,并重新按期望值决定这批零件要不要整修.【解】(1)先列出损益矩阵见表 11-19(2)修正先验概率见表11-20表11.4某工厂正在考虑是现在还是明年扩大生产规模问题. 由于可能出现的市场需求情况不一样,预期利润也不同•已知市场需求高( E i )、中(E 2)、低(E 3)的概率及不同方案时的预 期利润,如表11 — 16所示.表11— 16(单位:万元)肯定得8万元或0.9概率得10万和0.1概率失去1万;②肯定得6万元或0.8概率得10万 和0.2概率失去1万;③肯定得1万元或0.25概率得10万和0.75概率失去1万。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学(第3版)习题答案第1章线性规划 P36第2章线性规划的对偶理论 P74 第3章整数规划 P88 第4章目标规划 P105第5章运输与指派问题P142 第6章网络模型 P173 第7章网络计划 P195 第8章动态规划 P218 第9章排队论 P248 第10章存储论P277 第11章决策论P304第12章 多属性决策品P343 第13章博弈论P371 全书420页第1章 线性规划1.1工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.表1-23产品 资源 A B C 资源限量 材料(kg) 1.5 1.2 4 2500 设备(台时) 3 1.6 1.2 1400 利润(元/件)101412根据市场需求,预测三种产品最低月需求量分别是150、260和120,最高月需求是250、310和130.试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 1.2建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-24所示:表1-24 窗架所需材料规格及数量型号A 型号B 每套窗架需要材料长度(m ) 数量(根)长度(m) 数量(根)A 1:2 2B 1:2.5 2 A 2:1.53 B 2:23需要量(套)300400问怎样下料使得(1)用料最少;(2)余料最少. 【解】 第一步:求下料方案,见下表。
方案 一 二 三 四 五 六 七 八 九 十 需要量 B1 2.5 2 1 1 1 0 0 0 0 0 0 800 B2 2 0 1 0 0 2 1 1 0 0 0 1200 A1 2 0 0 1 0 0 1 0 2 1 0 600 A21.5120 2 3 900 余料(m) 0 0.5 0.5 1 1 1 010.5第二步:建立线性规划数学模型设x j (j =1,2,…,10)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为10112342567368947910min 28002120026002239000,1,2,,10jj j Z x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩∑ (2)余料最少数学模型为2345681012342567368947910min 0.50.50.52800212002*********0,1,2,,10j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩1.3某企业需要制定1~6月份产品A 的生产与销售计划。
已知产品A 每月底交货,市场需求没有限制,由于仓库容量有限,仓库最多库存产品A1000件,1月初仓库库存200件。
1~6月份产品A 的单件成本与售价如表1-25所示。
表1-25月份1 2 3 4 5 6 产品成本(元/件) 销售价格(元/件) 300 330 320 360 360 300 350 340 350 420 410 340 (1)1~6月份产品A 各生产与销售多少总利润最大,建立数学模型;(2)当1月初库存量为零并且要求6月底需要库存200件时,模型如何变化。
【解】设x j 、y j (j =1,2,…,6)分别为1~6月份的生产量和销售量,则数学模型为(1)112233445566111211223112233411223344511223344556max300350330340320350360420360410300340800800800800800Z x y x y x y x y x y x yxx y xx y x y xx y x y x y xx y x y x y x y xx y x y x y x y x y x=-+-+-+-+ -+-+≤-+≤-+-+≤-+-+-+≤-+-+-+-+≤-+-+-+-+-+≤111122112233112233441122334455112233445566800200200200200200200,0;1,2,,6j jx yx y x yx y x y x yx y x y x y x yx y x y x y x y x yx y x y x y x y x y x yx y j⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪-+≤⎨⎪-+-+≤⎪⎪-+-+-+≤⎪-+-+-+-+≤⎪⎪-+-+-+-+-+≤⎪-+-+-+-+-+-+≤⎪⎪≥=⎩(2)目标函数不变,前6个约束右端常数800改为1000,第7~11个约束右端常数200改为0,第12个约束“≤200”改为“=-200”。
1.4某投资人现有下列四种投资机会, 三年内每年年初都有3万元(不计利息)可供投资:方案一:在三年内投资人应在每年年初投资,一年结算一次,年收益率是20%,下一年可继续将本息投入获利;方案二:在三年内投资人应在第一年年初投资,两年结算一次,收益率是50%,下一年可继续将本息投入获利,这种投资最多不超过2万元;方案三:在三年内投资人应在第二年年初投资,两年结算一次,收益率是60%,这种投资最多不超过1.5万元;方案四:在三年内投资人应在第三年年初投资,一年结算一次,年收益率是30%,这种投资最多不超过1万元.投资人应采用怎样的投资决策使三年的总收益最大,建立数学模型.【解】是设x ij为第i年投入第j项目的资金数,变量表如下项目一项目二项目三项目四第1年第2年第3年x11x21x31x12x23x34数学模型为112131122334111211212312213134122334max 0.20.20.20.50.60.3300001.2300001.5 1.2300002000015000100000,1,,3;1,4ij Z x x x x x x x x x x x x x x x x x x x i j =+++++⎧+≤⎪-++≤⎪⎪--++≤⎪⎪≤⎨⎪≤⎪⎪≤⎪≥==⎪⎩最优解X=(30000,0,66000,0,109200,0);Z =847201.5 炼油厂计划生产三种成品油,不同的成品油由半成品油混合而成,例如高级汽油可以由中石脑油、重整汽油和裂化汽油混合,辛烷值不低于94,每桶利润5元,见表1-26。
表1-26成品油高级汽油 一般汽油 航空煤油 一般煤油 半成品油中石脑油 重整汽油 裂化汽油中石脑油 重整汽油 裂化汽油轻油、裂化油、重油、残油轻油、裂化油、重油、残油按10:4:3:1调合而成辛烷值 ≥94 ≥84蒸汽压:公斤/平方厘米≤1 利润(元/桶)5 4.2 31.5半成品油的辛烷值、气压、及每天可供应数量见表1-27。
表1-27问炼油厂每天生产多少桶成品油利润最大,建立数学模型。
解 设x ij 为第i (i =1,2,3,4)种成品油配第j (j =1,2,…,7)种半成品油的数量(桶)。
总利润:11121321222334353637444546475() 4.2()3() 1.5()Z x x x x x x x x x x x x x x =+++++++++++++高级汽油和一般汽油的辛烷值约束111213212223111213212223801151058011510594,8494x x x x x x x x x x x x ++++≥≤≤++++航空煤油蒸气压约束34353637343536371.50.60.051x x x x x x x x ++≤++++一般煤油比例约束44454647:::10:4:3:1x x x x =半成品油1中石脑油 2重整汽油 3裂化汽油 4轻油 5裂化油 6重油 7残油辛烷值 80 115 105 蒸汽压:公斤/平方厘米 1.0 1.5 0.60.05 每天供应数量(桶)2000 1000 1500 1200 1000 1000800即4546444546471043,,431x x x x x x === 半成品油供应量约束1121122213233444354536463747200010001500120010001000800x x x x x x x x x x x x x x +≤+≤+≤+≤+≤+≤+≤ 整理后得到111213212223343536374445464711121321222321222335363744454546464max 555 4.2 4.2 4.23333 1.5 1.5 1.5 1.5142111014211104312100.50.40.95041003403Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =+++++++++++++-++≥-++≤-++≥--≤-=-=-7112112221323344435453646374702000100015001200100010008000;1,2,3,4;1,2,,7ij x x x x x x x x x x x x x x x i j ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪=⎪⎪+≤⎨⎪+≤⎪⎪+≤⎪+≤⎪⎪+≤⎪+≤⎪⎪+≤⎪≥==⎪⎩1.6图解下列线性规划并指出解的形式:(1) 12121212max 522835,0Z x x x x x x x x =++≤⎧⎪≤⎪⎨≤⎪⎪≥⎩【解】最优解X =(3,2);最优值Z=19(2)12 12121212max4453224,0Z x x x xx xx xx x=++≤⎧⎪+≥⎪⎨+≤⎪⎪≥⎩【解】有多重解。
最优解X(1)=(0,5/4);X(2)=(3,1/2)最优值Z=5(3)12 1212121212min32211410 2731,0Z x x x xx xx xx xx x=-++≤⎧⎪-+≤⎪⎪-≤⎨⎪-≤⎪⎪≥⎩【解】最优解X=(4,1);最优值Z=-10,有唯一最优解(4)12 1212212min4628830,0Z x x x xx xxx x=++≥⎧⎪+≤⎪⎨≤⎪⎪≥≥⎩【解】最优解X=(2,3);最优值Z=26,有唯一最优解(5) ⎪⎪⎩⎪⎪⎨⎧≥≤≥≥-+=0,6322max 21212121x x x x x x x x Z【解】无界解。
